Reactive Power Management Based on Voltage Sensitivity Analysis of Distribution System with High Penetration of Renewable Energies
Abstract
:1. Introduction
2. Minimization of Voltage Variation by Voltage Sensitivity Analysis
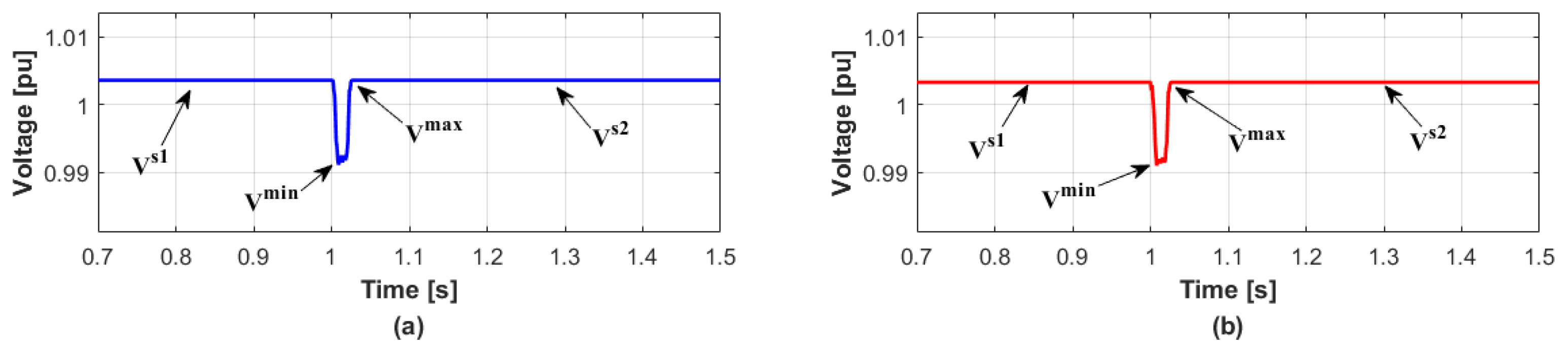
2.1. Measurement of Voltage Variation
2.2. Reactive Power Management Based on Voltage Sensitivity Analysis
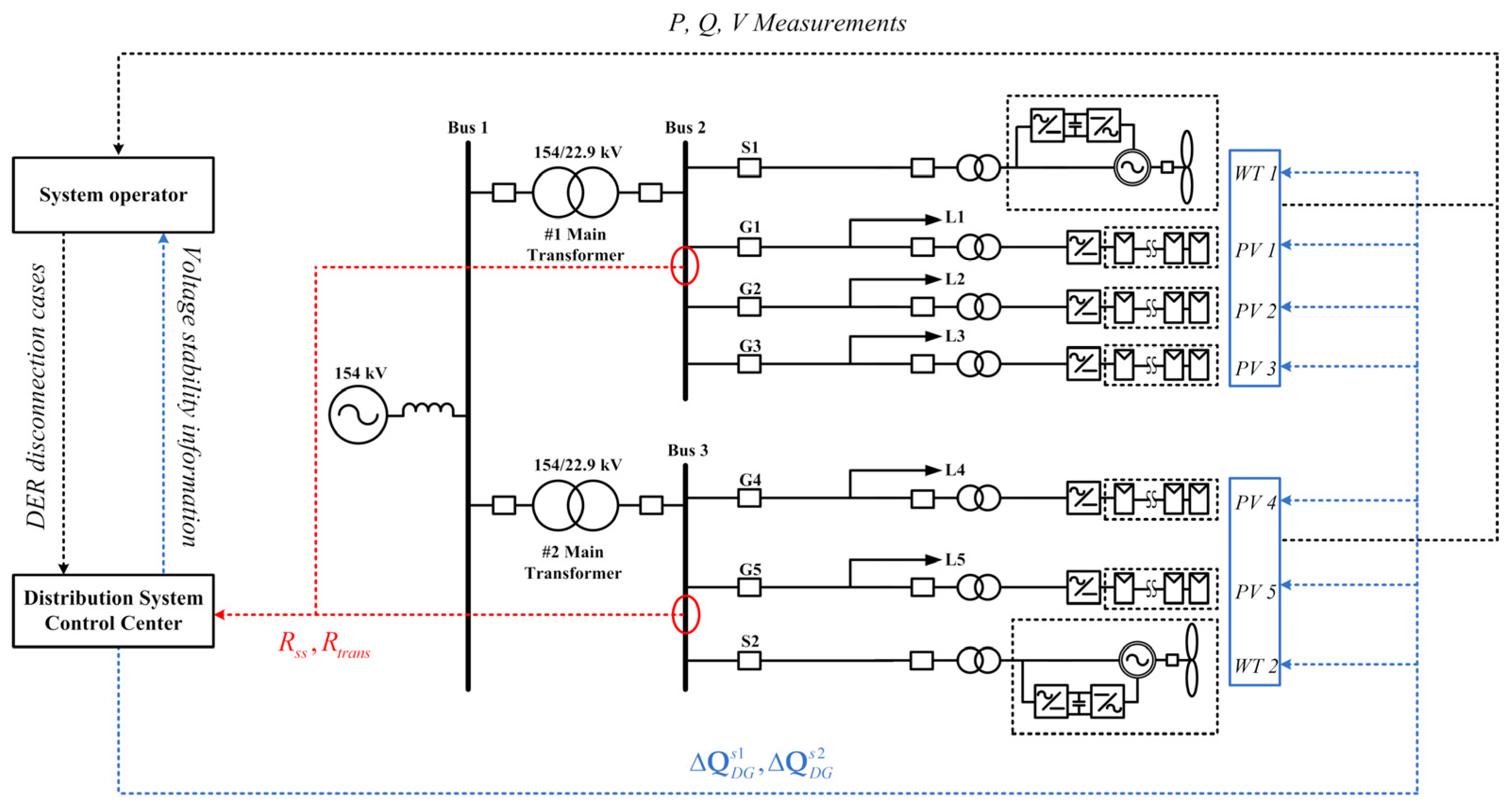
3. Implementation of the Proposed Method in Practical Distribution System
3.1. Implementation of the Proposed Reactive Power Management Method
3.2. Distribution System with High Penetration Level of DER
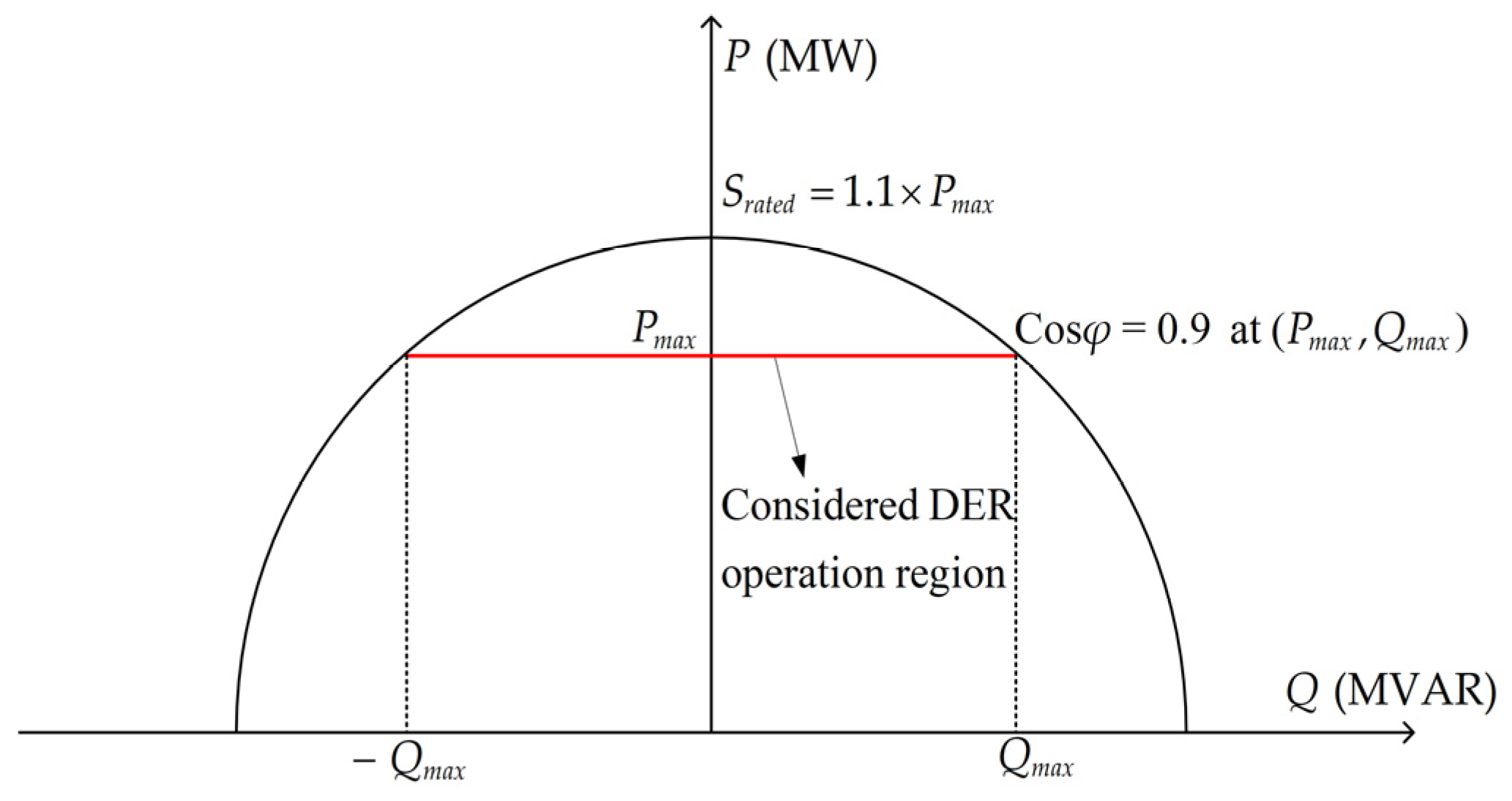
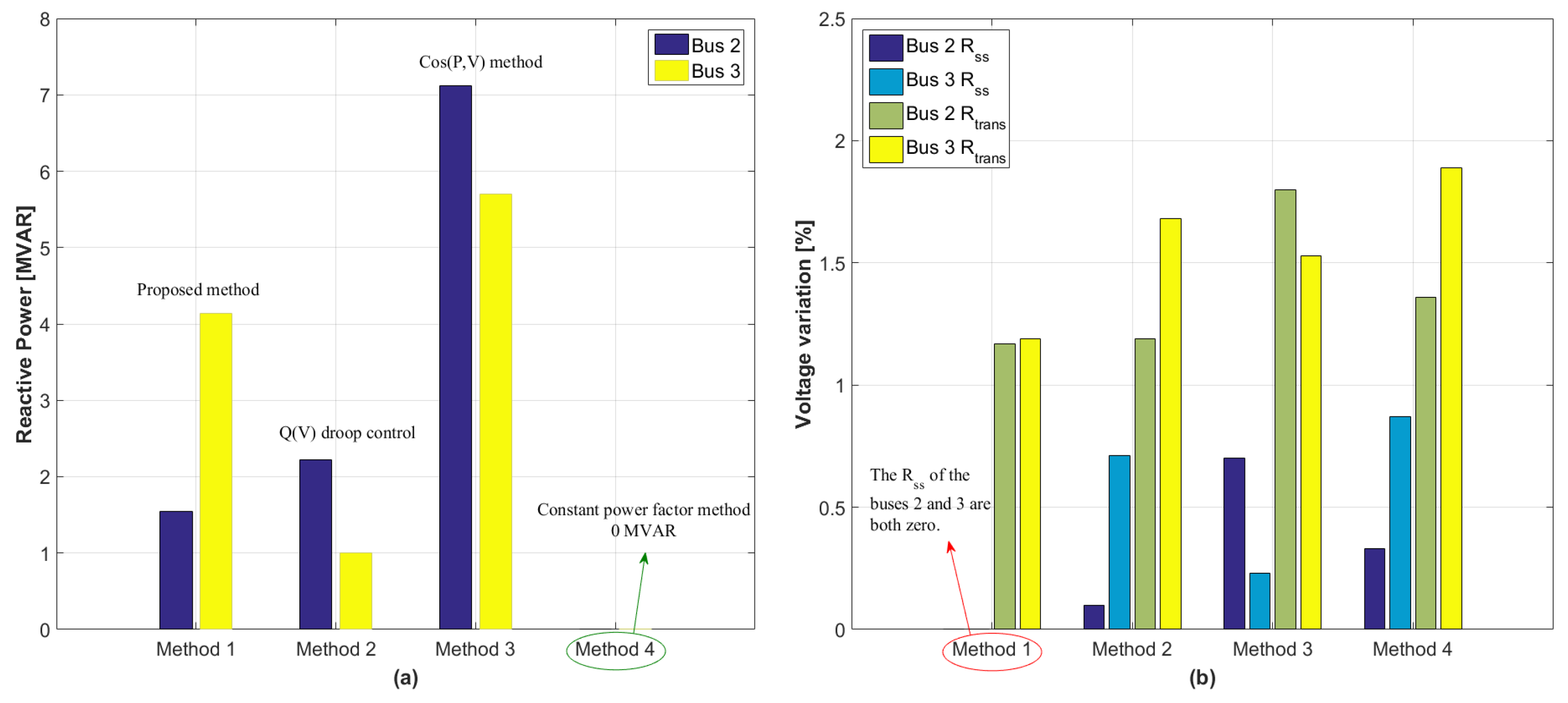
3.3. Maximum Reactive Power Generation of DER
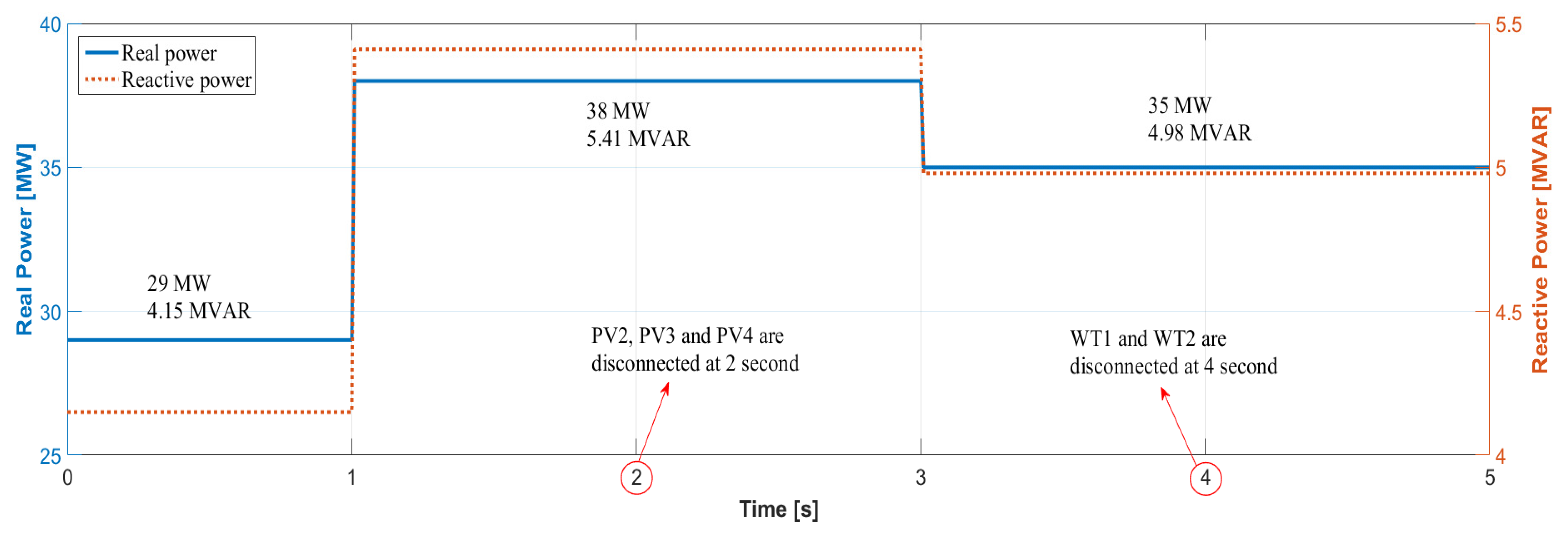
3.4. Cases Studies
4. Simulation Results
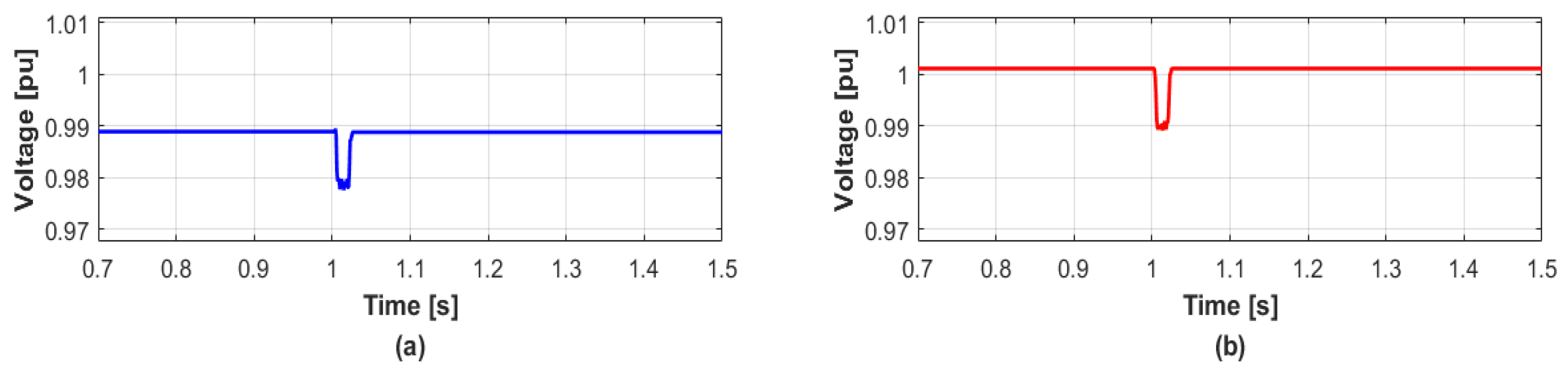
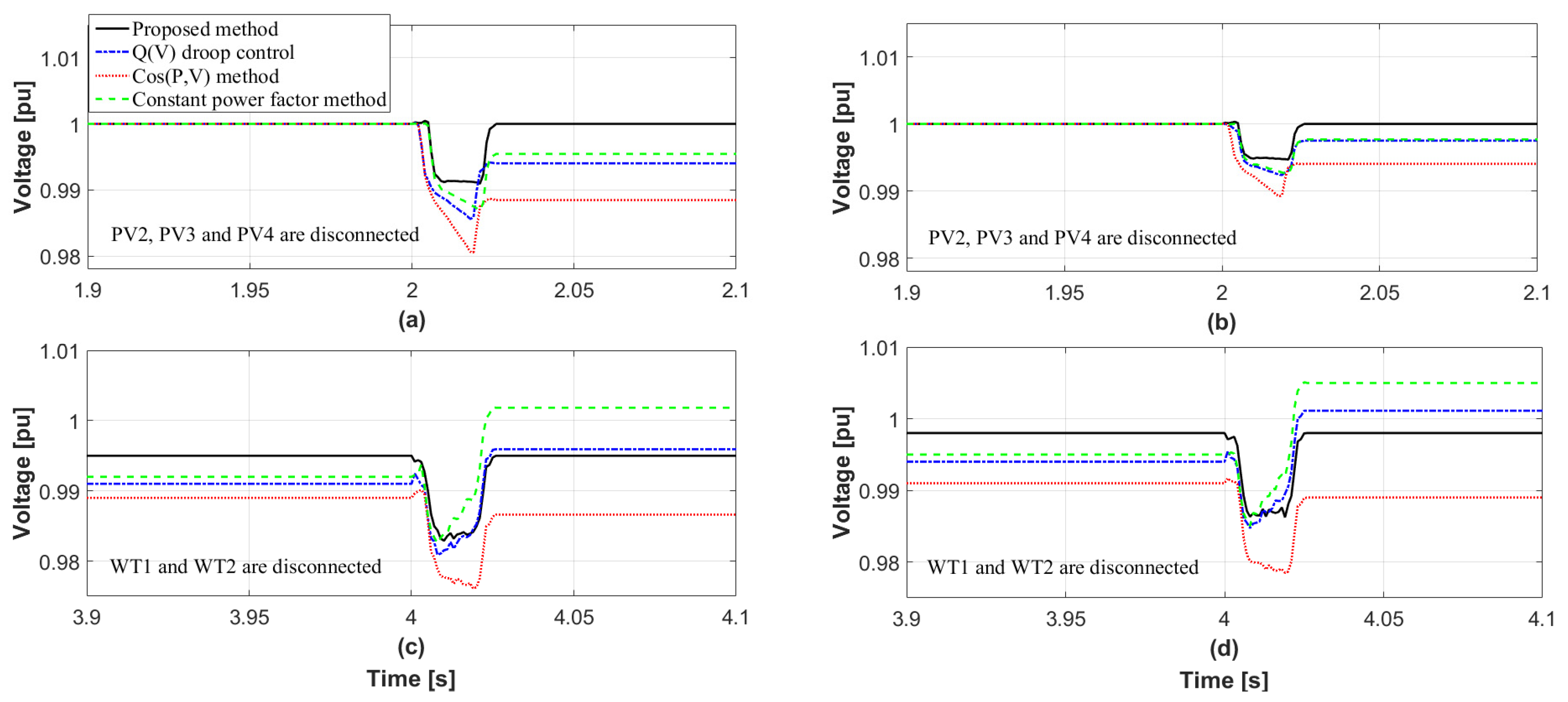
4.1. Case 1
4.2. Case 2
4.3. Case 3
4.4. Total Harmonic Distortion of System
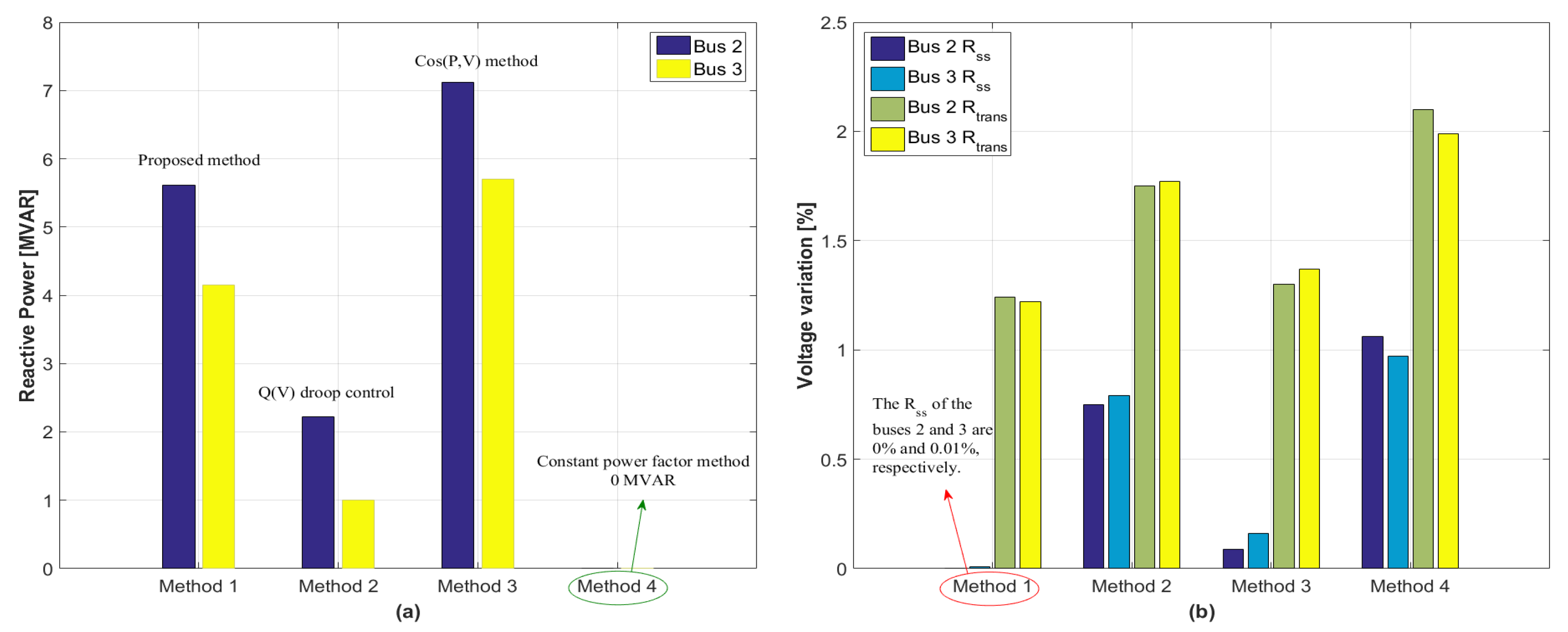
4.5. Changes of Voltage Sensitivity of System
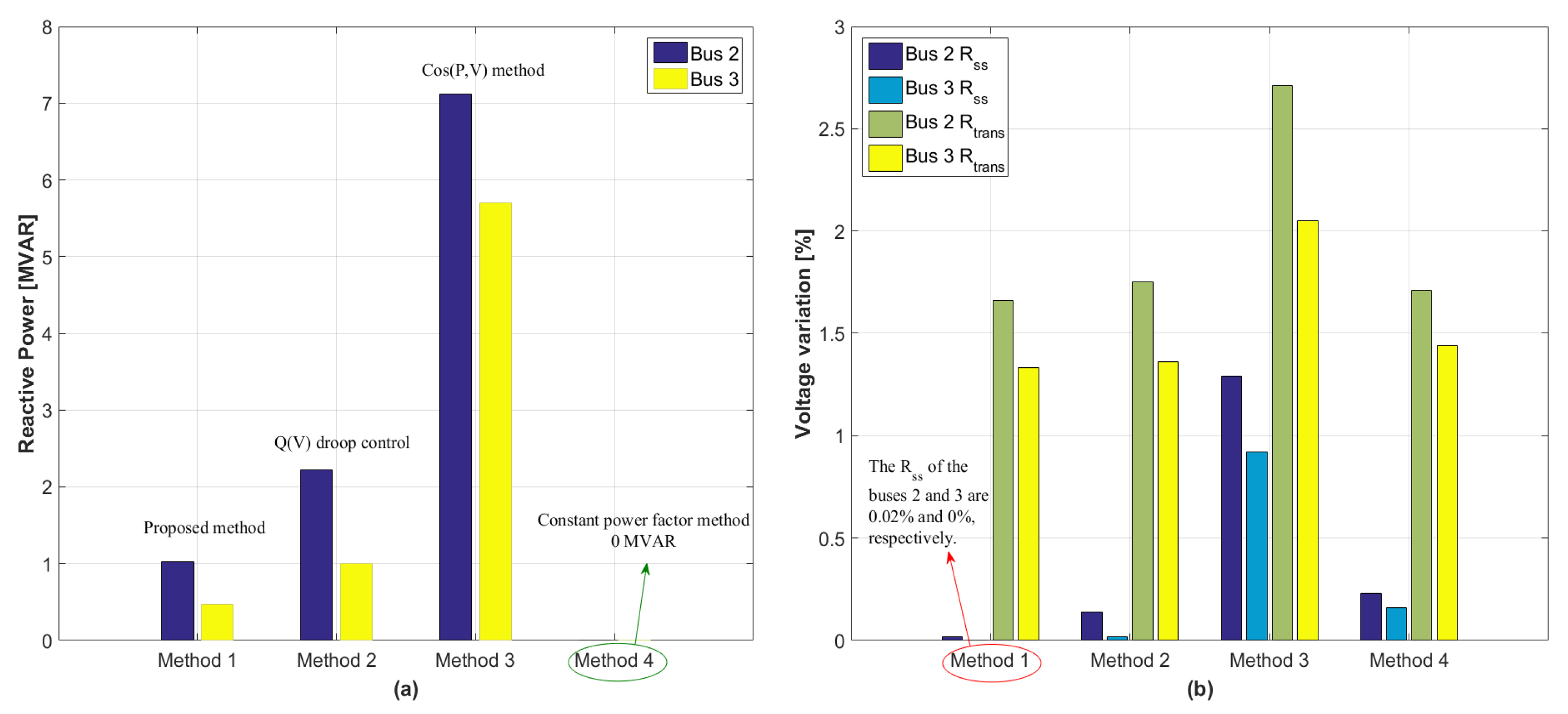
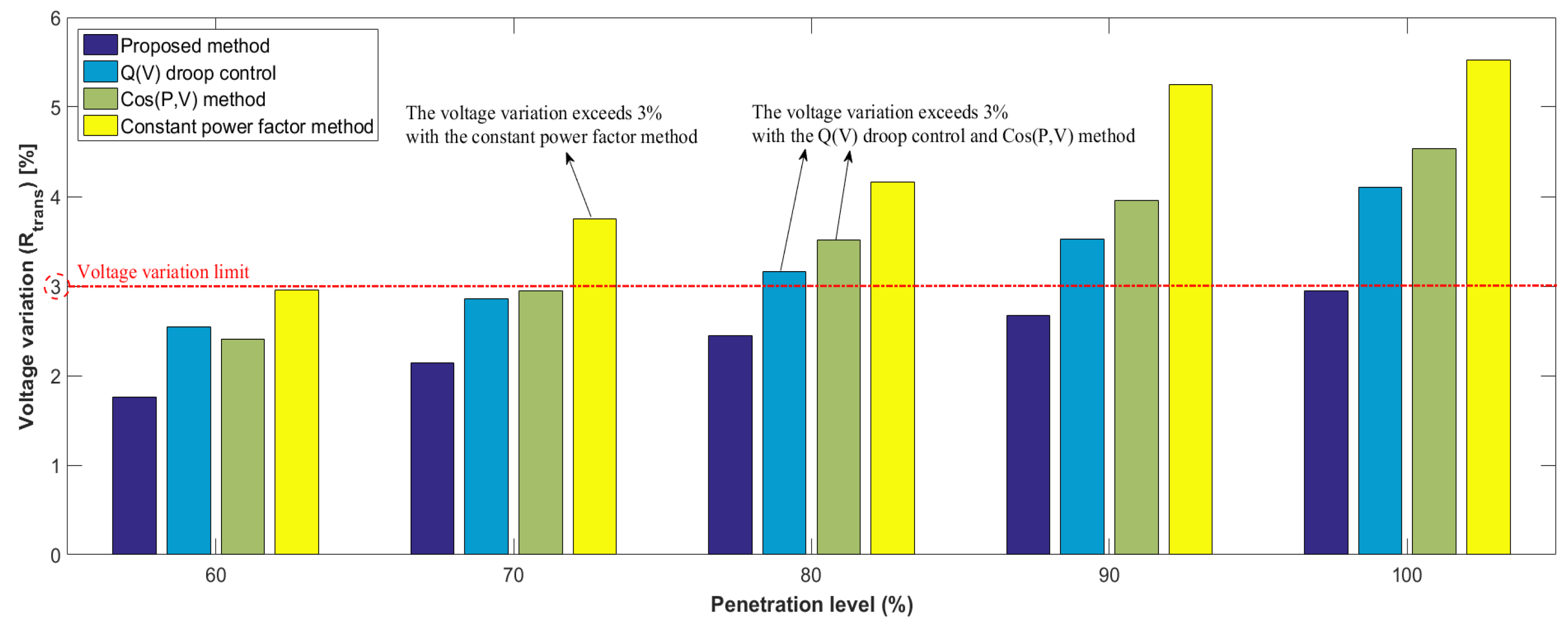
4.6. Increase of Penetration of DERs with Proposed Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AMI | advanced metering infrastructure |
| DER | distributed energy resource |
| DEMS | distribution energy management system |
| DFIG | doubly-fed induction generator |
| EMTP | electromagnetic transient program |
| ESS | energy storage system |
| OLTC | on-load tap changer |
| PCC | point of common coupling |
| PV | photovoltaic |
| SI | smart inverter |
| THD | total harmonic distortion |
Nomenclature
| Diagonal matrix with diagonal component ak | |
| Ratio of active power generation between and | |
| Deviation of active power generation at bus k | |
| Deviation of reactive power generation at bus k | |
| Active power variation of load at bus k | |
| Reactive power variation of load at bus k | |
| Reactive power generation at bus k, before the DER is disconnected | |
| Reactive power generation at bus k, after the DER is disconnected | |
| Reactive power generations of buses, to which the DERs are connected | |
| Reactive power generation of buses with DER connection, before the DER is disconnected | |
| Reactive power generation of buses with DER connection, after the DER is disconnected | |
| Voltage deviations at entire buses | |
| Voltage deviations at buses with DER connection | |
| Voltage deviation provided by reactive power compensation before the DER is disconnected | |
| Voltage deviation provided by reactive power compensation after the DER is disconnected | |
| Voltage phase angle at bus i | |
| Voltage phase angle at bus j | |
| Harmonic order | |
| Harmonic current of h th order | |
| Number of entire buses | |
| Active power generation of DERs | |
| Active powers at bus i | |
| Maximum active power generation of DERs | |
| Active power generation at bus k, before the DER is disconnected | |
| Active power generation at bus k, after the DER is disconnected | |
| Reactive powers at bus i | |
| Maximum reactive power generation | |
| Voltage variation in steady-state condition | |
| Voltage variation in transient condition | |
| Rated apparent power of the inverter | |
| Voltage sensitivity matrix | |
| Sensitivities of bus voltage magnitudes with respect to the active power | |
| Sensitivities of bus voltage magnitudes with respect to the reactive power | |
| Sensitivities of bus voltage angles with respect to the active power | |
| Sensitivities of bus voltage angles with respect to the reactive power | |
| Reconstructed matrix of S, which is voltage sensitivity matrix of DERs | |
| Reconstructed matrix of S, which is voltage sensitivity matrix of loads | |
| Submatrix of SDG, which is active power sensitivities with respect to the voltage | |
| Submatrix of SDG, which is reactive power sensitivities with respect to the voltage | |
| Submatrix of SLoad, which is active power sensitivities with respect to the voltage | |
| Submatrix of SLoad, which is reactive power sensitivities with respect to the voltage | |
| The before the DER is disconnected | |
| The after the DER is disconnected | |
| Voltage at bus i | |
| Voltage at bus j | |
| Steady state voltage before the occurrence of system disturbance | |
| Steady state voltage after the occurrence of system disturbance | |
| Maximum voltage during the transient period | |
| Minimum voltage during the transient period | |
| Rated voltage of the distribution system | |
| The at bus k | |
| The at bus k | |
| Voltage in the condition generating active power before the DER is disconnected | |
| Voltage in the condition generating active power after the DER is disconnected | |
| DER connected bus voltages in the condition of generating active power, before the specific DER is disconnected | |
| DER connected bus voltages in the condition of generating active power, after the specific DER is disconnected | |
| Admittance of line from bus i to j |
Appendix A
| Parameters of PV Inverter | |
|---|---|
| Frequency | 60 Hz |
| Step-up transformer | 22.9/0.38 kV, 100 MVA |
| L filter | 1 mH |
| DC source voltage | 40 V |
| DC-link capacitance | 1500 mF |
| Power controller proportional gain | 100 |
| Power controller integral gain | 10 |
| Reactive power controller proportional gain | 100 |
| Reactive power controller integral gain | 10 |
| d-axis current controller proportional gain | 10 |
| d-axis current controller integral gain | 1 |
| q-axis current controller proportional gain | 10 |
| q-axis current controller integral gain | 1 |
| Ls | 1.6 mH |
| Grid-Side Converter of DFIGs | |
|---|---|
| Rated AC voltage | 0.69 kV |
| Base DC voltage of DC bus | 1.45 kV |
| d-axis PI controller proportional gain | 2 |
| d-axis PI controller time constant | 0.01 |
| q-axis PI controller proportional gain | 2 |
| q-axis PI controller time constant | 0.01 |
| DC voltage PI controller proportional gain | 2 |
| DC voltage PI controller time constant | 0.01 |
| Grid side converter PLL integral gain | 500 |
| Grid side converter PLL proportional gain | 2000 |
| Rotor-Side Converter of DFIGs | |
|---|---|
| Rated AC voltage | 0.69 kV |
| d-axis PI controller proportional gain | 2 |
| d-axis PI controller time constant | 0.01 |
| q-axis PI controller proportional gain | 2 |
| q-axis PI controller time constant | 0.01 |
| Rotor side converter PLL integral gain | 200 |
| Rotor side converter PLL proportional gain | 2000 |
References
- Shayani, R.A.; Oliveira, M.A.G.D. Photovoltaic Generation Penetration Limits in Radial Distribution Systems. IEEE Trans. Power Syst. 2011, 26, 1625–1631. [Google Scholar] [CrossRef]
- Bank, J.; Mather, B.; Keller, J.; Coddington, M. High Penetration Photovoltaic Case Study Report. National Renewable Energy Lab (NREL). Available online: https://www.nrel.gov/docs/fy13osti/54742.pdf (accessed on 23 January 2019).
- Park, W.J.; Sung, B.C.; Song, K.-B.; Park, J.-W. Parameter Optimization of SFCL With Wind-Turbine Generation System Based on Its Protective Coordination. IEEE Trans. Appl. Supercond. 2011, 21, 2153–2156. [Google Scholar] [CrossRef]
- Long, C.; Ochoa, L.F. Voltage Control of PV-Rich LV networks: OLTC-Fitted Transformer and Capacitor Banks. IEEE Trans. Power Syst. 2016, 31, 4016–4025. [Google Scholar] [CrossRef]
- Varela, J.; Hatziargyriou, N.; Puglisi, L.J.; Rossi, M.; Abart, A.; Bletterie, B. The IGREENGrid Project: Increasing Hosting Capacity in Distribution Grids. IEEE Power Energy Mag. 2017, 15, 30–40. [Google Scholar] [CrossRef]
- Demirok, E.; González, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local Reactive Power Control Methods for Overvoltage Prevention of Distributed Solar Inverters in Low-Voltage Grids. IEEE J. Photovolt. 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Safayet, A.; Fajri, P.; Husain, I. Reactive Power Management for Overvoltage Prevention at High PV Penetration in a Low-Voltage Distribution System. IEEE Trans. Ind. Appl. 2017, 53, 5786–5794. [Google Scholar] [CrossRef]
- Vasquez, J.C.; Mastromauro, R.A.; Guerrero, J.M.; Liserre, M. Voltage Support Provided by a Droop-Controlled Multifunctional Inverter. IEEE Trans. Ind. Electron. 2009, 56, 4510–4519. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kim, G.-H.; Lee, J.-D.; Cho, C. New Requirements of the Voltage/VAR Function for Smart Inverter in Distributed Generation Control. Energies 2016, 9, 929. [Google Scholar] [CrossRef]
- Malekpour, A.R.; Pahwa, A. A Dynamic Operational Scheme for Residential PV Smart Inverters. IEEE Trans. Smart Grid 2017, 8, 2258–2267. [Google Scholar] [CrossRef]
- DeBlasio, R.; Photovoltaics, D.G.; Storage, E. IEEE Application Guide for IEEE Std 1547, IEEE Standard for Inter-connecting Distributed Resources with Electric Power Systems; IEEE Std 1574.2-2008; The Institute of Electrical and Electronics Engineers: New York, NY, USA, 2009. [Google Scholar]
- Trindade, F.C.L.; Ferreira, T.S.D.; Lopes, M.G.; Freitas, W. Mitigation of Fast Voltage Variations During Cloud Transients in Distribution Systems with PV Solar Farms. IEEE Trans. Power Deliv. 2017, 32, 921–932. [Google Scholar] [CrossRef]
- Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. A Multi-Mode Control Strategy for Var Support by Solar PV Inverters in Distribution Networks. IEEE Trans. Power Syst. 2015, 30, 1316–1326. [Google Scholar] [CrossRef]
- Giannitrapani, A.; Paoletti, S.; Vicino, A.; Zarrilli, D. Optimal Allocation of Energy Storage Systems for Voltage Control in LV Distribution Networks. IEEE Trans. Smart Grid 2017, 8, 2859–2870. [Google Scholar] [CrossRef]
- Jalali, A.; Aldeen, M. Risk-Based Stochastic Allocation of ESS to Ensure Voltage Stability Margin for Distribution Systems. IEEE Trans. Power Syst. 2019, 34, 1264–1277. [Google Scholar] [CrossRef]
- Wang, L.; Bai, F.; Yan, R.; Saha, T.K. Real-Time Coordinated Voltage Control of PV Inverters and Energy Storage for Weak Networks With High PV Penetration. IEEE Trans. Power Syst. 2018, 33, 3383–3395. [Google Scholar] [CrossRef]
- Zhao, H.; Hong, M.; Lin, W.; Loparo, K.A. Voltage and Frequency Regulation of Microgrid With Battery Energy Storage Systems. IEEE Trans. Smart Grid 2019, 10, 414–424. [Google Scholar] [CrossRef]
- Zeraati, M.; Golshan, M.E.H.; Guerrero, J.M. Distributed Control of Battery Energy Storage Systems for Voltage Regulation in Distribution Networks With High PV Penetration. IEEE Trans. Smart Grid 2018, 9, 3582–3593. [Google Scholar] [CrossRef]
- Bahramipanah, M.; Torregrossa, D.; Cherkaoui, R.; Paolone, M. A Decentralized Adaptive Model-Based Real-Time Control for Active Distribution Networks Using Battery Energy Storage Systems. IEEE Trans. Smart Grid 2018, 9, 3406–3418. [Google Scholar] [CrossRef]
- Mohammadi, F. Power Management Strategy in Multi-Terminal VSC-HVDC System. In Proceedings of the National Conference on Applied Research in Electrical, Mechanical, Computer and IT Engineering, Schiraz, Iran, 4 October 2018. [Google Scholar]
- Aghatehrani, R.; Kavasseri, R. Reactive Power Management of a DFIG Wind System in Microgrids Based on Voltage Sensitivity Analysis. IEEE Trans. Sustain. Energy 2011, 2, 451–458. [Google Scholar] [CrossRef]
- Wang, L.; Liang, D.H.; Crossland, A.F.; Taylor, P.C.; Jones, D.; Wade, N.S. Coordination of Multiple Energy Storage Units in a Low-Voltage Distribution Network. IEEE Trans. Smart Grid 2015, 6, 2906–2918. [Google Scholar] [CrossRef]
- Hashemi, S.; Østergaard, J. Efficient Control of Energy Storage for Increasing the PV Hosting Capacity of LV Grids. IEEE Trans. Smart Grid 2018, 9, 2295–2303. [Google Scholar]
- Wang, P.; Liang, D.H.; Yi, J.; Lyons, P.F.; Davison, P.J.; Taylor, P.C. Integrating Electrical Energy Storage Into Coordinated Voltage Control Schemes for Distribution Networks. IEEE Trans. Smart Grid 2014, 5, 1018–1032. [Google Scholar] [CrossRef]
- Kim, J.; Baek, S.-M.; Park, J.-W. Allowable Capacity Estimation of DGs for High Renewable Penetration to Distribution System. In Proceedings of the IEEE Ind. Appl. Soc. Annul. Meeting, Portland, OR, USA, 23–27 September 2018. [Google Scholar]


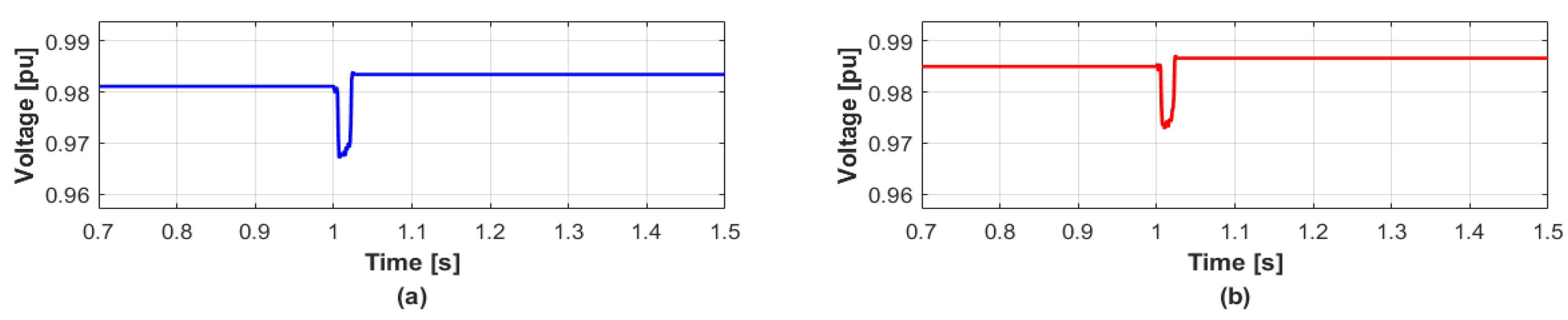
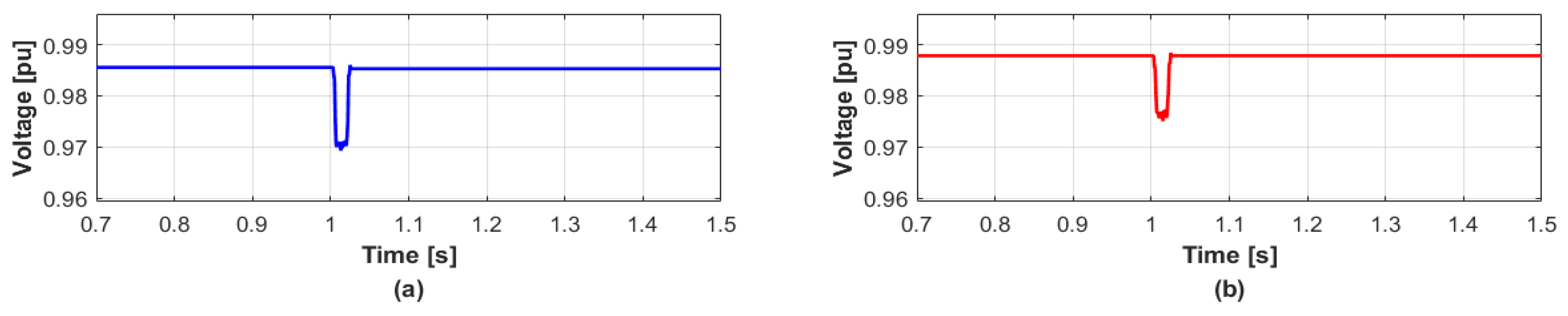
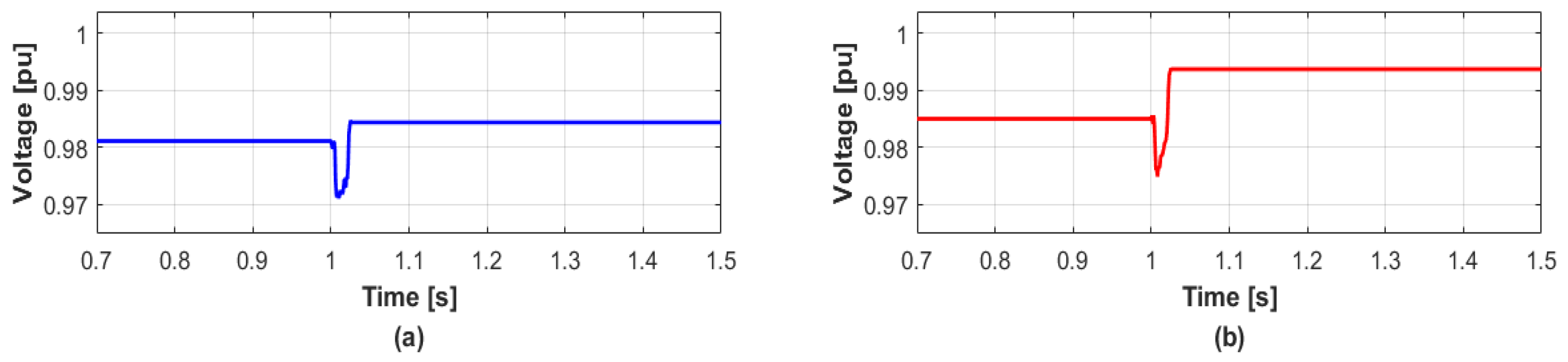
| DERs. | Before Disconnection | After Disconnection |
|---|---|---|
| DERs with disconnection | − | 0 |
| DERs without disconnection | ||
| Total DERs |
| Generations | |
| PV1, PV2, PV3, PV4, PV5 | 10 MW |
| WT1, WT2 | 20 MW |
| System Parameters | |
| 154 kV Line Impedance | 1.328 + j0.0267 Ω |
| #1 Main Transformer | j0.3122 Ω |
| #2 Main Transformer | j0.3093 Ω |
| S1, S2 | 0.1017 + j0.4446 Ω |
| G1, G2, G3, G4, G5 | 0.1819 + j0.3912 Ω/km |
| Load | |
| Total Load | 29 MW 4.15 MVAR |
| Case | DER Disconnection | Total Disconnection Capacity |
|---|---|---|
| 1 | WT1, WT2 | 40 MW |
| 2 | PV1, PV2, PV3, PV4, PV5 | 50 MW |
| 3 | PV1, PV2, WT2 | 40 MW |
| Bus | Without Q Compensation | Proposed Method | ||||||
|---|---|---|---|---|---|---|---|---|
| (pu) | (pu) | (%) | (%) | (pu) | (pu) | (%) | (%) | |
| 2 | 0.9811 | 0.9917 | 1.06 | 2.10 | 1.0036 | 1.0036 | 0.00 | 1.24 |
| 3 | 0.9850 | 0.9947 | 0.97 | 1.99 | 1.0033 | 1.0034 | 0.01 | 1.22 |
| Method | Reactive Power Generation |
|---|---|
| 1 | Proposed method |
| 2 | Q(V) droop control |
| 3 | Cos (P,V) method |
| 4 | Constant power factor method (cosφ = 1) |
| Bus | Without Q Compensation | Proposed Method | ||||||
|---|---|---|---|---|---|---|---|---|
| (pu) | (pu) | (%) | (%) | (pu) | (pu) | (%) | (%) | |
| 2 | 0.9811 | 0.9834 | 0.23 | 1.71 | 0.9856 | 0.9854 | 0.02 | 1.66 |
| 3 | 0.9850 | 0.9866 | 0.16 | 1.44 | 0.9879 | 0.9879 | 0.00 | 1.33 |
| Bus | Without Q Compensation | Proposed Method | ||||||
|---|---|---|---|---|---|---|---|---|
| (pu) | (pu) | (%) | (%) | (pu) | (pu) | (%) | (%) | |
| 2 | 0.9811 | 0.9844 | 0.33 | 1.36 | 0.9889 | 0.9889 | 0.00 | 1.17 |
| 3 | 0.9850 | 0.9937 | 0.87 | 1.89 | 1.0011 | 1.0011 | 0.00 | 1.19 |
| Case | Proposed Method | Q(V) Droop Control | Cos (P,V) Method | Constant Power Factor Method (cosφ = 1) |
|---|---|---|---|---|
| 1 | 2.14% | 2.18% | 2.16% | 2.13% |
| 2 | 2.11% | 2.25% | 2.12% | 2.12% |
| 3 | 2.26% | 2.11% | 2.19% | 2.17% |
| Method | Bus 2 | Bus 3 | ||
|---|---|---|---|---|
| Proposed Method | 0.00 | 0.94 | 0.00 | 0.56 |
| Q(V) droop control | 0.59 | 1.45 | 0.24 | 0.76 |
| Cos (P,V) method | 1.15 | 1.96 | 0.59 | 1.09 |
| Constant power factor method | 0.45 | 1.31 | 0.23 | 0.74 |
| Method | Bus 2 | Bus 3 | ||
|---|---|---|---|---|
| Proposed Method | 0.00 | 1.20 | 0.00 | 1.17 |
| Q(V) droop control | 0.49 | 1.50 | 0.71 | 1.63 |
| Cos (P,V) method | 0.23 | 1.41 | 0.19 | 1.32 |
| Constant power factor method | 0.98 | 1.94 | 0.99 | 2.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.; Kim, J.; Park, J.-W.; Baek, S.-M. Reactive Power Management Based on Voltage Sensitivity Analysis of Distribution System with High Penetration of Renewable Energies. Energies 2019, 12, 1493. https://doi.org/10.3390/en12081493
Kang S, Kim J, Park J-W, Baek S-M. Reactive Power Management Based on Voltage Sensitivity Analysis of Distribution System with High Penetration of Renewable Energies. Energies. 2019; 12(8):1493. https://doi.org/10.3390/en12081493
Chicago/Turabian StyleKang, SeokJu, Jaewoo Kim, Jung-Wook Park, and Seung-Mook Baek. 2019. "Reactive Power Management Based on Voltage Sensitivity Analysis of Distribution System with High Penetration of Renewable Energies" Energies 12, no. 8: 1493. https://doi.org/10.3390/en12081493
APA StyleKang, S., Kim, J., Park, J.-W., & Baek, S.-M. (2019). Reactive Power Management Based on Voltage Sensitivity Analysis of Distribution System with High Penetration of Renewable Energies. Energies, 12(8), 1493. https://doi.org/10.3390/en12081493







