Mitigating Impulsive Noise for Wavelet-OFDM Powerline Communication
Abstract
:1. Introduction
2. System Model
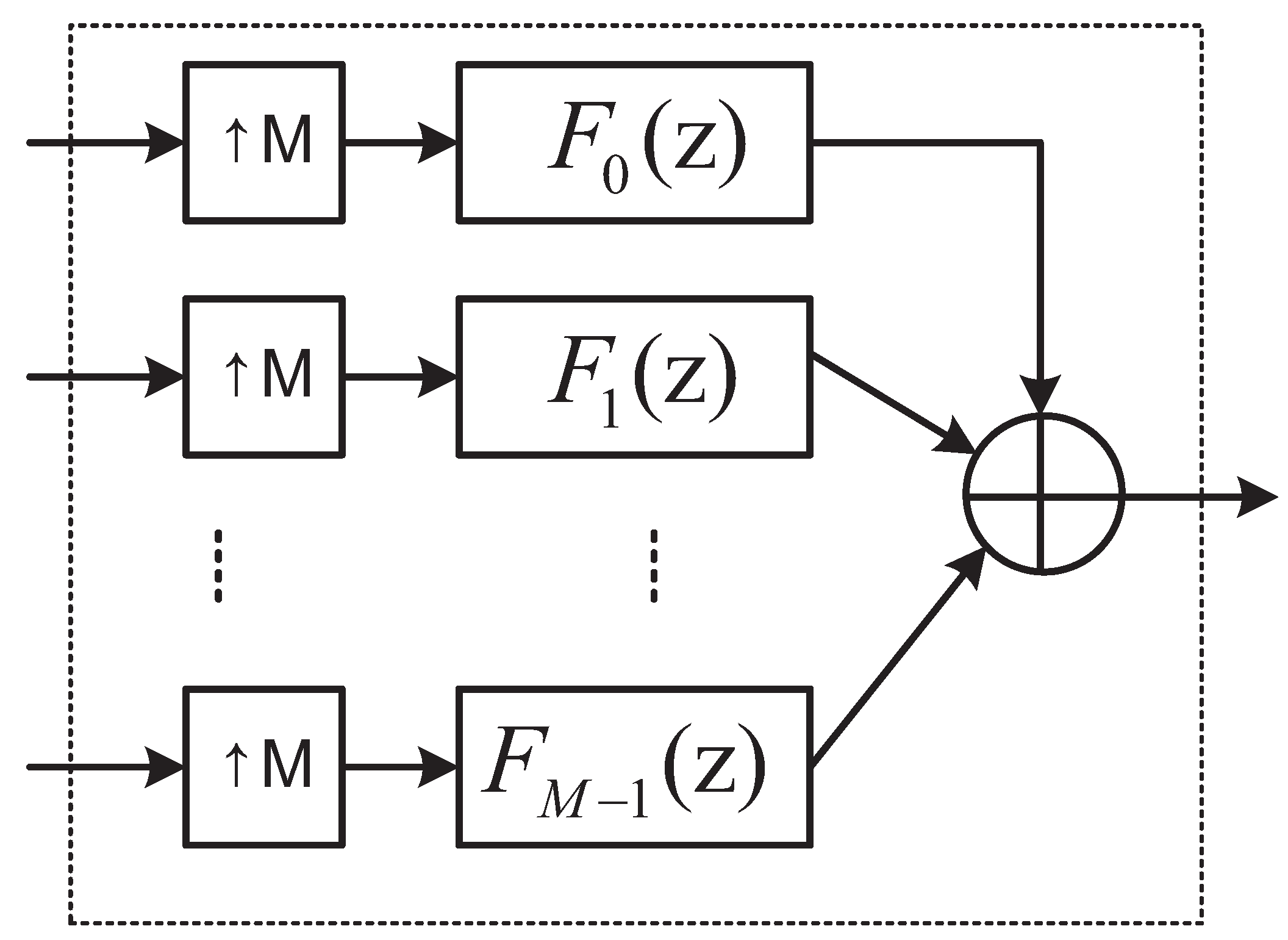
2.1. Transmission Using IDWT
2.2. Powerline Channel Model
2.3. Additive Noise Model
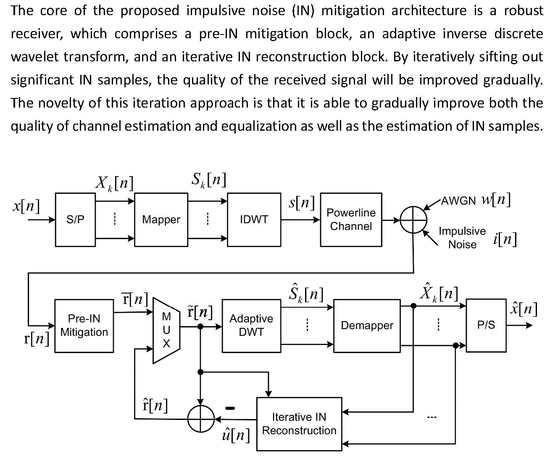
2.4. Proposed Receiving Block
3. Proposed IN Mitigation Scheme
3.1. Pre-IN Mitigation
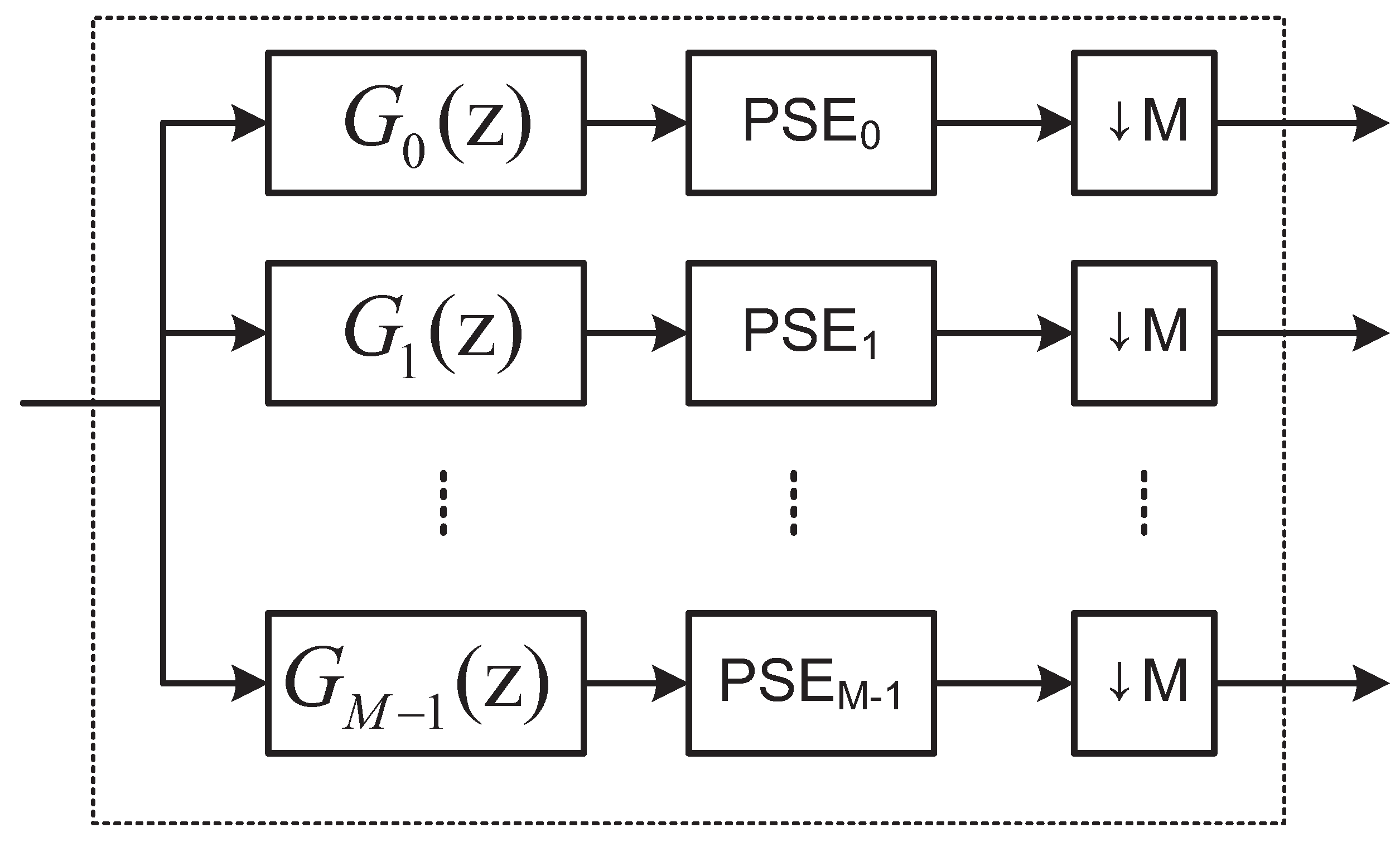
3.2. Adaptive DWT
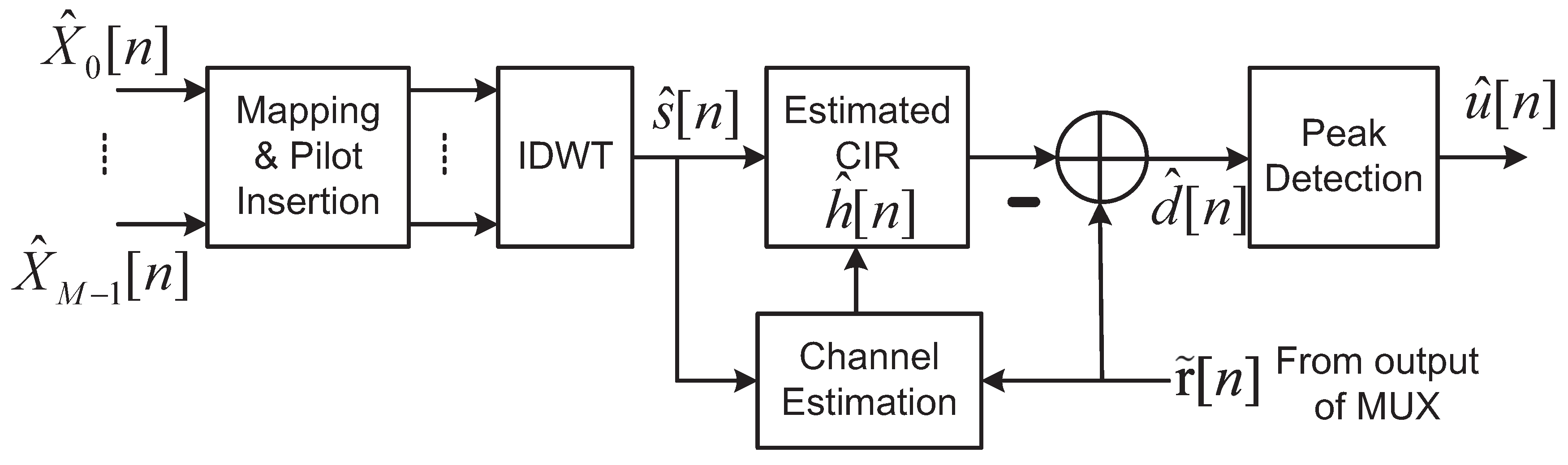
3.3. Iterative IN Reconstruction
3.4. Computational Complexity
- To train the coefficients of the , the calculation of Equations (11)–(13) is necessary. The computation of the variable step-size needs 9 multiplier, one divider, 6 adders, and one square-root operation. The calculation of the error signal requires multipliers and adders. The weight updating recursion needs multipliers, one divider, and adders. Thus, for M per-subchannel equalizers, it totally requires multipliers, adders, dividers, and M square-root operations.
- In addition to one additional IDWT operation, the main computation burden in the iterative IN reconstruction block is resulted from the calculation of Equations (19)–(21). Assuming that the channel estimator is implemented by an FIR filter of length , then the calculation of the recursion (19) needs multipliers, one divider, and adders; the calculation of Equation (20) needs multipliers and adders; the calculation of Equation (21) needs 9 multiplier, one divider, 6 adders, and one square-root operation. Thus, it requires about multiplier, 7 dividers, adders, and one square-root operation in total.
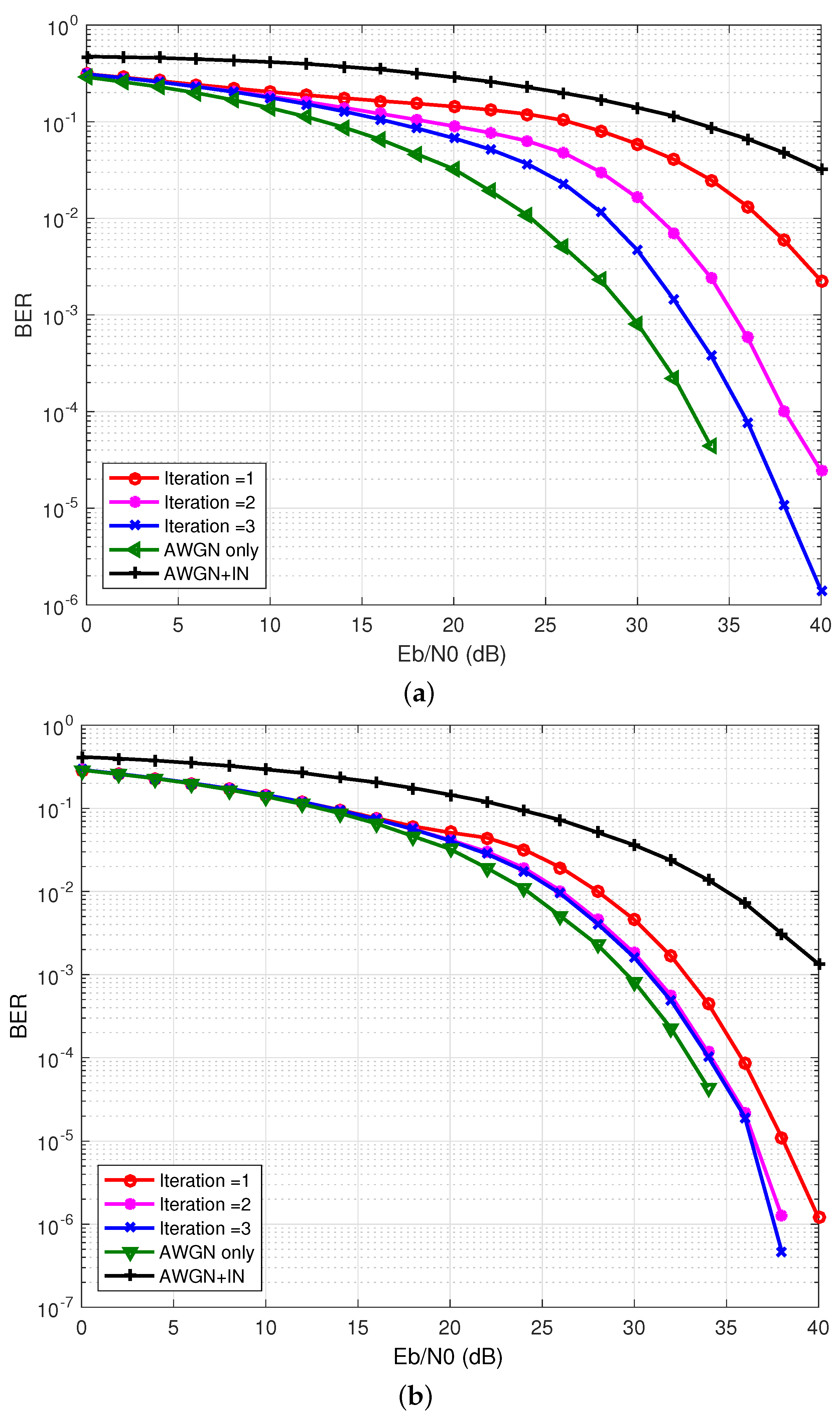
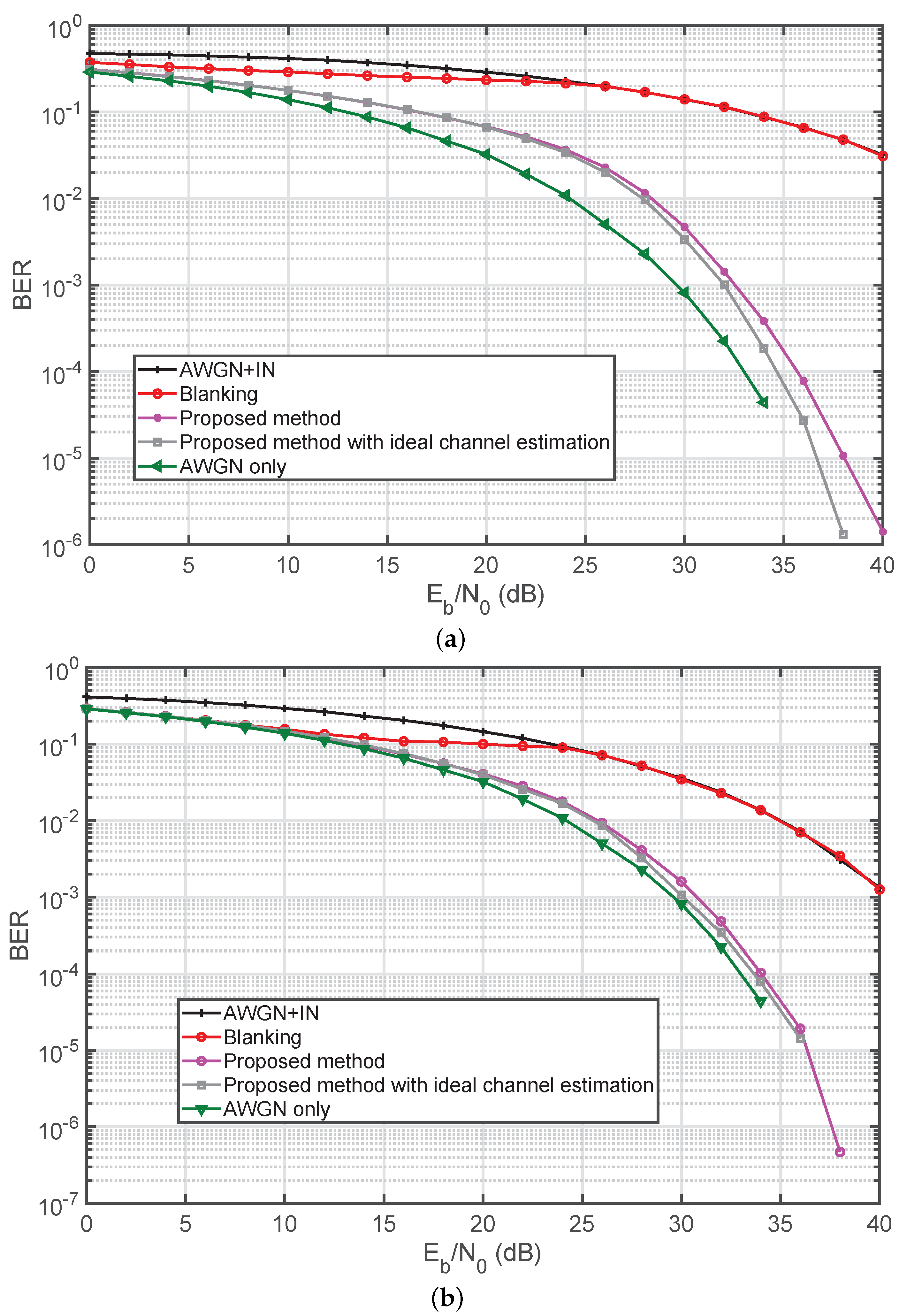
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ikpehai, A.; Adebisi, B.; Rabie, K.M. Broadband PLC for Clustered Advanced Metering Infrastructure (AMI) Architecture. Energies 2016, 9. [Google Scholar] [CrossRef]
- Kim, D.S.; Chung, B.J.; Chung, Y.M. Statistical Learning for Service Quality Estimation in Broadband PLC AMI. Energies 2019, 12. [Google Scholar] [CrossRef]
- Zhang, J.; Hasandka, A.; Wei, J.; Alam, S.M.S.; Elgindy, T.; Florita, A.R.; Hodge, B.M. Hybrid Communication Architectures for Distributed Smart Grid Applications. Energies 2018, 11. [Google Scholar] [CrossRef]
- Zambroni de Souza, A.C.; Castilla, M. Microgrids Design and Implementation, 1st ed.; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Graf, N.; Tsokalo, I.; Lehnert, R. Validating broadband PLC for smart grid applications with field trials. In Proceedings of the 2017 IEEE International Conference on Smart Grid Communications (SmartGridComm), Dresden, Germany, 23–27 October 2017; pp. 497–502. [Google Scholar]
- Zhang, J.; Meng, J. Noise Resistant OFDM for Power-Line Communication Systems. IEEE Trans. Power Deliv. 2010, 25, 693–701. [Google Scholar] [CrossRef]
- Gianaroli, F.; Pancaldi, F.; Sironi, E.; Vigilante, M.; Vitetta, G.M.; Barbieri, A. Statistical Modeling of Periodic Impulsive Noise in Indoor Power-Line Channels. IEEE Trans. Power Deliv. 2012, 27, 1276–1283. [Google Scholar] [CrossRef]
- Andreadou, N.; Pavlidou, F.N. Modeling the Noise on the OFDM Power-Line Communications System. IEEE Trans. Power Deliv. 2010, 25, 150–157. [Google Scholar] [CrossRef]
- Suraweera, H.; Armstrong, J. Noise Bucket Effect for Impulse Noise in OFDM. Electron. Lett. 2004, 40, 1156–1157. [Google Scholar] [CrossRef]
- Ghosh, M. Analysis of the Effect of Impulse Noise on Multicarrier and Single Carrier QAM Systems. IEEE Trans. Commun. 1996, 44, 145–147. [Google Scholar] [CrossRef]
- IEEE Standard for Broadband over Power Line Networks: Medium Access Control and Physical Layer Specifications; IEEE Std 1901-2010; IEEE Standards Association: Piscataway, NJ, USA, 2010; pp. 1–1586. [CrossRef]
- Koga, H.; Kodama, N.; Konishi, T. High-speed power line communication system based on wavelet OFDM. In Proceedings of the 2003 IEEE 7th International Symposium on Power Line Communications and Its Applications, Kyoto, Japan, 26–28 March 2003; pp. 226–231. [Google Scholar]
- Zhidkov, S. Analysis and Comparison of Several Simple Impulsive Noise Mitigation Schemes for OFDM Receivers. IEEE Trans. Commun. 2008, 56, 5–9. [Google Scholar] [CrossRef]
- Papilaya, V.N.; Vinck, A.J.H. Investigation on a new combined impulsive noise mitigation scheme for OFDM transmission. In Proceedings of the 2013 IEEE 17th International Symposium on Power Line Communications and Its Applications, Johannesburg, South Africa, 24–27 March 2013; pp. 86–91. [Google Scholar]
- Kim, Y.; Bae, J.N.; Kim, J.Y. Performance of Power Line Communication Systems with Noise Reduction Scheme for Smart Grid Applications. IEEE Trans. Consum. Electron. 2011, 57, 46–52. [Google Scholar] [CrossRef]
- Juwono, F.; Guo, Q.; Huang, D.; Wong, K.P. Deep Clipping for Impulsive Noise Mitigation in OFDM-Based Power-Line Communications. IEEE Trans. Power Deliv. 2014, 29, 1335–1343. [Google Scholar] [CrossRef]
- Ndo, G.; Siohan, P.; Hamon, M. Adaptive Noise Mitigation in Impulsive Environment: Application to Power-Line Communications. IEEE Trans. Power Deliv. 2010, 25, 647–656. [Google Scholar] [CrossRef]
- Yih, C. Iterative Interference Cancellation for OFDM Signals With Blanking Nonlinearity in Impulsive Noise Channels. IEEE Signal Process. Lett. 2012, 19, 147–150. [Google Scholar] [CrossRef]
- Zhidkov, S. Impulsive noise suppression in OFDM based communication systems. IEEE Trans. Consum. Electron. 2003, 4, 944–948. [Google Scholar] [CrossRef]
- Chien, Y.; Chen, J.; Xu, S.S. A Multilayer Perceptron-Based Impulsive Noise Detector with Application to Power-Line-Based Sensor Networks. IEEE Access 2018, 6, 21778–21787. [Google Scholar] [CrossRef]
- Barazideh, R.; Niknam, S.; Natarajan, B. Impulsive Noise Detection in OFDM-based Systems: A Deep Learning Perspective. In Proceedings of the 2019 IEEE 9th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 7–9 January 2019; pp. 937–942. [Google Scholar] [CrossRef]
- Chien, Y.R. Iterative Channel Estimation and Impulsive Noise Mitigation Algorithm for OFDM-Based Receivers With Application to Power-Line Communications. IEEE Trans. Power Deliv. 2015, 30, 2435–2442. [Google Scholar] [CrossRef]
- Khan, A.; Shin, S.Y. Linear precoded wavelet OFDM-based PLC system with overlap FDE for impulse noise mitigation. Int. J. Commun. Syst. 2017, 30, e3349. [Google Scholar] [CrossRef]
- Paleologu, C.; Benesty, J.; Ciochina, S. A Variable Step-Size Affine Projection Algorithm Designed for Acoustic Echo Cancellation. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 1466–1478. [Google Scholar] [CrossRef]
- Zimmermann, M.; Dostert, K. A Multipath Model for the Power Line Channel. IEEE Trans. Commun. 2002, 50, 553–559. [Google Scholar] [CrossRef]
- Zimmermann, M.; Dostert, K. Analysis and modeling of impulsive noise in broad-band powerline communications. IEEE Trans. Electromagn. Compat. 2002, 44, 249–258. [Google Scholar] [CrossRef]
- Pighi, R.; Franceschini, M.; Ferrari, G.; Raheli, R. Fundamental performance limits of communications systems impaired by impulse noise. IEEE Trans. Commun. 2009, 57, 171–182. [Google Scholar] [CrossRef]
- Chien, Y.; Chen, Y.; Tsao, H. Signal-quality-aware impulsive noise mitigation for OFDM-based power-line communications. In Proceedings of the 2015 IEEE International Conference on Consumer Electronics—Taiwan, Taipei, Taiwan, 6–8 June 2015; pp. 174–175. [Google Scholar] [CrossRef]

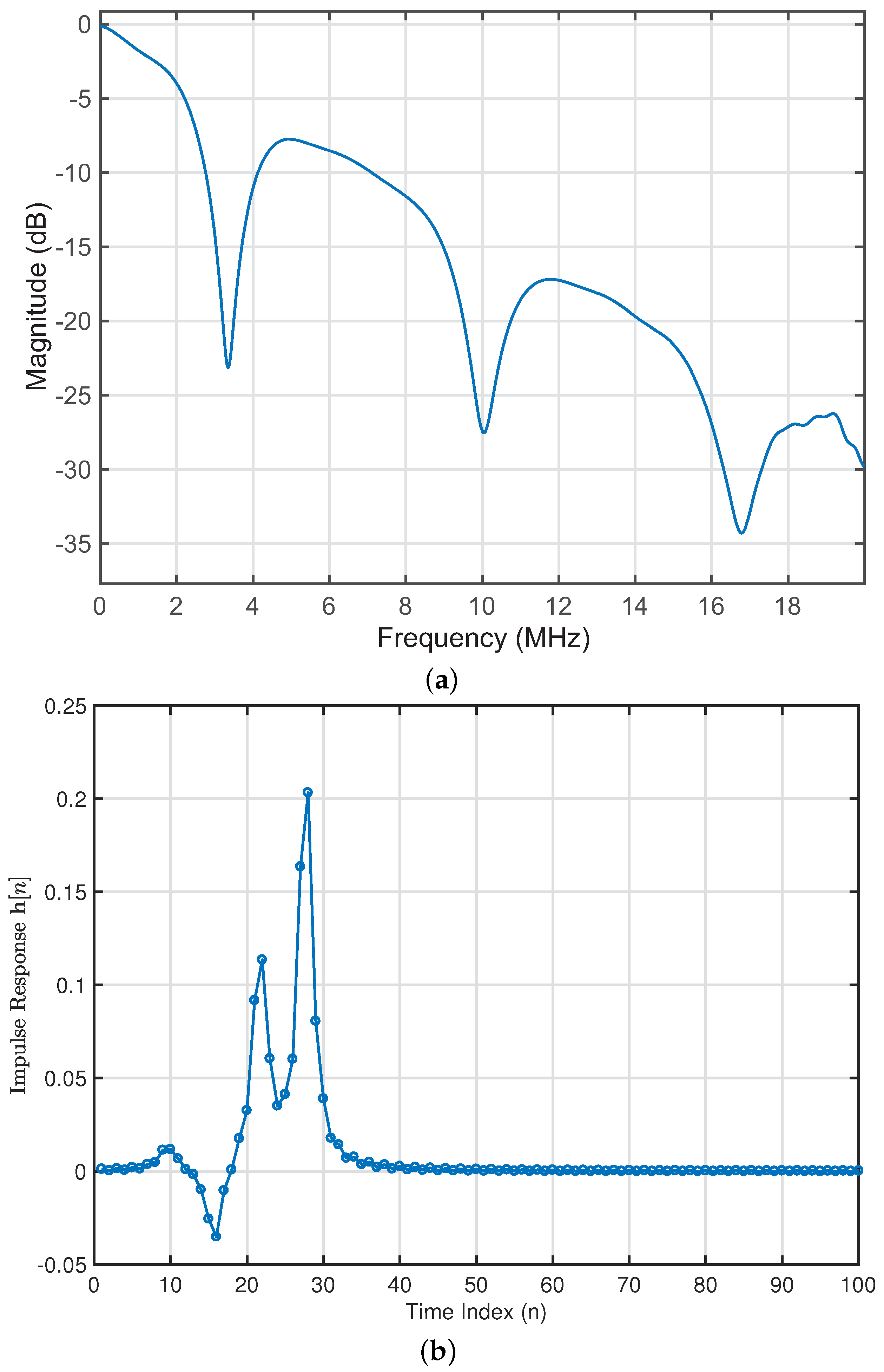
| Attenuation Parameters | |||||
| Path Parameters | |||||
| i | i | ||||
| 1 | 0.64 | 200 | 3 | −0.15 | 244.8 |
| 2 | 0.38 | 222.4 | 4 | 0.05 | 267.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chien, Y.-R.; Yu, H.-C. Mitigating Impulsive Noise for Wavelet-OFDM Powerline Communication. Energies 2019, 12, 1567. https://doi.org/10.3390/en12081567
Chien Y-R, Yu H-C. Mitigating Impulsive Noise for Wavelet-OFDM Powerline Communication. Energies. 2019; 12(8):1567. https://doi.org/10.3390/en12081567
Chicago/Turabian StyleChien, Ying-Ren, and Hao-Chun Yu. 2019. "Mitigating Impulsive Noise for Wavelet-OFDM Powerline Communication" Energies 12, no. 8: 1567. https://doi.org/10.3390/en12081567
APA StyleChien, Y.-R., & Yu, H.-C. (2019). Mitigating Impulsive Noise for Wavelet-OFDM Powerline Communication. Energies, 12(8), 1567. https://doi.org/10.3390/en12081567