Elimination of Common Mode Voltage in Three-To-Six-Phase Matrix Converter
Abstract
:1. Introduction
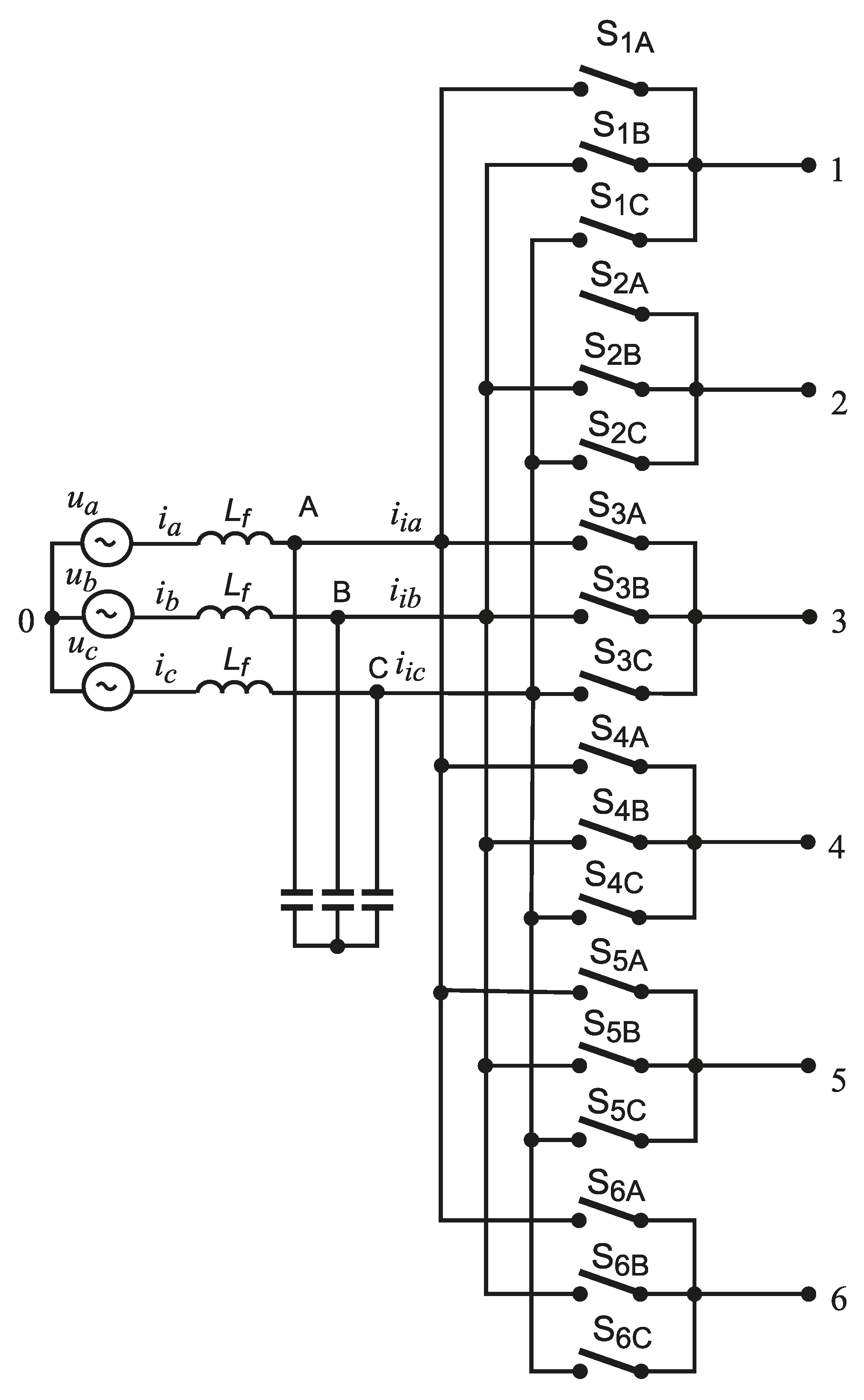
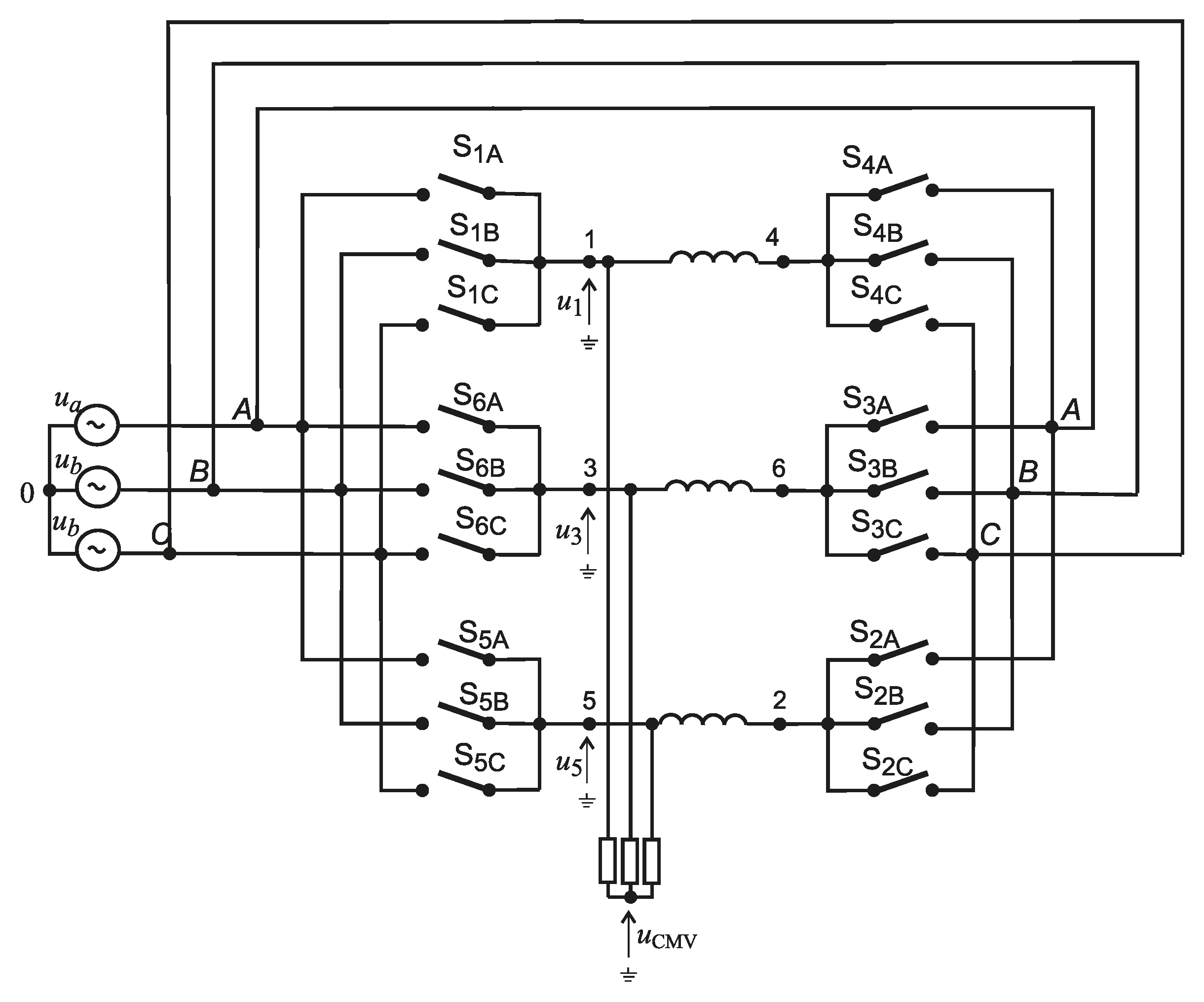
2. Three-To-Six Matrix Converter
2.1. Topology of Multiphase Matrix Converter
2.2. Output Voltage Space Vectors in Three-to-Six-Phase MC
- {6,0,0} All of the output phases are connected to the same input phase. This group consists of three possible switching combinations, i.e., either all output phases are connected to input phase A or input phase B or input phase C. {6,0,0} represents the switching conditions when all of the output phases are connected to input phase A. {0,6,0} represents the switching conditions when all of the output phases are connected to input phase B. {0,0,6} represents the switching conditions when all of the output phases are connected to input phase C. The voltage space vectors, representing these switching combinations have zero module and frequency. These are called zero vectors.
- {5,1,0} Five of the output phases are connected to the same input phase, and the sixth output phase is connected to any of the other two input phases. Here, 5 means five different output phases are connected to input phase A. The number 1 means that one output phase, other than the previous five, is connected to input phase B, and input phase C is not connected to any output phase. As such, there exist six different switching states ({5,1,0}, {1,5,0}, {1,0,5}, {0,1,5}, {0,5,1}, and {5,0,1}). Out of these, one switching state can have further six different combinations, i.e., every switching state has six combinations. This group hence consists of 6 × 6 = 36 switching combinations in all. Voltage space vectors representing these switching combination have a changeable module with maximum value amplitude of input phase voltage (6)), and fixed position on the complex plane. Here, all of switching combinations correspond to the active voltage space vectors.
- {4,0,2} Four of the output phases are connected to the same input phase and remaining two phases are connected to any of the other two input phases. Here exist six different switching states: {4,0,2}; {4,2,0}; {2,4,0}; {2,0,4}; {0,4,2}; and {0,2,4}. Every of sub-group have (6!/(4! × 2!)) × (2!/(2! ×0!)) = 15 combinations. Thus the total possible combination will be 6 × 15 = 90 switching combinations. The voltage space vectors in this group could be split up into three groups: 18 zero space vectors; 36 active voltage space vectors with a changeable module with maximum value and 36 active voltage space vectors with maximum value of the module equal the amplitude of input voltage .
- {4,1,1} Four of the output phases are connected to the same input phase and the two other output phases are connected to the other two input phases, respectively. As such, there exist three different switching states ({4,1,1}, {1,4,1}, and {1,1,4}). One sub-group can have (6!/(4! × 2!)) × (2!/(1! × 1!)) = 30 combinations. There are 3 sub-groups and thus the total possible combination will be 3 × 30 = 90 switching combinations. Among these 90 switching combinations 18 are represented by the active space voltage vectors with a changeable module with maximum value ; 36 are represented by rotating space voltage vectors with constant module equal and 36 combinations correspond to the space vectors with changeable both module and position on the complex plane.
- {3,0,3} Three of the output phases are connected to the same input phase and remaining three output phases are connected to another input phase. As such, there exist three different switching states: {3,3,0}, {0,3,3}, and {3,0,3}. One sub-group can have (6!/(3! × 3!)) × (3!/(3! × 0!)) = 20 combinations. There are 3 sub-groups and thus the total number of possible combination will be 3 × 20 = 60 switching combinations. In this group there are 6 zero space voltage vectors, 18 active voltage space vectors with a changeable module, with maximum value and 36 active space voltage vectors with maximum value of the module .
- {3,2,1} Three of the output phases are connected to the same input phase, two of them are connected to the same another input phase and the sixth output phase is connected to the third input phase. There exist six different switching states: {3,1,2}; {2,3,1}; {2,1,3}; {1,2,3}; {1,3,2} and {3,2,1}. One sub-group can have (6!/(3! × 3!)) × (3!/(2! × 1!)) × (1!/(1! × 0!)) = 60 combinations. There are 6 sub-groups and thus the total possible number of combination will be 6 × 60 = 360 switching combinations. Among these 360 switching combinations 72 are represented by rotating voltage space vectors with constant module equal , 144 switching combinations correspond to two groups of active voltage space vectors: with maximum value of module equal and second group—with maximum value of module equal . The next 144 switching combination are represented by the space vectors with changeable both, magnitude and position on the complex plane.
- {2,2,2} To every one input phases the two output phases are connected. One sub-group may have (6!/(2! × 4!)) × (4!/(2! × 2!)) × (2!/(2! × 0!)) = 90 combinations. As such, there is one sub-group and thus the total possible combination will be 1 × 90 = 90 switching combinations. In this group the active voltage vectors exist in the number of 36. Their maximum module is for 18 of them and − for the next 18. There are also 38 voltage space vectors with changeable both module and position on the complex plane and 6 zero vectors and 12 rotating voltage space vectors with modules equal .To sum up, among 729 possible switching combinations there are:
- 360 combinations with active voltage space vectors characterized by changeable modules and fixed position on the complex plane;
- 218 combinations with changeable both module and position on the complex plane;
- 33 zero vectors;
- 118 rotating space vectors with constant modules and constant angle speed on complex plane, half of them rotate in the negative direction (CW vectors), and the next half—in the positive direction (CCW vectors).
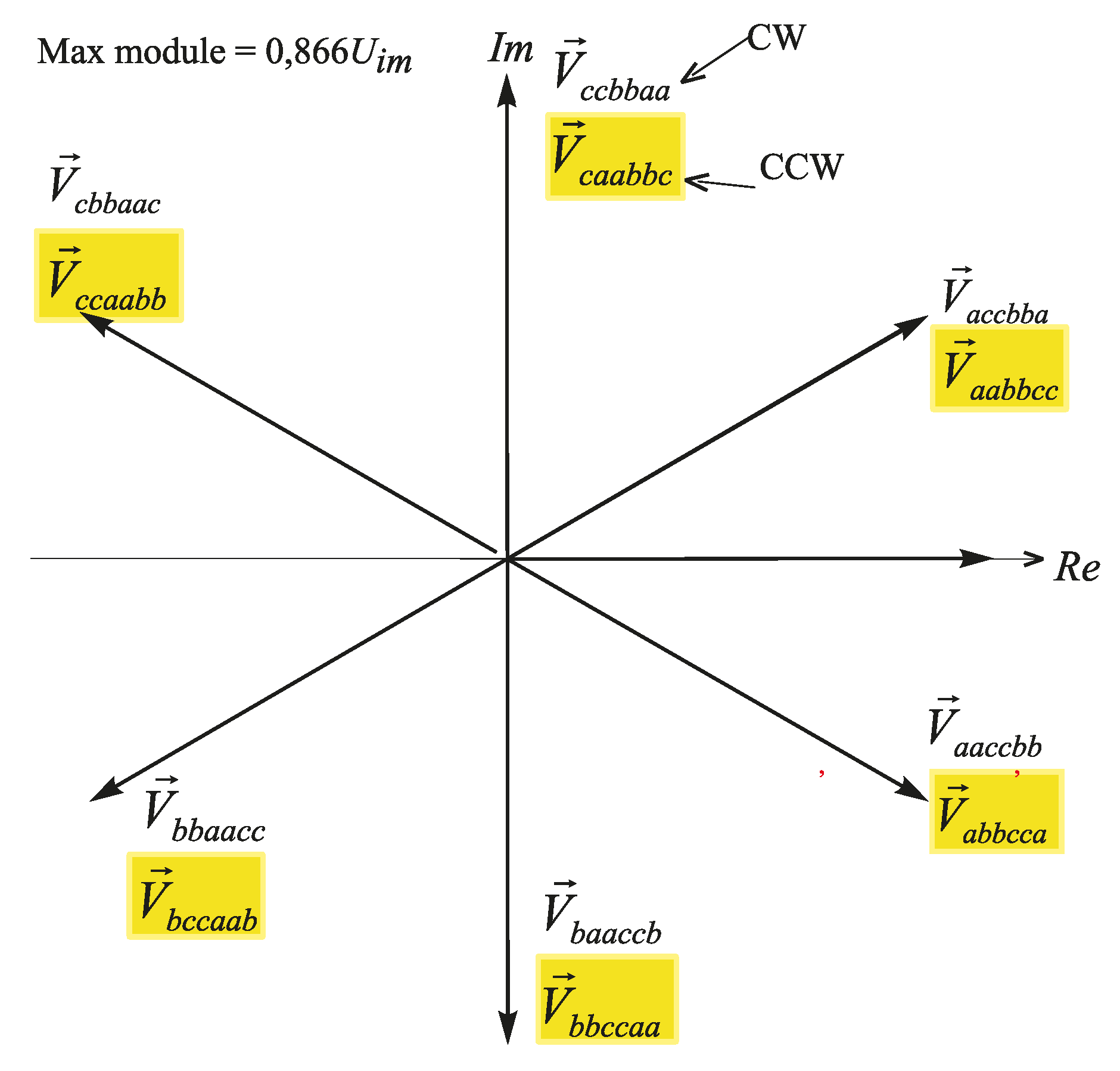
2.3. Output Voltage Space Vectors Reducing CMV in the Three-to-Six-Phase MC
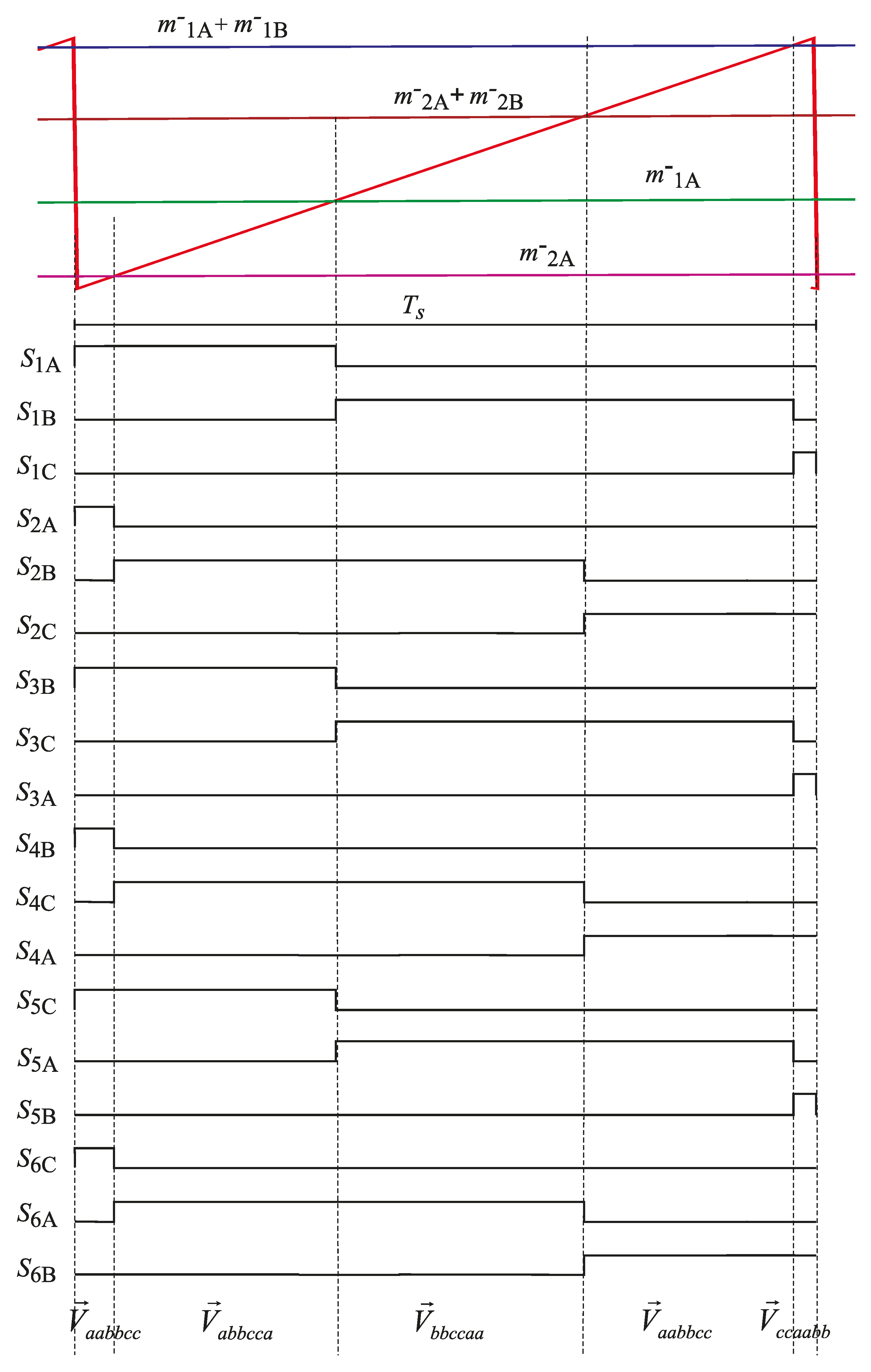
3. Proposed Modulation Method
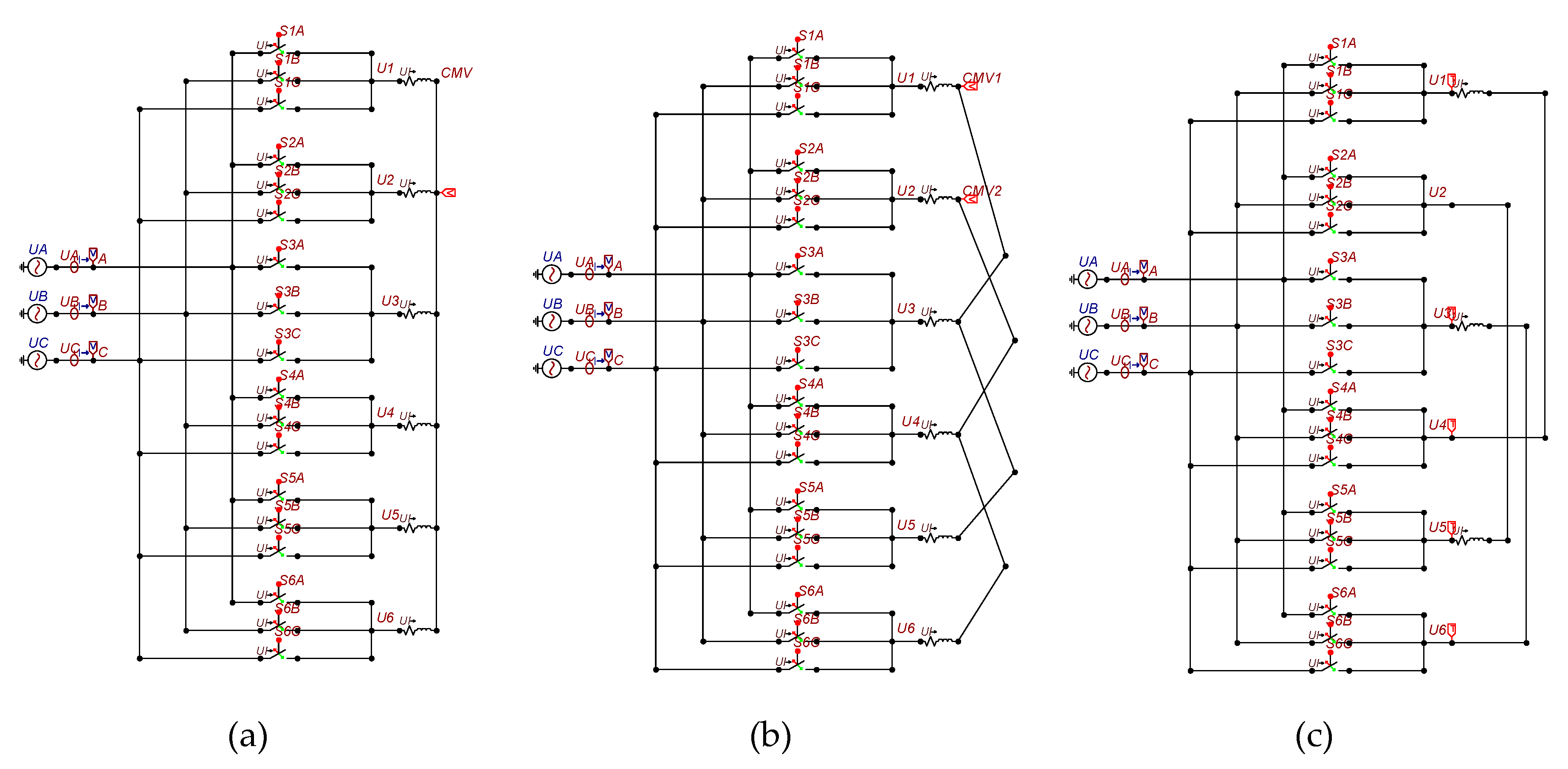
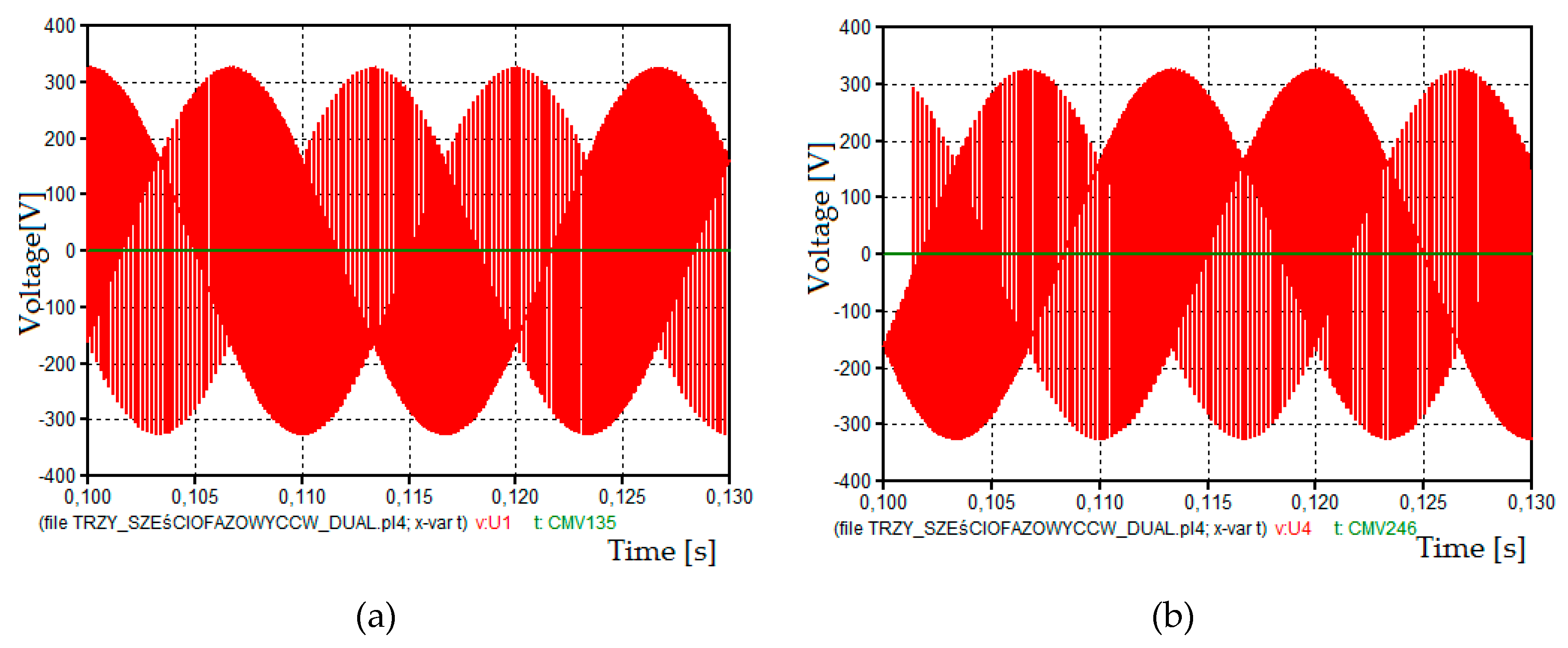
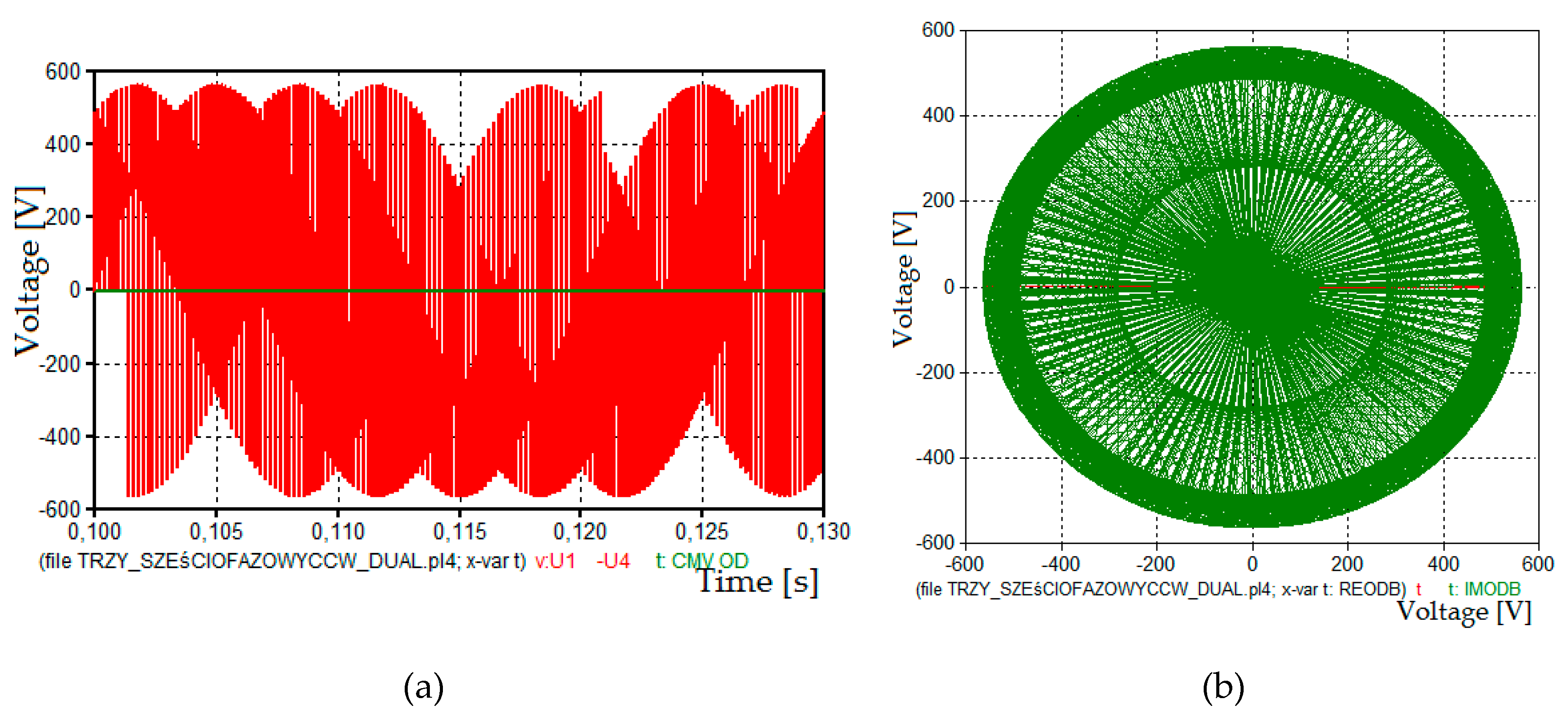
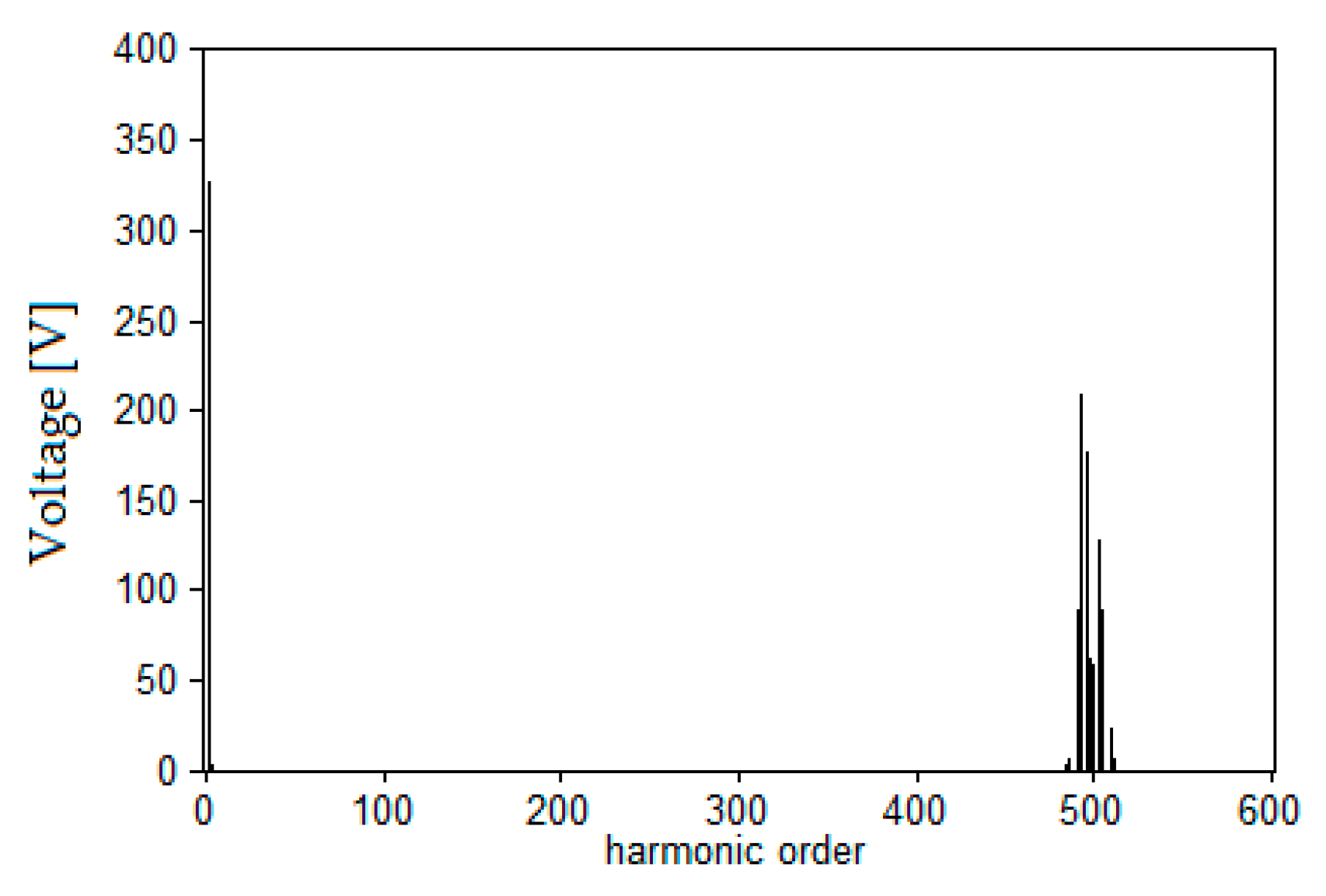
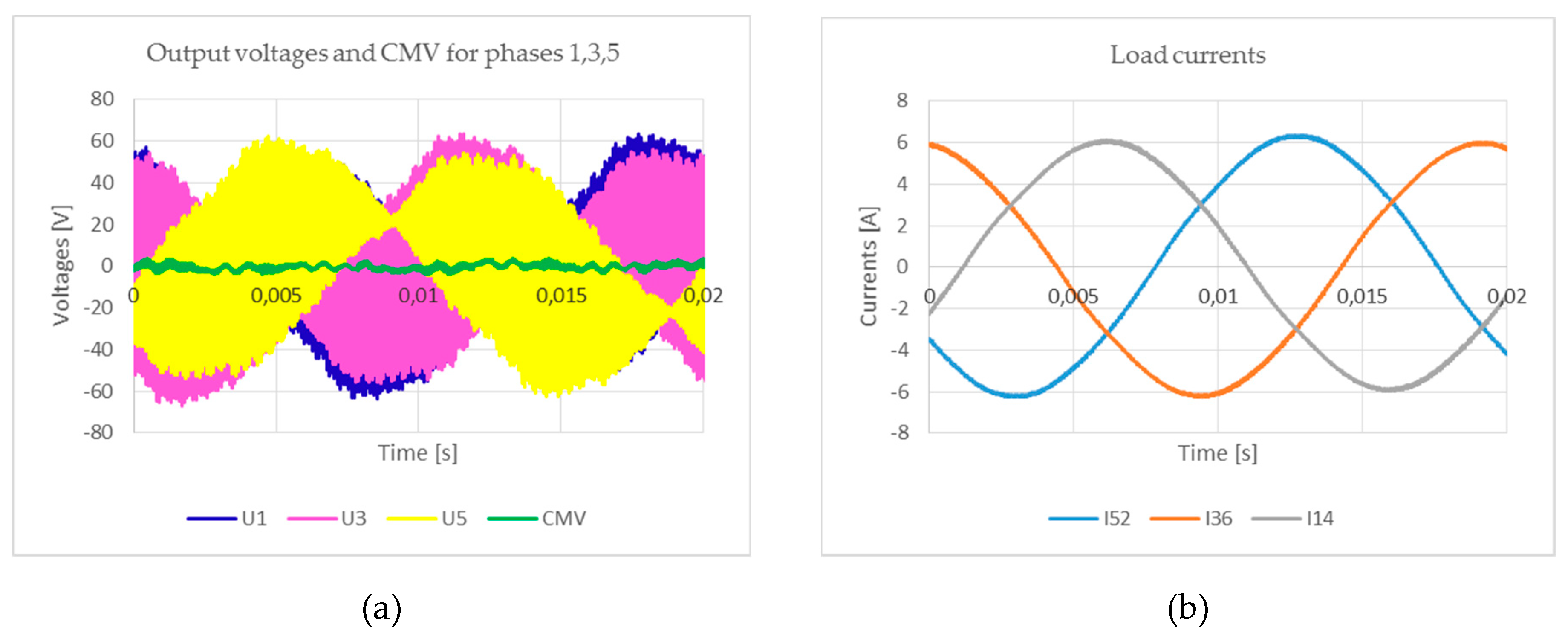
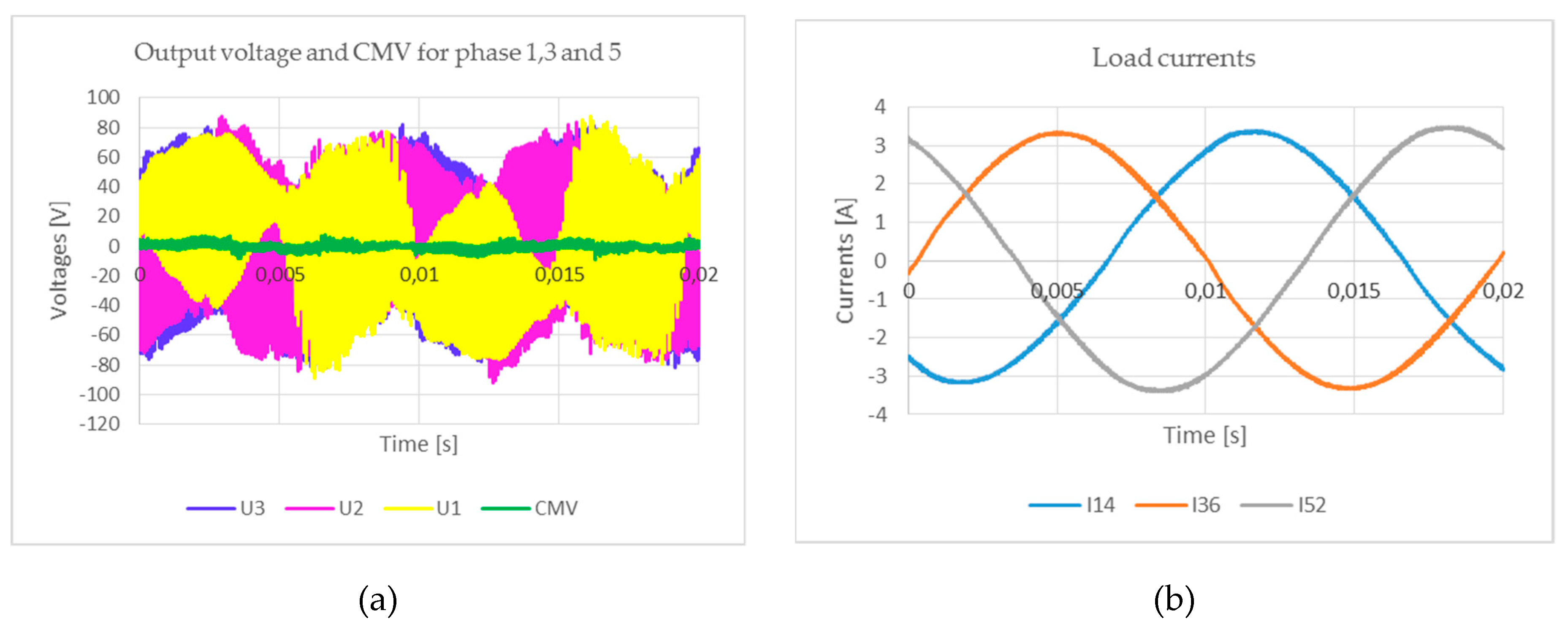
4. Simulation and Experiment
4.1. Simulation
4.2. Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alesina, A.; Venturini, M. Analysis and Design of Optimum–Amplitude Nine–Switch Direct AC–AC Converters. IEEE Trans. Power Electron. 1989, 4, 101–112. [Google Scholar] [CrossRef]
- Alesina, A.; Venturini, M. Solid–State power conversion: a Fourier analysis approach to generalized transformer synthesis. IEEE Trans. Circuits Syst. 1981, 28, 319–330. [Google Scholar] [CrossRef]
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electr. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Iqbali, A.; Abu-Rub, H.; Khan, M.R. Space vector PWM technique for a novel three-to-five phase matrix converter. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1875–1880. [Google Scholar] [CrossRef]
- Iqbal, A.; Ahmed, S.M.; Abu-Rub, H. Space Vector PWM Technique for a Three-to-Five-Phase Matrix Converter. IEEE Trans. Ind. Appl. 2012, 48, 697–707. [Google Scholar] [CrossRef]
- Ahmed, M.; Abu-Rub, H.; Salam, Z.; Kouzou, A. Space vector PWM technique for a novel three-to-seven phase matrix converter. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 4949–4954. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Iqbal, A.; Abu-Rub, H. Generalized Duty-Ratio-Based Pulsewidth Modulation Technique for a Three-to-k Phase Matrix Converter. IEEE Trans. Power Electron. 2011, 58, 3925–3937. [Google Scholar] [CrossRef]
- Saleh, M.; Iqbal, A.; Ahmed, K.M.; Kalam, A.; Abu-Rub, H. Carrier-based pulse width modulation technique for a three-to-five phase matrix converter for supplying five-phase two-motor drives. Int. J. Eng. Sci. Technol. 2010, 2, 67–78. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Abu-Rub, H.; Salarti, Z.; Rivera, M.; Ellabban, O. Generalized carrier based pulse width modulation technique for a three to n-phase dual matrix converter. In Proceedings of the IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3298–3304. [Google Scholar] [CrossRef]
- Ahmed, K.M.; Iqbal, A.; Abu-Rub, H. Carrier-based PWM technique of a novel three-to-seven-phase matrix converter. In Proceedings of the XIX International Conference on Electrical Machines-ICEM 2010, Rome, Italy, 6–8 September 2010. CD-ROM Paper No RF-004944. [Google Scholar]
- Ahmed, S.M.; Iqbal, A.; Abu-Rub, H.; Rodriguez, J.; Rojas, C.A.; Saleh, M. Simple Carrier-Based PWM Technique for a Three-to-Nine-Phase Direct AC–AC Converter. IEEE Trans. Power Electron. 2011, 58, 5014–5023. [Google Scholar] [CrossRef]
- Ali, M.; Iqbal, A.; Khan, M.R.; Ayyub, M.; Anees, M.A. Generalized Theory and Analysis of Scalar Modulation Techniques for a m x n Matrix Converter. IEEE Trans. Power Electron. 2017, 32, 4864–4877. [Google Scholar] [CrossRef]
- Iqbal, A.; Alammari, R.; Abu-Rub, H.; Ahmed, S.M. PWM scheme for dual matrix converters based five-phase open-end winding drive. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 1686–1690. [Google Scholar] [CrossRef]
- Ghalem, B.; Azeddine, B. Six-Phase Matrix Converter Fed Double Star Induction Motor. Acta Polytech. Hung. 2010, 7, 163–176. [Google Scholar]
- Saleh, M.; Iqbal, A.; Ahmed, S.M.; Abu Rub, H.; Kalam, A. Carrier based PWM technique for a three-to-six phase matrix converter for supplying six-phase two-motor drives. In Proceedings of the IECON 2011-37th Annual Conference of the IEEE Industrial Electronics Society, Victoria, Australia, 7–10 November 2011; pp. 3470–3475. [Google Scholar] [CrossRef]
- Bucknall, R.W.G.; Ciaramella, K.M. On the Conceptual Design and Performance of a Matrix Converter for Marine Electric Propulsion. IEEE Trans. Power Electron. 2010, 25, 1497–1508. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, R.; Cheng, F.; Yang, H. Six-phase induction machine driven by the matrix converter. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Espina, J.; Arias, A.; Balcells, J.; Ortega, C. Common mode output waveforms reduction for Matrix Converters drives. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 4499–4504. [Google Scholar] [CrossRef]
- Guan, Q.; Wheeler, Pa.; Guan, Q.S.; Yang, P. Common-mode voltage reduction for matrix converters using all valid switch states. IEEE Trans. Power Electron. 2016, 31, 8247–8259. [Google Scholar] [CrossRef]
- Padhee, V.; Sahoo, A.K.; Mohan, N. Modulation technique for common mode voltage reduction in a matrix converter drive operating with high voltage transfer ratio. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 1982–1988. [Google Scholar] [CrossRef]
- Ahmed, S.M.; Salam, Z.; Abu-Rub, H. Common-mode voltage elimination in a three-to-seven phase dual matrix converter feeding a seven phase open-end induction motor drive. In Proceedings of the 2014 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 13–14 October 2014; pp. 207–212. [Google Scholar] [CrossRef]
- Rzasa, J. Control of a matrix converter with reduction of a common mode voltage. IEEE Compat. Power Electron. 2005, 213–217. [Google Scholar]
- Mohapatra, K.K.; Mohan, N. Open-End Winding Induction Motor Driven with Matrix Converter for Common-Mode Elimination. In Proceedings of the 2006 International Conference on Power Electronic, Drives and Energy Systems, New Delhi, India, 12–15 December 2006; pp. 1–6. [Google Scholar]
- Rząsa, J. Research on Dual Matrix Cnverter Feeding an Open-End-Winding Load Controlled with the Use of Rotating Space Vectors. Part I. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society IECON 2013, Vienna, Austria, 10–13 November 2013; pp. 4917–4922. [Google Scholar]
- Rząsa, J.; Garus, G. Research on Dual Matrix Converter Feeding an Open-End-Winding Load Controlled with the Use of Rotating Space Vectors. Part II. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society IECON 2013, Vienna, Austria, 10–13 November 2013; pp. 4923–4928. [Google Scholar]
- Baranwal, R.; Basu, K.; Mohan, N. An alternative carrier based implementation of Space Vector PWM 420 for dual matrix converter drive with common mode voltage elimination. In Proceedings of the IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 1208–1213. [Google Scholar] [CrossRef]
- Rzasa, J. An Alternative Carrier-Based Implementation of Space Vector Modulation to Eliminate Common Mode Voltage in a Multilevel Matrix Converter. Electronics 2019, 8, 190. [Google Scholar] [CrossRef]
- Rząsa, J. Direct Voltage Sourced Matrix Converter; Oficyna Wydawnicza Politechniki Rzeszowskiej: Rzeszów, Poland, 2016; ISBN 978-83-7934-101-6. (in Polish) [Google Scholar]
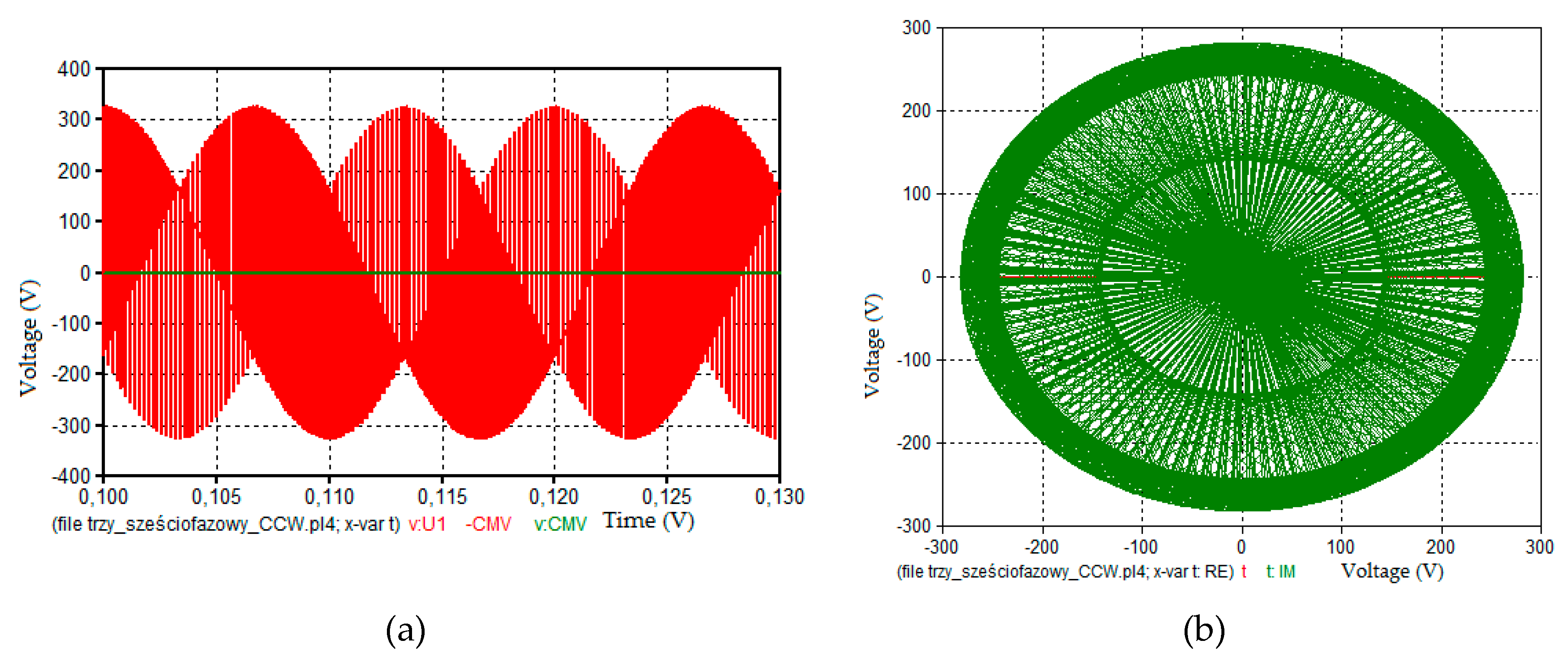
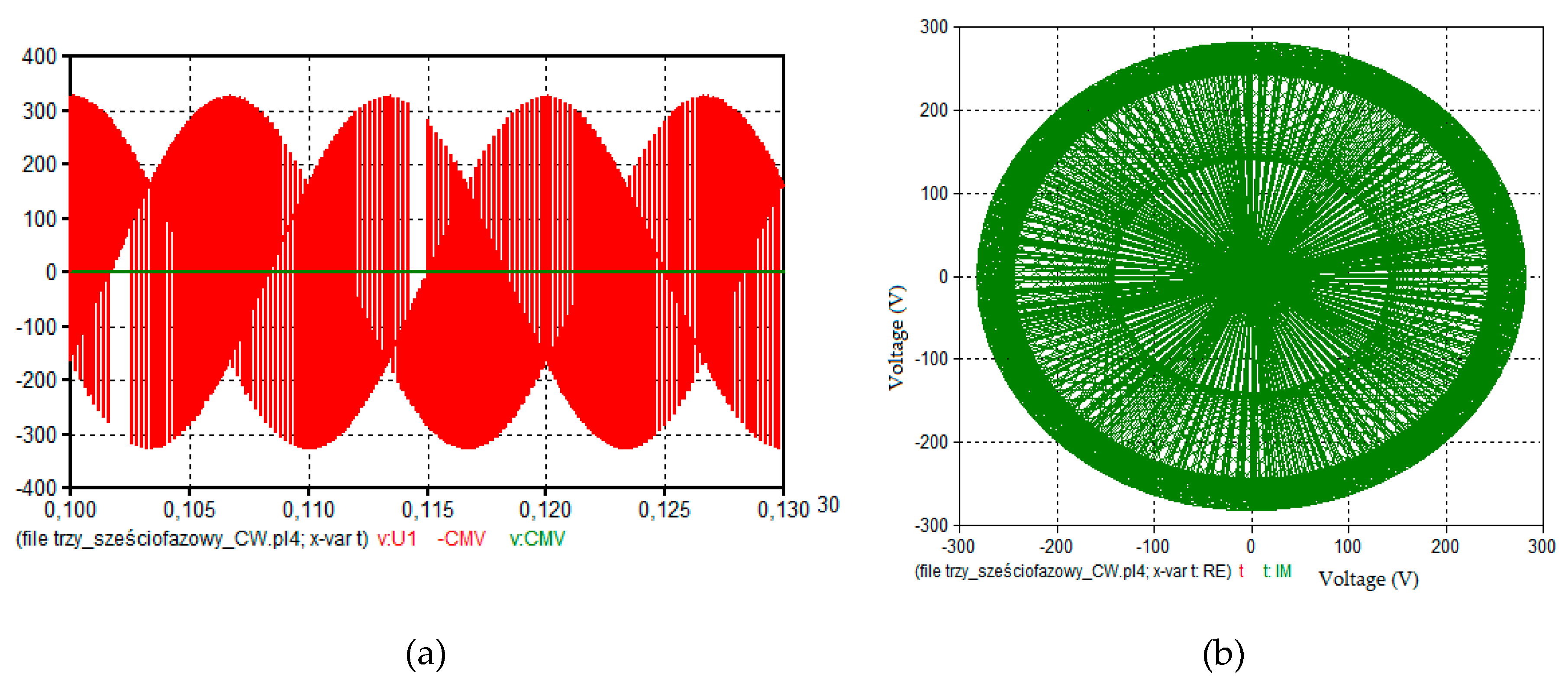
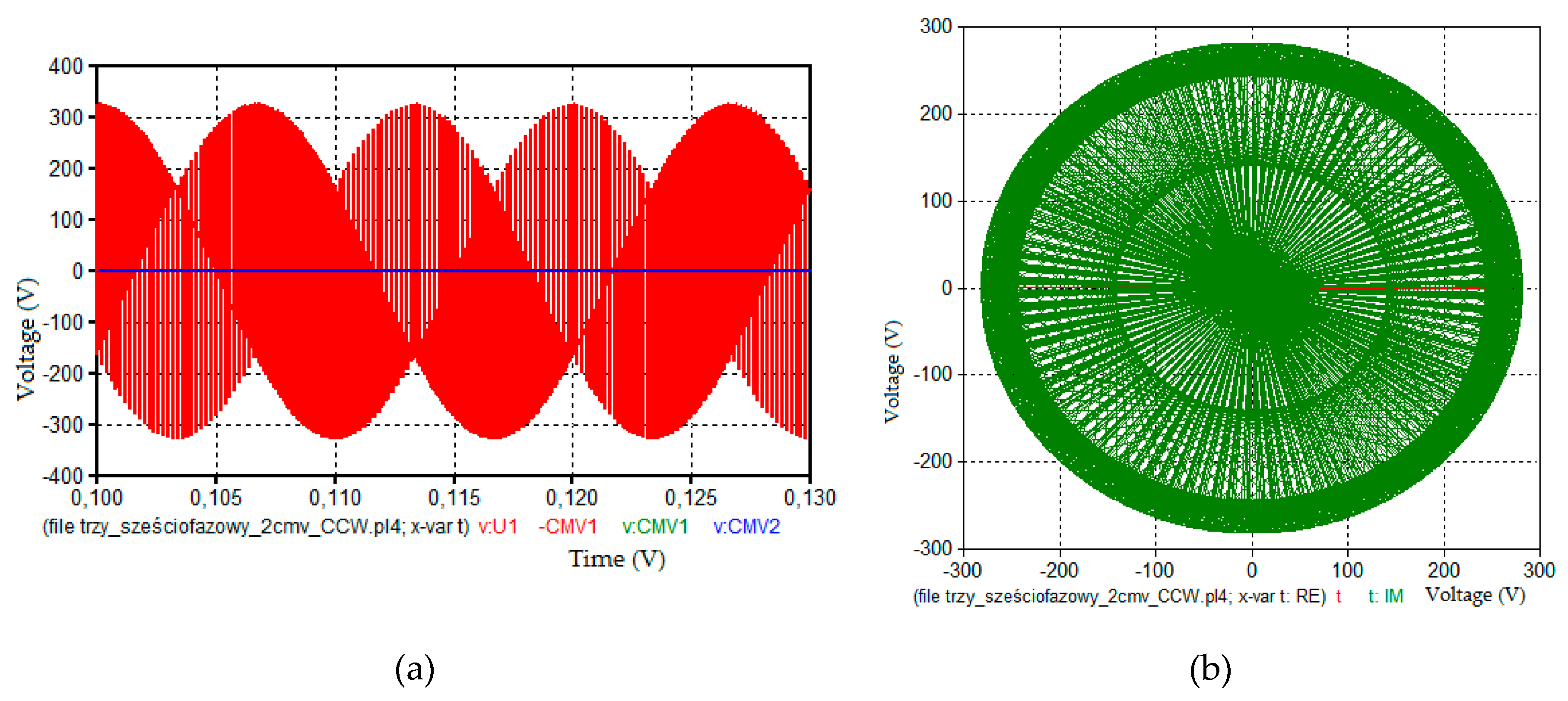
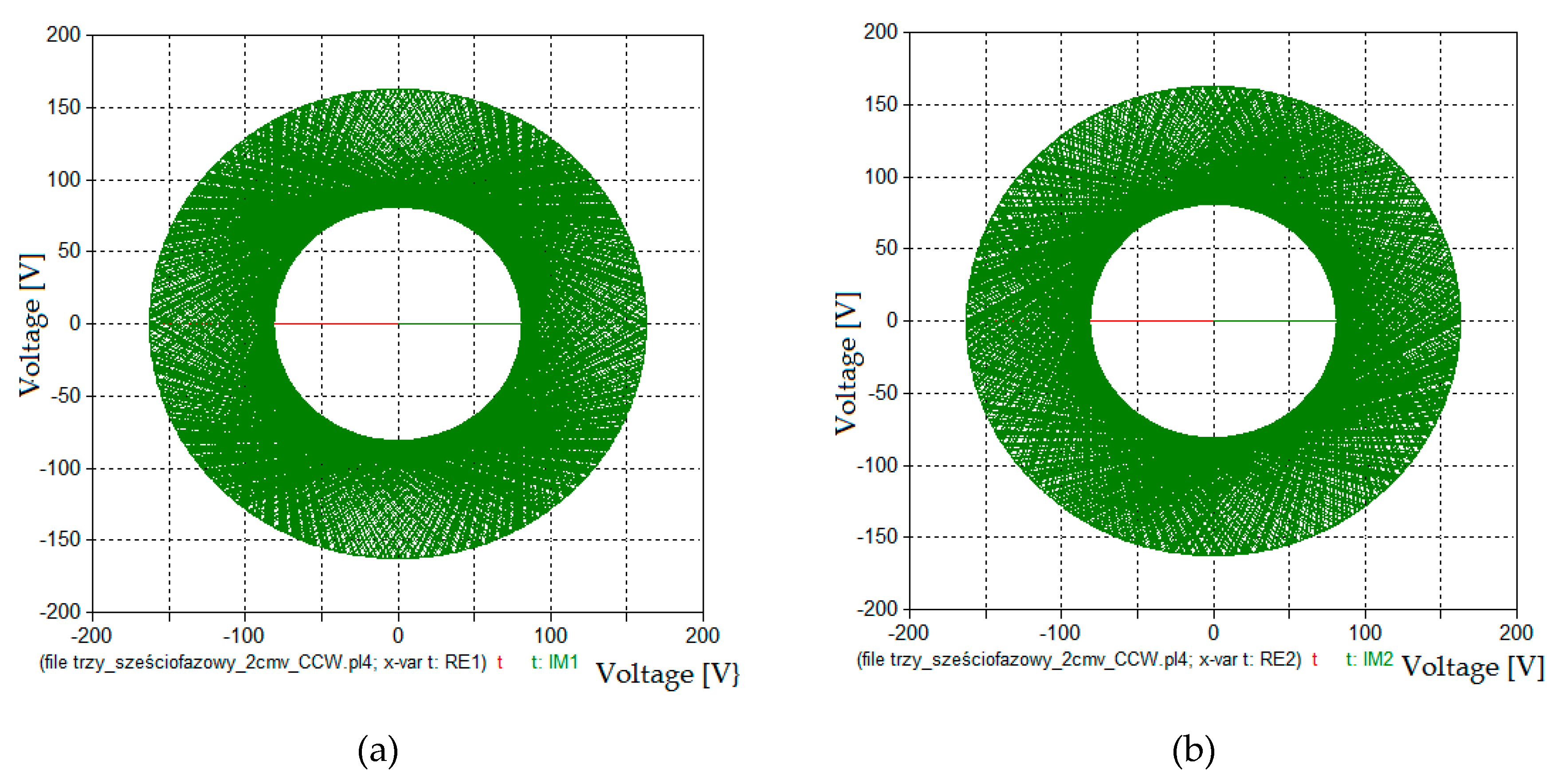

| Six-Phase Load | Six-Phase Load with Two Sets of Three-Phase Windings | Open-End Three Phase Load | |
|---|---|---|---|
| CW vectors | |||
| CCW vectors | |||
| Six-Phase Load | Six-Phase Load with Two Sets of Three-phase Windings | Open-End Three Phase Load | |
|---|---|---|---|
| Parameter Name | Parameter Value |
|---|---|
| input frequency f | 50 Hz |
| RMS value of input phase voltage | 60 V |
| carrier frequency | 5 kHz |
| load parameters | 4.5 Ω, 36 mH |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rząsa, J.; Sztajmec, E. Elimination of Common Mode Voltage in Three-To-Six-Phase Matrix Converter. Energies 2019, 12, 1662. https://doi.org/10.3390/en12091662
Rząsa J, Sztajmec E. Elimination of Common Mode Voltage in Three-To-Six-Phase Matrix Converter. Energies. 2019; 12(9):1662. https://doi.org/10.3390/en12091662
Chicago/Turabian StyleRząsa, Janina, and Elżbieta Sztajmec. 2019. "Elimination of Common Mode Voltage in Three-To-Six-Phase Matrix Converter" Energies 12, no. 9: 1662. https://doi.org/10.3390/en12091662
APA StyleRząsa, J., & Sztajmec, E. (2019). Elimination of Common Mode Voltage in Three-To-Six-Phase Matrix Converter. Energies, 12(9), 1662. https://doi.org/10.3390/en12091662






