Modelling of Passive Heat Removal Systems: A Review with Reference to the Framatome BWR Reactor KERENA: Part II
Abstract
:1. Introduction
2. Boiling Inside Inclined Tubes
2.1. 1D-Codes of Boiling
2.1.1. ATHLET
Subcooled Nucleate Boiling
Nucleate Boiling
Film Boiling
2.1.2. RELAP
Nucleate Boiling
Transition Boiling
Film Boiling
2.1.3. TRACE
Nucleate Boiling
Transition Boiling
Film Boiling
2.1.4. Boiling Heat Transfer Models in CFD
2.2. Experiments
3. Two-Phase Flow Instabilities
3.1. Static Instabilities
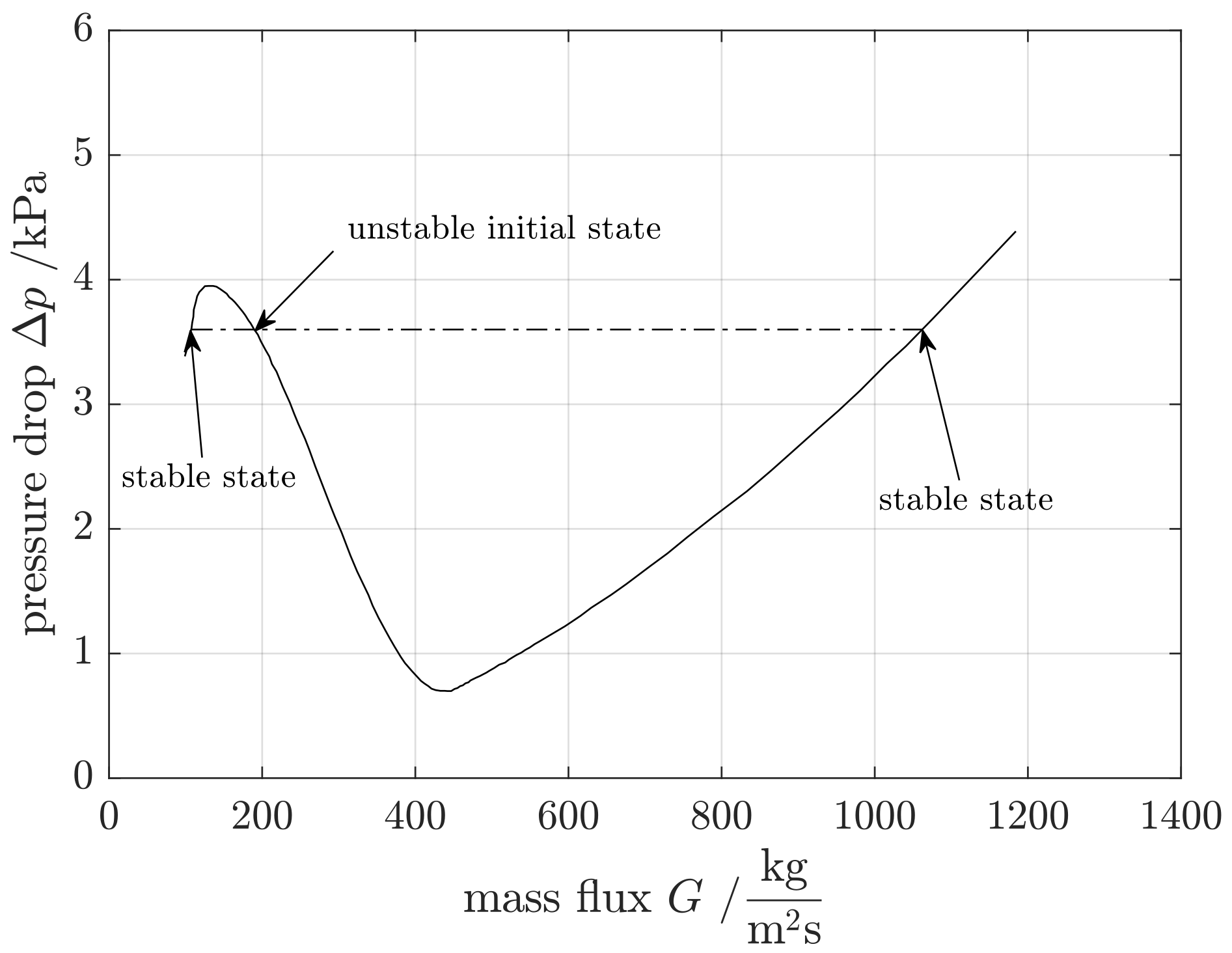
3.1.1. Ledinegg Instability
3.1.2. The Boiling Crisis
3.1.3. Flow Pattern Transition Instability
3.1.4. Geysering
3.2. Dynamic Instabilities
3.2.1. Acoustic Oscillation
3.2.2. Density Wave Oscillation
3.2.3. Thermally Induced Oscillations
3.2.4. Parallel Channel Instabilities
3.2.5. Pressure Drop Oscillations
3.2.6. Natural Circulation Instabilities
3.3. Experiments
- Increasing the single-phase flow pressure drop in the heated section
- Increasing the system pressure
- Decreasing the inlet subcooling
3.4. Numerical Investigations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AHWR | Advanced heavy water reactor |
| AST-500 | Soviet small nuclear reactor for district heating station, 500 MW thermal power |
| ATHLET | Analysis of thermal-hydraulics of leaks and transients |
| BWR | Boiling water reactor |
| CFD | Computational fluid dynamic |
| CHF | Critical heat flux |
| CIRCUS | Circulation during start-up, Delft University of Technology, Netherlands |
| DANTON | Dresdner Anlage für Naturumlauf mit teilweiser originaler Nachbildung, Technische Universität Dresden, Germany |
| DESIRE | Delft simulated reactor, Delft University of Technology, Netherlands |
| DFM | Drift-flux mixture |
| DWO | Density wave oscillation |
| GENEVA | Generische Einschleifen-Naturumlauf-Versuchsanlage, Technische Universität Dresden, Germany |
| GF | Ghost fluid |
| GRS | Gesellschaft für Anlagen und Reaktorsicherheit |
| HEM | Homogeneous equilibrium mixture model |
| HRTL-5 | Heating reactor test loop with a thermal power of about 5 MW, Tsinghua University, Beijing, China |
| INKA | Intgral Teststand Karlstein, AREVA, Karlstein, Germany |
| KATHY | Karlstein thermal hydraulic test loop, AREVA, Karlstein, Germany |
| LB | Lattice Boltzmann |
| LOCA | loss of coolant accidents |
| NHR-5 | 5 MW nuclear heating reactor, Institute of Nuclear Energy and Technology, Tsinghua University, Beijing, China |
| PANDA | Large scale, thermal-hydraulics test facility, Paul Scherrer Institute (PSI), Villigen, Switzerland |
| PCI | Parallel channel instabilities |
| PCL | Parallel channel loop, Bhabha atomic research centre, Trombay, Mumbai, India |
| PDO | Pressure drop oscillation |
| PUMA | Purdue university multi-dimensional integral test assembly, USA |
| PWR | Pressure water reactor |
| RELAP | Reactor excursion and leak analysis program |
| ROM | Reduced order model |
| SBLOCA | Small break loss of coolant accidents |
| SBWR | Simplified boiling water reactor |
| SIRIUS-N | Simulated reactivity feedback implemented into thermal-hydraulic stability for natural circulation BWR |
| TRACE | TRAC/RELAP Advanced computational engine |
| VoF | Volume-of-fluid |
| VOSET | Volume of fluid level set |
| Nomenclature | |
| Wall fraction cooled by single-phase convection | |
| Wall fraction cooled by quenching | |
| c | Relaxation factor |
| Isobar specific heat capacity [J/(kgK)] | |
| d | Droplet diameter [m] |
| D | Hydraulic diameter [m] |
| f | Fanning friction factor |
| F | Reynolds number factor |
| Fourier number | |
| g | Gravitational constant [] |
| G | Mass flux [] |
| Grashof number | |
| h | Heat transfer coefficient [] |
| i | Enthalpy [kJ/kg] |
| Jacob number | |
| K | Constant |
| L | Length [m] |
| Capillary length [m] | |
| M | Vertical stratification and mixture level tracking models multiplier |
| Mass flow [kg/s] | |
| Void fraction factor | |
| N | Exponent |
| Normal vector to the surface | |
| Phase change number | |
| Subcooling number | |
| Nusselt number | |
| p | Pressure [Pa] |
| Prandtl number | |
| Heat flow [W] | |
| Heat flux [] | |
| Volumetric heat generation rate [] | |
| R | Radiation terms |
| Reynolds number | |
| S | Boiling suppression factor |
| T | Temperature [K] |
| u | Averaged flow velocity at phase boundary [m/s] |
| x | Steam mass quality |
| Y | Constant |
| Latent heat of evaporation [kJ/kg] | |
| Greek | |
| Volume fraction | |
| Inclination angle /grad | |
| Vapor film thickness | |
| Non-dimensional vapor film thickness | |
| One dimensional delta function of normal coordinate n | |
| Thermal conductivity [W/(mK)] | |
| Dynamic viscosity [kg/(ms)] | |
| Density [] | |
| Surface tension [N/m] | |
| Boiling delay time [s] | |
| Emissivity | |
| Indices | |
| b | Bubble |
| CHF | Critical heat flux |
| E | Evaporation |
| ext | External |
| F | Convection |
| int | Internal |
| l | Liquid |
| mac | Macroscopic |
| mic | Microscopic |
| Q | Quenching |
| rel | Relative |
| sat | Saturation |
| tar | Target |
| tot | Total |
| TP | Two-phase |
| v | Vapor |
| w | Wall |
References
- Moonesi, A.S.; Zhang, Y.; Viereckl, F.; Manthey, R. Modelling of passive heat removal systems: A review with reference to the Framatome BWR reactor KERENA: Part I. Energies 2019, 13, 35. [Google Scholar] [CrossRef] [Green Version]
- Moonesi, A.S.; Bieberle, A.; Von der Cron, D.; Ding, W.; Krepper, E.; Lucas, D.; Hampel, U. Flow morphology and heat transfer analysis in an inclined condensation pipe part II: Numerical investigations. Nuclear Eng. Des. 2020. not yet published. [Google Scholar]
- Cheng, L.; Ribatski, G.; Thome, J.R. Two-Phase Flow Patterns and Flow-Pattern Maps: Fundamentals and Applications. Appl. Mech. Rev. 2008, 61, 050802. [Google Scholar] [CrossRef]
- Auban, O.; Paladino, D.; Zboray, R. Experimental investigation of natural-circulation flow behavior under low-power/low-pressure conditions in the large-scale PANDA facility. Nucl. Technol. 2004, 148, 294–312. [Google Scholar] [CrossRef]
- Furuya, M.; Inada, F.; van der Hagen, T. Flashing-induced density wave oscillations in a natural circulation BWR—Mechanism of instability and stability map. Nucl. Eng. Des. 2005, 235, 1557–1569. [Google Scholar] [CrossRef]
- Wallis, G.B.; Heasley, J.H. Oscillations in Two-Phase Flow Systems. J. Heat Transf. 1961, 83, 363. [Google Scholar] [CrossRef]
- Ishii, M. Thermally Induced Flow Instabilities in Two-Phase Mixtures in Thermal Equilibrium. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 1971. [Google Scholar]
- Bouré, J.A.; Bergles, A.E.; Tong, L.S. Review of two-phase flow instability. Nucl. Eng. Des. 1973, 25, 165–192. [Google Scholar] [CrossRef]
- Kakaç, S.; Veziroglu, T.N. A Review of Two-Phase Flow Instabilities. In Advances in Two-Phase Flow and Heat Transfer; Kakaç, S., Ishii, M., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 1983; pp. 577–667. [Google Scholar] [CrossRef]
- Prasad, G.V.D.; Pandey, M.; Kalra, M.S. Review of research on flow instabilities in natural circulation boiling systems. Prog. Nucl. Energy 2007, 49, 429–451. [Google Scholar] [CrossRef]
- Kakac, S.; Bon, B. A Review of two-phase flow dynamic instabilities in tube boiling systems. Int. J. Heat Mass Transf. 2008, 51, 399–433. [Google Scholar] [CrossRef]
- Nayak, A.K.; Vijayan, P.K. Flow Instabilities in Boiling Two-Phase Natural Circulation Systems: A Review. Sci. Technol. Nucl. Install. 2008, 2008, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, S.; Basu, D.N.; Das, P.K. Two-Phase Natural Circulation Loops: A Review of the Recent Advances. Heat Transf. Eng. 2012, 33, 461–482. [Google Scholar] [CrossRef]
- Ruspini, L.C.; Marcel, C.P.; Clausse, A. Two-phase flow instabilities: A review. Int. J. Heat Mass Transf. 2014, 71, 521–548. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure. VDI-Wärmeatlas, 10th ed.; VDI Buch, Springer: Berlin, Germany, 2006. [Google Scholar]
- Collier, J.G.; Thome, J.R. Convective Boiling and Condensation, 3rd ed.; reprint 2001 ed.; The Oxford Engineering Science Series; Clarendon Press: Oxford, UK; Oxford University Press: New York, NY, USA, 2001; p. 38. [Google Scholar]
- Lerchl, G.; Austregesilo, H.; Schöffel, P.; Von der Cron, D.; Weyermann, F. ATHLET 3.1A: User’s Manual, 1st ed.; GRS gmbH: Garching, Germany, 2016. [Google Scholar]
- Chen, J.C. Correlation for Boiling Heat Transfer to Saturated Fluids in Convective Flow. Ind. Eng. Chem. Process Des. Dev. 1966, 5, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Liesch, K.J.; Raemhild, G.; Hofmann, K. Zur Bestimmung des Wärmeübergangs und der kritischen Heizflächenbelastung im Hinblick auf besondere Verhältnisse in den Kühlkanälen eines DWR bei schweren Kühlmittelverluststörfällen; MRR-15: TU-München, Germany, 1975. [Google Scholar]
- Gröber, H.; Erk, S.; Grigull, U. Die Grundgesetze der Wärmeübertragung; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar] [CrossRef]
- Vojtek, I. Auswertung der 25-Stabbündel-Versuche mit dem Rechenprogramm BRUDI-VA; GRS-A-208; GRS: Gaithersburg, MD, USA, 1978.
- Berenson, P.J. Film-Boiling Heat Transfer From a Horizontal Surface. J. Heat Transf. 1961, 83, 351–356. [Google Scholar] [CrossRef]
- Bromley, L.A.; LeRoy, N.R.; Robbers, J.A. Heat Transfer in Forced Convection Film Boiling. Ind. Eng. Chem. 1953, 45, 2639–2646. [Google Scholar] [CrossRef]
- The RELAP5-3D© Code Development Team. RELAP5-3D© Code Manual Volume IV: Models and Correlations; Idaho National Laboratory: Idaho Falls, IE, USA, 2012.
- Bjornard, T.A.; Griffith, P. PWR Blowdown Heat Transfer. In Winter Annual Meeting; Thermal and Hydraulic Aspects of Nuclear Reactor Safety; American Society of Mechanical Engineers: Atlanta, GA, USA, 1977; Volume I, Light Water Reactors. [Google Scholar]
- Sudo, Y.; Murao, Y. Film Boiling Heat Transfer during Reflood Process; Japan Atomic Energy Research Inst.: Tokyo, Japan, 1976. [Google Scholar]
- Sun, K.H.; Gonzales-Santalo, J.M.; Tien, C.L. Calculations of Combined Radiation and Convection Heat Transfer in Rod Bundles Under Emergency Cooling Conditions. Trans. ASME J. Heat Transf. 1976, 98, 414–420. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Cess, R.D. Radiation Heat Transfer; Brooks/Cole Pub. Co: Belmont, CA, USA, 1970. [Google Scholar]
- NRC, U.S. TRACE V5.0 p2: Theory Manual; Office of Nuclear Regulatory Research; U.S. Nuclear Regulatory Commission: Washington, DC, USA, 2010.
- Steiner, D.; Taborek, J. Flow Boiling Heat Transfer in Vertical Tubes Correlated by an Asymptotic Model. Heat Transf. Eng. 1992, 13, 43–69. [Google Scholar] [CrossRef]
- Cooper, M.G. Heat Flow Rates in Saturated Nucleate Pool Boiling-A Wide-Ranging Examination Using Reduced Properties. Adv. Heat Transf. 1984, 16, 157–239. [Google Scholar] [CrossRef]
- Gorenflo, D. (Ed.) Pool Boiling, VDI-Heat Atlas; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Holman, J.P. Heat Transfer; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Lee, R.C.; Nydahl, J.E. Numerical Calculation of Bubble Growth in Nucleate Boiling From Inception Through Departure. J. Heat Transf. 1989, 111, 474. [Google Scholar] [CrossRef]
- Son, G.; Dhir, V.K.; Ramanujapu, N. Dynamics and Heat Transfer Associated With a Single Bubble During Nucleate Boiling on a Horizontal Surface. J. Heat Transf. 1999, 121, 623–631. [Google Scholar] [CrossRef]
- Tryggvason, G.; Lu, J. Direct Numerical Simulations of Flows with Phase Change. Procedia IUTAM 2015, 15, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Sato, Y.; Ničeno, B. A sharp-interface phase change model for a mass-conservative interface tracking method. J. Comput. Phys. 2013, 249, 127–161. [Google Scholar] [CrossRef]
- Sato, Y.; Niceno, B. A depletable micro-layer model for nucleate pool boiling. J. Comput. Phys. 2015, 300, 20–52. [Google Scholar] [CrossRef]
- Duan, X.; Phillips, B.; McKrell, T.; Buongiorno, J. Synchronized High-Speed Video, Infrared Thermometry, and Particle Image Velocimetry Data for Validation of Interface-Tracking Simulations of Nucleate Boiling Phenomena. Exp. Heat Transf. 2013, 26, 169–197. [Google Scholar] [CrossRef]
- Yabuki, T.; Nakabeppu, O. Heat transfer mechanisms in isolated bubble boiling of water observed with MEMS sensor. Int. J. Heat Mass Transf. 2014, 76, 286–297. [Google Scholar] [CrossRef]
- Sato, Y.; Niceno, B. Pool boiling simulation using an interface tracking method: From nucleate boiling to film boiling regime through critical heat flux. Int. J. Heat Mass Transf. 2018, 125, 876–890. [Google Scholar] [CrossRef]
- Drew, D.A.; Passman, S.L. Theory of Multicomponent Fluids; Applied Mathematical Sciences; Springer: New York, NY, USA, 1999; Volume 135. [Google Scholar]
- Ishii, M. Thermo-Fluid Dynamic Theory of Two-Phase Flow; Eyrolles: Paris, France, 1975. [Google Scholar]
- Yeoh, G.H.; Tu, J. Modelling Subcooled Boiling Flows; Nova Science Publ: New York, NY, USA, 2009. [Google Scholar]
- Judd, R.L.; Hwang, K.S. A Comprehensive Model for Nucleate Pool Boiling Heat Transfer Including Microlayer Evaporation. J. Heat Transf. 1976, 98, 623. [Google Scholar] [CrossRef]
- Kurul, N.; Podowski, M.Z. Multidimensional effects in forced convection subcooled boiling. In Proceeding of the 9th International Heat Transfer Conference; Begellhouse: Redding, CT, USA, 1990; pp. 21–26. [Google Scholar] [CrossRef]
- Kurul, N.; Podowski, M.Z. On the modeling of multidimensional effects in boiling channels. In Proceeding of the 27th National Heat Transfer Conference; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1991. [Google Scholar]
- Tolubinsky, V.I.; Kostanchuk, D.M. Vapour bubbles growth rate and heat transfer intensity at subcooled water boiling. In Proceedings of the 4th International Heat Transfer Conference; Begellhouse: Redding, CT, USA, 1970; pp. 1–11. [Google Scholar] [CrossRef]
- Kocamustafaogullari, G. Pressure dependence of bubble departure diameter for water. Int. Commun. Heat Mass Transf. 1983, 10, 501–509. [Google Scholar] [CrossRef]
- Ünal, H.C. Maximum bubble diameter, maximum bubble-growth time and bubble-growth rate during the subcooled nucleate flow boiling of water up to 17.7 MN/m2. Int. J. Heat Mass Transf. 1976, 19, 643–649. [Google Scholar] [CrossRef]
- Klausner, J.F.; Mei, R.; Bernhard, D.M.; Zeng, L.Z. Vapor bubble departure in forced convection boiling. Int. J. Heat Mass Transf. 1993, 36, 651–662. [Google Scholar] [CrossRef]
- Zeng, L.Z.; Klausner, J.F.; Mei, R. A unified model for the prediction of bubble detachment diameters in boiling systems—I. Pool boiling. Int. J. Heat Mass Transf. 1993, 36, 2261–2270. [Google Scholar] [CrossRef]
- Zeng, L.Z.; Klausner, J.F.; Bernhard, D.M.; Mei, R. A unified model for the prediction of bubble detachment diameters in boiling systems—II. Flow boiling. Int. J. Heat Mass Transf. 1993, 36, 2271–2279. [Google Scholar] [CrossRef]
- Krepper, E.; Rzehak, R. CFD for subcooled flow boiling: Simulation of DEBORA experiments. Nucl. Eng. Des. 2011, 241, 3851–3866. [Google Scholar] [CrossRef]
- Colombo, M.; Fairweather, M. Prediction of bubble departure in forced convection boiling: A mechanistic model. Int. J. Heat Mass Transf. 2015, 85, 135–146. [Google Scholar] [CrossRef]
- Ding, W.; Krepper, E.; Hampel, U. Evaluation of the microlayer contribution to bubble growth in horizontal pool boiling with a mechanistic model that considers dynamic contact angle and base expansion. Int. J. Heat Fluid Flow 2018, 72, 274–287. [Google Scholar] [CrossRef]
- Ding, W.; Krepper, E.; Hampel, U. The Implementation of an Activated Temperature-Dependent Wall Boiling Model in an Eulerian-Eulerian Computational Fluid Dynamics Approach for Predicting the Wall Boiling Process. Nucl. Technol. 2018, 205, 23–32. [Google Scholar] [CrossRef]
- Krepper, E.; Ding, W. Review of Subcooled Boiling Flow Models. In Handbook of Multiphase Flow Science and Technology; Yeoh, G.H., Ed.; Springer Singapore: Singapore, 2017. [Google Scholar]
- Lifante, C.; Frank, T.; Burns, A. Wall boiling modeling extension towards critical heat flux. In Proceedings of the 15th International Topical Meeting on Nuclear Reactor Thermalhydraulics, Pisa, Italy, 12–17 May 2013. [Google Scholar]
- Bartolomej, G.G. An experimental investigation of true volumetric vapour content with subcooled boiling in tubes. Therm. Eng. 1982, 29, 132–135. [Google Scholar]
- Hoyer, N. Calculation of dryout and post-dryout heat transfer for tube geometry. Int. J. Multiph. Flow 1998, 24, 319–334. [Google Scholar] [CrossRef]
- Bruder, M.; Sattelmayer, T. An Empirical Correlation for the Void Fraction at Critical Heat Flux Close to the Wall for Subcooled Flow Boiling of a Low Boiling Refrigerant. Heat Mass Transf. Res. J. 2018, 2, 14–28. [Google Scholar]
- Ding, W.; Geißler, T.; Krepper, E.; Hampel, U. Critical heat flux as a mass flux dependent local or global phenomenon: Theoretical analysis and experimental confirmation. Int. J. Therm. Sci. 2018, 130, 200–207. [Google Scholar] [CrossRef]
- Krepper, E.; Lucas, D.; Prasser, H.M. On the modelling of bubbly flow in vertical pipes. Nucl. Eng. Des. 2005, 235, 597–611. [Google Scholar] [CrossRef]
- Krepper, E.; Rzehak, R.; Lifante, C.; Frank, T. CFD for subcooled flow boiling: Coupling wall boiling and population balance models. Nucl. Eng. Des. 2013, 255, 330–346. [Google Scholar] [CrossRef]
- Hänsch, S.; Lucas, D.; Krepper, E.; Höhne, T. A multi-field two-fluid concept for transitions between different scales of interfacial structures. Int. J. Multiph. Flow 2012, 47, 171–182. [Google Scholar] [CrossRef]
- Höhne, T.; Krepper, E.; Montoya, G.; Lucas, D. CFD-simulation of boiling in a heated pipe including flow pattern transitions using the GENTOP concept. Nucl. Eng. Des. 2017, 322, 165–176. [Google Scholar] [CrossRef]
- Gupta, A.; Saini, J.S.; Varma, H.K. Boiling heat transfer in small horizontal tube bundles at low cross-flow velocities. Int. J. Heat Mass Transf. 1995, 38, 599–605. [Google Scholar] [CrossRef]
- Yu, W.; France, D.M.; Wambsganss, M.W.; Hull, J.R. Two-phase pressure drop, boiling heat transfer, and critical heat flux to water in a small-diameter horizontal tube. Int. J. Multiph. Flow 2002, 28, 927–941. [Google Scholar] [CrossRef]
- Wojtan, L.; Ursenbacher, T.; Thome, J.R. Investigation of flow boiling in horizontal tubes: Part I—A new diabatic two-phase flow pattern map. Int. J. Heat Mass Transf. 2005, 48, 2955–2969. [Google Scholar] [CrossRef]
- Wojtan, L.; Ursenbacher, T.; Thome, J.R. Investigation of flow boiling in horizontal tubes: Part II—Development of a new heat transfer model for stratified-wavy, dryout and mist flow regimes. Int. J. Heat Mass Transf. 2005, 48, 2970–2985. [Google Scholar] [CrossRef]
- Wojtan, L.; Ursenbacher, T.; Thome, J.R. Measurement of dynamic void fractions in stratified types of flow. Exp. Therm. Fluid Sci. 2005, 29, 383–392. [Google Scholar] [CrossRef]
- Kundu, A.; Kumar, R.; Gupta, A. Flow boiling heat transfer characteristics of R407C inside a smooth tube with different tube inclinations. Int. J. Refrig. 2014, 45, 1–12. [Google Scholar] [CrossRef]
- Yadigaroglu, G. Two-phase flow instabilities and propagation phenomena. In Thermohydraulics of Two-Phase Systems for Industrial Design and Nuclear Engineering, A von Karman Inst. Book; Hemisphere Publishing Corporation; McGraw-Hill Book Company: Washington, DC, USA, 1978; Volume 2, pp. 353–403. [Google Scholar]
- Ledinegg, M. Unstabilität der Strömung bei natürlichem und Zwangumlauf. Die Wärme 1938, 8, 891–898. [Google Scholar]
- Daleas, R.S.; Bergles, A.E. Effects of upstream compressibility on subcooled critical heat flux. In Proceedings of the ASME/AIChE Conference on Heat Transfer and Exhibit, Los Angeles, CA, USA, 8–11 August 1965. [Google Scholar]
- Padki, M.M.; Palmer, K.; Kakaç, S.; Veziroǧlu, T.N. Bifurcation analysis of pressure-drop oscillations and the Ledinegg instability. Int. J. Heat Mass Transf. 1992, 35, 525–532. [Google Scholar] [CrossRef]
- Maulbetsch, J.; Griffith, P. A study of system-induced instabilities in forced convection flows with subcooled boiling. In Proceedings of the 3rd International Heat Transfer Conference; Begellhouse: Redding, CT, USA, 1966; pp. 247–257. [Google Scholar]
- Nayak, A.K.; Vijayan, P.K.; Saha, D.; Venkat Raj, V.; Aritomi, M. Linear Analysis of Thermo-hydraulic Instabilities of the Advanced Heavy Water Reactor (AHWR). J. Nucl. Sci. Technol. 1998, 35, 768–778. [Google Scholar] [CrossRef]
- Rao, Y.F.; Fukuda, K.; Kaneshima, R. Analytical study of coupled neutronic and thermodynamic instabilities in a boiling channel. Nucl. Eng. Des. 1995, 154, 133–144. [Google Scholar] [CrossRef]
- Ruspini, L.C.; Dorao, C.A.; Fernandino, M. Dynamic simulation of Ledinegg instability. J. Nat. Gas Sci. Eng. 2010, 2, 211–216. [Google Scholar] [CrossRef]
- Fuhrmann, H. Wärmeübertrager: Apparate und ihre Berechnung; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1987. [Google Scholar]
- Theofanous, T.G. The boiling crisis in nuclear reactor safety and performance. Int. J. Multiph. Flow 1980, 6, 69–95. [Google Scholar] [CrossRef]
- Kutateladze, S.S.; Leont’ev, A.I. Some applications of the asymptotic theory of the turbulent boundary layer. In Proceedings of the 3rd International Heat Transfer Conference; Begellhouse: Redding, CT, USA, 1966. [Google Scholar]
- Tong, L.S. Boundary-layer analysis of the flow boiling crisis. Int. J. Heat Mass Transf. 1968, 11, 1208–1211. [Google Scholar] [CrossRef]
- Kim, Y.I.; Baek, W.P.; Chang, S.H. Critical heat flux under flow oscillation of water at low-pressure, low-flow conditions. Nucl. Eng. Des. 1999, 193, 131–143. [Google Scholar] [CrossRef]
- Nikolayev, V.; Garrabos, Y.; Lecoutre, C.; Charignon, T.; Hitz, D.; Chatain, D.; Guillaument, R.; Marre, S.; Beysens, D. Boiling Crisis Dynamics: Low Gravity Experiments at High Pressure. Microgravity Sci. Technol. 2015, 27, 253–260. [Google Scholar] [CrossRef]
- Griffith, P.; Wallis, G.B. Two-Phase Slug Flow. J. Heat Transf. 1961, 83, 307. [Google Scholar] [CrossRef]
- Haberstroh, R.; Griffith, P. The Transition from the Annular to the Slug Flow Regime in Two-Phase Flow; Massachusetts Institute of Technology: Cambridge, MA, USA, 1964. [Google Scholar]
- Krussenberg, A.K.; Prasser, H.M.; Schaffrath, A. A new criterion for the identification of the bubble slug transition in vertical tubes. Kerntechnik 2000, 65, 7–13. [Google Scholar]
- Taitel, Y.; Bornea, D.; Dukler, A.E. Modelling flow pattern transitions for steady upward gas-liquid flow in vertical tubes. AIChE J. 1980, 26, 345–354. [Google Scholar] [CrossRef]
- Jeng, H.R.; Pan, C. Analysis of two-phase flow characteristics in a natural circulation loop using the drift-flux model taking flow pattern change and subcooled boiling into consideration. Ann. Nucl. Energy 1999, 26, 1227–1251. [Google Scholar] [CrossRef]
- Aritomi, M.; Chiang, J.H.; Mori, M. Geysering in parallel boiling channels. Nucl. Eng. Des. 1993, 141, 111–121. [Google Scholar] [CrossRef]
- Griffith, P. Geysering in Liquid-Filled Lines; ASME Paper, 62-HT-39; American Society of Mechanical Engineers: New York, NY, USA, 1962; pp. 1–13. [Google Scholar]
- Ozawa, M.; Nakanishi, S.; Ishigai, S.; Mizuta, Y.; Tarui, H. Flow Instabilities in Boiling Channels: Part 1 Pressure Drop Oscillation. Bull. JSME 1979, 22, 1113–1118. [Google Scholar] [CrossRef]
- Aritomi, M.; Nakahashi, T.; Chiang, J.H.; Mori, M.; Wataru, M. Transient behavior of natural circulation for boiling two-phase flow—Experimental results. In Proceedings of the 6th Proceedings of the Nuclear Thermal Hydraulics, American Nuclear Society Winter Meeting, Washington, DC, USA, 11–15 November 1990; pp. 313–320. [Google Scholar]
- Marcel, C.P. Experimental and Numerical Stability Investigations on Natural Circulation Boiling Water Reactors. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Cloppenborg, T.; Schuster, C.; Hurtado, A. Two-phase flow phenomena along an adiabatic riser—An experimental study at the test-facility GENEVA. Int. J. Multiph. Flow 2015, 72, 112–132. [Google Scholar] [CrossRef]
- Cloppenborg, T. Passive Wärmeabfuhr-Generische Untersuchungen zum thermohydraulischen Systemverhalten eines zweiphasigen Naturumlaufs. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2015. [Google Scholar]
- Bishop, A.A.; Sandberg, R.O.; Tong, L.S. Forced Convection Heat Transfer to Water at Near-Critical Temperatures and Supercritical Pressures; Westinghouse Electric Corp., Pittsburgh, Pa. Atomic Power Div; USAEC Report WCAP-2056-Part IIIB; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1964.
- Bergles, A.E.; Goldberg, P.; Maulbetsch, J.S. Acoustic oscillations in a high pressure single channel boiling system. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969; pp. 535–550. [Google Scholar]
- Davies, A.L. The speed of sound in mixtures of water and steam. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969; pp. 626–638. [Google Scholar]
- Davies, A.L.; Potter, R. Hydraulic stability: An analysis of the causes of unstable flow in parallel channels. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969; pp. 225–266. [Google Scholar]
- Ruspini, L.C. Experimental and Numerical Investigation on Two-Phase Flow Instabilities. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2013. [Google Scholar]
- Fukuda, K.; Kobori, T. Classification of Two-Phase Flow Instability by Density Wave Oscillation Model. J. Nucl. Sci. Technol. 1979, 16, 95–108. [Google Scholar] [CrossRef]
- Van Bragt, D. Analytical Modeling of Boiling Water Reactor Dynamics. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1998. [Google Scholar]
- Yadigaroglu, G.; Bergles, A.E. An Experimental and Theoretical Study of Wave Oscillations in Two-Phase Flow; MIT Engineering Projects Laboratory: Cambridge, UK, 1969. [Google Scholar]
- Yadigaroglu, G.; Bergles, A.E. Fundamental and Higher-Mode Density-Wave Oscillations in Two-Phase Flow. J. Heat Transf. 1972, 94, 189. [Google Scholar] [CrossRef]
- Achard, J.L.; Drew, D.A.; Lahey, R.T. The analysis of nonlinear density-wave oscillations in boiling channels. J. Fluid Mech. 1985, 155, 213. [Google Scholar] [CrossRef]
- Fukuda, K.; Kobori, T. Two-phase flow instability in parallel channels. In Proceedings of the 6th International Heat Transfer Conference; Begellhouse: Redding, CT, USA, 1978; pp. 369–374. [Google Scholar]
- Inada, F.; Furuya, M.; Yasuo, A. Thermo-hydraulic instability of boiling natural circulation loop induced by flashing (analytical consideration). Nucl. Eng. Des. 2000, 200, 187–199. [Google Scholar] [CrossRef]
- Schuster, C. Betriebsverhalten eines Kreislaufs mit Naturumlaufströmung. Kernenergie 1991, 34, 260–263. [Google Scholar]
- Schuster, C. Experimentelle Untersuchung des Betriebsverhaltens eines Kreislaufs mit ein- und zweiphasiger Naturumlaufströmung. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 1992. [Google Scholar]
- Schuster, C.; Knorr, J.; Ringel, H.; Prasser, H.M.; Zippe, W. Flashing induced two-phase flow at the natural circulation loop DANTON-Experimental investigations. In Proceedings of the 3rd European Thermal Sciences Conference, 10–13 September 2000; Hahne, E., Heidemann, W., Spindler, K., Eds.; Springer: Heidelberg, Germany, 2000; pp. 1065–1070. [Google Scholar]
- Furuya, M.; Manera, A.; van Bragt, D.; van der Hagen, T.H.J.J.; de Kruijf, W.J.M. Effect of Liquid Density Differences on Boiling Two-Phase Flow Stability. J. Nucl. Sci. Technol. 2002, 39, 1094–1098. [Google Scholar] [CrossRef]
- Manera, A. Experimental and Analytical Investigations on Flashing-Induced Instabilities in Natural Circulation Two-Phase Systems: Applications to the Startup of Boiling Water Reactors. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2003. [Google Scholar]
- Manera, A.; van der Hagen, T.H.J.J. Stability of natural-circulation-cooled boiling water reactors during startup: Experimental results. Nucl. Technol. 2003, 143, 77–88. [Google Scholar] [CrossRef]
- Kakac, S.; Veziroglu, T.N.; Akyuzlu, K.; Berkol, O. Sustained and transient boiling flow instabilities in a cross-connected four-parallel-channel upflow system. In Proceedings of the 5th International Heat Transfer Conference; Begellhouse: Redding, CT, USA, 1974; pp. 235–239. [Google Scholar]
- Berenson, P.J. Flow Stability in Multitube Forced-Convection Vaporizers; Air Force Aero Propulsion Laboratory, Research and Technology Division: Los Angeles, CA, USA, 1964. [Google Scholar]
- Aritomi, M.; Aoki, S.; Inoue, A. Thermo-hydraulic instabilities in parallel boiling channel systems. Nucl. Eng. Des. 1984, 95, 105–116. [Google Scholar] [CrossRef]
- Aritomi, M.; Chiang, J.H.; Nakahashi, T.; Wataru, M.; Mori, M. Fundamental Study on Thermo-Hydraulics during Start-Up in Natural Circulation Boiling Water Reactors, (I). J. Nucl. Sci. Technol. 1992, 29, 631–641. [Google Scholar] [CrossRef]
- Dijkman, F.J.; Tummers, J.F.; Spigt, C.L. The stability characteristics of a boiling system with natural and forced convection circulation. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969; pp. 307–323. [Google Scholar]
- Mathisen, R.P. Out of pile channel instability in the loop skalvan. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969; pp. 19–63. [Google Scholar]
- Schuster, C.; Ellinger, A.; Knorr, J. Analysis of flow instabilities at the natural circulation loop DANTON with regard to non-linear effects. Heat Mass Transf. 2000, 36, 557–565. [Google Scholar] [CrossRef]
- Bouré, J.A.; Mihaila, A. The oscillatory behavior of heated channels. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969. [Google Scholar]
- Wu, C.Y.; Wang, S.B.; Pan, C. Chaotic oscillations in a low pressure two-phase natural circulation loop under low power and high inlet subcooling conditions. Nucl. Eng. Des. 1996, 162, 223–232. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Yao, M.S.; Bo, J.H.; Wu, S.R. Experimental simulation study on start-up of the 5 MW nuclear heating reactor. Nucl. Eng. Des. 1995, 158, 111–123. [Google Scholar] [CrossRef]
- Kleiss, E.B. On the Determination of Boiling Water Reactor cHaracteristics by Noise Analysis. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1983. [Google Scholar]
- Stekelenburg, A.J.C. Statics and Dynamics of a Natural Ciculation Cooled Boiling Water Reactor. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1994. [Google Scholar]
- Van der Hagen, T. Stability Monitoring of a Natural-Circulation-Cooled Boilingwater Reactor. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1989. [Google Scholar]
- Inada, F.; Furuya, M.; Yasuo, A.; Tabata, H.; Yoshioka, Y.; Kim, H.T. Thermo-hydraulic instability of natural circulation BWRs at low pressure start-up: Experimental estimation of instability region with test facility considering scaling law. In 3rd International Conference on Nuclear Engineering; The American Society of Mechanical Engineers, Ed.; ASME: New York, NY, USA, 1995; Volume 1. [Google Scholar]
- Kok, H.V. Experiments on a Natural Circulation Loop, from Void-Fraction to Coupled Nuclear Thermal-Hydraulic Dynamics. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1998. [Google Scholar]
- Zboray, R. An Experimental and Modelling Study of Natural-Circulation Boiling Water Reactor Dynamics. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2002. [Google Scholar]
- Paladino, D.; Auban, O.; Huggenberger, M.; Dreier, J. A PANDA integral test on the effect of light gas on a Passive Containment Cooling System (PCCS). Nucl. Eng. Des. 2011, 241, 4551–4561. [Google Scholar] [CrossRef]
- Paladino, D.; Dreier, J. PANDA: A Multipurpose Integral Test Facility for LWR Safety Investigations. Sci. Technol. Nucl. Install. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Kuran, S.; Xu, Y.; Sun, X.; Cheng, L.; Yoon, H.J.; Revankar, S.T.; Ishii, M.; Wang, W. Startup transient simulation for natural circulation boiling water reactors in PUMA facility. Nucl. Eng. Des. 2006, 236, 2365–2375. [Google Scholar] [CrossRef]
- Jain, V.; Nayak, A.K.; Vijayan, P.K.; Saha, D.; Sinha, R.K. Experimental investigation on the flow instability behavior of a multi-channel boiling natural circulation loop at low-pressures. Exp. Therm. Fluid Sci. 2010, 34, 776–787. [Google Scholar] [CrossRef]
- Cloppenborg, T.; Schuster, C.; Hurtado, A. Generic Experimental Investigations of Thermohydraulic Instabilities With Void Fraction Measurement at Natural Circulation Test Facility Geneva. In 22nd International Conference on Nuclear Engineering; The American Society of Mechanical Engineers, Ed.; ASME: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Zuber, N. Flow Excursions and Oscillations in Boiling, Two-Phase Flow Systems with Heat Addition. In Proceedings of the Symposium on Two-Phase Flow Dynamics; Technological University of Eindhoven and EURATOM, Ed.; Commission of the European Communities: Brussels, Belgium, 1969; pp. 1071–1089. [Google Scholar]
- Uddin, R.; Dorning, J.J. Some nonlinear dynamics of a heated channel. Nucl. Eng. Des. 1986, 93, 1–14. [Google Scholar] [CrossRef]
- Clausse, A.; Lahey, R.T. The analysis of periodic and strange attractors during density-wave oscillations in boiling flows. Chaos Solitons Fractals 1991, 1, 167–178. [Google Scholar] [CrossRef]
- Pinheiro Rosa, M.; Podowski, M.Z. Nonlinear effects in two-phase flow dynamics. Nucl. Eng. Des. 1994, 146, 277–288. [Google Scholar] [CrossRef]
- Dokhane, A. BWR-Stability and Bifurcation Analysis Using a Novel Reduced Order Model and the System Code RAMONA. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2004. [Google Scholar]
- Hassard, B.D.; Kazarinoff, N.D.; Wan, Y.H. Theory and Applications of Hopf Bifurcation; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 1981; Volume 41. [Google Scholar]
- Lange, C.; Hennig, D.; Hurtado, A. An advanced reduced order model for BWR stability analysis. Prog. Nucl. Energy 2011, 53, 139–160. [Google Scholar] [CrossRef]
- Prill, P. A Non-Linear Reduced Order Methology Applicable to Boiling Water Reactor Stability Analysis. Ph.D. Thesis, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2013. [Google Scholar]
- Achard, J.L.; Drew, D.A.; Lahey, R. The effect of gravity and friction on the stability of boiling flow in a channel. Chem. Eng. Commun. 1981, 11, 59–79. [Google Scholar] [CrossRef]
- Saha, P.; Zuber, N. An analytical study of the thermally induced two-phase flow instabilities including the effect of thermal non-equilibrium. Int. J. Heat Mass Transf. 1978, 21, 415–426. [Google Scholar] [CrossRef]
- Furuya, M.; Inada, F.; Yasuo, A. A study on thermo-hydraulic instability of boiling natural circulation loop with a chimney. 2. Experimental approach to clarify the flow instability in detail. Trans. Jpn. Soc. Mech. Eng. Ser. B 1995, 27, 4074–4080. [Google Scholar] [CrossRef] [Green Version]
- Karve, A.A.; Uddin, R.; Dorning, J.J. Stability analysis of BWR nuclear-coupled thermal-hydraulics using a simple model. Nucl. Eng. Des. 1997, 177, 155–177. [Google Scholar] [CrossRef]
- Van Bragt, D.; de Kruijf, W.; Manera, A.; van der Hagen, T.; van Dam, H. Analytical modeling of flashing-induced instabilities in a natural circulation cooled boiling water reactor. Nucl. Eng. Des. 2002, 215, 87–98. [Google Scholar] [CrossRef]
- Karve, A.A. Nuclear-Coupled Thermal-Hydraulic Stability Analysis of Boiling Water Reactors. Ph.D. Thesis, University of Virginia, Charlottesville, VA, USA, 1998. [Google Scholar]
- Saha, P.; Ishii, M.; Zuber, N. An Experimental Investigation of the Thermally Induced Flow Oscillations in Two-Phase Systems. J. Heat Transf. 1976, 98, 616. [Google Scholar] [CrossRef]
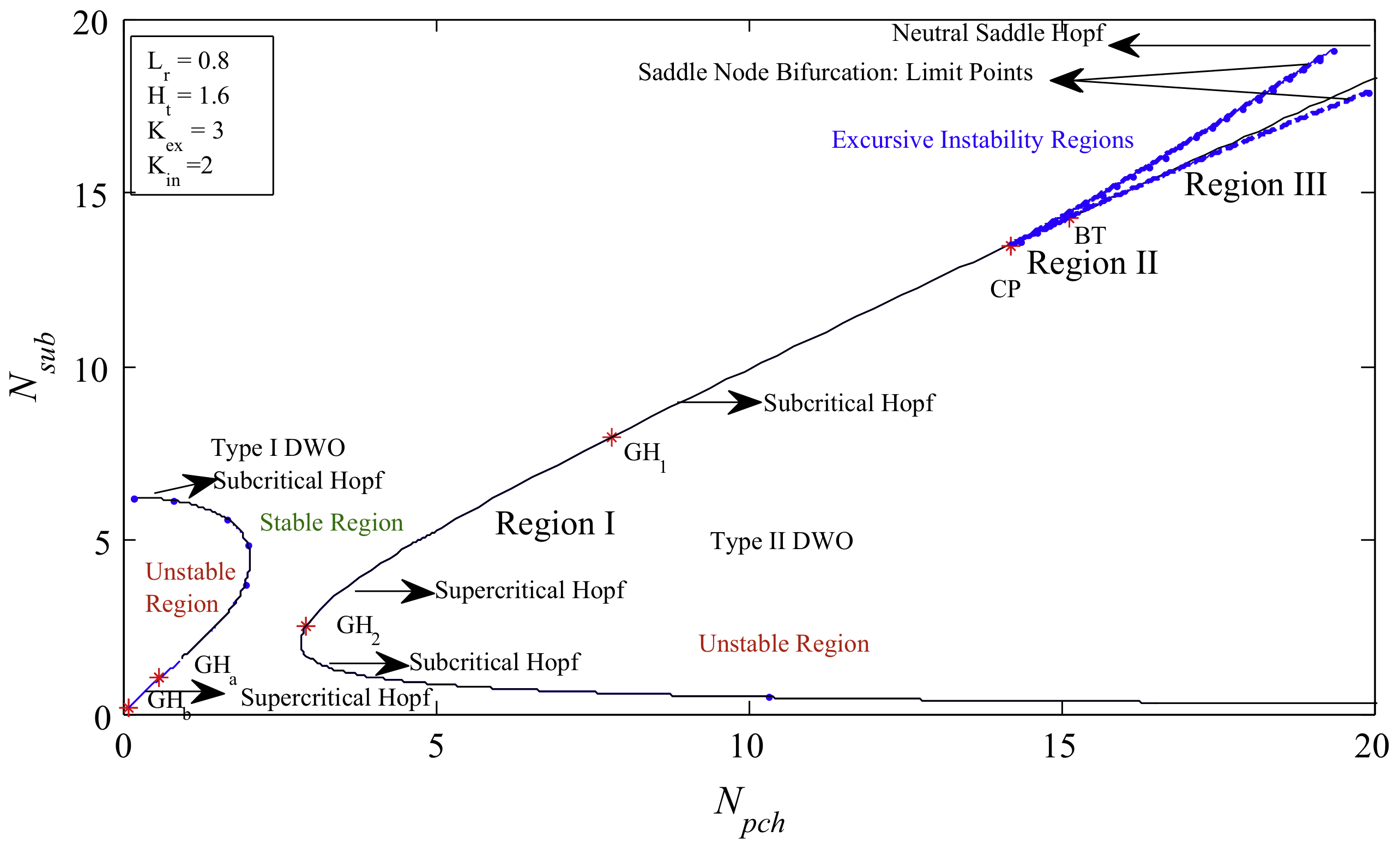
- Zhou, Q. Stability and Bifurcation Analyses of Reduced-Order Models of Forced and Natural Circulation BWRs. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign County, IL, USA, 2006. [Google Scholar]
- Lange, C. Advanced Nonlinear Stability Analysis of Boiling Water Nuclear Reactors. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2009. [Google Scholar]
- Solberg, K. Resultats des Essais de Instabilities sur la Boucle Culine et Comparison Avec Code de Calcul; Technical report; Centre d’Etudes Nucleaires de Grenoble: Grenoble, France, 1966. [Google Scholar]
- Paul, S.; Singh, S. Analysis of sub- and supercritical Hopf bifurcation with a reduced order model in natural circulation loop. Int. J. Heat Mass Transf. 2014, 77, 344–358. [Google Scholar] [CrossRef]
- Kumar, N.; Nayak, A.; Vijayan, P.; Saha, D. Experimental investigations on two-phase natural circulation in a closed rectangular loop. In Proceedings of the 2nd Japan-Korea Symposium on Nuclear Thermal Hydraulics and Safety, Atomic Energy Society of Japan, Tokyo (Japan), Korean Nuclear Society (KNS), Fukuoka, Japan, 15–18 October 2000; pp. 369–373. [Google Scholar]
- Pandey, V.; Singh, S. Characterization of stability limits of Ledinegg instability and density wave oscillations for two-phase flow in natural circulation loops. Chem. Eng. Sci. 2017, 168, 204–224. [Google Scholar] [CrossRef]
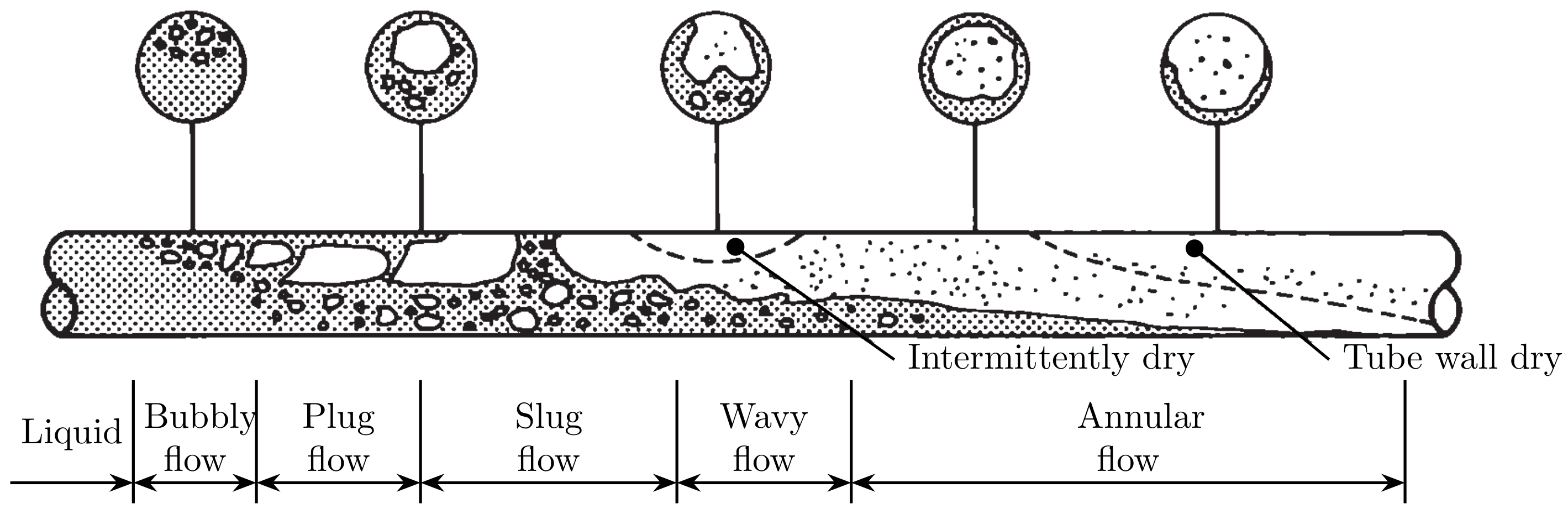

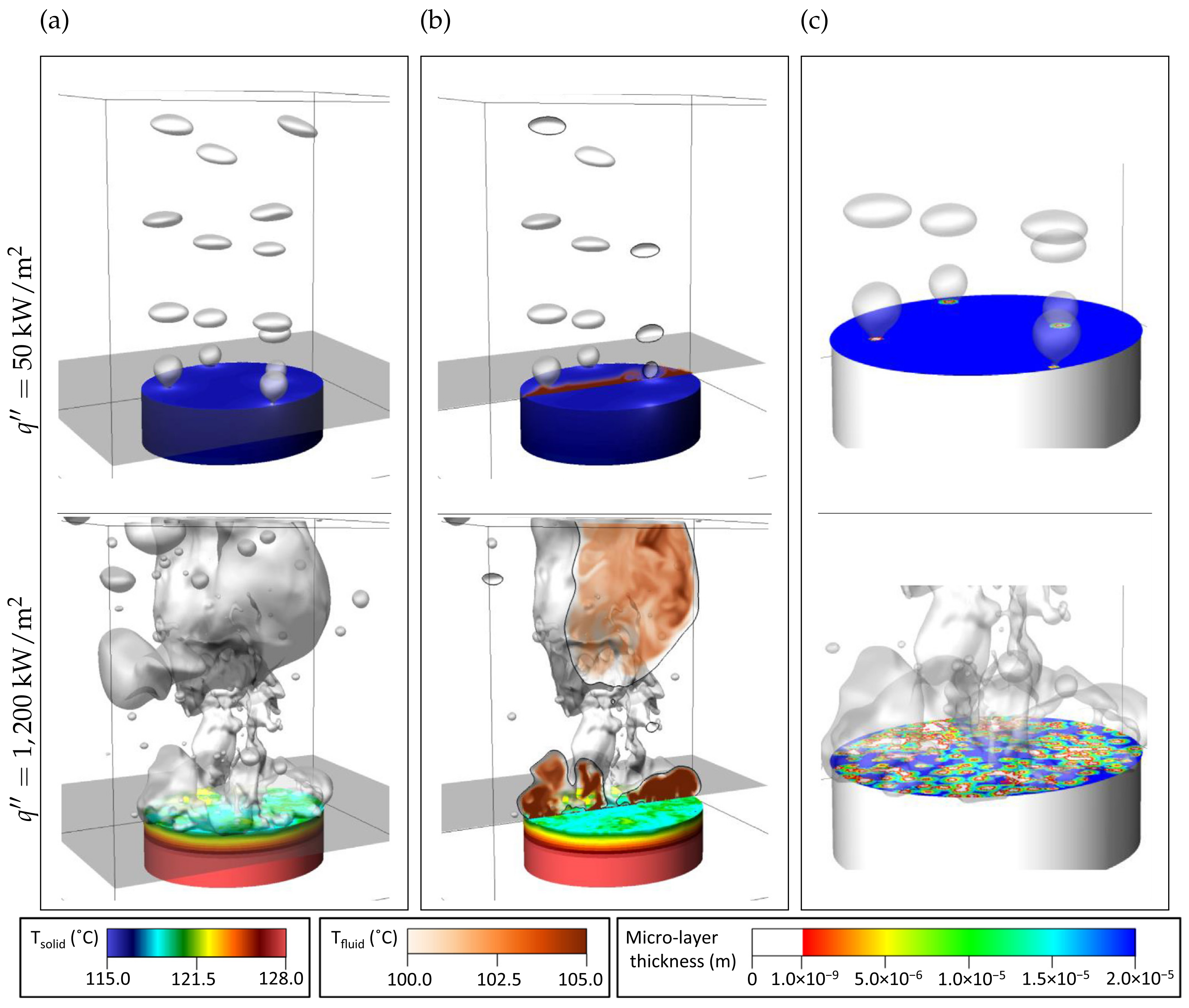
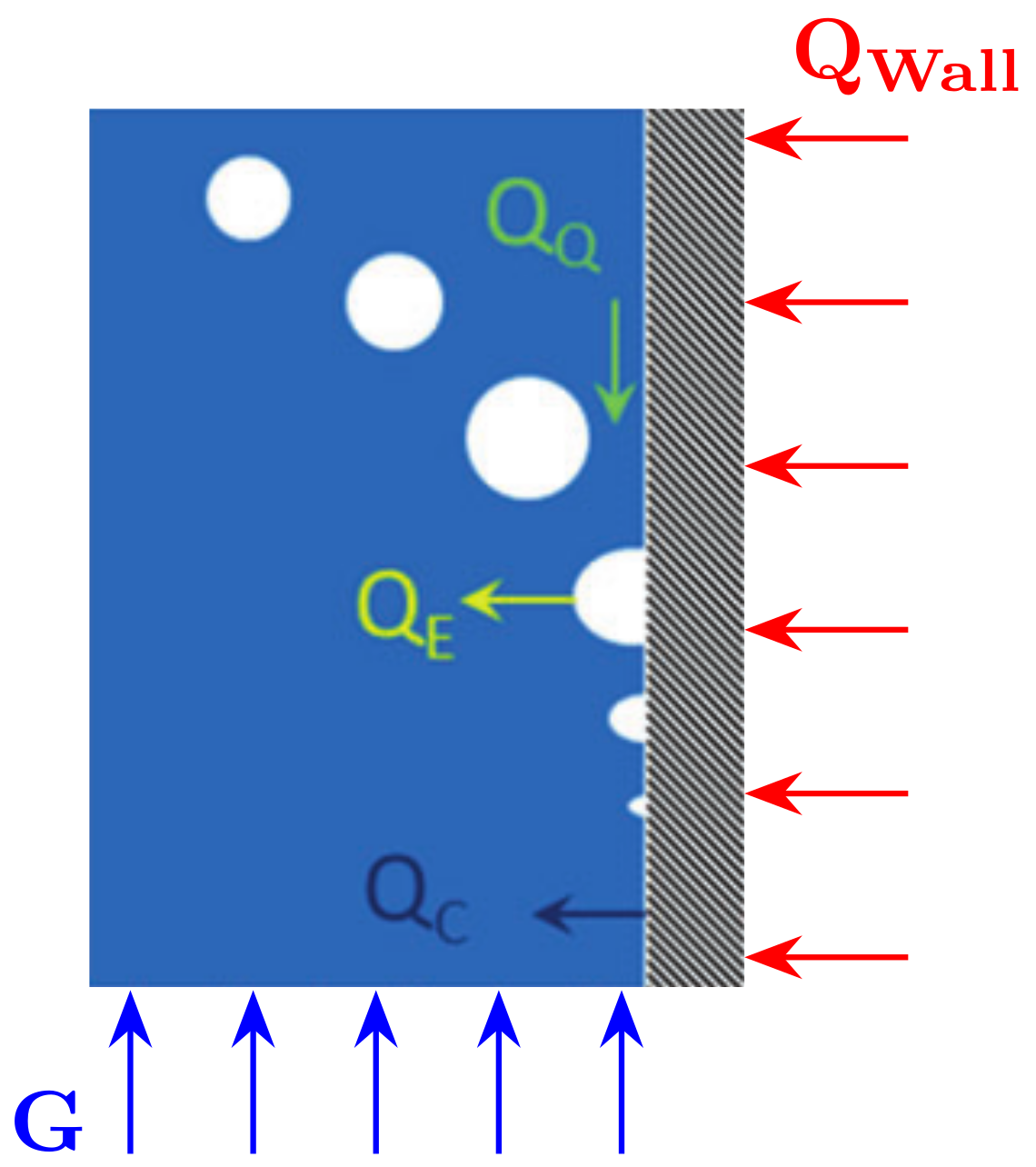
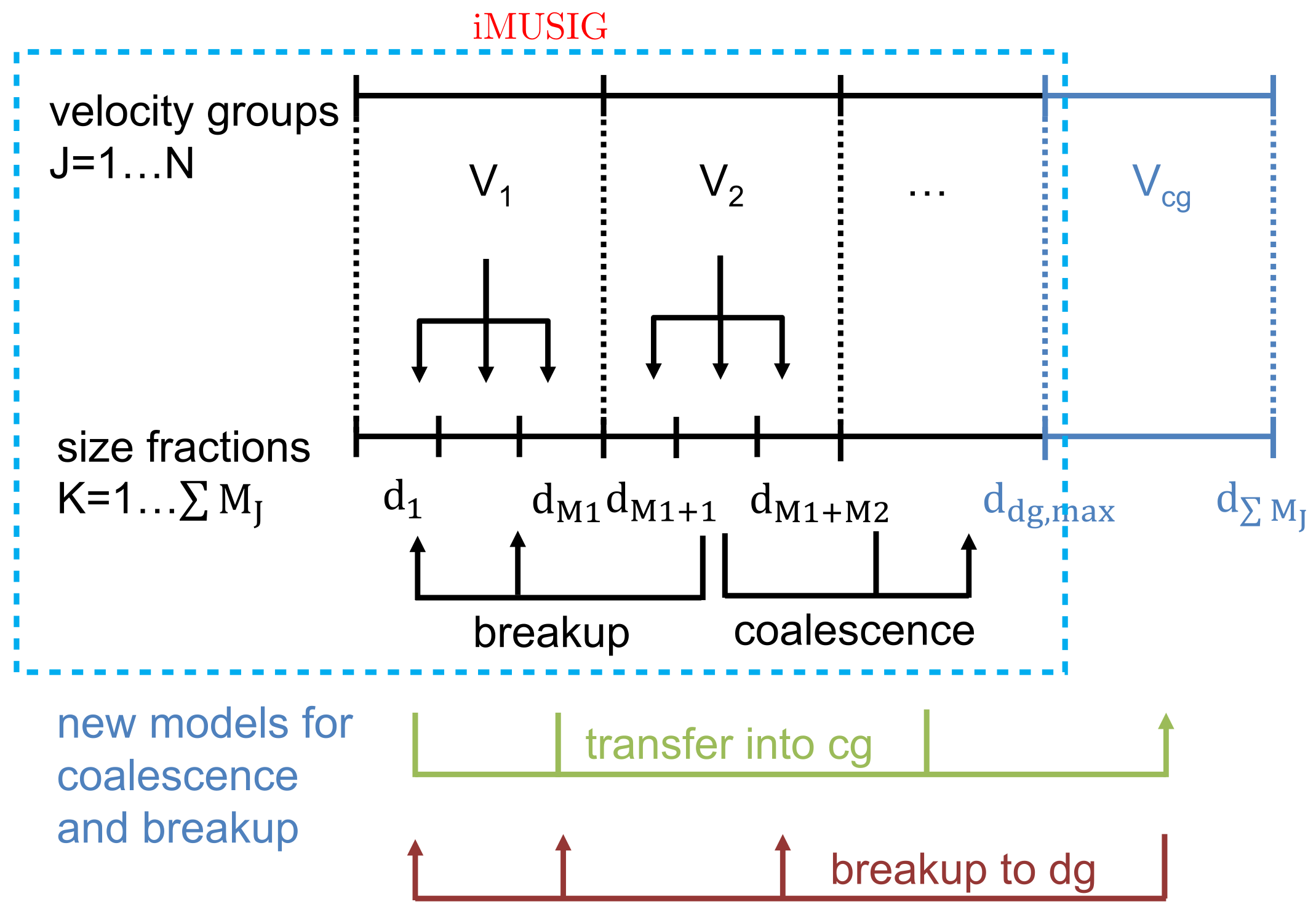
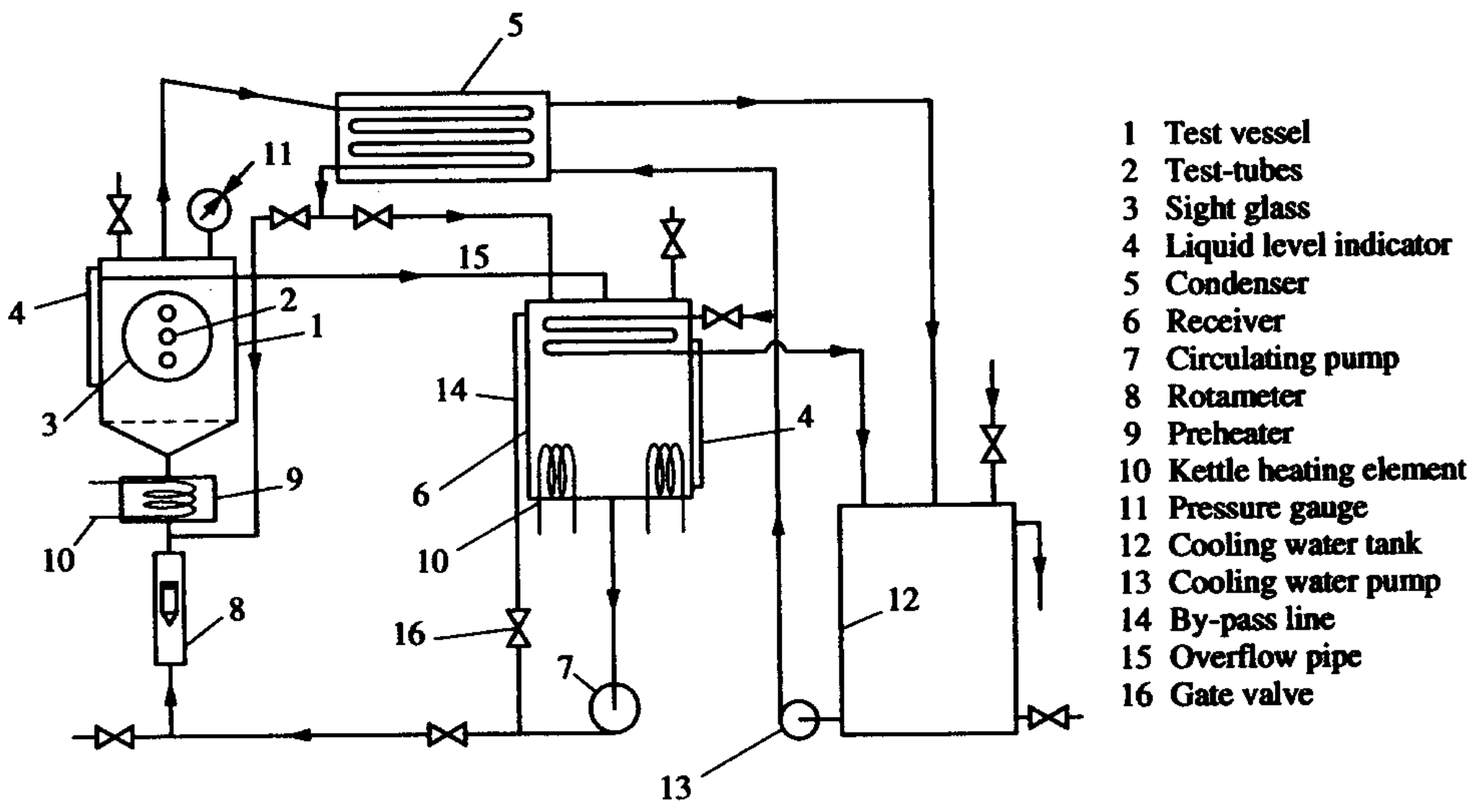
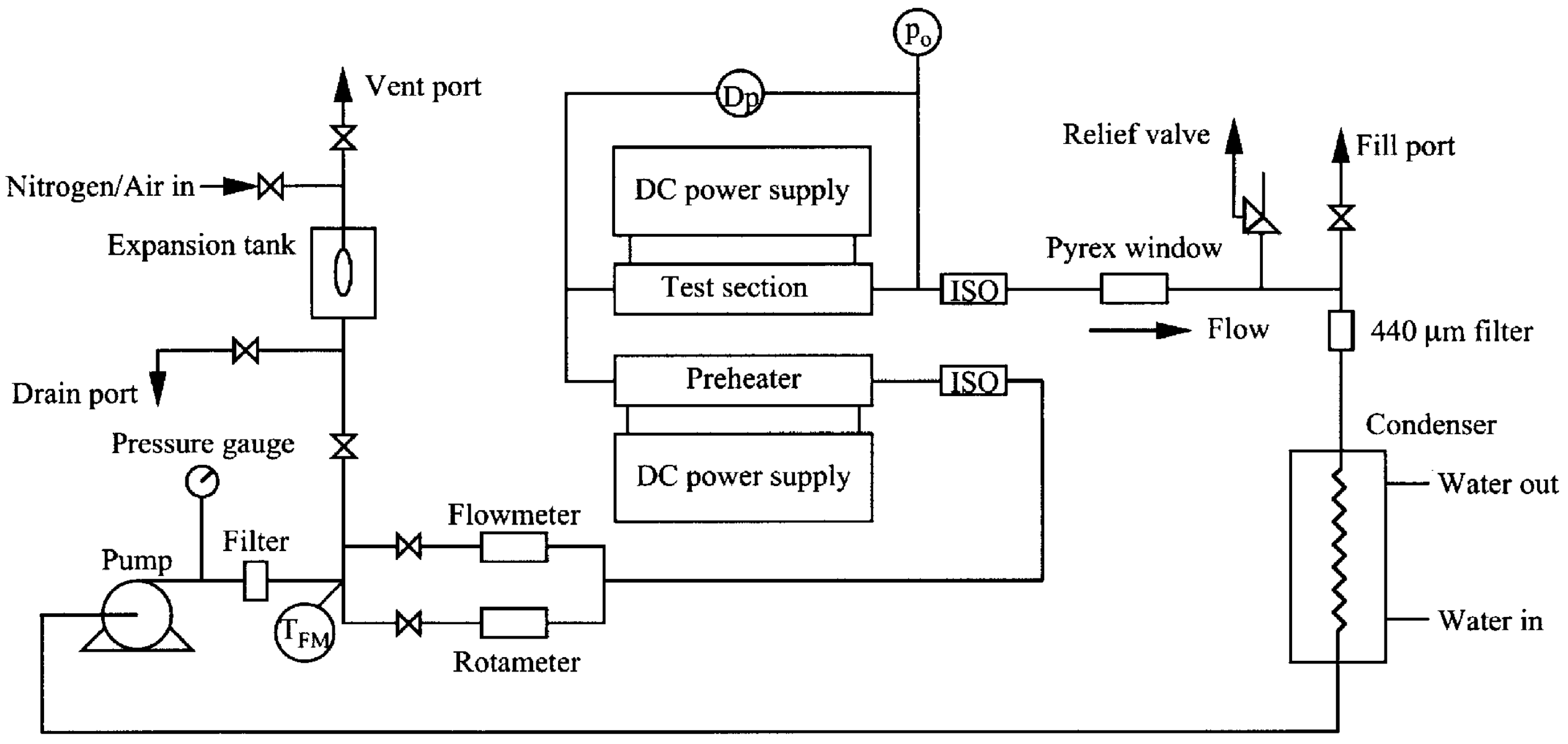
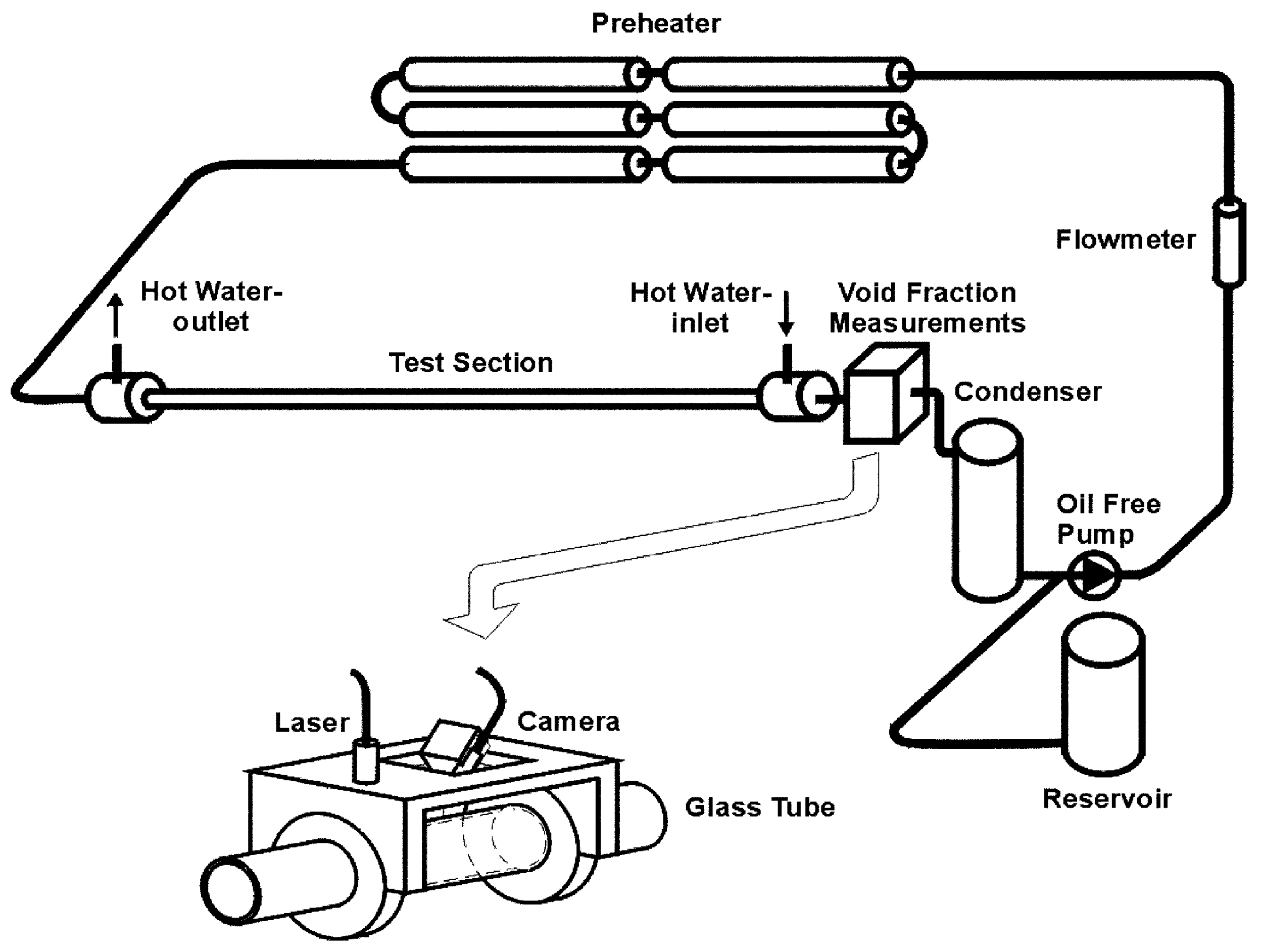


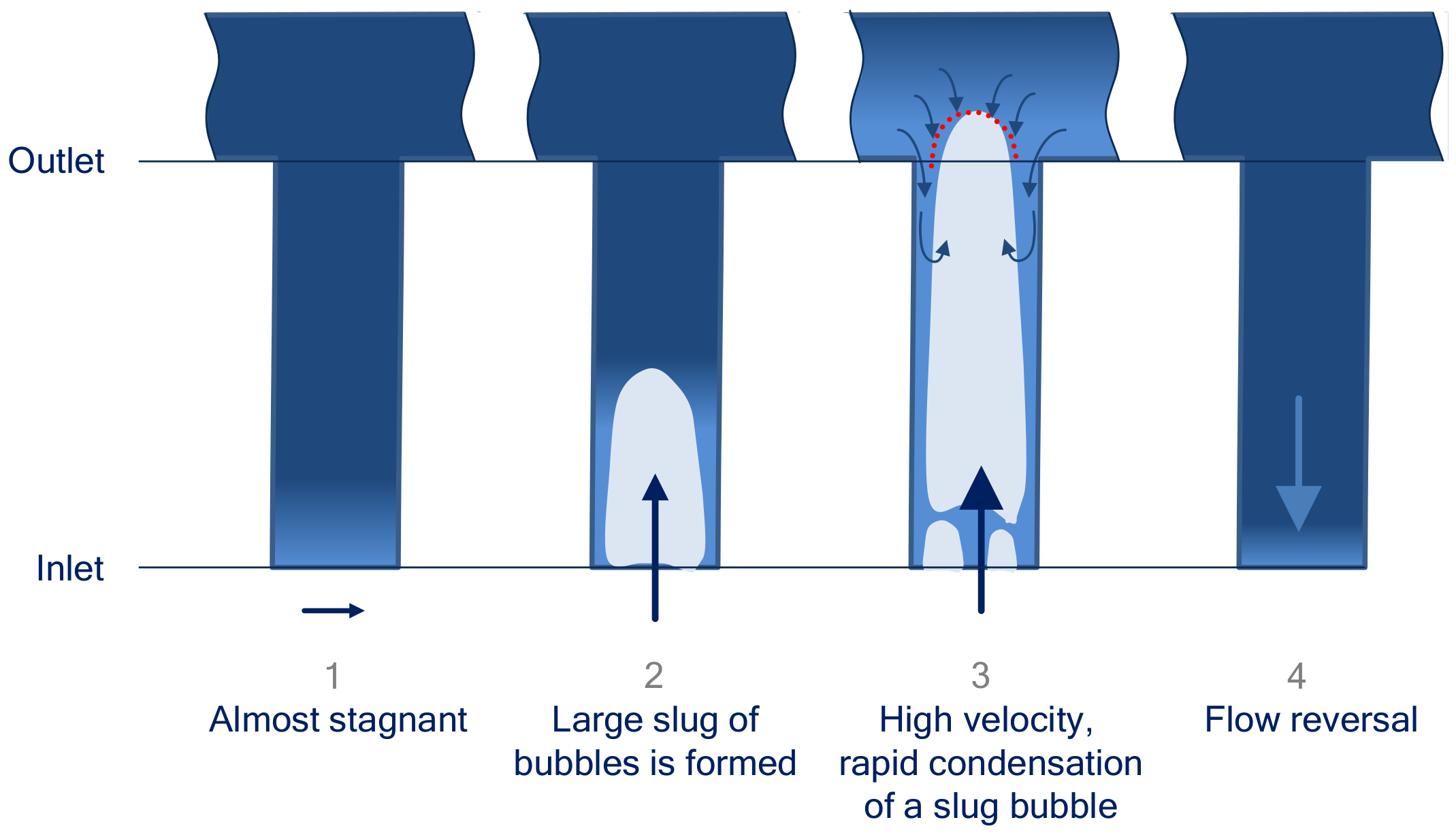
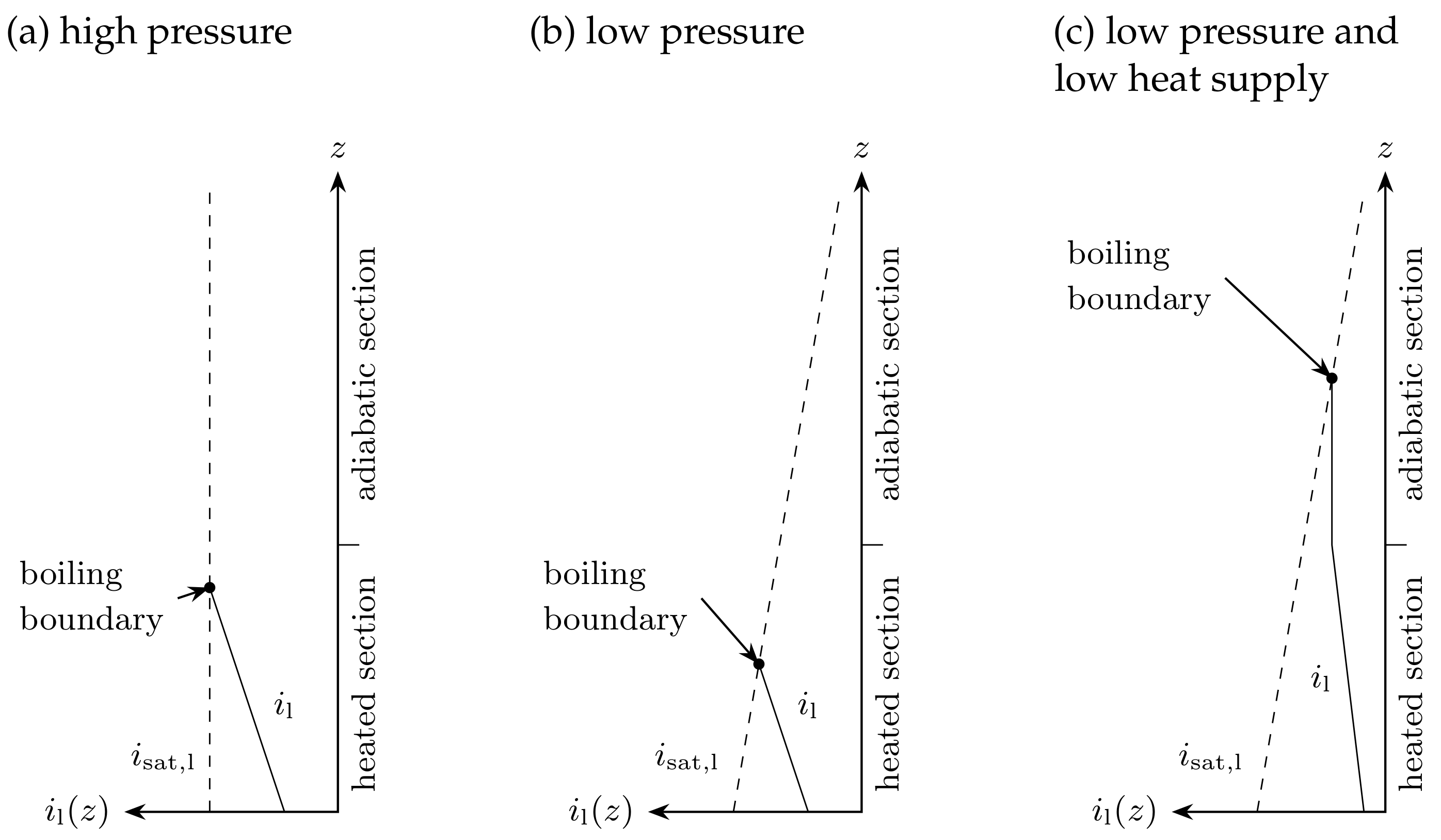

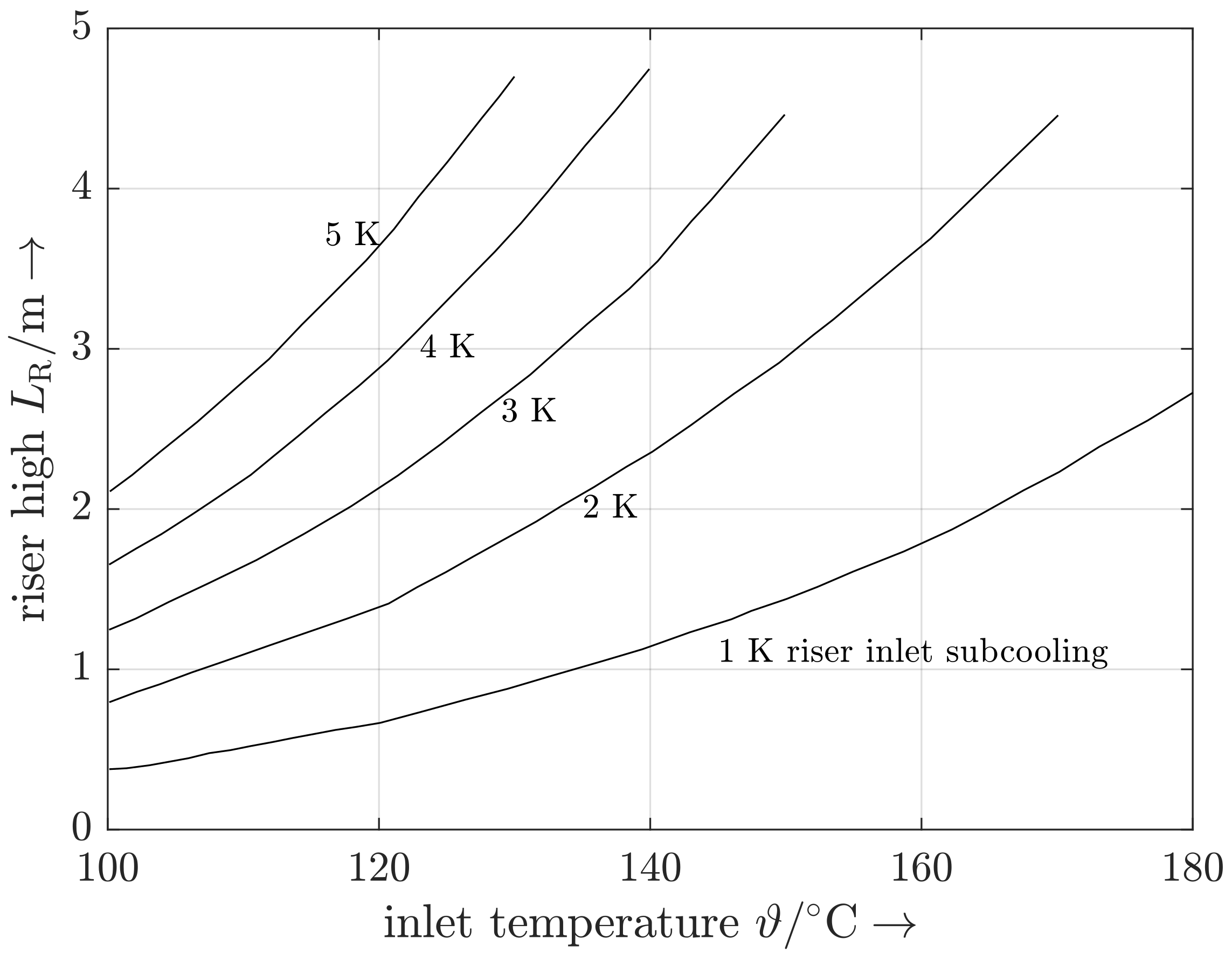
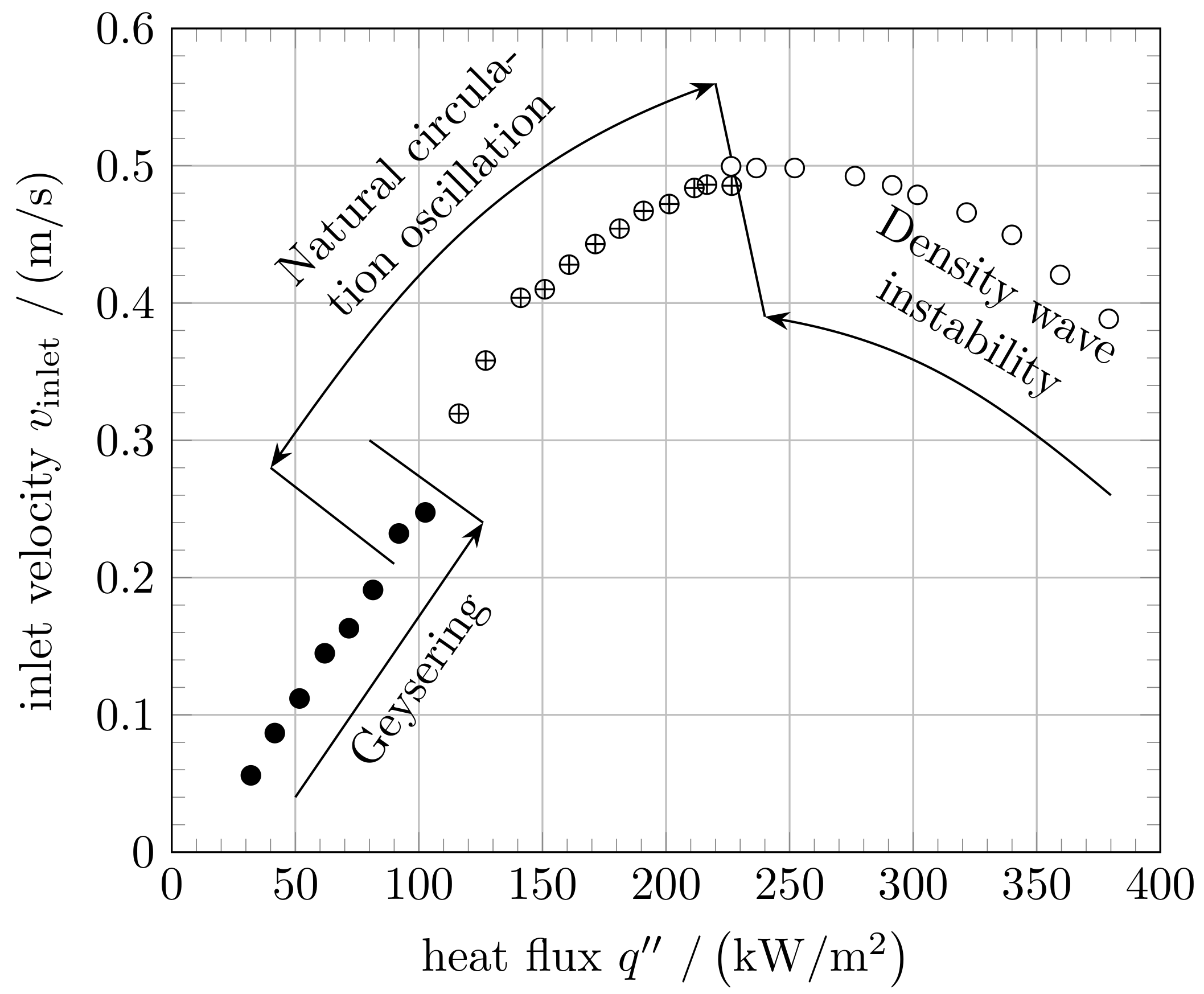
| Classification | Type | Mechanism | Characteristic |
|---|---|---|---|
| Fundamental static instabilities | Ledinegg instability | Sudden large change of flow parameters to a new stable operating point | |
| Boiling crisis | Ineffective removal of heat from heated surface | High wall temperatures and flow oscillations | |
| Fundamental relaxation instabilities | Flow pattern transition instability | Change from bubbly to annular flow | Cyclic flow pattern transition and flow oscillations |
| Compound relaxation instability | Geysering, bumping, chugging | Periodic adjustment of metastable conditions, caused of lack of nucleation sites | Periodic process of superheating and violent evaporation with possible expulsion and refilling |
| Classification | Type | Mechanism | Characteristic |
|---|---|---|---|
| Fundamental dynamic instabilities | Acoustic oscillations | Resonance of pressure waves | High frequencies (10 Hz to 100 Hz), related low amplitudes of flow oscillation |
| Density wave oscillations | Delay and feedback effects in relationship between flow rate, density and pressure drop | Low frequencies (≈1 Hz), large amplitudes of flow oscillations | |
| Compound dynamic instabilities | Thermal induced oscillations | Interaction of variable heat transfer coefficient with flow dynamic | Occurs in film boiling |
| BWR instabilities | Interaction of void reactivity coupling with flow dynamic and heat transfer | Strong only for a small fuel time constant and under low pressure | |
| Parallel channel instabilities | Interaction among small number of parallel channels | Various modes of flow redistribution | |
| Compound dynamic instability as secondary phenomena | Pressure drop oscillations | Flow excursion initiates dynamic interaction between channel and compressible volume | Very low frequency periodic process (≈0.1 Hz) |
| Test Facility | Geometric Characteristics | Operational Conditions | Authors and Findings |
|---|---|---|---|
| Dodewaard | Small BWR, 1.79 m fuel length, 164 fuel bundles | 183 MW thermal power, high pressure (7.5 MPa), 17.7 kW/m | Kleiss [128], Stekelenburg [129], van Bragt [106], van der Hagen [130]: DWOI, DWOII |
| DANTON | Vertical 3 m electrically heated section, 5.4 m adiabatic section | Low pressure (<2.5 MPa) | Schuster [113], variation of inlet flow resistance, flashing |
| SIRIUS-N | Vertical 1.7 m (2 channel) electrically heated section, 5.7 m chimney section | Low pressure (0.1 MPa to 0.5 MPa) | Inada et al. [131], Furuya et al. [5] |
| HRTL-5 | 0.58 m heated section height, 3 m riser length | Pressure <2 MPa, power | Jiang et al. [127]: geysering, flashing, DWOI |
| DESIRE (formerly SIDAS) | Scaled model of the Dodewaard natural circulation reactor. Freon-12 used as scaled liquid for 75 bar and 1.12 MW BWR, 35 electrically heated rods, 830 mm fuel length, riser length 1.1 m to 1.9 m | High pressure (because of scaling with Freon-12), 1.6 kW per rod, 8 bar to 13 bar | Kok [132], Zboray [133], Furuya et al. [115]: DWOII, supercritical Hopf bifurcation at the threshold of linear stability analysis, periodic-doubling bifurcation |
| PANDA | Large scale thermal hydraulic test facility for containment investigation, 1.3 m electrically heated section, 9.5 m riser length | 1.5 MW, Low pressure <10 bar | Auban et al. [4], Paladino et al. [134], Paladino and Dreier [135]: flashing, no limit-cycle oscillations |
| PUMA | Design to simulate transient behavior of LOCA for parallel electrically heated channels | Low pressure 1.03 MPa | Kuran et al. [136]: flashing |
| CIRCUS | Full-height scaled loop of Dodewaard, channels made of glass, 4 electrically heated fuel rods, 4 separate bypass channels, 3 m riser, fuel length 1.95 m | Low pressure (1 bar to 5 bar), 0 kW to 3 kW per rod | Manera [116], Manera and van der Hagen [117], Marcel [97]: flashing, DWOI |
| PCL | Based on BWR such as Indian AHWR, four parallel electrically heated channels with 0.8 m length, 2.8 m vertical riser | Pressure <20 bar, 200 kW (50 kW per channel) | Jain et al. [137]: DWOI and DWOII, PCI |
| GENEVA | Inclined 4 m (1–4 channel) steam heated section, vertical 6.5 m adiabatic section | Low pressure (1 atm at the top) | Cloppenborg et al. [98,99,138]: variation of number of channels, geysering, flashing |
| Author | Stability Anaylsis | Two-Phase Model | Notes |
|---|---|---|---|
| Zuber [139] | Linear | HEM | Discussion of the influence of the relative velocity, prediction of flow excursion, stability analysis in time domain |
| Ishii [7] | Linear by Mikhailov criterion (kind of Niquist) | DFM | Evaluation with experimental data |
| Achard et al. [147] | Linear, D-Partition method | HEM | Simplification of the model with subject of parallel channels, Prediction of the excursive instability for a zero-frequency limit |
| Achard et al. [109] | Linear and nonlinear | HEM |
|
| Uddin and Dorning [140] | Linear and nonlinear | HEM + DFM |
|
| Clausse and Lahey [141] | Nonlinear | HEM |
|
| Inada et al. [111] | Linear | DFM | |
| Karve et al. [150] | Linear and nonlinear | HEM | Model order reduction by weighted residual for enthalpy, eigenfunction expansion method/variational method for heat conduction
|
| van Bragt et al. [151] | Linear | HEM |
|
| Dokhane [143] | Linear and nonlinear | DFM | Complete BWR reduced order model: |
| Zhou [154] | Linear and nonlinear | HEM | Reduced order model for the natural circulation and the forced circulation BWR
|
| Lange [155] | Linear and nonlinear | DFM | BWR reduced order model with nuclear coupling
|
| Ruspini [104] | Linear | HEM | Numerical and experimental investigation of Ledinegg, PDO and DWO
|
| Prill [146] | Linear and nonlinear | HEM | Reduced order modeling by application of proper orthogonal decomposition
|
| Paul and Singh [157] | Linear and nonlinear | DFM | Nodalized reduced order model using weighted residual procedure for forced and natural circulation system, DWOI, DWOII
|
| Pandey and Singh [159] | Nonlinear | DFM | Based on the verified model of Paul and Singh [157]
|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manthey, R.; Viereckl, F.; Moonesi Shabestary, A.; Zhang, Y.; Ding, W.; Lucas, D.; Schuster, C.; Leyer, S.; Hurtado, A.; Hampel, U. Modelling of Passive Heat Removal Systems: A Review with Reference to the Framatome BWR Reactor KERENA: Part II. Energies 2020, 13, 109. https://doi.org/10.3390/en13010109
Manthey R, Viereckl F, Moonesi Shabestary A, Zhang Y, Ding W, Lucas D, Schuster C, Leyer S, Hurtado A, Hampel U. Modelling of Passive Heat Removal Systems: A Review with Reference to the Framatome BWR Reactor KERENA: Part II. Energies. 2020; 13(1):109. https://doi.org/10.3390/en13010109
Chicago/Turabian StyleManthey, René, Frances Viereckl, Amirhosein Moonesi Shabestary, Yu Zhang, Wei Ding, Dirk Lucas, Christoph Schuster, Stephan Leyer, Antonio Hurtado, and Uwe Hampel. 2020. "Modelling of Passive Heat Removal Systems: A Review with Reference to the Framatome BWR Reactor KERENA: Part II" Energies 13, no. 1: 109. https://doi.org/10.3390/en13010109
APA StyleManthey, R., Viereckl, F., Moonesi Shabestary, A., Zhang, Y., Ding, W., Lucas, D., Schuster, C., Leyer, S., Hurtado, A., & Hampel, U. (2020). Modelling of Passive Heat Removal Systems: A Review with Reference to the Framatome BWR Reactor KERENA: Part II. Energies, 13(1), 109. https://doi.org/10.3390/en13010109






