Stochastic Control for Intra-Region Probability Maximization of Multi-Machine Power Systems Based on the Quasi-Generalized Hamiltonian Theory

Abstract

With the penetration of renewable generation, electric vehicles and other random factors in power systems, the stochastic disturbances are increasing significantly, which are necessary to be handled for guarantying the security of systems. A novel stochastic optimal control strategy is proposed in this paper to reduce the impact of such stochastic continuous disturbances on power systems. The proposed method is effective in solving the problems caused by the stochastic continuous disturbances and has two significant advantages. First, a simplified and effective solution is proposed to analyze the system influenced by the stochastic disturbances. Second, a novel optimal control strategy is proposed in this paper to effectively reduce the impact of stochastic continuous disturbances. To be specific, a novel excitation controlled power systems model with stochastic disturbances is built in the quasi-generalized Hamiltonian form, which is further simplified into a lower-dimension model through the stochastic averaging method. Based on this Itô equation, a novel optimal control strategy to achieve the intra-region probability maximization is established for power systems by using the dynamic programming method. Finally, the intra-region probability increases in controlled systems, which confirms the effectiveness of the proposed control strategy. The proposed control method has advantages on controlling the fluctuation of system state variables within a desired region under the influence of stochastic disturbances, which means improving the security of stochastic systems. With more stochasticity in the future, the proposed control method based on the stochastic theory will play a novel way to relieve the impact of stochastic disturbances.

1. Introduction

There are many kinds of stochastic disturbances in the operation of power systems [1]. In the past decades, these random disturbances had less impact on the systems, because of their small intensity. However, recently, influenced by the renewable energy generation and electric vehicles, the impact of random factors on the power grid is increasing continuously [2,3].

More and more scholars are beginning to study the effects of these random disturbances [4,5,6,7,8,9,10,11,12,13]. Most of current research focuses on the power systems steady state. However, the dynamic security is also of concern as the power systems are dynamic systems. Although the intensity of most random excitation does not make systems unstable [14], the impact of the resulted fluctuations caused by random excitation needs to be considered. In this paper, the impact of stochastic disturbances is measured in the bounded fluctuation region, which is proposed in [2,3,15], and under this premise, the dynamic characteristics are further studied and controlled to reduce the fluctuation in the system. A novel method is applied in this paper as a supplement to the existing control methods. The proposed method has two significant advantages. First, a simplified and effective solution is proposed to analyze the system influenced by the stochastic disturbances. Second, a novel optimal control strategy is proposed in this paper to reduce the impact of stochastic continuous disturbances.

The disturbances are described by stochastic processes in this paper, and the states of power systems randomly fluctuate in this situation, which need to be analyzed and calculated by their statistical characteristics. The power systems model is a complex system, which makes it difficult to analyze analytically, especially after considering the uncertainties, so an appropriate simplification method is necessary. As we can see in references [16,17,18,19,20], the stochastic averaging method (SAM) put forward by Weiqiu can simplify the high-order stochastic system into a lower-order system, which will significantly reduce the power system dimensions and simplify the calculation. The power system transient energy function is selected as the system’s Hamiltonian function for applying the SAM, and the high-dimensional equations can be converted into low-dimensional diffusion equations based on this Hamiltonian function. According to references [1,3,15], by using the SAM, the calculation can be greatly simplified for analyzing power systems under stochastic disturbances, but the controller has not been considered in these references yet.

In the power systems, there are many new researches on the power systems control [21,22,23,24,25], but the influence of random factors was not considered. For a power system under the influence of stochastic factors, some analyses were done based on the stochastic averaging method [1,3,14,15,26,27], but the design of the controller was not involved. The stochastic power systems have multiple dimensions and strong nonlinearity, which is very difficult to control by using the traditional methods. Weiqiu’s researches [19,28,29,30,31,32,33] on the stochastic optimal control theory also have important guiding significance in this area. Based on the stochastic optimal control theory in these references, reference [34] considered the controller in a second-order model of the generator, and reference [35] studied an excitation controlled single-machine-infinity-bus (SMIB) power system. From the above references, it can be seen that the stochastic optimal control theory is a practical solution in the power system, and a more complex model can be further studied.

In this paper, an excitation controlled multi-machine power system model is introduced firstly, and the Gauss white noise is added into the model as the stochastic disturbances. By adopting the SAM, this stochastic system is simplified into a set of lower-dimension equations, which could greatly improve computational efficiency. According to the dynamic programming method, the intra-region probability maximization is selected as the control object to ensure systems security. Furthermore, a novel optimal control law (OCL) is built. The effectiveness is confirmed by the comparison between the intra-region probabilities of the system with and without control, and a Kolmogorov’s equation is adopted to achieve the analytical result of intra-region probability under OCL, and the analytical results fit well with the Monte Carlo results.

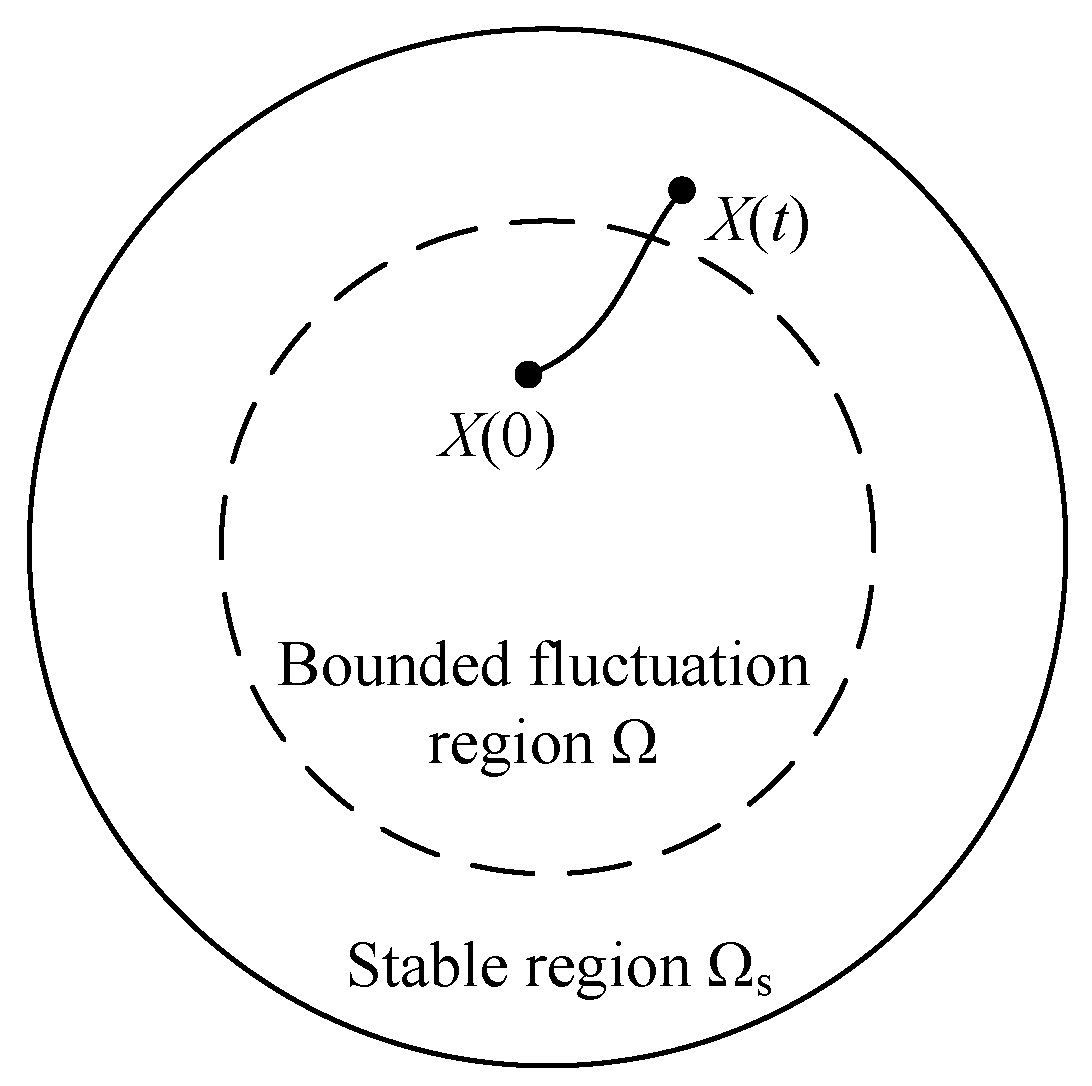
2. Intra-Region Probability and Transformation

2.1. Intra-Region Probability Definition

Assume that the initial state variable of the system is X(0), and it changes into X(t) at time t, as shown in Figure 1. If X(t) exceeds the stable region Ω_s, the system is unstable [36].

As the intensity of the stochastic disturbances generally does not make power systems unstable, whether the system states can be constrained in a smaller region Ω that can be tolerated by the actual systems is more meaningful, as shown as the dotted curve in Figure 1. This region is called bounded fluctuation region [15].

Because of the stochastic disturbances, X(t) becomes a stochastic process, and whether X(t) can remain in the Ω is a random event that should be expressed by probability, which is called intra-region probability [15].

2.2. Intra-Region Probability Transformation

The impact of stochastic disturbances is increasing continually with the development of the power systems, and a necessary control strategy is important to reduce the impact and to guarantee the systems security. In other words, it is to maximize the intra-region probability.

The bounded fluctuation region Ω of multi-machine systems is a hyperplane in a multidimensional space, which is hard to describe accurately. According to the power systems transient stability analysis method, there is correspondence between system state variables and system energy. In this paper, the correspondence between system state variables X(t) and system energy H is used to transfer the high-dimensional vector problem to a lower-dimensional energy problem [15]. As shown in Figure 2, assume that the initial value system transient energy function is H(0) = H₀, and it changes to H(t) at time t. H_max is the maximum energy within Ω, and H_cr is the critical energy. If X(t) is out of the Ω, H(t) will be greater than H_max.

3. SAM of Quasi-Generalized Hamiltonian Systems for Multi-Machine Power Systems

The multi-machine power systems model is too complex to analyze analytically, especially after considering stochastic disturbances. SAM is used in this paper to simplify the high-order system into a lower-order system.

The fundamental of SAM for quasi-generalized Hamiltonian systems is to average the fast-changing variables of systems, so as to obtain a simplified average equation for the system energy, which will reduce system dimensions and simplify the calculation.

First, whether the stochastic multi-machine power systems model has a Hamiltonian structure should be determined.

The model of excitation-controlled multi-machine systems is as follows [37]:

$$\begin{array}{c}\{\begin{array}{l}d{\delta }_i={\omega }_{\mathrm{N}}{\omega }_{i}dt\hfill \\ d{\omega }_i=\frac{1}{M_i}\left(P_{\mathrm{m}i}-D_i{\omega }_i-P_{\mathrm{e}i}\right)dt\hfill \\ d{E}_{\mathrm{q}i}^{\prime }=\frac{1}{T_{\mathrm{d}0i}^{\prime }}\left(-b_i{E}_{\mathrm{q}i}^{\prime }+c_i{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}+E_{\mathrm{fds}i}^{\prime }+u_{\mathrm{f}i}\right)dt\hfill \end{array}\\ i=1,\dots ,n\end{array}$$

(1)

and

$$\{\begin{array}{l}{P}_{\mathrm{e}i}=G_{ii}{E}_{\mathrm{q}i}^{\prime 2}-E_{\mathrm{q}i}^{\prime }{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\sin {\delta }_{ij}}\\ E_{\mathrm{fds}i}^{\prime }=b_i{E}_{\mathrm{q}is}^{\prime }-c_i{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j\mathrm{s}}^{\prime }{B}_{ij}\cos {\delta }_{ij\mathrm{s}}}\end{array}$$

(2)

where n is the number of generators, b_i:= 1 − (x_di − x^’_di)B_ii, c_i: = x_di − x^’_di, δ_ij: = δ_i − δ_j. ω_N is the synchronous speed; ω_i is the rotating speed of ith machine; δ_i and δ_j are respectively the rotor angle of ith and jth machines; M_i is the inertia coefficient of ith machine; P_mi is the mechanical power of ith machine; G_ii and B_ij are elements in the reduced admittance matrix; E^’_qi and E^’_qj are the q-axis transient voltage of the ith and jth machines, respectively; D_i is the damping coefficient of ith machine; T^’_d0i is the d-axis open-circuit transient time constant of ith machine; u_fi is the control variable of ith machine; x_di and x^’_di are respectively the d-axis reactance and d-axis transient reactance of ith machine; E^’_qis and E^’_qjs are respectively steady state value of E^’_qi and E^’_qj; and δ_ijs is the steady state value of δ_ij. The steady state (δ_is, ω_is, E^’_qis) of the system satisfies the following conditions:

$$\{\begin{array}{l}{\omega }_{i\mathrm{s}}=0\\ P_{\mathrm{m}i}=G_{ii}{E}_{\mathrm{q}i\mathrm{s}}^{\prime 2}-E_{\mathrm{q}i\mathrm{s}}^{\prime }{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j\mathrm{s}}^{\prime }{B}_{ij}\sin {\delta }_{ij\mathrm{s}}}\\ E_{\mathrm{fds}i}^{\prime }=b_i{E}_{\mathrm{q}i\mathrm{s}}^{\prime }-c_i{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j\mathrm{s}}^{\prime }{B}_{ij}\cos {\delta }_{ij\mathrm{s}}}\end{array}$$

where δ_ijs: = δ_is − δ_js.

The product of stochastic disturbances intensity σ_i and standard Gaussian white noise W_i(t) is added into the second formula in (1) as the stochastic disturbances, which is then expressed as follows:

$$\begin{array}{c}\{\begin{array}{l}d{\delta }_i={\omega }_{\mathrm{N}}{\omega }_{i}dt\hfill \\ d{\omega }_i=\frac{1}{M_i}\left(P_{\mathrm{m}i}-D_i{\omega }_i-P_{\mathrm{e}i}+{\sigma }_i{W}_i(t)\right)dt\hfill \\ d{E}_{\mathrm{q}i}^{\prime }=\frac{1}{T_{\mathrm{d}0i}^{\prime }}\left(-b_i{E}_{\mathrm{q}i}^{\prime }+c_i{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}+E_{\mathrm{fds}i}^{\prime }+u_{\mathrm{f}i}\right)dt\hfill \end{array}\\ i=1,\dots ,n\end{array}$$

(3)

Solving (3) requires a lot of computation because of its high-order and the stochastic disturbances, and SAM is used for solving this problem.

The derivative of Brownian motion A_i(t) is W_i(t), which is as follows:

$$d{A}_i(t)/dt=W_i(t).$$

(4)

Therefore, Equation (3) can be converted into the Itô stochastic differential equations (SDEs), which is as follows:

$$\begin{array}{c}\{\begin{array}{l}d{\delta }_i={\omega }_{\mathrm{N}}{\omega }_{i}dt\hfill \\ d{\omega }_i=\frac{1}{M_i}\left(P_{\mathrm{m}i}-D_i{\omega }_i-P_{\mathrm{e}i}\right)dt+\frac{{\sigma }_i}{M_i}d{A}_i\left(t\right)\hfill \\ d{E}_{\mathrm{q}i}^{\prime }=\frac{1}{T_{\mathrm{d}0i}^{\prime }}\left(-b_i{E}_{\mathrm{q}i}^{\prime }+c_i{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}+E_{\mathrm{fds}i}^{\prime }+u_{\mathrm{f}i}\right)dt\hfill \end{array}\\ i=1,\dots ,n\end{array}$$

(5)

The control variables u_fi in (5) are the stochastic optimal control variables, which will be further calculated in the following section. The stochastic optimal control is a supplement to the existing control methods.

Obviously, the Itô SDEs (5) is not a conservative system, which does not satisfy the conditions of a classic Hamiltonian system. However, it will be a quasi-generalized Hamiltonian system if coefficients D_i and σ_i are small [17]. The following part will establish the Hamiltonian structure.

The energy function of multi-machine power systems (1) is as follows [37]:

$$\begin{array}{ll}\hfill H=& \frac{1}{2}{\displaystyle \sum _{i=1}^n{M}_i{\omega }_{\mathrm{N}}{\omega }_i^2}+{\displaystyle \sum _{i=1}^n{P}_{\mathrm{m}i}^{\prime }\left({\delta }_{i\mathrm{s}}-{\delta }_i\right)}+\frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1,j\ne i}^n\left(E_{\mathrm{q}i\mathrm{s}}^{\prime }{E}_{\mathrm{q}j\mathrm{s}}^{\prime }{B}_{ij}\cos {\delta }_{ij\mathrm{s}}-E_{\mathrm{q}i}^{\prime }{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}\right)}}\hfill \\ \hfill & +{\displaystyle \sum _{i=1}^n\frac{b_i}{2c_i}{\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fds}i}^{\prime }\right)}^2}\hfill \end{array}$$

(6)

where

$$P_{mi}^{\prime }=E_{\mathrm{q}i\mathrm{s}}^{\prime }{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j\mathrm{s}}^{\prime }{B}_{ij}\sin {\delta }_{ij\mathrm{s}}}$$

$$E_{\mathrm{fds}i}^{\prime }=b_i{E}_{\mathrm{q}is}^{\prime }-c_i{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j\mathrm{s}}^{\prime }{B}_{ij}\cos {\delta }_{ij\mathrm{s}}}$$

The partial derivatives for each system state variables of the energy function shown in (6) are as follows:

$$\begin{array}{c}\{\begin{array}{l}\frac{\partial H}{\partial {\delta }_i}=-P_{\mathrm{m}i}^{\prime }+E_{\mathrm{q}i}^{\prime }{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\sin {\delta }_{ij}}\\ \frac{\partial H}{\partial {\omega }_i}=M_i{\omega }_{\mathrm{N}}{\omega }_i\\ \frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}=\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fds}i}^{\prime }\right)-{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}\end{array}\\ i=1,\dots ,n\end{array}$$

(7)

Substituting these partial derivatives in (7) into (5), Equation (5) can be rewritten, which is as shown in (8).

$$\begin{array}{c}\{\begin{array}{l}d{\delta }_i=\frac{1}{M_i}\frac{\partial H}{\partial {\omega }_i}dt\\ d{\omega }_i=\left(-\frac{1}{M_i}\frac{\partial H}{\partial {\delta }_i}-\frac{D_i}{M_i^2{\omega }_{\mathrm{N}}}\frac{\partial H}{\partial {\omega }_i}\right)dt+\frac{{\sigma }_i}{M_i}d{A}_i\left(t\right)\\ d{E}_{\mathrm{q}i}^{\prime }=-\frac{c_i}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}dt+\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}dt\end{array}\\ i=1,\dots ,n\end{array}$$

(8)

Equation (8) is the Itô stochastic differential function, and the matrix form of (8) is as shown in (9).

$${\dot{\mathit{x}}}_i=\left({\mathit{J}}_i-{\mathit{R}}_i\right)\partial H/\partial {\mathit{x}}_i+{\mathit{g}}_i{\mathit{u}}_{\mathrm{f}i},i=1,\dots ,n$$

(9)

and

$$\begin{gathered} {\mathit{x}}_i=\left[\begin{array}{c}{\delta }_i\\ {\omega }_i\\ E_{\mathrm{q}i}^{\prime }\end{array}\right], {\mathit{J}}_i=\left[\begin{array}{ccc}0& 1/M_i& 0\\ -1/M_i& 0& 0\\ 0& 0& 0\end{array}\right], \\ {\mathit{R}}_i=\left[\begin{array}{ccc}0& 0& 0\\ 0& D_i/\left(M_i^2{\omega }_i\right)& 0\\ 0& 0& c_i/T_{\mathrm{d}0i}^{\prime }\end{array}\right], {\mathit{g}}_i=\left[\begin{array}{c}0\\ 0\\ 1/T_{\mathrm{d}0i}^{\prime }\end{array}\right], \end{gathered}$$

where J_i is called the structural matrix, and J_i = −J_i^T, R_i ≥ 0, therefore, Equation (9) has the structure of a Hamiltonian system and energy function (6) can be regarded as the Hamiltonian function. Equation (9) is the quasi-generalized Hamiltonian equation for system (5) [37].

As mentioned above, there is no theoretical tool to calculate the stochastic system (9) analytically because of the stochasticity, so the SAM which is a powerful tool is used to simplify it.

Compared with the Hamiltonian systems, there is a special property of generalized Hamiltonian systems, which is called the Casimir function. When the structural matrix of the system is a singular matrix, where the rank of the structural matrix r is smaller than the system dimensions m, there are m-r independent Casimir functions, which are defined by [17]:

$${\displaystyle \sum _{j=1}^n{J}_{ij}\frac{\partial C_k}{\partial x_i}\frac{\partial F}{\partial x_j}}=0,k=1,\dots ,m-r$$

(10)

where J is the structural matrix of the system, C is the Casimir functions, and F is any function of x with continuous first-order derivatives.

Casimir functions are not unique in the system, and choosing the appropriate Casimir functions can help reduce the system dimensions and further study on the system stability.

In (9), J_i is a singular matrix, and the rank of J_i is 2. Therefore, there is one Casimir function for one generator. According to the J_i, if the Casimir function C_i(x) is the function of E^′_qi, Equation (10) is true. Therefore, the Casimir functions of system (5) can be chosen as:

$$C_i=\frac{b_i}{2c_i}{\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fds}i}^{\prime }\right)}^2,i=1,2,\dots ,n$$

(11)

Furthermore, the partial derivative of (11) is as follows:

$$\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}=\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fds}i}^{\prime }\right),i=1,2,\dots ,n$$

(12)

If there is no stochastic disturbance in (8), the full differential equations of the Hamiltonian and the Casimir function are as follows.

$$\{\begin{array}{l}dH={\displaystyle \sum _{i=1}^n\left(\frac{\partial H}{\partial {\delta }_i}d{\delta }_i+\frac{\partial H}{\partial {\omega }_i}d{\omega }_i+\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}d{E}_{\mathrm{q}i}^{\prime }\right)}\\ d{C}_i=\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}d{E}_{\mathrm{q}i}^{\prime },i=1,2,\dots ,n\end{array}$$

(13)

According to Itô lemma [38], when the stochastic excitations are considered into (8), the Wong-Zakai correction term 1/2 × (σ_i²/M_i²) × (∂²H/∂ω_i²) should be added to the first formula of (13). Then, Equation (13) can be rewritten by substituting (7) and (8) into (13), which is as shown in (14).

$$\{\begin{array}{ll}\hfill dH=& {\displaystyle \sum _{i=1}^n\left(-D_i{\omega }_{\mathrm{N}}{\omega }_i^2+\frac{{\sigma }_i^2{\omega }_{\mathrm{N}}}{2M_i}\right)}dt-{\displaystyle \sum _{i=1}^n\frac{c_i}{T_{\mathrm{d}0i}^{\prime }}{\left(\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)-{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}\right)}^2}dt\hfill \\ \hfill & +{\displaystyle \sum _{i=1}^n\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\left(\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)-{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}\right)}dt+{\displaystyle \sum _{i=1}^n{\sigma }_i{\omega }_{\mathrm{N}}{\omega }_i}d{A}_i\left(t\right)\hfill \\ \hfill d{C}_i=& -\frac{c_i}{T_{\mathrm{d}0i}^{\prime }}{\left(\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)\right)}^{2}dt-\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right){\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}dt\hfill \\ \hfill & +\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)dt\hfill \end{array},i=1,2,\dots ,n$$

(14)

Equation (14) is too complex to get an analytical result, so the SAM is adopted here to transform the system state variables into system energy. The averaging Itô functions are as shown in (15) and (16):

$$\{\begin{array}{l}dH=\left({\overline{m}}_H\left(H,\mathit{C}\right)+{\displaystyle \sum _{i=1}^n\langle \frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}\rangle }\right)dt+{\sigma }_{HH}\left(H,\mathit{C}\right)dA\left(t\right)\\ d{C}_i=\left({\overline{m}}_{C_i}\left(H,\mathit{C}\right)+\langle \frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}\rangle \right)dt,i=1,2,\dots ,n\end{array}$$

(15)

and

$$\{\begin{array}{l}\begin{array}{ll}\hfill {\overline{m}}_H\left(H,\mathit{C}\right)=& \frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}({\displaystyle \sum _{i=1}^n\left(-D_i{\omega }_{\mathrm{N}}{\omega }_i^2+\frac{{\sigma }_i^2{\omega }_{\mathrm{N}}}{2M_i}\right)}}\hfill \\ \hfill & -{\displaystyle \sum _{i=1}^n\frac{c_i}{T_{\mathrm{d}0i}^{\prime }}{\left(\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)-{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}\right)}^2}\hfill \\ \hfill & +\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\left(\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)-{\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}\right))/\left(M_1{\omega }_{\mathrm{N}}{\omega }_1\right)d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n\hfill \\ \hfill {\overline{m}}_{C_i}\left(H,\mathit{C}\right)=& \frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}(-\frac{c_i}{T_{\mathrm{d}0i}^{\prime }}{\left(\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right)\right)}^2}-\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right){\displaystyle \sum _{j=1,j\ne i}^n{E}_{\mathrm{q}j}^{\prime }{B}_{ij}\cos {\delta }_{ij}}\hfill \\ \hfill & +\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{b_i}{c_i}\left(E_{\mathrm{q}i}^{\prime }-\frac{1}{b_i}{E}_{\mathrm{fdsi}}^{\prime }\right))/\left(M_1{\omega }_{\mathrm{N}}{\omega }_1\right)d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n\hfill \end{array}\\ {\sigma }_{HH}^2\left(H,\mathit{C}\right)=\frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}{\displaystyle \sum _{i=1}^n{\left({\sigma }_i{\omega }_{\mathrm{N}}{\omega }_i\right)}^2}/\left(M_1{\omega }_{\mathrm{N}}{\omega }_1\right)}d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n\\ {\displaystyle \sum _{i=1}^n\langle \frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}\rangle }=\frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}{\displaystyle \sum _{i=1}^n\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}}/\left(M_1{\omega }_{\mathrm{N}}{\omega }_1\right)}d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n\\ \langle \frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}\rangle =\frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}/\left(M_1{\omega }_{\mathrm{N}}{\omega }_1\right)}d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n\\ T\left(H,\mathit{C}\right)={\displaystyle {\int }_{\mathsf{\Omega }}1/\left(M_1{\omega }_{\mathrm{N}}{\omega }_1\right)d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n}\\ \mathsf{\Omega }=\left\{\left({\omega }_2,\dots {\omega }_n,{\delta }_1,\dots {\delta }_n\right)|H\left(0,{\omega }_2,\dots {\omega }_n,{\delta }_1,\dots {\delta }_n,C_1,\dots C_n\right)<H,C_i\left(E_{\mathrm{q}1}^{\prime },\dots E_{\mathrm{q}n}^{\prime }\right)<C_i\right\}\end{array}$$

(16)

where H ∈ [0, H_max] and C_i ∈ [0, C_imax], H_max is the energy maximum of the bounded fluctuation area, and C_imax is the maximum of Casimir function. Actually, H and C_i in (15) are diffusion processes, in which m_H(H, C) and m_Ci(H, C) are drift coefficients and σ_HH(H, C) is diffusion coefficient. The selection of the Ω is very important to calculate those coefficients, which will influence the final effect of the control strategy. H_max is selected as described in Section 2, and C_imax is the maximum value of Casimir function when H ∈ [0, H_max].

Equation (15) is function of H and C_i, and the order of the averaging Itô functions (15) is n + 1, and the order of (3) is 3n. Obviously, the dimension is reduced after using the SAM, which means this method could simplify the system model.

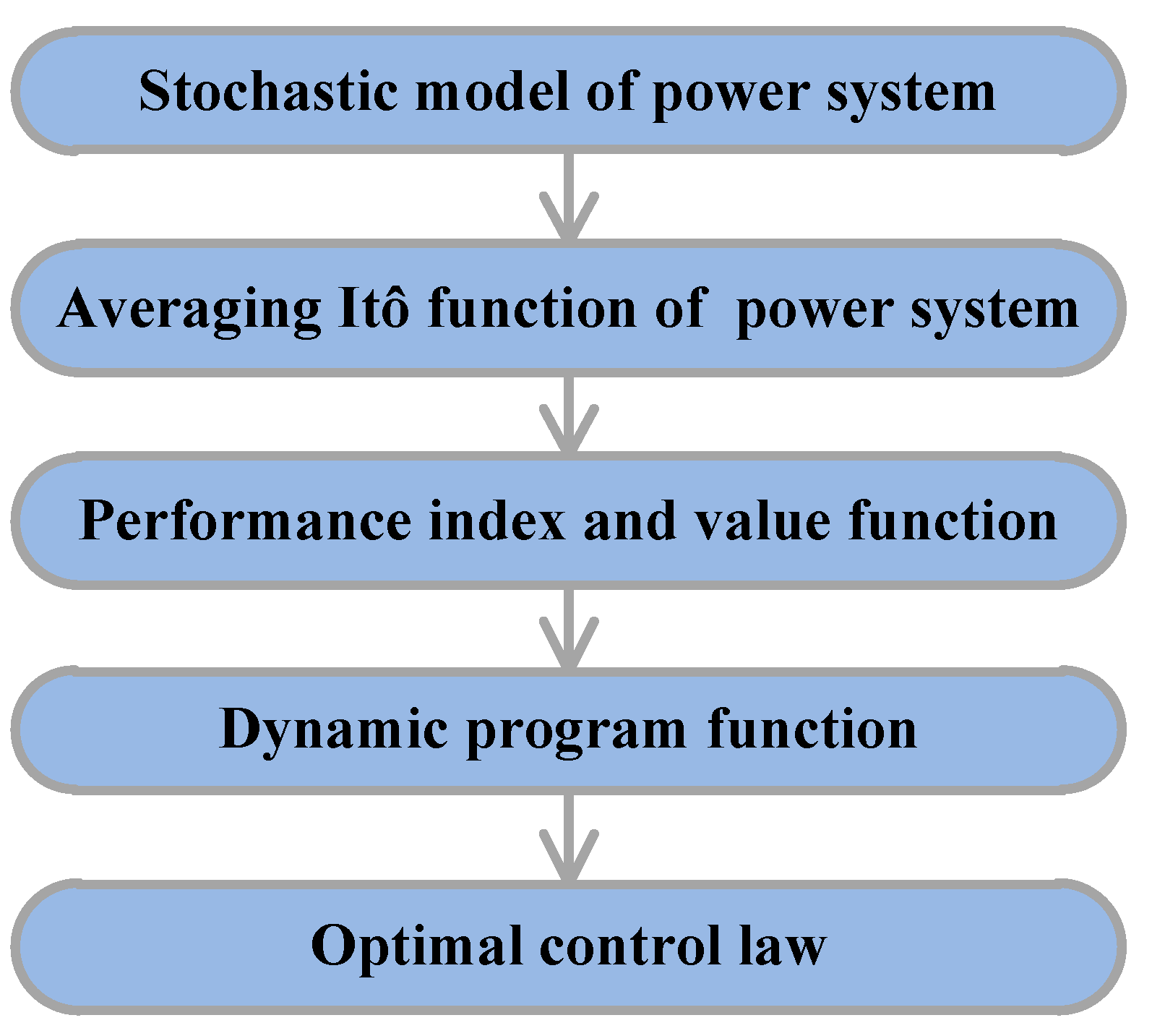
4. Stochastic Optimal Control for Maximizing Intra-Region Probability

The stochastic optimal control theory is a powerful tool to provide control strategies for the stochastic systems, and it is adopted here to obtain the control strategies for the stochastic power system described by the averaging Itô function (15).

4.1. Procedure of the Stochastic Optimal Control

A specific stochastic optimal control problem is determined by the stochastic model of controlled system, constraints on control, performance index and the time interval of control.

The procedure of stochastic optimal control on power system is shown in Figure 3.

As shown in Figure 3, the stochastic model of controlled power system is introduced in Section 3, and the rest of stochastic optimal control method will be introduced in the following parts.

4.2. Performance Index

Usually, the control objective is to achieve an extremum value of the optimization function. The optimization function is called as the performance index in this paper, and it is also known as the cost function in the optimization field [18]. Due to the stochastic disturbance, the system states variables and system energy are changed into stochastic processes, so it is not appropriate to use the same performance index used in the deterministic analysis. The intra-region probability is selected as performance index in this paper, which is as shown in (17), and the goal of control is to maximize it.

$$J\left(\mathit{u}\right):=P\left(\mathit{X}\left(t\right)\in \mathsf{\Omega },t_0\le t\le t_{\mathrm{f}}\right)$$

(17)

where u is the control law, X is the system variables vector, t₀ and t_f are the beginning and termination time of the control, respectively. The symbol P means the probability.

According to the analysis in Section 2, the analysis of state variables can be transferred into the system energy. Therefore, the performance index related to the system energy is as shown in (18).

$$J\left({\mathit{u}}_{\mathrm{f}}\right):=P\left\{\begin{array}{l}H\left(s,{\mathit{u}}_{\mathrm{f}}\right)\in \left[0,H_{\max }\right),\\ C_i\left(s,u_{\mathrm{f}i}\right)\in \left[0,C_{i\max }\right),\\ t_0<s\le t_{\mathrm{f}}\end{array}\right\},i=1,2,\dots ,n$$

(18)

where H_max is the energy maximum of the bounded fluctuation area, and C_imax is the maximum of Casimir function. u_f is the control law, and t₀ and t_f are the beginning and termination time of the control, respectively.

4.3. Stochastic Dynamic Programming Method

There are two solutions for stochastic optimal control problems. One is Pontryagin’s extremum principle based on the variational method, and another one is the dynamic programming method based on Bellman’s equation [18]. The second method can give solutions of the original problem with different initial times and states, which is more practical for the research on power systems than the first one, so the second method is used in this paper.

In the dynamic programming method [18], the value function is an important tool. According to the performance index shown in (18), the value function is further deduced as follows:

$$\begin{array}{l}V\left(H,\mathit{C},t\right)=\\ \underset{u\in U}{\sup }P\{H\left(s,{\mathit{u}}_{\mathrm{f}}\right)\in \left[0,H_{\max }\right),C_i\left(s,u_{\mathrm{f}i}\right)\in \left[0,C_{i\max }\right),t_0<s\le t_{\mathrm{f}}|H\left(t_0,{\mathit{u}}_{\mathrm{f}}\right)\in \left[0,H_{\max }\right),C_i\left(t_0,u_{\mathrm{f}i}\right)\in \left[0,C_{i\max }\right)\}\\ i=1,2,\dots ,n\end{array}$$

(19)

The dynamic programming equation based on the value function (19) can be further established as follows:

$$\frac{\partial V}{\partial t}=-\underset{u\in U}{\sup }(\frac{1}{2}{\sigma }_{HH}^2\left(H,\mathit{C}\right)\frac{{\partial }^{2}V}{\partial H^2}+\left[{\overline{m}}_H\left(H,\mathit{C}\right)+{\displaystyle \sum _{i=1}^n\langle \frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}\rangle }\right]\frac{\partial V}{\partial H}+{\displaystyle \sum _{i=1}^n\left[{\overline{m}}_{C_i}\left(H,\mathit{C}\right)+\langle \frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}\rangle \right]\frac{\partial V}{\partial C_i}})$$

(20)

where the corresponding boundary conditions are

$$\begin{gathered} V\left(H_{\max },\mathit{C},t\right)=0, V\left(H,{\mathit{C}}_{\max },t\right)=0, \\ V\left(0,\mathit{C},t\right)=\mathrm{finite}, V\left(H,0,t\right)=\mathrm{finite}, \end{gathered}$$

and the final condition is

$$V\left(H,\mathit{C},t_f\right)=1,H\in \left[0,H_{\max }\right),\mathit{C}\in \left[0,{\mathit{C}}_{\max }\right).$$

When the left side of (20) can achieve the minimum value, the OCL is obtained.

Practically, the control constraints should be considered. In this paper, constraints of the control signal being in the reasonable region which systems can be tolerated are used. The control constraints are taken as |u_fi/T^′_d0i| ≤ K_i. Equation (20) is difficult to be calculated directly, but when |u_fi/T^′_d0i| = K_i and the value of u_fi/T^′_d0i makes (21) positive, the left side of (20) can obtain the minimum value.

$$\frac{u_{\mathrm{f}i}}{T_{\mathrm{d}0i}^{\prime }}\left(\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}\frac{\partial V}{\partial H}+\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}\frac{\partial V}{\partial C_i}\right),i=1,\dots ,n$$

(21)

Furthermore, the OCL is as shown as follows:

$$\frac{u_{\mathrm{f}i}^{*}}{T_{\mathrm{d}0i}^{\prime }}=K_i\mathrm{sgn}\left(\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}\frac{\partial V}{\partial H}+\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}\frac{\partial V}{\partial C_i}\right),\hspace{1em}i=1,\dots ,n$$

(22)

Substituting (22) into (15), one obtains the optimized stochastic averaging function and its coefficients, as follows:

$$\begin{array}{l}dH=m_H\left(H,\mathit{C}\right)dt+{\sigma }_{HH}\left(H,\mathit{C}\right)dA\left(t\right)\\ dC=m_C\left(H,\mathit{C}\right)dt\end{array}$$

(23)

where

$$\begin{array}{c}{m}_H\left(H,\mathit{C}\right)={\overline{m}}_H\left(H,\mathit{C}\right)+\frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}\frac{u_{\mathrm{f}i}^{*}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial H}{\partial E_{\mathrm{q}i}^{\prime }}/\frac{\partial H}{\partial {\omega }_1}d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n}\\ m_C\left(H,\mathit{C}\right)={\overline{m}}_C\left(H,\mathit{C}\right)+\frac{1}{T\left(H,\mathit{C}\right)}{\displaystyle {\int }_{\mathsf{\Omega }}\frac{u_{\mathrm{f}i}^{*}}{T_{\mathrm{d}0i}^{\prime }}\frac{\partial C_i}{\partial E_{\mathrm{q}i}^{\prime }}/\frac{\partial H}{\partial {\omega }_1}d{\omega }_2\dots d{\omega }_{n}d{\delta }_1\dots d{\delta }_n}\\ i=1,\dots ,n\end{array}$$

4.4. Conditional Intra-Region Probability Function

A conditional intra-region probability function is introduced, as shown in (24), to indicate the intra-region probability under certain initial conditions within (0, t].

$$\begin{array}{l}R\left(t|H_0,{\mathit{C}}_0\right):=\\ P\{H\left(s\right)\in \left[0,H_{\max }\right),C_i\left(s\right)\in \left[0,C_{i\max }\right],s\in \left(0,t\right]|\\ H\left(0\right)=H_0\in \left[0,H_{\max }\right),C_i\left(0\right)=C_{i0}\in \left[0,C_{i\max }\right)\}\end{array}$$

(24)

The conditional intra-region probability function satisfies backward Kolmogorov Equation (25).

$$\frac{\partial R}{\partial t}=m_H\left(H_0,{\mathit{C}}_0\right)\frac{\partial R}{\partial H_0}+m_C\left(H_0,{\mathit{C}}_0\right)\frac{\partial R}{\partial {\mathit{C}}_0}+\frac{1}{2}{\sigma }_{HH}^2\left(H_0,{\mathit{C}}_0\right)\frac{{\partial }^{2}R}{\partial H_0^2}$$

(25)

where the corresponding boundary conditions are

$$R\left(t|H_{\max },{\mathit{C}}_0\right)=0,R\left(t|H_0,{\mathit{C}}_{\max }\right)=0,$$

and the initial condition is

$$R\left(0|H_0,{\mathit{C}}_0\right)=1,$$

where m_H(H₀, C₀), m_C(H₀, C₀) and σ²_HH(H₀,C₀) are calculated by m_H(H, C), m_C(H, C) and σ²_HH(H, C) in (23) when H = H₀ and C = C₀. H₀ and C₀ are the initial values of function H and C, respectively.

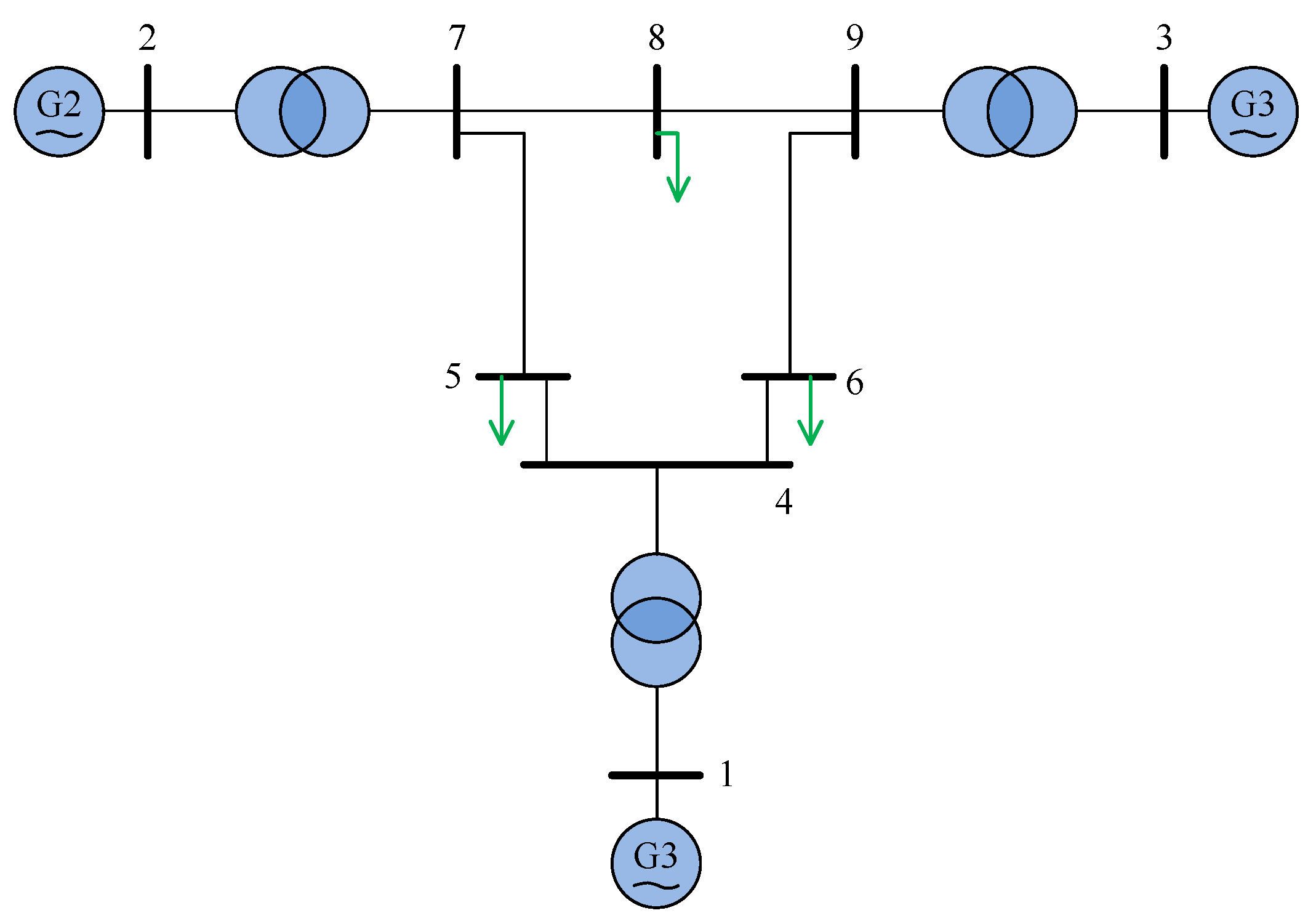
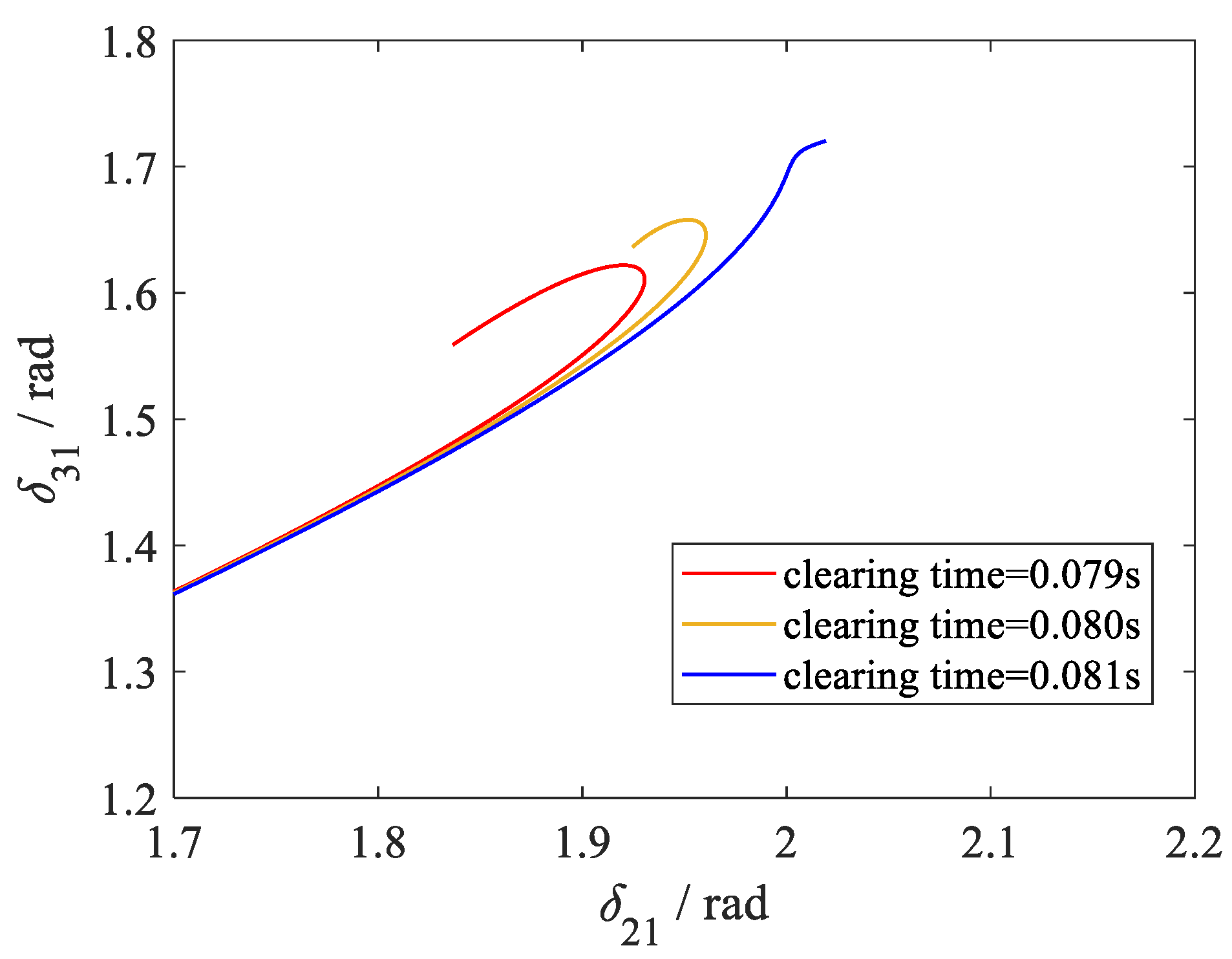
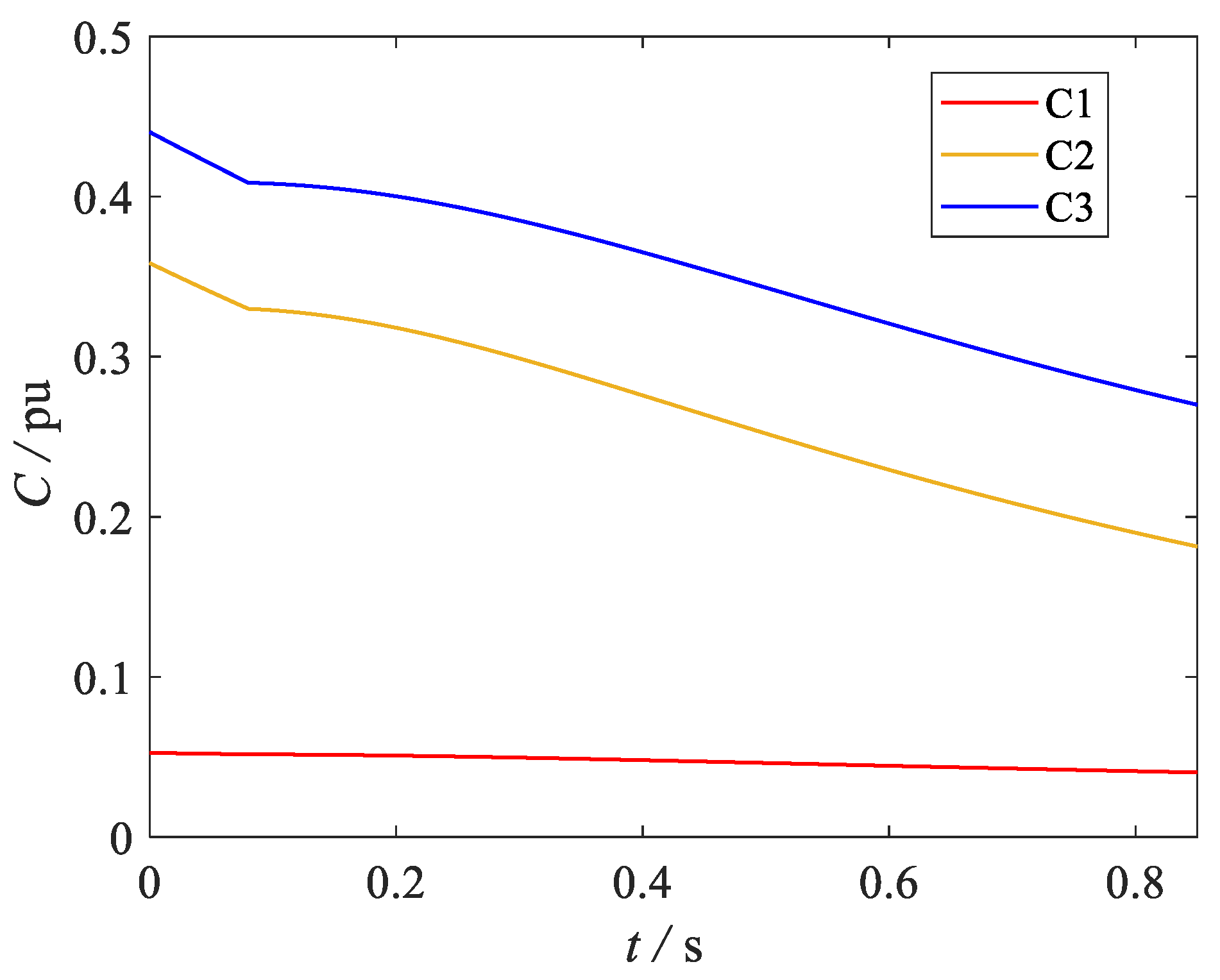
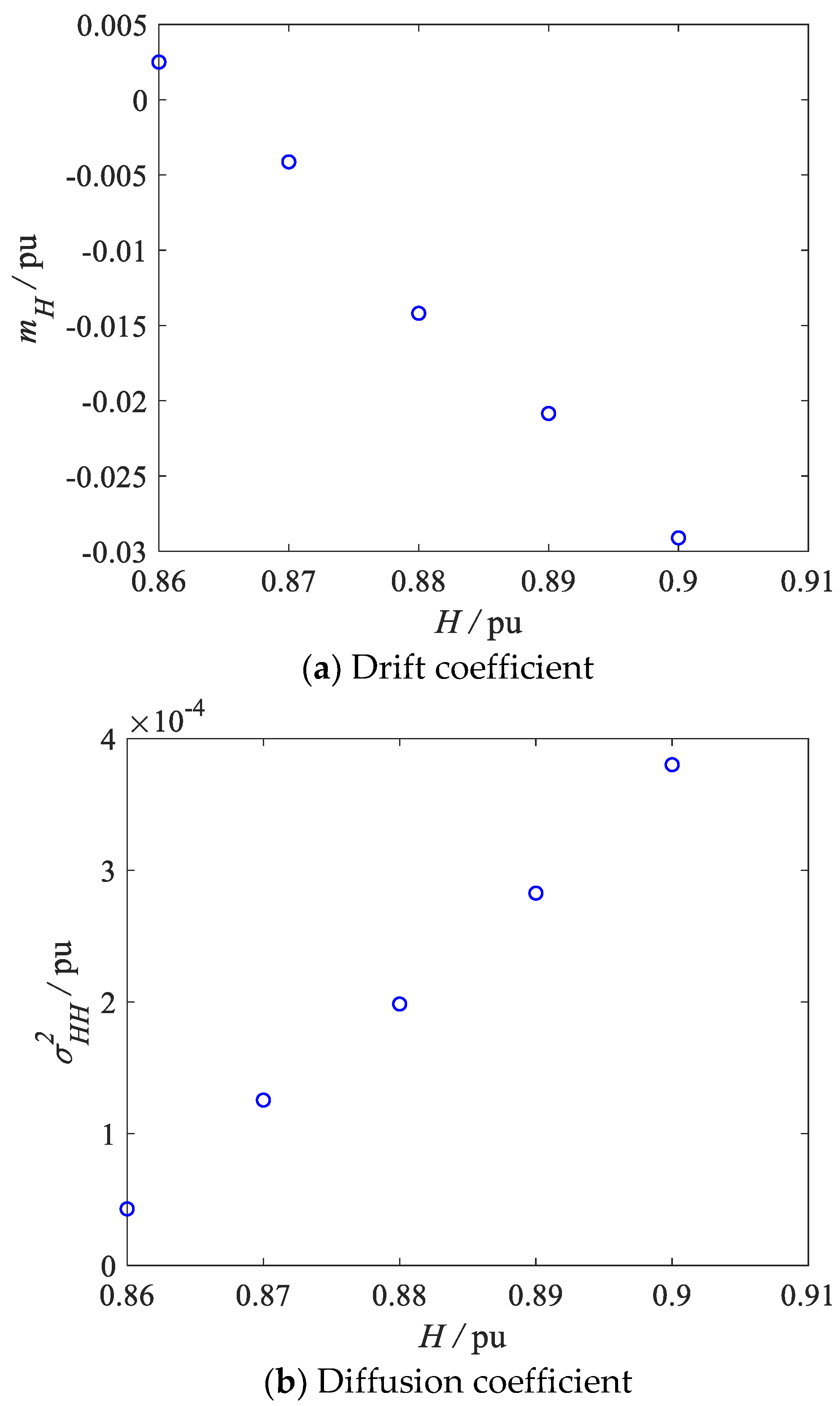
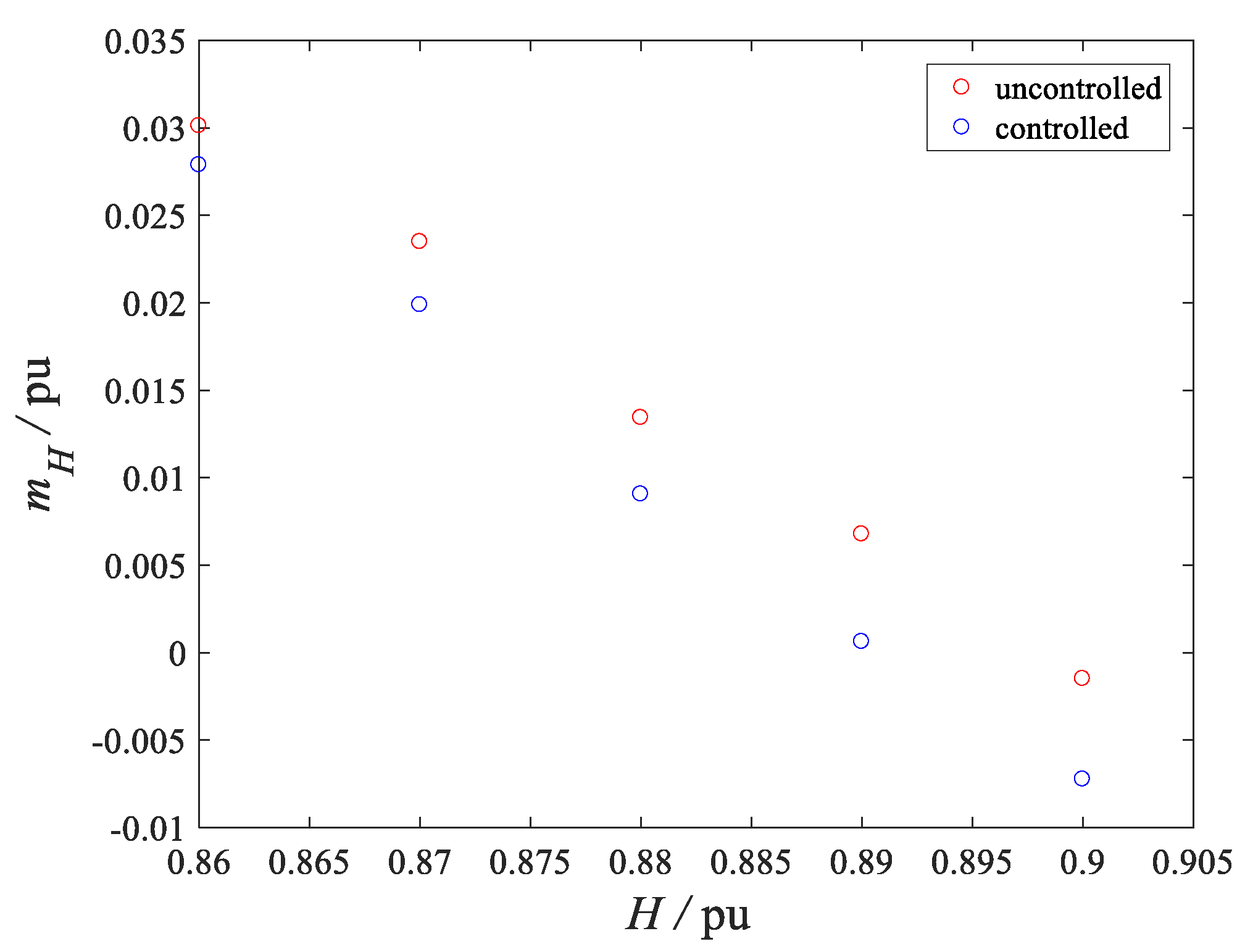
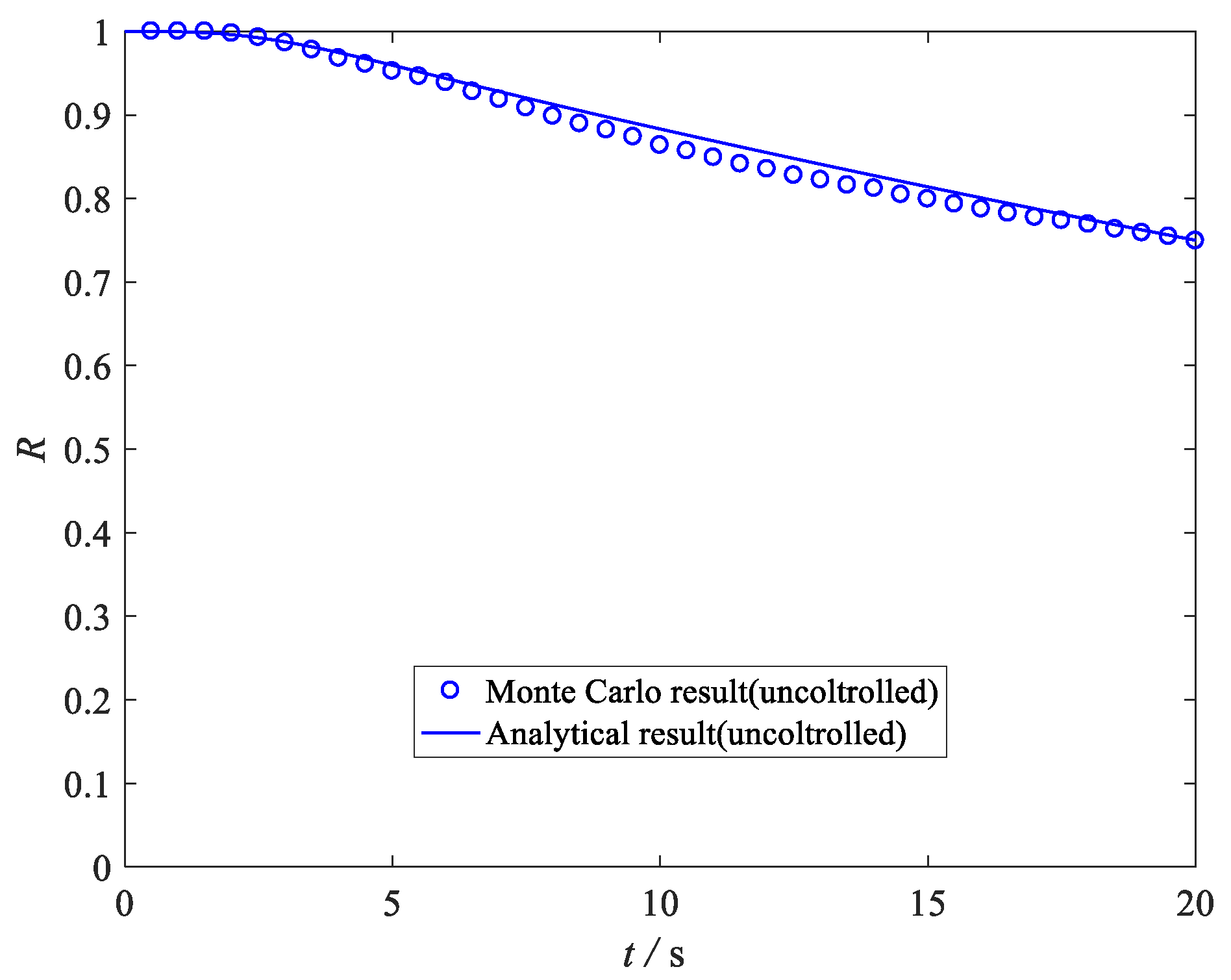
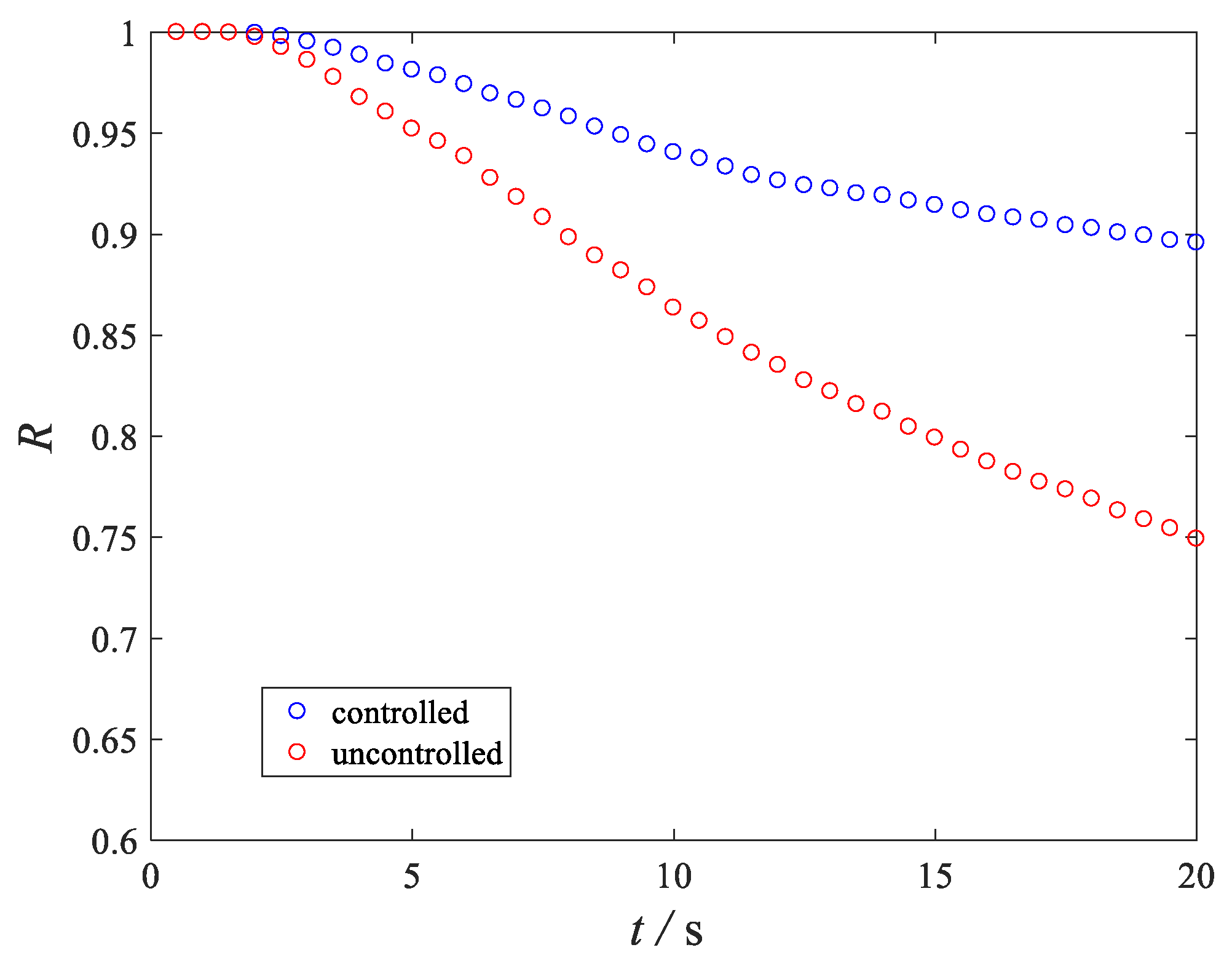
5. Case Study

A modified three-machine nine-bus system, whose structure is shown in Figure 4, is studied in this paper. The model used in this paper is a simplified model, where only the generators nodes are kept, and other nodes in the network are eliminated. The parameters of this original three-machine nine-bus system can be found in [39]. The original system is modified by adding the proposed stochastic control and stochastic disturbances.

The stochastic disturbance is added to the generator G2, which is also the only generator with the proposed stochastic optimal control.

The maximum potential energy point is determined through the rotor angle trajectory due to potential energy boundary surface (PEBS) method [36]. Obviously, the critical energy of the system is different under different faults. In this paper, a three-phase grounding short is added between Bus 5 and Bus 7. The clearing time changes from 0.07 to 0.09 s, and the time interval is 0.001 s. The rotor angle motion trajectories under different fault clearing time are shown in Figure 5.

Choose the clearing time = 0.080 s, the maximum potential energy point can be found and the value is 0.9857, which is also the value of the critical energy of the system.

Meanwhile, the Casimir function is found to be decreasing as the system energy is increasing, and the initial value of Casimir function is the maximum, as shown in Figure 6.

It can be seen that the Casimir function value is always in the region, so it is not necessary to consider it in the intra-region probability. Furthermore, the intra-region probability function (24) becomes as:

$$R\left(t|H_0\right)=P\left\{H\left(s\right)\in \left[0,H_{\max }\right),s\in \left(0,t\right]|H\left(0\right)=H_0\in \left[0,H_{\max }\right)\right\}$$

(26)

A new backward Kolmogorov equation is satisfied by (26), which is as follows:

$$\partial R/\partial t=m_H\left(H_0,{\mathit{C}}_0\right)\frac{\partial R}{\partial H_0}+\frac{1}{2}{\sigma }_{HH}^2\left(H_0,{\mathit{C}}_0\right)\frac{{\partial }^{2}R}{\partial H_0^2}$$

(27)

where R(0|H₀) = 1, R(t|H_max) = 0 and R(t|H₀) = 0.

According to (15), the numerical solution of coefficients m_H(H) and σ²_HH (H) of uncontrolled system are as shown in Figure 7.

Consider the OCL (22) into the coefficient, and it will only influence the m_H(H), which is as shown in Figure 8.

As shown in Figure 8, drift coefficient m_H(H) decreases after considering the OCL. As shown in (27), as the drift coefficient decreases, the derivative of energy H decreases, which means the growth of energy H will slow down at the corresponding time point, and the intra-region probability will increase at the same time point. Hence, the proposed control method could improve the system dynamic performance.

Use m_H(H) and σ²_HH (H) into (27), the results of probability function (26) are as shown in Figure 9 and Figure 10.

Substituting the OCL into (5) and solving the function by Monte Carlo method, the results are as shown in Figure 9.

Figure 9 is the comparison between Monte Carlo results and analytical results. As shown in Figure 9, the analytical results fit well with the Monte Carlo results, which verify the accuracy of the stochastic averaging method.

Figure 10 is the comparison between controlled and uncontrolled system. As shown in Figure 10, the intra-region probability increases when the OCL is adopted, which means the proposed control strategy can effectively keep the systems states in the desired region and improve the intra-region probability.

The state variables comparison between controlled and uncontrolled system is as shown in Figure 11.

Figure 11 is the state variables comparison between controlled and uncontrolled system under the stochastic disturbances. As shown in Figure 11, the fluctuation region of controlled system is smaller than the uncontrolled system, which means the proposed control strategy is effective on reducing the system fluctuations.

As shown in Figure 9, Figure 10 and Figure 11, the stochastic averaging method is accuracy in analyzing the stochastic power system, and the proposed control strategy is also effective in reducing the stochastic fluctuations in the system under stochastic continuous disturbances.

6. Conclusions

In this paper, the Gauss white noise is added into an excitation controlled power systems model as the stochastic disturbances. This proposed stochastic system offers a better description of the controlled stochastic power systems, which cannot be replaced by the deterministic system. As the systems model becomes more complex with the stochasticity, SAM is adopted here to simplify the high-dimension systems into a lower-dimension stochastic averaging Itô function. The theoretical deduction shows the effectiveness of the method. The optimal control problem of stochastic multi-machine power systems is addressed by adopting the dynamic programming method. Based on the control object which is achieving the maximum probability in the bounded fluctuation area, and the OCL is determined by dynamic programming equation. From the simulation results, the intra-region probability has been improved in the controlled system, which means the proposed OCL is effective to reduce the impact of the stochastic factors and to guarantee systems security. A conditional intra-region probability function which satisfies the backward Kolmogorov’s equation has been introduced, which makes the probability can be calculated analytically. The proposed method is accurate as the analytical results are close to the Monte Carlo results.

In modern power systems, the stochastic disturbances in power systems are irregular and unpredictable, and the impact will become more and more obvious in modern power systems. The control strategy proposed in this paper offers a new way to reduce such impact and ensure the security of systems.