A Model-Based Design Approach for Stability Assessment, Control Tuning and Verification in Off-Grid Hybrid Power Plants
Abstract
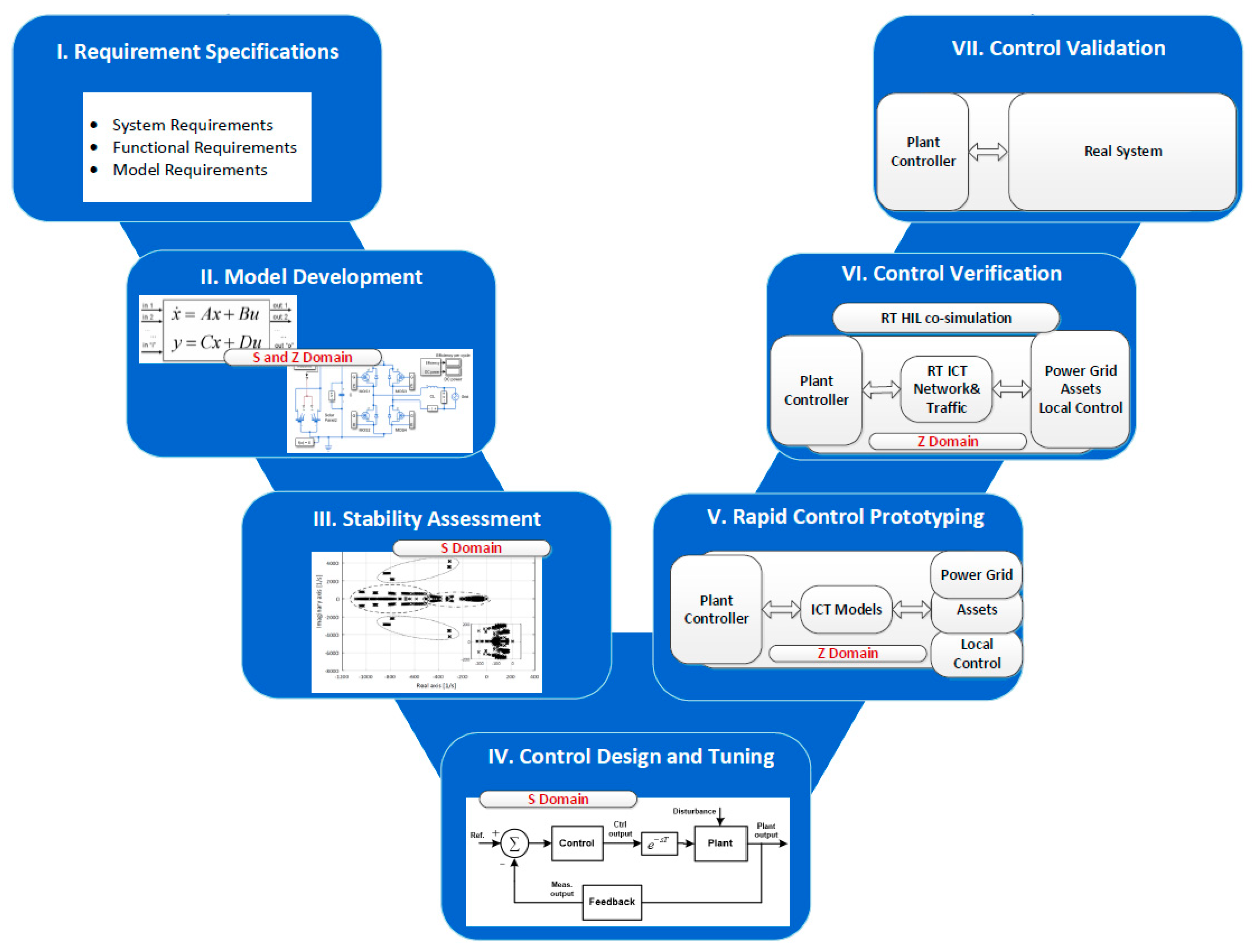
:1. Introduction
2. Step I: Requirement Specifications
2.1. Step Ia: Defining System Requirements
2.2. Step Ib: Defining Functional Requirements
2.3. Step Ic: Defining Modeling Requirements
- Linearized models are required for stability assessment and control tuning in frequency domain.
- The model bandwidth shall be limited to a minimum value that enables the assessment of voltage and frequency stability and control.
- Numerical models are required that are applicable for RCP and control verification purposes. Computational effort of model execution shall be taken into account to achieve accelerated off-line simulation studies during RCP stage and to ensure real-time capability for RT-HIL testing.
- Simulation platforms must be carefully selected to reduce the modeling effort by re-using developed models throughout various MBD stages shown in Figure 1.
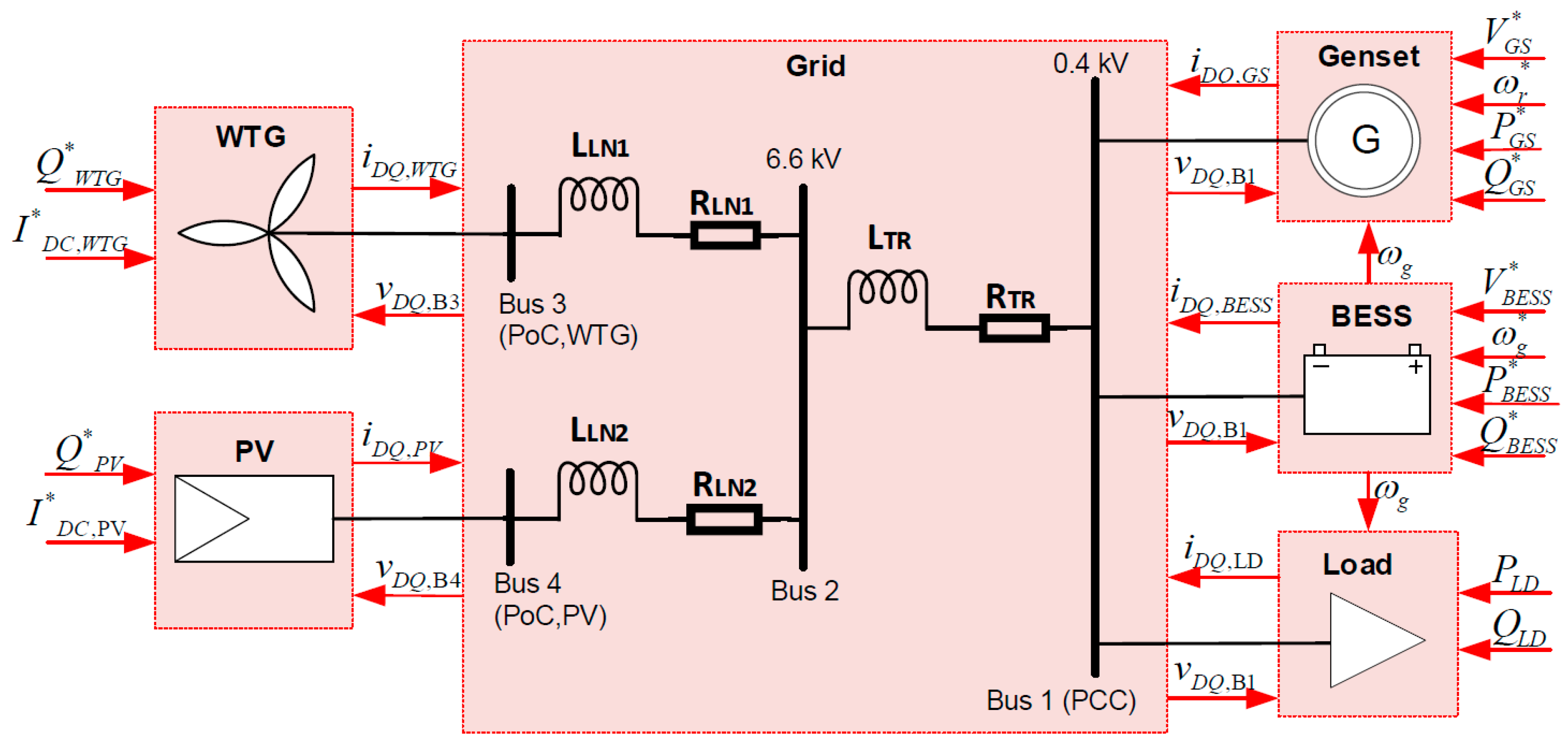
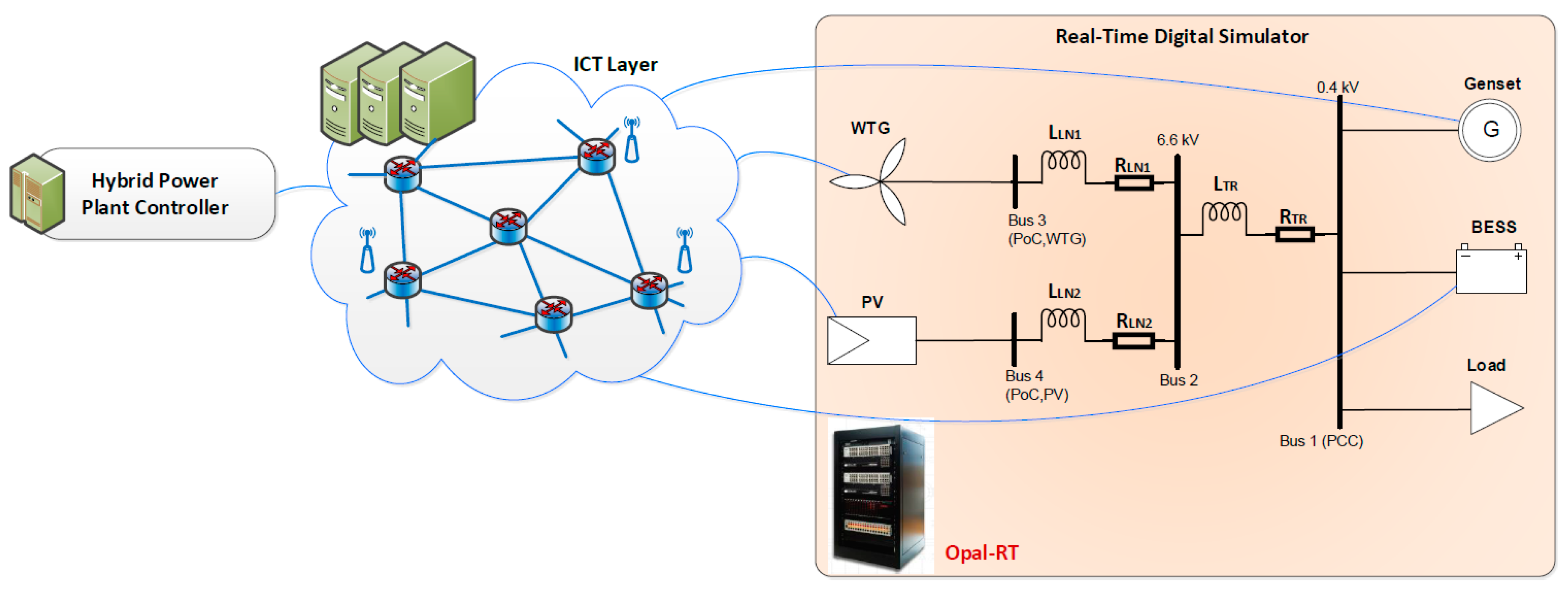
3. Step II: Modeling of Hybrid Power Plant
3.1. Step IIa: Modeling Plant Components in State-Space
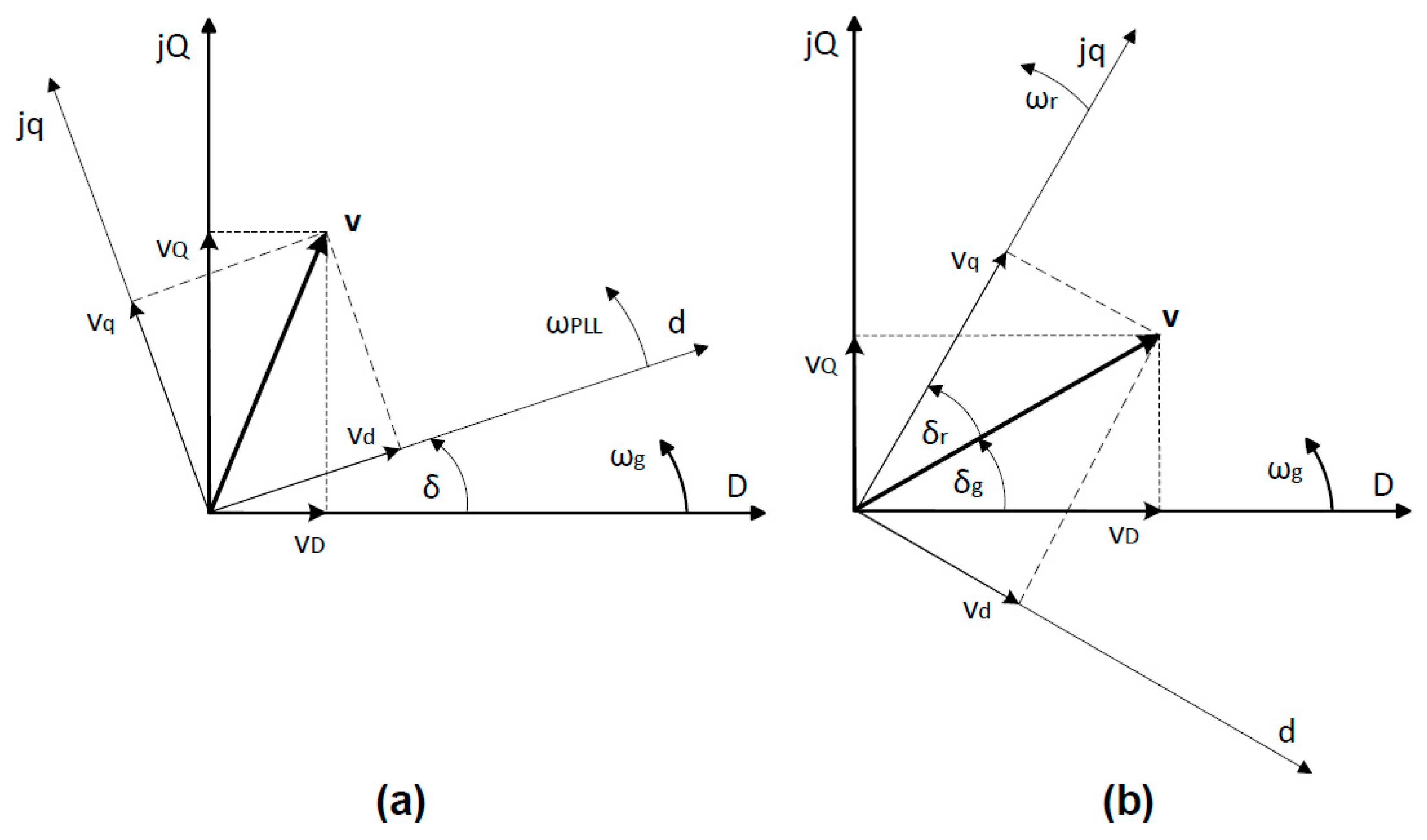
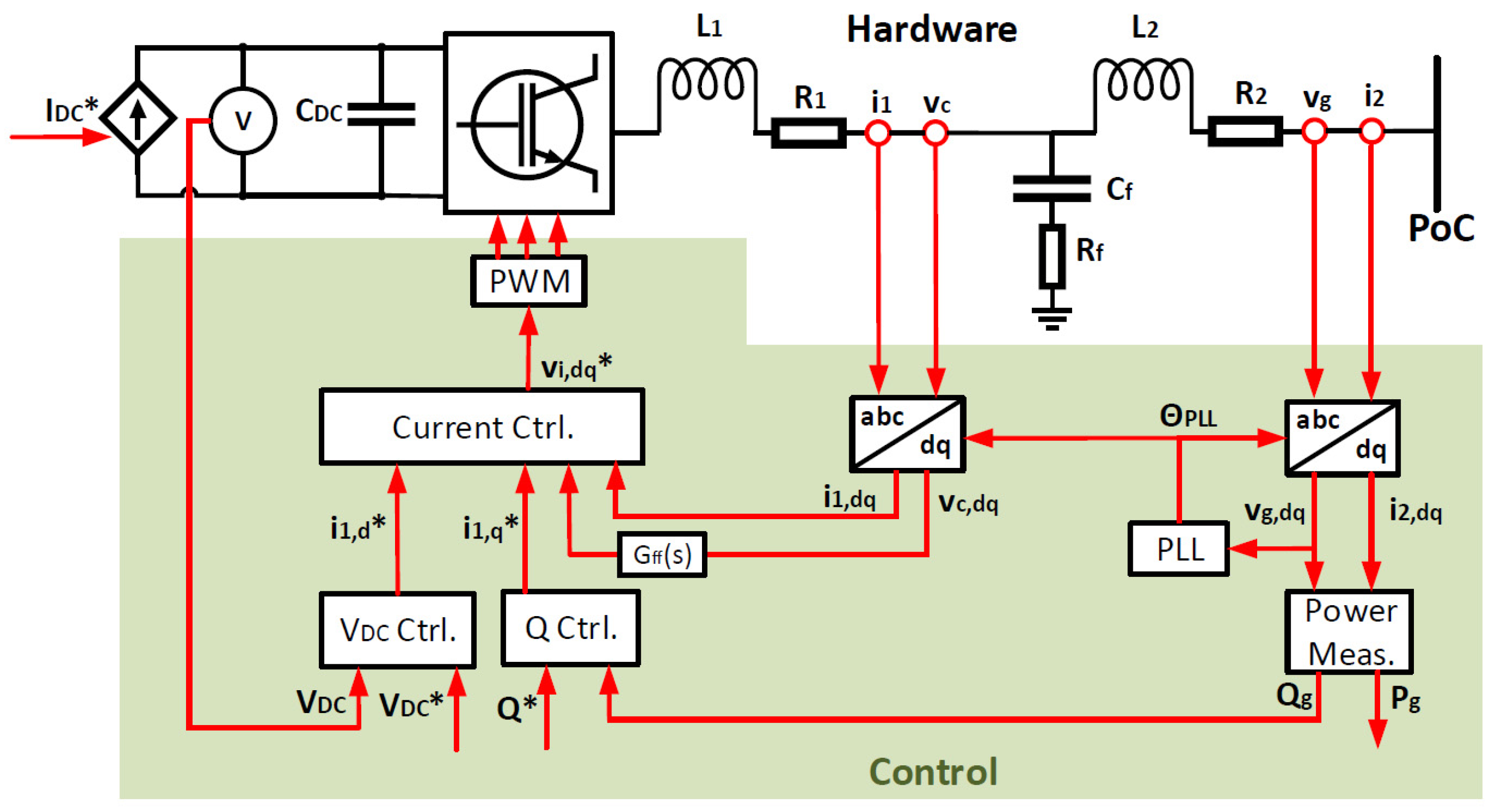
3.1.1. Grid-Forming Inverter
- , , , , and refer to the dynamic states of LCL filter. Note that it is necessary to represent the filter capacitance, as the voltage is controlled in this control structure.
- and are the state variables of the current controller (PI).
- and are the state variables of the outer voltage controller of type PI.
- and refer to the dynamics of a low pass filter (LPF) for power measurements, leading to an average value for active and reactive power.
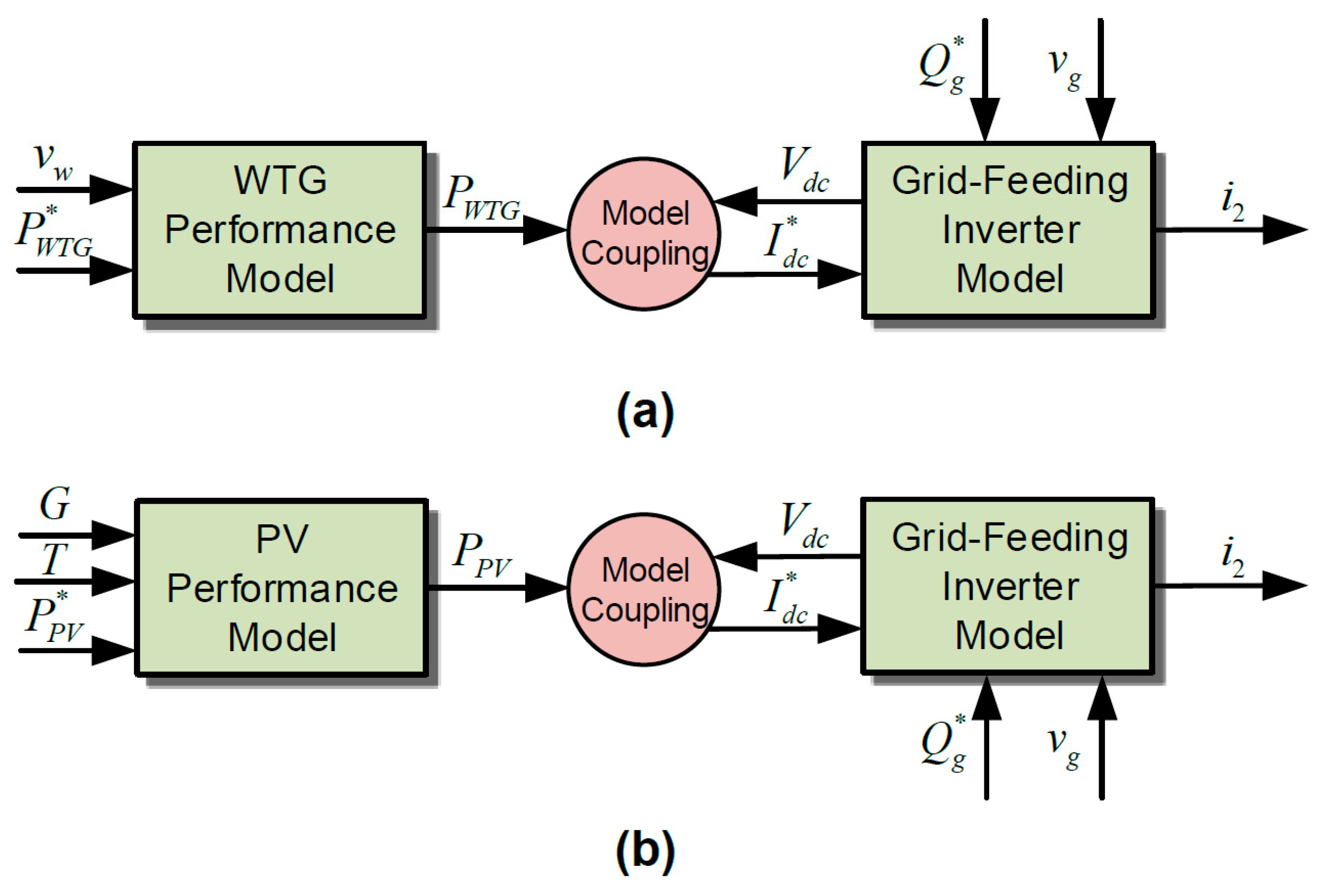
3.1.2. Grid-Feeding Inverter
- The dynamic states of LCL filter and current controller are the same as in grid-forming control mode. Note that it is not mandatory to represent the filter capacitance for the intended studies in this paper, as harmonics are not of concern. It is nevertheless retained to align the modeling representation of grid-forming and grid-feeding inverter control structure.
- and relate to the PI controllers of DC link voltage and reactive power respectively.
- corresponds to the dynamic of DC-link capacitor and to a LPF for reactive power measurement.
- belongs to a first-order filter of the phase-locked loop (PLL) and is the phase angle dynamic as a derivative of the grid frequency.
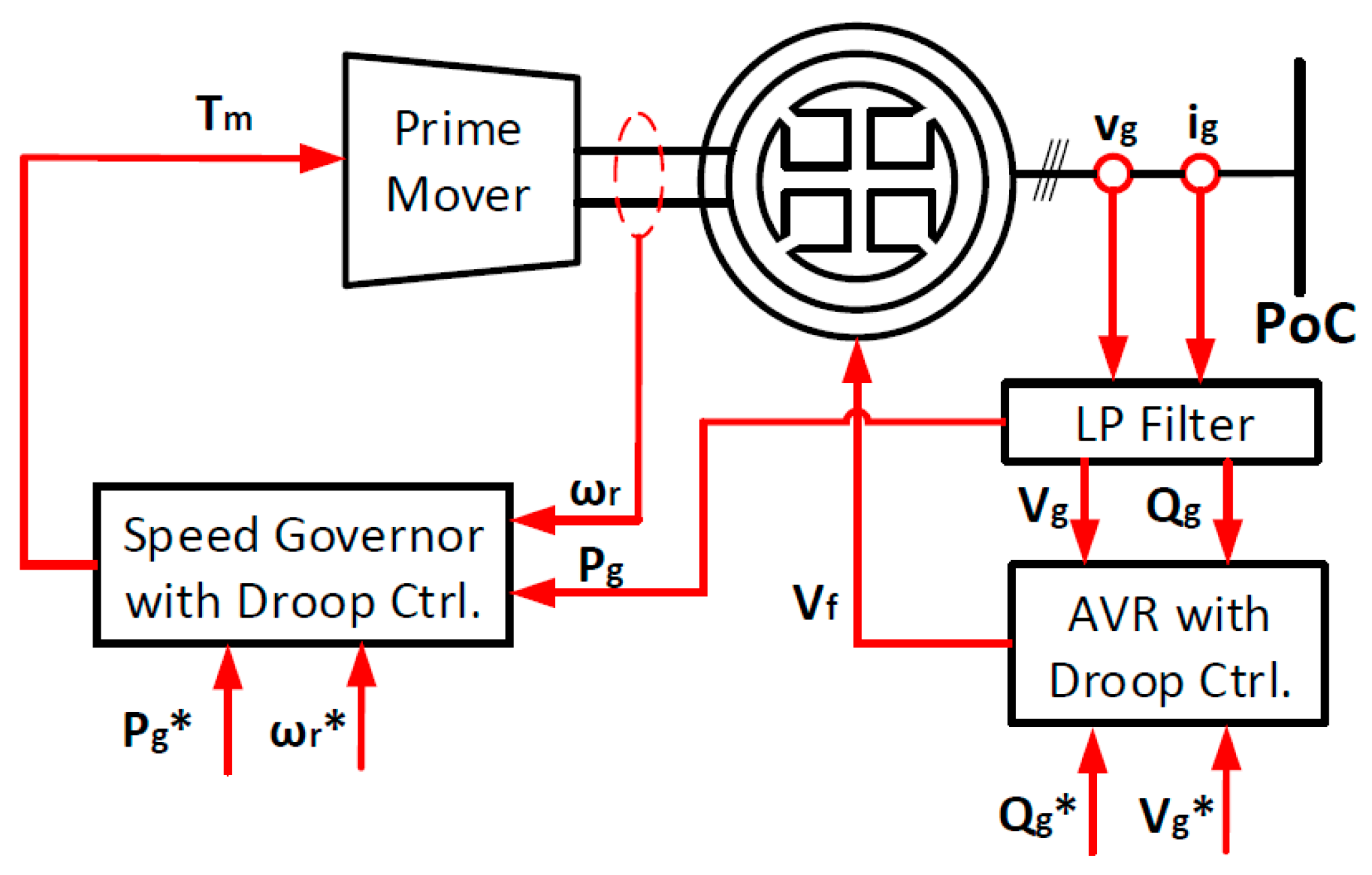
3.1.3. Generator Set
- The first five state variables result from the stator and rotor flux dynamics. and are the stator currents, and are currents in the damper winding and is the field winding current [26].
- The rotor dynamics are expressed by the swing equation (Equation (13)). It should be noted that is the rotor angular speed deviation from the grid angular frequency. is the inertia time constant, the damping factor coefficient and and the mechanical and electrical torques. An expression for the rotor angle displacement is given in Equation (14) [30].
- , and refer to the dynamics of a LPF for voltage and current measurement, leading to an average value for active and reactive power.
- and are the derivative and integral states of the governor PID controller, while relates to the change in mechanical torque due to prime mover dynamics (fuel actuator and combustion engine).
- and are the derivative and integral states of the AVR, while corresponds to the dynamics of the excitation voltage.
3.2. Step IIb: Merging of State-Space Models
3.3. Step IIc: Developing Discrete-Time Domain Models for Control Verification
4. Voltage and Frequency Stability Assessment
4.1. Step IIIa: Defining Relevant Operating Sccenarios
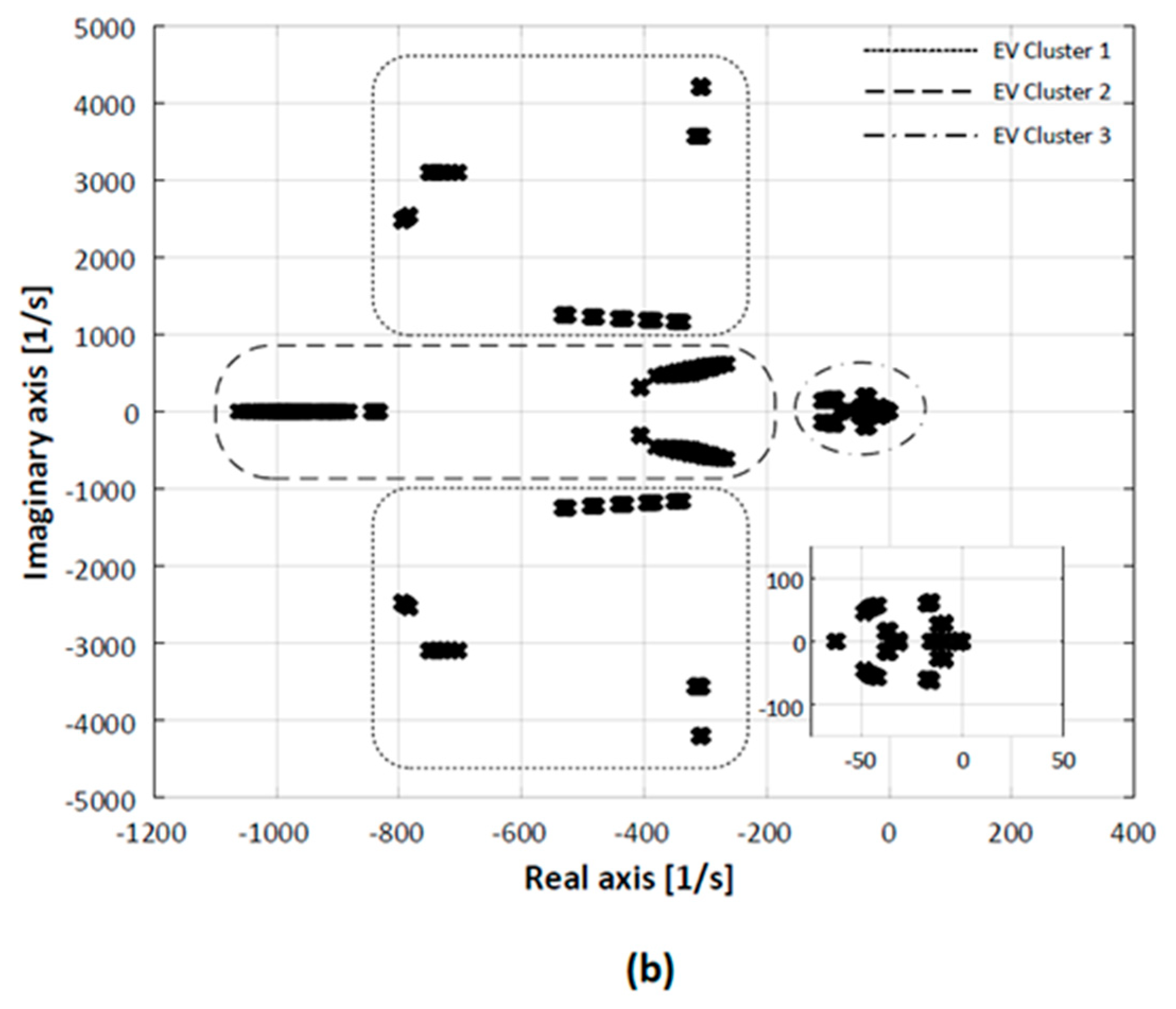
4.2. Step IIIb: Clustering of Eigenvalues
4.3. Step IIIc: Applying Corrective Measures for System Stability
4.4. Step IIId: Performing Sensitivity Analysis
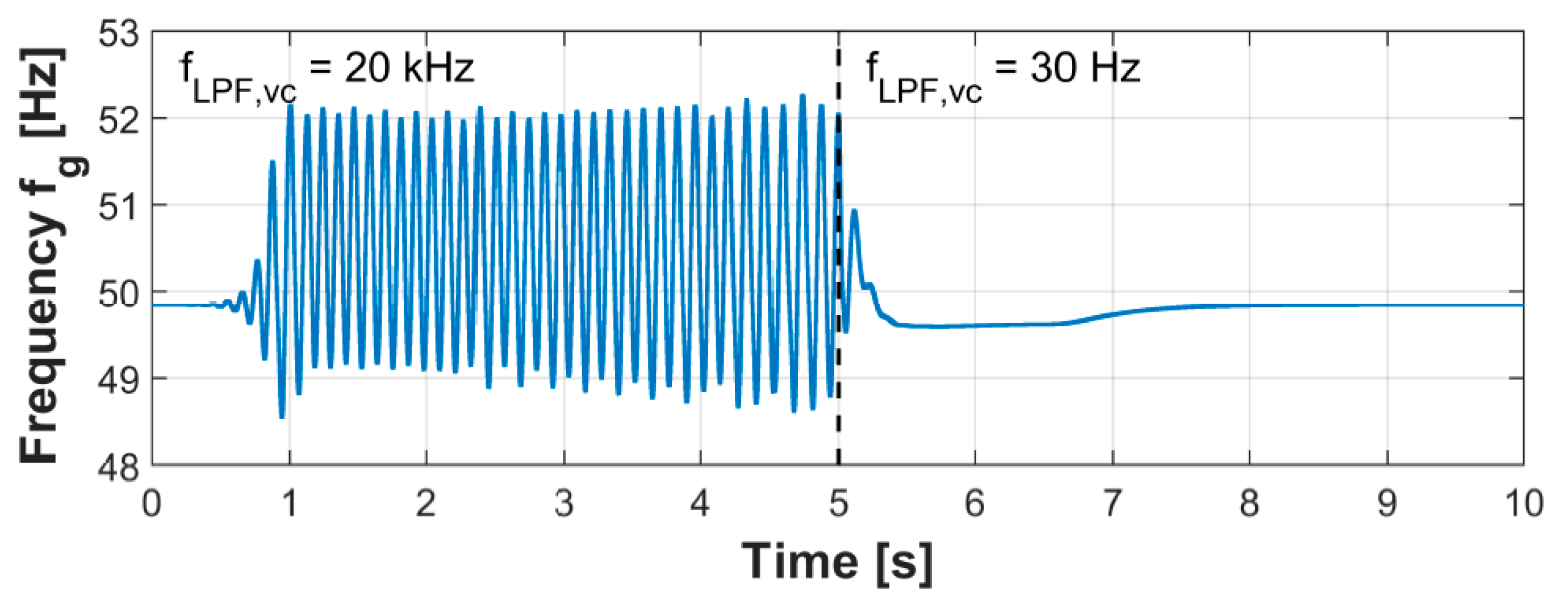
4.4.1. Test Case 1: Power Measurement Filter of Grid-Forming Inverter
4.4.2. Test Case 2: Frequency/Active Power Droop Characteristic
5. Step IV: Design and Tuning of Hybrid Power Plant Controller
5.1. Step IVa: Designing Hybrid Power Plant Controller
5.2. Step IVb: Assessing Control Performance
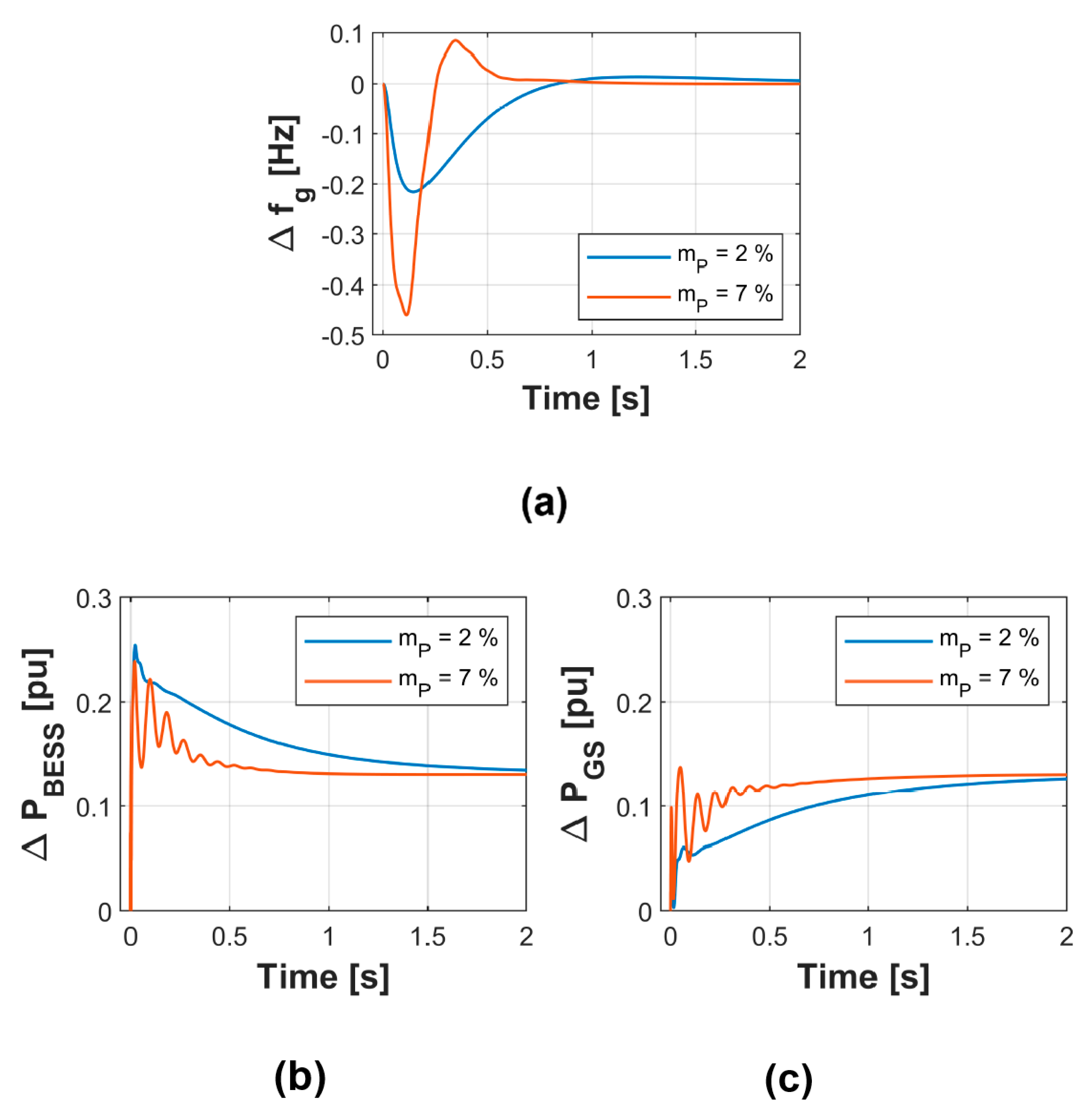
5.2.1. Test Case 1: Frequency Control
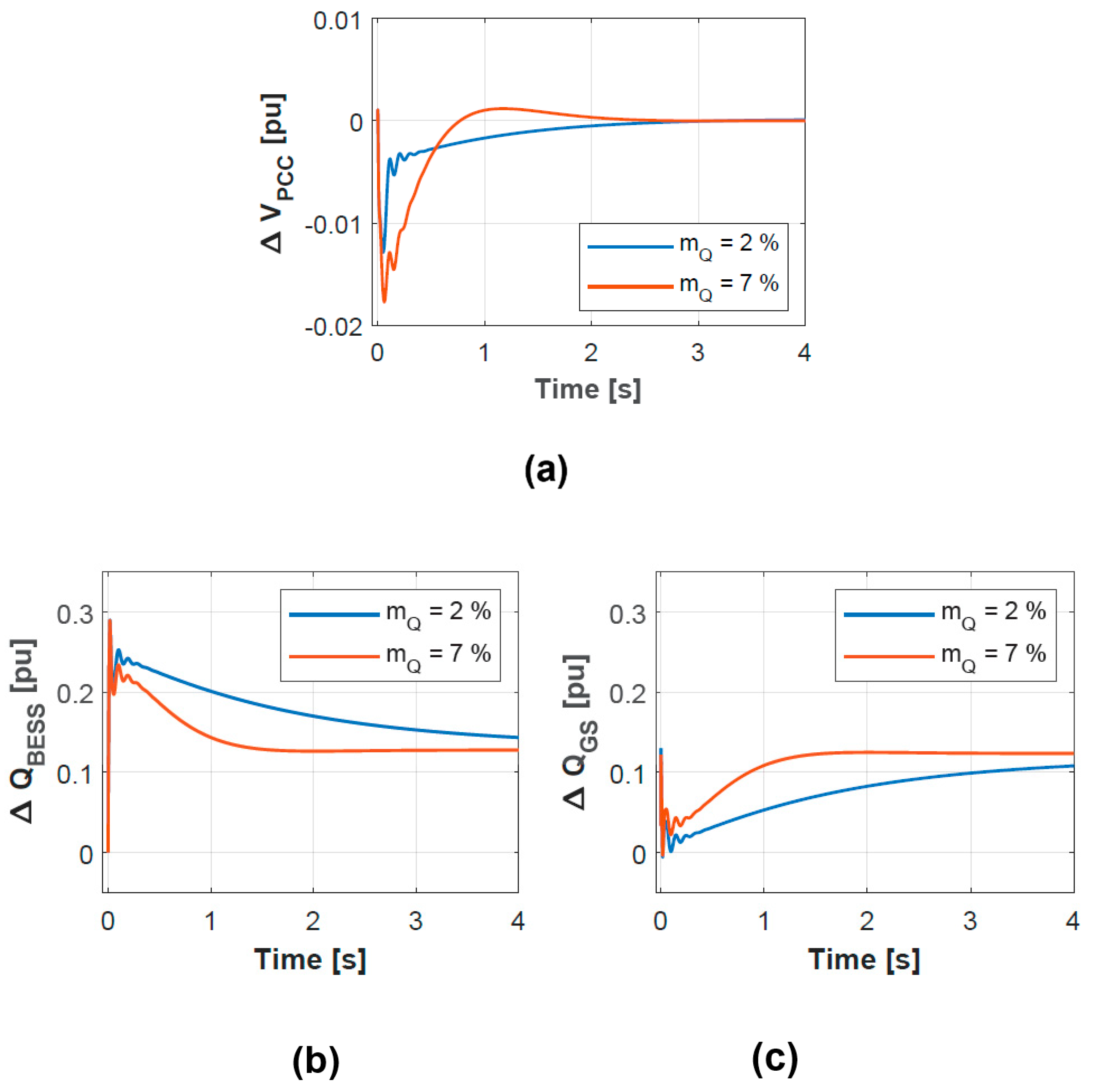
5.2.2. Test Case 2: Voltage Control
5.3. Step IVc: Control Tuning
- Frequency requirements: Figure 14 has shown that the frequency Nadir is deteriorated for large droop gains. Under-frequency load shedding (UFLS) schemes might be triggered depending on the occurring event (e.g., loss of unit) and UFLS characteristic. Detailed numerical simulations are required in order to assess such requirements.
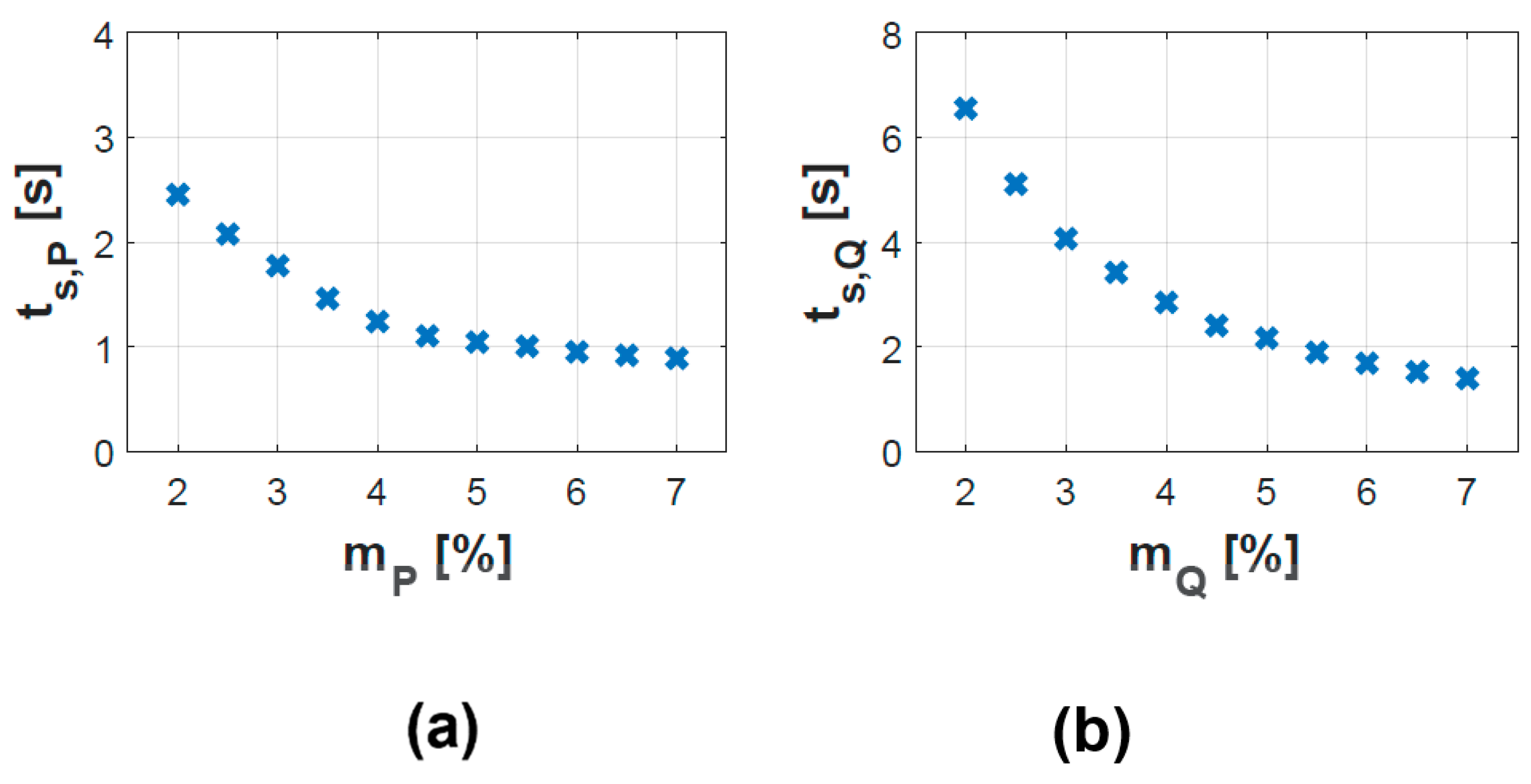
- Power sharing performance: Figure 16 summarizes in numbers how the settling time of active and reactive power increases with decreasing droop gains of BESS and genset. Proper droop gains shall be chosen according to the desired update rate of active and reactive power dispatch. Such a function is required, e.g., for BESS state-of-charge regulation and to avoid underloading/overloading of gensets according to dynamic fluctuations of renewable power. If active and reactive power setpoints are dispatched, e.g., every 3 s, the minimum droop gains shall be and in order to allow settlement of the respective parameters (Figure 16).
- Control sampling rate: According to Equation (26) the required sampling rate and hence the signal exchange between HPPC and DERs depends on the desired speed of secondary controller. In order to achieve the settling times depicted in Figure 16, the sampling rate must be for and for . Hence, the computational power of the control platform and communication latency issues shall be well assessed prior to selecting a certain droop gain.
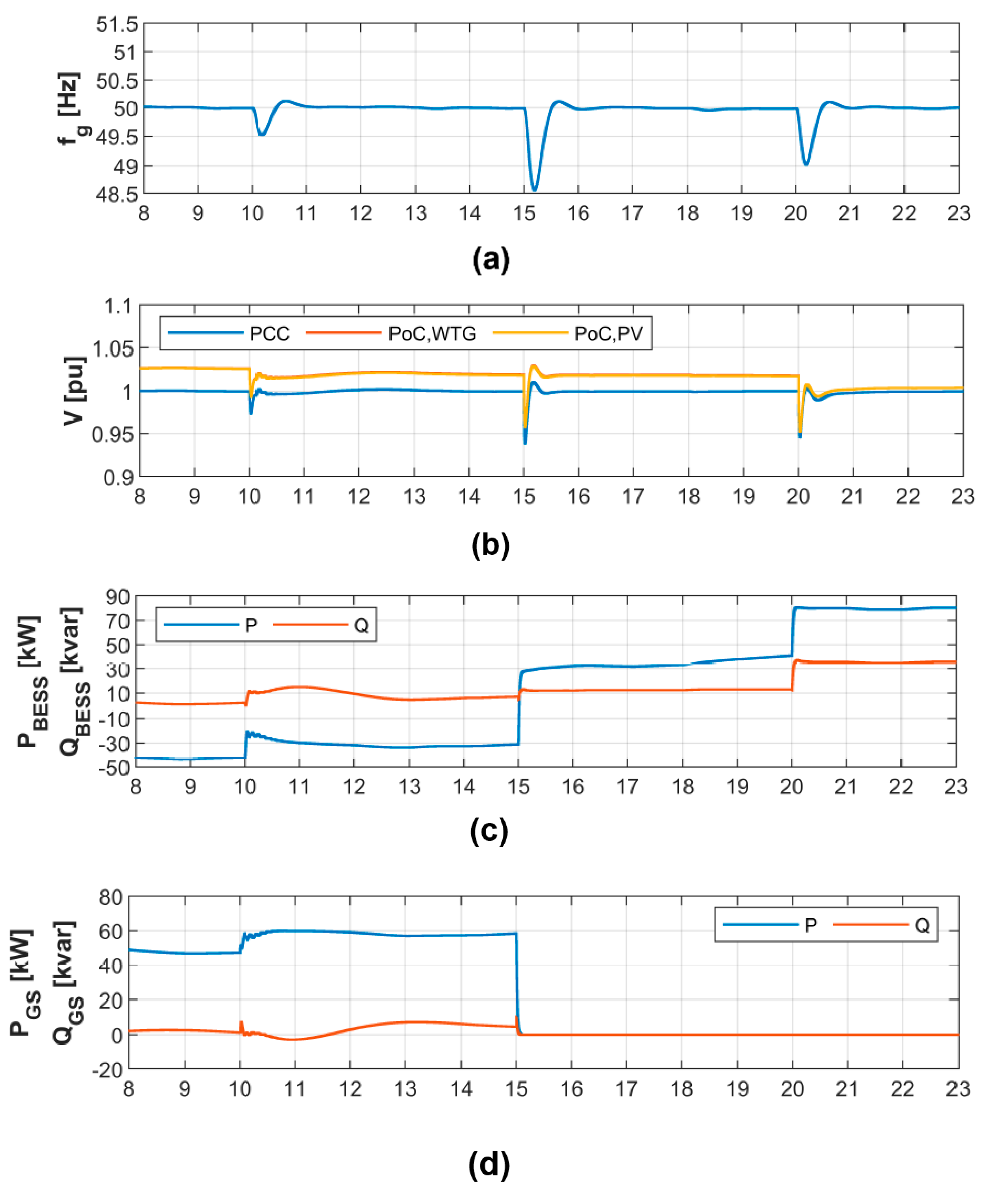
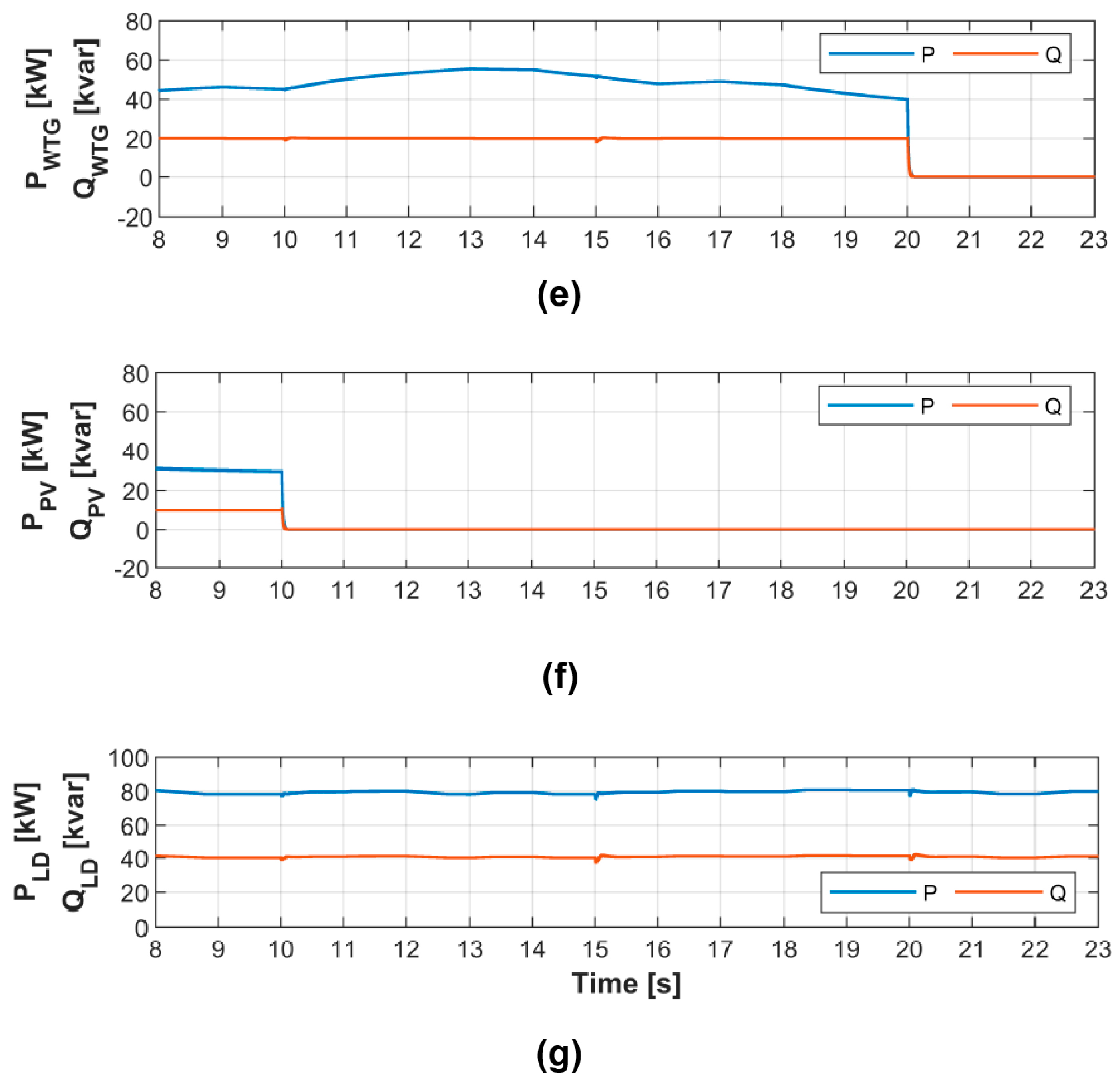
6. Step V: Rapid Control Prototyping
- 0.
- Operation with all DERs until ;
- 1.
- Disconnection of PV at ;
- 2.
- Disconnection of genset at ;
- 3.
- Disconnection of WTG at .
7. Step VI and VII: Control Verification and Validation
7.1. Step VI: Real-Time Hardware-in-the-Loop Verification
7.2. Step VII: On-Site Testing
8. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Elkadragy, M.M.; Baumann, M.; Moore, N.; Weil, M.; Lemmertz, N. Contrastive Techno-Economic Analysis Concept for Off-Grid Hybrid Renewable Electricity Systems Based on comparative case studies within Canada and Uganda. In Proceedings of the 3rd International Hybrid Power Systems Workshop, Tenerife, Spain, 8–9 May 2018; Energynautics: Darmstadt, Germany. [Google Scholar]
- Bitaraf, H.; Buchholz, B. Reducing energy costs and environmental impacts of off-grid mines. In Proceedings of the 3rd International Hybrid Power Systems Workshop, Tenerife, Spain, 8–9 May 2018; Energynautics: Darmstadt, Germany. [Google Scholar]
- Petersen, L.; Iov, F.; Tarnowski, G.C.; Carrejo, C. Optimal and Modular Configuration of Wind Integrated Hybrid Power Plants for Off-Grid Systems. In Proceedings of the 3rd International Hybrid Power Systems Workshop, Tenerife, Spain, 8–9 May 2018; Energynautics: Darmstadt, Germany. [Google Scholar]
- Kumar, R.; Gupta, R.A.; Bansal, A.K. Economic analysis and power management of a stand-alone wind/photovoltaic hybrid energy system using biogeography based optimization algorithm. Swarm Evol. Comput. 2013, 8, 33–43. [Google Scholar] [CrossRef]
- Maitra, A.; Rogers, L.; Handa, R. Program on Technology Innovation: Microgrid Implementations: Literature Review, Report; Electric Power Research Institute: Palo Alto, CA, USA, 2016; Available online: epri.com (accessed on 30 November 2019).
- Hafez, O.; Bhattacharya, K. Optimal planning and design of a renewable energy based supply system for microgrids. Renew. Energy 2012, 45, 7–15. [Google Scholar] [CrossRef]
- Ghiani, E.; Vertuccio, C.; Pilo, F. Optimal sizing of multi-generation set for off-grid rural electrification. In Proceedings of the IEEE Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Cañizares, C.A. Microgrid Stability Definitions, Analysis and Modeling; IEEE Power & Energy Society: Piscataway, NJ, USA, 2018. [Google Scholar]
- Pogaku, N.; Member, S.; Prodanovic, M.; Green, T.C.; Member, S. Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef] [Green Version]
- Etemadi, A.H.; Iravani, R. Eigenvalue and Robustness Analysis of a Decentralized Voltage Control Scheme for an Islanded Multi-DER Microgrid. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Tang, X.; Deng, W.; Qi, Z. Investigation of the dynamic stability of microgrid. IEEE Trans. Power Syst. 2014, 29, 698–706. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, M.R.; Lehn, P.W. Small-signal dynamic model of a micro-grid including conventional and electronically interfaced distributed resources. IET Gener. Transm. Distrib. 2007, 1, 324. [Google Scholar] [CrossRef] [Green Version]
- Gkountaras, A. Modeling Techniques and Control Strategies for Inverter Dominated Microgrids. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2017. Available online: depositonce.tu-berlin.de (accessed on 30 November 2019).
- Rocabert, J.; Luna, A.; Blaabjerg, F. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuna, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Matas, J.; Garcia de Vicuna, L.; Castilla, M.; Miret, J. Decentralized Control for Parallel Operation of Distributed Generation Inverters Using Resistive Output Impedance. IEEE Trans. Ind. Electron. 2007, 54, 994–1004. [Google Scholar] [CrossRef]
- Hadisupadmo, S.; Hadiputro, A.N.; Widyotriatmo, A. A Small Signal State Space Model of Inverter-Based Microgrid Control on Single Phase AC Power Network. Internetworking Indones. J. 2016, 8, 71–76. [Google Scholar]
- Petersen, L.; Iov, F.; Tarnowski, G.C.; Raghuchandra, K.B. Methodological Framework for Stability Analysis, Control Design and Verification in Hybrid Power Plants. In Proceedings of the 4th International Hybrid Power Systems Workshop, Crete, Greece, 22–23 May 2019; Energynautics: Darmstadt, Germany, 2019. [Google Scholar]
- EirGrid. Operating Security Standards; EirGrid: Dublin, Ireland, 2011. [Google Scholar]
- IEC 62257. Recommendations for Renewable Energy and Hybrid Systems for Rural Electrification—Part 2: From Requirements to a Range of Electrification Systems; International Electrotechnical Commission: Geneva, Switzerland, 2016. [Google Scholar]
- IEEE Standards Department. P2030.7/D11 Draft Standard for Specification of Microgrid Controllers; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Steinhart, C.J.; Finkel, M.; Gratza, M.; Witzmann, R.; Kerber, G.; Verteilnetz, L.E.W.; Germany, G. Determination of Load Frequency Dependence in Island Power Supply. In Proceedings of the 24th International Conference on Electricity Distribution, Glasgow, UK, 12–15 June 2017; pp. 12–15. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw-Hill, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Petersen, L.; Kryezi, F.; Iov, F. Design and tuning of wind power plant voltage controller with embedded application of wind turbines and STATCOMs. IET Renew. Power Gener. 2017, 11, 216–225. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Mao, C.; Lu, J.; Wang, D. Small-signal modelling and analysis of wind turbine with direct drive permanent magnet synchronous generator connected to power grid. IET Renew. Power Gener. 2012, 6, 48–58. [Google Scholar] [CrossRef]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability; Wiley-IEEE Press: Hoboken, NJ, USA, 1995; ISBN 007035958X. [Google Scholar]
- Knudsen, J. Modeling, Control and Optimization for Diesel-Driven Generator Sets. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2017. Available online: vbn.aau.dk (accessed on 30 November 2019).
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control and Applications; IEEE Press: Piscataway, NJ, USA; John Wiley: Hoboken, NJ, USA, 2010; ISBN 9780470521564. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; ISBN 9780470057513. [Google Scholar]
- Sabor, O. Small-Signal Modelling and Stability Analysis of a Traditional Generation Unit and a Virtual Synchronous Machine in Grid-Connected Operation. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. Available online: repository.tudelft.nl (accessed on 30 November 2019).
- Petersen, L.; Iov, F.; Tarnowski, G.C.; Gevorgian, V.; Koralewicz, P.; Stroe, D.-I. Validating Performance Models for Hybrid Power Plant Control Assessment. Energies 2019, 12, 4330. [Google Scholar] [CrossRef] [Green Version]
- European Commission. Network Code on Requirements for Grid Connection of Generators; European Network of Transmission System Operators for Electricity: Brussels, Belgium, 2016. [Google Scholar]
- Garcia, J.M. Voltage Control in Wind Power Plants with Doubly Fed Generators. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2010. Available online: vbn.aau.dk (accessed on 30 November 2019).
- Iov, F.; Shahid, K.; Petersen, L.; Olsen, L.R. RePlan Project: D5.1—Verification of Ancillary Services in Large Scale Power System, Project Report, Aalborg, Denmark. 2018. Available online: www.replanproject.dk (accessed on 30 November 2019).
- Smart Energy Systems Laboratory at Aalborg University. Available online: www.et.aau.dk/laboratories/power-systems-laboratories/smart-energy-systems (accessed on 30 November 2019).

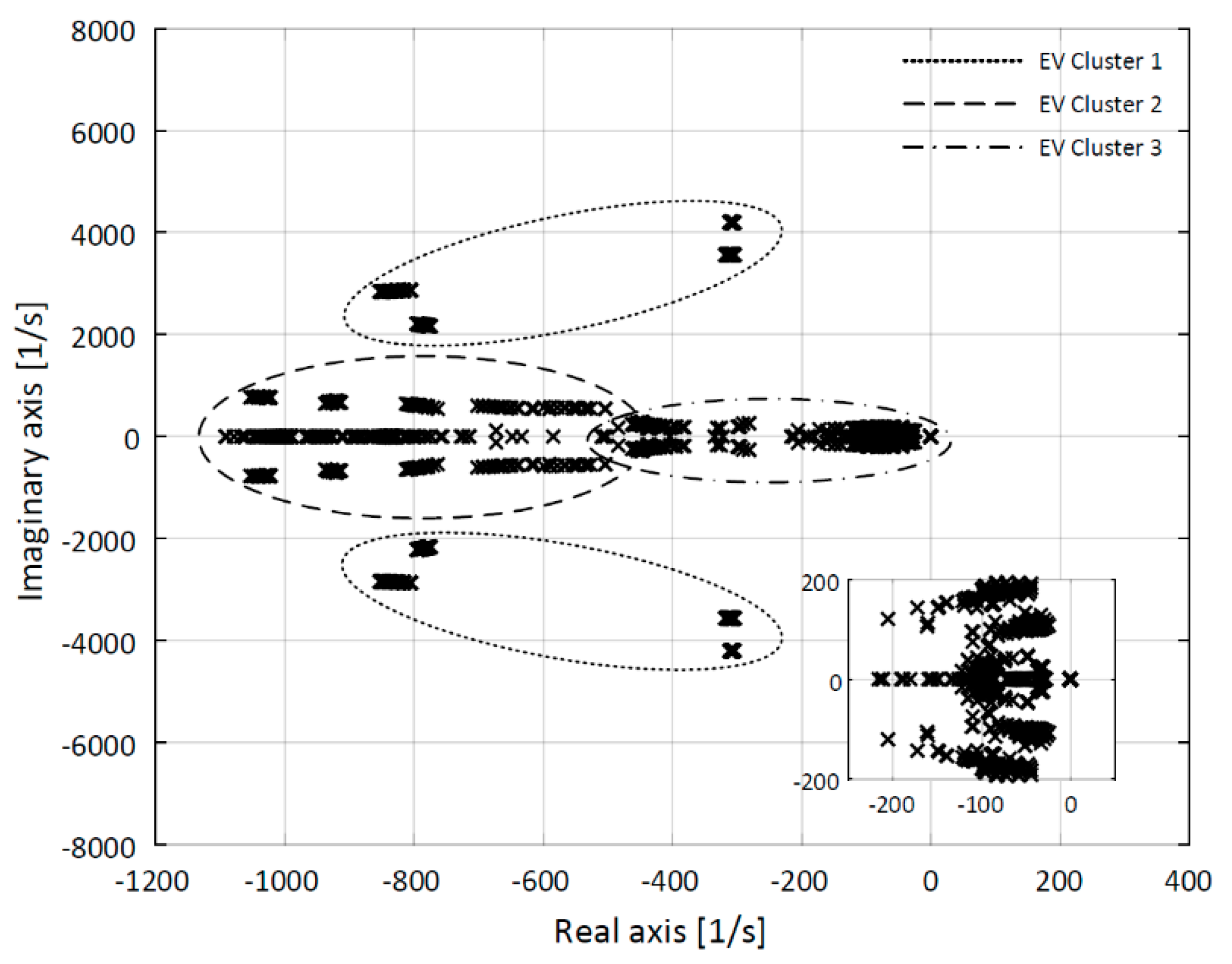




| EV Cluster | Eigenfrequency [Hz] | Damping Ratio [-] | Associated Dominant State Variables |
|---|---|---|---|
| 1 | {185, 20 × 103} | {0.03, 0.79} | Plant inductances and capacitances |
| 2 | {130, 160} | 1 | Inverter inner current control loops |
| 3 | {5, 30} | {0.39, 1} | Inverter outer control loops |
| EV Cluster | Eigenfrequency [Hz] | Damping Ratio [-] | Associated Dominant State Variables |
|---|---|---|---|
| 1 | {225, 20 × 103} | {0.03, 0.76} | Plant inductances and capacitances |
| 2 | {80, 160} | {0.61, 1} | Inverter inner current control loops, SG flux |
| 3 | {0.3, 34} | {0.19, 1} | Inverter outer control loops, SG flux, excitation system, genset mechanical time constants and control loops |
| BESS | Genset | WTG | PV | HPPC | |
|---|---|---|---|---|---|
| [kW] | - | ||||
| [kW] | - | ||||
| [%] | - | - | - | ||
| [ms] | - | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petersen, L.; Iov, F.; Tarnowski, G.C. A Model-Based Design Approach for Stability Assessment, Control Tuning and Verification in Off-Grid Hybrid Power Plants. Energies 2020, 13, 49. https://doi.org/10.3390/en13010049
Petersen L, Iov F, Tarnowski GC. A Model-Based Design Approach for Stability Assessment, Control Tuning and Verification in Off-Grid Hybrid Power Plants. Energies. 2020; 13(1):49. https://doi.org/10.3390/en13010049
Chicago/Turabian StylePetersen, Lennart, Florin Iov, and German Claudio Tarnowski. 2020. "A Model-Based Design Approach for Stability Assessment, Control Tuning and Verification in Off-Grid Hybrid Power Plants" Energies 13, no. 1: 49. https://doi.org/10.3390/en13010049





