A Coordinated Voltage and Reactive Power Control Architecture for Large PV Power Plants
Abstract
:1. Introduction
2. Hierarchical Voltage Control Architecture
3. Power Plants Modeling
3.1. Large RES Production Power Plants
3.2. Traditional Power Plants
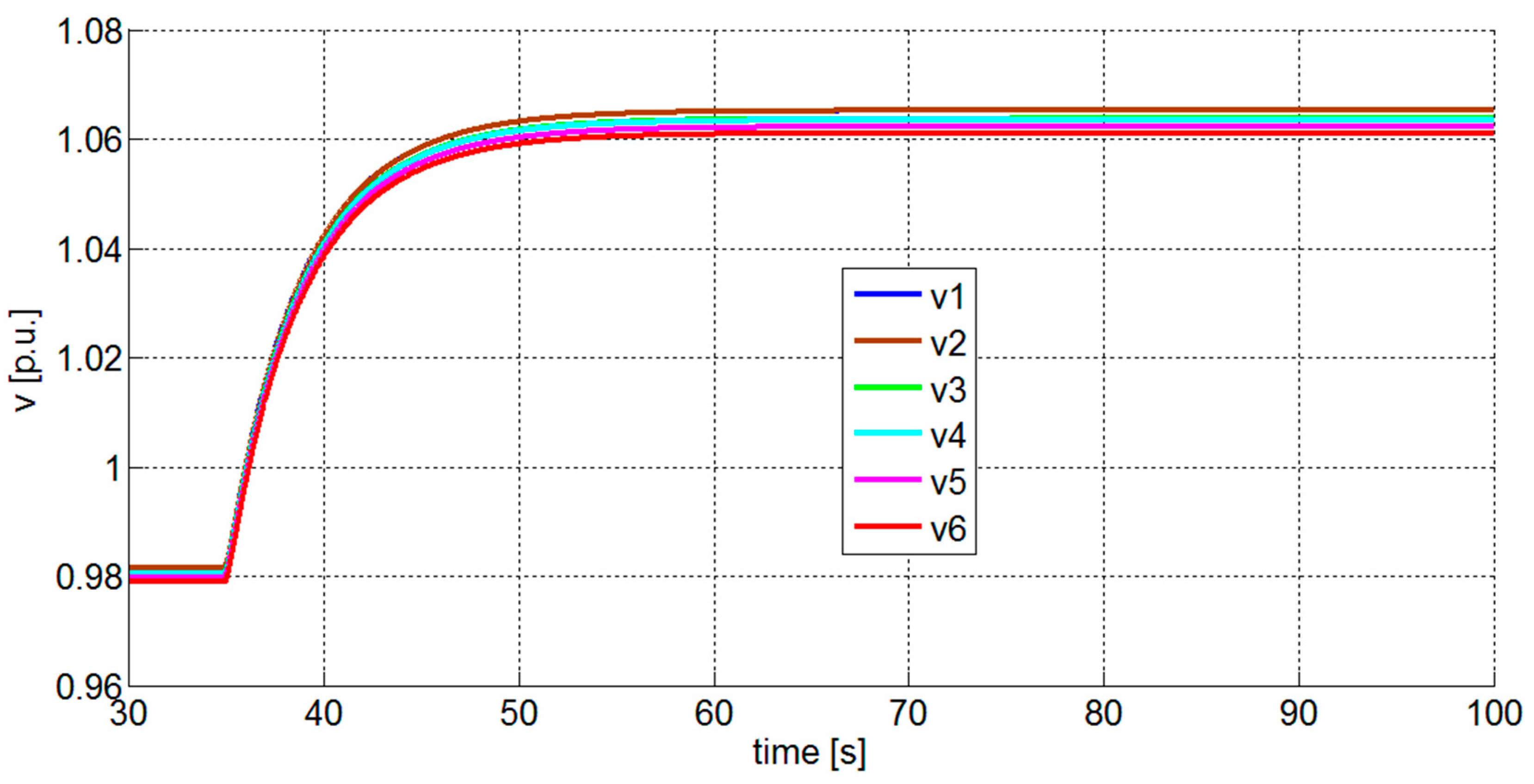
4. Case Studies
4.1. Case A) 940 MVA Combined-Cycle Power Plant
4.2. Case B) Synchronous Condenser of 160 MVA
4.3. Case C) PV Power Plant of 46.8 MWp
5. Results and Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AVR | Automatic Voltage Regulator |
| BVR | Busbar Voltage Regulator |
| DD | Dynamic Decoupling |
| DGs | Distributed Generators |
| GRPRs | Generator Reactive Power Regulators |
| HV | High Voltage |
| LV | Low Voltage |
| MIMO | Multiple-Input-Multiple-Output |
| MV | Medium Voltage |
| PI | Proportional-Integral |
| POC | Point Of Connection |
| PV | Photovoltaic |
| RES | Renewable Energy Sources |
| RPR | Reactive Power Regulator |
| SFC | Static Frequency Converter |
| SISO | Single-Input-Single-Output |
| STATCOM | Static Synchronous Compensator |
| SVR | Secondary Voltage Regulation |
| TSO | Transmission System Operator |
| VPP | Virtual Power Plants |
| VSC | Voltage Source Converter |
| VSN | Virtual Smart Network |
References
- van Wyk, A.A.L.; Khan, M.A.; Barendse, P. Impact of over/under and voltage unbalanced supplies on Energy-Efficient motors. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 1380–1385. [Google Scholar]
- Jahmeerbacus, I.; Bhurtun, C. Energy efficiency and power quality issues of AC voltage controllers in instant water heaters. In Proceedings of the 2012 20th Domestic Use of Energy Conference, Cape Town, South Africa, 3–4 April 2012; pp. 139–144. [Google Scholar]
- Lipsky, A.; Braunstein, A.; Miteva, N.; Slonim, M. Electric power quality and efficiency of power supply. In Proceedings of the 21st IEEE Convention of the Electrical and Electronic Engineers in Israel. Proceedings (Cat. No.00EX377), Tel-Aviv, Israel, 11–12 April 2000; pp. 222–225. [Google Scholar]
- Fusco, G.; Russo, M. Adaptive Voltage Control System; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Chiandone, M.; Sulligoi, G.; Massucco, S.; Silvestro, F. Hierarchical voltage regulation of transmission systems with renewable power plants: An overview of the Italian case. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014; pp. 1–5. [Google Scholar]
- Mousavi, O.A.; Cherkaoui, R. Literature Survey on Fundamental Issues of Voltage and Reactive Power Control; École polytechnique fédérale de Lausanne: Lausanne, Switzerland, 2011. [Google Scholar]
- Mohandes, B.; el Moursi, M.S.; Hatziargyriou, N.D.; el Khatib, S. A review of power system flexibility with high penetration of renewables. IEEE Trans. Power Syst. 2019, 34, 3140–3155. [Google Scholar] [CrossRef]
- Sun, H.; Guo, Q.; Qi, J.; Ajjarapu, V.; Bravo, R.; Chow, J.; Li, Z.; Moghe, R.; Nasr-Azadani, E.; Tamrakar, U.; et al. Review of challenges and research opportunities for voltage control in smart grids. IEEE Trans. Power Syst. 2019, 34, 2790–2801. [Google Scholar] [CrossRef] [Green Version]
- Vita, V.; Alimardan, T.; Ekonomou, L. The impact of distributed generation in the distribution networks’ voltage profile and energy losses. In Proceedings of the 9th IEEE European Modelling Symposium on Mathematical Modelling and Computer Simulation, Madrid, Spain, 6–8 October 2015; pp. 260–265. [Google Scholar]
- Ceaki, O.; Seritan, G.; Vatu, R.; Mancasi, M. Analysis of power quality improvement in smart grids. In Proceedings of the 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2017; pp. 797–801. [Google Scholar]
- Nieto, A.; Vita, V.; Maris, T.I. Power quality improvement in power grids with the integration of energy storage systems. Int. J. Eng. Res. Technol. 2016, 5, 438–443. [Google Scholar]
- European Commission. EU Energy in Figures—Statistical Pocketbook 2016; Publications Office of the European Union: Brussels, Belgium, 2016.
- The International Renewable Energy Agency. Renewable Energy Statistics 2016; IRENA: Abu Dhabi, UAE, 2016. [Google Scholar]
- Renewable Energy Policy Network for the 21st Century (REN21). Renewables 2014 Global Status Report; REN21: Paris, France, 2014. [Google Scholar]
- GSE S.p.A. Rapporto Statistico 2014—Solare Fotovoltaico; GSE S.p.A.: Rome, Italy, 2015. [Google Scholar]
- Petinrin, J.O.; Shaaban, M. Impact of renewable generation on voltage control in distribution systems. Renew. Sustain. Energy Rev. 2016, 65, 770–783. [Google Scholar] [CrossRef]
- Pfeiffer, R. Brief status on CENELEC standards related to Connection Network Code. In Proceedings of the 3rd Grid Connection Stakeholder Committee Meeting, Brussels, Belgium, 8 September 2016. [Google Scholar]
- Bründlinger, R. Advanced smart inverter and DER functions Requirements in latest European Grid Codes and future trends. In Proceedings of the Solar Canada 2015 Conference, Toronto, ON, Canada, 7–8 December 2015. [Google Scholar]
- ENTSO-E. Implementation Guideline for Network Code “Requirements for Grid Connection Applicable to all Generators”; ENTSO-E: Brussels, Belgium, 2013. [Google Scholar]
- The European Commission. Commission Regulation (EU) 2016/631 of 14 April 2016 Establishing a Network Code on Requirements for Grid Connection of Generators; Official Journal of the European Union: Brussels, Belgium, 2016. [Google Scholar]
- Arrinda, J.; Barrena, J.A.; Rodríguez, M.A.; Guerrero, A. Analysis of massive integration of renewable power plants under new regulatory frameworks. In Proceedings of the 2014 International Conference on Renewable Energy Research and Application (ICRERA), Milwaukee, WI, USA, 19–22 October 2014; pp. 462–467. [Google Scholar]
- Varma, R.K.; Salama, M. Large-scale photovoltaic solar power integration in transmission and distribution networks. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–4. [Google Scholar]
- Delfino, F.; Procopio, R.; Rossi, M.; Ronda, G. Integration of large-size photovoltaic systems into the distribution grids: A P-Q chart approach to assess reactive support capability. IET Renew. Power Gener. 2010, 4, 329–340. [Google Scholar] [CrossRef]
- Tyll, H.K.; Schettle, F. Historical overview on dynamic reactive power compensation solutions from the begin of AC power transmission towards present applications. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–7. [Google Scholar]
- Ghasemi, M.A.; Parniani, M. Prevention of distribution network overvoltage by adaptive droop-based active and reactive power control of PV systems. Electric Power Syst. Res. 2016, 133, 313–327. [Google Scholar] [CrossRef]
- Hashemi, M.; Agelidis, V. Evaluation of voltage regulation mitigation methods due to high penetration of PV generation in residential areas. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; pp. 1180–1189. [Google Scholar]
- Hasheminamin, M.; Agelidis, V.G.; Ahmadi, A.; Siano, P.; Teodorescu, R. Single-point reactive power control method on voltage rise mitigation in residential networks with high PV penetration. Renew. Energy 2018, 119, 504–512. [Google Scholar] [CrossRef]
- Rallabandi, V.; Akeyo, O.M.; Ionel, D.M. Modeling of a multi-megawatt grid connected PV system with integrated batteries. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 1146–1151. [Google Scholar]
- Olival, P.C.; Madureira, A.G.; Matos, M. Advanced voltage control for smart microgrids using distributed energy resources. Electr. Power Syst. Res. 2017, 146, 132–140. [Google Scholar] [CrossRef]
- Jayasekara, N.; Wolfs, P.; Masoum, M.A.S. An optimal management strategy for distributed storages in distribution networks with high penetrations of PV. Electr. Power Syst. Res. 2014, 116, 147–157. [Google Scholar] [CrossRef]
- Ko, H.; Bruey, S.; Jatskevich, J.; Dumont, G.; Moshref, A. A PI Control of DFIG-Based Wind Farm for Voltage Regulation at Remote Location. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar]
- Baalbergen, F.; Gibescu, M.; van der Sluis, L. Voltage stability consequences of decentralized generation and possibilities for intelligent control. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010; pp. 1–8. [Google Scholar]
- Zhao, J.; Li, X.; Hao, J.; Lu, J. Reactive power control of wind farm made up with doubly fed induction generators in distribution system. Electr. Power Syst. Res. 2010, 80, 698–706. [Google Scholar] [CrossRef]
- El-Fouly, T.H.M.; El-Saadany, E.F.; Salama, M.M.A. Voltage regulation of wind farms equipped with variable-speed doubly-fed induction generators wind turbines. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Qin, N.; Bak, C.L.; Abildgaard, H. Automatic voltage control system with market price employing large wind farms. Electr. Power Syst. Res. 2018, 157, 93–105. [Google Scholar] [CrossRef]
- Mastromauro, R.A.; Orlando, N.A.; Ricchiuto, D.; Liserre, M.; Dell’Aquila, A. Hierarchical control of a small wind turbine system for active integration in LV distribution network. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 426–433. [Google Scholar]
- Koraki, D.; Strunz, K. Wind and solar power integration in electricity markets and distribution networks through service-centric virtual power plants. IEEE Trans. Power Syst. 2018, 33, 473–485. [Google Scholar] [CrossRef]
- Unger, D.; Spitalny, L.; Myrzik, J.M.A. Voltage control by small hydro power plants integrated into a virtual power plant. In Proceedings of the 2012 IEEE Energytech, Cleveland, OH, USA, 29–31 May 2012; pp. 1–6. [Google Scholar]
- Dielmann, K.; van der Velden, A. Virtual power plants (VPP)—A new perspective for energy generation? In Proceedings of the 9th International Scientific and Practical Conference of Students, Post-graduates Modern Techniques and Technologies, 2003, MTT 2003, Tomsk, Russia, 7–11 April 2003. [Google Scholar]
- Pudjianto, D.; Ramsay, C.; Strbac, G. Virtual power plant and system integration of distributed energy resources. IET Renew. Power Gener. 2007, 1, 10–16. [Google Scholar] [CrossRef]
- Ricerca Sistema Energetico (RSE). Definizione dei Concetti e Delle Architetture di Gestione, Controllo e Comunicazione di Microreti e Virtual Power Plant; Progetto RdS—Trasmissione e Distribuzione; RSE: Milan, Italy, 2006. [Google Scholar]
- Arcidiacono, V. Automatic Voltage and Reactive Power Control in Transmission Systems. In Proceedings of the 1983 CIGRE-IFAC Symposium, Florence, Italy, 26–28 September 1983. Survey paper. [Google Scholar]
- Paul, J.P.; Leost, J.Y.; Tesseron, J.M. Survey of the Secondary Voltage Control in France: Present Realization and Investigations. IEEE Trans. Power Syst. 1987, 2, 505–511. [Google Scholar] [CrossRef]
- Sancha, J.L.; Fernandez, J.L.; Cortes, A.; Abarca, J.T. Secondary voltage control: Analysis, solutions and simulation results for the Spanish transmission system. IEEE Trans. Power Syst. 1996, 11, 630–638. [Google Scholar] [CrossRef]
- Automatic System for Voltage Regulation (SART) for Electric Power Plant, GRTN Document nr. DRRPX03019. Available online: http://www.terna.it/LinkClick.aspx?fileticket=irZ1FD%2BYxUE%3D&tabid=106&mid=468 (accessed on 11 April 2020).
- Lagonotte, P.; Sabonnadiere, J.C.; Leost, J.Y.; Paul, J.P. Structural analysis of the electrical system: Application to secondary voltage control in France. IEEE Trans. Power Syst. 1989, 4, 479–486. [Google Scholar] [CrossRef]
- Sancha, J.L.; Fernandez, J.L.; Martinez, F.; Salle, C. Spanish practices in reactive power management and voltage control. In Proceedings of the IEE Colloquium on International Practices in Reactive Power Control, London, UK, 7 April 1993; pp. 3/1–3/4. [Google Scholar]
- Sulligoi, G.; Chiandone, M.; Arcidiacono, V. NewSART automatic voltage and reactive power regulator for secondary voltage regulation: Design and application. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Arcidiacono, V.; Menis, R.; Sulligoi, G. Improving power quality in all electric ships using a voltage and VAR integrated regulator. In Proceedings of the 2007 IEEE Electric Ship Technologies Symposium, Arlington, VA, USA, 21–23 May 2007; pp. 322–327. [Google Scholar]
- TERNA. Sistema Automatico per la Regolazione di Tensione (SART) per Centrali Elettriche di Produzione. Annex A16 to the National Grid Code, GRTN Document nr. DRRPX03019. Available online: http://collaudo.download.terna.it/terna/0000/0105/33.pdf(accessed on 11 April 2020).
- Tamimi, B.; Cañizares, C.; Bhattacharya, K. Modeling and performance analysis of large solar photo-voltaic generation on voltage stability and inter-area oscillations. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
- Vasquez, J.C.; Mastromauro, R.A.; Liserre, J.M. Voltage support provided by a droop-controlled multifunctional inverter. IEEE Trans. Ind. Electron. 2009, 56, 4510–4519. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E.; Liserre, M.; Mastromauro, R.A. Online Optimal Reactive Power Control Strategy of PV Inverters. IEEE Trans. Ind. Electron. 2011, 58, 4549–4558. [Google Scholar] [CrossRef]
- Campaner, R.; Chiandone, M.; Arcidiacono, V.; Sulligoi, G.; Milano, F. Automatic voltage control of a cluster of hydro power plants to operate as a virtual power plant. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 2153–2158. [Google Scholar]
- Chiandone, M.; Campaner, R.; Arcidiacono, V.; Sulligoi, G.; Milano, F. Automatic voltage and reactive power regulator for wind farms participating to TSO voltage regulation. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–5. [Google Scholar]
- Chiandone, M.; Campaner, R.; Pavan, A.M.; Arcidiacono, V.; Milano, F.; Sulligoi, G. Coordinated voltage control of multi-converter power plants operating in transmission systems. The case of photovoltaics. In Proceedings of the 2015 International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 506–510. [Google Scholar]
- Gao, B.; Morison, G.K.; Kundur, P. Voltage Stability evaluation using modal analysis. IEEE Trans. Power Syst. 1992, 7, 1529–1542. [Google Scholar] [CrossRef]
- Carvalho, P.M.; Correia, P.F.; Ferreira, L.A. Distributed reactive power generation control for voltage rise mitigation in distribution networks. IEEE Trans. Power Syst. 2008, 23, 766–772. [Google Scholar] [CrossRef]
- Milano, F. A python-based software tool for power system analysis. In Proceedings of the IEEE PES General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]




















| Line Type | Graphic Symbol | R | X | C |
|---|---|---|---|---|
| (Ω/km) | (Ω/km) | (μF/km) | ||
| RG7H1R 3 × 1 × 240 mm2 |  | 0.0754 | 0.12 | 0.25 |
| RG7H1R 3 × 1 × 120 mm2 |  | 0.153 | 0.11 | 0.32 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiandone, M.; Campaner, R.; Bosich, D.; Sulligoi, G. A Coordinated Voltage and Reactive Power Control Architecture for Large PV Power Plants. Energies 2020, 13, 2441. https://doi.org/10.3390/en13102441
Chiandone M, Campaner R, Bosich D, Sulligoi G. A Coordinated Voltage and Reactive Power Control Architecture for Large PV Power Plants. Energies. 2020; 13(10):2441. https://doi.org/10.3390/en13102441
Chicago/Turabian StyleChiandone, Massimiliano, Riccardo Campaner, Daniele Bosich, and Giorgio Sulligoi. 2020. "A Coordinated Voltage and Reactive Power Control Architecture for Large PV Power Plants" Energies 13, no. 10: 2441. https://doi.org/10.3390/en13102441
APA StyleChiandone, M., Campaner, R., Bosich, D., & Sulligoi, G. (2020). A Coordinated Voltage and Reactive Power Control Architecture for Large PV Power Plants. Energies, 13(10), 2441. https://doi.org/10.3390/en13102441






