Dynamic Voltage Support of Converters during Grid Faults in Accordance with National Grid Code Requirements
Abstract
:1. Introduction
1.1. Requirements and Relevant Standards for the Behavior of Converters during Grid Faults
1.1.1. LVRT
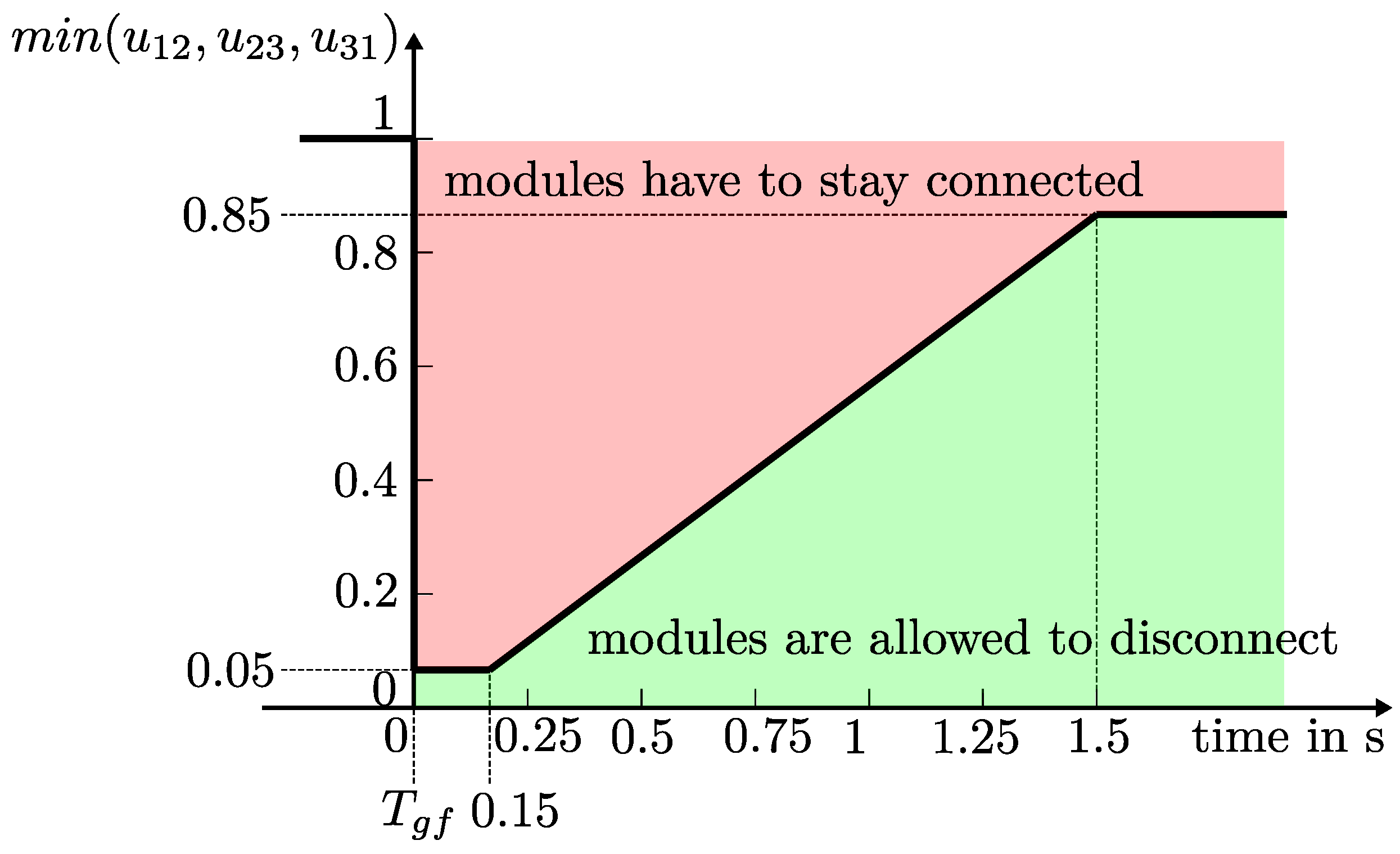
1.1.2. Dynamic Voltage Support during Grid Faults
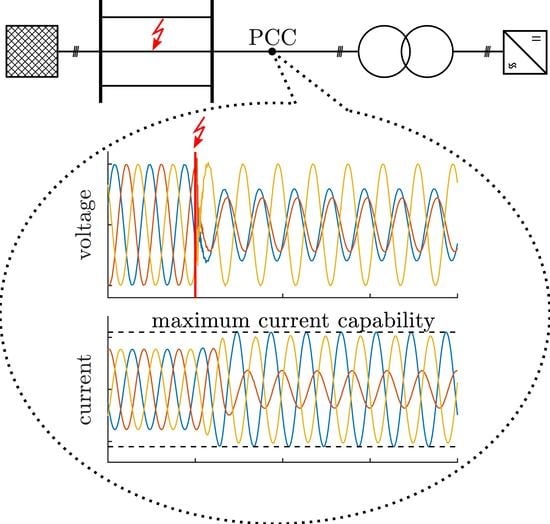
1.2. Current Limitation
2. Simulation
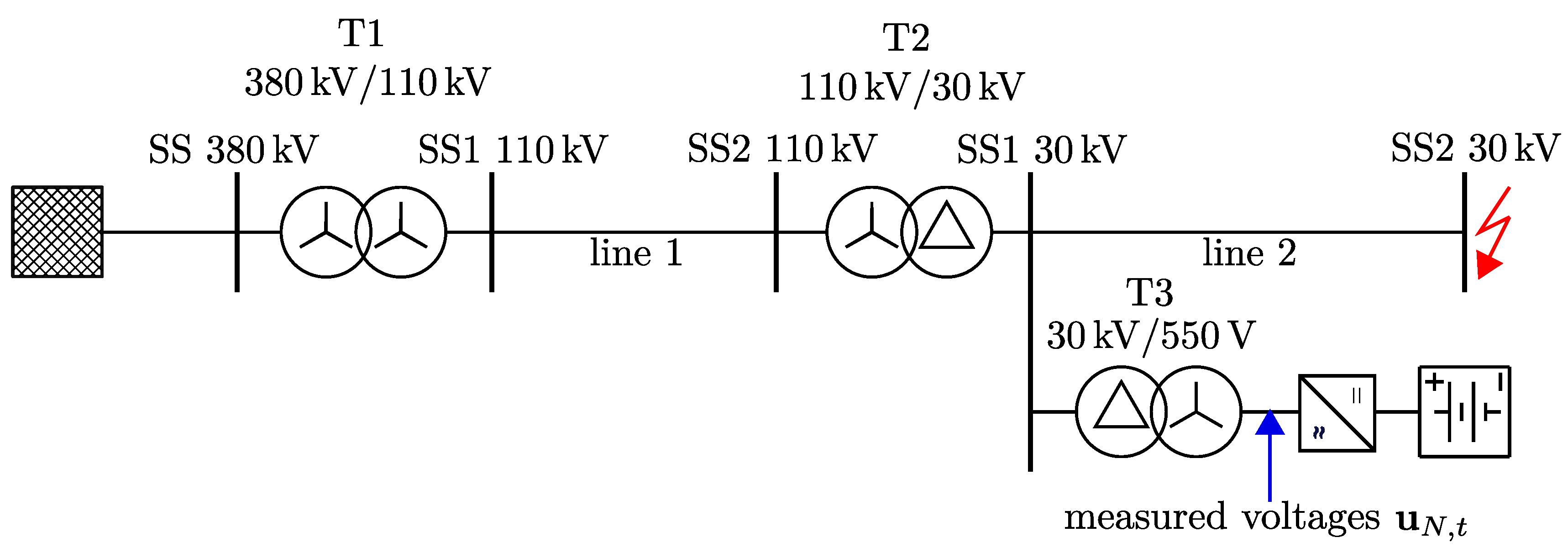
2.1. Description of the Model
| Algorithm 1: Implementation of a current limitation according to Section 1.2 |
 |
2.2. LC-Filter Design Considerations and Tuning of the Inverter Current Control
2.3. Application of the Model
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
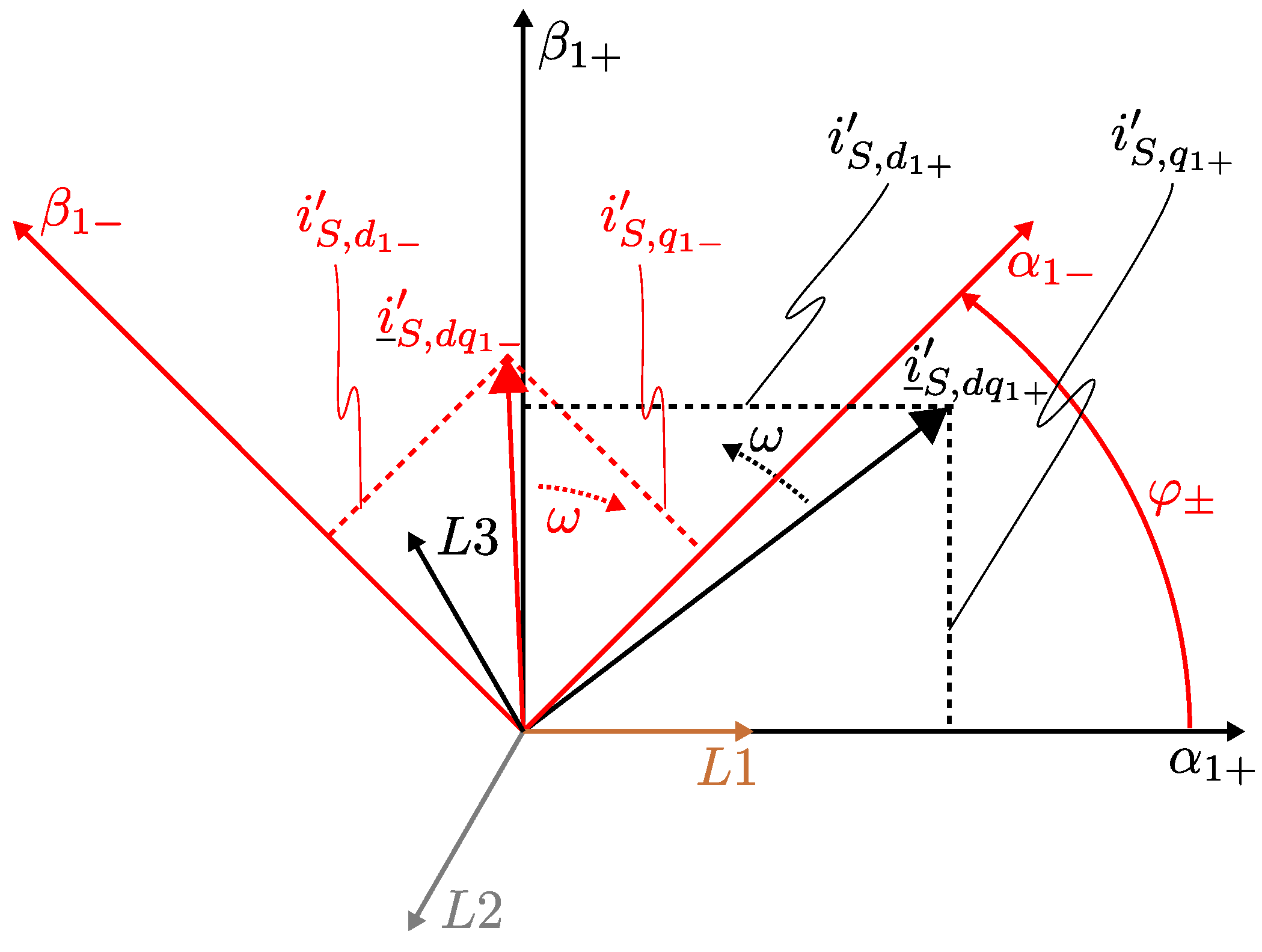
Appendix A. Calculation of the Positive- and Negative-Sequence Voltages in the Sequence Analyzer
Appendix B. List of Symbols
| normalized instantaneous current vector | |
| instantaneous value of the current in phase L1 | |
| instantaneous value of the current in phase L2 | |
| instantaneous value of the current in phase L3 | |
| peak value of the current capability | |
| current space vector in the -plane | |
| current space vector in the dq-plane | |
| positive-sequence component of the current space vector | |
| negative-sequence component of the current space vector | |
| reference value of the direct/active, positive-sequence component of the normalized current space vector | |
| reference value of the quadrature/reactive, positive-sequence component of the normalized current space vector | |
| reference value of the direct/active, negative-sequence component of the normalized current space vector | |
| reference value of the quadrature/reactive, negative-sequence component of the normalized current space vector | |
| limited reference value of the direct/active, positive-sequence component of the normalized current space vector | |
| limited reference value of the quadrature/reactive, positive-sequence component of the normalized current space vector | |
| limited reference value of the direct/active, negative-sequence component of the normalized current space vector | |
| limited reference value of the quadrature/reactive, negative-sequence component of the normalized current space vector | |
| direct/active, positive-sequence component of the normalized current output space vector | |
| quadrature/reactive, positive-sequence component of the normalized current output space vector | |
| direct/active, negative-sequence component of the normalized current output space vector | |
| quadrature/reactive, negative-sequence component of the normalized current output space vector | |
| phase-to-phase root-mean-square voltage vector | |
| nominal phase-to-phase voltage | |
| normalized phase-to-phase root-mean-square voltage vector | |
| normalized phase-to-phase root-mean-square voltage between L1-L2 | |
| normalized phase-to-phase root-mean-square voltage between L2-L3 | |
| normalized phase-to-phase root-mean-square voltage between L3-L1 | |
| normalized phase-to-neutral instantaneous voltage vector | |
| normalized phase-to-neutral instantaneous reference voltage vector | |
| normalized phase-to-neutral instantaneous voltage in L1 | |
| normalized phase-to-neutral instantaneous voltage in L2 | |
| normalized phase-to-neutral instantaneous voltage in L3 | |
| normalized voltage space vector in the dq-plane | |
| direct/active, positive-sequence component of the normalized voltage output space vector | |
| quadrature/reactive, positive-sequence component of the normalized voltage output space vector | |
| direct/active, negative-sequence component of the normalized voltage output space vector | |
| quadrature/reactive, negative-sequence component of the normalized voltage output space vector | |
| reference value of the direct/active, positive-sequence component of the normalized voltage output space vector | |
| reference value of the quadrature/reactive, positive-sequence component of the normalized voltage output space vector | |
| reference value of the direct/active, negative-sequence component of the normalized voltage output space vector | |
| reference value of the quadrature/reactive, negative-sequence component of the normalized voltage output space vector | |
| complex value of the normalized positive-sequence voltage | |
| complex value of the normalized negative-sequence voltage | |
| magnitude of the normalized positive-sequence voltage | |
| magnitude of the normalized negative-sequence voltage | |
| angle of the normalized positive-sequence voltage | |
| angle between the positive- and negative sequence voltage | |
| 1-minute average of the mean value of the phase-to-phase voltages | |
| DC-link voltage | |
| instantaneous phase-to-neutral voltage in L1 at the inverter output | |
| instantaneous phase-to-neutral voltage in L2 at the inverter output | |
| instantaneous phase-to-neutral voltage in L3 at the inverter output | |
| starting time of a grid fault | |
| p | normalized active power output of the converter |
| q | normalized reactive power output of the converter |
| reference value of the active power | |
| reference value of the reactive power | |
| angular frequency | |
| nominal angular frequency | |
| L | inductance of the LC-filter |
| l | normalized inductance of the LC-filter |
| R | resistance of the LC-filter |
| C | capacitance of the LC-filter |
| time constant of the current control loop | |
| proportional controller gain of the current control loop | |
| integral controller gain of the current control loop | |
| proportional factor of the reactive current injection in the positive-sequence system | |
| proportional factor of the reactive current injection in the negative-sequence system | |
| switching frequency of the switching control | |
| nominal apparent power of the converter | |
| maximum current ripple at the converter output | |
| transfer function of the current controller | |
| process transfer function of the current control loop | |
| loop gain of the current control loop |
References
- Erlich, I.; Neumann, T.; Shewarega, F.; Schegner, P.; Meyer, J. Wind turbine negative sequence current control and its effect on power system protection. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- VDE. VDE-AR-N 4110: Technische Regeln für den Anschluss von Kundenanlagen an das Mittelspannungsnetz und deren Betrieb (TAR Mittelspannung). 2017. Available online: https://www.vde.com/de/fnn/arbeitsgebiete/tar/tar-mittelspannung-vde-ar-n-4110 (accessed on 9 May 2020).
- E-Control. Technische und organisatorische Regeln für Betreiber und Benutzer von Netzen: TOR Erzeuger: Anschluss und Parallelbetrieb von Stromerzeugungsanlagen des Typs B. 2019. Available online: https://www.e-control.at/documents/1785851/1811582/TOR+Erzeuger+Typ+B+V1.0.pdf/a9a7e5ae-5842-caa9-d2c0-93be4b6e0802?t=1562757801048 (accessed on 9 May 2020).
- Castilla, M.; Miret, J.; Sosa, J.L.; Matas, J.; de Vicu na, L.G. Grid-fault control scheme for three-phase photovoltaic inverters with adjustable power quality characteristics. IEEE Trans. Power Electron. 2010, 25, 2930–2940. [Google Scholar] [CrossRef]
- Chaudhary, S.K.; Teodorescu, R.; Rodriguez, P.; Kjaer, P.C.; Gole, A.M. Negative sequence current control in wind power plants with VSC-HVDC connection. IEEE Trans. Sustain. Energy 2012, 3, 535–544. [Google Scholar] [CrossRef]
- Mortazavian, S.; Shabestary, M.M.; Mohamed, Y.A.R.I. Analysis and dynamic performance improvement of grid-connected voltage–source converters under unbalanced network conditions. IEEE Trans. Power Electron. 2016, 32, 8134–8149. [Google Scholar] [CrossRef]
- Camacho, A.; Castilla, M.; Miret, J.; Borrell, A.; de Vicu na, L.G. Active and reactive power strategies with peak current limitation for distributed generation inverters during unbalanced grid faults. IEEE Trans. Ind. Electron. 2014, 62, 1515–1525. [Google Scholar] [CrossRef] [Green Version]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 29. [Google Scholar]
- Jia, J.; Yang, G.; Nielsen, A.H. Investigation of grid-connected voltage source converter performance under unbalanced faults. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 609–613. [Google Scholar]
- Du, X.; Wu, Y.; Gu, S.; Tai, H.M.; Sun, P.; Ji, Y. Power oscillation analysis and control of three-phase grid-connected voltage source converters under unbalanced grid faults. IET Power Electron. 2016, 9, 2162–2173. [Google Scholar] [CrossRef]
- Rodriguez, P.; Timbus, A.V.; Teodorescu, R.; Liserre, M.; Blaabjerg, F. Flexible active power control of distributed power generation systems during grid faults. IEEE Trans. Ind. Electron. 2007, 54, 2583–2592. [Google Scholar] [CrossRef]
- López, M.A.G.; de Vicu na, J.L.G.; Miret, J.; Castilla, M.; Guzmán, R. Control strategy for grid-connected three-phase inverters during voltage sags to meet grid codes and to maximize power delivery capability. IEEE Trans. Power Electron. 2018, 33, 9360–9374. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.; Lee, K.J.; Lee, J.P.; Yoo, D.W.; Kim, H.J. Implementation of fault ride-through techniques of grid-connected inverter for distributed energy resources with adaptive low-pass notch PLL. IEEE Trans. Power Electron. 2014, 30, 2859–2871. [Google Scholar] [CrossRef]
- Göksu, Ö.; Teodorescu, R.; Bak, C.L.; Iov, F.; Kjær, P.C. Impact of wind power plant reactive current injection during asymmetrical grid faults. IET Renew. Power Gener. 2013, 7, 484–492. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current reference generation based on next generation grid code requirements of grid-tied converters during asymmetrical faults. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef] [Green Version]
- Wurm, M. 110-und 30-kV-Netzkurzschlussversuche mit einem 2, 2-MWh-Batteriespeicher. E I Elektrotechnik Und Inf. 2019, 136, 21–30. [Google Scholar] [CrossRef]
- European Union. Commission Regulation (EU) 2016/631; Establishing a Network Code on Requirements for Grid Connection of Generators (RfG). 2016. Available online: http://data.europa.eu/eli/reg/2016/631/oj (accessed on 9 May 2020).
- IEC 60909-0:2016. Short-Circuit Currents in Three-Phase a.c. Systems—Part 0: Calculation of Currents. 2016. Available online: https://webstore.iec.ch/publication/24100 (accessed on 9 May 2020).
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A review of passive power filters for three-phase grid-connected voltage-source converters. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 54–69. [Google Scholar] [CrossRef] [Green Version]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Marchgraber, J.; Gawlik, W.; Wurm, M. Modellierung der dynamischen Netzstützung von über Umrichter angebundenen Erzeugungsanlagen und Speichern. E I Elektrotechnik Und Inf. 2019, 136, 31–38. [Google Scholar] [CrossRef] [Green Version]
- FGW. Technische Richtlinien für Erzeugungseinheiten und -anlagen; Teil 3 (TR3); Bestimmung der elektrischen Eigenschaften von Erzeugungseinheiten und -anlagen am Mittel-, Hoch- und Höchstspannungsnetz. 2017. Available online: https://wind-fgw.de/wp-content/uploads/2018/10/FGW/Teil3/Rev25/preview/180901-1.pdf (accessed on 9 May 2020).




| Parameter | Value |
|---|---|
| 550 | |
| 650 kVA | |
| 900 | |
| 8 | |
| L | 280 |
| R | 1 |
| C | 342 |
| pu | |
| 20 | |
| 14 pu | |
| 50 pu |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchgraber, J.; Gawlik, W. Dynamic Voltage Support of Converters during Grid Faults in Accordance with National Grid Code Requirements. Energies 2020, 13, 2484. https://doi.org/10.3390/en13102484
Marchgraber J, Gawlik W. Dynamic Voltage Support of Converters during Grid Faults in Accordance with National Grid Code Requirements. Energies. 2020; 13(10):2484. https://doi.org/10.3390/en13102484
Chicago/Turabian StyleMarchgraber, Jürgen, and Wolfgang Gawlik. 2020. "Dynamic Voltage Support of Converters during Grid Faults in Accordance with National Grid Code Requirements" Energies 13, no. 10: 2484. https://doi.org/10.3390/en13102484