Interleaved High Step-Up DC–DC Converter with Voltage-Lift and Voltage-Stack Techniques for Photovoltaic Systems †
Abstract
1. Introduction
- (1)
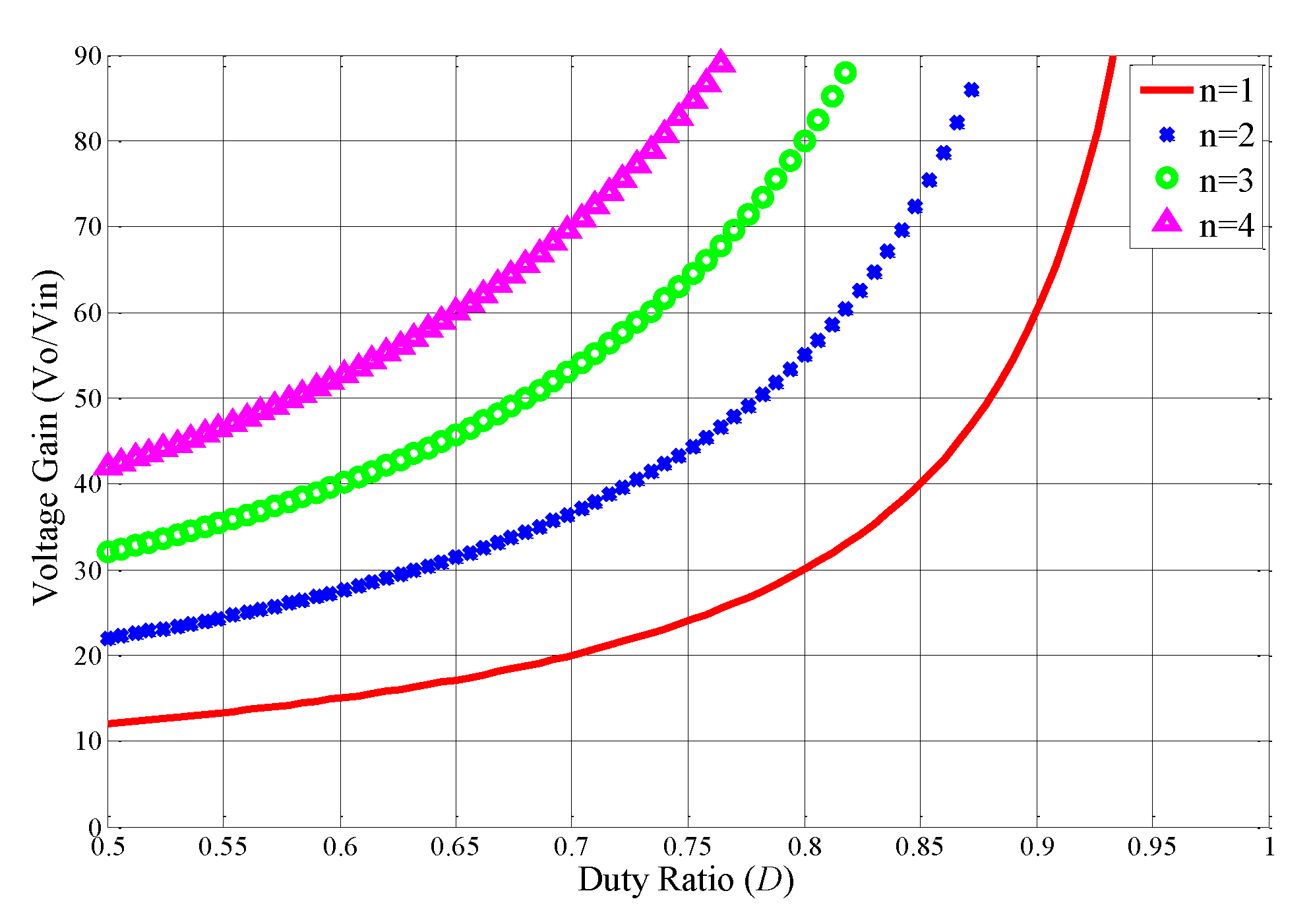
- By designing a proper turns ratio for the coupled inductors, the high voltage conversion ratio can be obtained whilst operating at an appropriate duty ratio.
- (2)
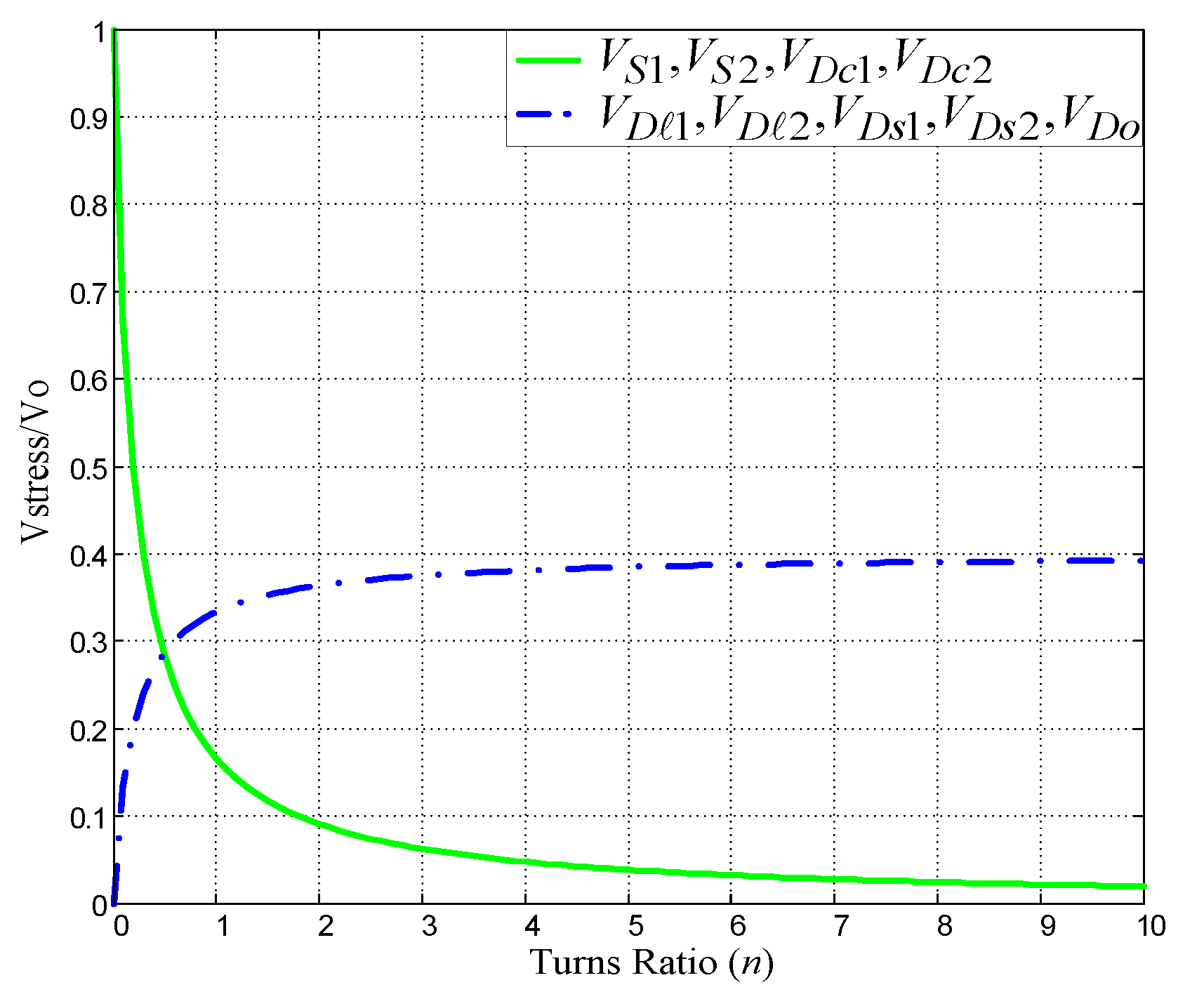
- The voltage stresses on the power switches are greatly less than the output voltage, so the power switches with lower on-state resistances are utilized to decrease the conduction losses.
- (3)
- The power switches achieve zero-current switching at turn on, and the switching losses can thereby be reduced.
- (4)
- The diode reverse-recovery problem is effectively alleviated by the leakage inductances of the coupled inductors.
- (5)
- The leakage inductor energy can be recycled to suppress the voltage spikes on the power switches.
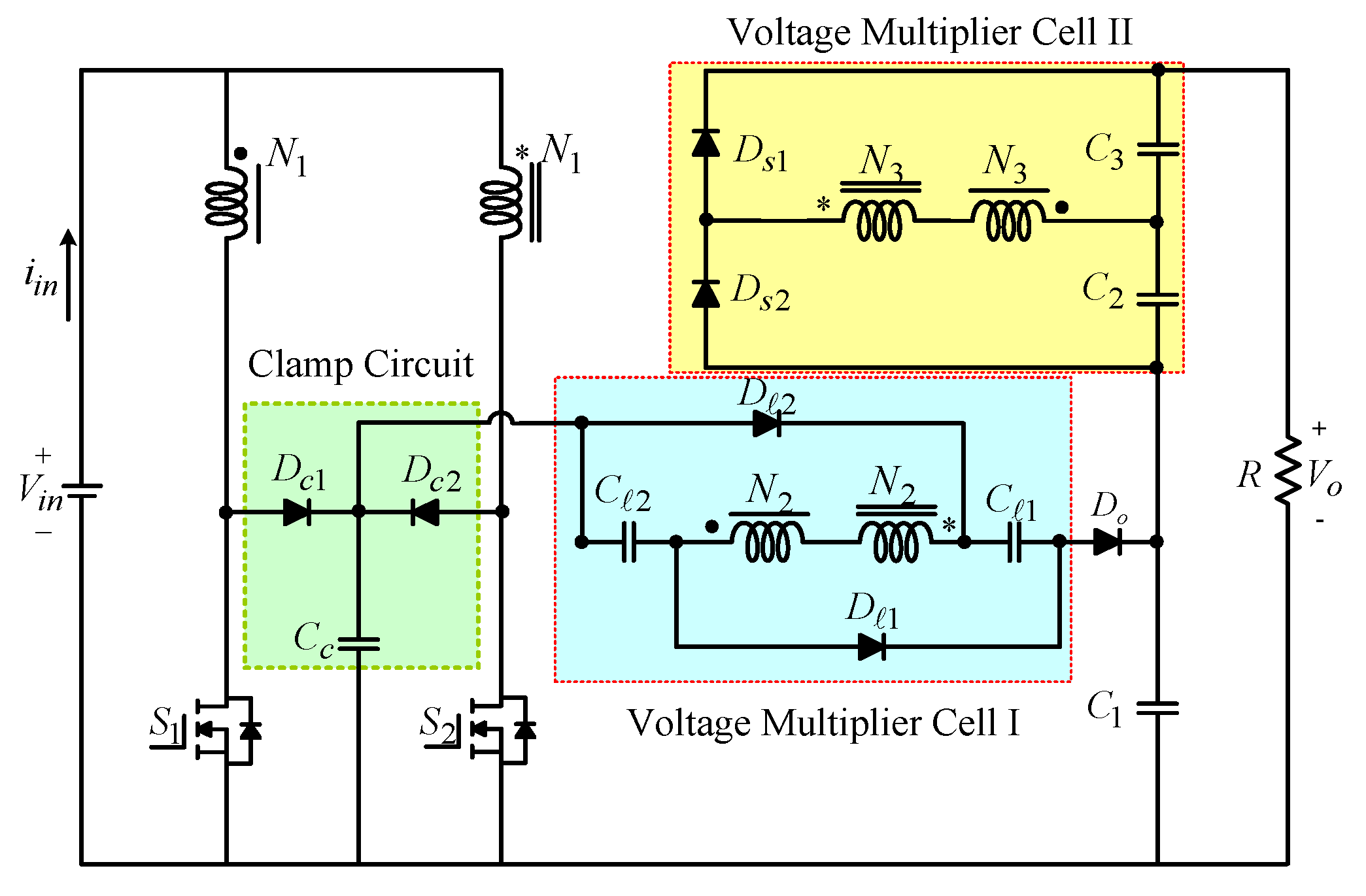
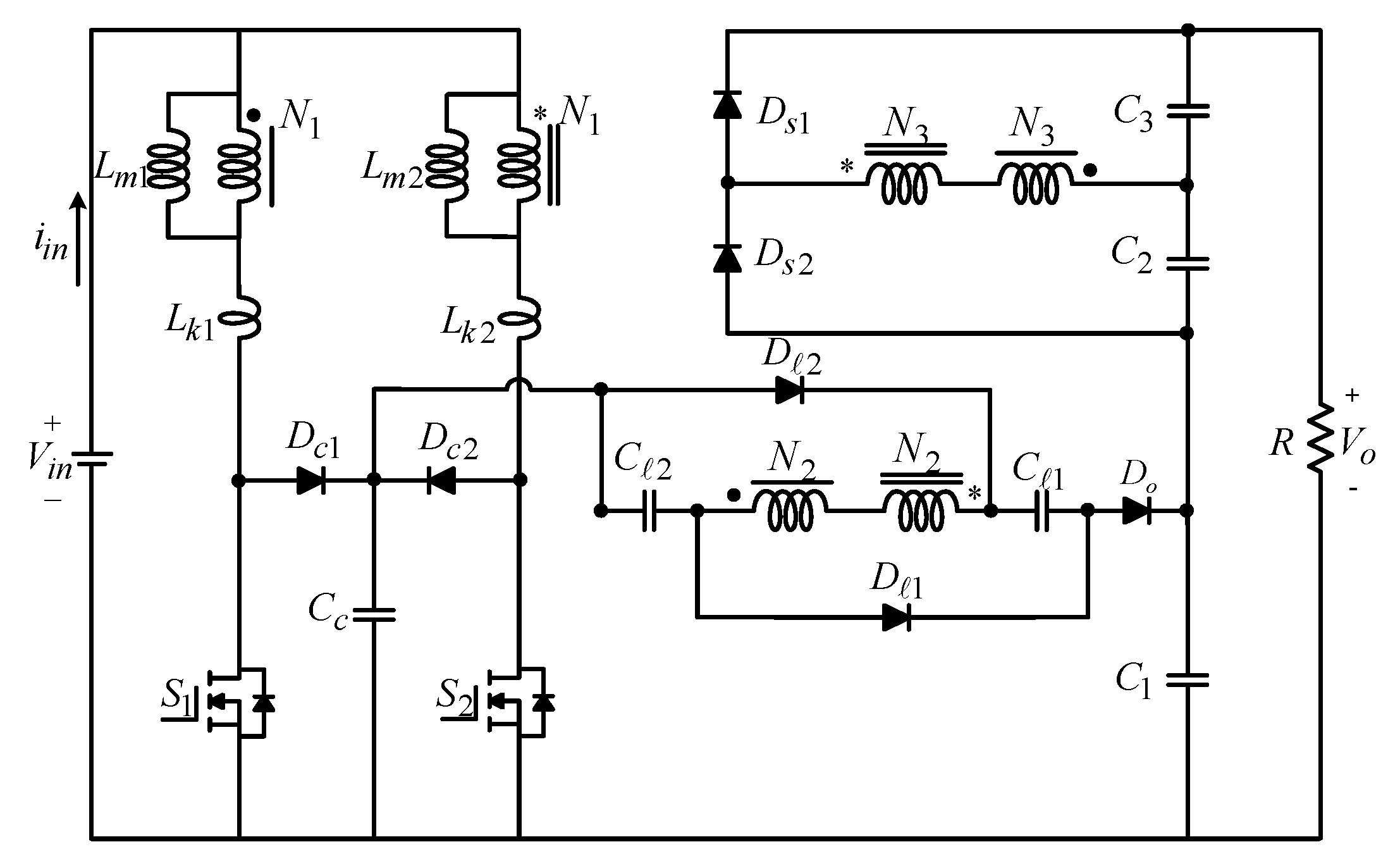
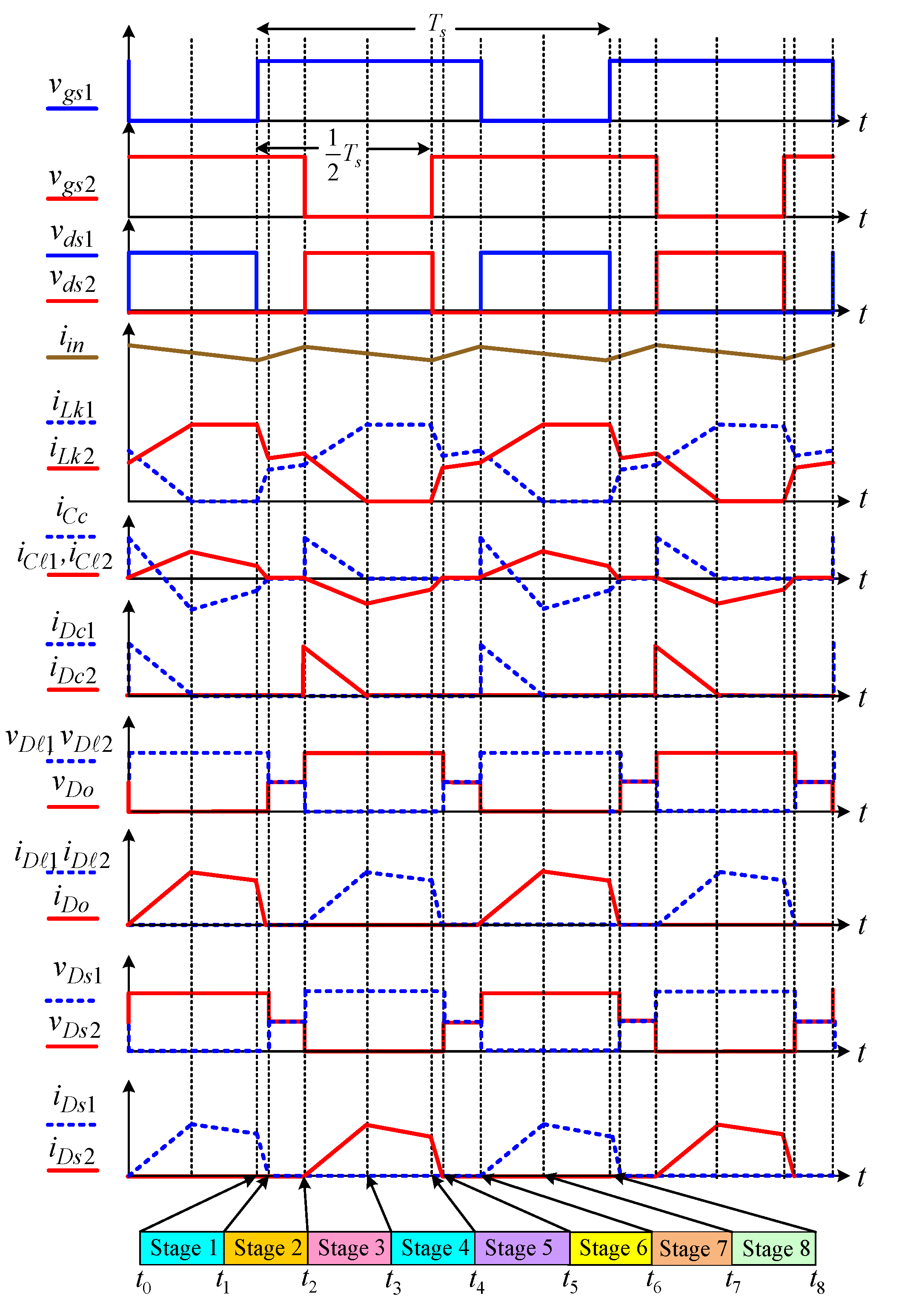
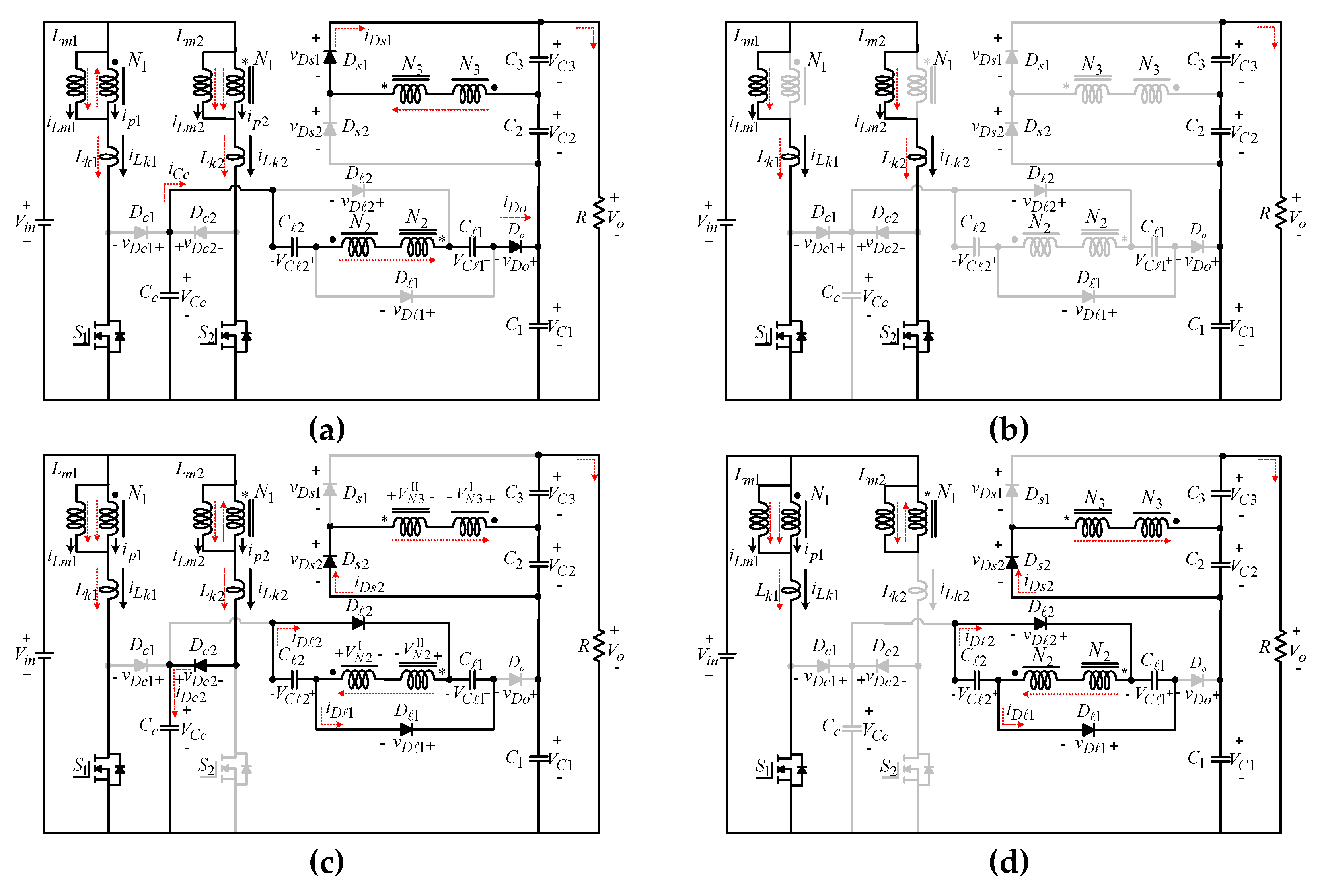
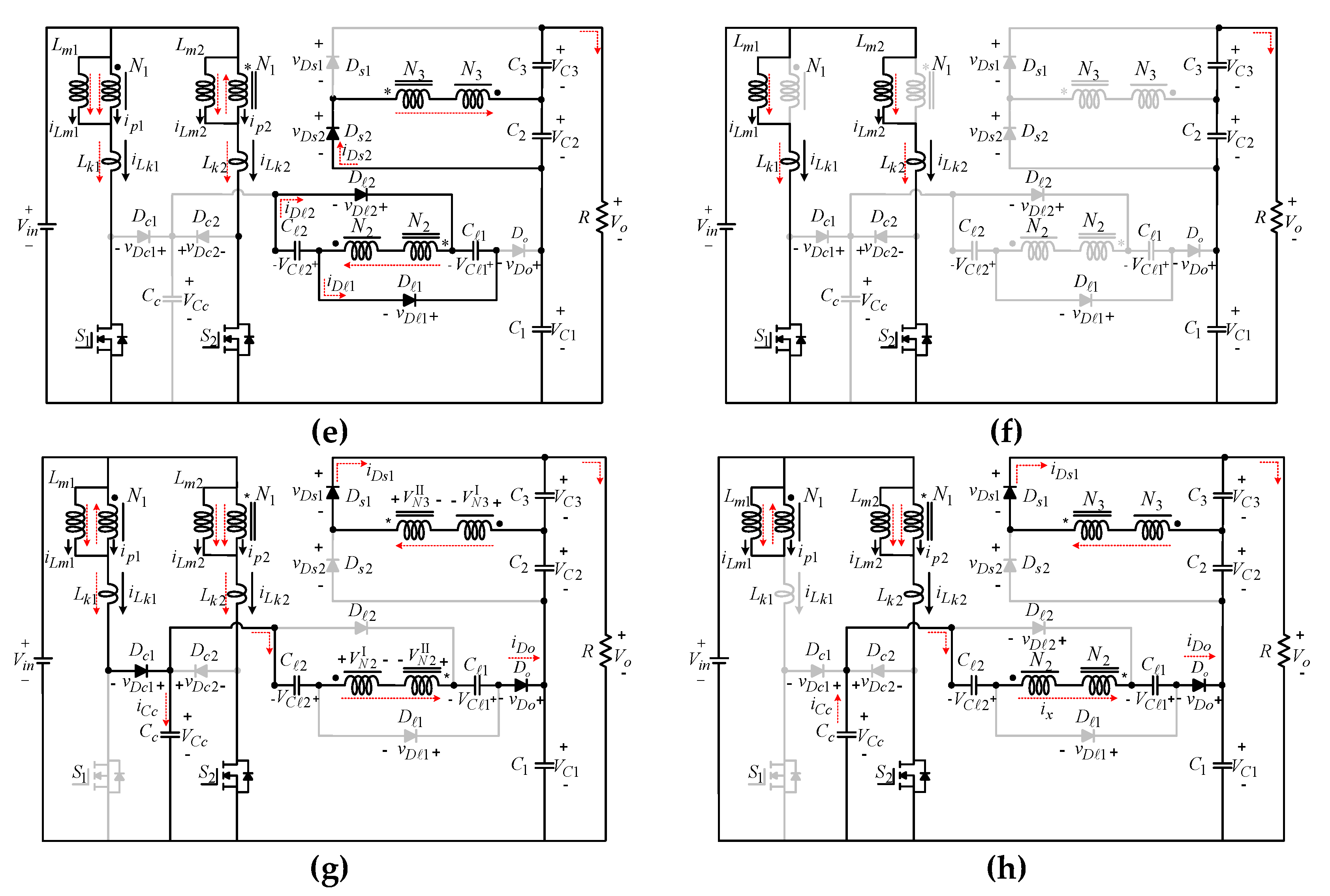
2. Circuit Description and Operating Principle
3. Steady-State Analysis
3.1. Voltage Gain Derivation
- (1)
- All of the semiconductors are regarded as ideal. The on-state resistance of the switches and the forward voltage drop of the diodes are ignored.
- (2)
- The leakage inductances are neglected.
- (3)
- The magnetizing inductances of the coupled inductors are regarded as the same; that is, .
3.2. Voltage Stresses on Semiconductor Devices
3.3. Design Considerations
3.3.1. Design of Coupled Inductors
3.3.2. Design of Capacitors
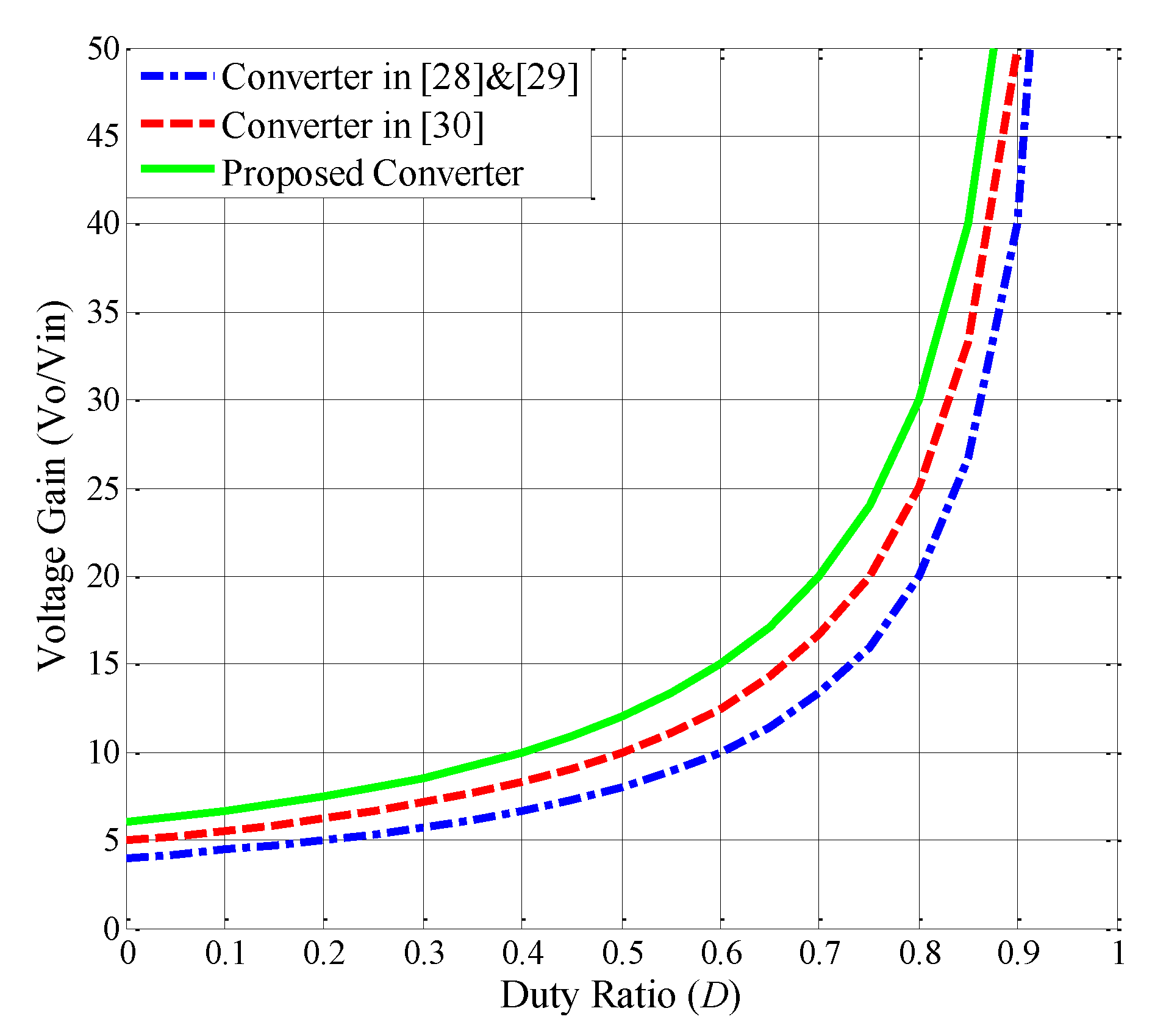
3.4. Performance Comparison
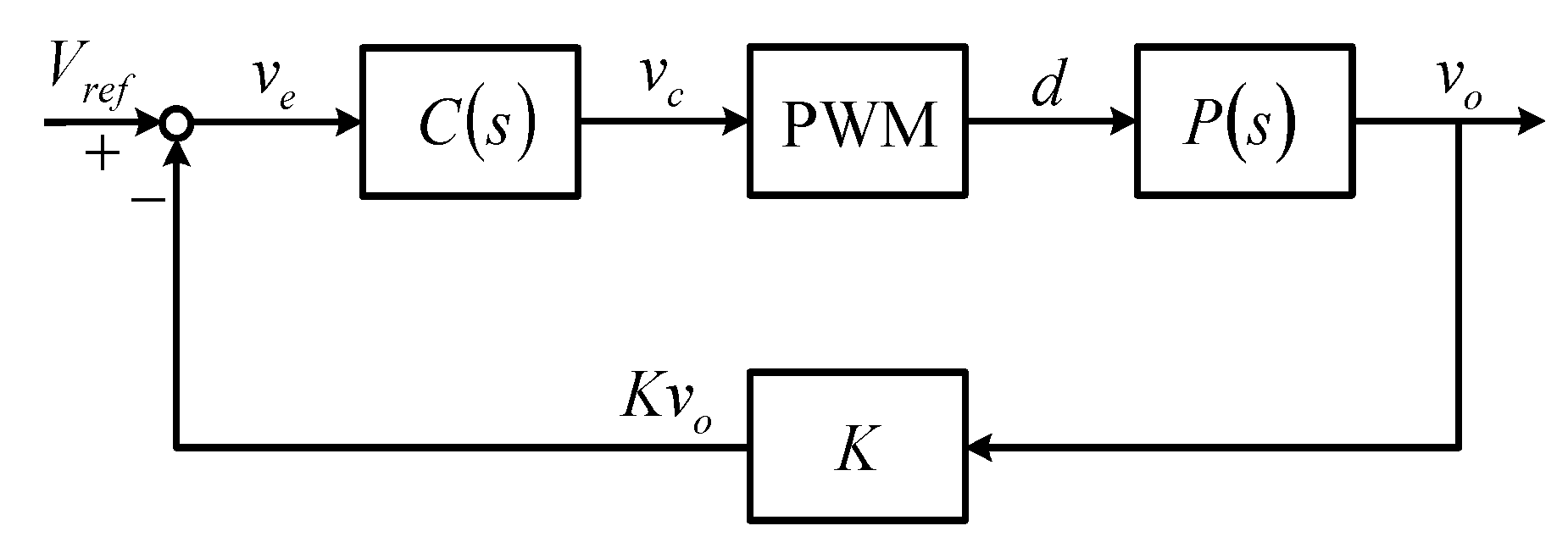
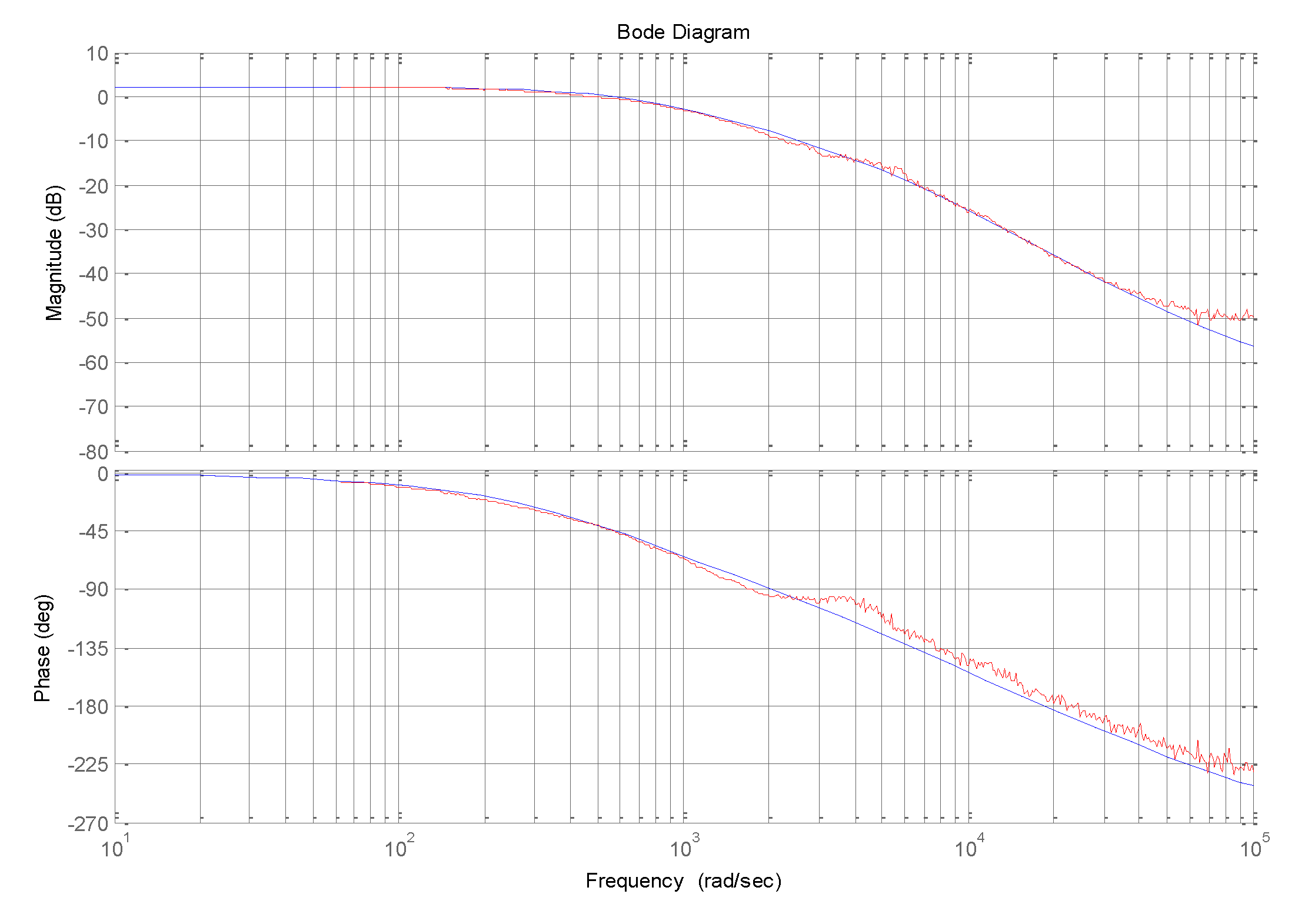
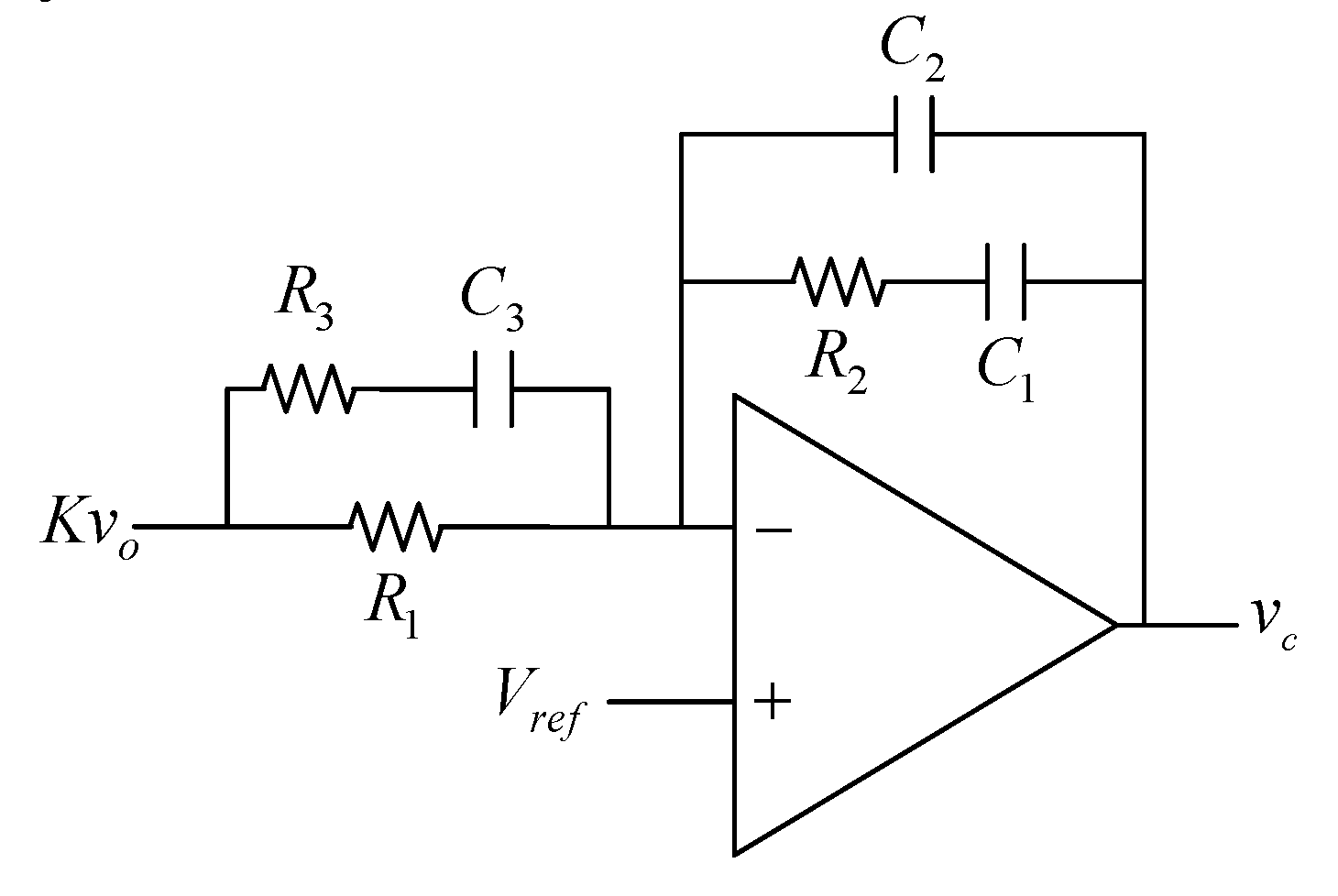
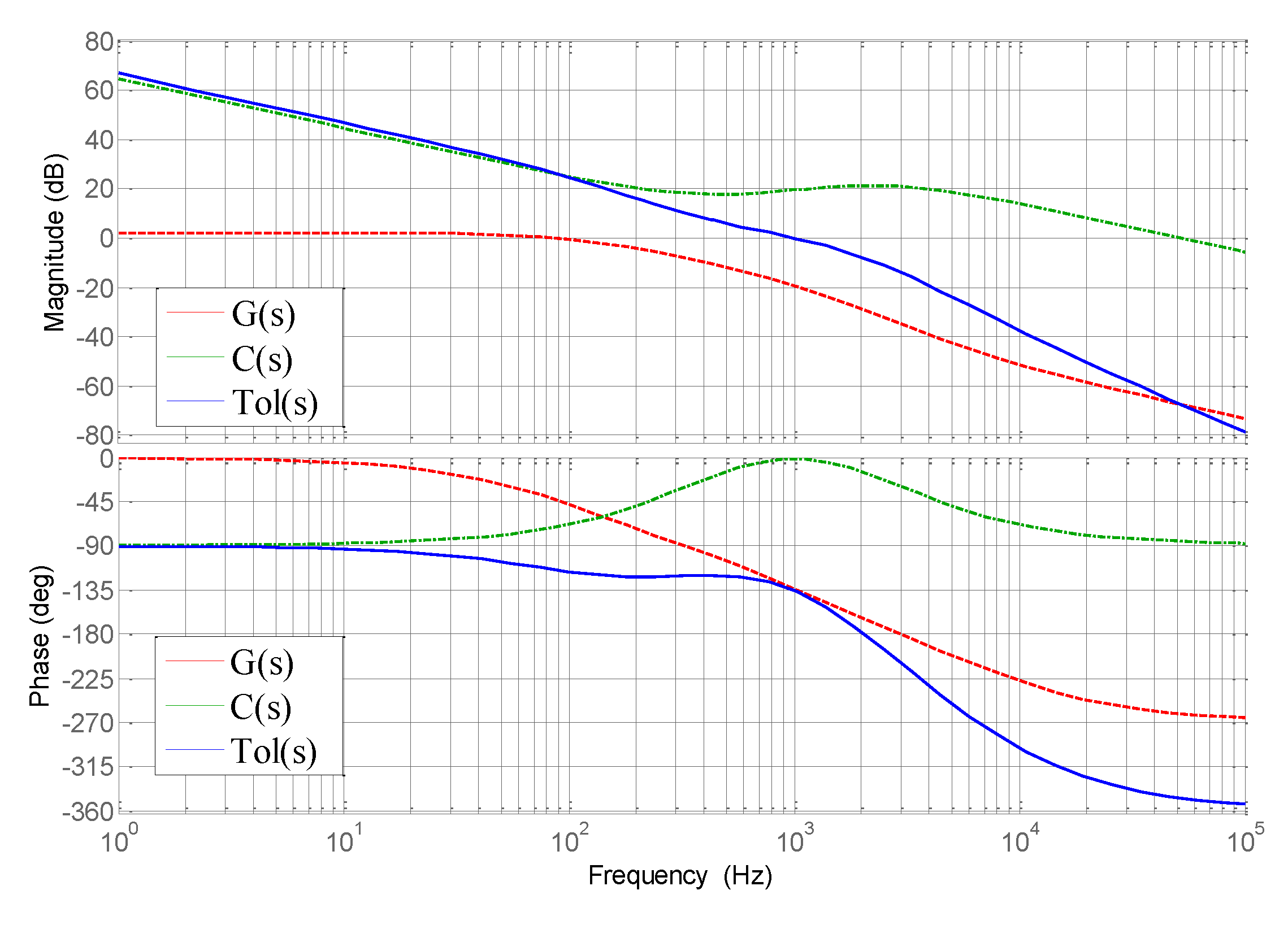
4. Controller Design
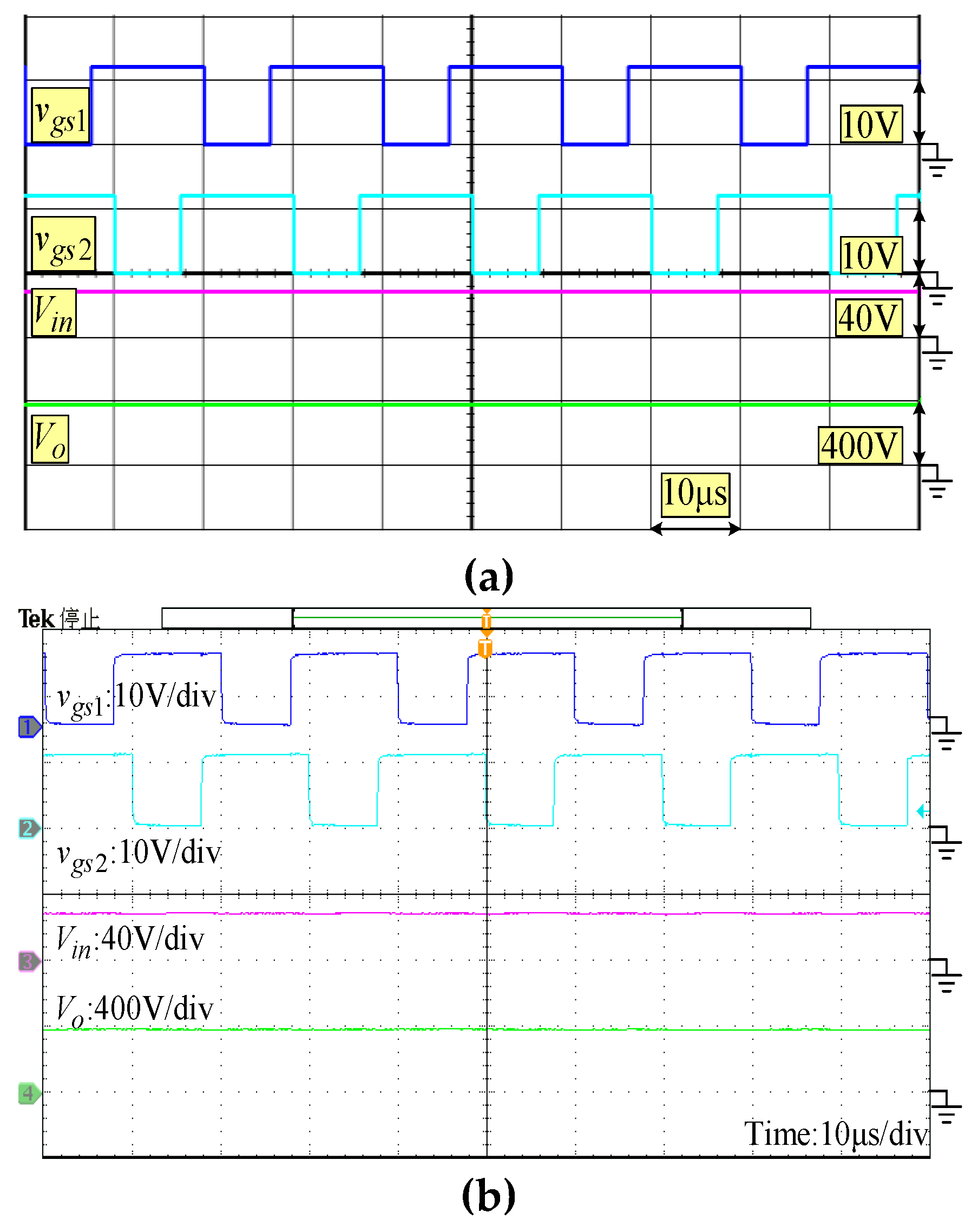
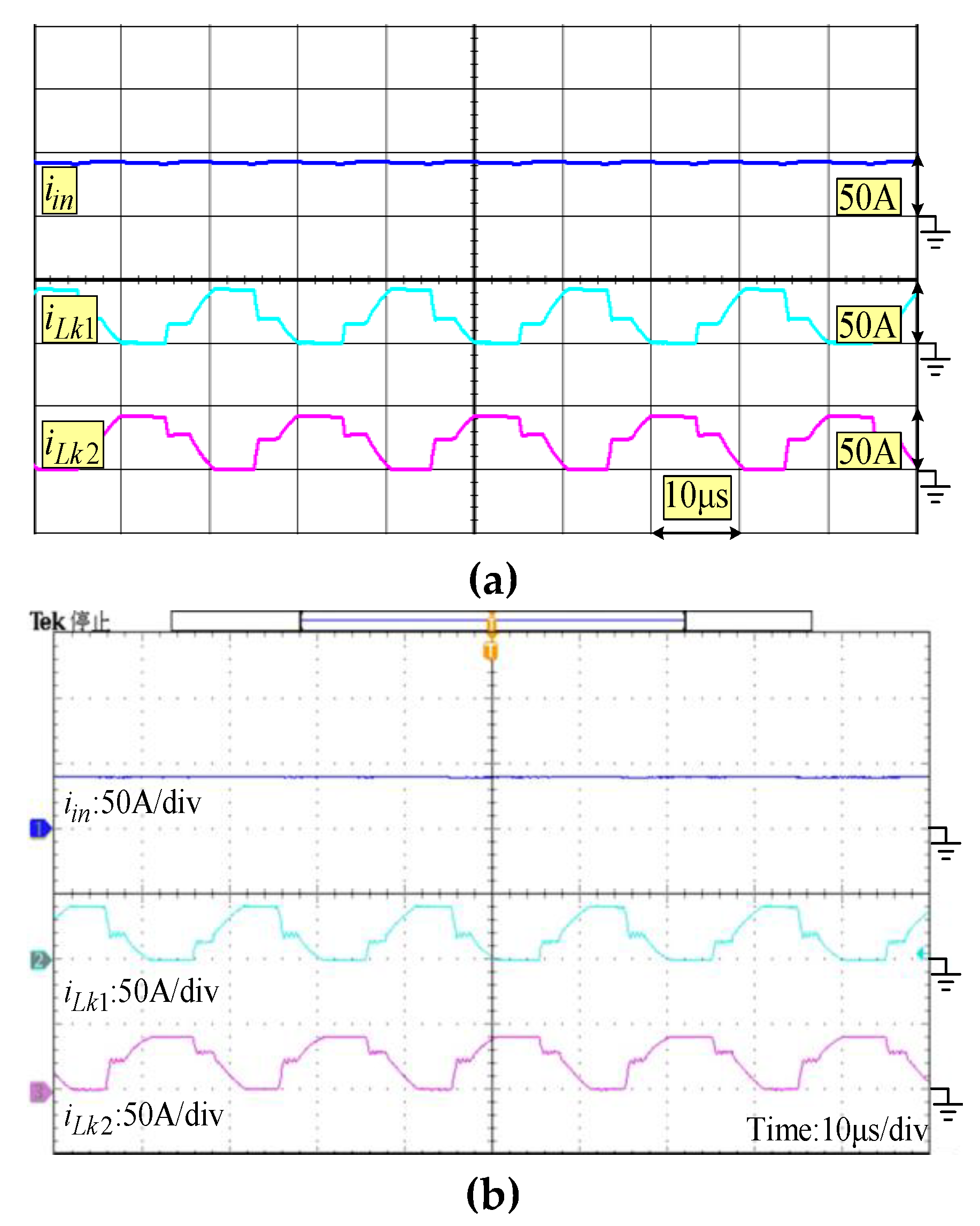
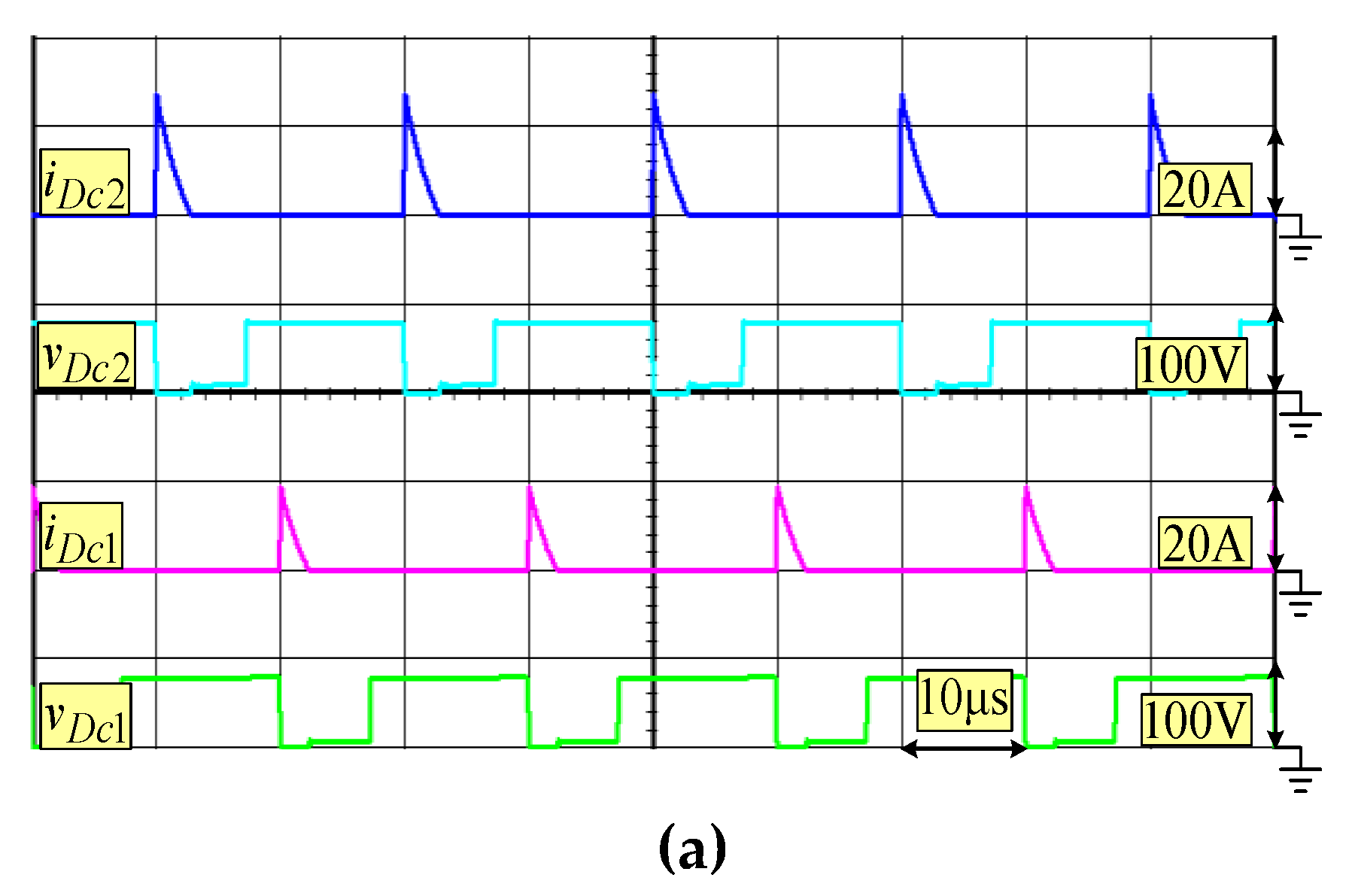
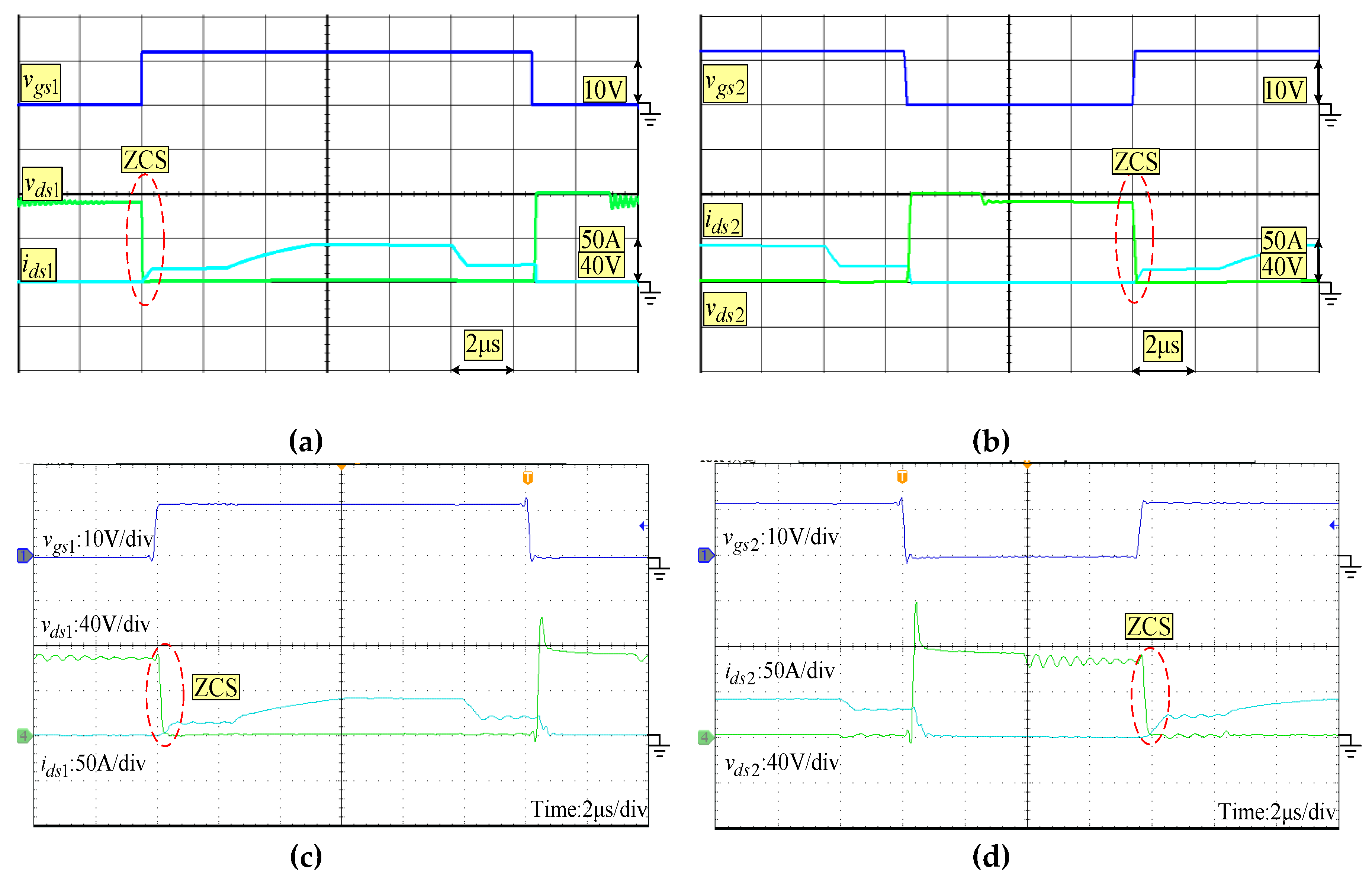
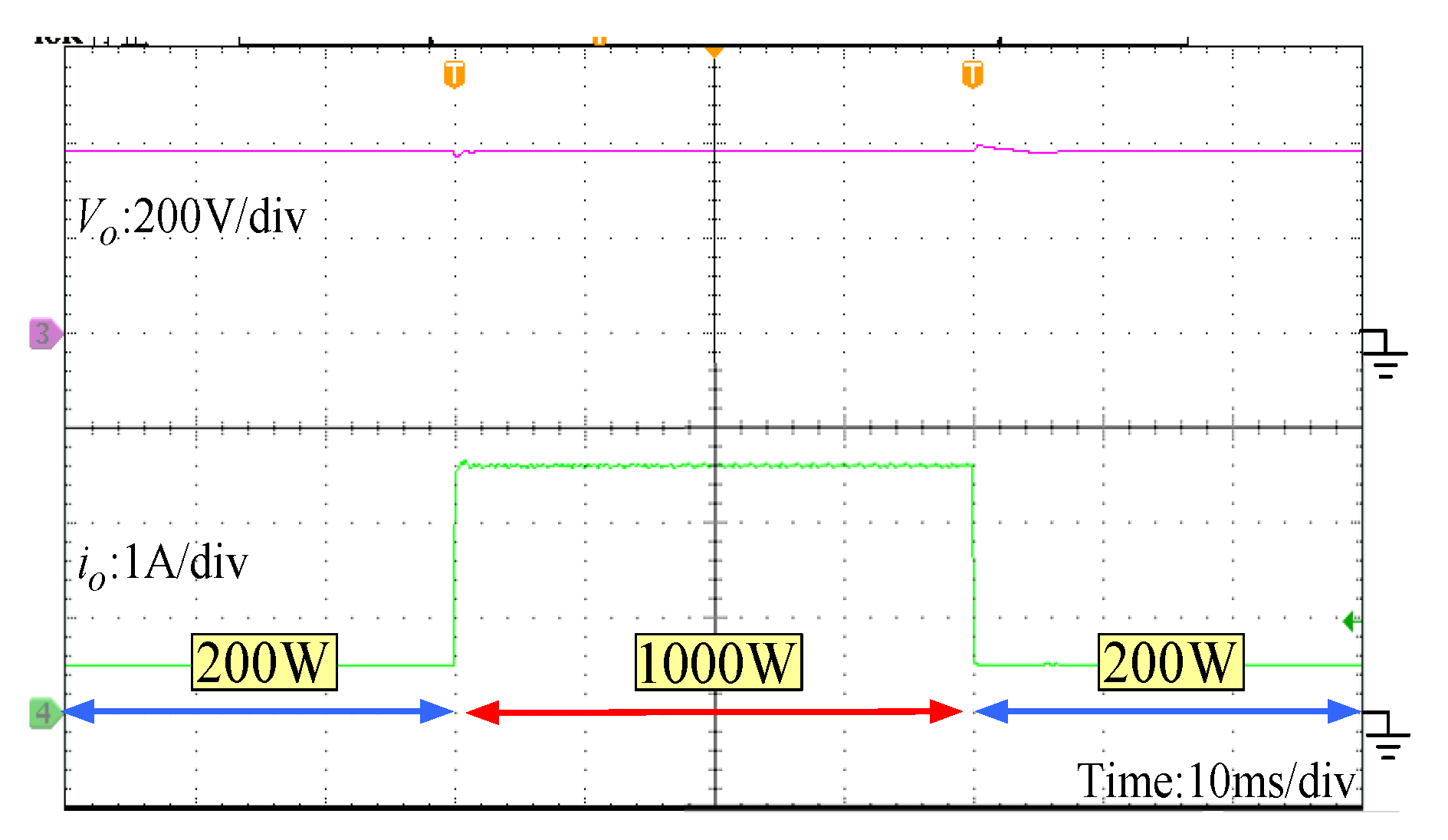
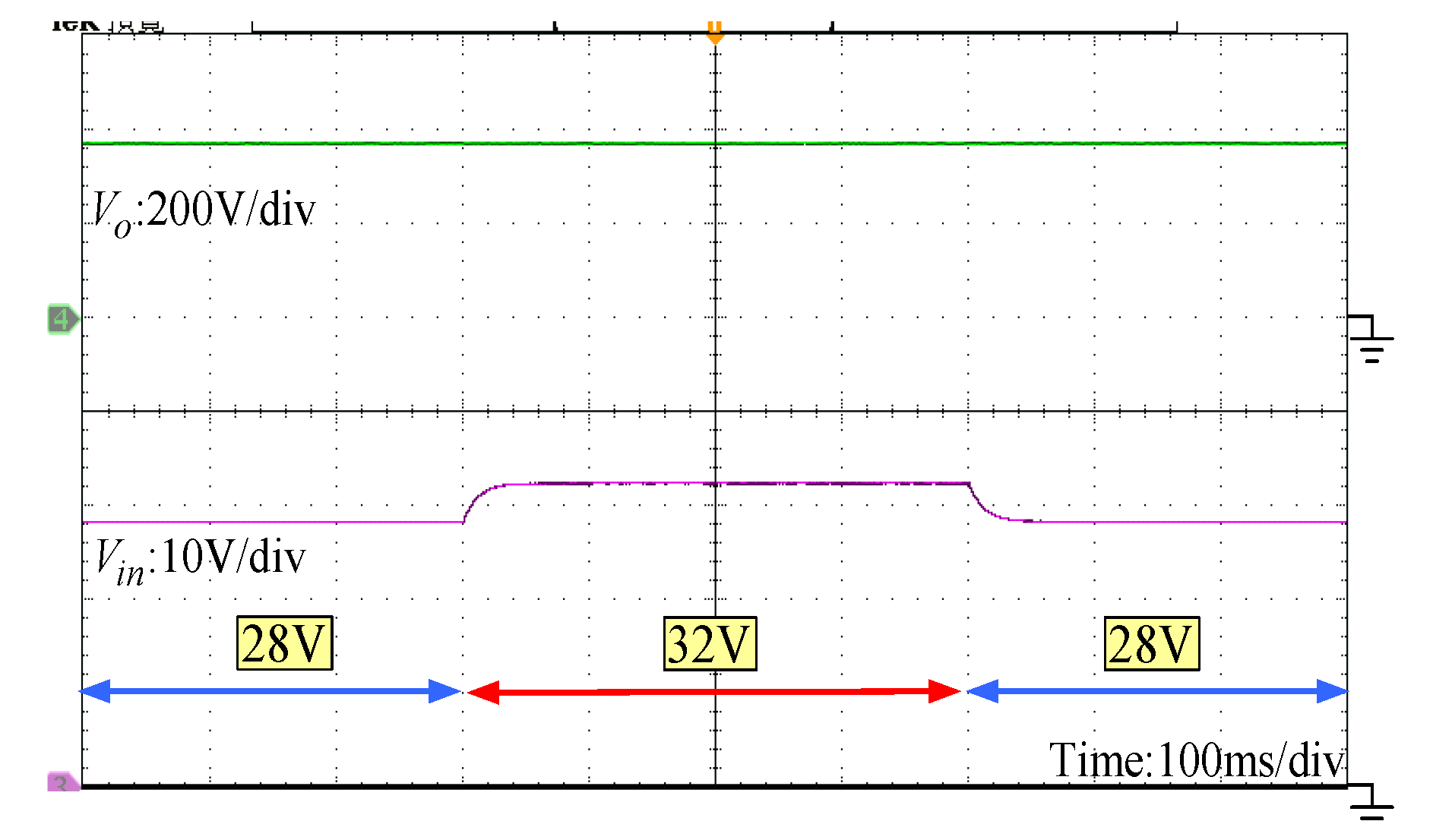
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ajami, A.; Ardi, H.; Farakhor, A. A novel high step-up DC-DC converter based on integrating coupled inductor and switched-capacitor techniques for renewable energy applications. IEEE Trans. Power Electron. 2015, 30, 4255–4263. [Google Scholar] [CrossRef]
- Yang, B.; Li, W.; Zhao, Y.; He, X. Design and analysis of a grid connected PV power system. IEEE Trans. Power Electron. 2010, 25, 992–1000. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; PortilloGuisado, R.C.; Prats, M.A.M.; Leon, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Andrade, A.M.; Schuch, L.; Martins, M.L.S. Analysis and design of high-efficiency hybrid high step-up DC–DC converter for distributed PV generation systems. IEEE Trans. Ind. Electron. 2019, 66, 3860–3868. [Google Scholar] [CrossRef]
- Tofoli, F.L.; Pereira, D.C.; Paula, W.J.; Junior, D.S.O. Survey on non-isolated high-voltage step-up DC–DC topologies based on the boost converter. IET Power Electron. 2015, 8, 2044–2057. [Google Scholar] [CrossRef]
- Wong, Y.S.; Chen, J.F.; Liu, K.B.; Hsieh, Y.P. A novel high step-up DC-DC converter with coupled inductor and switched clamp capacitor techniques for photovoltaic systems. Energies 2017, 10, 378–394. [Google Scholar] [CrossRef]
- Hu, X.; Gong, C. A high voltage gain DC-DC converter integrating coupled-inductor and diode-capacitor techniques. IEEE Trans. Power Electron. 2014, 29, 789–800. [Google Scholar]
- Farakhor, A.; Abapour, M.; Sabahi, M.; Farkoush, S.G.; Oh, S.R.; Rhee, S.B. A study on an improved three-winding coupled inductor based dc/dc boost converter with continuous input current. Energies 2020, 13, 1780. [Google Scholar] [CrossRef]
- Tseng, K.C.; Lin, J.T.; Huang, C.C. High step-up converter with three-winding coupled inductor for fuel cell energy source applications. IEEE Trans. Power Electron. 2015, 30, 574–581. [Google Scholar] [CrossRef]
- Yu, D.; Yang, J.; Xu, R.; Xia, Z.; Iu, H.H.; Fernando, T. A family of module-integrated high step-up converters with dual coupled inductors. IEEE Access 2018, 6, 16256–16266. [Google Scholar] [CrossRef]
- Azizkandi, M.E.; Sedaghati, F.; Shayeghi, H.; Blaabjerg, F. Two- and three-winding coupled-inductor-based high step-up DC–DC converters for sustainable energy applications. IET Power Electron. 2020, 13, 144–156. [Google Scholar]
- Gao, Y.; Liu, H.; Ai, J. Novel high step-up DC–DC converter with three-winding-coupled-inductors and its derivatives for a distributed generation system. Energies 2018, 11, 3428. [Google Scholar] [CrossRef]
- Azizkandi, M.E.; Sedaghati, F.; Shayeghi, H.; Blaabjerg, F. A high voltage gain DC–DC converter based on three winding coupled inductor and voltage multiplier cell. IEEE Tran. Power Electron. 2020, 35, 4558–4567. [Google Scholar] [CrossRef]
- Wei, C.L.; Shih, M.H. Design of a switched-capacitor DC-DC converter with a wide input voltage range. IEEE Trans. Circuits Syst. 2013, 60, 1648–1656. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, D.; Wang, T.; Xu, Z. Hybrid switched-inductor converters for high step-up conversion. IEEE Trans. Ind. Electron. 2015, 62, 1480–1490. [Google Scholar] [CrossRef]
- Axelrod, B.; Berkovich, Y.; Ioinovici, A. Switched-capacitor/switched-inductor structures for getting transformerless hybrid DC–DC PWM converters. IEEE Trans. Circuits Syst. 2008, 55, 687–696. [Google Scholar] [CrossRef]
- Salvador, M.A.; Lazzarin, T.B.; Coelho, R.F. High step-up DC-DC converter with active switched-inductor and passive switched-capacitor networks. IEEE Trans. Ind. Electron. 2018, 65, 5644–5654. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, Y.; Zhang, B.; Qiu, D.; Xie, F. High step-up DC–DC converter with active switched LC-network for photovoltaic systems. IEEE Trans. Energy Convers. 2019, 34, 321–329. [Google Scholar] [CrossRef]
- Duong, T.D.; Nguyen, M.K.; Tran, T.T.; Lim, Y.C.; Choi, J.H. Transformerless high step-up DC-DC converters with switched-capacitor network. Electronics 2019, 8, 1420. [Google Scholar] [CrossRef]
- Lakshmi, M.; Hemamalini, S. Nonisolated high gain DC-DC converter for DC microgrids. IEEE Trans. Ind. Electron. 2018, 65, 1205–1212. [Google Scholar] [CrossRef]
- Bhaskar, M.S.; Meraj, M.; Iqbal, A.; Padamanaban, S.; Maroti, P.K.; Alammari, R. High gain transformer-less double-duty-triple-mode DC/DC converter for DC microgrid. IEEE Access 2019, 7, 36353–36370. [Google Scholar] [CrossRef]
- Tseng, K.C.; Chen, C.T.; Cheng, C.A. A high-efficiency high step-up interleaved converter with a voltage multiplier for electric vehicle power management applications. J. Power Electron. 2016, 16, 414–424. [Google Scholar] [CrossRef]
- Zhou, W.B.; Zhu, X.; Luo, Q.M.; Chen, S. Interleaved non-isolated high step-up dc/dc converter based on the diode-capacitor multiplier. IET Power Electron. 2014, 7, 390–397. [Google Scholar] [CrossRef]
- Li, W.; Zhao, Y.; Deng, Y.; He, X. Interleaved converter with voltage multiplier cell for high step-up and high-efficiency conversion. IEEE Trans. Power Electron. 2010, 25, 2397–2408. [Google Scholar] [CrossRef]
- Li, W.; Xiang, X.; Li, C.; Li, W.; He, X. Interleaved high step-up ZVT converter with built-in transformer voltage doubler cell for distributed PV generation system. IEEE Trans. Power Electron. 2013, 28, 300–313. [Google Scholar] [CrossRef]
- Li, W.; Xiang, X.; Hu, Y.; He, X. High step-up interleaved converter with built-in transformer voltage multiplier cells for sustainable energy applications. IEEE Trans. Power Electron. 2014, 29, 2829–2836. [Google Scholar] [CrossRef]
- Nouri, T.; Vosoughi, N.; Hosseini, S.H.; Babaei, E.; Sabahi, M. An interleaved high step-up converter with coupled inductor and built-in transformer voltage multiplier cell techniques. IEEE Trans. Ind. Electron. 2019, 66, 1894–1905. [Google Scholar] [CrossRef]
- Li, W.; Zhao, Y.; Wu, J.; He, X. Interleaved high step-up converter with winding-cross-coupled inductors and voltage multiplier cells. IEEE Trans. Power Electron. 2012, 27, 133–143. [Google Scholar] [CrossRef]
- He, L.; Liao, Y. An advanced current-autobalance high step-up converter with a multicoupled inductor and voltage multiplier for a renewable power generation system. IEEE Trans. Power Electron. 2016, 31, 6992–7005. [Google Scholar]
- Nouri, T.; Hosseini, S.H.; Babaei, E.; Ebrahimi, J. Interleaved high step-up DC–DC converter based on three-winding high-frequency coupled inductor and voltage multiplier cell. IET Power Electron. 2015, 8, 175–189. [Google Scholar] [CrossRef]
- Venable, D. The K factor: A new mathematical tool for stability analysis and synthesis. Proc. Powercon 1983, 10. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.196.6850&rep=rep1&type=pdf (accessed on 10 May 2020).
- Cao, L. Type III compensator design for power converters. Power Electron. Technol. 2011, 1, 20–25. [Google Scholar]
- Chen, S.J.; Yang, S.P.; Huang, C.M.; Chen, Y.H. High step-up interleaved converter with three-winding coupled inductors and voltage multiplier cells. In Proceedings of the 20th IEEE International Conference on Industrial Technology (ICIT), Melbourne, VIC, Australia, 13–15 February 2019; pp. 458–463. [Google Scholar]



| Converter | Converter in [28] | Converter in [29] | Converter in [30] | Proposed Converter |
|---|---|---|---|---|
| Voltage gain | ||||
| Voltage stress on switches | ||||
| Maximum diode voltage stress | ||||
| Quantities of switches | 2 | 2 | 2 | 2 |
| Quantities of diodes | 6 | 6 | 8 | 7 |
| Quantities of capacitors | 5 | 5 | 7 | 6 |
| Quantities of coupled inductors | 2 | 2 | 2 | 2 |
| Maximal efficiency at output power | 95.8% at 500W | 97.2% at 400W | 97% at 524W | 98% at 100W |
| Parameter/Description | Specification/Value |
|---|---|
| Input voltage Vin | 28 V |
| Output voltage Vo | 380 V |
| Rated output power Po | 1000 W |
| Switching frequency fs | 50 kHz |
| Magnetizing inductance Lm | 69 µH |
| Leakage inductance Lk | 0.7 µH |
| Turns ratio n | 1 |
| Power switches S1 and S2 | IRFP4668 |
| Diodes DC1, DC2, , , DS1, DS2 and Do | 60CPQ150 |
| Clamp capacitor CC | 147 µF |
| Lift capacitors and | 147 µF |
| Output capacitors C1, C2 and C3 | 120 µF |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-J.; Yang, S.-P.; Huang, C.-M.; Chen, Y.-H. Interleaved High Step-Up DC–DC Converter with Voltage-Lift and Voltage-Stack Techniques for Photovoltaic Systems. Energies 2020, 13, 2537. https://doi.org/10.3390/en13102537
Chen S-J, Yang S-P, Huang C-M, Chen Y-H. Interleaved High Step-Up DC–DC Converter with Voltage-Lift and Voltage-Stack Techniques for Photovoltaic Systems. Energies. 2020; 13(10):2537. https://doi.org/10.3390/en13102537
Chicago/Turabian StyleChen, Shin-Ju, Sung-Pei Yang, Chao-Ming Huang, and Yu-Hua Chen. 2020. "Interleaved High Step-Up DC–DC Converter with Voltage-Lift and Voltage-Stack Techniques for Photovoltaic Systems" Energies 13, no. 10: 2537. https://doi.org/10.3390/en13102537
APA StyleChen, S.-J., Yang, S.-P., Huang, C.-M., & Chen, Y.-H. (2020). Interleaved High Step-Up DC–DC Converter with Voltage-Lift and Voltage-Stack Techniques for Photovoltaic Systems. Energies, 13(10), 2537. https://doi.org/10.3390/en13102537





