Effect of Porous Medium and Copper Heat Sink on Cooling of Heat-Generating Element
Abstract
1. Introduction
2. Basic Equations
- inside the porous layer
- inside the copper heat sink
- inside the heat-generating element
- inside the porous insertion
- inside the copper heat sink
- inside the heat-generating element
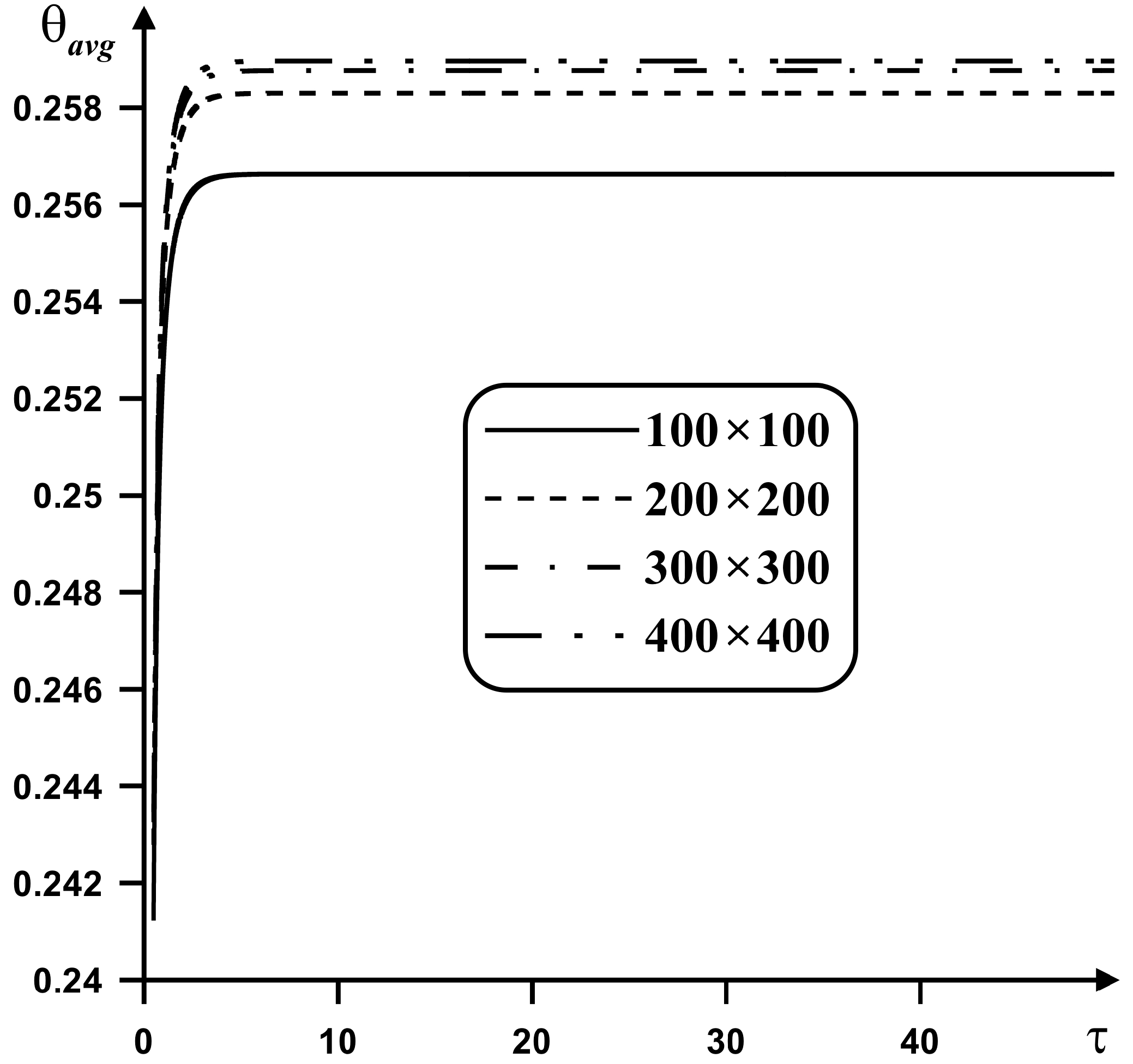
3. Numerical Technique
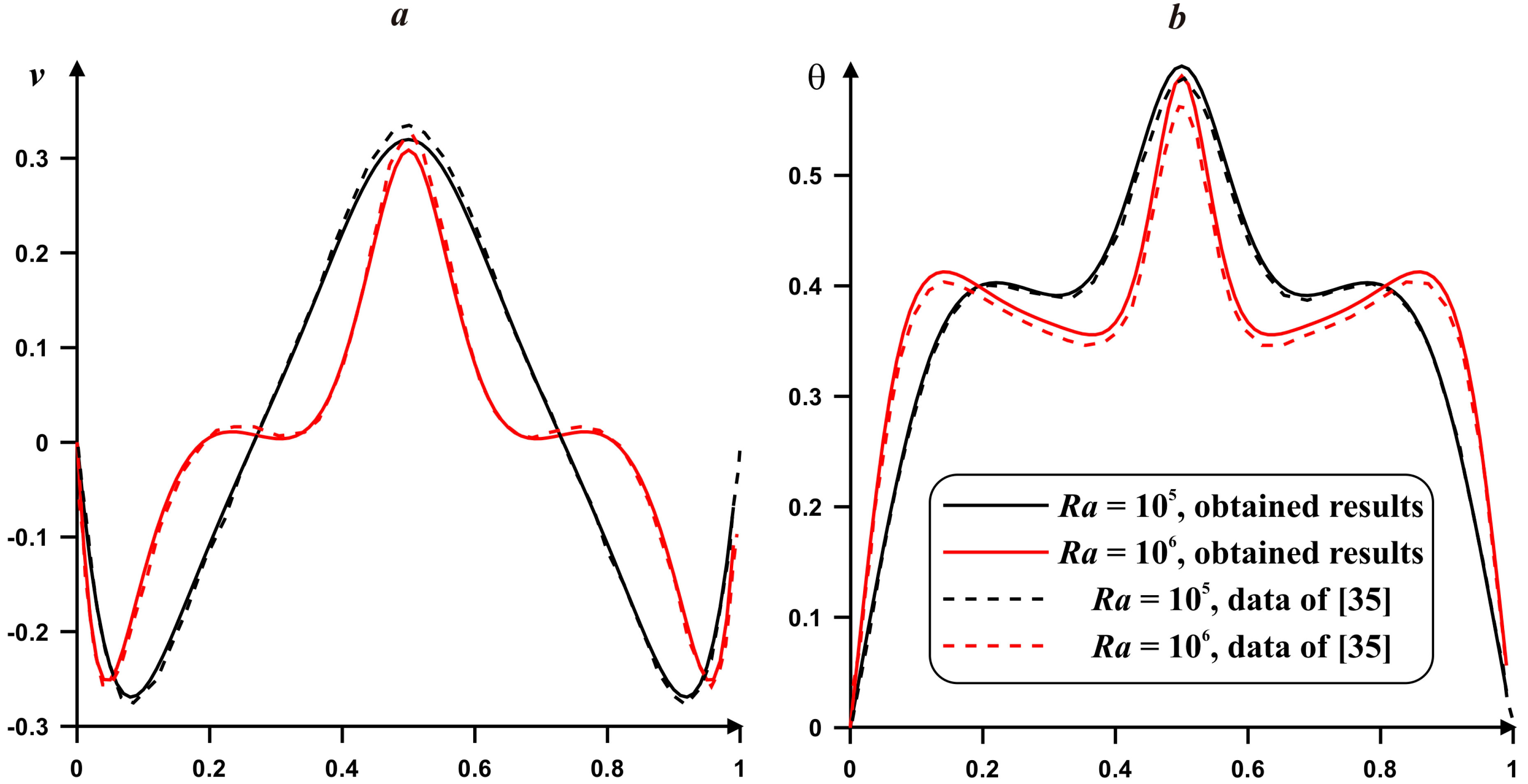
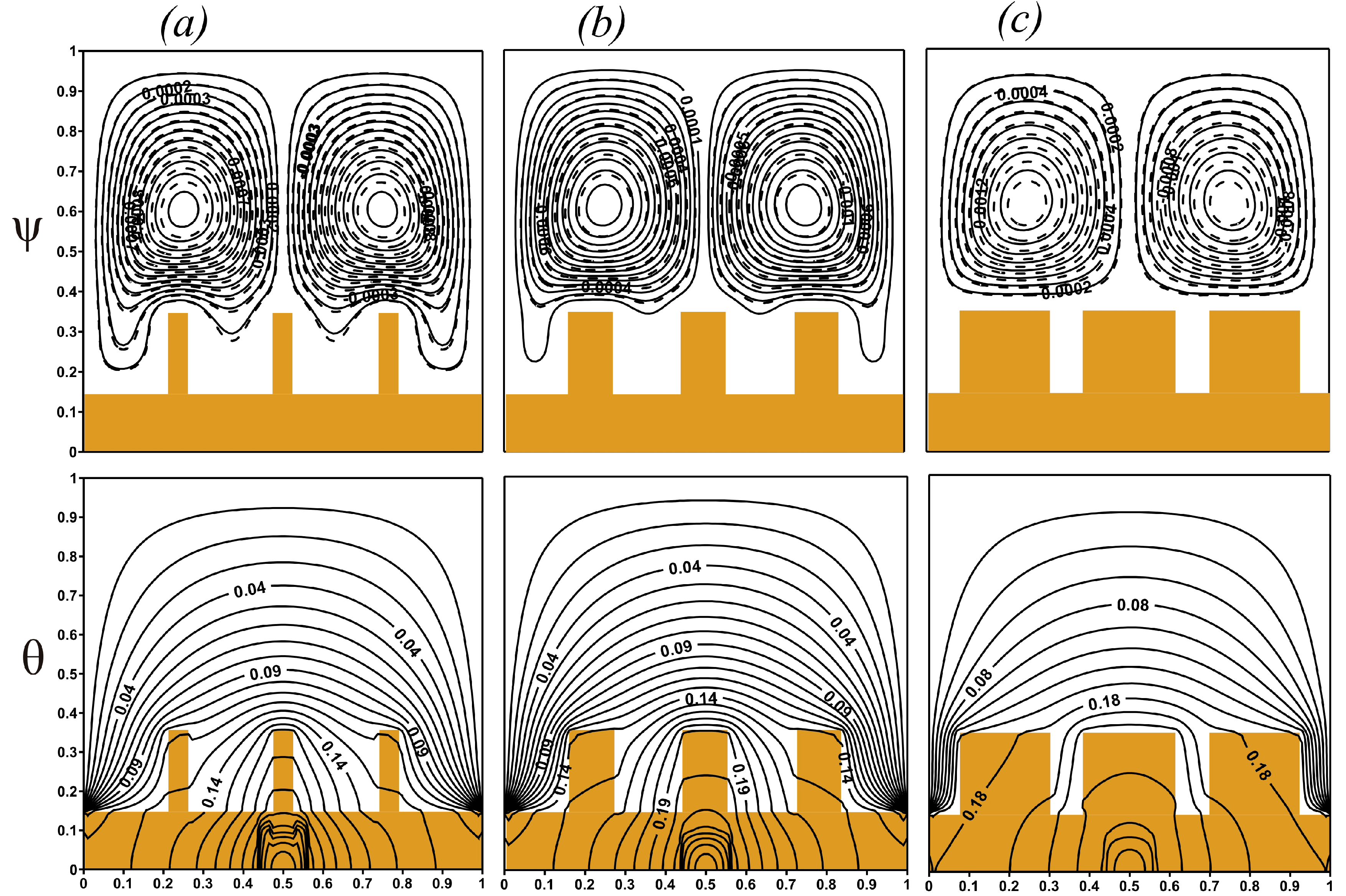
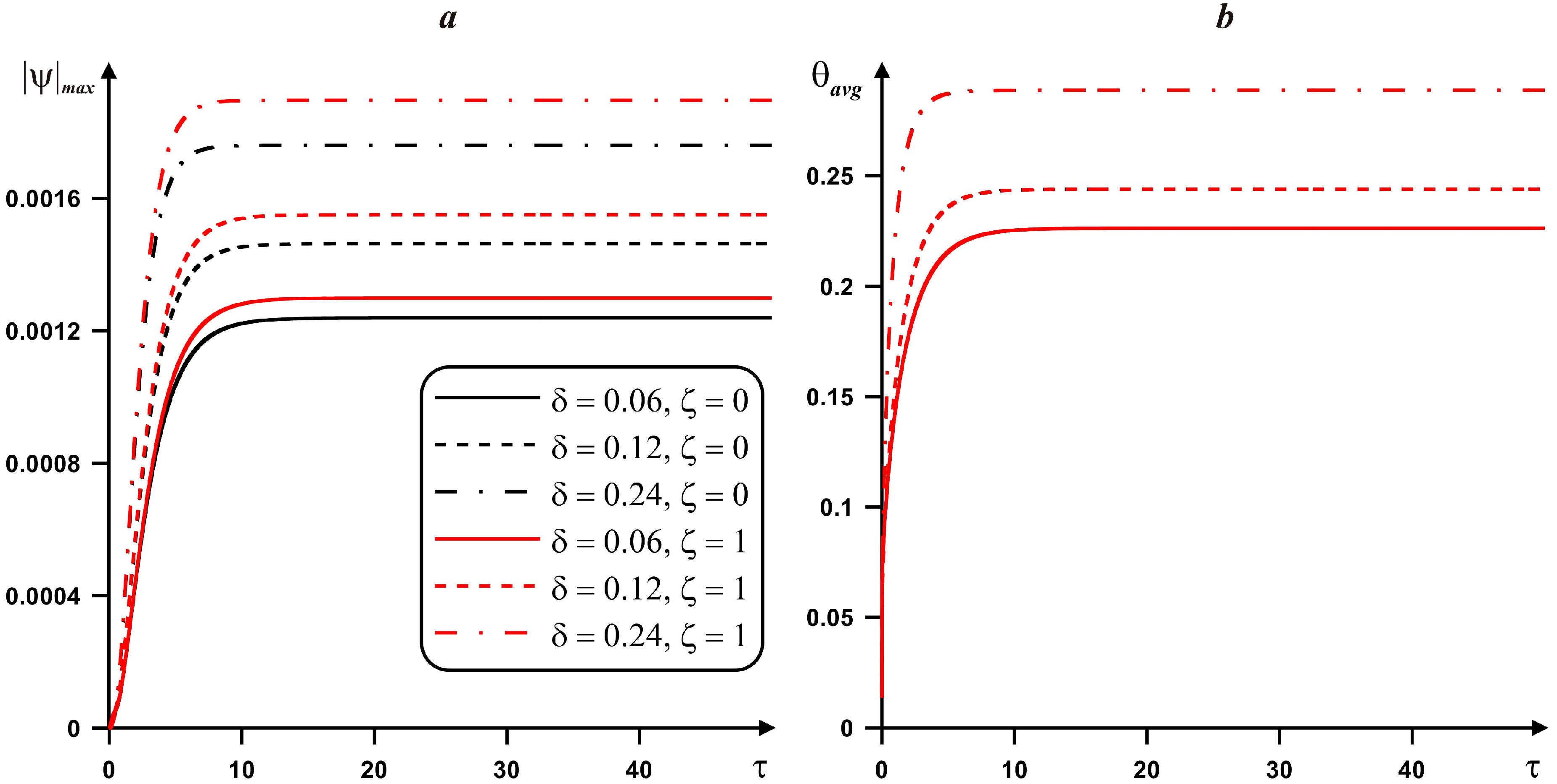
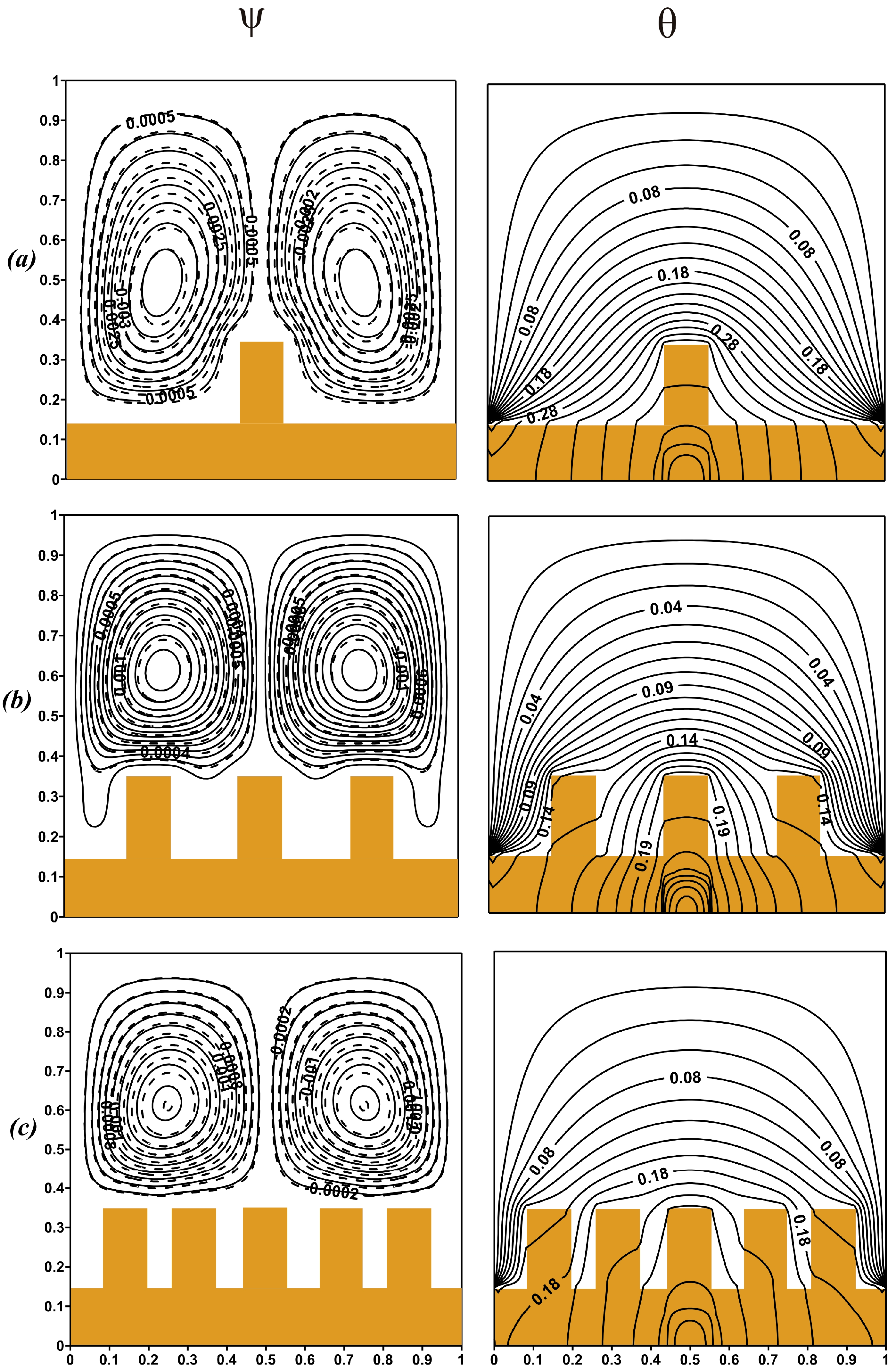
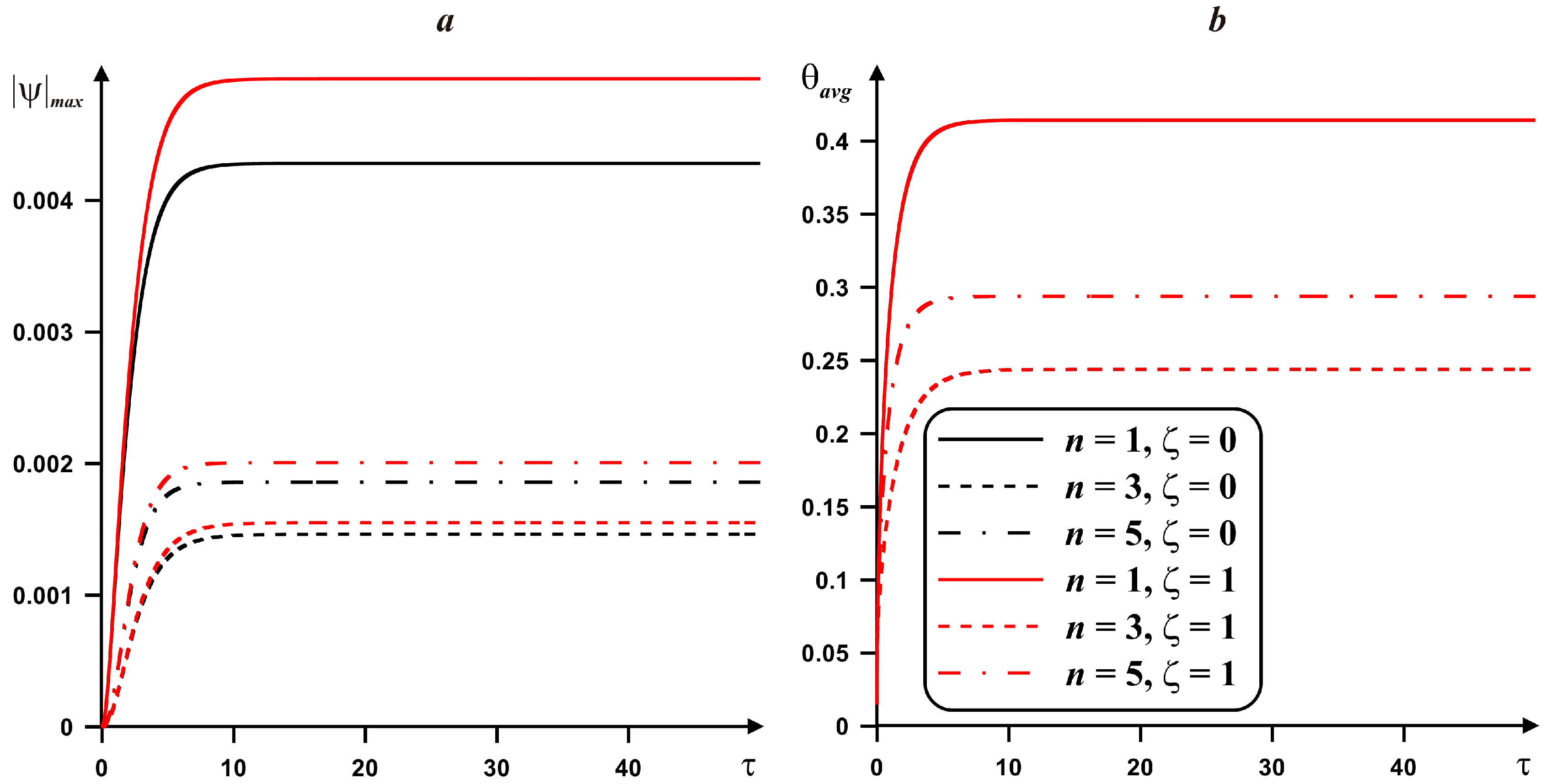
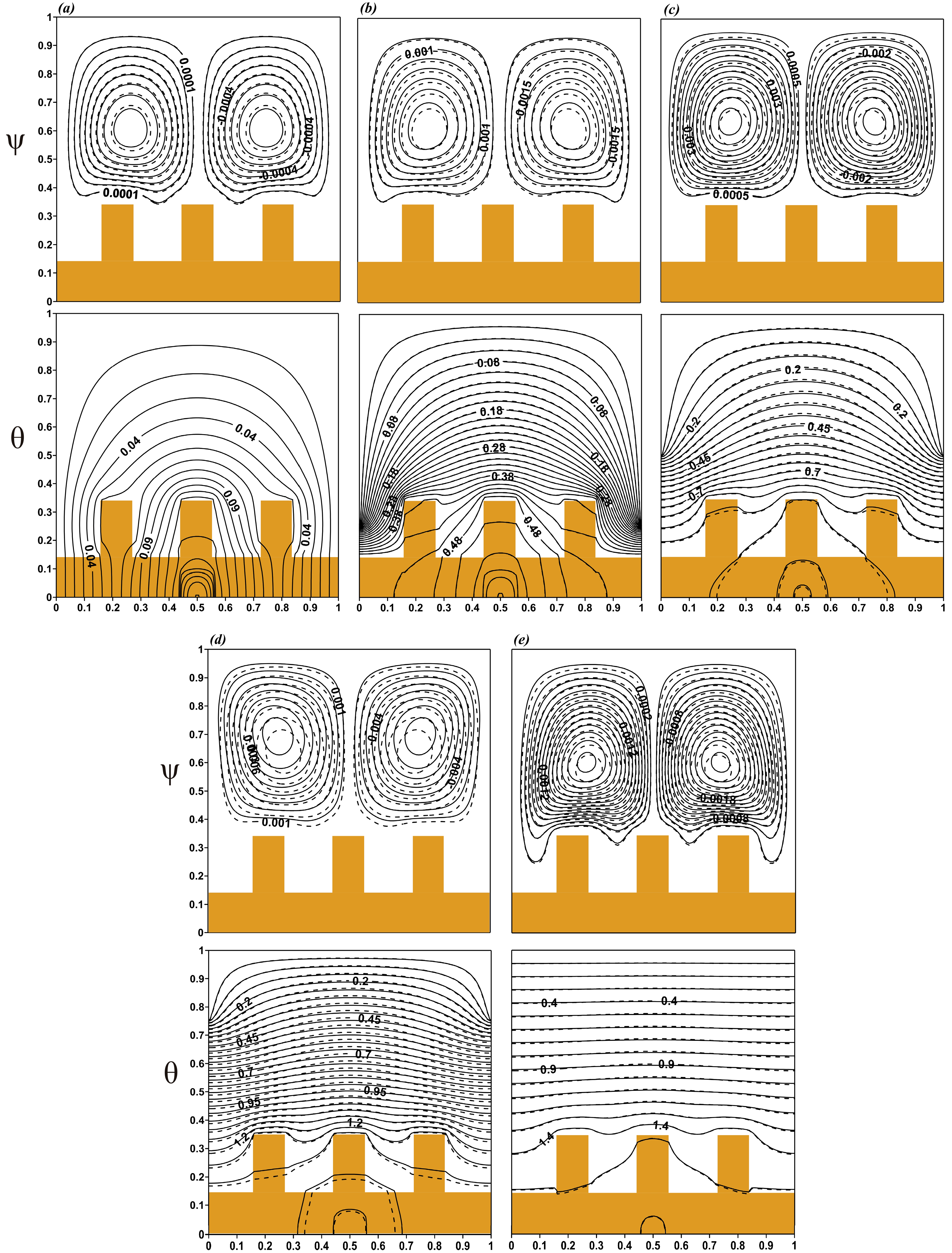
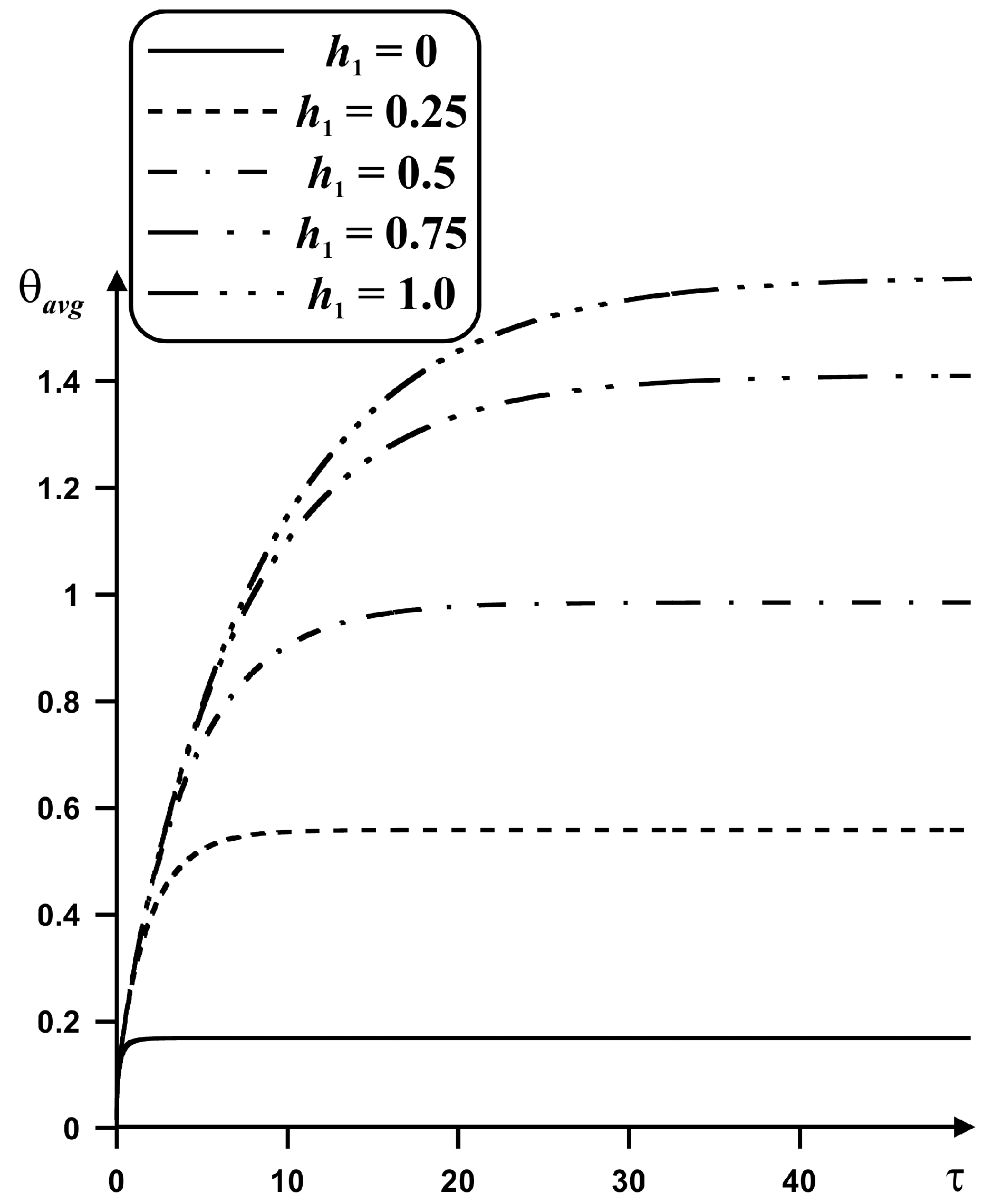
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| c | heat capacity [J⋅kg−1⋅K−1] |
| Da = K/L2 | Darcy number [–] |
| g | gravity acceleration [m⋅s−2] |
| H | dimensional height of the radiator fins [m] |
| H1 | dimensional height of the adiabatic part of vertical walls [m] |
| h | dimensionless height of the radiator fins [–] |
| h1 | dimensionless height of the adiabatic part of vertical walls [–] |
| K | porous layer permeability [m2] |
| L | size of the enclosure [m] |
| n | number of fins [–] |
| Os = QL2/(λhsΔT) | Ostrogradsky number [–] |
| p | static pressure [Pa] |
| Pr = μ0/(ρα) | Prandtl number [–] |
| Q | volumetric heat flux [W⋅m−3] |
| Ra = ρgβΔTL3/(αμ0) | Rayleigh number [–] |
| T | dimensional temperature [K] |
| Tc | cold wall temperature [K] |
| t | dimensional time [s] |
| dimensional velocity components [m⋅s−1] | |
| u, v | dimensionless velocity components [–] |
| dimensional coordinates [m] | |
| x, y | dimensionless coordinates [–] |
| w | dimensional width of the fins [m] |
| Greek symbols | |
| α | heat diffusivity [m2⋅s−1] |
| β | thermal expansion coefficient [K−1] |
| δ | non-dimensional fins width [–] |
| ΔT = Tref − Tc | temperature difference [K] |
| ε | porosity of the porous insertion [–] |
| overall specific heat ratio [–] | |
| θ | non-dimensional temperature [–] |
| λ | thermal conductivity [W⋅m−1⋅K−1] |
| variable dynamic viscosity [Pa⋅s] | |
| μ0 | dynamic viscosity at reference temperature [Pa⋅s] |
| μ = exp(−ζθ) | non-dimensional dynamic viscosity [–] |
| ζ | viscosity changeable parameter [–] |
| ρ | fluid density [kg⋅m−3] |
| τ | non-dimensional time [–] |
| stream function [m2⋅s−1] | |
| ψ | non-dimensional stream function [–] |
| vorticity [s−1] | |
| ω | non-dimensional vorticity [–] |
| Subscripts | |
| c | cold |
| eff | effective |
| f | fluid |
| hs | heat source |
| pm | porous material |
| r | radiator |
| ref | reference |
| s | solid porous matrix |
References
- Bairi, A.; Zarco-Pernia, E.; De Maria, J.M.G. A review on natural convection in enclosures for engineering applications. The particular case of the parallelogrammic diode cavity. Appl. Therm. Eng. 2014, 63, 304–322. [Google Scholar] [CrossRef]
- Florio, L.; Harnoy, A. Combination technique for improving natural convection cooling in electronics. Int. J. Therm. Sci. 2007, 46, 76–92. [Google Scholar] [CrossRef]
- Zhang, K.; Li, M.-J.; Wang, F.-L.; He, Y.-L. Experimental and numerical investigation of natural convection heat transfer of W-type fin arrays. Int. J. Heat Mass Transf. 2020, 152, 119315. [Google Scholar] [CrossRef]
- Adhikari, R.C.; Wood, D.H.; Pahlevani, M. Optimizing rectangular fins for natural convection cooling using CFD. Therm. Sci. Eng. Prog. 2020, 17, 100484. [Google Scholar] [CrossRef]
- Hyun, J.M.; Lee, J.W. Transient natural convection in a square cavity of a fluid with temperature-dependent viscosity. Int. J. Heat Fluid Flow 1988, 9, 278–285. [Google Scholar] [CrossRef]
- He, B.; Lu, S.; Gao, D.; Chen, W.; Lin, F. Lattice Boltzmann simulation of double diffusive natural convection in heterogeneously porous media of a fluid with temperature-dependent viscosity. Chin. J. Phys. 2020, 63, 186–200. [Google Scholar] [CrossRef]
- De Castro, C.A.N.; Li, S.F.Y.; Nagashima, A.; Trengove, R.; Wakeham, W.A. Standard Reference Data for the Thermal Conductivity of Liquids. J. Phys. Chem. Ref. Data 1986, 15, 1073. [Google Scholar] [CrossRef]
- Charitidou, E.; Molidou, C.; Assael, M.J. The thermal conductivity and viscosity of benzene. Int. J. Thermophys. 1988, 9, 37–45. [Google Scholar] [CrossRef]
- Hasona, W.; El-Shekhipy, A.; Ibrahim, M. Combined effects of magnetohydrodynamic and temperature dependent viscosity on peristaltic flow of Jeffrey nanofluid through a porous medium: Applications to oil refinement. Int. J. Heat Mass Transf. 2018, 126, 700–714. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Shanakhat, I.; Shehzad, S. Entropy generation analysis for peristalsis of nanofluid with temperature dependent viscosity and Hall effects. J. Magn. Magn. Mater. 2019, 474, 434–441. [Google Scholar] [CrossRef]
- Tlili, I.; Bhatti, M.; Hamad, S.M.; Barzinjy, A.A.; Sheikholeslami, M.; Shafee, A.; Nguyen, T.K.; Ali, J.A. Macroscopic modeling for convection of Hybrid nanofluid with magnetic effects. Phys. A Stat. Mech. Appl. 2019, 534, 122136. [Google Scholar] [CrossRef]
- Dogonchi, A.; Seyyedi, S.M.; Hashemi-Tilehnoee, M.; Chamkha, A.J.; Ganji, D. Investigation of natural convection of magnetic nanofluid in an enclosure with a porous medium considering Brownian motion. Case Stud. Therm. Eng. 2019, 14, 100502. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Chamkha, A.J.; Wen, D. Natural convective flow and heat transfer of Nano-Encapsulated Phase Change Materials (NEPCMs) in a cavity. Int. J. Heat Mass Transf. 2019, 138, 738–749. [Google Scholar] [CrossRef]
- Zadeh, S.M.H.; Sabour, M.; Sazgar, S.; Ghalambaz, M. Free convection flow and heat transfer of nanofluids in a cavity with conjugate solid triangular blocks: Employing Buongiorno’s mathematical model. Phys. A Stat. Mech. Appl. 2020, 538, 122826. [Google Scholar] [CrossRef]
- Singh, J.; Bajaj, R. Stability of temperature modulated convection in a vertical fluid-layer. Appl. Math. Model. 2018, 61, 408–420. [Google Scholar] [CrossRef]
- Singh, J.; Kaur, P.; Bajaj, R. Bicritical states in a vertical layer of fluid under two frequency temperature modulation. Phys. Rev. E 2020, 101, 023109. [Google Scholar] [CrossRef]
- Sadeghi, R.; Shadloo, M.S.; Hopp-Hirschler, M.; Hadjadj, A.; Nieken, U. Three-dimensional lattice Boltzmann simulations of high density ratio two-phase flows in porous media. Comput. Math. Appl. 2018, 75, 2445–2465. [Google Scholar] [CrossRef]
- Zhao, F.-Y.; Liu, D.; Tang, G.-F. Natural convection in an enclosure with localized heating and salting from below. Int. J. Heat Mass Transf. 2008, 51, 2889–2904. [Google Scholar] [CrossRef]
- Maghsoudi, P.; Siavashi, M. Application of nanofluid and optimization of pore size arrangement of heterogeneous porous media to enhance mixed convection inside a two-sided lid-driven cavity. J. Therm. Anal. Calorim. 2018, 135, 947–961. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A. Thermal instability in a porous medium layer saturated by a nanofluid. Int. J. Heat Mass Transf. 2009, 52, 5796–5801. [Google Scholar] [CrossRef]
- Hooman, K.; Gurgenci, H. Effects of Temperature-Dependent Viscosity on Forced Convection Inside a Porous Medium. Transp. Porous Media 2008, 75, 249–267. [Google Scholar] [CrossRef]
- Seth, G.; Hussain, S.; Sarkar, S. Hydromagnetic natural convection flow with heat and mass transfer of a chemically reacting and heat absorbing fluid past an accelerated moving vertical plate with ramped temperature and ramped surface concentration through a porous medium. J. Egypt. Math. Soc. 2015, 23, 197–207. [Google Scholar] [CrossRef]
- Rashidi, S.; Kashefi, M.H.; Kimc, K.C.; Samimi-Abianeh, O. Potentials of porous materials for energy management in heat exchangers—A comprehensive review. Appl. Energy 2019, 243, 206–232. [Google Scholar] [CrossRef]
- Ahmed, H.E.; Salman, B.; Kherbeet, A.; Ahmed, M. Optimization of thermal design of heat sinks: A review. Int. J. Heat Mass Transf. 2018, 118, 129–153. [Google Scholar] [CrossRef]
- Zheng, X.; Qi, Z. A comprehensive review of offset strip fin and its applications. Appl. Therm. Eng. 2018, 139, 61–75. [Google Scholar] [CrossRef]
- Alihosseini, Y.; Targhi, M.Z.; Heyhat, M.M.; Ghorbani, N. Effect of a micro heat sink geometric design on thermo-hydraulic performance: A review. Appl. Therm. Eng. 2020, 170, 114974. [Google Scholar] [CrossRef]
- Smolka, J.; Biro, O.; Nowak, A. Numerical Simulation and Experimental Validation of Coupled Flow, Heat Transfer and Electromagnetic Problems in Electrical Transformers. Arch. Comput. Methods Eng. 2009, 16, 319–355. [Google Scholar] [CrossRef]
- Zhao, H.; Li, B.; Wang, W.; Hu, Y.; Wang, Y. Water cooling radiator for solid state power supply in fast-axial-flow CO2 laser. Front. Optoelectron. 2016, 9, 585–591. [Google Scholar] [CrossRef]
- Qiu, T.; Wen, D.; Hong, W.; Liu, Y. Heat transfer performance of a porous copper micro-channel heat sink. J. Therm. Anal. Calorim. 2019, 139, 1453–1462. [Google Scholar] [CrossRef]
- Bar-Cohen, A.; Iyengar, M. Design and optimization of air-cooled heat sinks for sustainable development. IEEE Trans. Compon. Packag. Technol. 2002, 25, 584–591. [Google Scholar] [CrossRef]
- Zhao, D.; Tan, G. A review of thermoelectric cooling: Materials, modeling and applications. Appl. Therm. Eng. 2014, 66, 15–24. [Google Scholar] [CrossRef]
- Astanina, M.S.; Sheremet, M.; Umavathi, J. Unsteady natural convection in a partially porous cavity having a heat-generating source using local thermal non-equilibrium model. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1902–1919. [Google Scholar] [CrossRef]
- Mikhailenko, S.A.; Sheremet, M.A.; Mahian, O. Effects of uniform rotation and porous layer on free convection in an enclosure having local heat source. Int. J. Therm. Sci. 2019, 138, 276–284. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Buonomo, B.; Manca, O.; Sheremet, M.A. Heat transfer performance of the finned nano-enhanced phase change material system under the inclination influence. Int. J. Heat Mass Transf. 2019, 135, 1063–1072. [Google Scholar] [CrossRef]
- AlAmiri, A.; Khanafer, K.; Pop, I. Buoyancy-induced flow and heat transfer in a partially divided square enclosure. Int. J. Heat Mass Transf. 2009, 52, 3818–3828. [Google Scholar] [CrossRef]
- Astanina, M.; Rashidi, M.M.; Sheremet, M.; Lorenzini, G. Effect of porous insertion on convective energy transport in a chamber filled with a temperature-dependent viscosity liquid in the presence of a heat source term. Int. J. Heat Mass Transf. 2019, 144, 118530. [Google Scholar] [CrossRef]

| Characteristics of Materials | ρ, kg/m3 | c, J/(kg⋅K) | λ, W/(m⋅K) |
|---|---|---|---|
| Fluid (water) | 997.1 | 4179 | 0.613 |
| Solid structure (aluminum foam) | 2700 | 897 | 205 |
| Heat sink (copper) | 8920 | 385 | 401 |
| Heat-generating element (silicon) | 2330 | 710 | 150 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astanina, M.; Sheremet, M.; Mahabaleshwar, U.S.; Singh, J. Effect of Porous Medium and Copper Heat Sink on Cooling of Heat-Generating Element. Energies 2020, 13, 2538. https://doi.org/10.3390/en13102538
Astanina M, Sheremet M, Mahabaleshwar US, Singh J. Effect of Porous Medium and Copper Heat Sink on Cooling of Heat-Generating Element. Energies. 2020; 13(10):2538. https://doi.org/10.3390/en13102538
Chicago/Turabian StyleAstanina, Marina, Mikhail Sheremet, U. S. Mahabaleshwar, and Jitender Singh. 2020. "Effect of Porous Medium and Copper Heat Sink on Cooling of Heat-Generating Element" Energies 13, no. 10: 2538. https://doi.org/10.3390/en13102538
APA StyleAstanina, M., Sheremet, M., Mahabaleshwar, U. S., & Singh, J. (2020). Effect of Porous Medium and Copper Heat Sink on Cooling of Heat-Generating Element. Energies, 13(10), 2538. https://doi.org/10.3390/en13102538






