Recovery and Utilization of Low-Grade Waste Heat in the Oil-Refining Industry Using Heat Engines and Heat Pumps: An International Technoeconomic Comparison
Abstract
:1. Introduction
1.1. Definition of Low-Grade Heat
1.2. Estimates of Low-Grade Heat within the Oil Refining Industry
1.3. Aims of the Present Study
2. Technologies for the Recovery and Re-Use of Surplus Low-Grade Heat
2.1. Onsite Heat Recovery and Re-Use with Heat Exchangers/District Heating
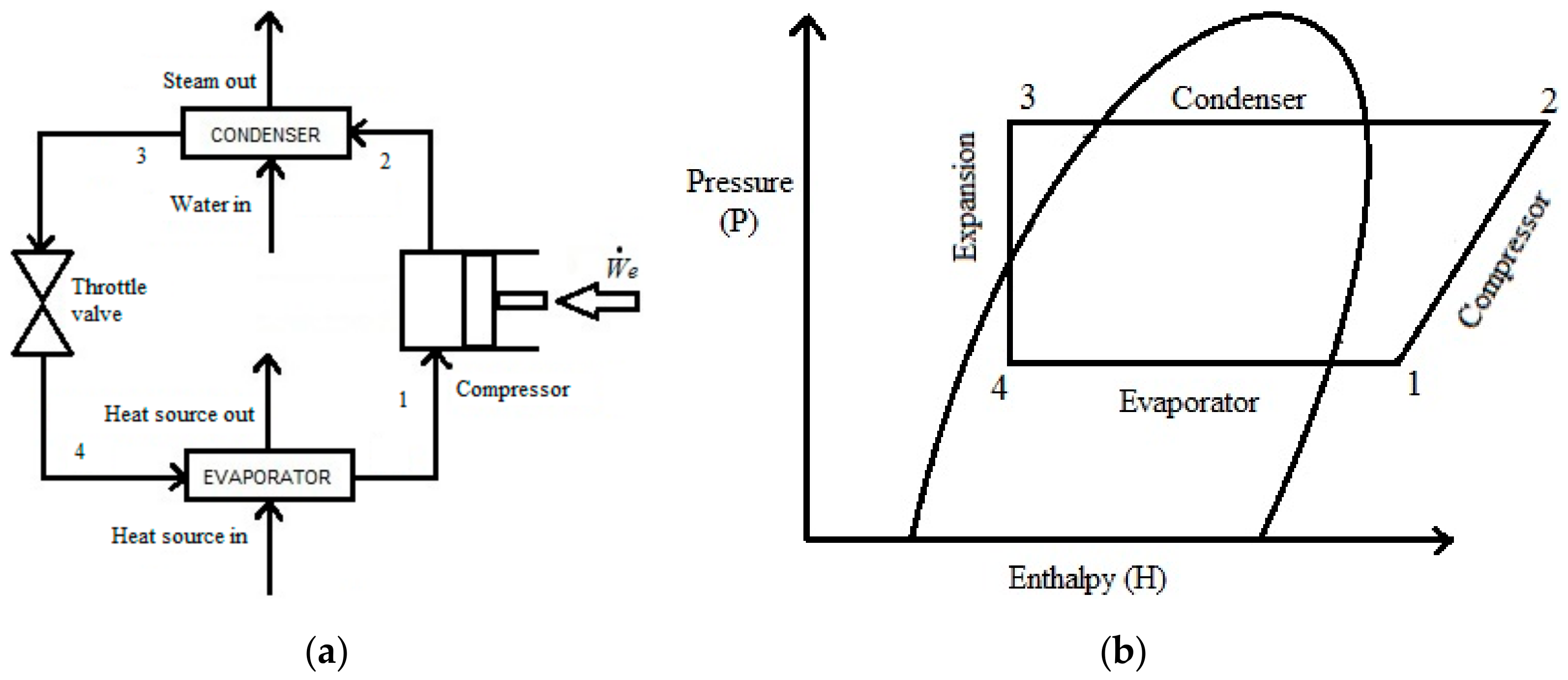
2.2. Power Cycle for Heat-To-Electricity Conversion
2.3. Heat Pumps for Temperature Upgrading
3. Theoretical and Empirical Models of Heat Engines and Heat Pumps
3.1. Heat Engines
3.1.1. Reversible (Carnot) and Endoreversible (Novikov) Heat Engine
3.1.2. Varying Heat-Source Temperature Heat Engine
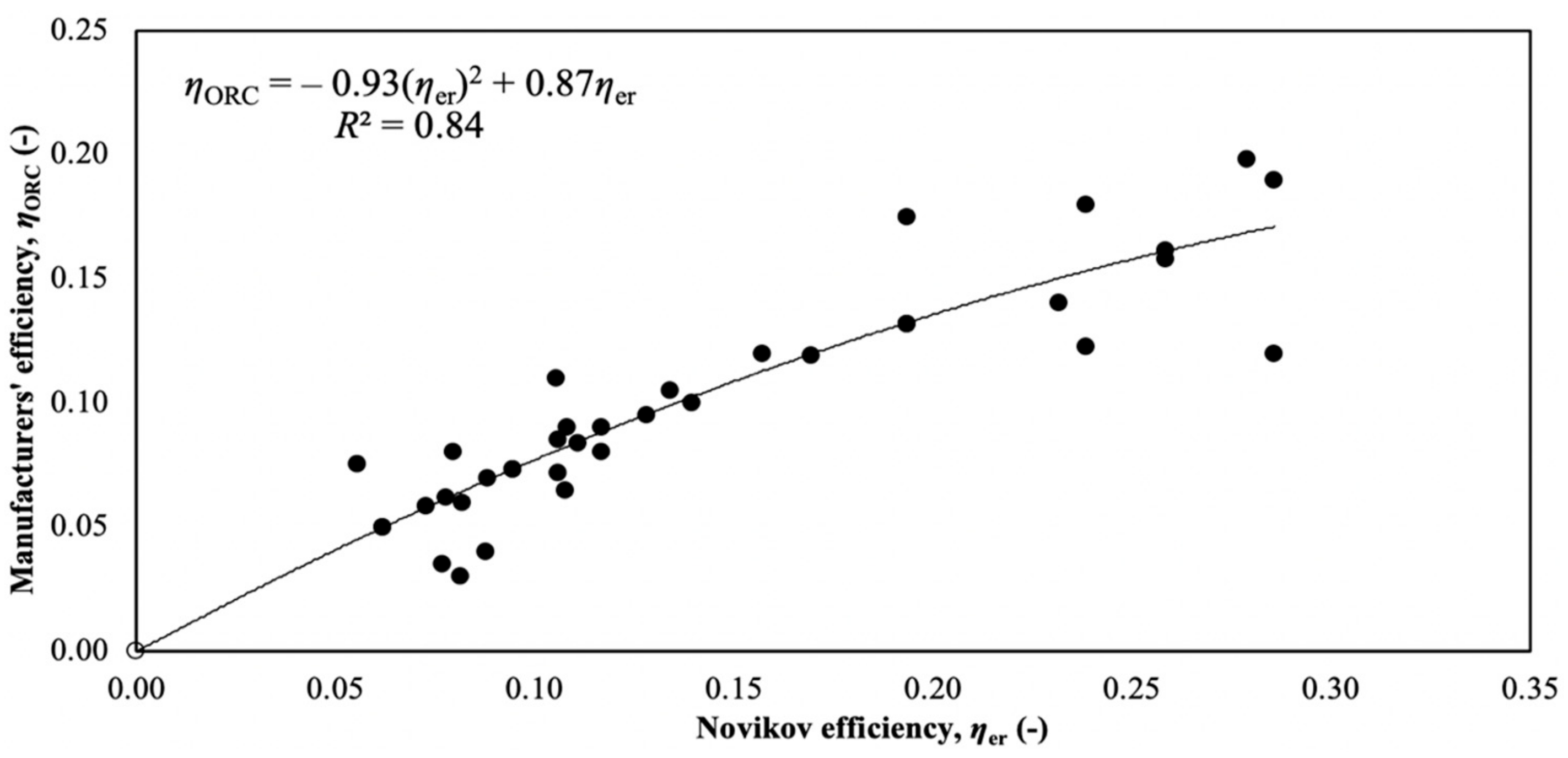
3.1.3. Practical ORC Engine Efficiencies
3.2. Heat Pumps
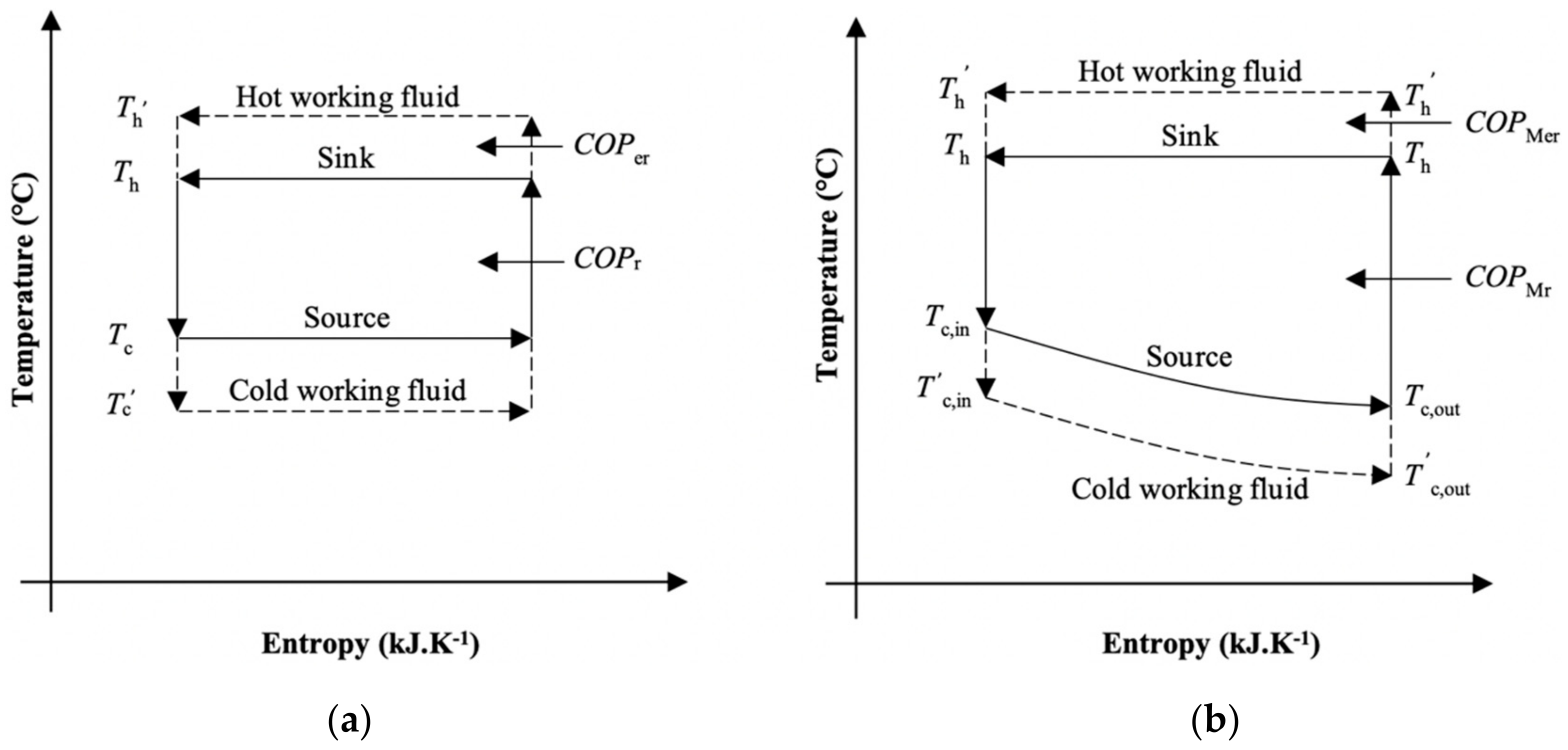
3.2.1. Reversible (Carnot) and Endoreversible Heat Pump
3.2.2. Varying Heat-Source Temperature Heat Pump
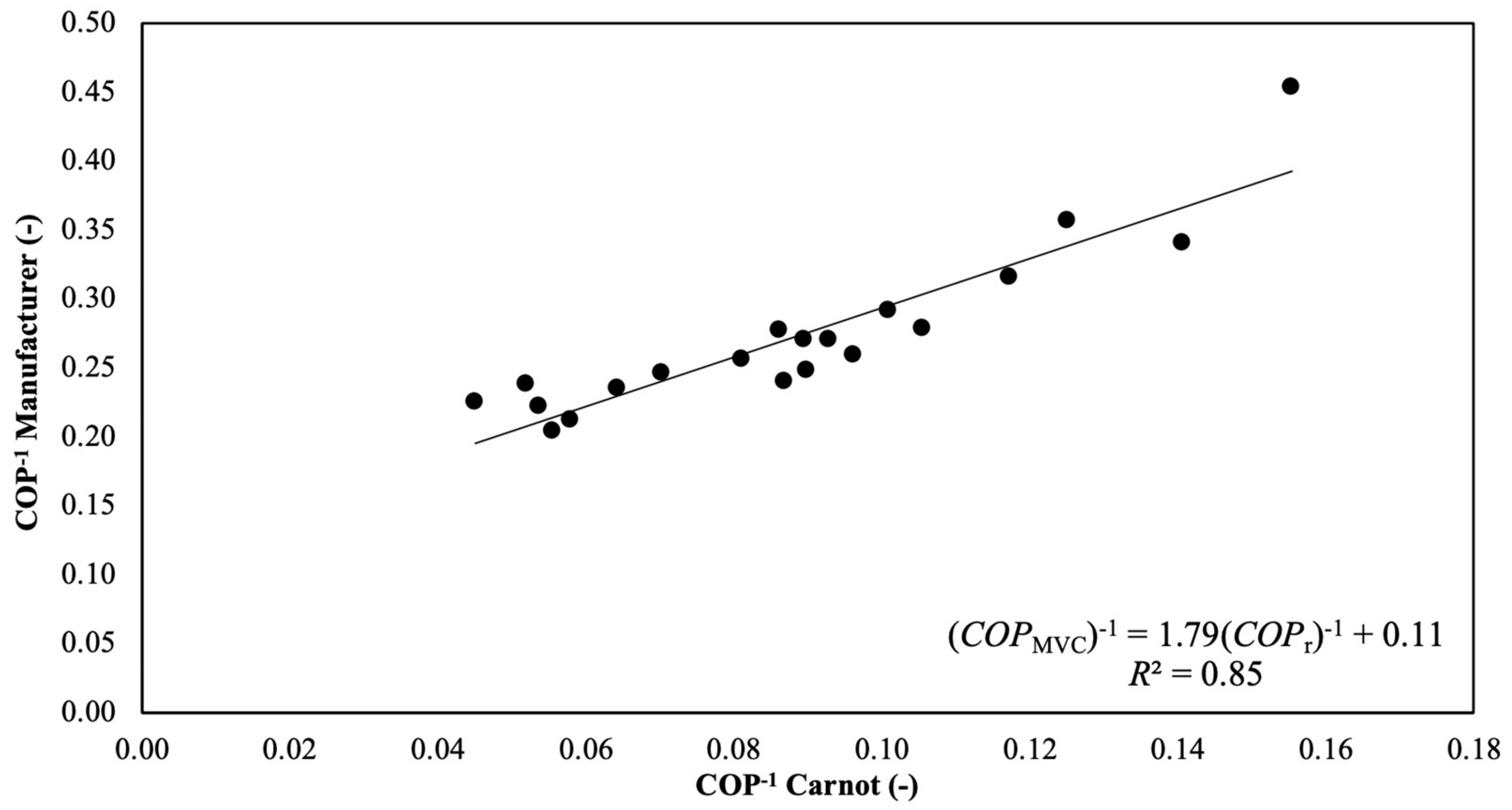
3.2.3. Practical COPs of MVC Heat Pumps
3.3. Economics of Low-Grade Heat Recovery Using ORC Engines and MVC Heat Pumps
4. Results and Discussion
4.1. Comparison of Theoretical Models against Empirical Predictions
4.2. Economics of Low-Grade Heat Recovery and Utilization
4.3. Comparison of Monetary Benefits across Global Regions
5. Conclusions
- Data from manufacturers on ORC engine thermal efficiencies and MVC heat pump COPs can be used to derive empirical relationships for predicting the performance of these technologies. In this work, expressions were derived for heat engines (Equation (8)) converting heat sources with temperatures up to 330 °C to electricity, as well as heat pumps (Equation (20) upgrading heat by temperature lifts up to 80 °C, that can predict actual performance within 4% for the former and 8% for the latter.
- The thermal efficiencies of commercially available ORC engines are well represented by a theoretical expression derived for an endoreversible heat engine operating with a decreasing heat-source temperature. The predictions were checked for heat sources with temperatures in the range of 65–145 °C and thermal-energy contents of 0.5–2.5 MW, with errors of around 4–5% on average.
- The COPs of commercially available MVC heat pumps are well represented by a similar theoretical expression for an endoreversible heat pump operating with a decreasing heat-source temperature, although less well than for the heat engines, with errors around 10–15% on average. A best match with actual COPs was obtained when upgrading heat sources with temperatures in the range of 120–140 °C. The theoretical expression was derived by proposing a modification (Equation (21)) to a temperature parameter in the Blanchard expression [76].
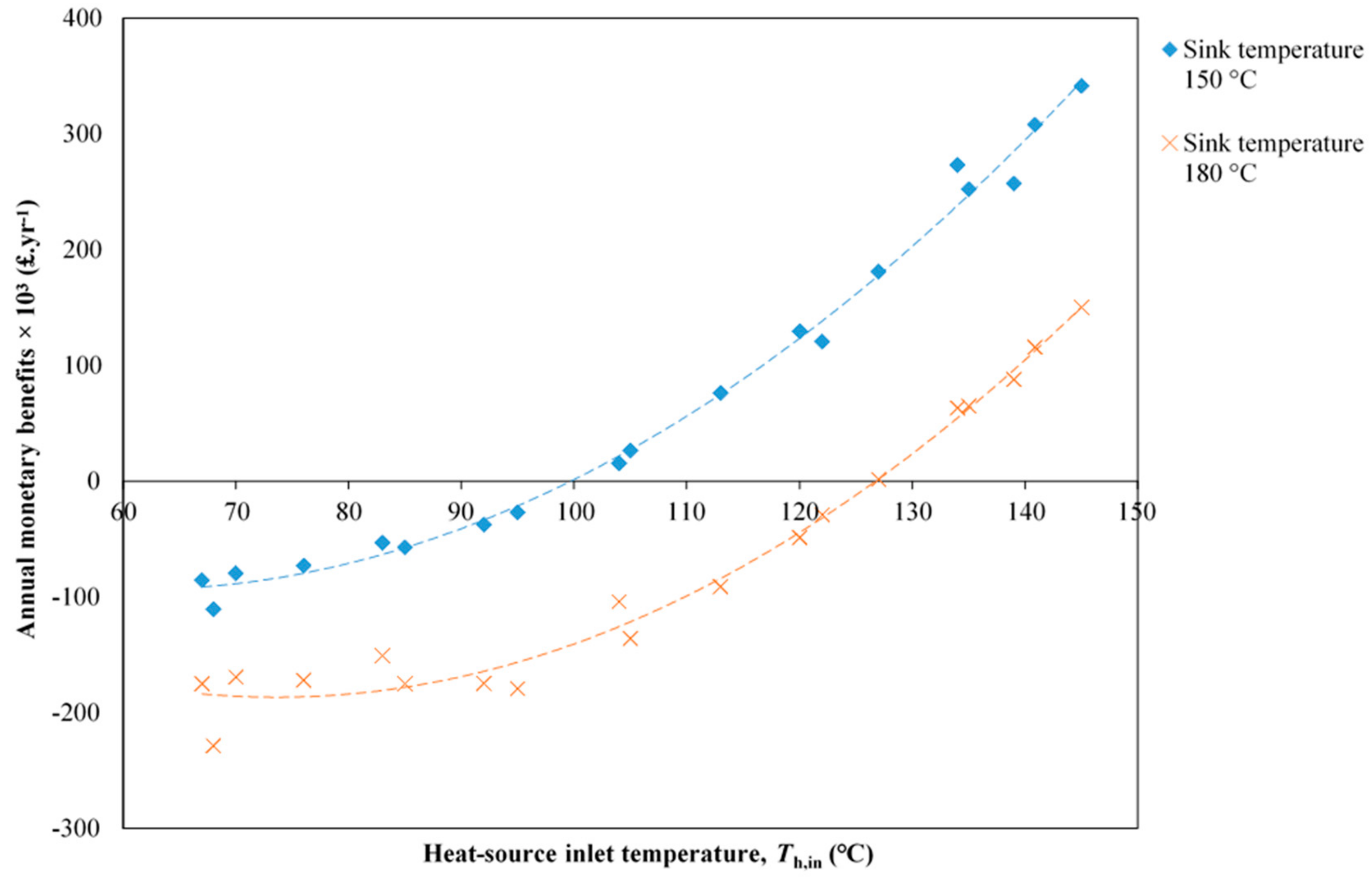
- The economics of low-grade waste heat recovery are strongly dependent not only on the heat-source temperatures but also on the heat-sink temperatures, with different sensitivities for ORC engines and MVC heat pumps. In the case of China (used as an example), electrical power generation with ORC engines was found to suffer a (small) reduction in monetary benefits amounting to £10,000–£20,000 for the heat sources considered in this work (listed in Table 5) for a 20 °C increase in the sink temperature (representing a change in the ambient temperature, either seasonal or geographical). In the case of MVC heat pumps, an increase of 30 °C in the sink temperature (representing a need or decision to generate medium-temperature stream rather than low-pressure steam) was found to reduce the monetary benefits by a rather larger £100,000–£200,000 for the same heat sources.
- Electrical power generation with ORC engines showed positive returns when streams with temperatures higher than 70 °C were considered from our list of investigated waste-heat sources, whereas for the generation of steam, economic feasibility is more strongly dependent on gas and electricity prices, as well as the choice of low- vs. medium-pressure steam generation. Returns can become negative more easily than for power generation. Positive annual benefits typically result when streams with temperatures above 100 °C are used for steam generation.
- In China, low-pressure steam generation with MVC heat pumps showed better annual benefits than power generation with ORC engines for streams with temperatures above ~110 °C and thermal-energy contents above 1.5 MW. For a waste-heat source temperature below ~110 °C or thermal-energy content less than 1.5 MW, ORC engines for electricity generation are monetarily more beneficial than MVC heat pumps for LP steam generation. MVC heat pumps and LP steam generation appear preferable when temperature lifts are less than 40 °C and COPs exceed 4.
- A similar crossover point, but at a higher heat-source temperature (~135 °C) and a higher thermal content (2.5 MW), exists for India. However, in countries such as Saudi Arabia, the UK and USA, the use of MVC heat pumps was not found to yield financial benefits in our investigated cases.
- Payback periods are in the range of two-to-eight years for electricity generation with ORC engines. In cases where low-pressure steam generation with MVC heat pumps is economically promising, the payback periods are highly influenced by the temperature lift and COP.
- Given data for one or more waste-heat streams, technoeconomic analyses and comparisons between ORC and MVC heat pump systems may be easily and rapidly performed using the efficiency models proposed in this work, which are sufficiently good representations of commercially available products to warrant their use in such integration studies. For later-stage design, it is necessary to employ more advanced/detailed models, such as in Refs. [85,86,87,88].
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| AB | Annual monetary benefits, £.yr−1 |
| ACE | Annualized capital expenditure, £.yr−1 |
| AF | Annualization factor |
| Ratio of absolute outlet temperature to inlet temperature of waste heat stream | |
| Ratio of absolute heat-sink temperature to inlet temperature of waste heat stream | |
| CC | Capital cost |
| Ce | Unit cost of electricity, £.Wh−1 |
| Cg | Unit cost of natural gas, £.Wh−1 |
| COP | Coefficient of performance |
| COPMVC | COP of (real) MVC heat pump |
| COPr | COP of (theoretical) reversible (Carnot) heat pump |
| COPer | COP of (theoretical) endoreversible heat pump |
| COPMr | COP of (theoretical) reversible heat pump with source varying temperature |
| COPMer | COP of (theoretical) endoreversible heat pump with source varying temperature |
| EEC | Cost of extra electricity consumed, £.yr−1 |
| i | Interest rate |
| , | Heat capacity rates of hot and cold streams, W.K−1 |
| MVC | Mechanical vapour compression |
| ORC | Organic Rankine cycle |
| PBP | Payback period, years |
| n | Number of years of operating life of the equipment |
| , | Thermal energy delivered to or extracted from hot and cold reservoirs/streams, Wth |
| SAE | Savings due to avoided purchase of electricity, £.yr−1 |
| SSG | Savings due to avoided generated steam, £.yr−1 |
| Th, Tc | Temperatures of hot and cold reservoirs, K |
| To | Sink temperature, K |
| Th,in, Tc,in | Inlet temperatures of hot and cold streams, K |
| Th,out, Tc,out | Outlet temperatures of hot and cold streams, K |
| Tk | Variable temperature used in correlations for endoreversible heat pumps, K |
| Electrical power, We | |
| Thermal power, Wth | |
| Greek | |
| Thermal efficiency of heat engine | |
| Thermal efficiency of (theoretical) reversible (Carnot) engine | |
| Thermal efficiency of (theoretical) endoreversible (Novikov) engine | |
| Thermal efficiency of (theoretical) reversible engine with varying source temperature | |
| Thermal efficiency of (theoretical) endoreversible engine with varying source temperature | |
| Thermal efficiency of (real) ORC engine |
Appendix A
| Cg, £.kWh−1 | Ce, £.kWh−1 | |
|---|---|---|
| UK | 0.016 | 0.14 |
| China | 0.022 | 0.07 |
| India | 0.018 | 0.08 |
| Saudi Arabia | 0.002 | 0.005 |
| USA | 0.006 | 0.12 |
- 1 GBP = 1.5 USD
- MVC heat pump—200 £.kWth−1
- ORC—2000 £.kWe−1
- 8000 h per year of operation of the facility.
- 20 years (n) of operating lifetime of the equipment.
- Interest rate, i = 5%
References
- Energy and Climate Change Committee. Energy and Climate Change—Third Report. UK Oil RefiningReport for UK House of Commons. 2013. Available online: https://publications.parliament.uk/pa/cm201314/cmselect/cmenergy/340/34002.htm (accessed on 3 April 2020).
- Element Energy; Ecofys; Imperial College; Stevenson, P.; Hyde, R. The Potential for Recovering and Using Surplus Heat from Industry. Report for UK Department of Energy & Climate Change. (Larksdown Environmental Services); (RHEnergy); 2014. Available online: https://www.gov.uk/government/publications/the-potential-for-recovering-and-using-surplus-heat-from-industry (accessed on 3 April 2020).
- McKenna, R.C.; Norman, J.B. Spatial modelling of industrial heat loads and recovery potentials in the UK. Energy Policy 2010, 38, 5878–5891. [Google Scholar] [CrossRef]
- Jouhara, H.; Khordehgah, N.; Almahmoud, S.; Delpech, B.; Chauhan, A.; Tassou, S.A. Waste heat recovery technologies and applications. Therm. Sci. Eng. Prog. 2018, 6, 268–289. [Google Scholar] [CrossRef]
- Waters, L. Energy Consumption in the UK. Report for Department for Business, Energy & Industrial Strategy; 2019. Available online: www.gov.uk/government/collections/energy-consumption-in-the-uk (accessed on 3 April 2020).
- Papapetrou, M.; Kosmadakis, G.; Cipollina, A.; La Commare, U.; Micale, G. Industrial waste heat: Estimation of the technically available resource in the EU per industrial sector, temperature level and country. Appl. Therm. Eng. 2018, 138, 207–216. [Google Scholar] [CrossRef]
- CE-HEAT Project. Available online: www.interreg-central.eu/content.node/CE-HEAT.html (accessed on 3 April 2020).
- Luo, A.; Fang, H.; Xia, J.; Lin, B.; Jiang, Y. Mapping potentials of low-grade industrial waste heat in Northern China. Resour. Conserv. Recycl. 2017, 125, 335–348. [Google Scholar] [CrossRef]
- BCS. Waste Heat Recovery: Technology and Opportunities in U.S. Industry. Report for US Department of Energy; 2008. Available online: www.eere.energy.gov/manufacturing/intensiveprocesses/pdfs/waste_heat_recovery.pdf (accessed on 3 May 2020).
- Ebrahimi, K.; Jones, G.F.; Fleischer, A.S. A review of data center cooling technology, operating conditions and the corresponding low-grade waste heat recovery opportunities. Renew. Sustain. Energy Rev. 2014, 31, 622–638. [Google Scholar] [CrossRef]
- Olsen, D.; Liem, P.; Abdelouadoud, Y.; Wellig, B. Thermal energy storage integration based on pinch analysis–Methodology and application. Chem. Ing. Tech. 2017, 89, 598–606. [Google Scholar] [CrossRef]
- Bagajewicz, M.; Valtinson, G.; Nguyen Thanh, D. Retrofit of crude units preheating trains: Mathematical programming versus pinch technology. Ind. Eng. Chem. Res. 2013, 52, 14913–14926. [Google Scholar] [CrossRef]
- Nemet, A.; Jide Isafiade, A.; Klemeš, J.J.; Kravanja, Z. Two-step MILP/MINLP approach for the synthesis of large-scale HENs. Chem. Eng. Sci. 2019, 197, 432–448. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Varbanov, P.S.; Walmsley, T.G.; Jia, X. New directions in the implementation of pinch methodology (PM). Renew. Sustain. Energy Rev. 2018, 98, 439–468. [Google Scholar] [CrossRef]
- Ferland, K.; Papar, R.; Quinn, J.; Kumar, S. Low Temperature Waste Energy Recovery at Chemical Plants and Refineries. In Proceedings of the 35th Industrial Energy Technology Conference (IETC 2013), New Orleans, LA, USA, 21–24 May 2013; Energy Systems Laboratory, Texas A&M Engineering Experiment Station: College Station, TX, USA, 2013. [Google Scholar]
- Hammond, G.P.; Norman, J.B. Heat recovery opportunities in UK industry. Appl. Energy 2014, 116, 387–397. [Google Scholar] [CrossRef] [Green Version]
- Sinclair, D.A.J. The Climate Change Levy and Enhanced Capital Allowances–Focus on Waste Heat Recovery Equipment. Master’s Thesis, Heriot-Watt University, Edinburgh, UK, 2001. [Google Scholar]
- Brückner, S.; Liu, S.; Miró, L.; Radspieler, M.; Cabeza, L.F.; Lävemann, E. Industrial waste heat recovery technologies: An economic analysis of heat transformation technologies. Appl. Energy 2015, 151, 157–167. [Google Scholar] [CrossRef]
- Ammar, Y.; Joyce, S.; Norman, R.; Wang, Y.; Roskilly, A.P. Low grade thermal energy sources and uses from the process industry in the UK. Appl. Energy 2012, 89, 3–20. [Google Scholar] [CrossRef]
- Crook, A.W. Profiting from Low-Grade Heat: Thermodynamic Cycles for Low-Temperature Heat Sources; Institute of Electrical Engineers: London, UK, 1994. [Google Scholar]
- Little, A.B.; Garimella, S. Comparative assessment of alternative cycles for waste heat recovery and upgrade. Energy 2011, 36, 4492–4504. [Google Scholar] [CrossRef]
- Öhman, H.; Lundqvist, P. Comparison and analysis of performance using low temperature power cycles. Appl. Therm. Eng. 2013, 52, 160–169. [Google Scholar] [CrossRef]
- Fischer, J. Comparison of trilateral cycles and organic Rankine cycles. Energy 2011, 36, 6208–6219. [Google Scholar] [CrossRef]
- Ling-Chin, J.; Bao, H.; Ma, Z.; Taylor, W.; Roskilly, A.P. State-of-the-Art Technologies on Low-Grade Heat Recovery and Utilization in Industry. Intechopen Book, Ch. 4. 2018. Available online: http://dx.doi.org/10.5772/intechopen.78701 (accessed on 3 April 2020).
- Haddad, C.; Périlhona, C.; Danlosa, A.; François, M.-X.; Descombesa, G. Some efficient solutions to recover low and medium waste heat: Competitiveness of the thermoacoustic technology. Energy Procedia 2014, 50, 1056–1069. [Google Scholar] [CrossRef]
- Van de Bor, D.M.; Infante Ferreira, C.A.; Kiss, A.A. Low grade waste heat recovery using heat pumps and power cycles. Energy 2015, 8, 864–873. [Google Scholar] [CrossRef]
- Crowe, R. Capturing Waste Heat with Organic Rankine Cycle Systems. Available online: https://www.renewableenergyworld.com/2011/01/24/capturing-waste-heat-with-organic-rankine-cycle-systems/ (accessed on 3 April 2020).
- Brasz, J.J. Low Temperature/Small Capacity ORC System Development. In Proceedings of the 1st International Seminar on ORC Power Systems, Delft, The Netherlands, 22–23 September 2011. [Google Scholar]
- Law, R.; Harvey, A.; Reay, D. Opportunities for low-grade heat recovery in the UK food processing industry. Appl. Therm. Eng. 2012, 53, 188–196. [Google Scholar] [CrossRef]
- Johansson, D.; Rootzén, J.; Berntsson, T.; Johnsson, F. Assessment of strategies for CO2 abatement in the European petroleum refining industry. Energy 2012, 42, 375–386. [Google Scholar] [CrossRef] [Green Version]
- BRE; University of Edinburgh; Centre for Sustainable Energy. Research into Barriers to Deployment of District Heating Networks. Report for UK Department of Energy & Climate Change; 2013. Available online: https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/191542/Barriers_to_deployment_of_district_heating_networks_2204.pdf (accessed on 3 April 2020).
- Freeman, J.; Hellgardt, K.; Markides, C.N. An Assessment of solar–thermal collector designs for small-scale combined heating and power applications in the United Kingdom. Heat Transf. Eng. 2015, 36, 1332–1347. [Google Scholar] [CrossRef] [Green Version]
- Freeman, J.; Hellgardt, K.; Markides, C.N. An assessment of solar-powered organic Rankine cycle systems for combined heating and power in UK domestic applications. Appl. Energy 2015, 138, 605–620. [Google Scholar] [CrossRef] [Green Version]
- Oyewunmi, O.A.; Markides, C.N. Thermo-economic and heat transfer optimization of working-fluid mixtures in a low-temperature organic Rankine cycle system. Energies 2016, 9, 448. [Google Scholar] [CrossRef] [Green Version]
- Oyewunmi, O.A.; Taleb, A.I.; Haslam, A.J.; Markides, C. An assessment of working-fluid mixtures using SAFT-VR MIE for use in organic Rankine cycle systems for waste-heat recovery. Comput. Therm. Sci. 2014, 6, 301–316. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Taleb, A.I.; Haslam, A.J.; Markides, C.N. On the use of SAFT-VR Mie for assessing large-glide fluorocarbon working-fluid mixtures in organic Rankine cycles. Appl. Energy 2016, 163, 263–282. [Google Scholar] [CrossRef] [Green Version]
- Cedillos Alvarado, D.; Acha, S.; Shah, N.; Markides, C.N. A technology selection and operation (TSO) optimisation model for distributed energy systems: Mathematical formulation and case study. Appl. Energy 2016, 180, 491–503. [Google Scholar] [CrossRef]
- Law, R.; Harvey, A.; Reay, D. Techno-economic comparison of a high temperature heat pump and an organic Rankine cycle machine for low-grade waste heat recovery in UK industry. Int. J. Low-Carbon Technol. 2013, 8, i47–i54. [Google Scholar] [CrossRef]
- Arvay, P.; Muller, M.R.; Ramdeen, V.; Cunningham, G. Economic Implementation of the Organic Rankine Cycle in Industry. In Proceedings of the 2011 American Council for an Energy Efficient Economy (ACEEE) Summer Study on Energy Efficiency in Industry, New York, NY, USA, 23–26 July 2011; pp. 1–12. [Google Scholar]
- Jung, H.C.; Krumdieck, S.; Vranjes, T. Feasibility assessment of refinery waste heat-to-power conversion using an organic Rankine cycle. Energy Convers. Manag. 2014, 77, 396–407. [Google Scholar] [CrossRef]
- Mitsuo, M.B.; Silva, J.A.M.; Oliveira, S.J. Are ORCs a Good Option for Waste Heat Recovery in a Petroleum Refinery? In Proceedings of the 27th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS 2014), Turku, Finland, 15–19 June 2014; Zevenhoven, R., Ed.; Thermal and Flow Engineering Laboratory, Abo Akademi University: Turku, Finland, 2014. [Google Scholar]
- Oluleye, G.; Jobson, M.; Smith, R. A hierarchical approach for evaluation of waste heat utilization opportunities. Chem. Eng. Trans. 2014, 39, 1093–1098. [Google Scholar] [CrossRef]
- Chen, C.-L.; Li, P.-Y.; Le, S.N.T. Organic Rankine cycle for waste heat recovery in a refinery. Ind. Eng. Chem. Res. 2016, 55, 3262–3275. [Google Scholar] [CrossRef]
- Meacher, J. Organic Rankine Cycle Systems for Waste Heat Recovery in Refineries and Chemical Process Plants. In Proceedings of the 3rd Industrial Energy Technology Conference (IETC), Houston, TX, USA, 26–29 April 1981; Energy Systems Laboratory, Texas A&M Engineering Experiment Station: College Station, TX, USA, 1981. [Google Scholar]
- Berntsson, T.; Elmeroth, L.P.; Algehed, J.; Hektor, E.; Franck, P.-Å.; Åsblad, A.; Johnsson, F.; Lyngfelt, A.; Gevert, B.; Chalmers EnergiCentrum, Chalmers University of Technology; et al. Towards a Sustainable Oil Refinery. Pre-Study for Larger Co-Operation ProjectsReport for Preem. 2008. Available online: http://publications.lib.chalmers.se/records/fulltext/69752.pdf (accessed on 3 April 2020).
- Varga, Z.; Rabi, I.; Farkas, C. Waste heat recovery with organic Rankine cycle in the petroleum industry. Chem. Eng. Trans. 2012, 29, 301–306. [Google Scholar] [CrossRef]
- Fuji Oil Company. Low-Temperature Waste Heat Utilize System; Report for Fuji Oil Company; Fuji Oil Company: Tokyo, Japan, 2019. [Google Scholar]
- DRD Power. Huntsman UK Trials New Waste-Heat Power System. Available online: http://drdpower.co.uk/huntsman-uk-trials-new-waste-heat-power-system (accessed on 3 April 2020).
- Markides, C.N. The role of pumped and waste heat technologies in a high-efficiency sustainable energy future for the UK. Appl. Therm. Eng. 2013, 53, 197–209. [Google Scholar] [CrossRef]
- Nag, P.K.; Gupta, A.V.S.S.K.S. Exergy analysis of the Kalina cycle. Appl. Therm. Eng. 1998, 18, 427–439. [Google Scholar] [CrossRef]
- Arslan, O. Exergoeconomic evaluation of electricity generation by the medium temperature geothermal resources, using a Kalina cycle: Simav case study. Int. J. Therm. Sci. 2010, 49, 1866–1873. [Google Scholar] [CrossRef]
- Ogriseck, S. Integration of Kalina cycle in a combined heat and power plant, a case study. Appl. Therm. Eng. 2009, 29, 2843–2848. [Google Scholar] [CrossRef] [Green Version]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tian, H.; Shu, G.; Zhao, M.; Markides, C.N.; Hu, C. Potential of carbon dioxide transcritical power cycle waste-heat recovery systems for heavy-duty truck engines. Appl. Energy 2019, 250, 1581–1599. [Google Scholar] [CrossRef]
- Song, J.; Li, X.; Ren, X.; Tian, H.; Shu, G.; Gu, C.; Markides, C.N. Thermodynamic and economic investigations of transcritical CO2-cycle systems with integrated radial-inflow turbine performance predictions. Appl. Therm. Eng. 2020, 165, 114604. [Google Scholar] [CrossRef]
- Zamfirescu, C.; Dincer, I. Thermodynamic analysis of a novel ammonia–water trilateral Rankine cycle. Thermochim. Acta 2008, 477, 7–15. [Google Scholar] [CrossRef]
- Ajimotokan, H.A.; Sher, I. Thermodynamic performance simulation and design optimisation of trilateral-cycle engines for waste heat recovery-to-power generation. Appl. Energy 2015, 154, 26–34. [Google Scholar] [CrossRef]
- Yari, M.; Mehr, A.S.; Zare, V.; Mahmoudi, S.M.S.; Rosen, M.A. Exergoeconomic comparison of TLC (trilateral Rankine cycle), ORC (organic Rankine cycle) and Kalina cycle using a low grade heat source. Energy 2015, 83, 712–722. [Google Scholar] [CrossRef]
- Markides, C.N.; Smith, T.C.B. A dynamic model for the efficiency optimization of an oscillatory low grade heat engine. Energy 2011, 36, 6967–6980. [Google Scholar] [CrossRef] [Green Version]
- Solanki, R.; Galindo, A.; Markides, C.N. Dynamic modelling of a two-phase thermofluidic oscillator for efficient low grade heat utilization: Effect of fluid inertia. Appl. Energy 2012, 89, 156–163. [Google Scholar] [CrossRef]
- Solanki, R.; Mathie, R.; Galindo, A.; Markides, C.N. Modelling of a two-phase thermofluidic oscillator for low-grade heat utilisation: Accounting for irreversible thermal losses. Appl. Energy 2013, 106, 337–354. [Google Scholar] [CrossRef]
- Solanki, R.; Galindo, A.; Markides, C.N. The role of heat exchange on the behaviour of an oscillatory two-phase low-grade heat engine. Appl. Therm. Eng. 2013, 53, 177–187. [Google Scholar] [CrossRef]
- Kirmse, C.J.W.; Oyewunmi, O.A.; Taleb, A.I.; Haslam, A.J.; Markides, C.N. A two-phase single-reciprocating-piston heat conversion engine: Non-linear dynamic modelling. Appl. Energy 2017, 186, 359–375. [Google Scholar] [CrossRef] [Green Version]
- Markides, C.N.; Gupta, A. Experimental investigation of a thermally powered central heating circulator: Pumping characteristics. Appl. Energy 2013, 110, 132–146. [Google Scholar] [CrossRef] [Green Version]
- Markides, C.N.; Solanki, R.; Galindo, A. Working fluid selection for a two-phase thermofluidic oscillator: Effect of thermodynamic properties. Appl. Energy 2014, 124, 167–185. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Kirmse, C.J.W.; Haslam, A.J.; Müller, E.A.; Markides, C.N. Working-fluid selection and performance investigation of a two-phase single-reciprocating-piston heat-conversion engine. Appl. Energy 2017, 186, 376–395. [Google Scholar] [CrossRef] [Green Version]
- Palanisamy, K.; Taleb, A.I.; Markides, C.N. Optimizing the non-inertive-feedback thermofluidic engine for the conversion of low-grade heat to pumping work. Heat Transf. Eng. 2015, 36, 1303–1320. [Google Scholar] [CrossRef] [Green Version]
- Taleb, A.I.; Timmer, M.A.G.; El-Shazly, M.Y.; Samoilov, A.; Kirillov, V.A.; Markides, C.N. A single-reciprocating-piston two-phase thermofluidic prime-mover. Energy 2016, 104, 250–265. [Google Scholar] [CrossRef] [Green Version]
- Kirmse, C.J.W.; Oyewunmi, O.A.; Haslam, A.J.; Markides, C.N. Comparison of a novel organic-fluid thermofluidic heat converter and an organic Rankine cycle heat engine. Energies 2016, 9, 479. [Google Scholar] [CrossRef] [Green Version]
- Macwan, S. The Kalina Cycle. A Major Breakthrough in Efficient Heat to Power Generation. In Proceedings of the National Combined Heat & Power and Waste Heat to Power (CHP2013 & WHP2013) Conference and Trade Show, Houston, TX, USA, 7–9 October 2013. [Google Scholar]
- Kalina Power. Kalina Cycle. Available online: www.kalinapower.com (accessed on 3 April 2020).
- Chen, H.; Yogi Goswami, D.; Stefanakos, E. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Cao, X.-Q.; Yang, W.-W.; Zhou, F.; He, Y.-L. Performance analysis of different high-temperature heat pump systems for low-grade waste heat recovery. Appl. Therm. Eng. 2014, 71, 291–300. [Google Scholar] [CrossRef]
- Kiss, A.A.; Landaeta, S.J.F.; Ferreira, C.A.I. Mastering heat pumps selection for energy efficient distillation. Chem. Eng. Trans. 2012, 29, 397–402. [Google Scholar] [CrossRef]
- Markides, C.N. Low-concentration solar-power systems based on organic Rankine cycles for distributed-scale applications: Overview and further developments. Front. Energy Res. 2015, 3, 47. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, C.H. Coefficient of performance for finite speed heat pump. J. Appl. Phys. 1980, 51, 2471–2472. [Google Scholar] [CrossRef]
- Jincan, C. The general performance characteristics of an irreversible absorption heat pump operating between four temperature levels. J. Phys. D: Appl. Phys. 1999, 32, 1428–1433. [Google Scholar] [CrossRef]
- Sun, F.; Chen, W.; Chen, L.; Wu, C. Optimal performance of an endoreversible Carnot heat pump. Energy Convers. Manag. 1997, 38, 1439–1443. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, D.; Kang, Y. Local stability analysis of a class of endoreversible heat pumps. J. Appl. Phys. 2007, 102, 034905. [Google Scholar] [CrossRef]
- Sahin, B.; Kodal, A. Finite time thermoeconomic optimization for endoreversible refrigerators and heat pumps. Energy Convers. Manag. 1999, 40, 951–960. [Google Scholar] [CrossRef]
- Oluleye, G.; Jobson, M.; Smith, R.; Perry, S.J. Evaluating the potential of a process site for waste heat recovery. Chem. Eng. Trans. 2014, 39, 1069–1074. [Google Scholar] [CrossRef]
- Aneke, M.; Agnew, B.; Underwood, C. Power Generation through the use of Waste Heat Energy from Process Industries: A Greener Approach to Reducing CO2 Emission & Global Warming in Nigeria. In Proceedings of the 2nd FUTO 2011 Alternative and Renewable Energy Conference, Owerri, Nigeria, 16–19 May 2010; Greenfield Education Service: Beijing, China, 2011. [Google Scholar]
- Fraser, D.M.; Gillespie, N. The application of pinch technology to retrofit energy integration of an entire oil refinery. Trans. IChemE Part A: Chem. Eng. Res. Des. 1992, 70A, 395–406. [Google Scholar]
- Barve, S.; (ThyssenKrupp Industries, Mumbai, Maharashtra, India). Personal communication, 2015.
- Schuster, S.; Markides, C.N.; White, A.J. Design and off-design optimisation of an organic Rankine cycle (ORC) system with an integrated radial turbine model. Appl. Therm. Eng. 2020, 174, 115192. [Google Scholar] [CrossRef]
- Van Kleef, L.M.T.; Oyewunmi, O.A.; Markides, C.N. Multi-objective thermo-economic optimization of organic Rankine cycle (ORC) power systems in waste-heat recovery applications using computer-aided molecular design techniques. Appl. Energy 2019, 251, 112513. [Google Scholar] [CrossRef]
- Chatzopoulou, M.A.; Lecompte, S.; De Paepe, M.; Markides, C.N. Off-design optimisation of organic Rankine cycle (ORC) engines with different heat exchangers and volumetric expanders in waste heat recovery applications. Appl. Energy 2019, 253, 113442. [Google Scholar] [CrossRef]
- Pantaleo, A.M.; Simpson, M.; Rotolo, G.; Distaso, E.; Oyewunmi, O.A.; Sapin, P.; De Palma, P.; Markides, C.N. Thermoeconomic optimisation of small-scale organic Rankine cycle systems based on screw vs. piston expander maps in waste heat recovery applications. Energy Convers. Manag. 2019, 200, 112053. [Google Scholar] [CrossRef]
- International Gas Union. Wholesale Gas Price Survey. 2016 Edition. Available online: www.igu.org/sites/default/files/node-news_item-field_file/IGU_wholesalegasprice_survey0509_2016.pdf (accessed on 3 April 2020).
- Statista Research Department. Electricity Prices by Country in 2015. Available online: www.statista.com/statistics/477995/global-prices-of-electricity-by-select-country (accessed on 3 April 2020).
- Exchange Rates UK. Historical Exchange Rates for GBP/USD Currency Conversion in 2015. Available online: www.exchangerates.org.uk (accessed on 3 April 2020).











| Stream Type | Phase | Waste Energy Sources | Temperature (°C) |
|---|---|---|---|
| Process | Liquid | Distillation cuts to be cooled | 82–104 |
| Process | Gas | Overhead condensers | 65–148 |
| Process | Liquid | Run-down and product streams | 176–232 |
| Process | Gas and liquid | Product/gas to air coolers | 112 |
| Industry | Process | Stream Type | Thermal-Energy Content (MW) | Temperature (°C) |
|---|---|---|---|---|
| Oil | Furnace exhaust | Gas | 2080 | 340 |
| Oil | Boiler exhaust | Gas | 615 | 230 |
| Oil | Condensate | Liquid | 1520 | 82 |
| Oil | Process water | Liquid | 925 | 50 |
| Oil | Condenser cooling water | Liquid | 2310 | 45 |
| Refinery | Refining Capacity (bbl.day−1) | Waste Heat Streams Type | Thermal-Energy Content (MW) | Temperature (°C) |
|---|---|---|---|---|
| Essar Stanlow | 296,000 | Liquid | 2050 | 70–90 |
| Gas | 30 | 150 | ||
| Esso Fawley | 270,000 | Liquid | 2850 | 70–90 |
| Gas | 425 | 150 | ||
| Murco Milford Haven # | 108,000 | Liquid | 1070 | 70–90 |
| Gas | 158 | 150 | ||
| Petroineos Grangemouth | 200,000 | Liquid | 1780 | 70–90 |
| Gas | 264 | 150 | ||
| Phillips 66 Humber | 221,000 | Liquid | 2050 | 70–90 |
| Gas | 304 | 150 | ||
| Total Lindsey * | 207,000 | Liquid | 1960 | 70–90 |
| Gas | 292 | 150 | ||
| Valero Energy Ltd. | 270,000 | Liquid | 1870 | 70–90 |
| Gas | 278 | 150 |
| Heat Sources | Preferred Utilization Temperature (°C) | Typical Efficiency/COP | Capital Cost | Payback Period (Years) | Key Parameters | Constraints | |
|---|---|---|---|---|---|---|---|
| Heat exchangers | Most heat sources | 50–300 | >90% | Vary; typical: £4–200 m−2 | <2 | Amount of heat recovered | Temp. gradients in heat exchanger |
| Heat upgrade with heat pumps | Waste-water streams, flue gases, distillation cuts being cooled | 80–150 | 3–5, up to 8 in rare cases | £150–200 kW−1 | 3–5 | Inlet/outlet temp. of compressor | Boiling point of working fluid |
| Electricity generation with ORC engines | Air coolers, water coolers, furnace flue gases, gas turbine exhaust, excess low-press. steam | 100–300 | 10–20% | £1000–2000 kW−1 | 4–5 | Working fluid, turbine inlet temp., condenser outlet temp. | Boiling point of working fluid |
| Heat transport for district heating | Excess low-press. steam, unrecycled steam condensate, waste water | 50–100 (water) 100–150 (steam) | 25–75% | £900–1000 m−1 | Depends on energy prices | Supply/return temp. | Policies, geographical |
| Stream No. | Th,in (°C) | Th,out (°C) | Heat Capacity Rate (, kW.K−1) | Thermal Energy Available , MW) | Reference |
|---|---|---|---|---|---|
| 1 | 113 | 62 | 35.0 | 1.78 $ | [81] |
| 2 | 134 | 63 | 38.0 | 2.70 $ | |
| 3 | 67 | 60 | 80.0 | 0.56 $ | [82] |
| 4 | 68 | 58 | 75.0 | 0.75 $ | |
| 5 | 70 | 57 | 45.0 | 0.58 $ | |
| 6 | 76 | 51 | 28.0 | 0.70 $ | |
| 7 | 105 | 55 | 32.0 $ | 1.60 | [83] |
| 8 | 104 | 60 | 26.5 $ | 1.16 | |
| 9 | 145 | 61 | 32.0 $ | 2.68 | |
| 10 | 140 | 64 | 34.0 $ | 2.61 | |
| 11 | 127 | 61 | 33.0 $ | 2.18 | |
| 12 | 95 | 45 | 27.0 $ | 1.35 | |
| 13 | 135 | 59 | 32.0 $ | 2.43 | |
| 14 | 92 | 50 | 28.0 $ | 1.17 | [84] |
| 15 | 83 | 57 | 29.0 $ | 0.75 | |
| 16 | 139 | 55 | 27.0 $ | 2.26 | |
| 17 | 120 | 62 | 35.0 $ | 2.03 | |
| 18 | 122 | 60 | 28.0 $ | 1.74 | |
| 19 | 85 | 55 | 31.0 $ | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gangar, N.; Macchietto, S.; Markides, C.N. Recovery and Utilization of Low-Grade Waste Heat in the Oil-Refining Industry Using Heat Engines and Heat Pumps: An International Technoeconomic Comparison. Energies 2020, 13, 2560. https://doi.org/10.3390/en13102560
Gangar N, Macchietto S, Markides CN. Recovery and Utilization of Low-Grade Waste Heat in the Oil-Refining Industry Using Heat Engines and Heat Pumps: An International Technoeconomic Comparison. Energies. 2020; 13(10):2560. https://doi.org/10.3390/en13102560
Chicago/Turabian StyleGangar, Nikunj, Sandro Macchietto, and Christos N. Markides. 2020. "Recovery and Utilization of Low-Grade Waste Heat in the Oil-Refining Industry Using Heat Engines and Heat Pumps: An International Technoeconomic Comparison" Energies 13, no. 10: 2560. https://doi.org/10.3390/en13102560
APA StyleGangar, N., Macchietto, S., & Markides, C. N. (2020). Recovery and Utilization of Low-Grade Waste Heat in the Oil-Refining Industry Using Heat Engines and Heat Pumps: An International Technoeconomic Comparison. Energies, 13(10), 2560. https://doi.org/10.3390/en13102560






