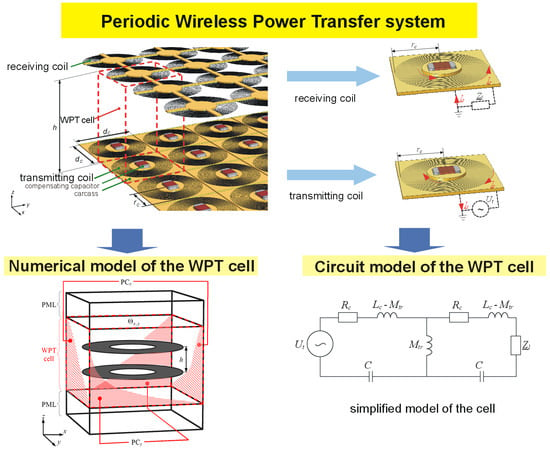
Numerical and Circuit Modeling of the Low-Power Periodic WPT Systems
Abstract
1. Introduction
2. Materials and Methods
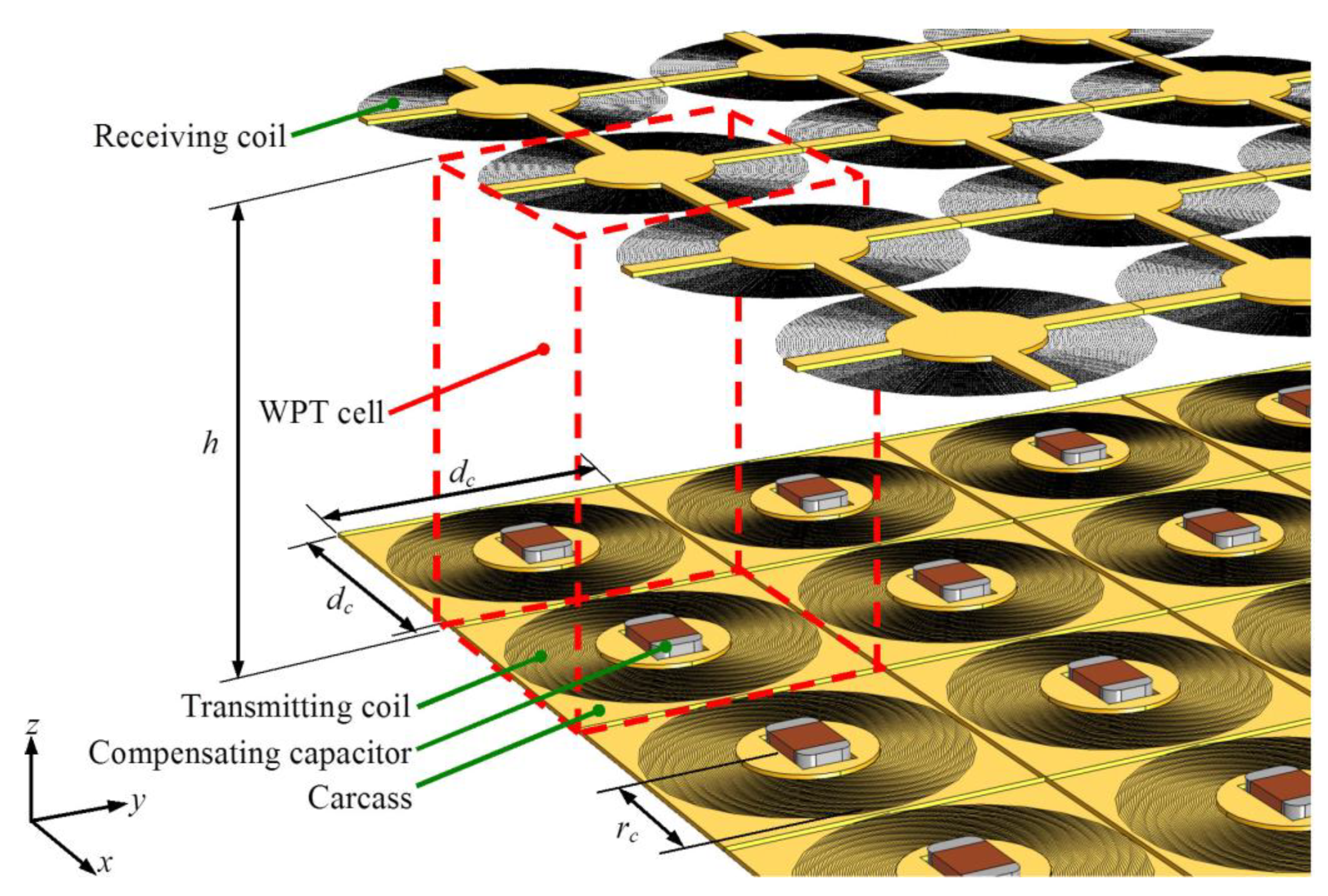
2.1. Periodic Wireless Power Transfer System
2.2. Modeling Approach
- Numerical model of periodic WPT system, with necessary simplifications and boundary conditions.
- Circuit model as an alternative for numerical model.
2.3. Numerical Model
- Coil geometry,
- Winding structure, number of WPT cells,
- Electrical elements (e.g., compensating capacitors, loads) connected to coils.
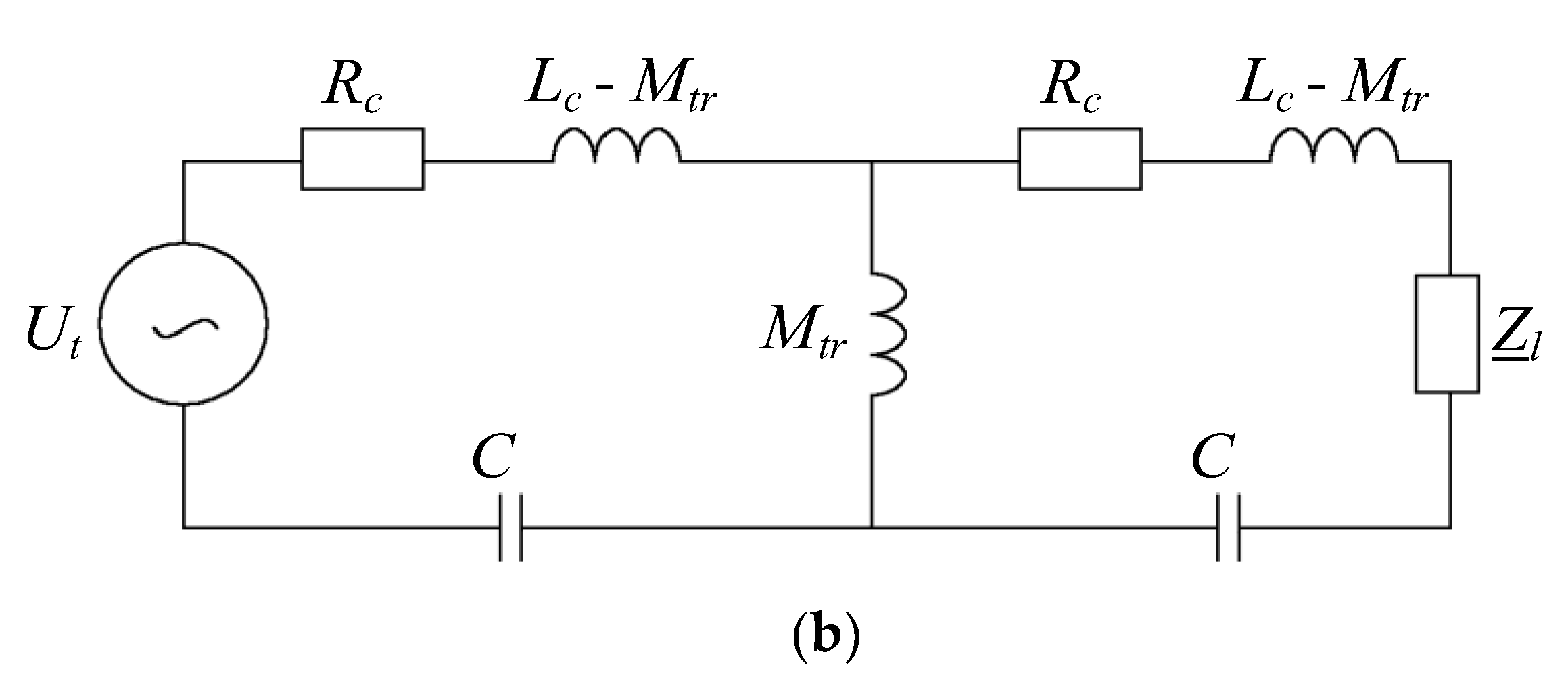
2.4. Circuit Model
- Only coupling between adjacent coils is considered (|a|max = |b|max = 1),
- The system is periodic and symmetrical (Mx+a,y+b = Mx−a,y−b),
- Mutual inductances of coils adjacent to Θx,y are assumed to be approximately equal (Mx+a,y ≈ Mx,y+b ≈ Mx+a,y+b),
3. Results and Discussion
3.1. Analyzed Models
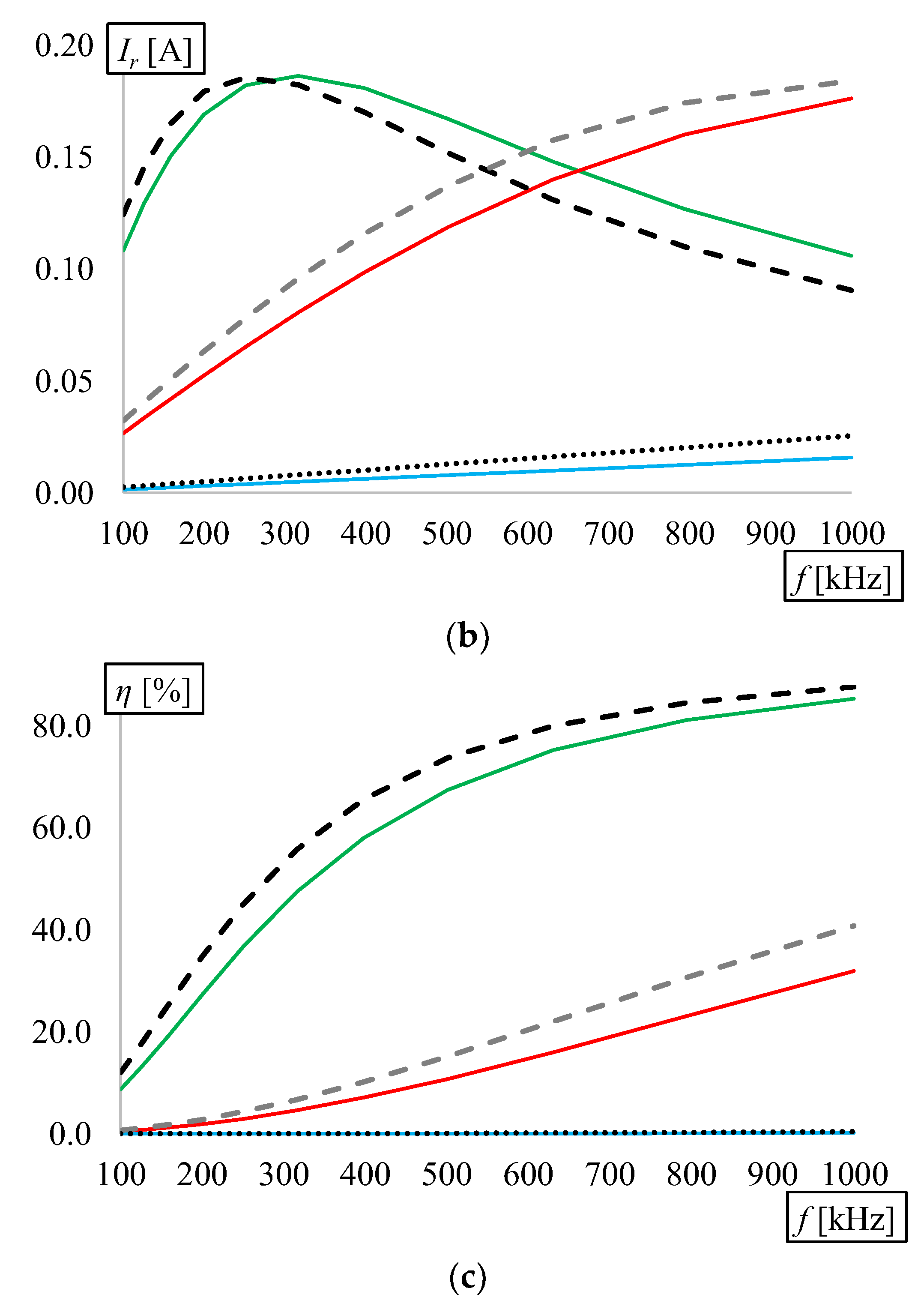
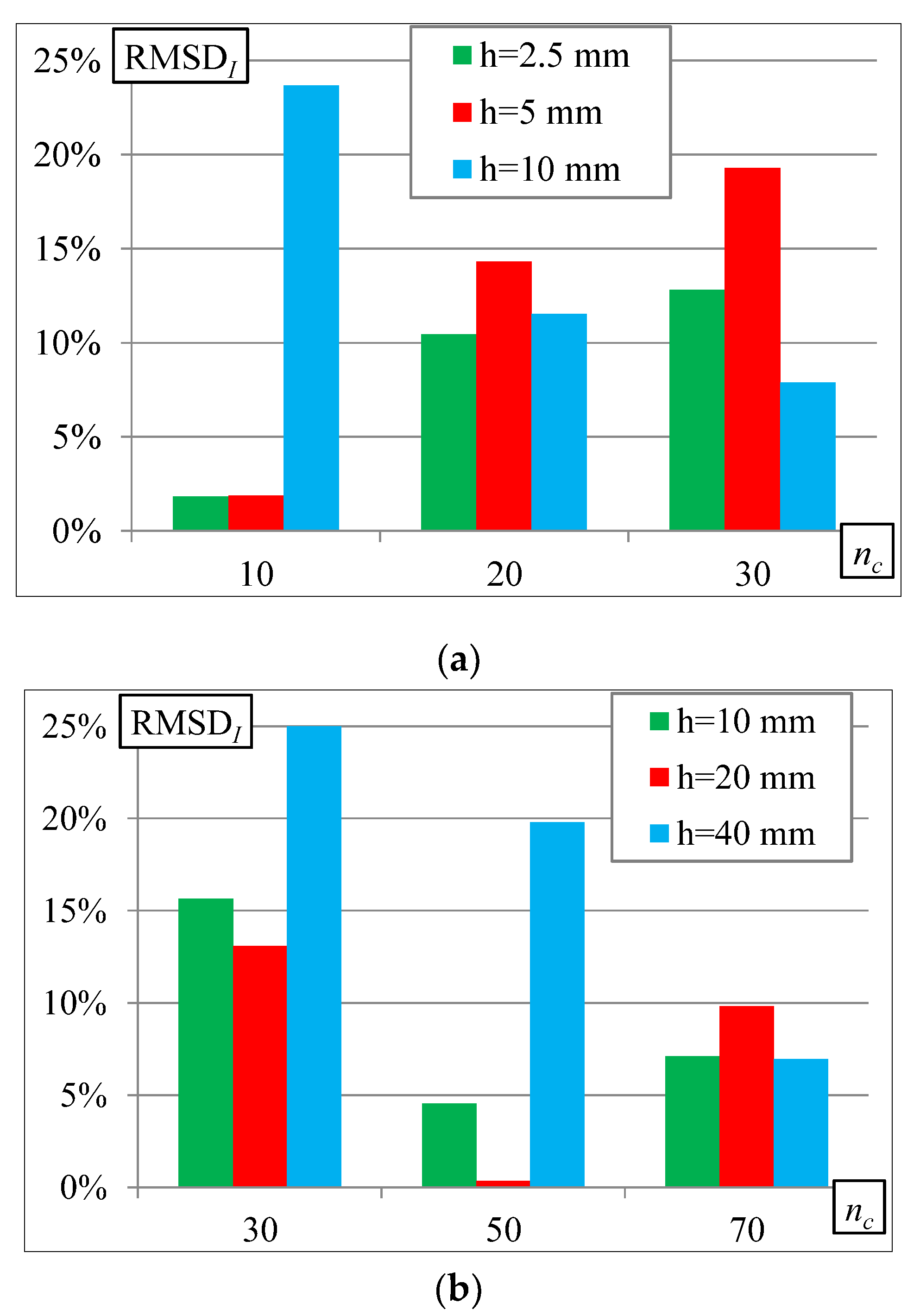
3.2. Model Comparison and Electrical Parameters
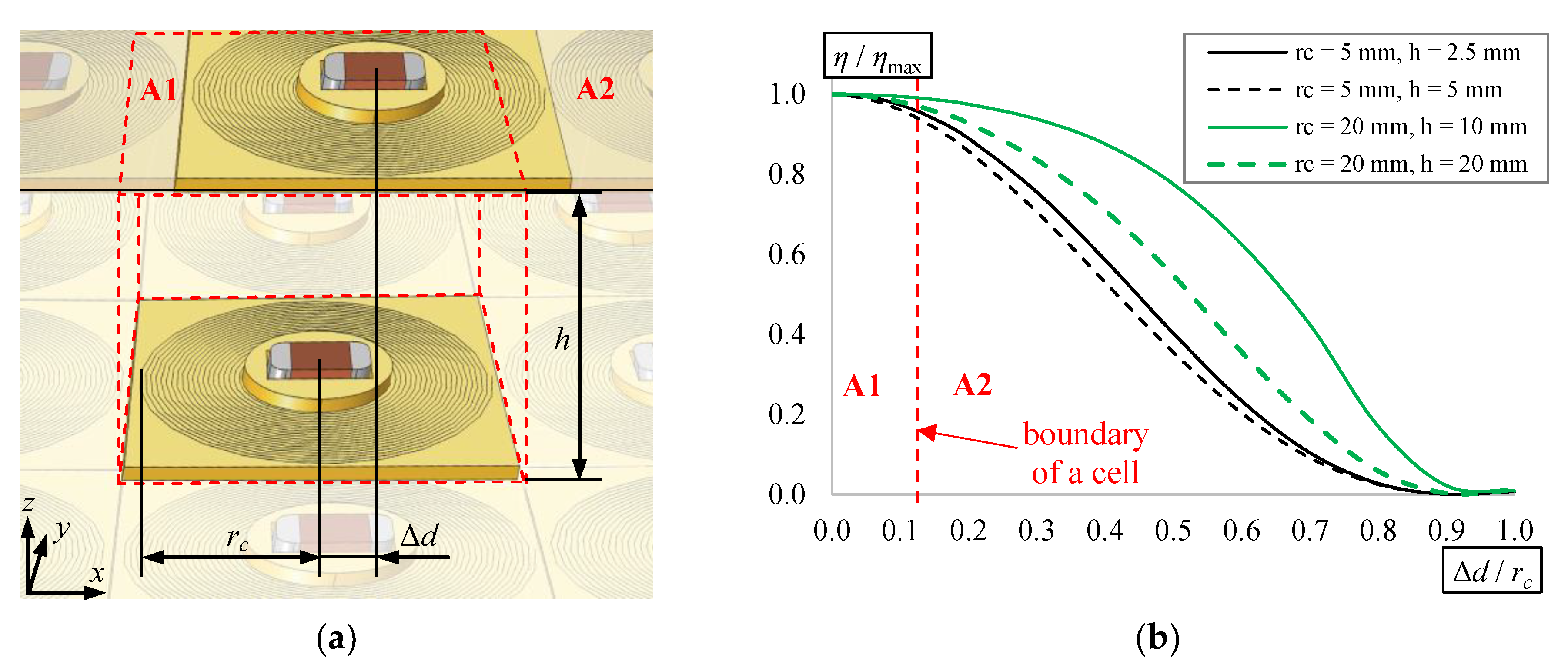
3.3. Horizontal Misalignment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barman, S.D.; Reza, A.W.; Kumar, N.; Karim, M.E.; Munir, A.B. Wireless powering by magnetic resonant coupling: Recent trends in wireless power transfer system and its applications. Renew. Sust. Energ. Rev. 2015, 51, 1525–1552. [Google Scholar] [CrossRef]
- Osowski, S.; Siwek, K. Data mining of electricity consumption in small power region. In Proceedings of the 19th International Conference Computational Problems of Electrical Engineering (CPEE), Banska Stiavnica, Slovakia, 9–12 September 2018; pp. 1–4. [Google Scholar]
- Luo, Z.; Wei, X. Analysis of square and circular planar spiral coils in wireless power transfer system for electric vehicles. IEEE Trans. Ind. Electron. 2018, 65, 331–341. [Google Scholar] [CrossRef]
- Batra, T.; Schaltz, E.; Ahn, S. Effect of ferrite addition above the base ferrite on the coupling factor of wireless power transfer for vehicle applications. J. Appl. Phys. 2015, 117. [Google Scholar] [CrossRef]
- Eteng, A.A.; Rahim, S.K.A.; Leow, C.Y.; Chew, B.W.; Vandenbosch, G.A.E. Two-stage design method for enhanced inductive energy transmission with Q-constrained planar square loops. PLoS ONE 2016, 11, e0148808. [Google Scholar] [CrossRef][Green Version]
- Kim, T.-H.; Yun, G.-H.; Lee, W.Y. Asymmetric coil structures for highly efficient wireless power transfer systems. IEEE Trans. Microw. Theory. Tech. 2018, 66, 3443–3451. [Google Scholar] [CrossRef]
- Rim, C.T.; Mi, C. Wireless Power Transfer for Electric Vehicles and Mobile Devices; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 473–490. [Google Scholar]
- Fujimoto, K.; Itoh, K. Antennas for Small Mobile Terminals, 2nd ed.; Artech House: Norwood, MA, USA, 2018; pp. 30–70. [Google Scholar]
- Zhang, Z.; Pang, H.; Georgiadis, A.; Cecati, C. Wireless power transfer—An overview. IEEE Trans. Ind. Electron. 2019, 66, 1044–1058. [Google Scholar] [CrossRef]
- Rozman, M.; Fernando, M.; Adebisi, B.; Rabie, K.M.; Collins, T.; Kharel, R.; Ikpehai, A. A new technique for reducing size of a WPT system using two-loop strongly-resonant inductors. Energies 2017, 10, 1614. [Google Scholar] [CrossRef]
- Liu, X.; Wang, G. A novel wireless power transfer system with double intermediate resonant coils. IEEE Trans. Ind. Electron. 2016, 63, 2174–2180. [Google Scholar] [CrossRef]
- El Rayes, M.M.; Nagib, G.; Abdelaal, W.G.A. A review on wireless power transfer. IJETT 2016, 40, 272–280. [Google Scholar] [CrossRef]
- Re, P.D.H.; Podilchak, S.K.; Rotenberg, S.; Goussetis, G.; Lee, J. Circularly polarized retrodirective antenna array for wireless power transmission. In Proceedings of the 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 891–895. [Google Scholar]
- Nikoletseas, S.; Yang, Y.; Georgiadis, A. Wireless Power Transfer Algorithms, Technologies and Applications in Ad Hoc Communication Networks; Springer: Cham, Switzerland, 2016; pp. 31–51. [Google Scholar]
- Stevens, C.J. Magnetoinductive waves and wireless power transfer. IEEE Trans. Power Electron. 2015, 30, 6182–6190. [Google Scholar] [CrossRef]
- Zhong, W.; Lee, C.K.; Hui, S.Y.R. General analysis on the use of Tesla’s resonators in domino forms for wireless power transfer. IEEE Trans. Ind. Electron. 2013, 60, 261–270. [Google Scholar] [CrossRef]
- Alberto, J.; Reggiani, U.; Sandrolini, L.; Albuquerque, H. Accurate calculation of the power transfer and efficiency in resonator arrays for inductive power transfer. PIER 2019, 83, 61–76. [Google Scholar] [CrossRef]
- Alberto, J.; Reggiani, U.; Sandrolini, L.; Albuquerque, H. Fast calculation and analysis of the equivalent impedance of a wireless power transfer system using an array of magnetically coupled resonators. PIER B 2018, 80, 101–112. [Google Scholar] [CrossRef][Green Version]
- Martin, P.; Ho, B.J.; Grupen, N.; Muñoz, S.; Srivastasa, M. An iBeacon primer for indoor localization. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings (BuildSys’14), Memphis, TN, USA, 3–6 November 2014; pp. 190–191. [Google Scholar]
- Li, X.; Zhang, H.; Peng, F.; Li, Y.; Yang, T.; Wang, B.; Fang, D. A wireless magnetic resonance energy transfer system for micro implantable medical sensors. Sensors 2012, 12, 10292–10308. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Abu-Siada, A.; Sutinjo, A. State-of-the-art literature review of WPT: Current limitations and solutions on IPT. Electr. Power Syst. Res. 2018, 154, 493–502. [Google Scholar] [CrossRef]
- Fitzpatrick, D.C. Implantable Electronic Medical Devices; Academic Press: San Diego, CA, USA, 2014; pp. 7–35. [Google Scholar]
- Wang, B.; Yerazunis, W.; Teo, K.H. Wireless power transfer: Metamaterials and array of coupled resonators. Proc. IEEE 2013, 101, 1359–1368. [Google Scholar] [CrossRef]
- Kanoun, O. Lecture Notes on Impedance Spectroscopy; CRC Press: Boca Raton, FL, USA, 2015; Volume 5, pp. 63–71. [Google Scholar]
- Meeker, D.C. Continuum Representation of Wound Coils Via an Equivalent Foil Approach. Available online: http://www.femm.info/examples/prox/notes.pdf (accessed on 3 April 2020).
- Meeker, D.C. An improved continuum skin and proximity effect model for hexagonally packed wires. J. Comput. Appl. Math. 2012, 236, 4635–4644. [Google Scholar] [CrossRef]
- Mohan, S.S.; del Mar Hershenson, M.; Boyd, S.P.; Lee, T.H. Simple Accurate expressions for planar spiral inductances. IEEE J. Solid-State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
- Raju, S.; Wu, R.; Chan, M.; Yue, C.P. Modeling of mutual coupling between planar inductors in wireless power applications. IEEE Trans. Power Electron. 2014, 29, 481–490. [Google Scholar] [CrossRef]
- Tal, N.; Morag, Y.; Levron, Y. Magnetic induction antenna arrays for MIMO and multiple-frequency communication systems. PIER C 2017, 75, 155–167. [Google Scholar] [CrossRef][Green Version]
- Liu, S.; Su, J.; Lai, J. Accurate expressions of mutual inductance and their calculation of archimedean spiral coils. Energies 2019, 12, 2017. [Google Scholar] [CrossRef]





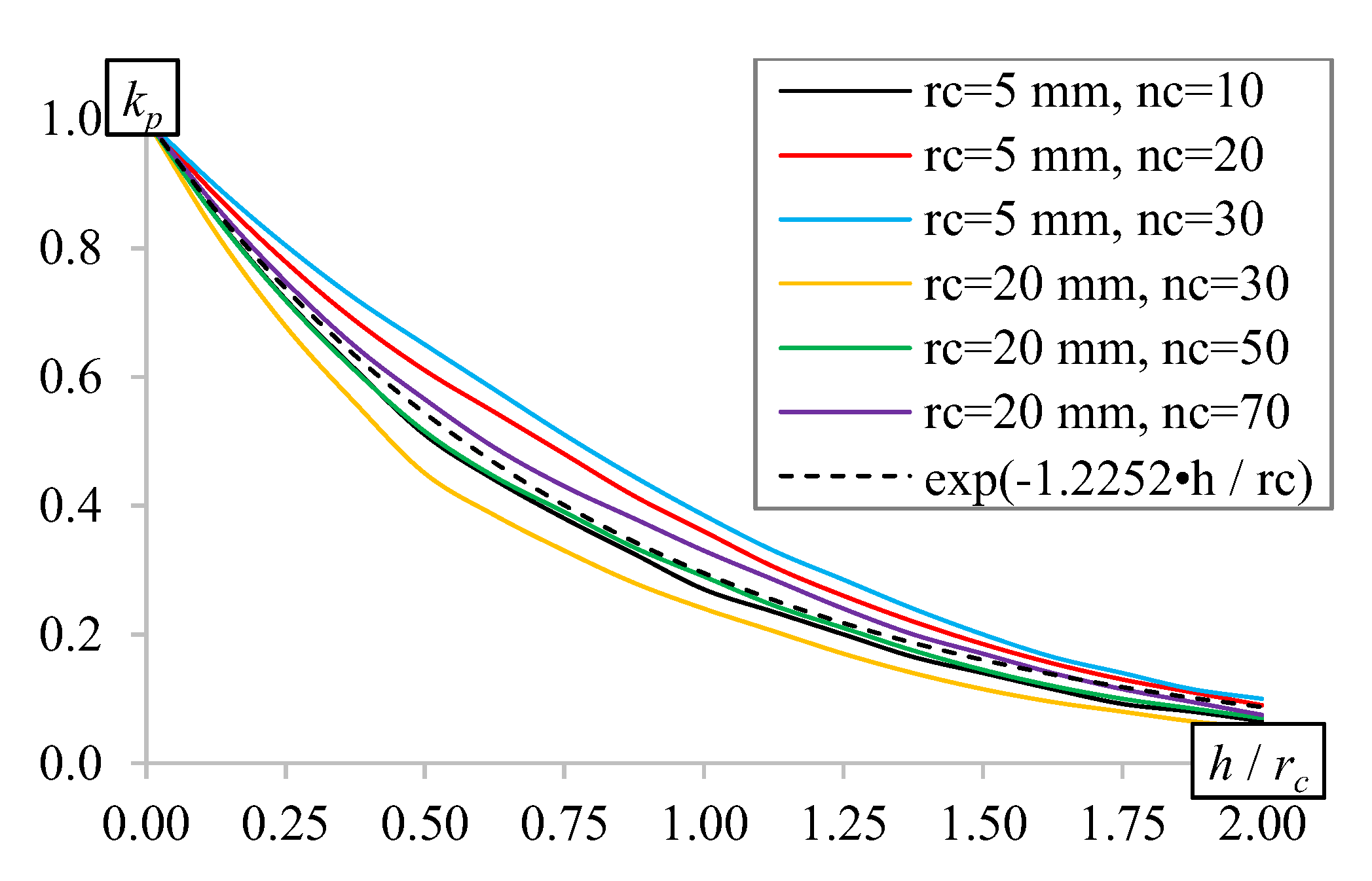







| rc (mm) | nc | h (mm) | ||
|---|---|---|---|---|
| 0.5rc | rc | 2rc | ||
| 5 | 10 | 2.5 | 5.0 | 10.0 |
| 20 | 2.5 | 5.0 | 10.0 | |
| 30 | 2.5 | 5.0 | 10.0 | |
| 20 | 30 | 10.0 | 20.0 | 40.0 |
| 50 | 10.0 | 20.0 | 40.0 | |
| 70 | 10.0 | 20.0 | 40.0 | |
| rc (mm) | nc | Rc (Ω) | Lself (H) | Mperiod (H) | Cc (F) | h = 0.5rc | h = rc | h = 2rc | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mz (H) | kp | Mz (H) | kp | Mz (H) | kp | ||||||
| 5 | 10 | 0.274 | 1.41 × 10−6 | 3.78 × 10−8 | 2.28 × 10−8 | 3.68 × 10−7 | 0.542 | 1.54 × 10−7 | 0.293 | 4.06 × 10−8 | 0.086 |
| 20 | 0.453 | 3.14 × 10−6 | 6.97 × 10−8 | 9.80 × 10−9 | 8.96 × 10−7 | 0.542 | 3.56 × 10−7 | 0.293 | 8.74 × 10−8 | 0.086 | |
| 30 | 0.535 | 3.84 × 10−6 | 7.74 × 10−8 | 7.86 × 10−9 | 1.08 × 10−6 | 0.542 | 4.21 × 10−7 | 0.293 | 1.01 × 10−7 | 0.086 | |
| 20 | 30 | 3.393 | 5.97 × 10−5 | 1.62 × 10−6 | 5.41 × 10−10 | 1.53 × 10−5 | 0.542 | 6.47 × 10−6 | 0.293 | 1.73 × 10−6 | 0.086 |
| 50 | 5.175 | 1.22 × 10−4 | 3.00 × 10−6 | 2.60 × 10−10 | 3.45 × 10−5 | 0.542 | 1.41 × 10−5 | 0.293 | 3.60 × 10−6 | 0.086 | |
| 70 | 6.574 | 1.78 × 10−4 | 3.99 × 10−6 | 1.73 × 10−10 | 5.27 × 10−5 | 0.542 | 2.10 × 10−5 | 0.293 | 5.17 × 10−6 | 0.086 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steckiewicz, A.; Stankiewicz, J.M.; Choroszucho, A. Numerical and Circuit Modeling of the Low-Power Periodic WPT Systems. Energies 2020, 13, 2651. https://doi.org/10.3390/en13102651
Steckiewicz A, Stankiewicz JM, Choroszucho A. Numerical and Circuit Modeling of the Low-Power Periodic WPT Systems. Energies. 2020; 13(10):2651. https://doi.org/10.3390/en13102651
Chicago/Turabian StyleSteckiewicz, Adam, Jacek Maciej Stankiewicz, and Agnieszka Choroszucho. 2020. "Numerical and Circuit Modeling of the Low-Power Periodic WPT Systems" Energies 13, no. 10: 2651. https://doi.org/10.3390/en13102651
APA StyleSteckiewicz, A., Stankiewicz, J. M., & Choroszucho, A. (2020). Numerical and Circuit Modeling of the Low-Power Periodic WPT Systems. Energies, 13(10), 2651. https://doi.org/10.3390/en13102651