A Novel Approach for the Determination of Sorption Equilibria and Sorption Enthalpy Used for MOF Aluminium Fumarate with Water
Abstract
:1. Introduction
- Volumetric uptake measurement;
- Stepwise volume and temperature perturbation;
- Frequency response analysis.
2. Materials and Methods
2.1. Material
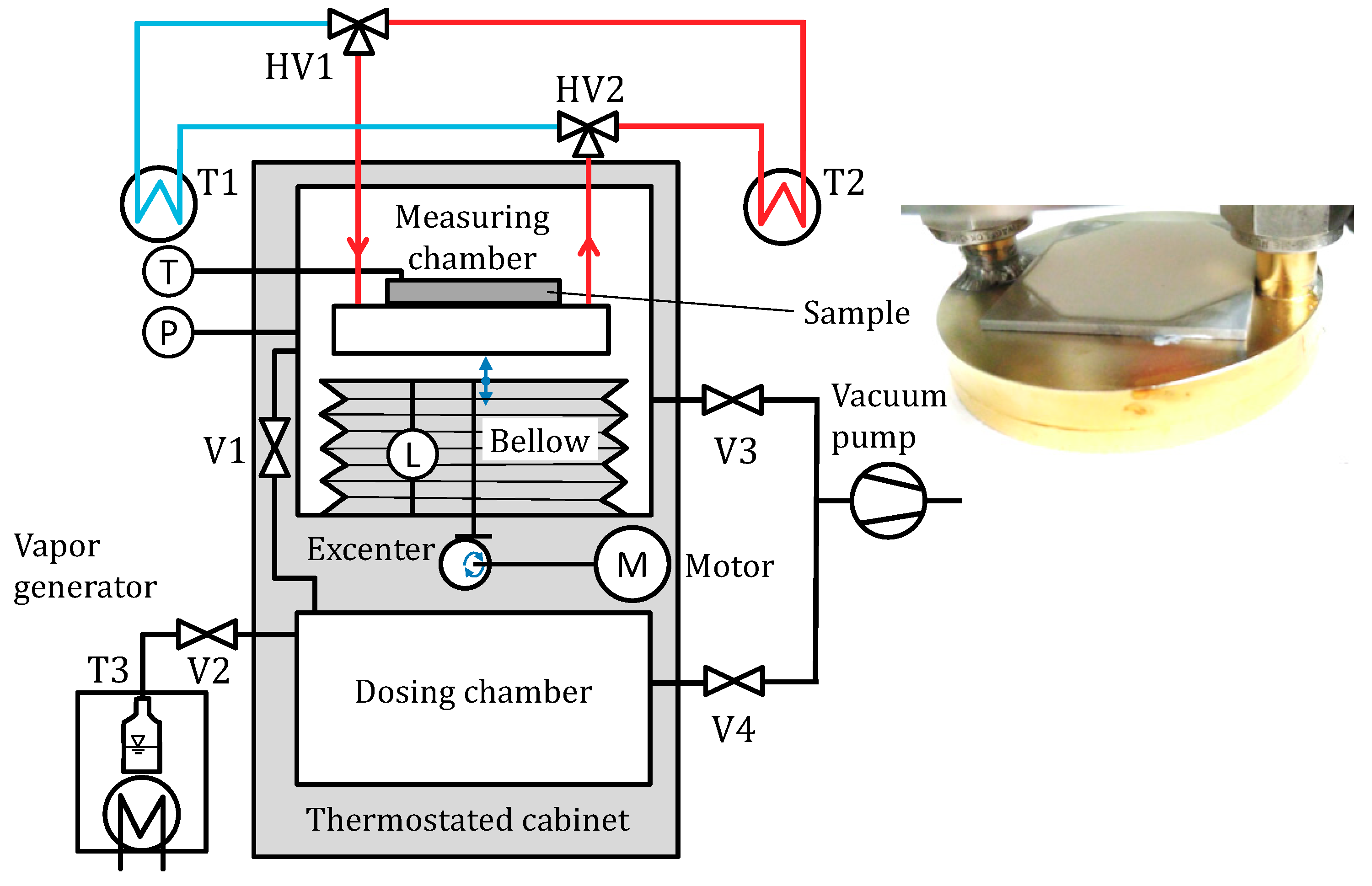
2.2. Apparatus
2.3. Procedure
2.4. Uncertainty Evaluation
3. Results and Discussion
3.1. Adsorption Equilibrium
3.2. Adsorption Enthalpy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| Ad-HX | Adsorber heat exchanger |
| Variables | |
| Temperature (K) | |
| Pressure (Pa) | |
| Loading (kgadsorbed/kgsorbent,dry) | |
| Effective loading (kgadsorbed/kgcomposite,dry) | |
| Volume (m3) | |
| Surface area (m2), adsorption potential (J/kg), Amplitude (any unit) | |
| Universal gas constant (J/(mol K)) | |
| Specific gas constant of water (J/(kg K)) | |
| Mass (kg) | |
| Time (s) | |
| Molar mass (kg/mol) | |
| Differential adsorption enthalpy (J/kgadsorbed) | |
| Indices | |
| w | Water |
| s | (Ad)sorbent, (ad)sorption |
| 0 | Temporal mean value |
| D | Dosing chamber |
| M | Measurement chamber |
| At constant volume | |
| At constant temperature | |
| ch | (Measurement) chamber |
| cmp | Composite |
| ct | Coating |
| rel | Relative |
References
- Meunier, F. Adsorption heat powered heat pumps. Appl. Therm. Eng. 2013, 61, 830–836. [Google Scholar] [CrossRef]
- Metcalf, S.J.; Critoph, R.E.; Tamainot-Telto, Z. Optimal cycle selection in carbon-ammonia adsorption cycles. Int. J. Refrig. 2012, 35, 571–580. [Google Scholar] [CrossRef]
- Wittstadt, U.; Füldner, G.; Laurenz, E.; Warlo, A.; Große, A.; Herrmann, R.; Schnabel, L.; Mittelbach, W. A novel adsorption module with fiber heat exchangers: Performance analysis based on driving temperature differences. Renew. Energy 2017, 110, 154–161. [Google Scholar] [CrossRef]
- Wang, D.C.; Li, Y.H.; Li, D.; Xia, Y.Z.; Zhang, J.P. A review on adsorption refrigeration technology and adsorption deterioration in physical adsorption systems. Renew. Sustain. Energy Rev. 2010, 14, 344–353. [Google Scholar] [CrossRef]
- Pang, S.C.; Masjuki, H.H.; Kalam, M.A.; Hazrat, M.A. Liquid absorption and solid adsorption system for household, industrial and automobile applications: A review. Renew. Sustain. Energy Rev. 2013, 28, 836–847. [Google Scholar] [CrossRef]
- Wilde, T.; Ott, M.; Auweter, A.; Meijer, I.; Ruch, P.; Hilger, M.; Kuhnert, S.; Huber, H. CooLMUC-2: A supercomputing cluster with heat recovery for adsorption cooling. In Thirty-third Annual Semiconductor Thermal Measurement and Management Symposium, Proceedings of 2017 33rd Thermal Measurement, Modeling & Management Symposium (SEMI-THERM), San Jose, CA, USA, 13–17 March 2017; Wesling, P., Ed.; IEEE: Piscataway, NJ, USA, 2017; pp. 115–121. ISBN 978-1-5386-1531-7. [Google Scholar]
- Zimmermann, S.; Meijer, I.; Tiwari, M.K.; Paredes, S.; Michel, B.; Poulikakos, D. Aquasar: A hot water cooled data center with direct energy reuse. Energy 2012, 43, 237–245. [Google Scholar] [CrossRef]
- Aristov, Y.I. Challenging offers of material science for adsorption heat transformation: A review. Appl. Therm. Eng. 2013, 50, 1610–1618. [Google Scholar] [CrossRef]
- Lenzen, D.; Zhao, J.; Ernst, S.-J.; Wahiduzzaman, M.; Ken Inge, A.; Fröhlich, D.; Xu, H.; Bart, H.-J.; Janiak, C.; Henninger, S.; et al. A metal-organic framework for efficient water-based ultra-low-temperature-driven cooling. Nat. Commun. 2019, 10, 3025. [Google Scholar] [CrossRef] [PubMed]
- Jeremias, F.; Fröhlich, D.; Janiak, C.; Henninger, S.K. Advancement of sorption-based heat transformation by a metal coating of highly-stable, hydrophilic aluminium fumarate MOF. RSC Adv. 2014, 4, 24073–24082. [Google Scholar] [CrossRef] [Green Version]
- Kummer, H.; Jeremias, F.; Warlo, A.; Füldner, G.; Fröhlich, D.; Janiak, C.; Gläser, R.; Henninger, S.K. A Functional Full-Scale Heat Exchanger Coated with Aluminum Fumarate Metal–Organic Framework for Adsorption Heat Transformation. Ind. Eng. Chem. Res. 2017, 56, 8393–8398. [Google Scholar] [CrossRef]
- Schnabel, L.; Füldner, G.; Velte, A.; Laurenz, E.; Bendix, P.; Kummer, H.; Wittstadt, U. Innovative Adsorbent Heat Exchangers: Design and Evaluation. In Innovative Heat Exchangers; Bart, H.J., Scholl, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 363–394. ISBN 978-3-319-71641-1. [Google Scholar]
- Kiener, C.; Müller, U.; Schubert, M. Organometallic Aluminum Fumerate Backbone Material. PCT/EP2007/053567, 9 April 2009. [Google Scholar]
- ASUE. Marktübersicht Gaswärmepumpen 2017/18. Available online: https://asue.de/sites/default/files/asue/themen/gaswaermepumpe_kaelte/2017/broschueren/ASUE_Marktuebersicht-Gaswaermepumpen_2017.pdf (accessed on 6 February 2019).
- Freni, A.; Dawoud, B.; Bonaccorsi, L.; Chmielewski, S.; Frazzica, A.; Calabrese, L.; Restuccia, G. Adsorption Heat Exchangers. In Characterization of zeolite-based coatings for adsorption heat pumps; Freni, A., Ed.; Springer: Cham, Switzerland, 2015; pp. 35–53. ISBN 978-3-319-09326-0. [Google Scholar]
- Graf, S.; Eibel, S.; Lanzerath, F.; Bardow, A. Validated Performance Prediction of Adsorption Chillers: Bridging the Gap from Gram-Scale Experiments to Full-Scale Chillers. Energy Technol. 2020, 1901130. [Google Scholar] [CrossRef]
- Bourdin, V.; Gray, P.G.; Grenier, P.; Terrier, M.F. An apparatus for adsorption dynamics studies using infrared measurement of the adsorbent temperature. Rev. Sci. Instrum. 1998, 69, 2130–2136. [Google Scholar] [CrossRef]
- Schnabel, L.; Tatlier, M.; Schmidt, F.; Erdem-Şenatalar, A. Adsorption kinetics of zeolite coatings directly crystallized on metal supports for heat pump applications (adsorption kinetics of zeolite coatings). Appl. Therm. Eng. 2010, 30, 1409–1416. [Google Scholar] [CrossRef]
- Frazzica, A.; Füldner, G.; Sapienza, A.; Freni, A.; Schnabel, L. Experimental and theoretical analysis of the kinetic performance of an adsorbent coating composition for use in adsorption chillers and heat pumps. Appl. Therm. Eng. 2014, 73, 1022–1031. [Google Scholar] [CrossRef]
- Velte, A.; Füldner, G.; Laurenz, E.; Schnabel, L. Advanced Measurement and Simulation Procedure for the Identification of Heat and Mass Transfer Parameters in Dynamic Adsorption Experiments. Energies 2017, 10, 1130. [Google Scholar] [CrossRef] [Green Version]
- Graf, S.; Lanzerath, F.; Sapienza, A.; Frazzica, A.; Freni, A.; Bardow, A. Prediction of SCP and COP for adsorption heat pumps and chillers by combining the large-temperature-jump method and dynamic modeling. Appl. Therm. Eng. 2016, 98, 900–909. [Google Scholar] [CrossRef]
- Aristov, Y.I.; Dawoud, B.; Glaznev, I.S.; Elyas, A. A new methodology of studying the dynamics of water sorption/desorption under real operating conditions of adsorption heat pumps: Experiment. Int. J. Heat Mass Transf. 2008, 51, 4966–4972. [Google Scholar] [CrossRef]
- Kummer, H.; Füldner, G.; Henninger, S.K. Versatile siloxane based adsorbent coatings for fast water adsorption processes in thermally driven chillers and heat pumps. Appl. Therm. Eng. 2015, 85, 1–8. [Google Scholar] [CrossRef]
- Füldner, G. Stofftransport und Adsorptionskinetik in porösen Adsorbenskompositen für Wärmetransformationsanwendungen. Ph.D. Thesis, Universiät Freiburg, Freiburg, Germany, 2015. [Google Scholar]
- Schnabel, L. Experimentelle und numerische Untersuchung der Adsorptionskinetik von Wasser an Adsorbens-Metallverbundstrukturen. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2009. [Google Scholar]
- JCGM. Guide to the Expression of Uncertainty in Measurement (GUM 1995 with Minor Corrections); Joint Committee for Guides in Metrology, JCGM: Sèvres, France, 2008; Volume 100. [Google Scholar]
- Elsayed, E.; AL-Dadah, R.; Mahmoud, S.; Elsayed, A.; Anderson, P.A. Aluminium fumarate and CPO-27(Ni) MOFs: Characterization and Thermodynamic Analysis for Adsorption Heat Pump Applications. Appl. Therm. Eng. 2016. [Google Scholar] [CrossRef]
- Dubinin, M.M.; Astakhov, V.A. Description of Adsorption Equilibria of Vapors on Zeolites over Wide Ranges of Temperature and Pressure. In Molecular Sieve Zeolites. 2: International Conference on Molecular Sieves 2; Flanigen, E.M., Sand, L.B., Eds.; American Chemical Society: Washington, DC, USA, 1971; pp. 69–85. ISBN 0-8412-0115-3. [Google Scholar]




| By Suspension Composition | By Comparison to Pure Adsorbent Uptake | ||||||
|---|---|---|---|---|---|---|---|
| Sample | (g/cm3) | ||||||
| Ct_140 | 134 ± 3 | 0.14 ± 0.04 | 0.51 ± 0.15 | 0.75 | 0.25 | 0.72 | 0.28 |
| Ct_240 | 217 ± 4 | 0.24 ± 0.05 | 0.48 ± 0.10 | 0.75 | 0.25 | 0.79 | 0.21 |
| Ct_610 | 563 ± 11 | 0.61 ± 0.07 | 0.49 ± 0.06 | 0.75 | 0.25 | 0.80 | 0.20 |
| Quantity | Range | Typical Uncertainty | Device |
|---|---|---|---|
| Chamber volume | 849–922 mL | 0.4 mL (20 °C), 1.3 mL (80 °C) | Schreiber Messtechnik LVDT |
| Chamber pressure | 0–100 mbar | 0.05 mbar (5 mbar), 0.15 mbar (100 mbar) | MKS Baratron 627B |
| Cold plate temperature | 20–95 °C | 0.1 K | 4-wired Pt100 |
| Sample surface temperature | 20–80 °C | Not applicable 1 | Heitronics KT15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laurenz, E.; Füldner, G.; Schnabel, L.; Schmitz, G. A Novel Approach for the Determination of Sorption Equilibria and Sorption Enthalpy Used for MOF Aluminium Fumarate with Water. Energies 2020, 13, 3003. https://doi.org/10.3390/en13113003
Laurenz E, Füldner G, Schnabel L, Schmitz G. A Novel Approach for the Determination of Sorption Equilibria and Sorption Enthalpy Used for MOF Aluminium Fumarate with Water. Energies. 2020; 13(11):3003. https://doi.org/10.3390/en13113003
Chicago/Turabian StyleLaurenz, Eric, Gerrit Füldner, Lena Schnabel, and Gerhard Schmitz. 2020. "A Novel Approach for the Determination of Sorption Equilibria and Sorption Enthalpy Used for MOF Aluminium Fumarate with Water" Energies 13, no. 11: 3003. https://doi.org/10.3390/en13113003
APA StyleLaurenz, E., Füldner, G., Schnabel, L., & Schmitz, G. (2020). A Novel Approach for the Determination of Sorption Equilibria and Sorption Enthalpy Used for MOF Aluminium Fumarate with Water. Energies, 13(11), 3003. https://doi.org/10.3390/en13113003






