A Sparse Spike Deconvolution Algorithm Based on a Recurrent Neural Network and the Iterative Shrinkage-Thresholding Algorithm
Abstract
:1. Introduction
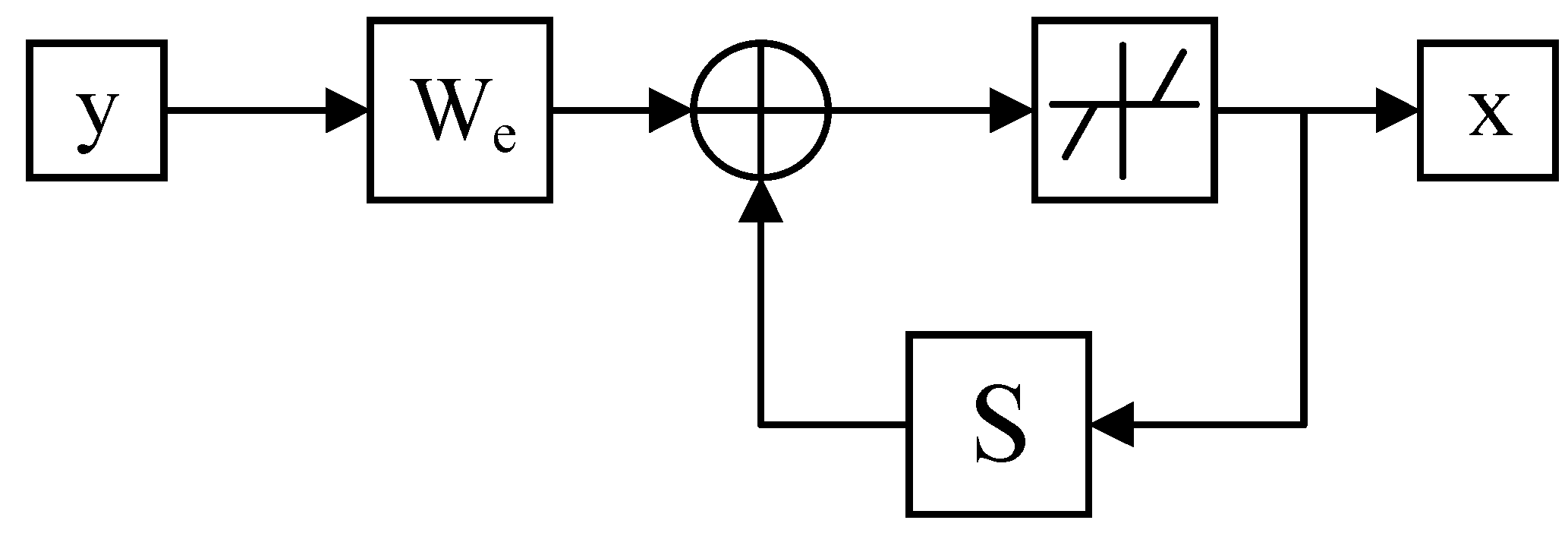
2. ISTA Algorithm
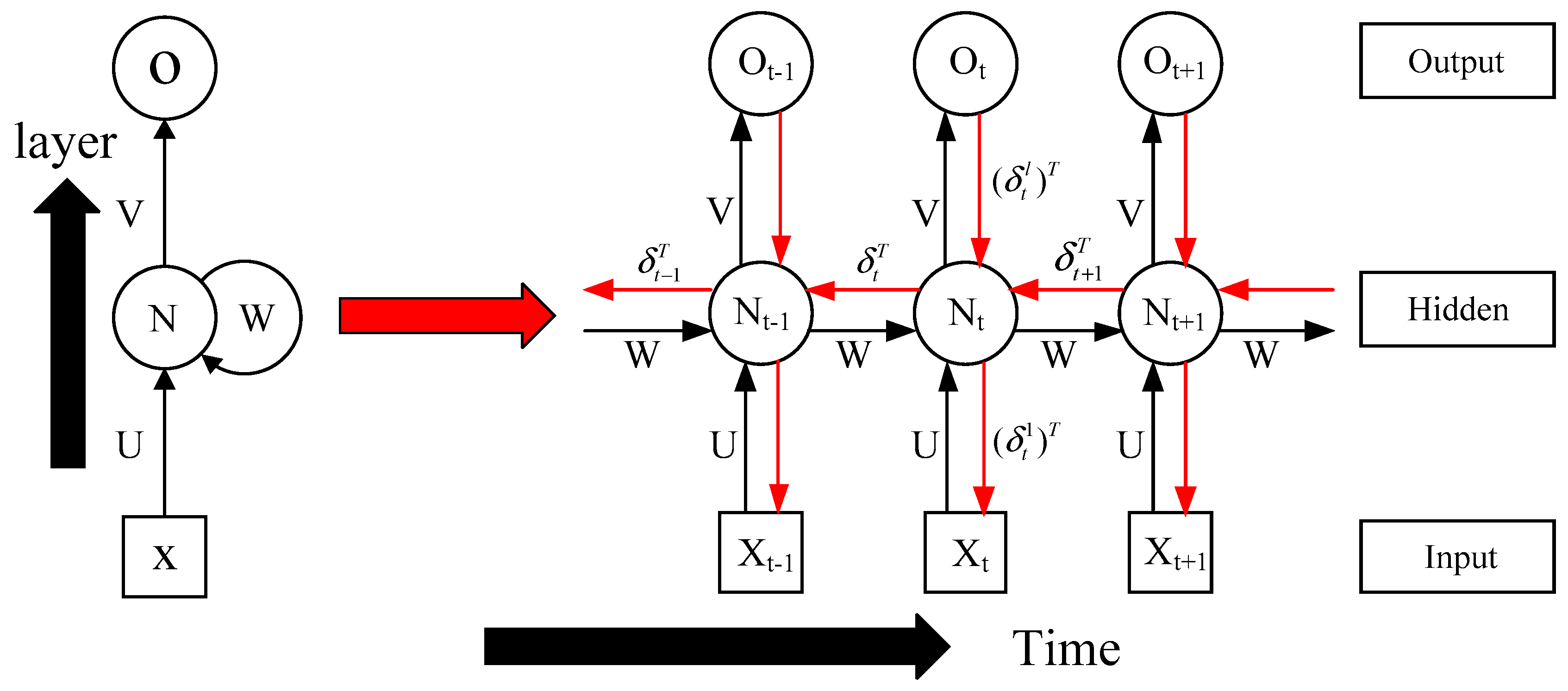
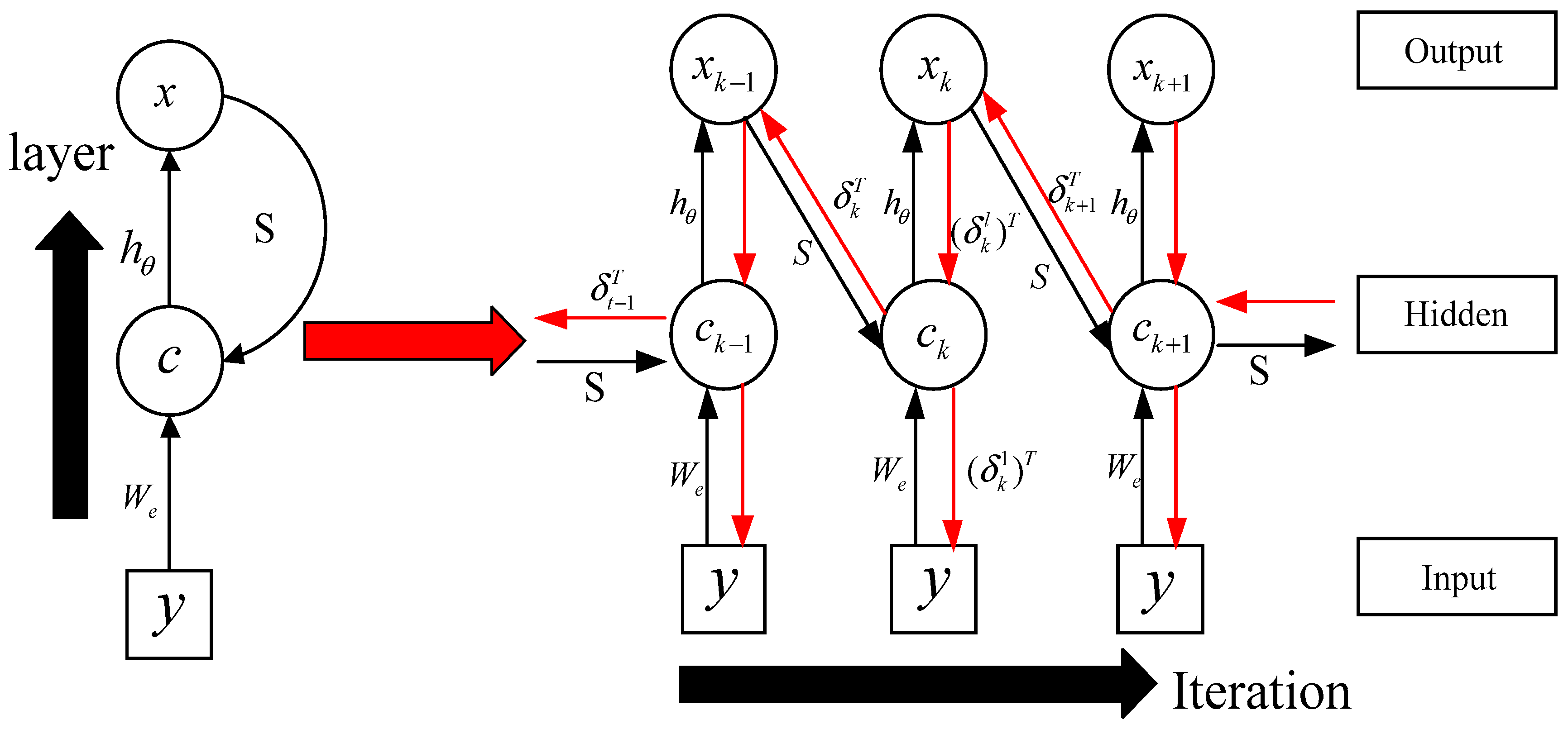
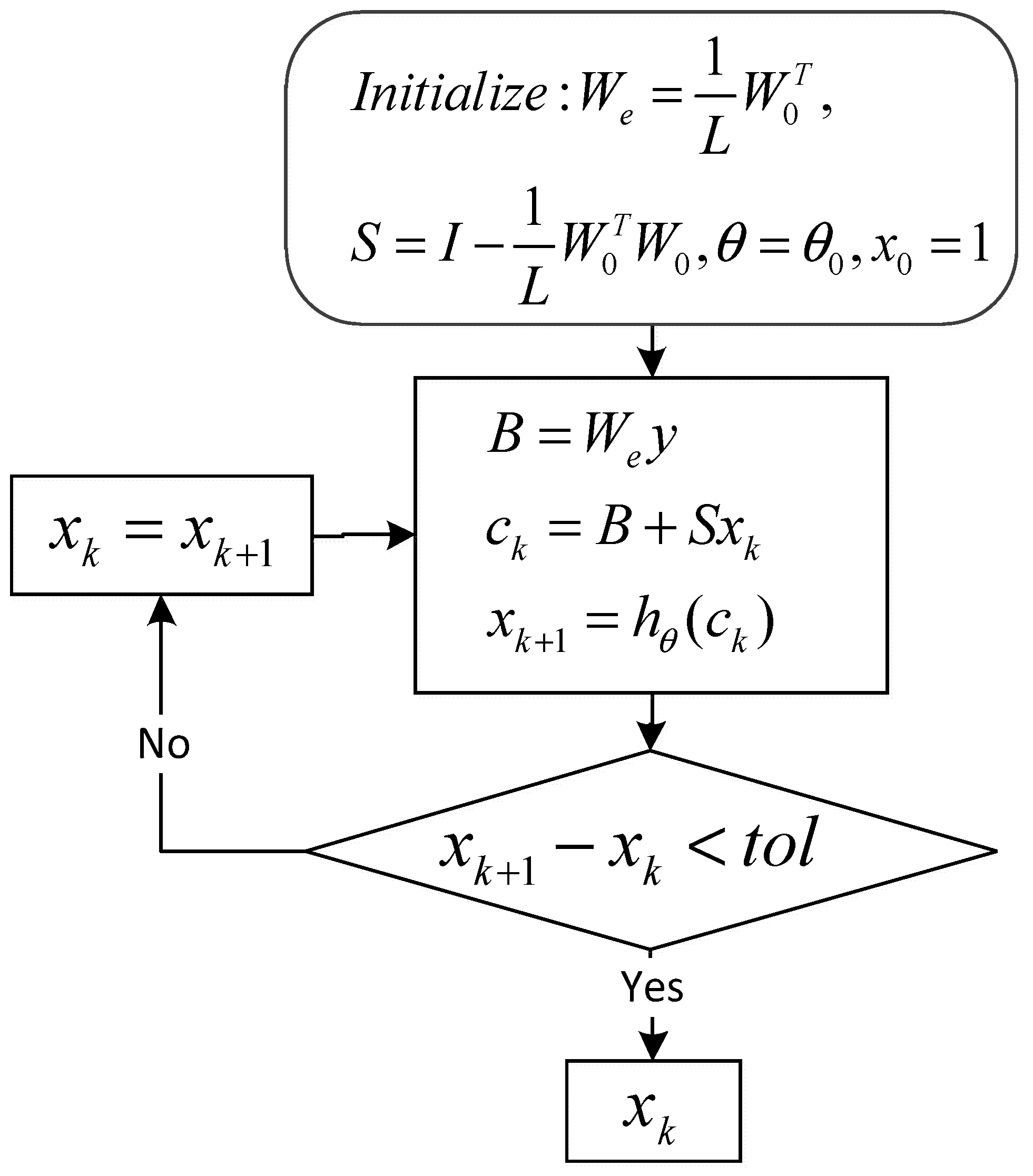
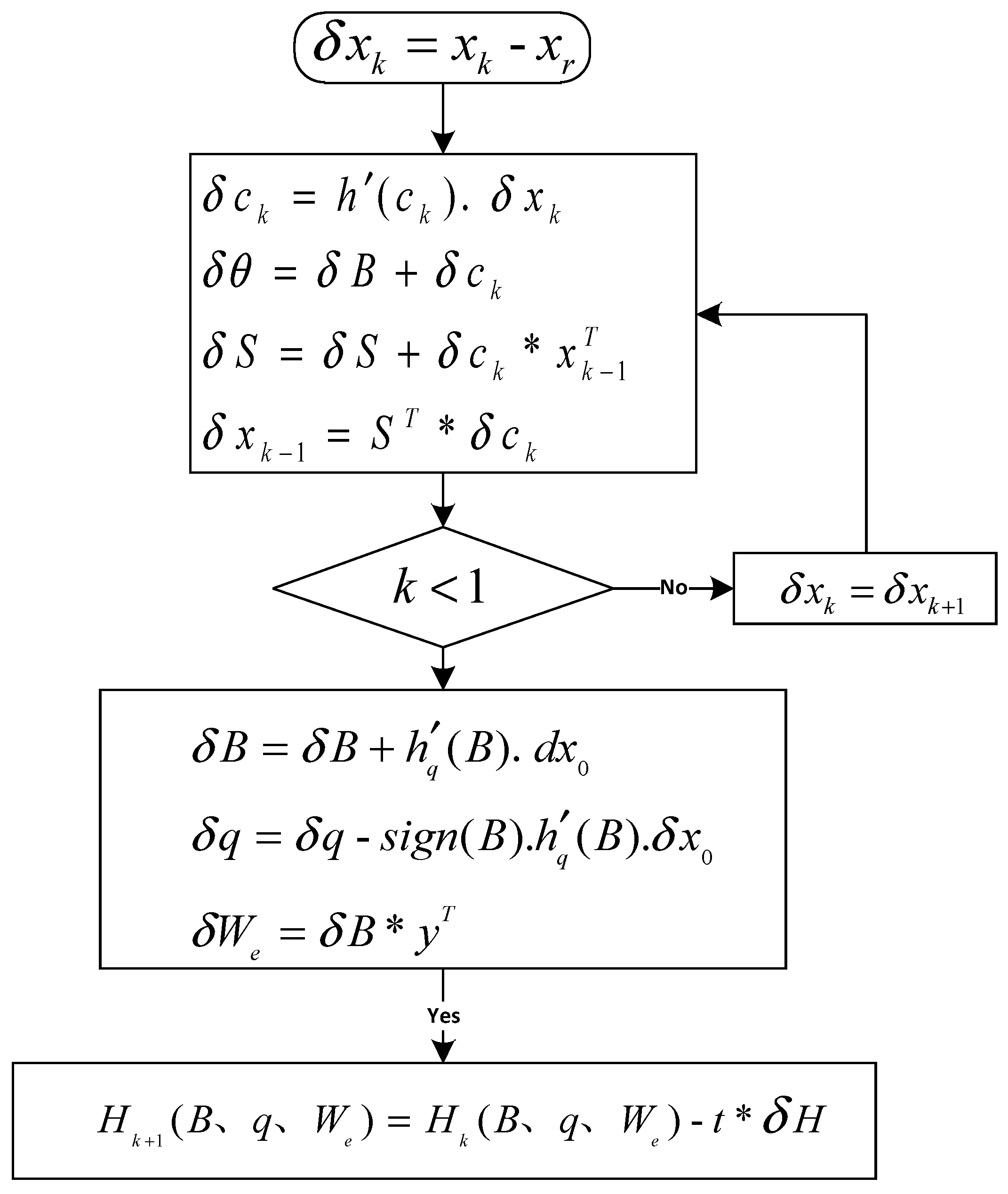
3. RNN-Like ISTA Algorithm
3.1. Forward Calculation
3.2. Error Backpropagation
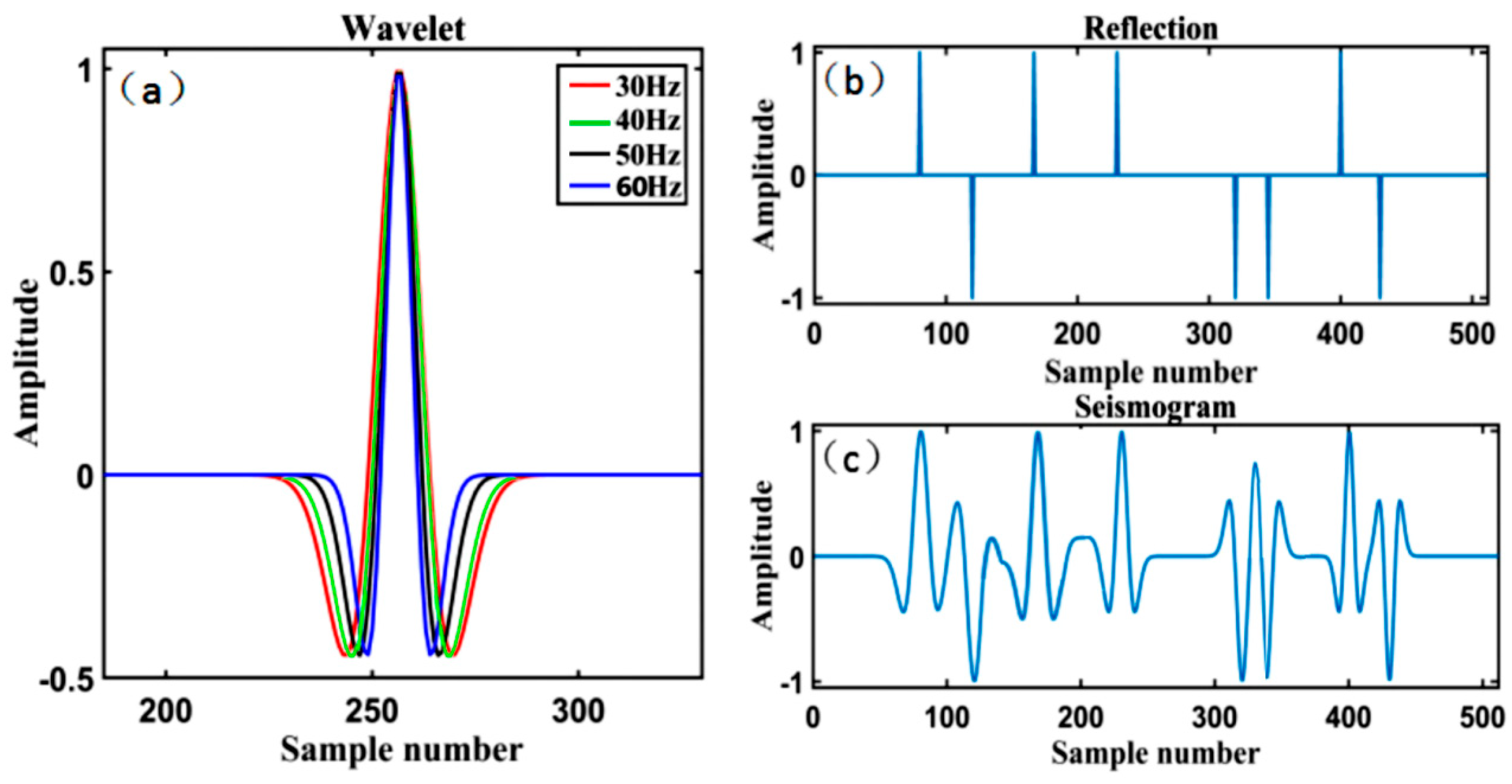
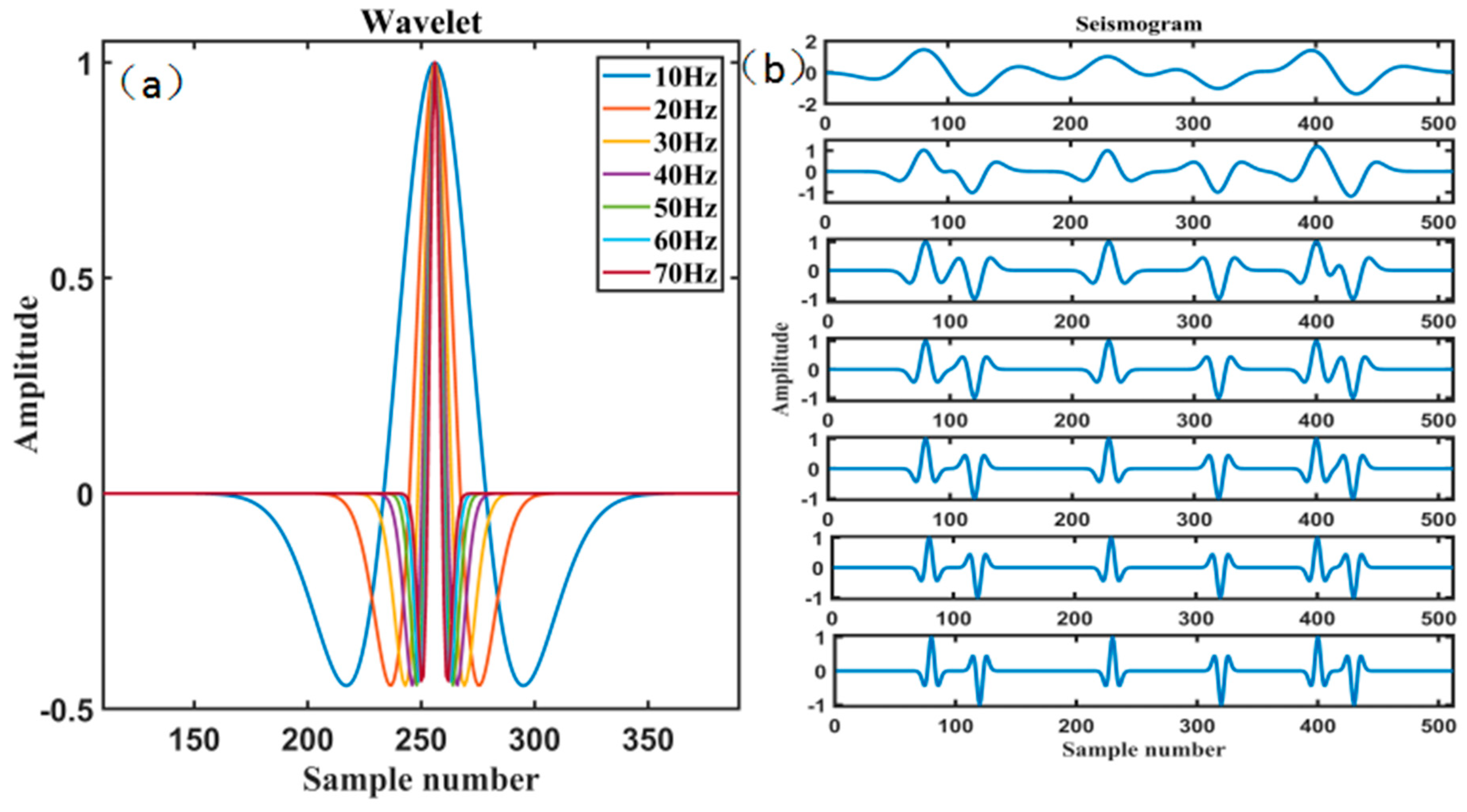
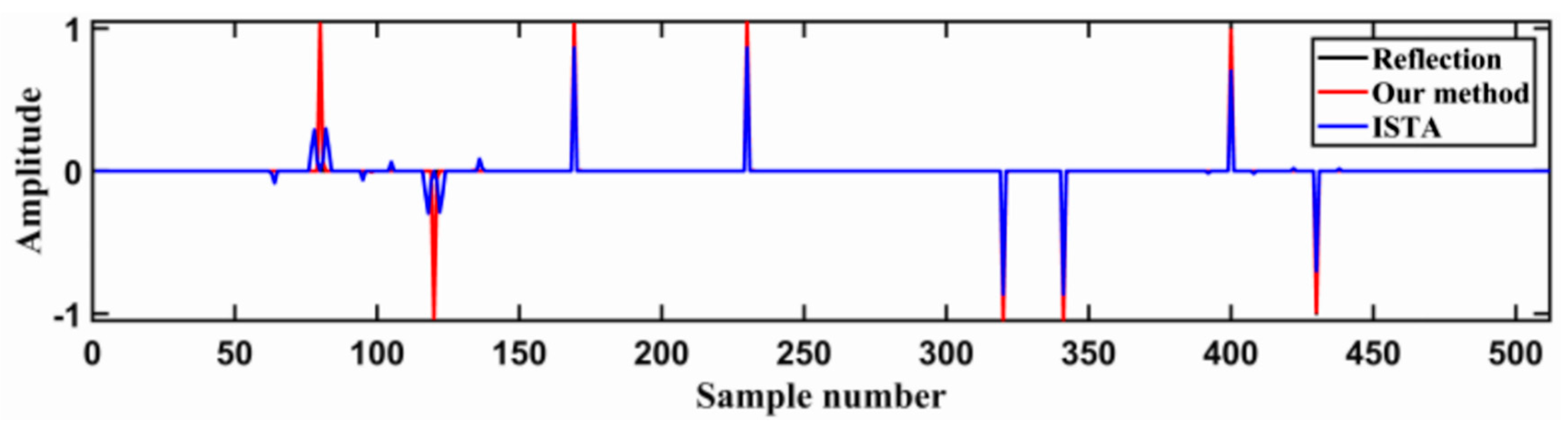
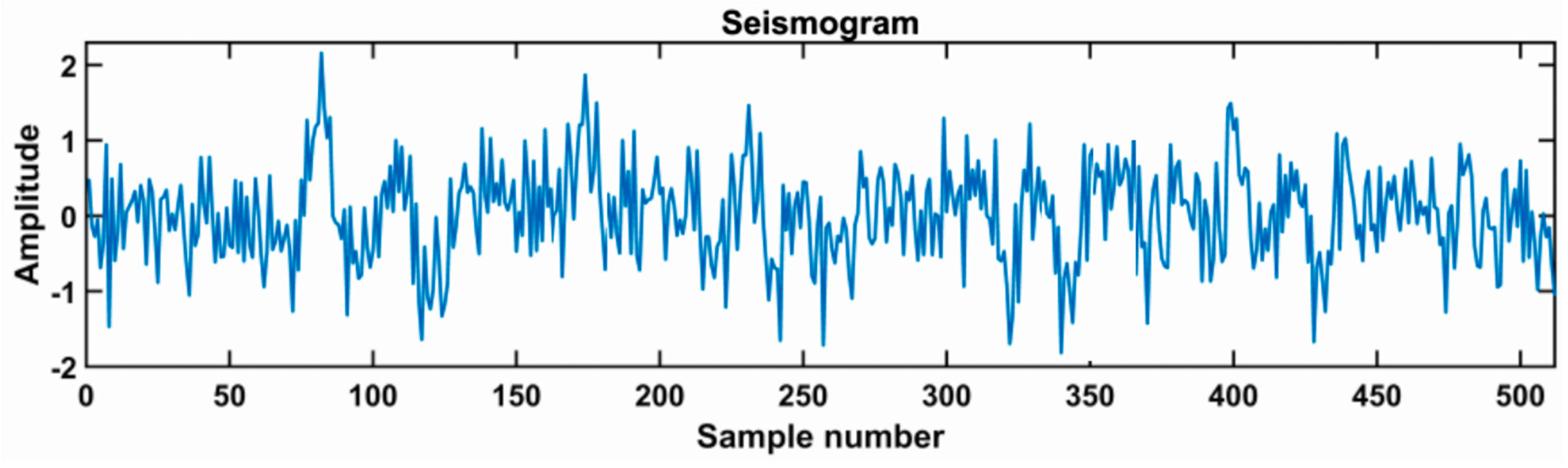
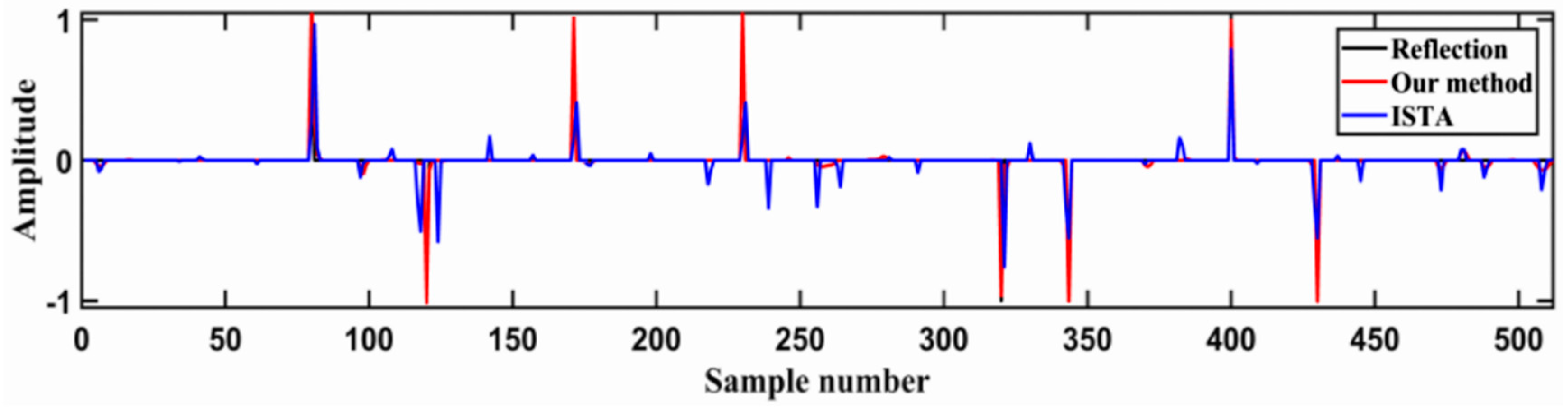
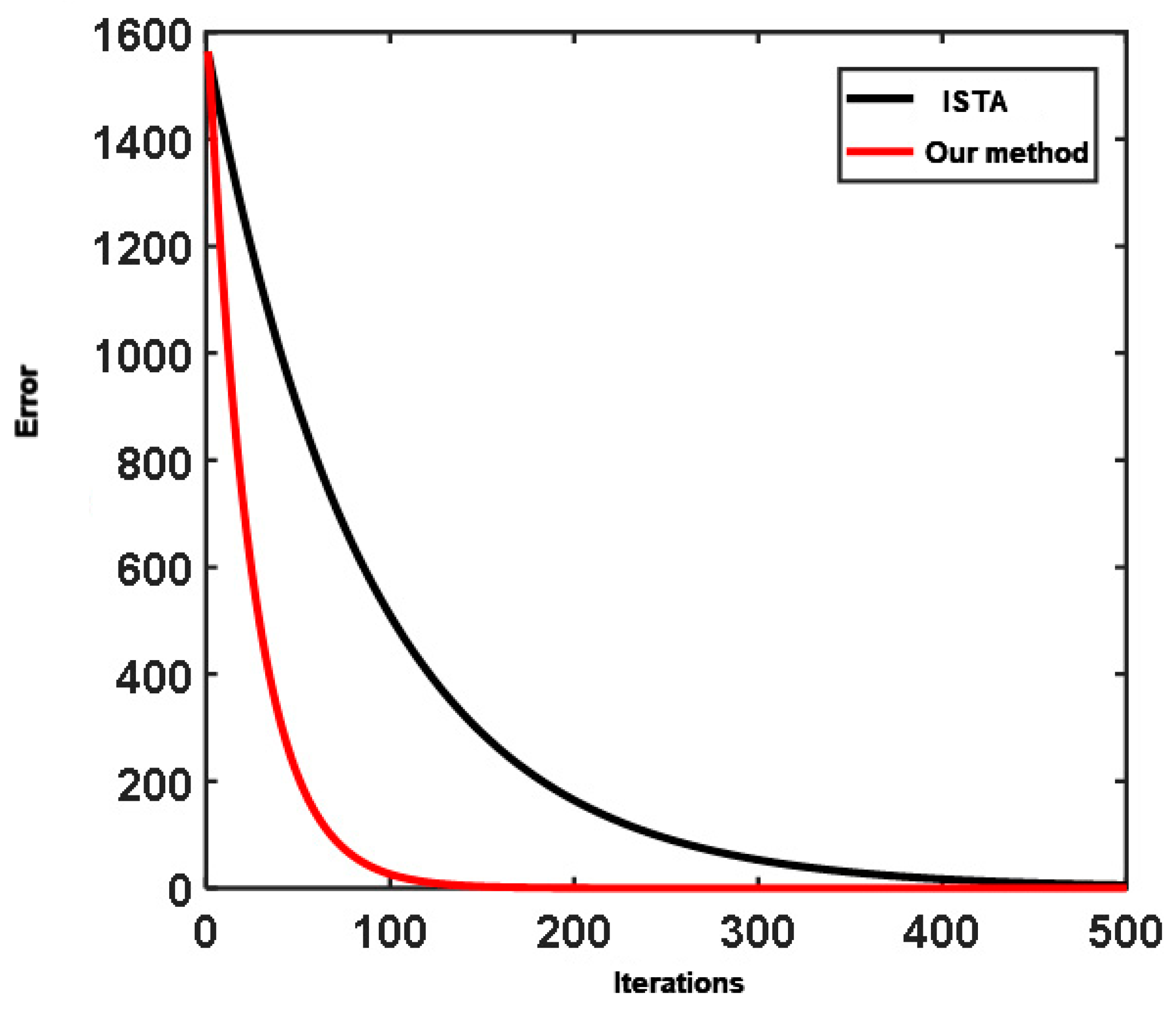
4. Theoretical Model Experiment
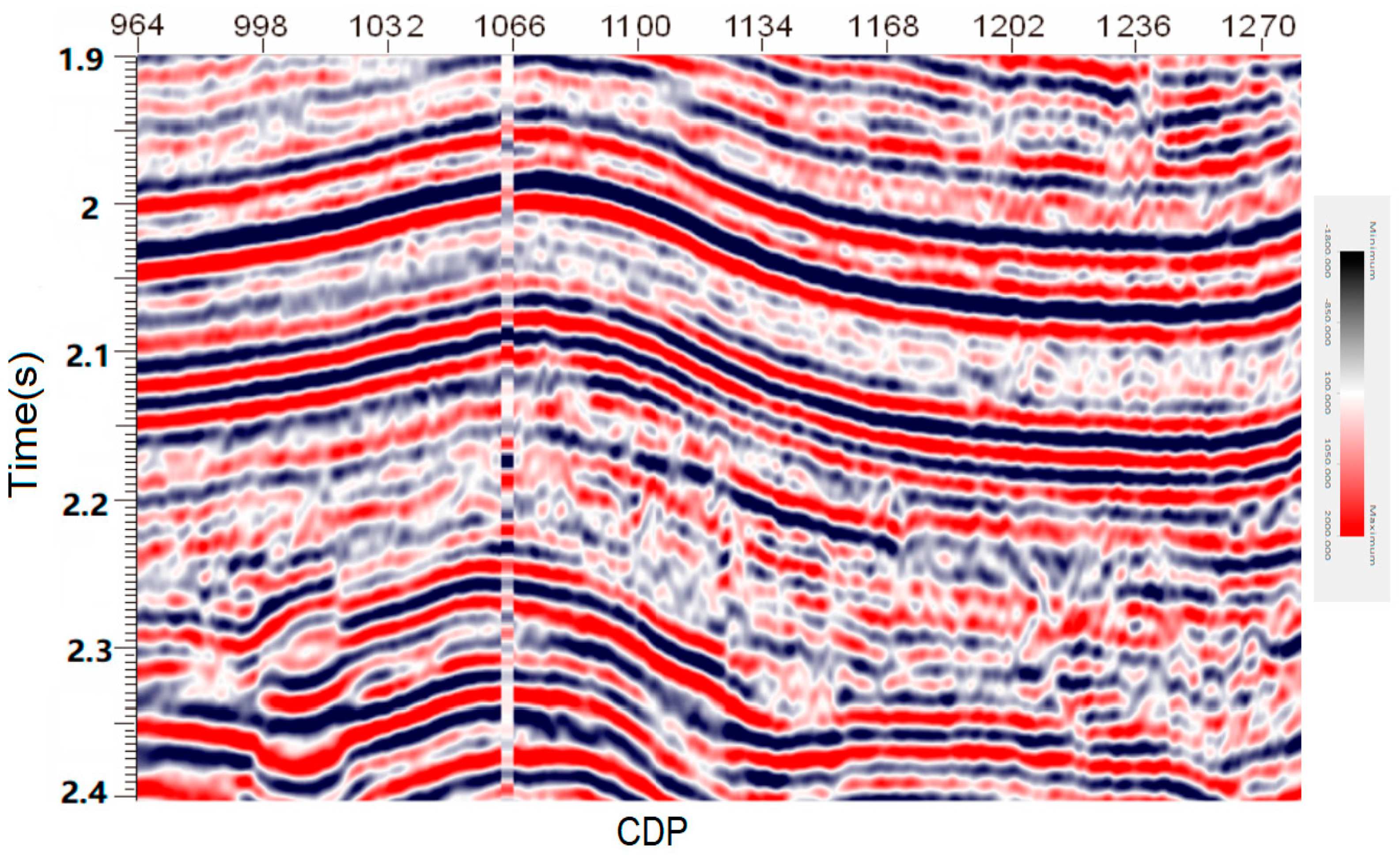
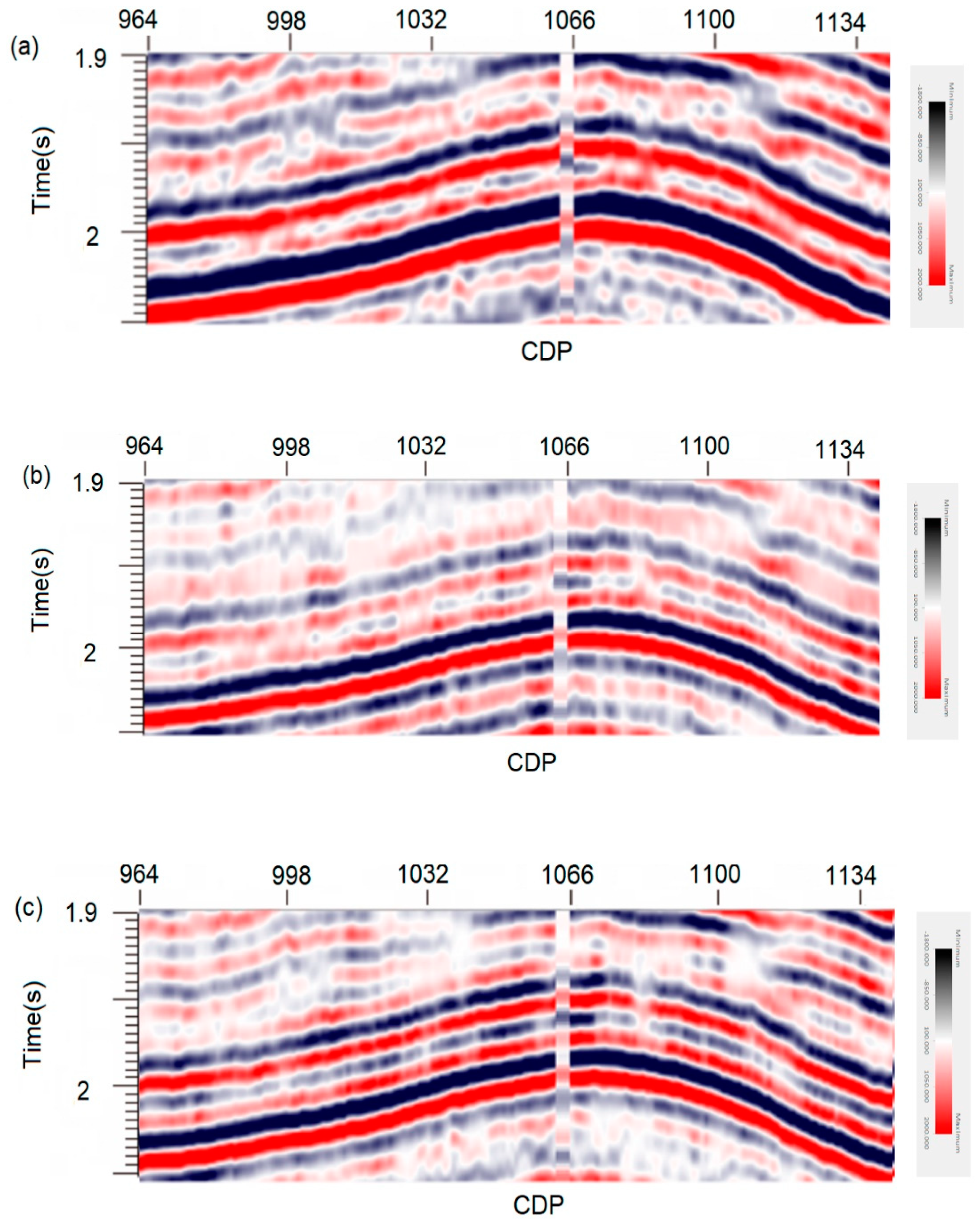
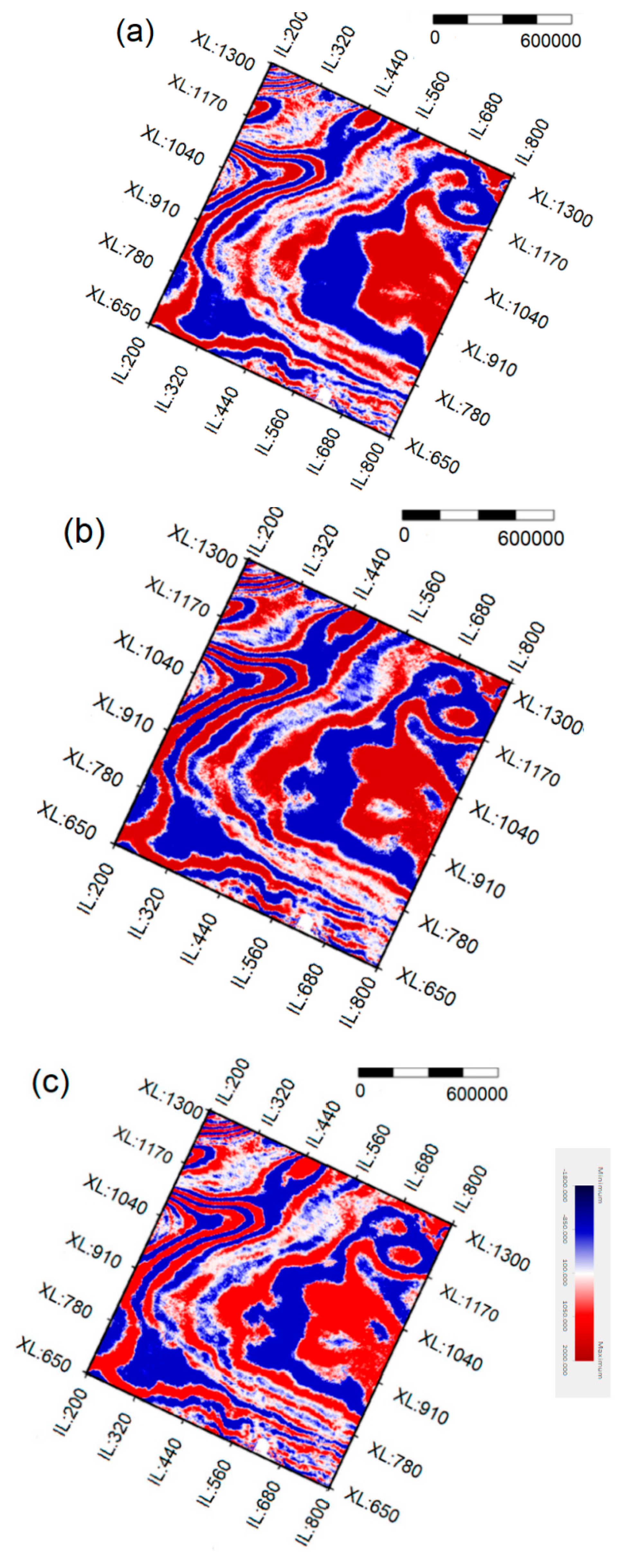
5. Real Data Processing
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Cai, T.T.; Wang, L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Trans. Inf. Theory 2011, 57, 4680–4688. [Google Scholar] [CrossRef]
- Chen, S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. Siam J. Sci. Comput. 1998, 20, 33–61. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressedsensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online dictionary learning for sparse coding. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 689–696. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. Siam J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics. Speech and Signal Processing, Vancouver, BC, Canada, 26–30 May 2013; Volume 38, pp. 6645–6649. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pineda, F.J. Generalization of back-propagation to recurrent neural networks. Phys. Rev. Lett. 1987, 59, 2229–2232. [Google Scholar] [CrossRef] [PubMed]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef] [Green Version]
- Kasać, J.; Deur, J.; Novaković, B.; Kolmanovsky, I. A conjugate gradient-based BPTT-like optimal control algorithm. In Proceedings of the IEEE International Conference on Control Applications, Petersburg, Russia, 8–10 July 2009; pp. 861–866. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, S.; Yan, K.; Lan, H.; Badal, J.; Qin, Z. A Sparse Spike Deconvolution Algorithm Based on a Recurrent Neural Network and the Iterative Shrinkage-Thresholding Algorithm. Energies 2020, 13, 3074. https://doi.org/10.3390/en13123074
Pan S, Yan K, Lan H, Badal J, Qin Z. A Sparse Spike Deconvolution Algorithm Based on a Recurrent Neural Network and the Iterative Shrinkage-Thresholding Algorithm. Energies. 2020; 13(12):3074. https://doi.org/10.3390/en13123074
Chicago/Turabian StylePan, Shulin, Ke Yan, Haiqiang Lan, José Badal, and Ziyu Qin. 2020. "A Sparse Spike Deconvolution Algorithm Based on a Recurrent Neural Network and the Iterative Shrinkage-Thresholding Algorithm" Energies 13, no. 12: 3074. https://doi.org/10.3390/en13123074




