Effective Electricity Theft Detection in Power Distribution Grids Using an Adaptive Neuro Fuzzy Inference System
Abstract
1. Introduction
- The adaptive neuro fuzzy inference system (ANFIS) is proposed and applied for first time in power theft detection for local low voltage power distribution network;
- Thirteen different scenarios possible to occur in the real world are established and presented analytically, in order to justify their importance in the proper operation of the power distribution network and they are used in the simulated and discussed case studies in the following;
- High success rates in power theft detection for most those realistic power theft scenarios were achieved; The adaptive neuro fuzzy inference system (ANFIS) is proposed, implemented and has achieved great success in classifying residential energy consumption patterns to be legal or illegal.
2. The Proposed Machine Learning Model Framework
2.1. The ANFIS Classification Method
2.2. Power Theft Scenarios
2.3. Electricity Consumption Data Preprocess and ANFIS Configuration
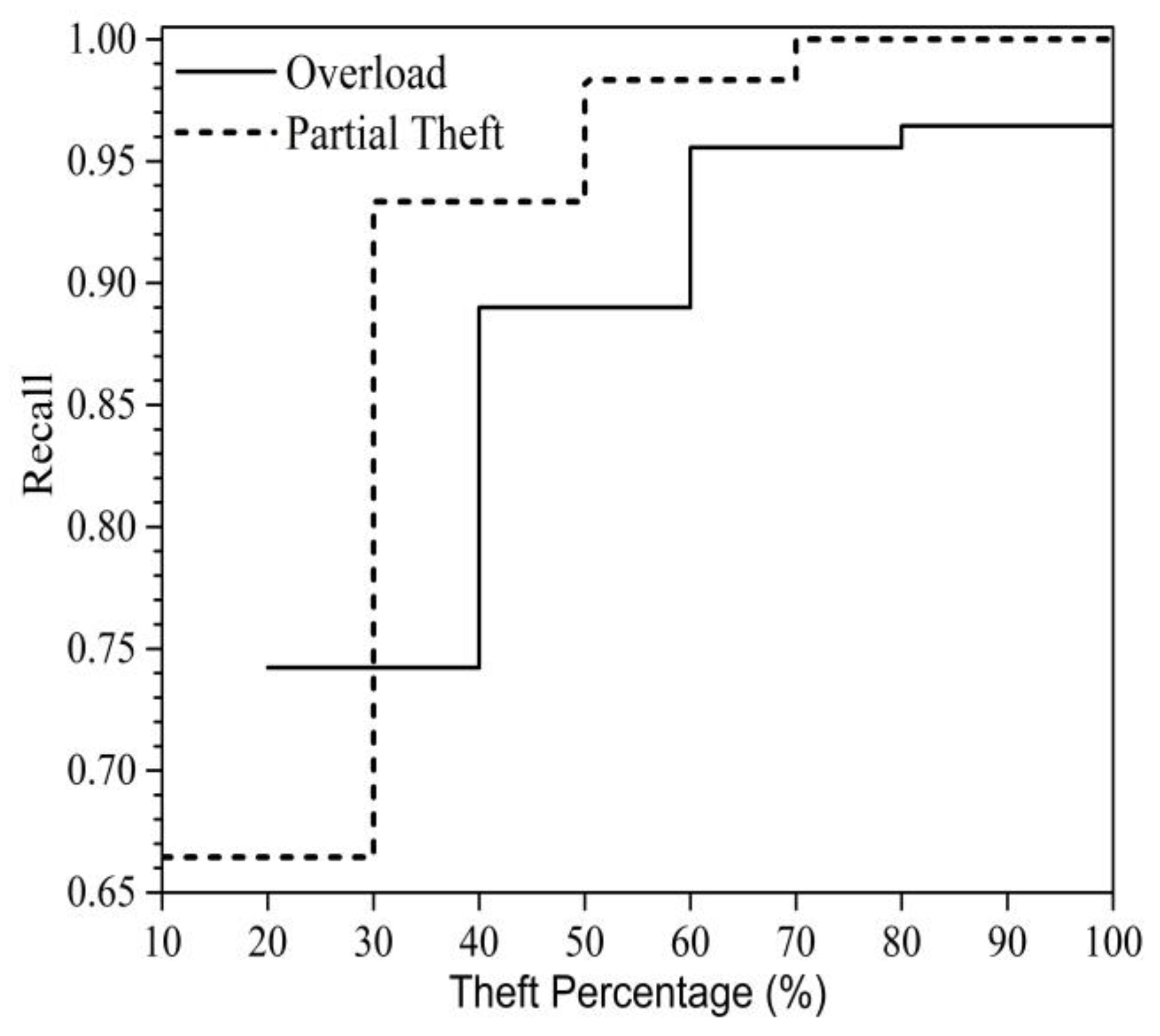
3. Performance and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Viegas, J.L.; Esteves, P.R.; Melício, R.; Mendes VM, F.; Vieira, S.M. Solutions for detection of non-technical losses in the electricity grid: A review. Renew. Sustain. Energy Rev. 2017, 80, 1256–1268. [Google Scholar] [CrossRef]
- Messinis, G.M.; Hatziargyriou, N.D. Hatziargyriou. Review of non-technical loss detection methods. Electr. Power Syst. Res. 2018, 158, 250–266. [Google Scholar] [CrossRef]
- Glauner, P.; Meira, J.; Valtchev, P.; State, R.; Bettinger, F. The Challenge of Non-Technical Loss Detection using Artificial Intelligence: A Survey. Int. J. Comput. Intell. Syst. (IJCIS) 2017, 10, 760–775. [Google Scholar] [CrossRef]
- Angelos EW, S.; Saavedra, O.R.; Cortés OA, C.; de Souza, A.N. Detection and identification of abnormalities in customer consumptions in power distribution systems. IEEE Trans. Power Deliv. 2011, 26, 2436–2442. [Google Scholar] [CrossRef]
- Nizar, A.H.; Dong, Z.Y.; Wang, Y. Power utility nontechnical loss analysis with extreme learning machine method. IEEE Trans. Power Syst. 2008, 23, 946–955. [Google Scholar] [CrossRef]
- Konstantinos, B.; Georgios, S. Efficient Power Theft Detection for Residential Consumers Using Mean Shift Data Mining Knowledge Discovery Process. Int. J. Artif. Intell. Appl. (IJAIA) 2019, 10, 69–85. [Google Scholar]
- Nagi, J.; Yap, K.S.; Tiong, S.K.; Ahmed, S.K.; Mohamad, M. Nontechnical loss detection for metered customers in power utility using support vector machines. IEEE Trans. Power Deliv. 2010, 25, 1162–1171. [Google Scholar] [CrossRef]
- Nagi, J.; Yap, K.S.; Tiong, S.K.; Ahmed, S.K.; Nagi, F. Improving SVM-based nontechnical loss detection in power utility using the fuzzy inference system. IEEE Trans. Power Deliv. 2011, 26, 1284–1285. [Google Scholar] [CrossRef]
- Ramos, C.C.O.; de Souza, A.N.; Falcão, A.X.; Papa, J.P. New insights on nontechnical losses characterization through evolutionary-based feature selection. IEEE Trans. Power Deliv. 2012, 27, 140–146. [Google Scholar] [CrossRef]
- Pereira, D.R.; Pazoti, M.A.; Pereira, L.A.M.; Rodrigues, D.; Ramos, C.O.; Souza, A.N.; Papa, J.P. Social-Spider Optimization-based Support Vector Machines applied for energy theft detection. Comput. Electr. Eng. 2016, 49, 25–38. [Google Scholar] [CrossRef]
- Costa, B.C.; Alberto, B.L.A.; Portela, A.M.; Maduro, W.; Eler, E.O. Fraud detection in electric power distribution networks using an Ann-based knowledge-discovery process. Int. J. Artif. Intell. Appl. 2013, 4, 17–23. [Google Scholar] [CrossRef]
- León, C.; Biscarri, F.; Monedero, I.; Guerrero, J.I.; Biscarri, J.; Millán, R. Variability and trend-based generalized rule induction model to NTL detection in power companies. IEEE Trans. Power Syst. 2011, 26, 1798–1807. [Google Scholar] [CrossRef]
- Ramos CC, O.; de Sousa, A.N.; Papa, J.P.; Falcao, A.X. A new approach for nontechnical losses detection based on optimum-path forest. IEEE Trans. Power Syst. 2011, 26, 181–189. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, Y.; Niu, X.; Dai, H.N.; Zhou, Y. Wide & Deep Convolutional Neural Networks for Electricity-Theft Detection to Secure Smart Grids. IEEE Trans. Veh. Technol. 2017, 14, 1606–1614. [Google Scholar]
- Wang, Y.; Chen, Q.; Gan, D.; Yang, J.; Kirschen, D.S.; Kang, C. Deep Learning-Based Socio-demographic Information Identification from Smart Meter Data. IEEE Trans. Smart Grid 2018, 10, 2593–2602. [Google Scholar] [CrossRef]
- Hasan, M.; Toma, R.N.; Nahid, A.A.; Islam, M.M.; Kim, J.M. Electricity Theft Detection in Smart Grid Systems: A CNN-LSTM Based Approach. Energies 2019, 12, 3310. [Google Scholar] [CrossRef]
- Bhat, R.R.; Trevizan, R.D.; Sengupta, R.; Li, X.; Bretas, A. Identifying nontechnical power loss via spatial and temporal deep learning. In Proceedings of the 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 272–279. [Google Scholar]
- Fenza, G.; Gallo, M.; Loia, V. Drift-aware methodology for anomaly detection in smart grid. IEEE Access 2019, 7, 9645–9657. [Google Scholar] [CrossRef]
- Marulli, F.; Visaggio, C.A. Adversarial deep learning for energy management in buildings. In Proceedings of the 2019 Summer Simulation Conference, Society for Computer Simulation International, Berlin, Germany, July 2019. [Google Scholar]
- Neto, E.A.A.; Coelho, J. Probabilistic methodology for technical and non-technical losses estimation in distribution system. Electr. Power Syst. Res. 2013, 97, 93–99. [Google Scholar] [CrossRef]
- Xiao, Z.; Xiao, Y.; Du, D.H.-C. Exploring malicious meter inspection in neighborhood area smart grids. IEEE Trans. Smart Grid 2013, 4, 214–226. [Google Scholar] [CrossRef]
- Liao, C.; Ten, C.W.; Hu, S. Strategic FRTU deployment considering cyber security in secondary distribution network. IEEE Trans. Smart Grid 2013, 4, 1264–1274. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, X.; Zomaya, A.; Wang, L.; Hu, S. A dynamic programming algorithm for leveraging probabilistic detection of energy theft in smart home. IEEE Trans. Emerg. Top. Comput. 2015, 3, 502–513. [Google Scholar] [CrossRef]
- Silva, L.G.d.; da Silva, A.A.P.; de Almeida-Filho, A.T. Allocation of power-quality monitors using the P-median to identify nontechnical losses. IEEE Trans. Power Deliv. 2016, 31, 2242–2249. [Google Scholar] [CrossRef]
- Jokar, P.; Arianpoo, N.; Leung, V.C.M. Electricity theft detection in AMI using customers’ consumption patterns. IEEE Trans. Smart Grid 2016, 7, 216–226. [Google Scholar] [CrossRef]
- Jindal, A.; Dua, A.; Kaur, K.; Singh, M.; Kumar, N.; Mishra, S. Decision tree and SVM-based data analytics for theft detection in smart grid. IEEE Trans. Ind. Inform. 2016, 12, 1005–1016. [Google Scholar] [CrossRef]
- Huang, S.-C.; Lo, Y.-L.; Lu, C.-N. Non-technical loss detection using state estimation and analysis of variance. IEEE Trans. Power Syst. 2013, 28, 2959–2966. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform 2018. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Kapetanakis, T.N.; Vardiambasis, I.O.; Lourakis, E.I.; Maras, A. Applying neuro-fuzzy soft computing techniques to the circular loop antenna radiation problem. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1673–1676. [Google Scholar] [CrossRef]
- Matlab Statistics and Machine Learning Toolbox 11.2, 2017; The MathWorks, Inc.: Natick, MA, USA, 2017.
- Ghasemi, A.A.; Gitizadeh, M. Detection of illegal consumers using pattern classification approach combined with Levenberg-Marquardt method in smart grid. Int. J. Electr. Power Energy Syst. 2018, 99, 363–375. [Google Scholar] [CrossRef]
- Buzau, M.M.; Tejedor-Aguilera, J.; Cruz-Romero, P.; Gómez-Expósito, A. Detection of non-technical losses using smart meter data and supervised learning. IEEE Trans. Smart Grid 2018, 10, 2661–2670. [Google Scholar] [CrossRef]
- Irish Social Science Data Archive. Available online: http://www.ucd.ie/issda/data/commissionforenergyregulationcer/ (accessed on 6 October 2019).
- Zheng, K.; Chen, Q.; Wang, Y.; Kang, C.; Xia, Q. A Novel Combined Data-Driven Approach for Electricity Theft Detection. IEEE Trans. Ind. Inform. 2018, 15, 1809–1819. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14; 1998; Available online: https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/ (accessed on 10 June 2016).
- Wu, Y.; Wang, H.; Zhang, B.; Du, K.L. Using radial basis function networks for function approximation and classification. ISRN Appl. Math. 2012, 2012, 1–34. [Google Scholar] [CrossRef]











| Scenario | Power Theft (%) |
|---|---|
| PTi: Partially stealing | i = 1: 10%–30% |
| i = 2: 30%–50% | |
| i = 3: 50%–70% | |
| i = 4: 70%–90% | |
| Ok: Abruptly increased consumption | k = 1: 20%–40% |
| k = 2: 40%–60% | |
| k = 3: 60%–80% | |
| k = 4: 80%–100% | |
| PDm: Partially stealing electricity specific times of the day | m = 1: 80% from 12:00 p.m.–15:00 p.m. and 20:00 p.m.–22:00 p.m. |
| m = 2: 80% from 12:00 p.m.–15:00 p.m. | |
| Mn: combination of PTi, Ok, PDm | n = 1: PT3, O3 |
| n = 2: PT3, O3, PD1 | |
| n = 3: PT3, O3, PD1, PD2 |
| Model | ANFIS |
|---|---|
| MF type | Generalized bell-shaped |
| Number of MFs | 4 |
| Output MF | Constant |
| Training dataset | 327 |
| Checking dataset | 327 |
| Testing dataset | 327 |
| Number of epochs | 200 |
| Features | Definition |
|---|---|
| mean | |
| median | The middle value of observations |
| skewness | |
| entropy | |
| standard deviation | |
| kurtosis | |
| variance | |
| Energy | |
| Load factor |
| Accuracy | Recall | F1 | Precision | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ANFIS | SVM | RBF | ANFIS | SVM | RBF | ANFIS | SVM | RBF | ANFIS | SVM | RBF | |
| O1 | 0.87 | 0.72 | 0.80 | 0.74 | 0.13 | 0.57 | 0.78 | 0.22 | 0.64 | 0.81 | 0.69 | 0.72 |
| O2 | 0.94 | 0.79 | 0.84 | 0.89 | 0.42 | 0.68 | 0.90 | 0.55 | 0.72 | 0.92 | 0.79 | 0.77 |
| O3 | 0.98 | 0.85 | 0.90 | 0.96 | 0.61 | 0.83 | 0.96 | 0.71 | 0.84 | 0.97 | 0.85 | 0.85 |
| O4 | 0.98 | 0.89 | 0.95 | 0.96 | 0.74 | 0.93 | 0.97 | 0.81 | 0.91 | 0.98 | 0.90 | 0.90 |
| PT1 | 0.87 | 0.69 | 0.80 | 0.66 | 0.00 | 0.50 | 0.75 | 0.09 | 0.61 | 0.86 | 1.00 | 0.78 |
| PT2 | 0.97 | 0.91 | 0.95 | 0.93 | 0.71 | 0.91 | 0.95 | 0.83 | 0.92 | 0.97 | 0.99 | 0.93 |
| PT3 | 0.99 | 0.97 | 0.98 | 0.98 | 0.91 | 0.98 | 0.98 | 0.95 | 0.97 | 0.98 | 1.00 | 0.96 |
| PT4 | 1.00 | 0.99 | 0.99 | 1.00 | 0.97 | 1.00 | 1.00 | 0.98 | 0.98 | 0.99 | 1.00 | 0.97 |
| PD1 | 0.99 | 0.96 | 0.98 | 0.97 | 0.89 | 0.97 | 0.98 | 0.94 | 0.96 | 0.99 | 0.99 | 0.96 |
| PD2 | 0.95 | 0.91 | 0.95 | 0.89 | 0.72 | 0.90 | 0.92 | 0.84 | 0.91 | 0.96 | 0.99 | 0.94 |
| M1 | 0.93 | 0.88 | 0.73 | 0.96 | 0.65 | 0.14 | 0.88 | 0.76 | 0.23 | 0.82 | 0.93 | 0.82 |
| M2 | 0.83 | 0.87 | 0.83 | 0.92 | 0.59 | 0.48 | 0.66 | 0.73 | 0.63 | 0.52 | 0.96 | 0.94 |
| M3 | 0.69 | 0.77 | 0.77 | 0.89 | 0.27 | 0.27 | 0.44 | 0.42 | 0.41 | 0.29 | 0.97 | 0.91 |
| Power Theft Scenario | RMSE |
|---|---|
| PT1, PT2, PT3, PT4 | 0.640, 0.350, 0.184, 0.082 |
| O1, O2, O3, O4 | 1.184, 0.844, 0.631, 0.537 |
| PD1, PD2 | 0.660, 1.518 |
| M1, M2, M3 | 0.531, 0.850, 1.436 |
| Ref | Data Source | Number of Consumers | Sampling Time (Min) 1 | ML Algorithm | Accuracy | Precision | Recall | AUC |
|---|---|---|---|---|---|---|---|---|
| [25] | Irish | ~5000 | 30 | SVM | – | – | 0.94 | – |
| [36] | Irish | ~5000 | 30 | CFSFDP | – | – | – | 0.98 |
| [33] | - | - | 15 | PNN, LM | 0.96 | – | – | – |
| [34] | Endesa | 57,304 | 288 | K-means, KNN, LR, XGBoost | – | – | – | 0.91 |
| [6] | Artificial | 1100 | 15 | Mean shift, DBSCAN | – | – | 0.96 | – |
| [17] | IEEE 123 bus feeder | 12,180 | - | CNN, LSTM | – | 0.97 | 0.97 | – |
| [16] | State Grid of China | 17,120 | - | CNN, LSTM | 0.89 | 0.90 | 0.87 | – |
| ANFIS | Irish | 3273 | 30 | ANFIS | 0.99 | 0.99 | 0.99 | 0.99 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blazakis, K.V.; Kapetanakis, T.N.; Stavrakakis, G.S. Effective Electricity Theft Detection in Power Distribution Grids Using an Adaptive Neuro Fuzzy Inference System. Energies 2020, 13, 3110. https://doi.org/10.3390/en13123110
Blazakis KV, Kapetanakis TN, Stavrakakis GS. Effective Electricity Theft Detection in Power Distribution Grids Using an Adaptive Neuro Fuzzy Inference System. Energies. 2020; 13(12):3110. https://doi.org/10.3390/en13123110
Chicago/Turabian StyleBlazakis, Konstantinos V., Theodoros N. Kapetanakis, and George S. Stavrakakis. 2020. "Effective Electricity Theft Detection in Power Distribution Grids Using an Adaptive Neuro Fuzzy Inference System" Energies 13, no. 12: 3110. https://doi.org/10.3390/en13123110
APA StyleBlazakis, K. V., Kapetanakis, T. N., & Stavrakakis, G. S. (2020). Effective Electricity Theft Detection in Power Distribution Grids Using an Adaptive Neuro Fuzzy Inference System. Energies, 13(12), 3110. https://doi.org/10.3390/en13123110






