Numerical Simulation of the Flow in a Kaplan Turbine Model during Transient Operation from the Best Efficiency Point to Part Load †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Case
2.2. Numerical Model
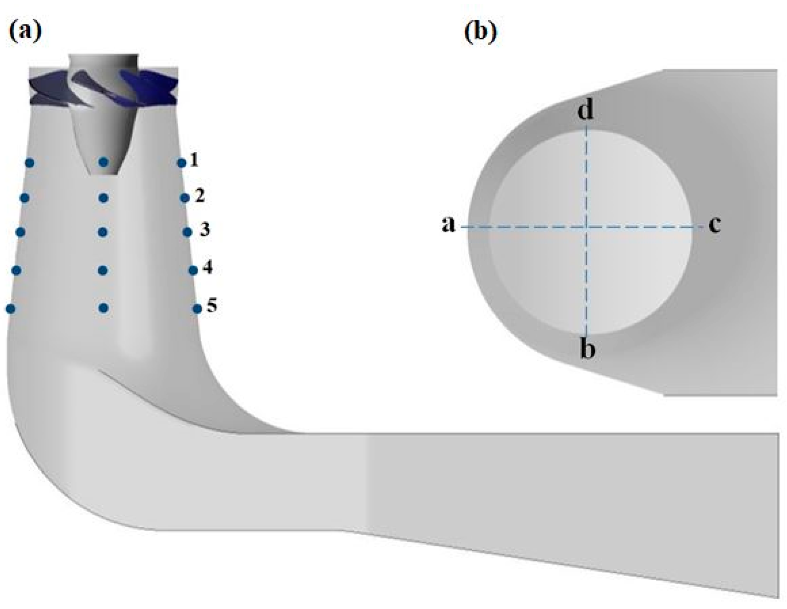
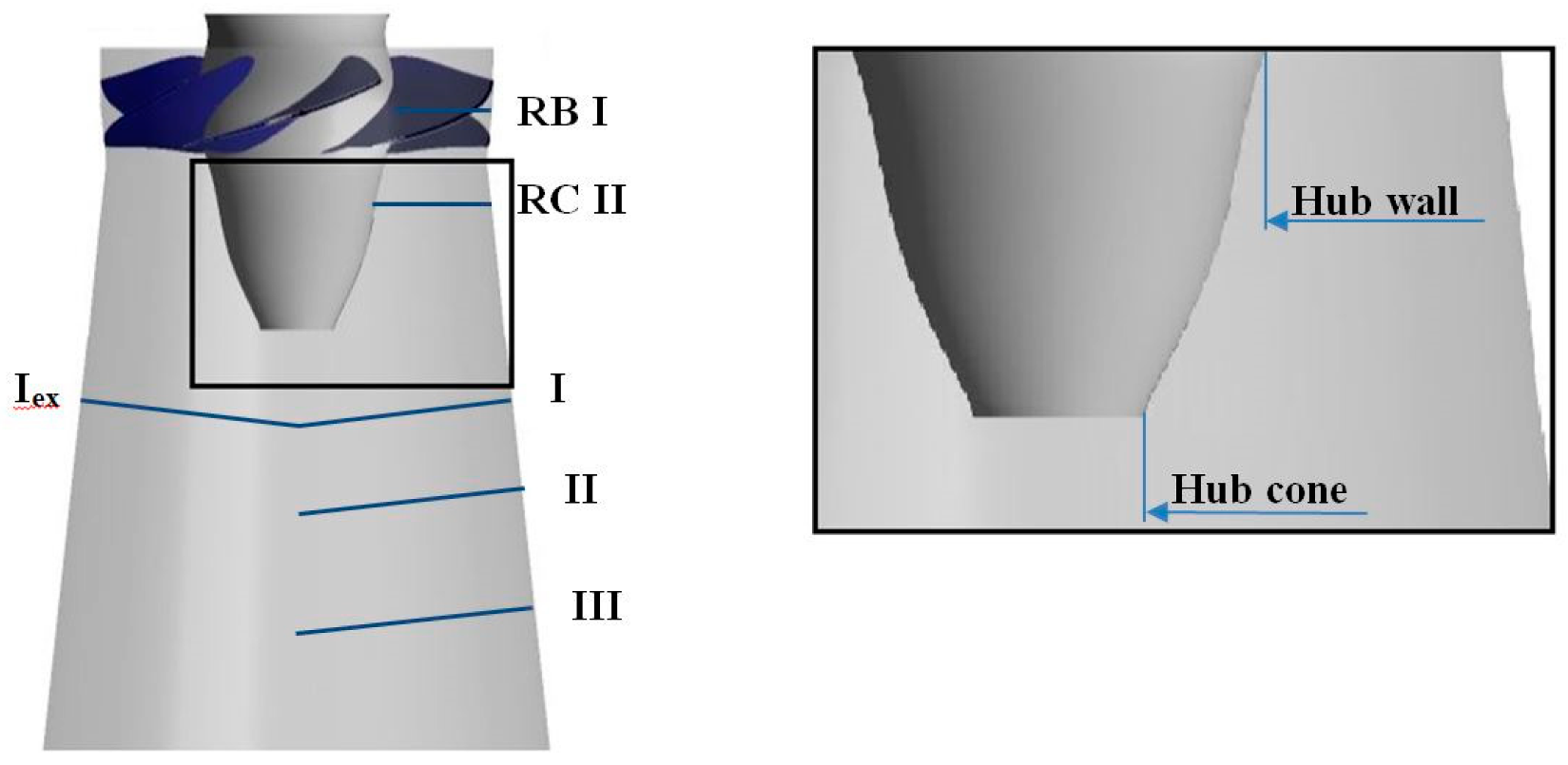
2.1.1. Analysis Domain
2.1.2. Mesh
2.1.3. Boundary Conditions
2.1.4. Time Step Sensitivity Analysis
3. Results and Discussion
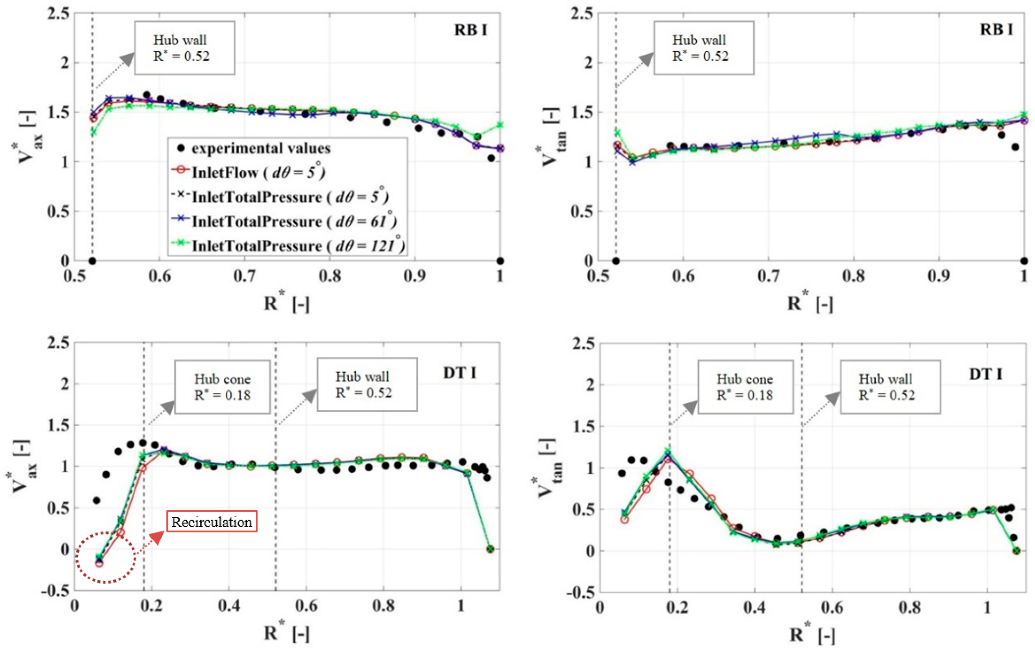
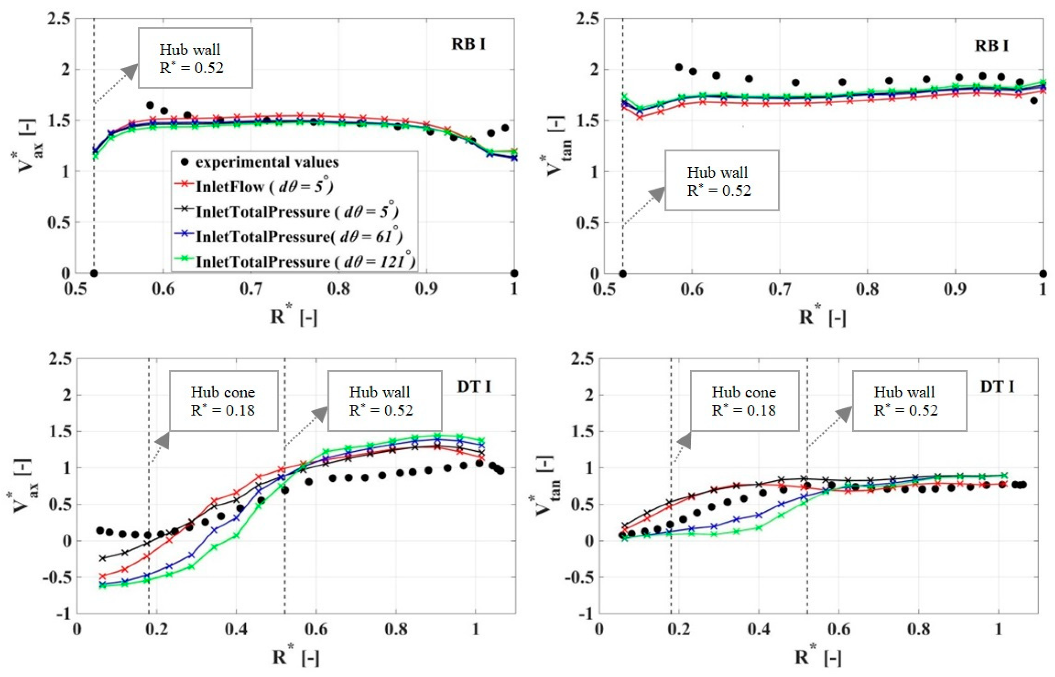
3.1. Validation with Experimental Velocity Profiles
3.2. Inlet Boundary Conditions
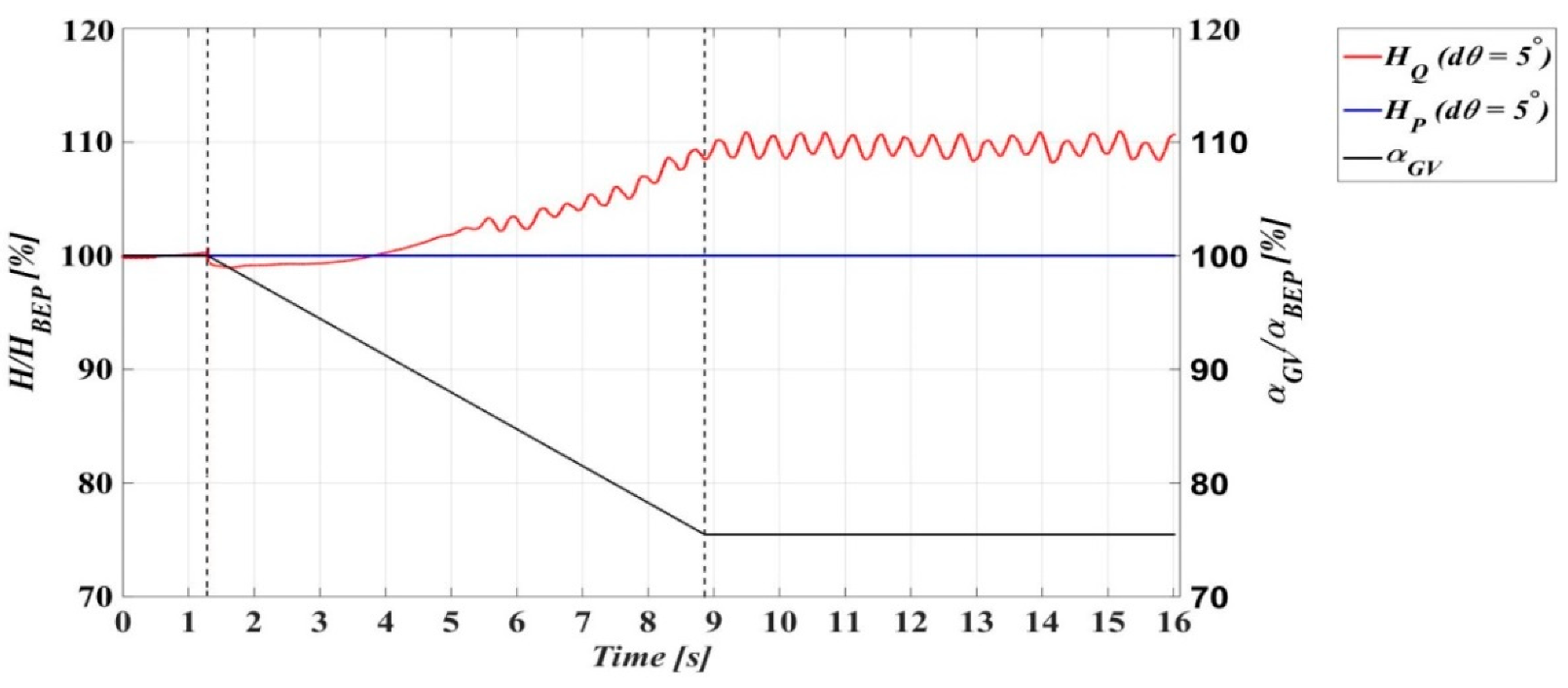
3.2.1. Main Parameters
3.2.2. Pressure Oscillations
3.3. Rotating Vortex Rope
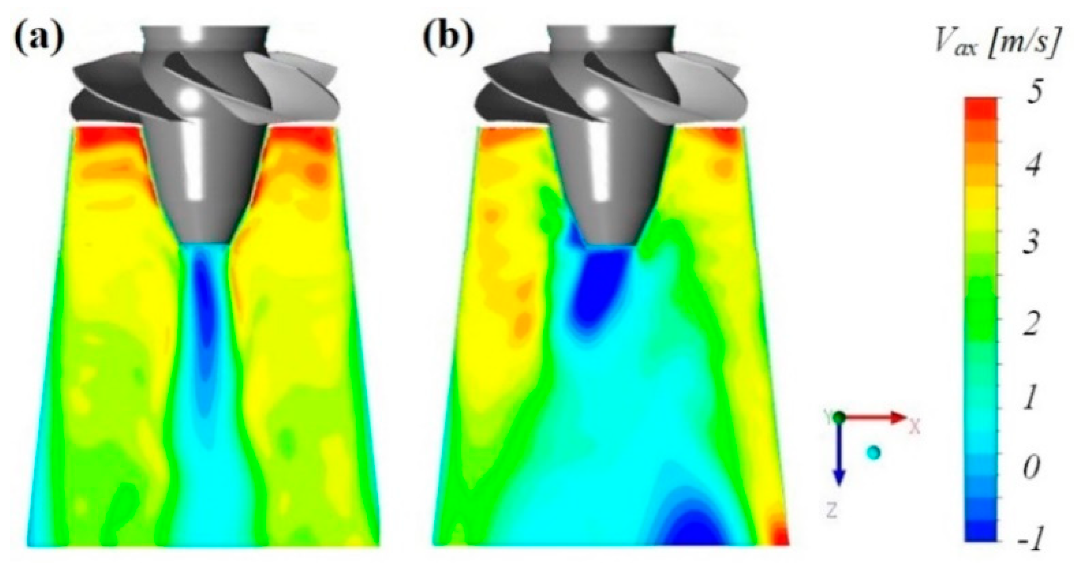
3.3.1. Flow Structure
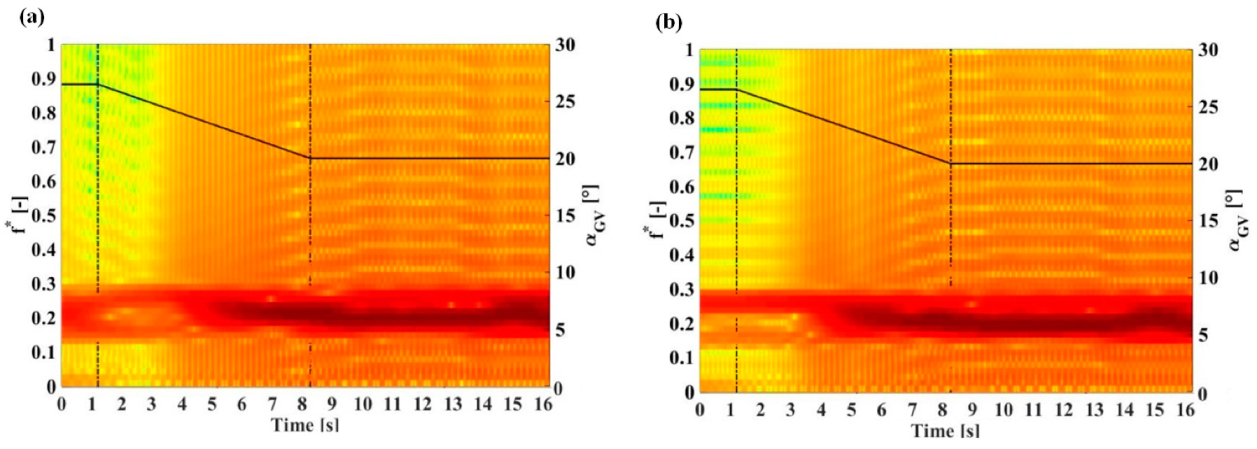
3.3.2. Spectral Analysis
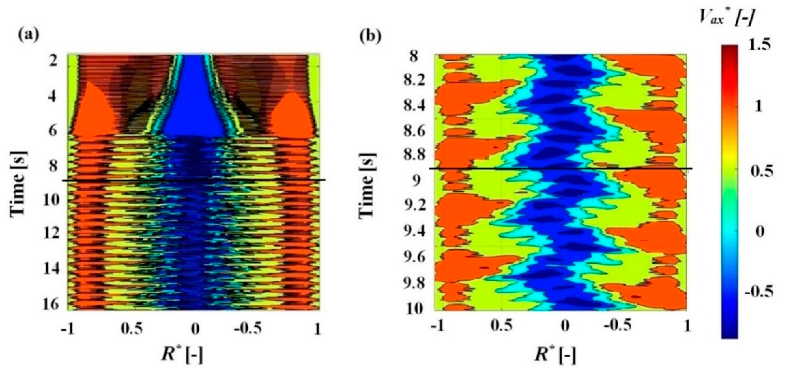
3.3.3. Decomposition of the Rotating Vortex Rope
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Banshwar, A.; Sharma, N.K.; Sood, Y.R.; Shrivastava, R. Market based procurement of energy and ancillary services from renewable energy sources in deregulated environment. Renew. Energy 2017, 101, 1390–1400. [Google Scholar] [CrossRef]
- Amiri, K.; Cervantes, M.J.; Mulu, B. Experimental investigation of the hydraulic loads on the runner of a Kaplan turbine model and the corresponding prototype. J. Hydraul. Res. 2015, 53, 452–465. [Google Scholar] [CrossRef]
- Goyal, R.; Cervantes, M.J.; Gandhi, B.K. Vortex rope formation in a high head model Francis turbine. J. Fluids Eng. 2017, 139, 041102. [Google Scholar] [CrossRef]
- Houde, S.; Fraser, R.; Ciocan, G.; Deschênes, C. Experimental study of the pressure fluctuations on propeller turbine runner blades: Part 2, transient conditions. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062061. [Google Scholar] [CrossRef] [Green Version]
- Chirag, T.; Cervantes, M.J.; Bhupendrakumar, G.; Dahlhaug, O.G. Pressure measurements on a high-head Francis turbine during load acceptance and rejection. J. Hydraul. Res. 2014, 52, 283–297. [Google Scholar] [CrossRef]
- Amiri, K.; Mulu, B.; Raisee, M.; Cervantes, M.J. Unsteady pressure measurements on the runner of a Kaplan turbine during load acceptance and load rejection. J. Hydraul. Res. 2016, 54, 1–18. [Google Scholar] [CrossRef]
- Ciocan, G.D.; Iliescu, M.S.; Vu, T.C.; Nennemann, B.; Avellan, F. Experimental study and numerical simulation of the FLINDT draft tube rotating vortex. J. Fluids Eng. 2006, 129, 146–158. [Google Scholar] [CrossRef]
- Favrel, A.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Study of the vortex-induced pressure excitation source in a Francis turbine draft tube by particle image velocimetry. Exp. Fluids 2015, 56. [Google Scholar] [CrossRef]
- Lipej, A.; Čelič, D.; Tartinville, B.; Mezine, M.; Hirsch, C. Reduction of CPU time for CFD analysis of hydraulic machinery development process. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 62011. [Google Scholar] [CrossRef] [Green Version]
- Židonis, A.; Aggidis, G. State of the art in numerical modelling of Pelton turbines. Renew. Sustain. Energy Rev. 2015, 45, 135–144. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J. State of the art in numerical simulation of high head Francis turbines. Renew. Energy Environ. Sustain. 2016, 1, 20. [Google Scholar] [CrossRef] [Green Version]
- Denton, J.D. Some limitations of turbomachinery CFD. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 735–745. [Google Scholar] [CrossRef]
- Tang, T. Moving mesh computations for computational fluid dynamics. Contemp. Math. 2005, 383, 141–173. [Google Scholar] [CrossRef] [Green Version]
- Matsushima, K.; Murayama, M.; Nakahashi, K. Unstructured dynamic mesh for large movement and deformation. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Perot, J.B.; Nallapati, R. A moving unstructured staggered mesh method for the simulation of incompressible free-surface flows. J. Comput. Phys. 2003, 184, 192–214. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.; Yuekun, S.; Yulin, W.; Leqin, W. Three dimensional flow simulation of load rejection of a prototype pump-turbine. Eng. Comput. 2013, 29, 417–426. [Google Scholar] [CrossRef]
- Kolšek, T.; Duhovnik, J.; Bergant, A. Simulation of unsteady flow and runner rotation during shut-down of an axial water turbine. J. Hydraul. Res. 2006, 44, 129–137. [Google Scholar] [CrossRef]
- Li, J.; Yu, J.; Wu, Y. 3D unsteady turbulent simulations of transients of the Francis turbine. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012001. [Google Scholar] [CrossRef]
- Mössinger, P.; Jester-Zürker, R.; Jung, A. Francis-99: Transient CFD simulation of load changes and turbine shutdown in a model sized high-head Francis turbine. J. Phys. Conf. Ser. 2017, 782, 12001. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, J.-M.; Flemming, F.; Qian, R.; Deschênes, C.; Coulson, S. Experimental and numerical investigations of inlet boundary conditions for a propeller turbine draft tube. In Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting, Montreal, QC, Canada, 1–5 August 2010. [Google Scholar] [CrossRef]
- Nilsson, H.; Cervantes, M.J. Effects of inlet boundary conditions, on the computed flow in the Turbine-99 draft tube, using OpenFOAM and CFX. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 32002. [Google Scholar] [CrossRef] [Green Version]
- Nicolle, J.; Giroux, A.M.; Morissette, J.F. CFD configurations for hydraulic turbine startup. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 32021. [Google Scholar] [CrossRef]
- Wilhelm, S.; Balarac, G.; Métais, O.; Ségoufin, C. Analysis of head losses in a turbine draft tube by means of 3D unsteady simulations. Flow Turbul. Combust. 2016, 97, 1255–1280. [Google Scholar] [CrossRef] [Green Version]
- Nicolet, C.; Arpe, J.; Avellan, F. Identification and modelling of pressure fluctuations of a Francis turbine scale model at part load operation. In Proceedings of the IAHR 22nd Symposium on Hydraulic Machinery and Systems, Stockholm, Sweden, 29 June–2 July 2004. [Google Scholar]
- Liu, S.; Li, S.; Wu, Y. Pressure fluctuation prediction of a model Kaplan turbine by unsteady turbulent flow simulation. J. Fluids Eng. 2009, 131, 101102. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S.; Dou, H.-S.; Wu, S.; Chen, T. Numerical prediction and similarity study of pressure fluctuation in a prototype Kaplan turbine and the model turbine. Comput. Fluids 2011, 56, 128–142. [Google Scholar] [CrossRef]
- Ruprecht, A.; Helmrich, T.; Aschenbrenner, T.; Scherer, T. Simulation of vortex rope in a turbine draft tube. In Proceedings of the Hydraulic Machinery and Systems 21st IAHR Symposium, Lausanne, Switzerland, 9–12 September 2002. [Google Scholar]
- Maddahian, R.; Cervantes, M.J.; Sotoudeh, N. Numerical investigation of the flow structure in a Kaplan draft tube at part load. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 22008. [Google Scholar] [CrossRef] [Green Version]
- Iovănel, R.G.; Bucur, D.M.; Dunca, G.; Cervantes, M.J. Numerical analysis of a Kaplan turbine model during transient operation. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022046. [Google Scholar] [CrossRef]
- Mulu, B.; Jonsson, P.; Cervantes, M.J. Experimental investigation of a Kaplan draft tube—Part I: Best efficiency point. Appl. Energy 2012, 93, 695–706. [Google Scholar] [CrossRef]
- Jonsson, P.; Mulu, B.; Cervantes, M.J. Experimental investigation of a Kaplan draft tube—Part II: Off-design conditions. Appl. Energy 2012, 94, 71–83. [Google Scholar] [CrossRef]
- Amiri, K.; Mulu, B.; Cervantes, M.J. Experimental investigation of the interblade flow in a Kaplan runner at several operating points using Laser Doppler Anemometry. J. Fluids Eng. 2015, 138, 021106. [Google Scholar] [CrossRef]
- Melot, M.; Nennemann, B.; Désy, N. Draft tube pressure pulsation predictions in Francis turbines with transient Computational Fluid Dynamics methodology. IOP Conf. Ser. Earth Environ. Sci. 2014, 22, 32002. [Google Scholar] [CrossRef] [Green Version]
- Alfonsi, G. Reynolds-averaged Navier–Stokes equations for turbulence modeling. Appl. Mech. Rev. 2009, 62, 040802. [Google Scholar] [CrossRef]
- Mulu, B.G.; Cervantes, M.J.; Devals, C.; Vu, T.C.; Guibault, F. Simulation-based investigation of unsteady flow in near-hub region of a Kaplan Turbine with experimental comparison. Eng. Appl. Comput. Fluid Mech. 2015, 9, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.; Carregal-Ferreira, J.; Esch, T.; Konno, B. The SST turbulence model with improved wall treatment for heat transfer predictions in gas turbines. In Proceedings of the International Gas Turbine Congress, Tokyo, Japan, 2–7 November 2003. [Google Scholar]
- Ansys 16.2 Documentation CFX Modelling guide 4.2. Modelling Flow Near the Wall. 2014. Available online: http://http://read.pudn.com/downloads500/ebook/2077964/cfx_mod.pdf (accessed on 12 June 2020).
- Trivedi, C.; Cervantes, M.J.; Dahlhaug, O.G. Experimental and numerical studies of a high-head Francis turbine: A review of the Francis-99 test case. Energies 2016, 9, 74. [Google Scholar] [CrossRef] [Green Version]
- Nicolle, J.; Cupillard, S. Prediction of dynamic blade loading of the Francis-99 turbine. J. Phys. Conf. Ser. 2015, 579, 012001. [Google Scholar] [CrossRef] [Green Version]
- Iovanel, R.G. Numerical Investigation of the Flow in a Kaplan Turbine. Ph.D. Thesis, Politehnica University of Bucharest, Bucharest, Romania, 2018. [Google Scholar]
- Nishi, M.; Kubota, T.; Matsunaga, S. Surging characteristics of conical and elbow type draft tubes. In Proceedings of the 12th IAHR Symposium on Hydraulic Machinery, Equipment, and Cavitation, Stirling, Scotland, 27–30 August 1984. [Google Scholar]











| Operating Point | BEP | PL |
|---|---|---|
| αGV (°) | 26.5 | 20 |
| Q (m3/s) | 0.69 | 0.62 |
| H (m) | 7.5 | 7.5 |
| Domain | No. of Elements (×106) | Minimum Angle (°) | Expansion Factor (–) | Aspect Ratio (–) | y+ (min/avg/max) (–) |
|---|---|---|---|---|---|
| Guide vane | 0.34 | 20.2 | 16 | 58 | 2.70/15.6/27.1 |
| Runner | 9.96 | 16.8 | 48 | 668 | 0.90/15.7/67.0 |
| Draft tube | 3.66 | 30.5 | 9 | 7635 | 0.02/1.12/4.40 |
| Case | Time Step dt [s] | Corresponding Runner Rotation dθ (°) |
|---|---|---|
| 1 | 0.001195 | 5 |
| 2 | 0.014579 | 61 |
| 3 | 0.028919 | 121 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iovănel, R.G.; Dunca, G.; Bucur, D.M.; Cervantes, M.J. Numerical Simulation of the Flow in a Kaplan Turbine Model during Transient Operation from the Best Efficiency Point to Part Load. Energies 2020, 13, 3129. https://doi.org/10.3390/en13123129
Iovănel RG, Dunca G, Bucur DM, Cervantes MJ. Numerical Simulation of the Flow in a Kaplan Turbine Model during Transient Operation from the Best Efficiency Point to Part Load. Energies. 2020; 13(12):3129. https://doi.org/10.3390/en13123129
Chicago/Turabian StyleIovănel, Raluca G., Georgiana Dunca, Diana M. Bucur, and Michel J. Cervantes. 2020. "Numerical Simulation of the Flow in a Kaplan Turbine Model during Transient Operation from the Best Efficiency Point to Part Load" Energies 13, no. 12: 3129. https://doi.org/10.3390/en13123129





