A Gini Coefficient-Based Impartial and Open Dispatching Model

Abstract

According to the existing widely applied impartial and open dispatching models, operation fairness was mainly emphasized, which severely restricted the optimization space of the economy of the overall system operation and affected the economic benefits. To solve the above problems, a scheduling model based on Gini coefficient under impartial and open dispatching principle is proposed in this paper, which can consider the balance between the fairness and economy of system operation. In the proposed model, the Gini coefficient is introduced to describe the fairness of electric energy completion rate among different generation units in the form of constraint conditions. Because the electricity production schedule can reflect the economic income of the electric power enterprise, and the Gini coefficient is used as an economic statistical indicator to evaluate the fairness in the overall distribution of income in social statistics, it is more appropriate to be used to measure the fairness of the power generation dispatching. The objective of the proposed model is to minimize the total operation costs. In the model, the balance between the system operation economy and fairness can be realized by adjusting the Gini coefficient value. The simulation results show that the proposed model is an extension of the traditional model. Compared with the traditional economic dispatching model and normal “impartial and open dispatching” model, the proposed model can better coordinate the relationship between fairness and economy. It could provide more choices for power generation dispatchers. It could also provide a reference for regulatory departments to formulate relevant policies by adjusting the threshold value of the Gini coefficient. Case studies show that the power dispatching decisions according to the proposed model can provide a scientific and fair reference basis for dispatching schemes, and could reduce the generation costs and also achieve optimal allocation of resources on the basis of ensuring fair dispatching.

1. Introduction

In the past several decades, impartial and open dispatching has generally been implemented in some countries like China, although power dispatching must be guaranteed for it to be open and fair. The assessed object of the impartial and open dispatching is the completion progress of the annual power generation plan issued by the government department, which requires the annual electric energy production completion rate of all the power plants to be approximately equal [1,2]. According to the national regulation, deviation of no more than 2–3% between the annual schedule is required.

The impartial and open principle should be felicitously considered in the power system scheduling process. The unit’s operation adjustment space would be limited strictly if the impartial and open dispatching principle is excessive emphasized, resulting in higher power generation costs of the power system. On the contrary, the excessive emphasis on operational economy will result in a serious imbalance among the units’ power generation progresses, leading to conflicts and disputes among various power generation producers, which may disrupt the generation order, but also reduce market efficiency. Therefore, in the dispatching, the reliability, economy, and fairness of the system operation should be comprehensively considered to reasonably arrange the unit commitment and load distribution schedule of the power units [3,4,5,6].

Literature Review and Discussion

Many researchers all over the world have studied the electricity dispatching model. In past decades, an hourly scheduling model in a local day-ahead electricity market was presented in [7], to maximize the operational profits managed by an energy service company. A two-stage robust scheduling approach for a hydrothermal power system was studied in [8]. In [9], a day ahead optimal scheduling model of generators using dynamic programming method was proposed. In [10,11,12], an optimal generation scheduling strategy in micro-grids was studied. The studies above studied the scheduling problem under different requirements using different methods. Nevertheless, the generation fairness was not considered. The preparation process and allocation strategy for annual generation schedules based on the annual utilization hours under the impartial and open dispatching principle have been proposed in [13]. Scheduling models according to the impartial and open dispatching principle were presented in [14,15], respectively, aiming at minimizing the deviation between the actual output and the target output, and minimizing the deviation between the annual planned electricity energy and the contracted electric energy. Multi-objective optimization models were presented in [16,17,18], considering the economy of the system operation on the basis of the impartial and open dispatching principle, with the objective of minimizing the power generation costs and minimizing the contracted energy deviation. Fuzzy methods were used to solve the model. In the existing methods mentioned above, the fairness is considered using the standard deviation index of the actual electricity and the planned electricity.

The issue of fairness involves many fields such as philosophy, ethics, politics, society, economy, and so on. The criteria for measuring fairness are also difficult to determine. Although, in the existing studies, the indicator constructed by the standard deviation can be used to measure the difference among units’ generation completion progresses [13,14,15,16,17,18,19], the threshold for judging fairness is difficult to determine, which leads to the following shortcomings:

(1)

The fairness of the unit’s generation schedule is over-emphasized, so that the system operation economic optimization space is reduced, which is not conducive to the resources optimizing configuration [20];

(2)

There is a lack of coordination between fairness and economy, which limits the diversity of the optimization objectives of the dispatching. As a result, the different fairness requirement in the different processes of scheduling is difficult to meet.

Among the above analyses, it is not difficult to find that existing studies usually consider only fairness or safety. Especially for the fairness of scheduling, some fairness indicators are also mentioned in many literature, but the determination of the fairness index threshold still needs to be further considered, and there is no authoritative definition. So, whether or not fairness is justified remains to be discussed.

Currently, in the international arena, the Gini coefficient is used to comprehensively examine the differences in income distribution among residents as an important analytical indicator. Through theoretical research and practice for more than half a century, there has been a basic consensus on the corresponding relationship between the values of the Gini coefficient and the levels of fairness. The Gini coefficient has been widely applied in many fields including traffic systems [21,22], environmental resources [23], and power systems [24,25]. An indicator to measure the fairness of the annual generation schedule based on the Gini coefficient was proposed in [25]. The correlation and difference between the Gini coefficient and the standard deviation were analyzed in [26].

According to China’s current electricity pricing system, the electric energy charge income is the main economic source of generation units. Therefore, the Gini coefficient is appropriate to be introduced into the impartial and open dispatching as a parameter to measure fairness, and the existing studies and practical results can be used as a basis for measuring the level of fairness when applying the Gini coefficient index. On the basis of the above understanding, an impartiality and openness of power dispatching model is proposed in this paper based on the Gini coefficient. According to the proposed model:

(1)

The differences among units’ generation energy progresses can be guaranteed in the specified range, which could give consideration to the interests of all the units;

(2)

The balance between economy and fairness can be achieved by adjusting the value of the Gini coefficient, thereby the economic optimizing space in the dispatching could be effectively expanded, and the overall operational economy is improved.

The model proposed in this paper can provide more choices and solutions for the dispatching department, and also provide a reference for the regulatory authorities to formulate relevant policies. Avoid situations where dispatchers make power generation plans based on experience, and the power generation plan is more scientific and accurate. At the same time, the system operation economy, reliability, and fairness could be comprehensively considered using the method proposed in this paper, and the model reduces the total cost of power generation effectively, so that the fairness of the generation progresses of units could be ensured while the overall resources optimizing configuration is implemented.

2. Impartial and Open Dispatching and Gini Coefficient

2.1. Impartial and Open Dispatching

Impartial and open dispatching refers to electric power dispatching institutions following the national laws and regulations and treating all market entities equally in terms of dispatching management and information disclosure in accordance with the principle of fairness and transparency on the premise of satisfying the safety, stability, and economic operation of the power system. Impartial and open dispatching should follow the following principles:

(1)

Abide by the relevant laws and regulations of the state, implement the national energy, environmental and industrial policies, and conscientiously implement the relevant national and industrial standards and regulations;

(2)

Ensure the safety, quality, and economic operation of the power system and give full play to its capabilities to meet the needs of the community;

(3)

Safeguard the legitimate rights and interests of power production enterprises, power grid operating enterprises, and power users;

(4)

Give full play to the role of the market in regulating the allocation of electricity resources.

Impartial and open dispatching is the basic principle and working goal of power dispatching, which is of great significance to guarantee the economic interests of power generation enterprises. At present, according to the impartial and open dispatching, it requires that the power dispatching organization should make rolling adjustments to the completion progress of the annual electricity purchase contracts, and the completion progress of annual generation contracts in the same grid should be roughly equivalent [27].

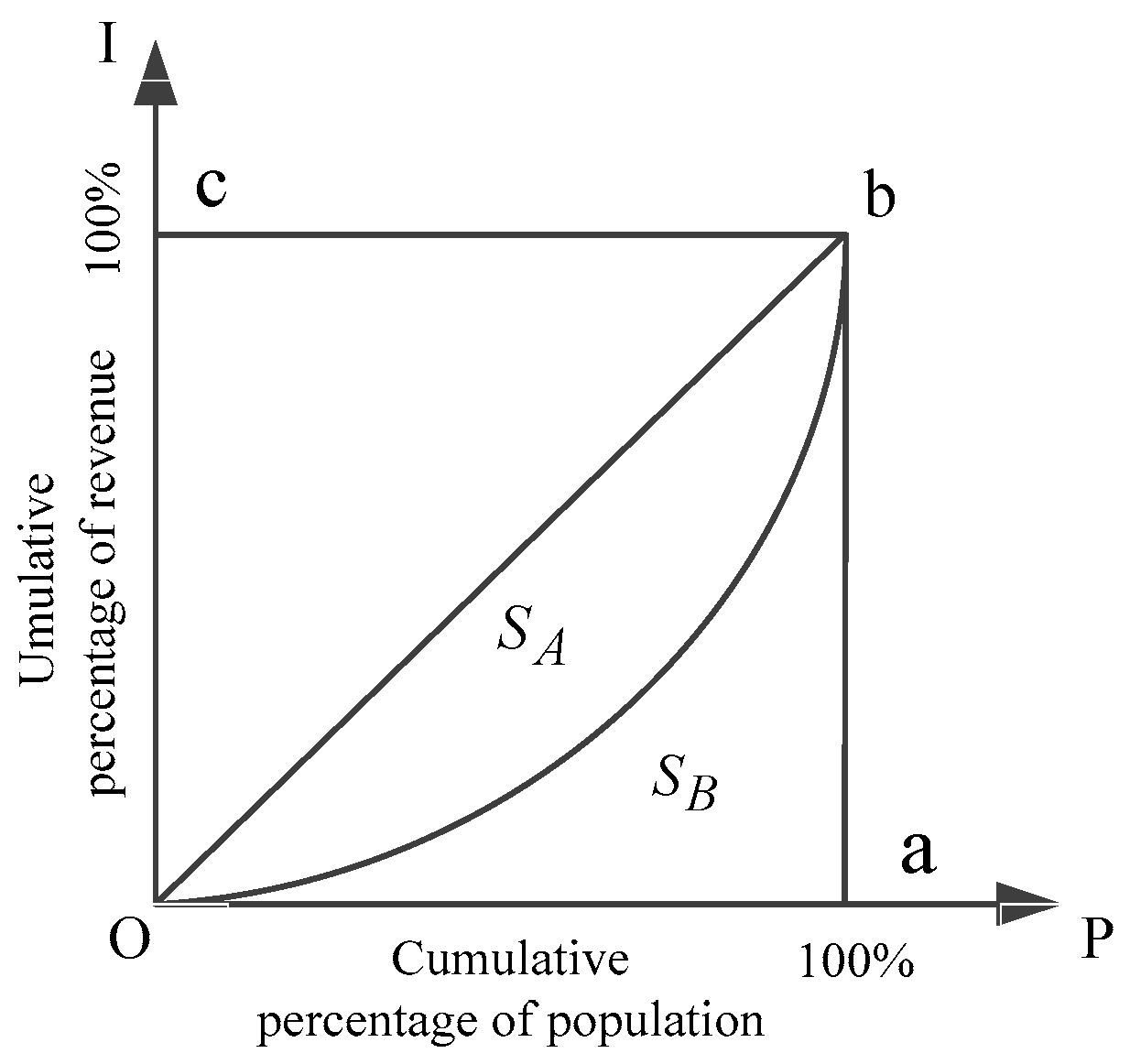
2.2. Gini Coefficient

2.2.1. Concept of Gini Coefficient

The Gini coefficient is an economic statistics indicator that reflects the fairness in general, which is used to reflect whether the distribution of income in social statistics is fair [28,29]. The Lorenz curve is the basis of the Gini coefficient, as shown in Figure 1.

On the basis of the Lorenz curve, the Gini coefficient is as follows:

$$G=\frac{S_A}{S_A+S_B}=\frac{2S_A}{2(S_A+S_B)}=\frac{2S_A}{1}=1-2S_B$$

(1)

The value of the Gini coefficient is equal to twice the value of the area, and is converted to the value of area for the convenience of calculation. It can be found from Equation (1) that, when the area of is zero, the allocation is absolutely fair. The larger the area, the greater the unevenness of the distribution. It is generally believed that, if the Gini coefficient is less than 0.4, it means fairness is basically reached, while if the Gini coefficient is less than 0.3, it means fairness is better.

The calculation methods of Gini coefficient mainly include the direct calculation method, regression curve method, cardinal equal division method, and group decomposition method [19]. Considering the characteristics of the above calculation methods and practical applications, the direct calculation method is applied in this paper, which does not depend on the Lorenz curve. The direct calculation method can ensure that the calculated Gini coefficient value is completely true and accurate without any errors.

2.2.2. Characteristics of the Gini Coefficient

As an index to measure fairness, the Gini coefficient mainly has the following characteristics.

The fairness based on the Gini coefficient does not require all data samples to be identical, but meets certain fairness conditions on the whole, reflecting the overall fairness of samples.

(1)

The Gini coefficient is of good observability, that is, fairness can be determined without comparing any data. When evaluating the fairness, the Gini coefficient ranges from 0 to 1, and the closer it is to 0, the fairer the distribution will be.

(2)

The calculation process of Gini coefficient is the processing of all data collection, which is more universal and reasonable than some other fair indicators such as extreme poor.

(3)

The Gini coefficient is an important international analysis index used to comprehensively investigate the income distribution differences among residents. It is an internationally recognized economic statistical index that can reasonably reflect the overall fairness.

According to the current electricity pricing system in China, the amount of power generation determined by the generation schedule directly determines the operating income of the units. The completing rate of progress of each generator is determined by the power system dispatching. Therefore, it is appropriate to apply the Gini coefficient to the generation dispatching model in the power system to measure the equilibrium degree of economic income among the generating companies.

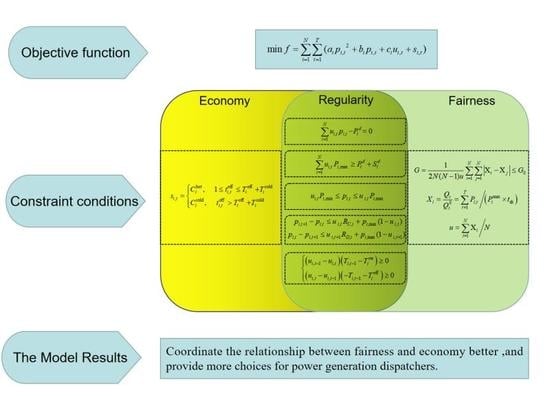
3. Mathematical Model

3.1. Mathematical Modeling

In order to comprehensively coordinate the two indicators, fairness and economy, the constraint method for mathematical modeling is used in this paper. This means the power generation costs are set as the objective function, and the fairness indicator is set as a constraint [30]. Using this method, the economic optimization space of the whole system can be increased to a certain extent, so as to improve the economic benefit of the whole system, on the basis of ensuring that the completion rate of each power generation unit is within the specified range, so as to safeguard the relevant interests of all parties.

3.1.1. Objective Function

According to the above modeling concept, the optimization objective of the impartiality and openness power dispatching model is to minimize the total power generation costs.

$$\min f={\displaystyle \sum _{i=1}^N{\displaystyle \sum _{t=1}^T({a_i{p}_{i,t}}^2}}+b_i{p}_{i,t}+c_i{u}_{i,t}+s_{i,t})$$

(2)

where, $a_i$, $b_i$, and $c_i$ are the power generation cost coefficients of unit $i$; $p_{i,t}$ is the scheduled output of unit $i$ at time interval $t$; $u_{i,t}$ is the commitment state of unit $i$ at time interval $t$; $s_{i,t}$ is the startup and shutdown costs of unit $i$ at time interval $t$; $N$ is the total number of units; and $T$ is the total number of time intervals.

3.1.2. Constraint Conditions

(1)

The power balance constraint of the system

$${\displaystyle \sum _{i=1}^N{u}_{i,t}{p}_{i,t}-P_t^d=0}$$

(3)

where $P_t^d$ is the total system load demand at time interval $t$.

(2)

The spinning reserve constraints of the system

$${\displaystyle \sum _{i=1}^N{u}_{i,t}{P}_{i,\max }}\ge P_t^d+S_t^d$$

(4)

where $P_{i,\max }$ is the maximum output of the unit $i$ at time $t$ and $S_t^d$ is the total spare capacity at time $t$.

(3)

The maximum and minimum output constrains

$$u_{i,t}{P}_{i,\min }\le p_{i,t}\le u_{i,t}{P}_{i,\max }$$

(5)

where $P_{i,\max }$ and $P_{i,\min }$ are the maximum and minimum output of the unit $i$, respectively.

(4)

The ramp rate constraints

$$p_{i,t+1}-p_{i,t}\le u_{i,t}{R}_{U,i}+p_{i,\max }(1-u_{i,t})$$

(6)

$$p_{i,t}-p_{i,t+1}\le u_{i,t+1}{R}_{D,i}+p_{i,\max }(1-u_{i,t+1})$$

(7)

where $R_{U,i}$ and $R_{D,i}$ are the maximum rate of upward ramping/downward ramping of unit $i$ in each time interval, respectively.

(5)

The minimum startup–shutdown time constraints

$$\{\begin{array}{l}\left(u_{i,t-1}-u_{i,t}\right)\left(T_{i,t-1}-T_i^{\mathrm{on}}\right)\ge 0\\ \left(u_{i,t}-u_{i,t-1}\right)\left(-T_{i,t-1}-T_i^{\mathrm{off}}\right)\ge 0\end{array}$$

(8)

where $T_i^{\mathrm{on}}$ and $T_i^{\mathrm{off}}$ are the minimum operating time and minimum offtime of the unit $i$, respectively; and $T_{i,t}$ is the continuous offtime or continuous operating time of the unit $i$ at time $t$.

(6)

The startup–shutdown cost constraint

The start-up costs of cold start and hot start are different. By judging the length of continuous offtime, the specific constraint conditions for cold start and hot start can be determined as follows:

$$s_{i,t}=\{\begin{array}{ll}{C}_i^{\mathrm{hot}},& 1\le t_{i,t}^{\mathrm{off}}\le T_i^{\mathrm{off}}+T_i^{\mathrm{cold}}\\ C_i^{\mathrm{cold}},& t_{i,t}^{\mathrm{off}}>T_i^{\mathrm{off}}+T_i^{\mathrm{cold}}\end{array}$$

(9)

where $t_{i,t}^{\mathrm{off}}$ is the continuous offtime of unit $i$ until time $t-1$; $T_i^{\mathrm{cold}}$ is the cold start time of unit $i$; and $C_i^{\mathrm{hot}}$ and $C_i^{\mathrm{cold}}$ are the costs of the unit $i$ in the case of cold start and hot start, respectively.

(7)

Generation fairness constraint

The Gini coefficient is introduced to model the fairness constraint of the complementation rate of electricity generation.

$$G=\frac{1}{2N(N-1)u}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N\left|{\mathrm{X}}_i-{\mathrm{X}}_j\right|}}\le G_0$$

(10)

where ${\mathrm{X}}_i$ and ${\mathrm{X}}_j$ are the scheduled power completion rates of unit $i$ and unit $j$, respectively; u is the average power completion rates of all units; and $G_0$ is the threshold value of the Gini coefficient, which can be set according to the actual fairness requirement, and the value range is 0~1.

$$X_i=\frac{Q_i}{Q_i^0}={\displaystyle \sum _{t=1}^T{P}_{i,t}}/\left(P_i^{\max }\times t_{\mathrm{sh}}\right)$$

(11)

where $Q_i^0$ and $Q_i$ are the completed electric energy according to the dispatching results and the daily planned energy of unit $i$, respectively.

$$u={\displaystyle \sum _{i=1}^N{\mathrm{X}}_i}/N$$

(12)

Substituting (12) into (10), the final fairness constraint formulation (13) can be obtained after shifting and simplifying.

$${\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^N\left|{\mathrm{X}}_i-{\mathrm{X}}_j\right|}}\le 2G_0(N-1){\displaystyle \sum _{i=1}^N{\mathrm{X}}_i}$$

(13)

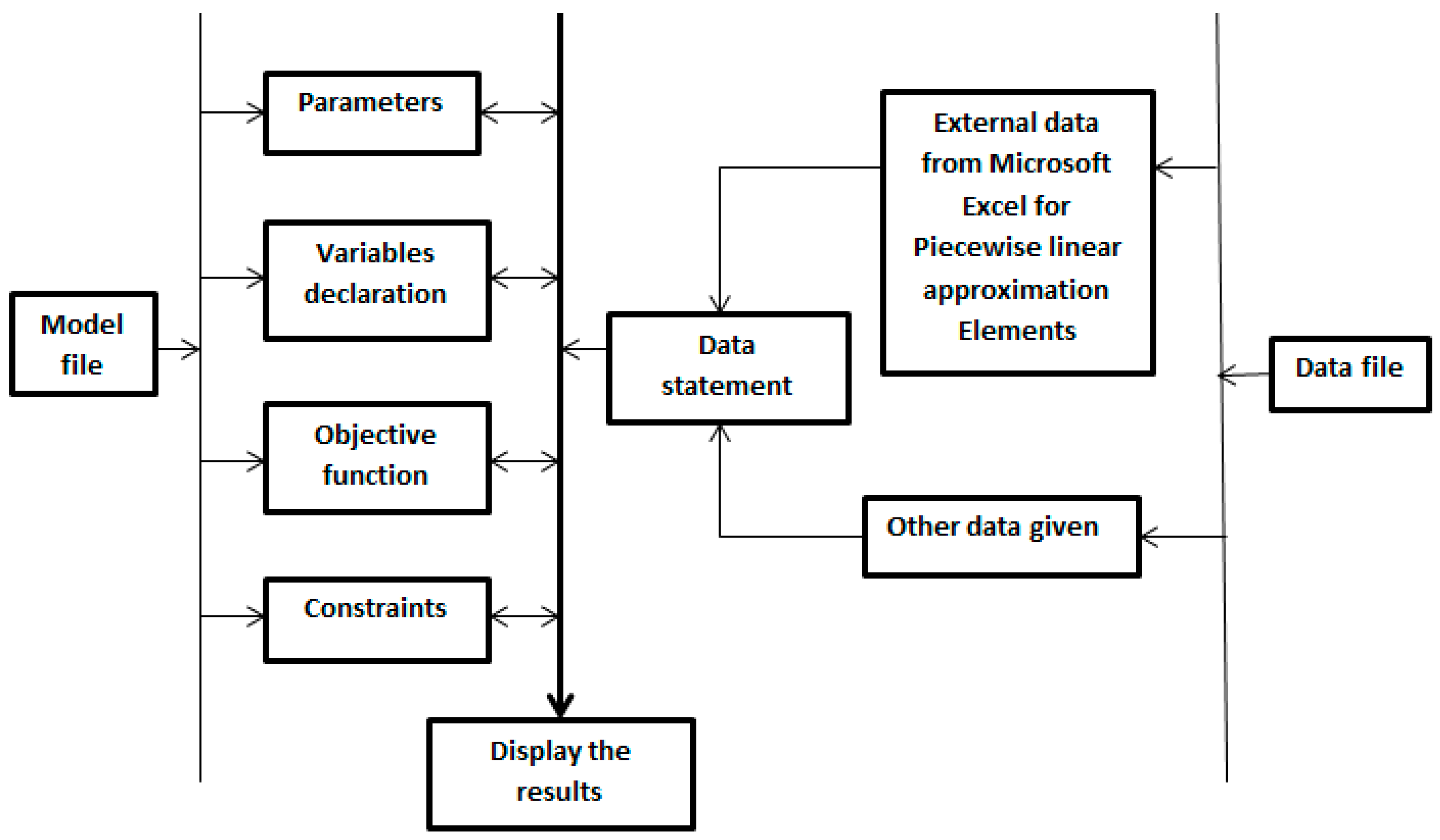
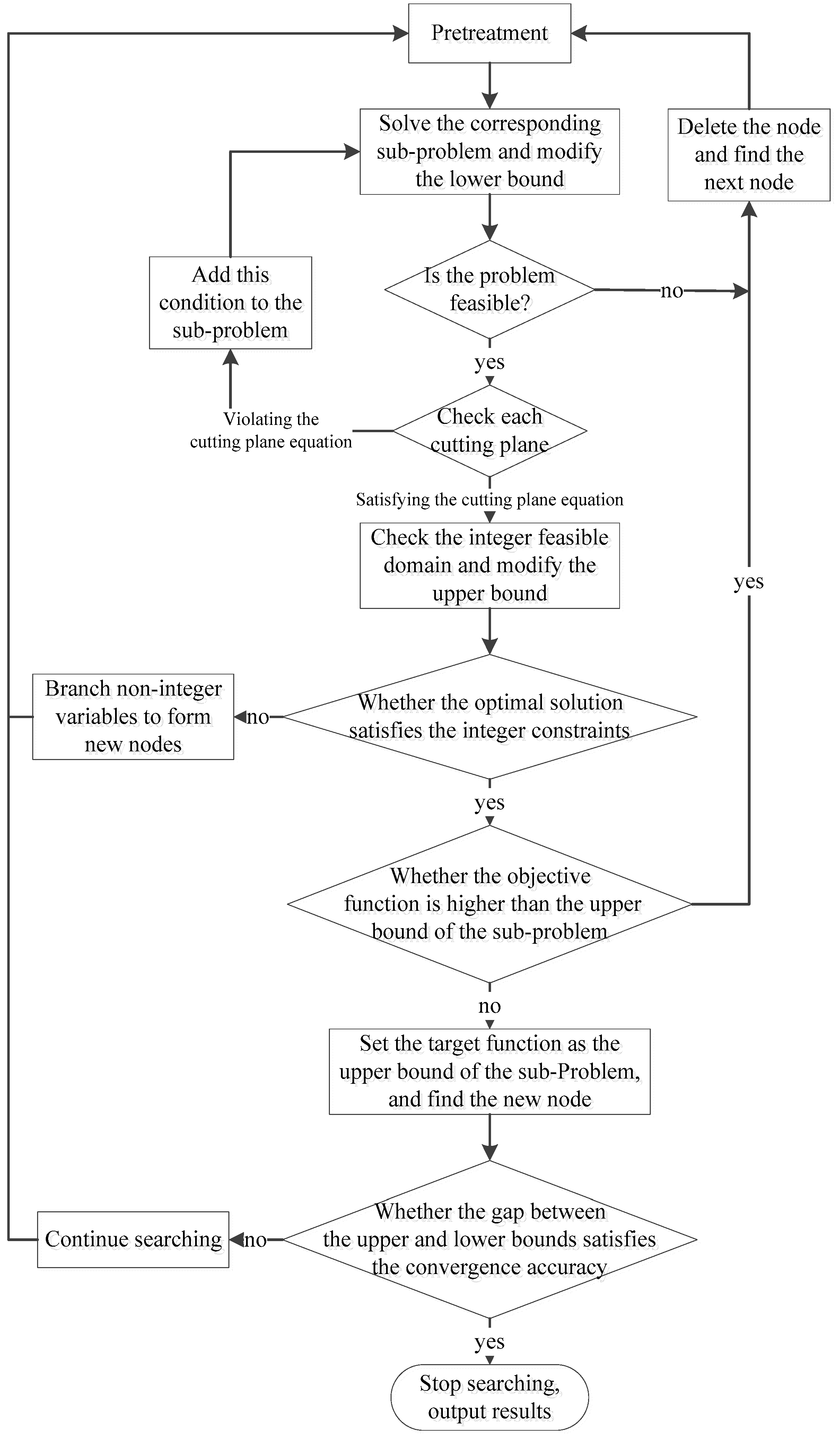
3.2. Solving Method

The model presented in this paper corresponds to the mixed integer quadratic programming problem, and the solving of such a problem usually adopts the branch and bound method [31,32]. In solving a large-scale mixed integer problem, as the quantity of discrete integral variable and complex constraints, the branch and bound method to solve the sub-problem of break out when the number of increased exponentially seriously affected the calculation efficiency; so, in solving combinatorial optimization such as a unit of this kind of large-scale mixed integer programming problem, the efficiency and the results of using a single method are usually unsatisfactory [33,34].

In order to solve the above problems, the business optimization package IBM ILOG CPLEX (IBM, Armonk, New York, NY, USA) is used to solve the model. Figure 2 depicts the schematic arrangement technique used to build wide projects such as the scheduling of hydrothermal power plants using IBM Ilog Cplex Optimization Studio. Two files are created, one for model statement and another for data. External data from Microsoft excel are connected to the optimization software by the use of the appropriate codes. Microsoft Excel is a good tool that can be easily used to write equation and formula; this leads to less effort in executing programming. At the same time, in order to solve the mixed integer programming problem, the CPLEX solver adds the cutting plane method on the branch and bound method to form an improved branch cutting plane method [35,36]. Its solving principle is based on the branch and bound method, and the branch optimization to solve the subproblem cutting plane method is used in the process of feasible solution searching. The binary tree optimization and the choice of branch were reduced, which can effectively reduce calculation time.

The solution flow of mixed integer programming by the CPLEX optimizer is shown in Figure 3. In order to solve the above problems, the paper uses the particular algorithm of the commercial optimization software ILOG CPLEX.

4. Simulation and Analysis

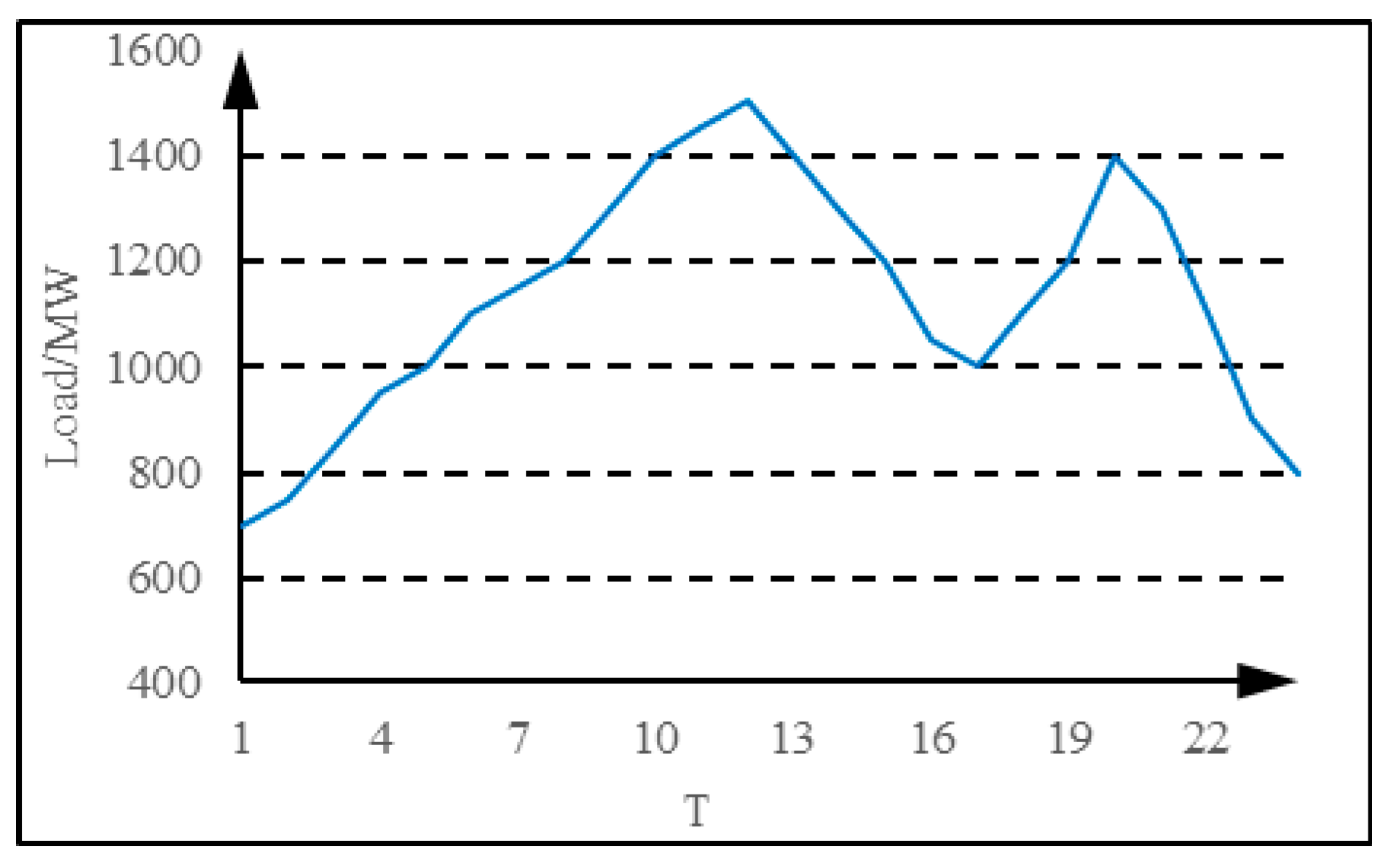
4.1. Simulation Condition

There are 10 units in the test system. The rationality and feasibility of the proposed model are verified by analyzing the simulation results, and the superiority is verified by comparing with the simulation results of other models. The parameters of units in the system are shown in

Table 1. Units’ parameters. MW, h, $.

Unit No.	Pmax	Pmin	$T_i^{\mathrm{on}}$	$T_i^{\mathrm{off}}$	$T_{\mathrm{inis}}$	$T_{\mathrm{cold}}$	a	b	c	${\alpha }_i$	${\beta }_i$	Rup
1	455	150	8	8	8	5	0.00048	16.19	1000	4500	9000	80
2	455	150	8	8	8	5	0.00031	17.26	970	5000	10,000	80
3	130	20	5	5	−5	4	0.00200	16.60	700	550	1100	20
4	130	20	5	5	−5	4	0.00211	16.50	680	560	1120	20
5	162	25	6	6	−6	4	0.00398	19.70	450	900	1800	30
6	80	20	3	3	−3	2	0.00712	22.26	370	170	340	10
7	85	25	3	3	−3	2	0.00079	27.74	480	260	520	10
8	55	10	1	1	−1	0	0.00413	25.92	660	30	60	5
9	55	10	1	1	−1	0	0.00222	27.27	665	30	60	5
10	55	10	1	1	−1	0	0.00173	27.79	670	30	60	5

, respectively. The simulation period is set to 30 days (one month), and the simulation step size (unit period) is set to 1 h. The calculation results of one typical day are shown below owing to page limit, the total system load of each period on this typical day is shown in Figure 4. The value of spinning reserve is set to 10% of the load demand, and the threshold value of Gini coefficient G0 is set to 0.4.

The simulation is programmed, run, and processed on a PC with a CPU of Intel(R) Pentium(R) CPU G630 @ 2.70 GHz, and the RAM is 4.0 G.

4.2. Simulation Results

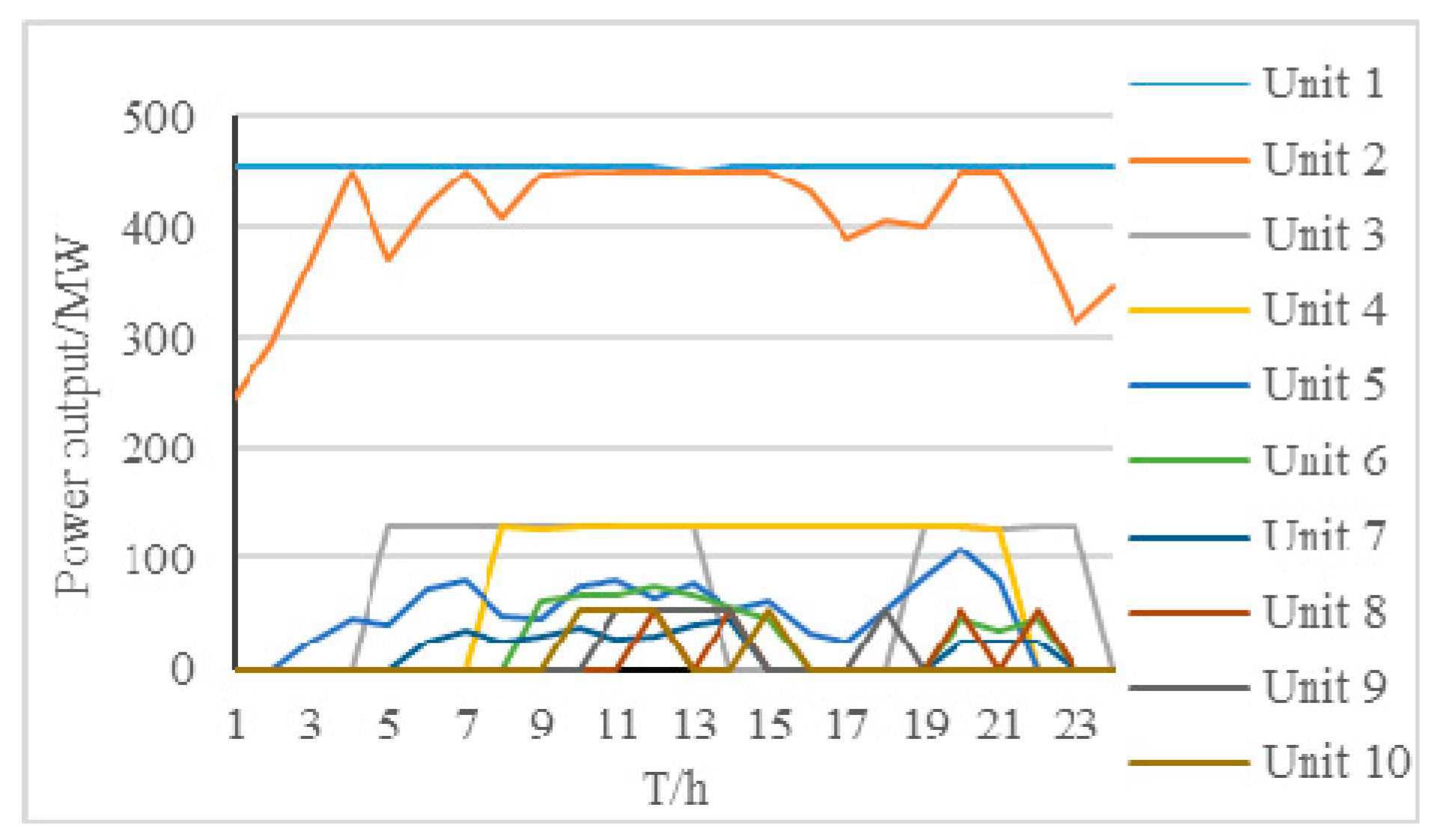
4.2.1. Unit Commitment and Output Schedule

First, it is simulated with the Gini coefficient set to 0.3. The total power generation cost was $17,468,276, and the program running time was 4.3 s. For the typical day, the unit commitment schedule and load dispatching schedule are shown in Figure 5 and Figure 6, respectively. From the 24 h generation schedule, it can be seen that, for large-scale units (units 1 and 2), there is no shutdown and the generation output did not change significantly during load following. The stability of output power can give full play to the operating efficiency of large-scale units. The small unit can meet the constraint demand of system load change through progressive output adjustment. Because of its lower start-up and shutdown cost, it is more suitable for following load fluctuation. Thus, the economy of the overall system operation can be ensured.

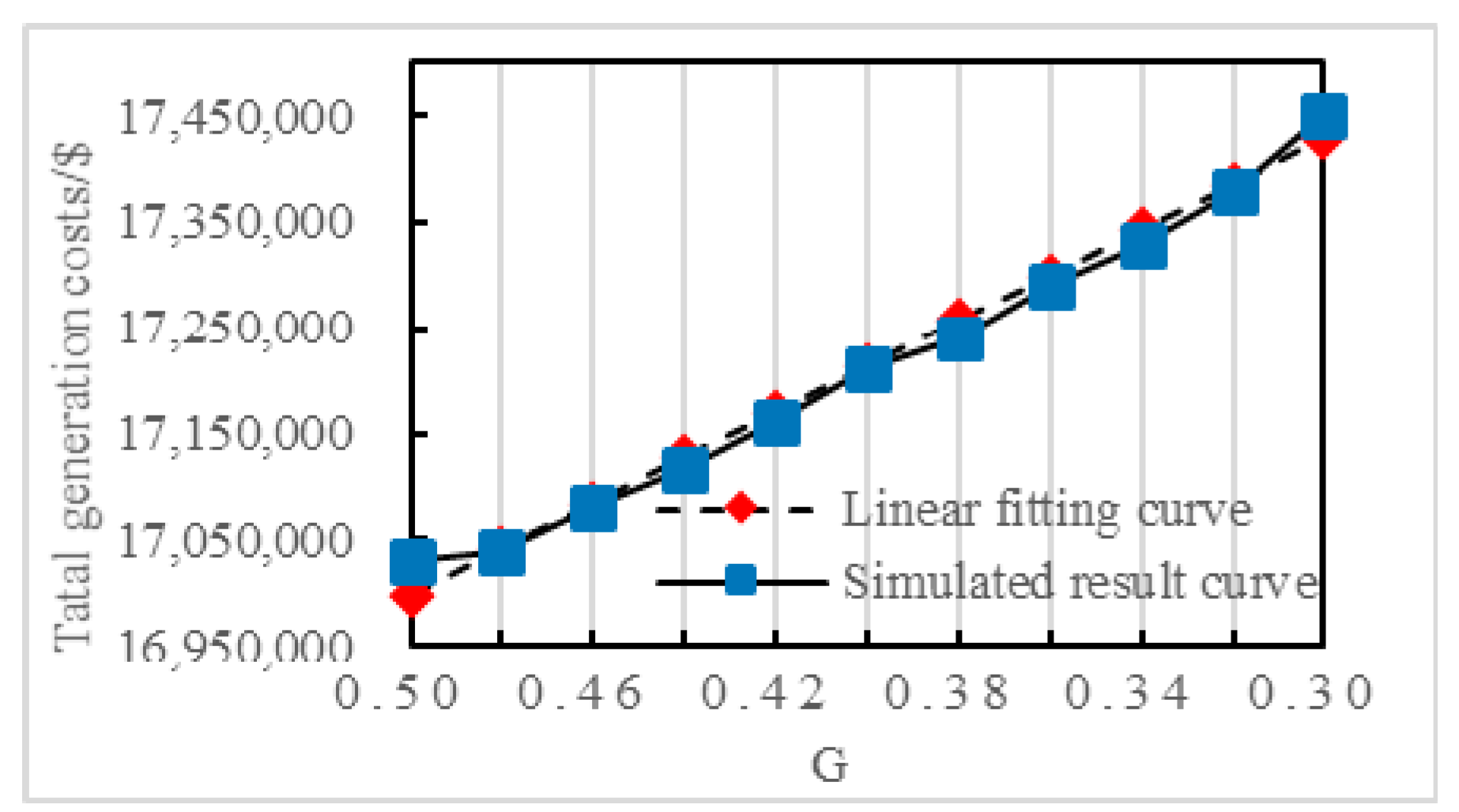
4.2.2. Simulation Results with Different Threshold Values of Gini Coefficient

Generally, the Gini coefficient value 0.4 is taken as the “warning line” to measure the fairness of economic income. Therefore, in the case studies, the Gini coefficient value is set around 0.4 to study the changes in fairness and operation economy. Specifically, within the range of 0.3~0.5, the threshold value of Gini coefficient is selected at an interval of 0.02, so as to study the changes in the objective function value (total cost). The changes of the total costs of power generation with different threshold value of Gini coefficient can be found in Figure 7. In order to more intuitively reflect and display the relationship between the two, it is drawn as a line graph.

From Figure 7, it can be seen that the relationship between the total cost and the Gini coefficient is negatively correlated. That is, with the increase in Gini coefficient value, the optimization space of the model becomes larger, so that there could be a more economical way to revise the model. However, owing to the increase in Gini coefficient, the fairness of power system operation is weaker.

The numerical simulation results show that the relationship between the Gini coefficient and the total power generation cost is approximately linear. Specifically, with the Gini coefficient being reduced by 0.05, correspondingly, the total cost increases by about $135,130, accounting for 1% to 2% of the total power generation cost.

4.2.3. Simulation Results with Different Dispatching Modes

In order to compare the effect of three different dispatching methods, which are the traditional economic dispatching model, the existing impartial and open scheduling model and the Gini coefficient-based impartial and open dispatching model are proposed in this paper, the power system operation is simulated according to the three methods respectively, and the results and effect of fairness and economy are compared and analyzed.

In the traditional economic dispatching, minimizing total power generation cost is taken as the objective function, and the fairness is not considered. The objective function of existing impartial and open dispatching model is to minimize the standard deviation of the completion rate of electric energy of all the units. The results of relevant fairness and economy can be obtained in Figure 7.

It can be seen from Figure 8 that, when using the traditional economic dispatching model, the lowest total cost of power generation can be obtained, while the generation overall fairness among the generators is not ideal. The results when using the traditional “impartial and open” dispatching model are more fair because it pays more attention to treat each unit equally, but the total costs are the highest. Using the Gini coefficient-based “impartial and open” dispatching model proposed in this paper, the operation economic could be improved on the basis of ensuring fairness to some extent because of the coordination of the two indicators.

It can be found combined with Figure 7 that, when the threshold value of Gini coefficient with the method presented in this paper is set as equal to the Gini coefficient values of the other two models, the total costs are the same, which shows that the model proposed in this paper is an extended model of the existing dispatching models. Different levels of balance between economy and equity can be achieved by adjusting threshold values of Gini coefficient according to different levels of fairness demand in actual system operation, so as to provide more choices for scheduling department, to realize the goal of fully and reasonably allocating scheduling resources under the “impartial and open scheduling principle”.

5. Conclusions

In order to achieve the balance between the fairness and economy of power system operation, an impartial and open dispatching model based on the Gini coefficient is proposed in this paper. The theoretical analysis and simulation results show the following:

• The proposed impartial and open dispatching model based on the Gini coefficient is an extended mode of the conventional dispatching model. The optimization space of system operation economy could be effectively improved on the premise of specifying fairness requirement by introducing the Gini coefficient in economics as an index to measure the fairness of electric energy completed progress in the form of constraint conditions.
• In power system operation, different levels of balance between economy and equity can be achieved by adjusting the threshold value of the Gini coefficient according to different levels of fairness demand, so as to provide more choices for scheduling department. Better balance between fairness and economy could be realized to improve the overall system operation efficiency. The recognition of the generation companies to the impartial and open scheduling scheme could be improved because of the use of the internationally recognized Gini coefficient indicator, which has the recommended fairness value range.
• The research in this paper is limited to the theoretical study of models and methods, and the proposed method cannot meet the computational requirements of optimal scheduling of large-scale power systems in terms of computational speed and computational convergence. However, the model presented in this paper has been put into trial operation in the monthly power generation scheduling in a provincial power grid in China. The next study content of the authors is to simplify the model and algorithm so that they could be applied to the actual dispatching work.