A Novel Market Clearing and Safety Checking Method for Multi-Type Units That Considers Flexible Loads
Abstract
:1. Introduction
2. Flexible Load Modeling and Its Mechanism
2.1. Flexible Load Modeling
2.1.1. Reducible Loads
2.1.2. Convertible Loads
2.1.3. Shiftable Loads
2.2. Mechanism Design
2.2.1. General Framework
2.2.2. Business Process
3. Market Clearing and Safety Checking Model
3.1. Market Clearing Model that Considers the Convertible Load
3.1.1. Generator Bidding
3.1.2. Demand Side Bidding
3.1.3. Market Clearing Model
- (1)
- System power balance constraint
- (2)
- Upper and lower limits of the unit
- (3)
- Climbing constraint of the unit
- (4)
- Convertible load constraint
3.2. Safety Checking Model That Considers the Reducible Loads
- (1)
- Balance between the adjustment and reduction
- (2)
- Upper and lower limit constraints before and after the unit adjustment.
- (3)
- Upper and lower limit constraint of the line transmission power..
- (4)
- Reduce load constraints.
- (5)
- Power distribution factor constraints
4. Solution Method
4.1. Linearization of the Cost Function
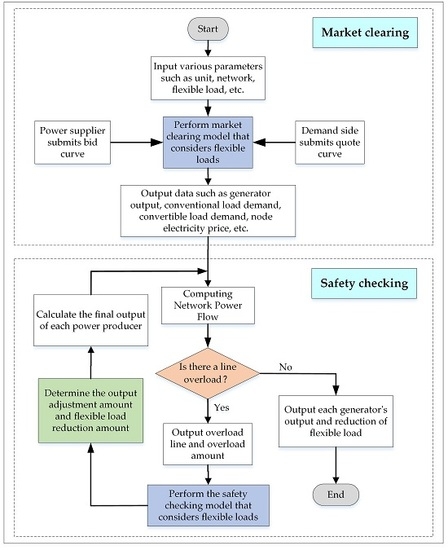
4.2. Market Clearing and Safety Checking Process
5. Case Analysis
5.1. Basic Date
5.2. Market Clearing
5.3. Safety Checking
5.4. Economic Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shareef, H.; Ahmed, M.S.; Mohamed, A.; Al Hassan, E. Review on Home Energy Management System Considering Demand Responses, Smart Technologies, and Intelligent Controllers. IEEE Access 2018, 6, 24498–24509. [Google Scholar] [CrossRef]
- Bahrami, S.; Sheikhi, A. From Demand Response in Smart Grid toward Integrated Demand Response in Smart Energy Hub. IEEE Trans. Smart Grid 2015, 7, 650–658. [Google Scholar] [CrossRef]
- Wang, K.; Hu, X.; Li, H.; Li, P.; Zeng, D.; Guo, S. A Survey on Energy Internet Communications for Sustainability. IEEE Trans. Sustain. Comput. 2017, 2, 231–254. [Google Scholar] [CrossRef]
- Wang, D.; Liu, L.; Jia, H.; Wang, W.; Zhi, Y.; Meng, Z.; Zhou, B. Tianjin University Review of key problems related to integrated energy distribution systems. CSEE J. Power Energy Syst. 2018, 4, 130–145. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Liu, G.; Shi, D.; Yi, Z.; Wang, Z.; Liu, G. Thermostatic Load Control for System Frequency Regulation Considering Daily Demand Profile and Progressive Recovery. IEEE Trans. Smart Grid 2019, 10, 6259–6270. [Google Scholar] [CrossRef]
- Tu, J.; Zhou, M.; Cui, H.; Li, F. An Equivalent Aggregated Model of Large-Scale Flexible Loads for Load Scheduling. IEEE Access 2019, 7, 143431–143444. [Google Scholar] [CrossRef]
- Liu, F.; Bie, Z.; Liu, S.; Li, G. Framework Design Transaction Mechanism and Key Issues of Energy Internet Market. Autom. Electr. Power Syst. 2018, 42, 114–123. [Google Scholar]
- Lezama, F.; Soares, J.; Hernandez-Leal, P.; Kaisers, M.; Pinto, T.; Vale, Z. Local Energy Markets: Paving the Path Toward Fully Transactive Energy Systems. IEEE Trans. Power Syst. 2019, 34, 4081–4088. [Google Scholar] [CrossRef] [Green Version]
- Lezama, F.; Soares, J.; Canizes, B.; Vale, Z. Flexibility management model of home appliances to support DSO requests in smart grids. Sustain. Cities Soc. 2020, 55, 102048. [Google Scholar] [CrossRef]
- Borenstein, S.; Bushnell, J.; Stoft, S. The Competitive Effects of Transmission Capacity in a Deregulated Electricity Industry. Natl. Bur. Econ. Res. 2000, 31, 294–325. [Google Scholar] [CrossRef] [Green Version]
- Di Somma, M.; Graditi, G.; Siano, P. Optimal Bidding Strategy for a DER Aggregator in the Day-Ahead Market in the Presence of Demand Flexibility. IEEE Trans. Ind. Electron. 2018, 66, 1509–1519. [Google Scholar] [CrossRef]
- Liu, P.; Ding, T.; He, Y.; Chen, T. Integrated Demand Response in Multi-Energy Market Based on Flexible Loads Classification. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 4346–4350. [Google Scholar]
- Chen, T.; Pourbabak, H.; Liang, Z.; Su, W. An Integrated eVoucher Mechanism for Flexible Loads in Real-Time Retail Electricity Market. IEEE Access 2017, 5, 2101–2110. [Google Scholar] [CrossRef]
- Hanif, S.; Creutzburg, P.; Gooi, H.B.; Hamacher, T. Pricing Mechanism for Flexible Loads Using Distribution Grid Hedging Rights. IEEE Trans. Power Syst. 2019, 34, 4048–4059. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Optimal Posturing in Day-Ahead Market Clearing for Uncertainties Considering Anticipated Real-Time Adjustment Costs. IEEE Syst. J. 2013, 9, 177–190. [Google Scholar] [CrossRef]
- Ye, H.; Ge, Y.; Shahidehpour, M.; Li, Z. Uncertainty Marginal Price, Transmission Reserve, and Day-Ahead Market Clearing With Robust Unit Commitment. IEEE Trans. Power Syst. 2017, 32, 1782–1795. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Yan, Z.; Chen, S.; Yang, L.; Li, X. Two-stage market clearing approach to mitigate generator collusion in Eastern China electricity market via system dynamics method. IET Gener. Transm. Distrib. 2019, 13, 3346–3353. [Google Scholar] [CrossRef]
- Tan, F.Z.; Chen, G.J.; Zhao, J.B. Joint optimization model of peak-valley time-of-use electricity price based on energy-saving dispatch oriented electricity generation and electricity sales. Proc. CSEE 2009, 29, 55–62. [Google Scholar]
- Streiffert, D.; Philbrick, R.; Ott, A. A mixed integer programming solution for market clearing and reliability analysis. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 3, pp. 2724–2731. [Google Scholar]
- Xavier, Á.S.; Qiu, F.; Wang, F.; Thimmapuram, P.R. Transmission Constraint Filtering in Large-Scale Security-Constrained Unit Commitment. IEEE Trans. Power Syst. 2019, 34, 2457–2460. [Google Scholar] [CrossRef]
- Chen, S.; Cheng, R.S. Operating Reserves Provision from Residential Users through Load Aggregators in Smart Grid: A Game Theoretic Approach. IEEE Trans. Smart Grid 2017, 10, 1588–1598. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-Khah, M.; Catalao, J.P.S. A Decentralized Electricity Market Scheme Enabling Demand Response Deployment. IEEE Trans. Power Syst. 2018, 33, 4218–4227. [Google Scholar] [CrossRef]
- Wang, S.; Bi, S.; Zhang, Y.J. Demand Response Management for Profit Maximizing Energy Loads in Real-Time Electricity Market. IEEE Trans. Power Syst. 2018, 33, 6387–6396. [Google Scholar] [CrossRef]
- Kong, P.-Y.; Karagiannidis, G.K. Charging Schemes for Plug-In Hybrid Electric Vehicles in Smart Grid: A Survey. IEEE Access 2016, 4, 6846–6875. [Google Scholar] [CrossRef]
- Baldick, R. Electricity Market Equilibrium Models: The Effect of Parameterization. IEEE Power Eng. Rev. 2002, 22, 53. [Google Scholar] [CrossRef]
- De Paola, A.; Angeli, D.; Strbac, G. Price-Based Schemes for Distributed Coordination of Flexible Demand in the Electricity Market. IEEE Trans. Smart Grid 2017, 8, 3104–3116. [Google Scholar] [CrossRef]
- Prabavathi, M.; Gnanadass, R. Electric power bidding model for practical utility system. Alex. Eng. J. 2018, 57, 277–286. [Google Scholar] [CrossRef]
- Verbič, G.; Canizares, C.A. Probabilistic Optimal Power Flow in Electricity Markets Based on a Two-Point Estimate Method. IEEE Trans. Power Syst. 2006, 21, 1883–1893. [Google Scholar] [CrossRef]
- Morales, J.M.; Ruiz, J.P. Point Estimate Schemes to Solve the Probabilistic Power Flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Luenberger, D.G. Linear and Nonlinear Programming, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Floudas, C.A. Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications; Oxford Univ. Press: New York, NY, USA, 1995. [Google Scholar]
- Chazarra, M.; Perez-Diaz, J.I.; Garcia-Gonzalez, J. Value of perfect information of spot prices in the joint energy and reserve hourly scheduling of pumped storage plants. In Proceedings of the 2016 13th International Conference on the European Energy Market (EEM), Porto, Portugal, 6–9 June 2016; pp. 1–6. [Google Scholar]
- Sotkiewicz, P.M.; Vignolo, J.M. Nodal Pricing for Distribution Networks: Efficient Pricing for Efficiency Enhancing DG. IEEE Trans. Power Syst. 2006, 21, 1013–1014. [Google Scholar] [CrossRef]
- Fernandez-Blanco, R.; Arroyo, J.M.; Alguacil, N. On the Solution of Revenue- and Network-Constrained Day-Ahead Market Clearing Under Marginal Pricing—Part II: Case Studies. IEEE Trans. Power Syst. 2017, 32, 220–227. [Google Scholar] [CrossRef]














| Power Plant | a | b | Lower Limit(MW) | Upper Limit(MW) | Climbing Uphill (MW/h) | Downhill (MW/h) |
|---|---|---|---|---|---|---|
| 1 | 0.00021 | 0.32 | 315.2 | 3152 | 2101 | 2101 |
| 24 | 0.00016 | 0.32 | 117 | 1170 | 780 | 780 |
| 26 | 6.6 × 10−5 | 0.325 | 117 | 1170 | 780 | 780 |
| 36 | 0.00016 | 0.29 | 44 | 440 | 293 | 293 |
| 52 | 6.2 × 10−5 | 0.35 | 196 | 1960 | 1307 | 1307 |
| 63 | 0.00005 | 0.01 | −1200 | 1200 | 1200 | 1200 |
| 68 | 0.00021 | 0.225 | 500 | 5000 | 3333 | 3333 |
| 69 | 0.00016 | 0.29 | 268 | 2680 | 1787 | 1787 |
| 73 | 0.00005 | 0.09 | 415.2 | 4152 | 2768 | 2768 |
| Power Plant | Quote Factor | Power Plant | Quote Factor |
|---|---|---|---|
| 1 | 1.03 | 63 | 1.01 |
| 24 | 1.02 | 68 | 1.02 |
| 26 | 0.98 | 69 | 0.98 |
| 36 | 0.96 | 73 | 1.00 |
| 52 | 0.99 | - | - |
| Node | Quote Factor | Node | Quote Factor | Node | Quote Factor |
|---|---|---|---|---|---|
| 2 | 1.03 | 25 | 1.01 | 48 | 1.03 |
| 3 | 1.02 | 26 | 0.99 | 49 | 1.02 |
| 4 | 0.98 | 27 | 1.01 | 50 | 0.98 |
| 5 | 0.96 | 28 | 1.03 | 51 | 0.96 |
| 6 | 0.99 | 29 | 1.02 | 52 | 0.99 |
| 7 | 1.01 | 30 | 0.98 | 53 | 1.01 |
| 8 | 1.03 | 31 | 0.96 | 54 | 1.03 |
| 9 | 1.02 | 32 | 0.99 | 55 | 1.02 |
| 10 | 0.98 | 33 | 1.01 | 56 | 0.98 |
| 11 | 0.96 | 34 | 1.03 | 57 | 0.96 |
| 12 | 0.99 | 35 | 1.02 | 58 | 0.99 |
| 13 | 1.01 | 36 | 0.98 | 59 | 1.01 |
| 14 | 1.03 | 37 | 0.96 | 60 | 1.03 |
| 15 | 1.02 | 38 | 0.99 | 61 | 1.02 |
| Plant | Case One(MW) | Case Two(MW) | Lower Limit(MW) | Upper Limit(MW) | ||
|---|---|---|---|---|---|---|
| Adjustment amount | Output after Adjustment | Adjustment Amount | Output after Adjustment | |||
| 1 | 0 | 2544. 52 | 0 | 2544.52 | 415.2 | 4152 |
| 24 | 0 | 1170.00 | 0 | 1170.00 | 117 | 1170 |
| 26 | 0 | 1170.00 | 0 | 1170.00 | 117 | 1170 |
| 36 | 0 | 440.00 | 0 | 440.00 | 44 | 440 |
| 52 | −423.16 | 1536. 84 | −417.55 | 1542.45 | 196 | 1960 |
| 63 | 423.16 | −776.84 | 285.27 | −914.73 | −1200 | 1200 |
| 68 | 0 | 3039.67 | 0 | 3039.67 | 600 | 6000 |
| 69 | 0 | 2160.00 | 0 | 2160.00 | 268 | 2680 |
| 73 | 0 | 1660. 80 | 0 | 1660.80 | 415.2 | 4152 |
| Cost | Unit Adjustment Cost (yuan) | Out-Of-Load Cost (yuan) | Total Cost (yuan) |
|---|---|---|---|
| Case One | 846,300 | 0 | 846,300 |
| Case Two | 702,800 | 132,300 | 835,100 |
| Difference | 143,500 | −132,300 | 11,200 |
| Case | Increase Capacity (MW) | Reduce Capacity (MW) |
|---|---|---|
| Case One | 6779.01 | 10,833.27 |
| Case Two | 7102.69 | 10,833.27 |
| Difference | 323.68 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, D.; Chen, W.; Zhang, C. A Novel Market Clearing and Safety Checking Method for Multi-Type Units That Considers Flexible Loads. Energies 2020, 13, 3771. https://doi.org/10.3390/en13153771
Hua D, Chen W, Zhang C. A Novel Market Clearing and Safety Checking Method for Multi-Type Units That Considers Flexible Loads. Energies. 2020; 13(15):3771. https://doi.org/10.3390/en13153771
Chicago/Turabian StyleHua, Dong, Wutao Chen, and Cong Zhang. 2020. "A Novel Market Clearing and Safety Checking Method for Multi-Type Units That Considers Flexible Loads" Energies 13, no. 15: 3771. https://doi.org/10.3390/en13153771
APA StyleHua, D., Chen, W., & Zhang, C. (2020). A Novel Market Clearing and Safety Checking Method for Multi-Type Units That Considers Flexible Loads. Energies, 13(15), 3771. https://doi.org/10.3390/en13153771