Pressure Loss Reduction in an Innovative Directional Poppet Control Valve
Abstract
1. Introduction
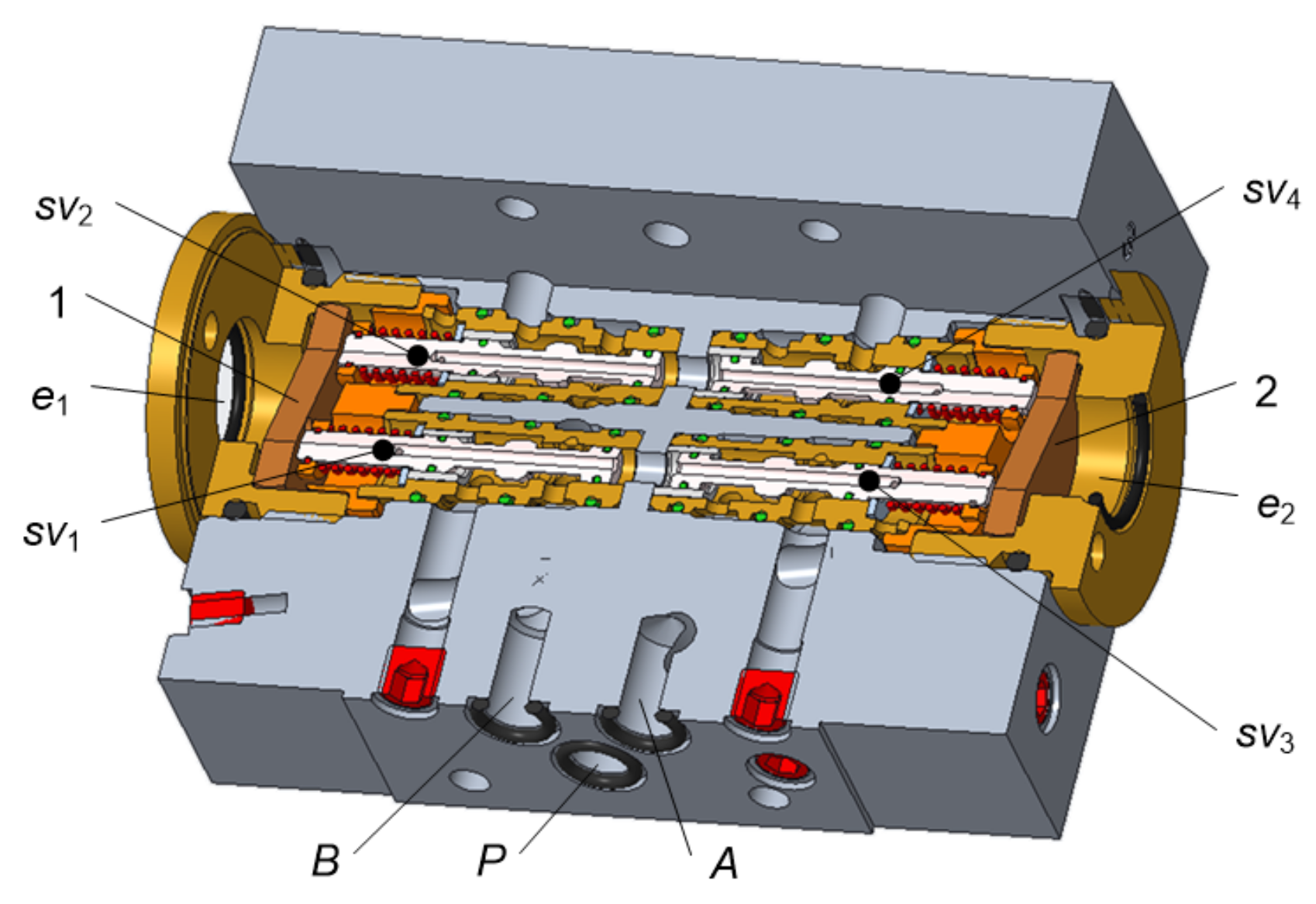
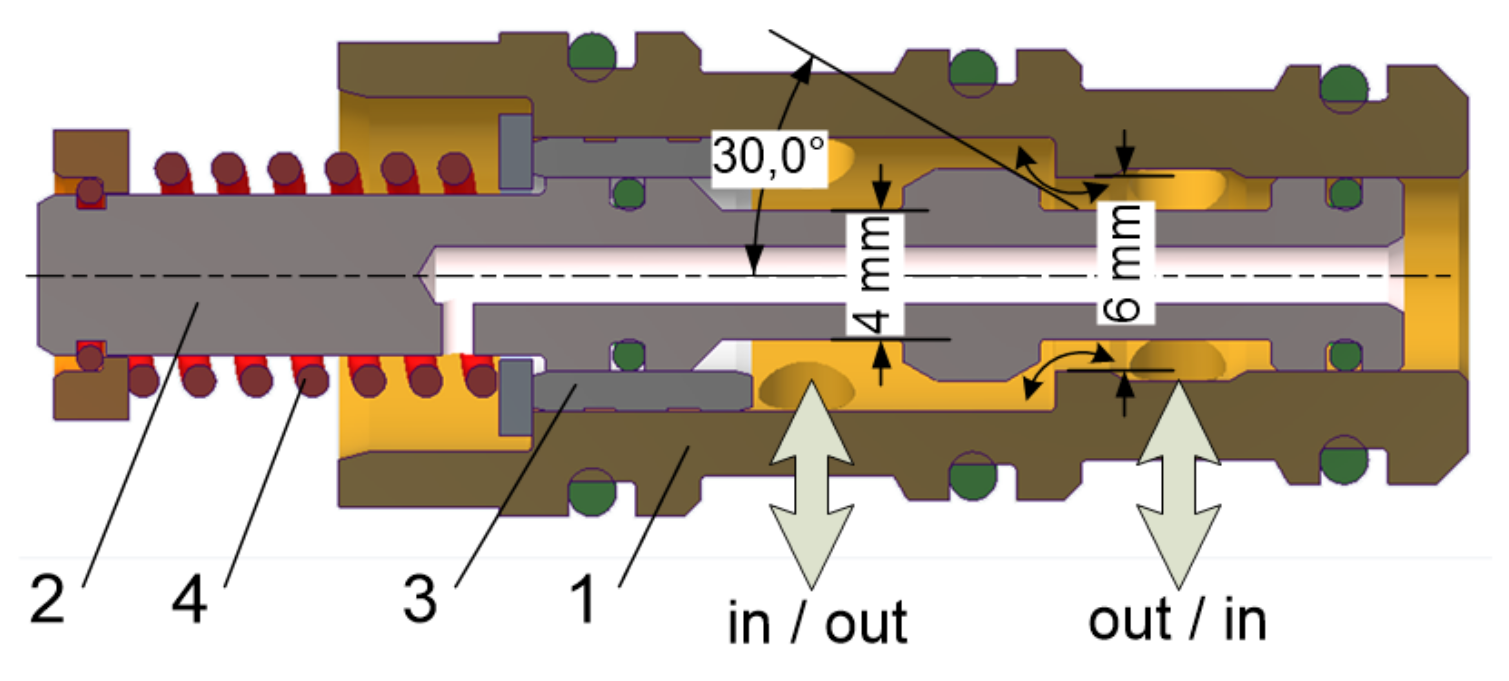
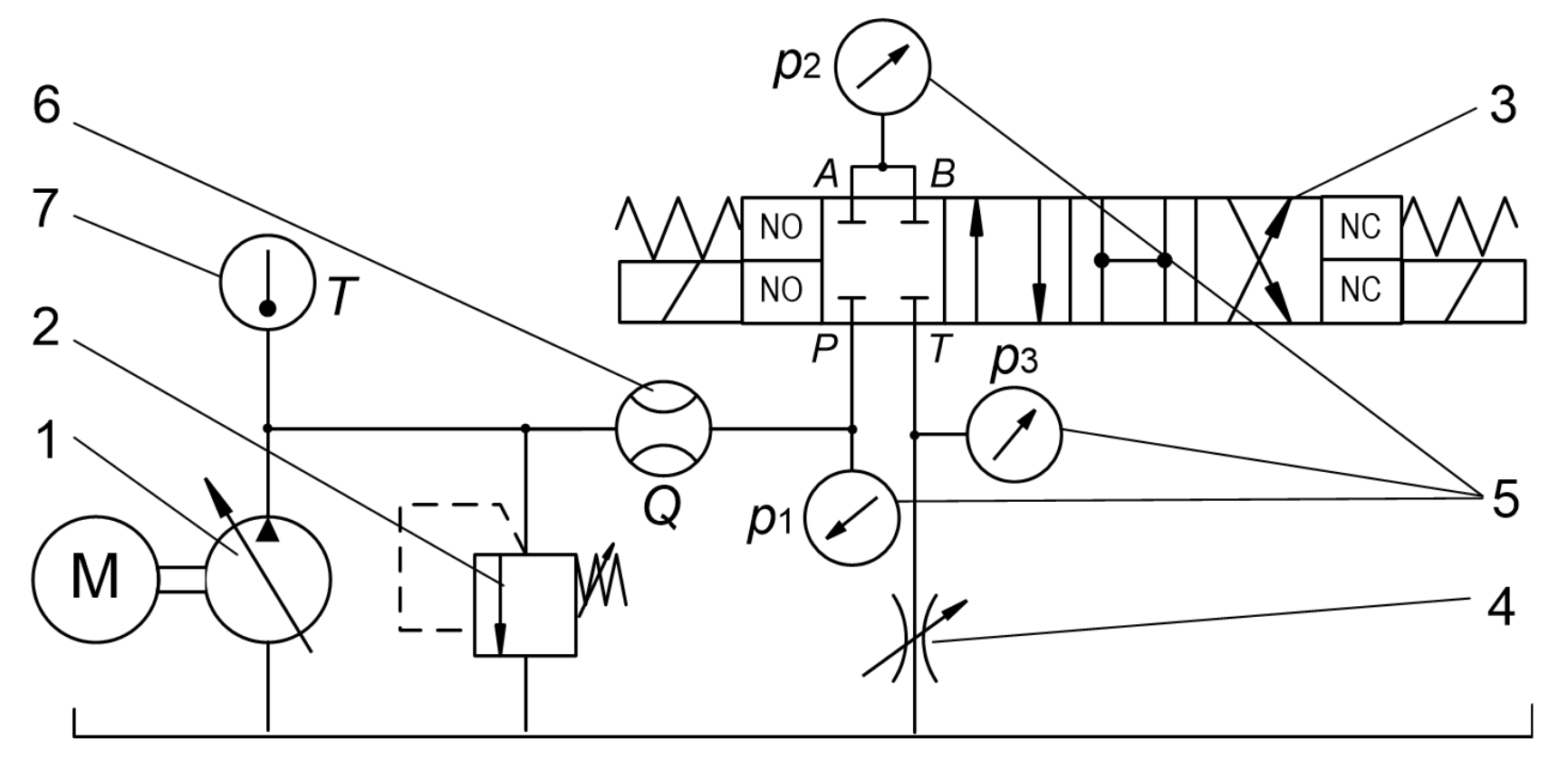
2. Working Principle of the Valve
3. Flow Analysis by Means of CFD Method
3.1. Geometrical Fluid Model
3.2. Discrete Model
3.3. CFD Model Parameters
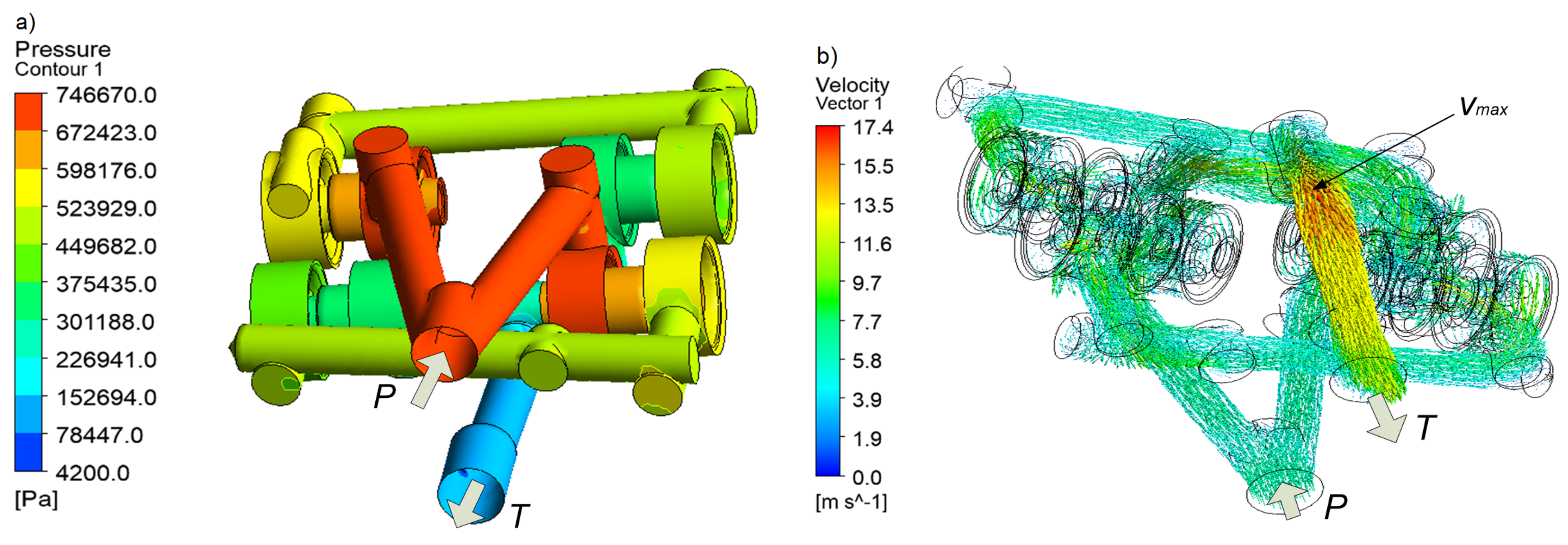
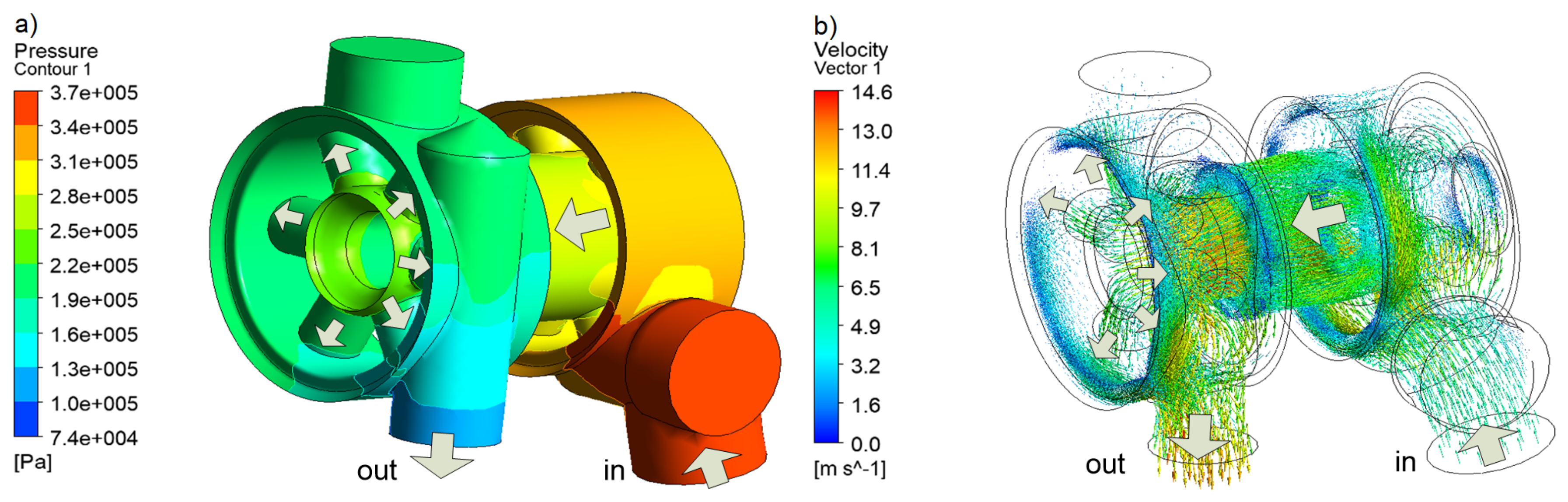
3.4. Results of CFD Simulations
3.4.1. and Flow Paths
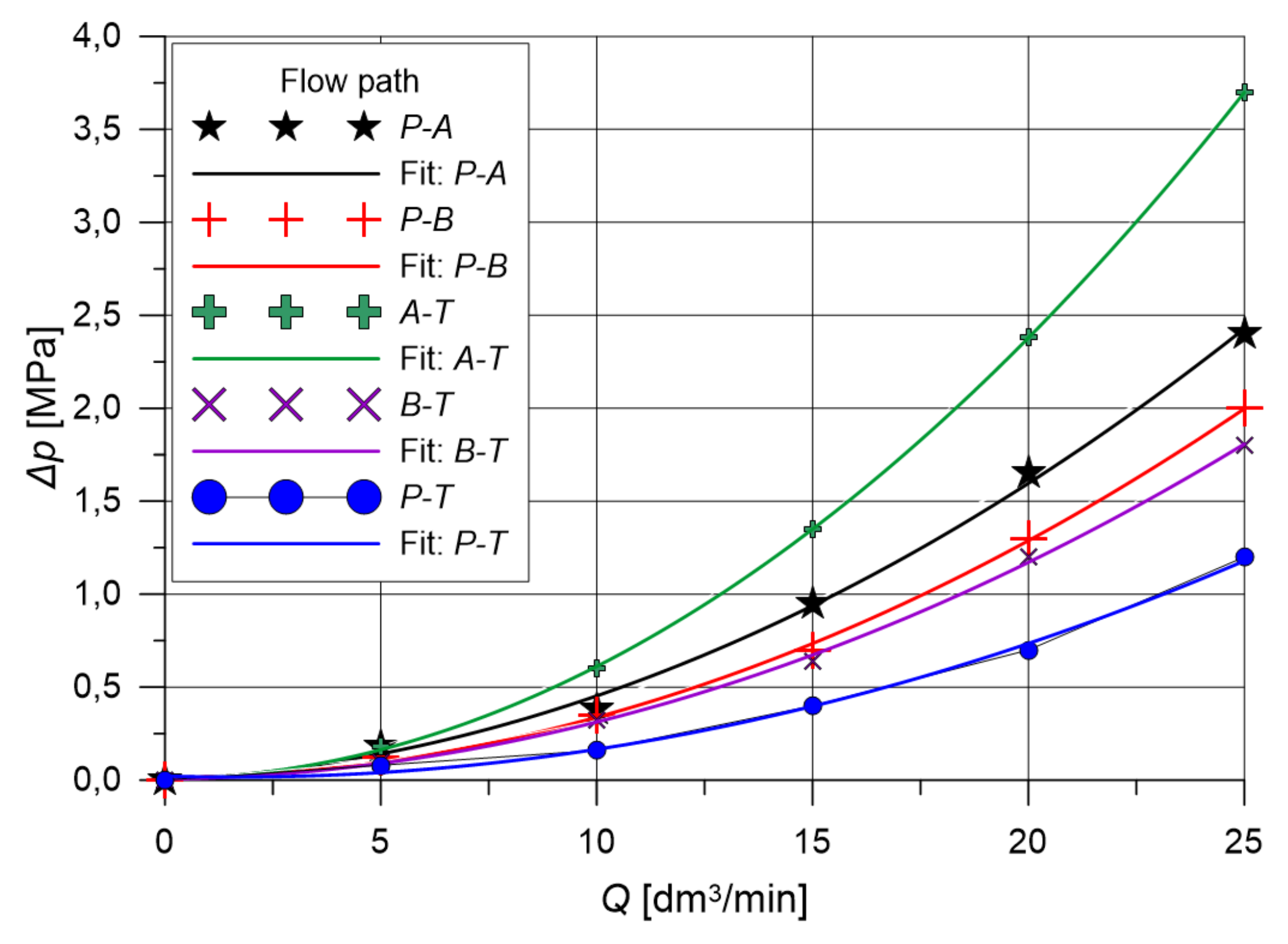
3.4.2. Determination of Flow Characteristics
3.4.3. Discussion of Simulation Results
4. Laboratory Experiments
5. Conclusions
- the available four operating positions is of significant practical importance, especially in the context of energy saving. This is particularly important in systems where there is a need to cut off the flow in one position of an actuator and open it in the another one. In case when the actuator is locked in the working position under a pressure of MPa and the flow rate of the relieved pump is 20 dm3 min−1, the power consumption is instantaneously reduced by approximately 5 kW;
- the use of poppet seat valves ensures full tightness between the flow paths, which is difficult to achieve with spool valves. Assuming a typical operating pressure MPa, the average power consumption can be reduced by 60 W due to avoiding the leaks;
- although the proposed solution control valve contains more elements than a typical spool valve, it is characterized by simpler geometry of flow channels and includes typical two-way cartridge valves which are easy to mount or replace;
- application of CAD methods together with CFD analysis is a useful and convenient tool in the search for new design solutions of hydraulic valves as well as introducing changes in the operating characteristics.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| poppet gap area (m2) | |
| turbulence model constants (-) | |
| hydraulic diameter (mm) | |
| energy components of turbulence model (J) | |
| I | turbulence intensity (-) |
| specific kinetic energy of turbulence and kinetic energy dissipation (m2 s−2, m2 s−3) | |
| ℓ | turbulence length scale (mm) |
| pressure, pressure drop (MPa) | |
| Q | volumetric flow rate (dm3 min−1) |
| Reynolds number (-) | |
| Prandtl numbers (-) | |
| fluid velocity component (m s−1) | |
| fluid dynamic viscosity (Pa s) | |
| poppet gap flow coefficient (-) | |
| eddy viscosity (-) | |
| fluid density (kg m−3) |
References
- Herakovic, N.; Duhovnik, J.; Simic, M. CFD simulation of flow force reduction in hydraulic valves. Teh. Vjesn./Tech. Gaz. 2015, 22, 453–463. [Google Scholar] [CrossRef]
- Huovinen, M.; Kolehmainen, J.; Koponen, P.; Nissilä, T.; Saarenrinne, P. Experimental and numerical study of a choke valve in a turbulent flow. Flow Meas. Instrum. 2015, 45, 151–161. [Google Scholar] [CrossRef]
- Šimic, M.; Debevec, M.; Herakovič, N. Modelling of Hydraulic Spool-Valves with Specially Designed Metering Edges. Stroj. Vestn.-J. Mech. Eng. 2014, 60, 77–83. [Google Scholar] [CrossRef]
- Amirante, R.; Distaso, E.; Tamburrano, P. Sliding spool design for reducing the actuation forces in direct operated proportional directional valves: Experimental validation. Energy Convers. Manag. 2016, 119, 399–410. [Google Scholar] [CrossRef]
- Park, S. Development of a proportional poppet-type water hydraulic valve. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 2099–2107. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G. CFD analysis of the characteristics of a proportional flow control valve with an innovative opening shape. Energy Convers. Manag. 2016, 123, 15–28. [Google Scholar] [CrossRef]
- Woldemariam, E.T.; Lemu, H.G.; Wang, G.G. CFD-Driven Valve Shape Optimization for Performance Improvement of a Micro Cross-Flow Turbine. Energies 2018, 11, 248. [Google Scholar] [CrossRef]
- Gomez, I.; Gonzalez-Mancera, A.; Newell, B.; Garcia-Bravo, J. Analysis of the Design of a Poppet Valve by Transitory Simulation. Energies 2019, 12. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, J.; Jing, C. Lumped Parameter Modelling of Cavitating Orifice Flow in Hydraulic Systems. Stroj. Vestn.-J. Mech. Eng. 2016, 62, 373–380. [Google Scholar] [CrossRef]
- Pan, X.; Wang, G.; Lu, Z. Flow field simulation and a flow model of servo-valve spool valve orifice. Energy Convers. Manag. 2011, 52, 3249–3256. [Google Scholar] [CrossRef]
- Sapra, M.; Bajaj, M.; Kundu, S.; Sharma, B. Experimental and CFD investigation of 100 mm size cone flow elements. Flow Meas. Instrum. 2011, 22, 469–474. [Google Scholar] [CrossRef]
- Ferreira, J.P.B.; Martins, N.M.; Covas, D.I. Ball Valve Behavior under Steady and Unsteady Conditions. J. Hydraul. Eng. 2018, 144, 04018005. [Google Scholar] [CrossRef]
- Brunone, B.; Morelli, R. Automatic control valve-induced transients in an operative pipe system. J. Hydraul. Eng. 1999, 125, 534–542. [Google Scholar] [CrossRef]
- Liao, Y.; Yuan, H.; Lian, Z.; Feng, J.; Guo, Y. Research and Analysis of the Hysteresis Characteristics of a Large Flow Directional Valve. Stroj. Vestn.-J. Mech. Eng. 2015, 61, 355–364. [Google Scholar] [CrossRef]
- El-Adawy, M.; Heikal, M.R.; Aziz, A.R.; Siddiqui, M.I.; Munir, S. Characterization of the Inlet Port Flow under Steady-State Conditions Using PIV and POD. Energies 2017, 10, 1950. [Google Scholar] [CrossRef]
- Rybarczyk, D.; Sedziak, D.; Owczarek, P.; Owczarkowski, A. Modelling of electrohydraulic drive with a valve controlled by synchronous motor. Adv. Intell. Syst. Comput. 2015, 350, 215–222. [Google Scholar]
- Wos, P.; Dindorf, R. Practical parallel position-force controller for electro-hydraulic servo drive using on-line identification. Int. J. Dyn. Control 2016, 4, 52–58. [Google Scholar] [CrossRef][Green Version]
- Stump, P.M.; Keller, N.; Vacca, A. Energy Management of Low-Pressure Systems Utilizing Pump-Unloading Valve and Accumulator. Energies 2019, 12, 4423. [Google Scholar] [CrossRef]
- Dindorf, R.; Wos, P. Force and position control of the integrated electro-hydraulic servo-drive. In Proceedings of the 20th International Carpathian Control Conference (ICCC), Krakow-Wieliczka, Poland, 26–29 May 2019. [Google Scholar] [CrossRef]
- Tamburrano, P.; Plummer, A.R.; De Palma, P.; Distaso, E.; Amirante, R. A Novel Servovalve Pilot Stage Actuated by a Piezo-Electric Ring Bender (Part II): Design Model and Full Simulation. Energies 2020, 13, 2267. [Google Scholar] [CrossRef]
- Lei, L.; Desheng, Z.; Jiyun, Z. Design and Research for the Water Low-pressure Large-flow Pilot-operated Solenoid Valve. Stroj. Vestn.-J. Mech. Eng. 2014, 60, 665–674. [Google Scholar] [CrossRef]
- Jin, Z.; Hong, W.; You, T.; Su, Y.; Li, X.; Xie, F. Effect of Multi-Factor Coupling on the Movement Characteristics of the Hydraulic Variable Valve Actuation. Energies 2020, 13, 2870. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G. Analysis of a proportional control valve flow coefficient with the usage of a CFD method. Flow Meas. Instrum. 2017, 53, 269–278. [Google Scholar] [CrossRef]
- Lisowski, E.; Filo, G.; Rajda, J. Analysis of flow forces in the initial phase of throttle gap opening in a proportional control valve. Flow Meas. Instrum. 2018, 59, 157–167. [Google Scholar] [CrossRef]
- Filo, G.; Lisowski, E.; Rajda, J. Flow analysis of a switching valve with innovative poppet head geometry by means of CFD method. Flow Meas. Instrum. 2019, 70, 101643. [Google Scholar] [CrossRef]
- ISO 4401:2005 Hydraulic Fluid Power—Four-Port Directional Control Valves—Mounting Surfaces. 2005. Available online: www.iso.org (accessed on 23 May 2020).
- Lisowski, E.; Filo, G.; Rajda, J. Pressure compensation using flow forces in a multi-section proportional directional control valve. Energy Convers. Manag. 2015, 103, 1052–1064. [Google Scholar] [CrossRef]
- ANSYS-Fluent: Users Guide, 13th ed.; ANSYS, Inc.: Canonsburg, PA, USA, 2011.

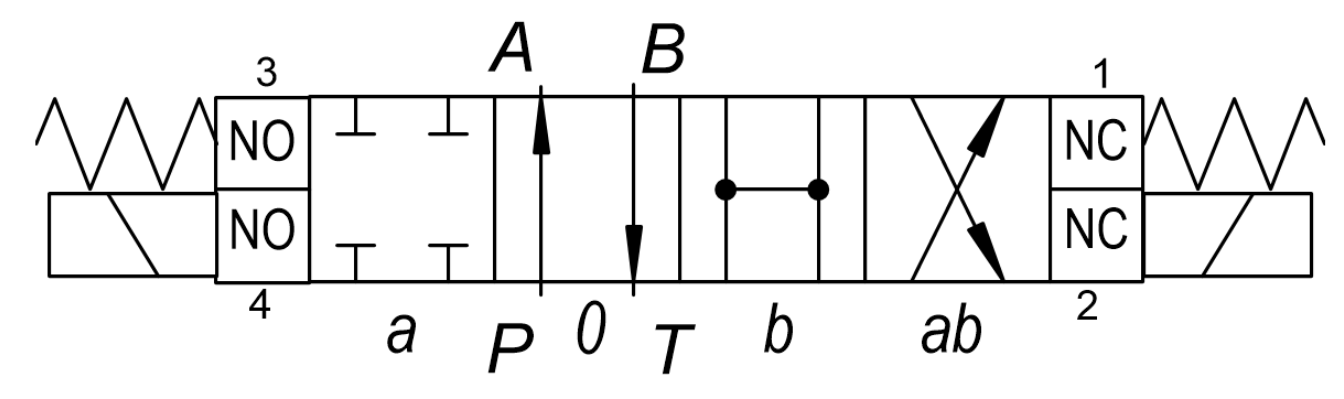


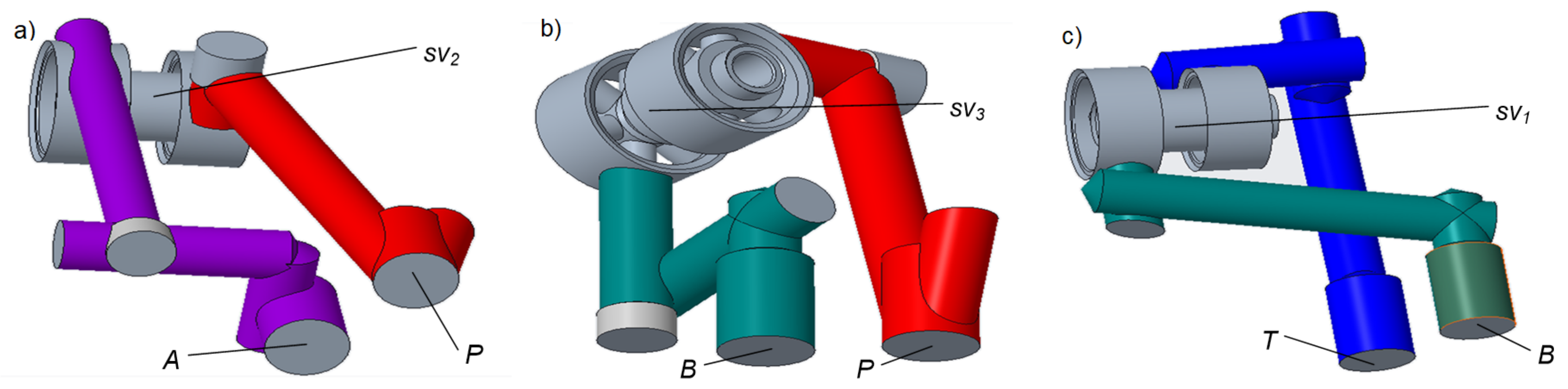

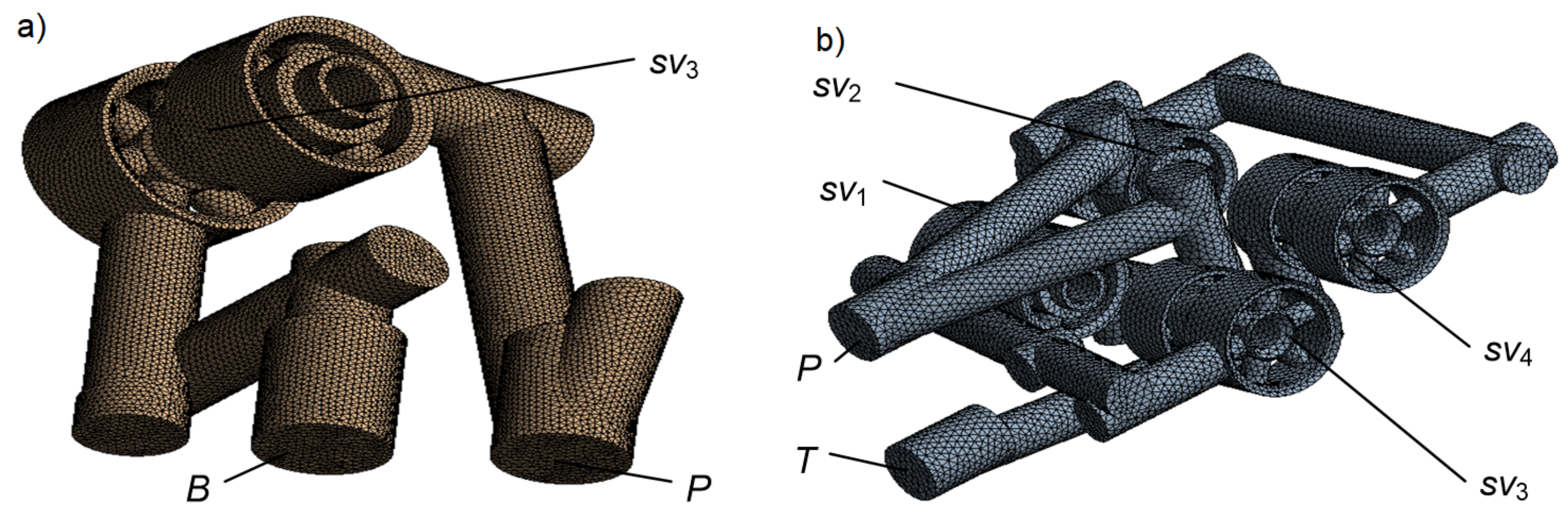



| Diagram | Number of NC | Number of NO |
|---|---|---|
 | 4 | 0 |
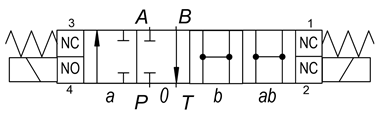 | 3 | 1 |
 | 3 | 1 |
 | 2 | 2 |
| Fluid Dynamic Viscosity | Fluid Density | Fluid Temperature | Turbulence Intensity | Length Scale | Min Inlet Flowrate | Max Inlet Flowrate | Outlet Pressure |
|---|---|---|---|---|---|---|---|
| 32.2 | 870 | 40.0 | 5.1 | 0.42 | 5.0 | 25.0 | 0.1 |
| mPa s | kg m−3 | °C | % | mm | dm3 min−1 | dm3 min−1 | MPa |
| Path Parameter | S/E | Q dm3min−1 | Average Diff.% | ||||
|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | |||
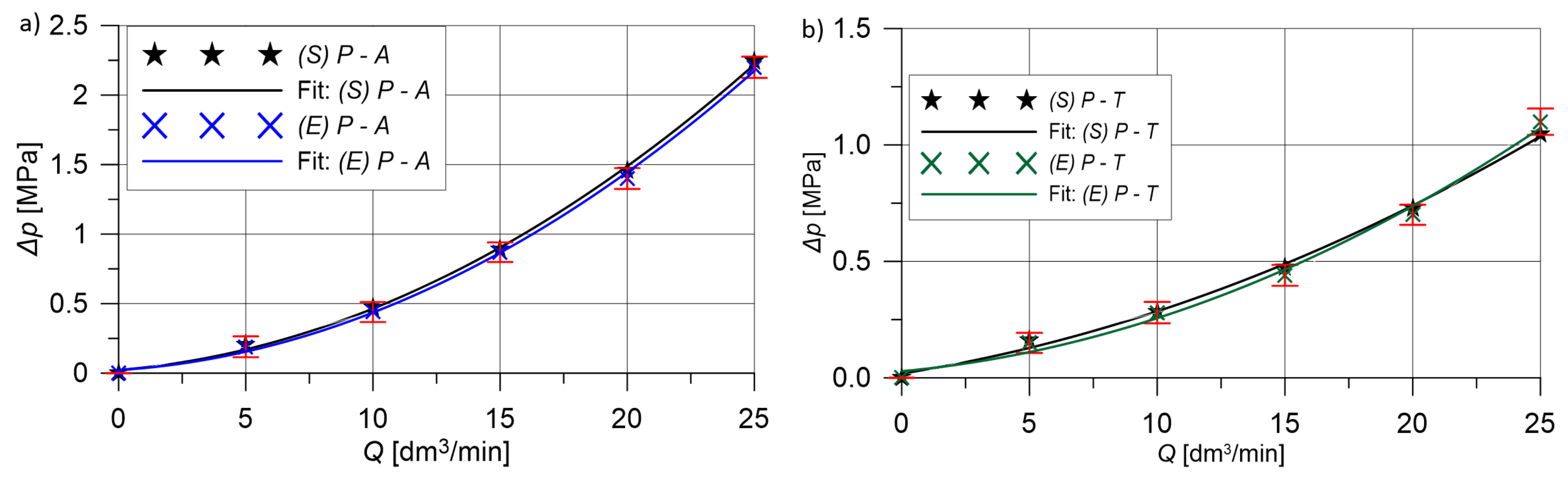
(MPa) | S | 0.21 | 0.47 | 0.89 | 1.46 | 2.24 | 4.71 |
| E | 0.19 | 0.44 | 0.87 | 1.40 | 2.20 | ||
(MPa) | S | 0.19 | 0.39 | 0.75 | 1.15 | 1.72 | 6.26 |
| E | 0.18 | 0.37 | 0.70 | 1.20 | 1.85 | ||
(MPa) | S | 0.20 | 0.42 | 0.76 | 1.23 | 1.82 | 5.13 |
| E | 0.18 | 0.38 | 0.74 | 1.20 | 1.80 | ||
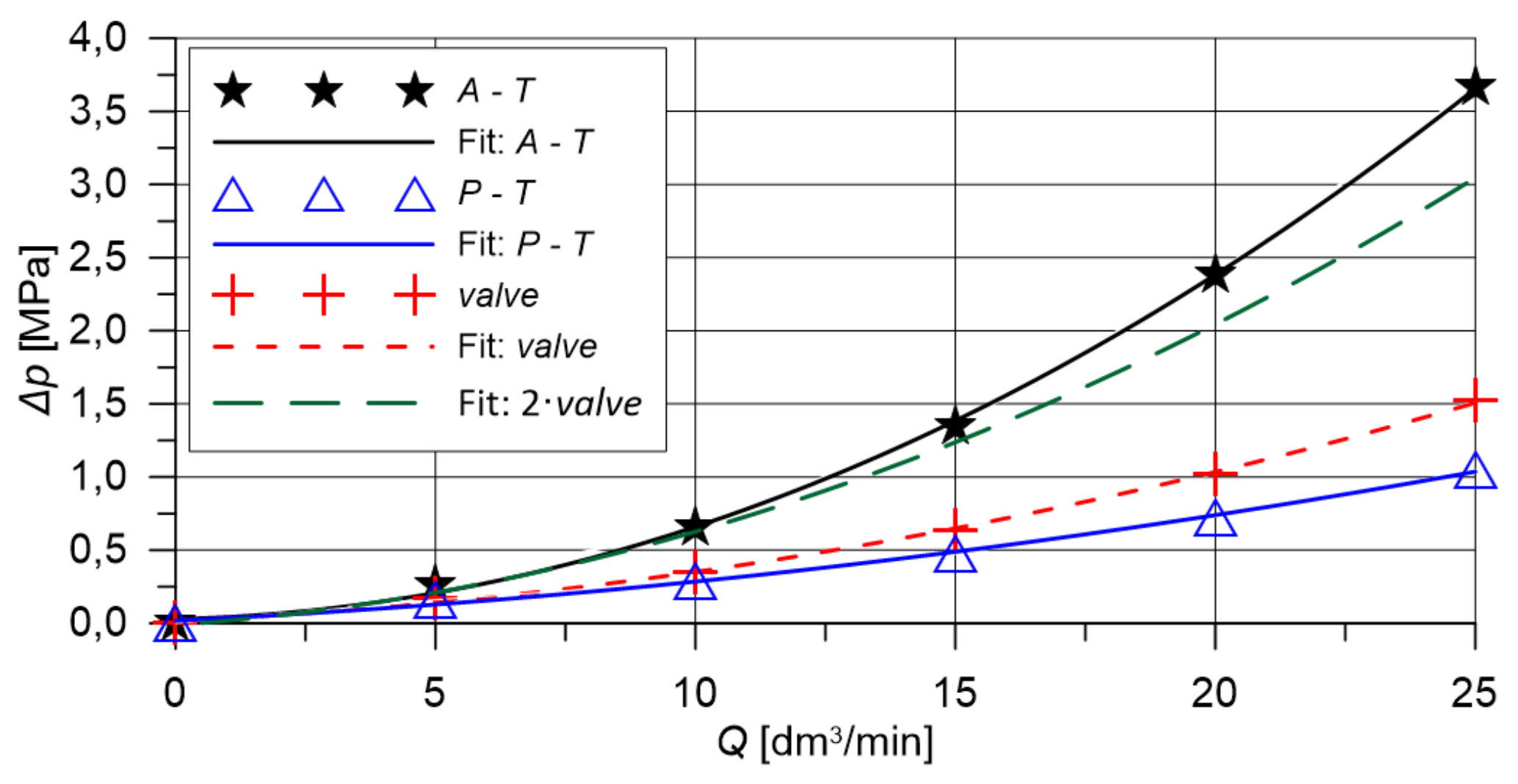
(MPa) | S | 0.27 | 0.65 | 1.35 | 2.38 | 3.66 | 5.00 |
| E | 0.25 | 0.60 | 1.35 | 2.30 | 3.40 | ||
(MPa) | S | 0.16 | 0.29 | 0.48 | 0.73 | 1.05 | 5.04 |
| E | 0.15 | 0.28 | 0.44 | 0.70 | 1.10 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filo, G.; Lisowski, E.; Rajda, J. Pressure Loss Reduction in an Innovative Directional Poppet Control Valve. Energies 2020, 13, 3149. https://doi.org/10.3390/en13123149
Filo G, Lisowski E, Rajda J. Pressure Loss Reduction in an Innovative Directional Poppet Control Valve. Energies. 2020; 13(12):3149. https://doi.org/10.3390/en13123149
Chicago/Turabian StyleFilo, Grzegorz, Edward Lisowski, and Janusz Rajda. 2020. "Pressure Loss Reduction in an Innovative Directional Poppet Control Valve" Energies 13, no. 12: 3149. https://doi.org/10.3390/en13123149
APA StyleFilo, G., Lisowski, E., & Rajda, J. (2020). Pressure Loss Reduction in an Innovative Directional Poppet Control Valve. Energies, 13(12), 3149. https://doi.org/10.3390/en13123149






