A Real-Time Dynamic Fuel Cell System Simulation for Model-Based Diagnostics and Control: Validation on Real Driving Data
Abstract
:1. Introduction
2. Fuel Cell Stack Model
2.1. Derivation of Model Equations
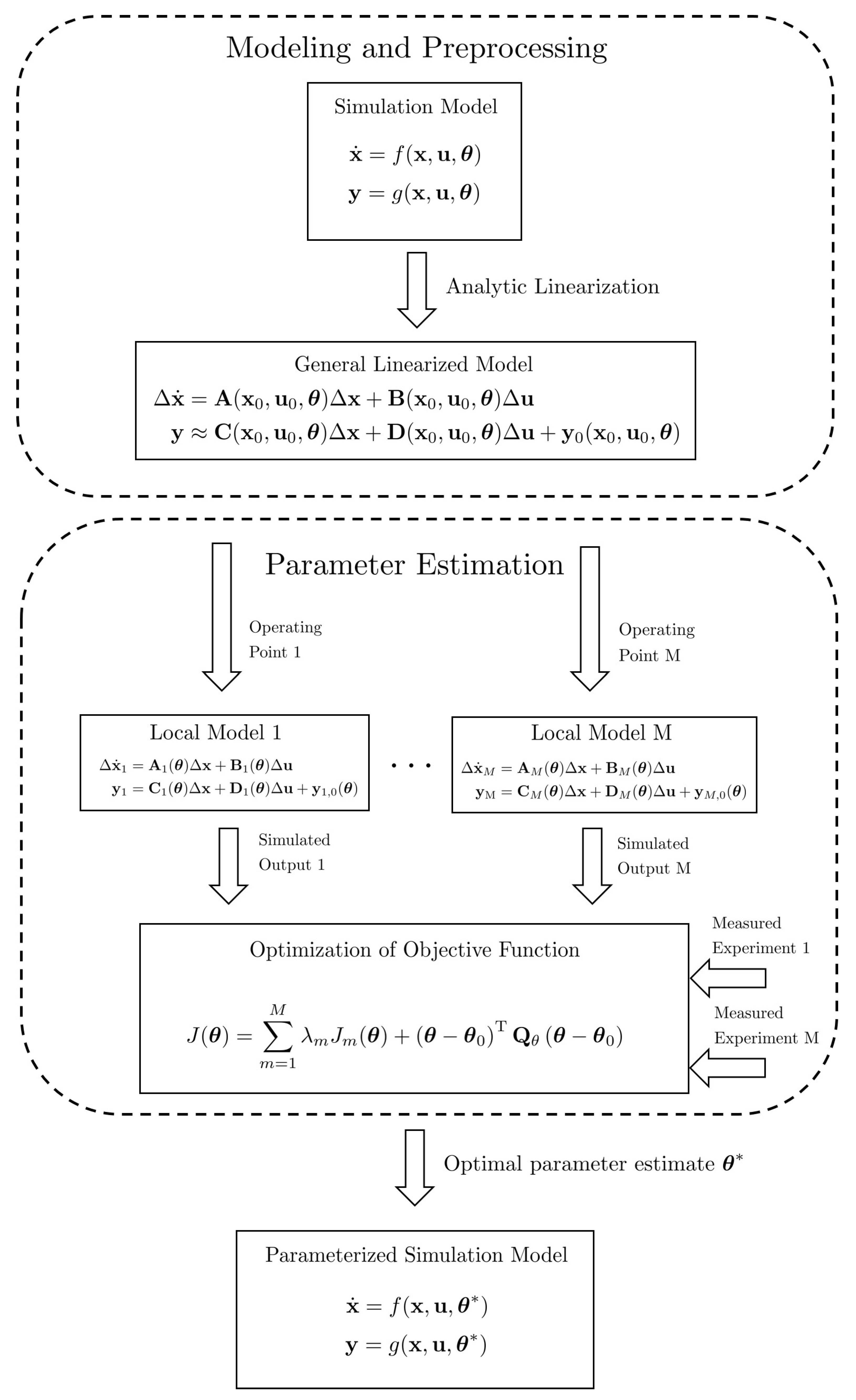
2.2. Model Parameterization
- The applied ordinary differential equation solver fails to provide a solution of the simulated output (e.g., due to numerical stiffness or improper parameter values during the optimization). As a result, the objective function (15) cannot be evaluated and the parameterizaton task fails.
- The optimization algorithm does not converge to a suitable solution. A restart of the optimization with different solvers, solver settings and weightings in the objective function is required.
- The experimental data is not informative enough or conversely, all desired parameters cannot be uniquely determined from the experimental data due (e.g., due to insufficient excitations, sensors or measurement errors).
2.3. Approximating Model Discontinuities
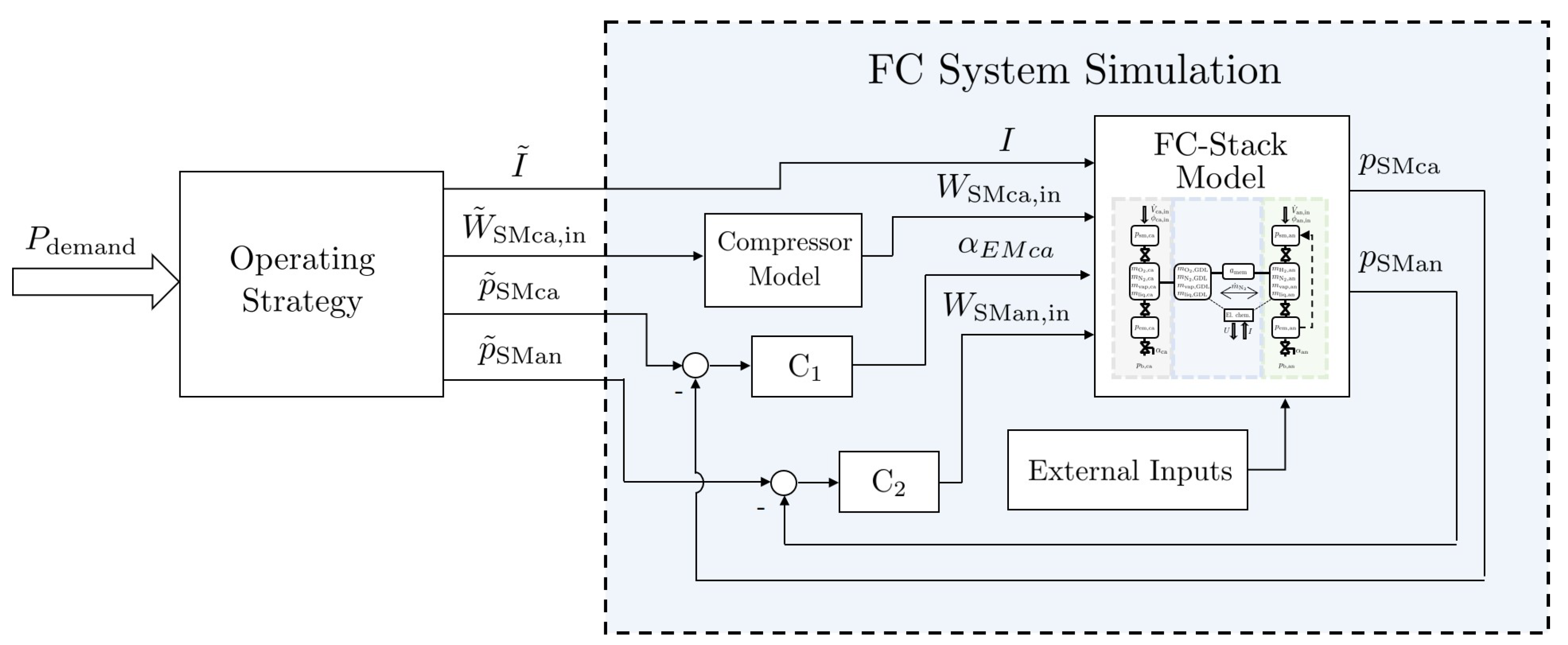
3. Fuel Cell System Simulation
- Stack Current ,
- Cathode inlet air flow ,
- Cathode supply manifold pressure ,
- Anode supply manifold pressure .
4. Results
4.1. Validation of the System Simulation
4.2. Investigation of Internal States
5. Discussion
- State Estimation and Fault Detection: To improve the accuracy with respect to unknown disturbances, measurement noise and emerging faults, the system simulation can be embedded into an observer algorithm to estimate (and correct) the simulation states based on available measurement data. The presented model, as it is continuously differentiatable, is especially suitable for estimation schemes based on successive linearization such as the extended Kalman filter [41]. Having a robust state estimation enables the on-line estimation of hazardous conditions such as fuel starvation, dry-out and flooding and excessive humidity cycles.
- Model Based Control: The fuel cell system is a strongly coupled multi-input multi-output system for which model-based control methodologies have become indespensible. In a nutshell, the task of the fuel cell system is to provide the required power at the highest possible system efficiency (e.g., considering parasitic consumptions such as the compressor), while taking into account safety and life-time related limitations. The verbal description of the control objective alone points in the direction of optimal control as a suitable candidate. The existence of desired safety-limits, which can be described as constraints either on the inputs, states, or outputs, suggests Model Predictive Control (MPC) [42,43] as a suitable methodology to balance the conflicting goals of life preservation, tracking performance and efficiency maximization. In this sense, the MPC rather takes over the task of planning the operating strategy, which is done on-line together with the a priori information predicted by the real-time model and the a-posteriori correction based on available measurements of the system.
- Improving the Operating Strategy Even in a non-optimal way it is straight forward to see that the availability of a dynamic fuel cell system simulation enables an engineer to refine the operating strategy with a fraction of the time and costs as opposed to the development at a real test stand. Additionally, all internal states are accessible during the transient operation, which are in general unknown on the real-system.
6. Conclusions
Author Contributions
Funding
Acknowledgments
- AVL List GmbH,
- ElringKlinger AG,
- HOERBIGER Ventilwerke GmbH & Co Kg,
- HyCentA Research GmbH,
- IESTA, Institut für Innovative Energie- und Stoffaustauschsysteme,
- MAGNA STEYR Engineering AG & Co KG,
- Technische Universität Graz, Institut für Chemische Verfahrenstechnik und Umwelttechnik,
- Technische Universität Wien, Institut für Mechanik und Mechatronik.
Conflicts of Interest
Abbreviations
| CL | Catalyst layer |
| CM | Center manifold |
| EM | Exit Manifold |
| FC | Fuel Cell |
| GDL | Gas diffusion layer |
| MPC | Model predictive control |
| OEM | Original equipment manufacturer |
| PEMFC | Polymer electrolyte membrane fuel cell |
| PWM | Pulse width modulation |
| SM | Supply Manifold |
Appendix A. Auxiliary Tables and Figures
| Source Terms | Descriptions |
|---|---|
The diffusion of oxygen, nitrogen and water vapor from the center manifold through the GDL to the catalyst layer is described by
| |
The massflow of oxygen due to the electrochemical reaction [44] is given by
| |
The permeation of nitrogen from cathode to anode through the membrane is considered via
| |
The generation of product water [44] is given by
| |
The massflow of hydrogen beeing reacted [44] is given by
| |
| Nitrogen crossover leads to the accumulation of Nitrogen in the anode, which is ejected when the purge valve is actuated. | |
The phase change of water vapor to liquid water in the anode center manifold is calculated analogously as for the cathode side. |
References
- Das, V.; Padmanaban, S.; Venkitusamy, K.; Selvamuthukumaran, R.; Blaabjerg, F.; Siano, P. Recent advances and challenges of fuel cell based power system architectures and control—A review. Renew. Sustain. Energy Rev. 2017, 73, 10–18. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X. A review of polymer electrolyte membrane fuel cell durability for vehicular applications: Degradation modes and experimental techniques. Energy Convers. Manag. 2019, 199, 112022. [Google Scholar] [CrossRef]
- Yousfi-Steiner, N.; Moçotéguy, P.; Candusso, D.; Hissel, D. A review on polymer electrolyte membrane fuel cell catalyst degradation and starvation issues: Causes, consequences and diagnostic for mitigation. J. Power Sources 2009, 194, 130–145. [Google Scholar] [CrossRef]
- Petrone, R.; Zheng, Z.; Hissel, D.; Péra, M.C.; Pianese, C.; Sorrentino, M.; Becherif, M.; Yousfi-Steiner, N. A review on model-based diagnosis methodologies for PEMFCs. Int. J. Hydrog. Energy 2013, 38, 7077–7091. [Google Scholar] [CrossRef]
- Liu, J.; Luo, W.; Yang, X.; Wu, L. Robust model-based fault diagnosis for PEM fuel cell air-feed system. IEEE Trans. Ind. Electron. 2016, 63, 3261–3270. [Google Scholar] [CrossRef] [Green Version]
- Escobet, T.; Feroldi, D.; De Lira, S.; Puig, V.; Quevedo, J.; Riera, J.; Serra, M. Model-based fault diagnosis in PEM fuel cell systems. J. Power Sources 2009, 192, 216–223. [Google Scholar] [CrossRef] [Green Version]
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of Fuel Cell Power Systems: Principles, Modeling, Analysis and Feedback Design; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Xu, L.; Hu, J.; Cheng, S.; Fang, C.; Li, J.; Ouyang, M.; Lehnert, W. Robust control of internal states in a polymer electrolyte membrane fuel cell air-feed system by considering actuator properties. Int. J. Hydrog. Energy 2017, 42, 13171–13191. [Google Scholar] [CrossRef]
- Pilloni, A.; Pisano, A.; Usai, E. Observer-based air excess ratio control of a PEM fuel cell system via high-order sliding mode. IEEE Trans. Ind. Electron. 2015, 62, 5236–5246. [Google Scholar] [CrossRef] [Green Version]
- Hong, L.; Chen, J.; Liu, Z.; Huang, L.; Wu, Z. A nonlinear control strategy for fuel delivery in PEM fuel cells considering nitrogen permeation. Int. J. Hydrog. Energy 2017, 42, 1565–1576. [Google Scholar] [CrossRef]
- Murschenhofer, D.; Kuzdas, D.; Braun, S.; Jakubek, S. A real-time capable quasi-2D proton exchange membrane fuel cell model. Energy Convers. Manag. 2018, 162, 159–175. [Google Scholar] [CrossRef]
- Pathapati, P.; Xue, X.; Tang, J. A new dynamic model for predicting transient phenomena in a PEM fuel cell system. Renew. Energy 2005, 30, 1–22. [Google Scholar] [CrossRef]
- Ziogou, C.; Voutetakis, S.; Papadopoulou, S.; Georgiadis, M.C. Modeling, simulation and experimental validation of a PEM fuel cell system. Comput. Chem. Eng. 2011, 35, 1886–1900. [Google Scholar] [CrossRef]
- Mo, Z.J.; Zhu, X.J.; Wei, L.Y.; Cao, G.Y. Parameter optimization for a PEMFC model with a hybrid genetic algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A comprehensive review on parameter estimation techniques for Proton Exchange Membrane fuel cell modelling. Renew. Sustain. Energy Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Rajasekar, N.; Jacob, B.; Balasubramanian, K.; Priya, K.; Sangeetha, K.; Babu, T.S. Comparative study of PEM fuel cell parameter extraction using Genetic Algorithm. Ain Shams Eng. J. 2015, 6, 1187–1194. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.; Min, K. Dynamic simulation of a fuel cell hybrid vehicle during the federal test procedure-75 driving cycle. Appl. Energy 2016, 161, 181–196. [Google Scholar] [CrossRef]
- Boulon, L.; Agbossou, K.; Hissel, D.; Sicard, P.; Bouscayrol, A.; Péra, M.C. A macroscopic PEM fuel cell model including water phenomena for vehicle simulation. Renew. Energy 2012, 46, 81–91. [Google Scholar] [CrossRef]
- Keytech4ev Project Homepage. Available online: http://www.iesta.at/keytech4ev/ (accessed on 20 May 2020).
- Hemmer, S.; Walters, M.; Tinz, S. Scalable Fuel Cell Systems for Commercial Vehicles. MTZ Worldw. 2019, 80, 64–71. [Google Scholar] [CrossRef]
- Zucrow, M.J.; Hoffman, J.D. Gas Dynamics. Volume 2—Multidimensional Flow; Wiley: Hoboken, NJ, USA, 1977. [Google Scholar]
- Kulikovsky, A. The voltage–current curve of a polymer electrolyte fuel cell: “Exact” and fitting equations. Electrochem. Commun. 2002, 4, 845–852. [Google Scholar] [CrossRef]
- Kulikovsky, A. A physically–based analytical polarization curve of a PEM fuel cell. J. Electrochem. Soc. 2014, 161, F263–F270. [Google Scholar] [CrossRef]
- Sonntag, R.E.; Borgnakke, C.; Van Wylen, G.J.; Van Wyk, S. Fundamentals of Thermodynamics; Wiley: New York, NY, USA, 1998; Volume 6. [Google Scholar]
- Birgersson, E.; Noponen, M.; Vynnycky, M. Analysis of a two-phase non-isothermal model for a PEFC. J. Electrochem. Soc. 2005, 152, A1021–A1034. [Google Scholar] [CrossRef]
- Xu, L.; Fang, C.; Hu, J.; Cheng, S.; Li, J.; Ouyang, M.; Lehnert, W. Parameter extraction and uncertainty analysis of a proton exchange membrane fuel cell system based on Monte Carlo simulation. Int. J. Hydrog. Energy 2017, 42, 2309–2326. [Google Scholar] [CrossRef]
- Khajeh-Hosseini-Dalasm, N.; Fushinobu, K.; Okazaki, K. Transient phase change in the cathode side of a PEM fuel cell. J. Electrochem. Soc. 2010, 157, B1358–B1369. [Google Scholar] [CrossRef]
- Liso, V.; Araya, S.S.; Olesen, A.C.; Nielsen, M.P.; Kær, S.K. Modeling and experimental validation of water mass balance in a PEM fuel cell stack. Int. J. Hydrog. Energy 2016, 41, 3079–3092. [Google Scholar] [CrossRef]
- Hissel, D.; Pera, M.C. Diagnostic & health management of fuel cell systems: Issues and solutions. Annu. Rev. Control 2016, 42, 201–211. [Google Scholar]
- Kravos, A.; Ritzberger, D.; Tavcar, G.; Hametner, C.; Jakubek, S.; Katrasnik, T. Thermodynamically consistent reduced dimensionality electrochemical model for proton exchange membrane fuel cell performance modelling and control. J. Power Sources 2020, 454, 227930. [Google Scholar] [CrossRef]
- Lennart, L. System Identification: Theory for the User; PTR Prentice Hall: Upper Saddle River, NJ, USA, 1999; pp. 1–14. [Google Scholar]
- Bohlin, T.P. Practical Grey-Box Process Identification: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kristensen, N.R.; Madsen, H.; Jørgensen, S.B. Parameter estimation in stochastic grey-box models. Automatica 2004, 40, 225–237. [Google Scholar] [CrossRef]
- Nelles, O.; Fink, A.; Isermann, R. Local linear model trees (LOLIMOT) toolbox for nonlinear system identification. IFAC Proc. Vol. 2000, 33, 845–850. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neural Networks and Fuzzy Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- MathWorks Symbolic Toolbox: Dcoumentatoin (R2019b). Available online: https://www.mathworks.com/help/symbolic/ (accessed on 30 October 2019).
- Grujicic, M.; Chittajallu, K.; Law, E.; Pukrushpan, J. Model-based control strategies in the dynamic interaction of air supply and fuel cell. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 487–499. [Google Scholar] [CrossRef]
- Bao, C.; Ouyang, M.; Yi, B. Modeling and control of air stream and hydrogen flow with recirculation in a PEM fuel cell system—I. Control-oriented modeling. Int. J. Hydrog. Energy 2006, 31, 1879–1896. [Google Scholar] [CrossRef]
- Dadvar, M.; Afshari, E. Analysis of design parameters in anodic recirculation system based on ejector technology for PEM fuel cells: A new approach in designing. Int. J. Hydrog. Energy 2014, 39, 12061–12073. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Z.; Wang, F.; Ouyang, Q.; Su, H. Optimal oxygen excess ratio control for PEM fuel cells. IEEE Trans. Control Syst. Technol. 2017, 26, 1711–1721. [Google Scholar] [CrossRef]
- Ribeiro, M.I. Kalman and Extended Kalman Filters: Concept, Derivation and Properties; Instituto Superior Técnico: Lisboa, Portugal, 2004; Volume 43. [Google Scholar]
- Morari, M.; Garcia, C.E.; Prett, D.M. Model predictive control: Theory and practice. IFAC Proc. Vol. 1988, 21, 1–12. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Pub: Madison, WI, USA, 2009. [Google Scholar]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Kocha, S.S.; Deliang Yang, J.; Yi, J.S. Characterization of gas crossover and its implications in PEM fuel cells. AIChE J. 2006, 52, 1916–1925. [Google Scholar] [CrossRef]





| Vehicle Platform | VW Passat GTE |
|---|---|
| Vehicle gross weight | 1746 kg |
| Battery capacity | 9.9 kWh |
| Battery power | 85 kW |
| Fuel cell system power | 55 kW |
| e-drive power | 100 kW |
| Hydrogen tank capacity | 4 kg |
| Number of tanks | 3 |
| Hydrogen consumption | 0.8 kg/100 km |
| Driving range | >500 km |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ritzberger, D.; Hametner, C.; Jakubek, S. A Real-Time Dynamic Fuel Cell System Simulation for Model-Based Diagnostics and Control: Validation on Real Driving Data. Energies 2020, 13, 3148. https://doi.org/10.3390/en13123148
Ritzberger D, Hametner C, Jakubek S. A Real-Time Dynamic Fuel Cell System Simulation for Model-Based Diagnostics and Control: Validation on Real Driving Data. Energies. 2020; 13(12):3148. https://doi.org/10.3390/en13123148
Chicago/Turabian StyleRitzberger, Daniel, Christoph Hametner, and Stefan Jakubek. 2020. "A Real-Time Dynamic Fuel Cell System Simulation for Model-Based Diagnostics and Control: Validation on Real Driving Data" Energies 13, no. 12: 3148. https://doi.org/10.3390/en13123148
APA StyleRitzberger, D., Hametner, C., & Jakubek, S. (2020). A Real-Time Dynamic Fuel Cell System Simulation for Model-Based Diagnostics and Control: Validation on Real Driving Data. Energies, 13(12), 3148. https://doi.org/10.3390/en13123148




