Security Assessment and Coordinated Emergency Control Strategy for Power Systems with Multi-Infeed HVDCs
Abstract
1. Introduction
- (1)
- A security assessment method based on EMT-TS hybrid simulation is achieved. DC and AC subsystems are modeled in EMTDC/PSCAD and PSS/E, respectively. The security assessment method can accurately identify the security and stability issues related to interactions between AC and DC subsystems while maintaining the high computational efficiency;
- (2)
- An emergency control strategy decision-making method that can coordinate HVDCs, pumped storages, and interruptible loads is developed subject to multiple security constraints. The decision-making method can minimize the control costs while maintaining the security and stability of the receiving-end system.
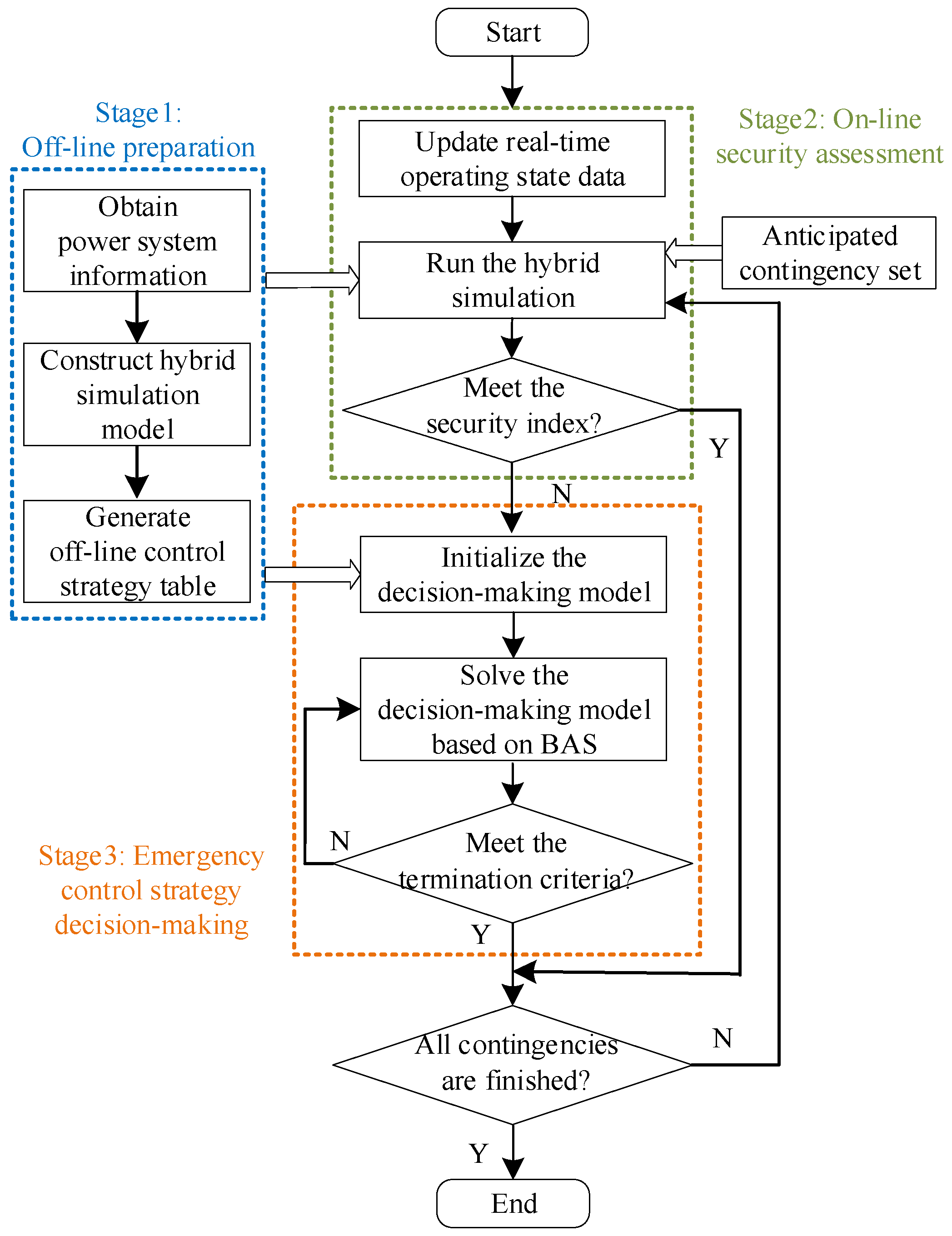
2. Procedure of the On-Line Pre-Decision-Making Scheme
- (1)
- Off-line preparation. Construct the EMT-TS hybrid model based on the information of the network topology, electrical parameters, control parameters, etc. Then, generate an off-line control strategy table under the anticipated contingency set and pre-determined typical operating conditions (different from the on-line control strategy table, various typical operating conditions need to be considered in the off-line control strategy table [39]), which will provide the initial solution of the decision-making model for the emergency control strategy;
- (2)
- On-line security assessment based on EMT-TS hybrid simulation. Update the real-time operating state data, including the operation mode of the system and the power flow of the main transmission section; choose one contingency from the anticipated contingency set and run the hybrid simulation. Then, identify possible security and stability issues according to the security indices. Finally, generate the assessment result for contingencies that cause security and stability issues, including the current operating condition, contingency, and power shortage in the receiving-end system; and
- (3)
- Emergency control strategy decision-making. Initialize the decision-making model with the operating condition and the control strategy. The operating condition is obtained from the assessment result. The control strategy, which is used as the initial solution, is determined based on the power shortage and the control strategy obtained through an approximate search of the off-line control strategy table. Then, solve the decision-making model based on the beetle antennae search (BAS) algorithm [40], a meta-heuristic algorithm developed by the inspiration of the beetle forging principle, until the termination criteria are met.
3. Security Assessment Based on EMT-TS Hybrid Simulation
3.1. Analysis of Commutation Failures and Blocking Events Simulation
3.2. Principle of EMT-TS Hybrid Simulation Modeling
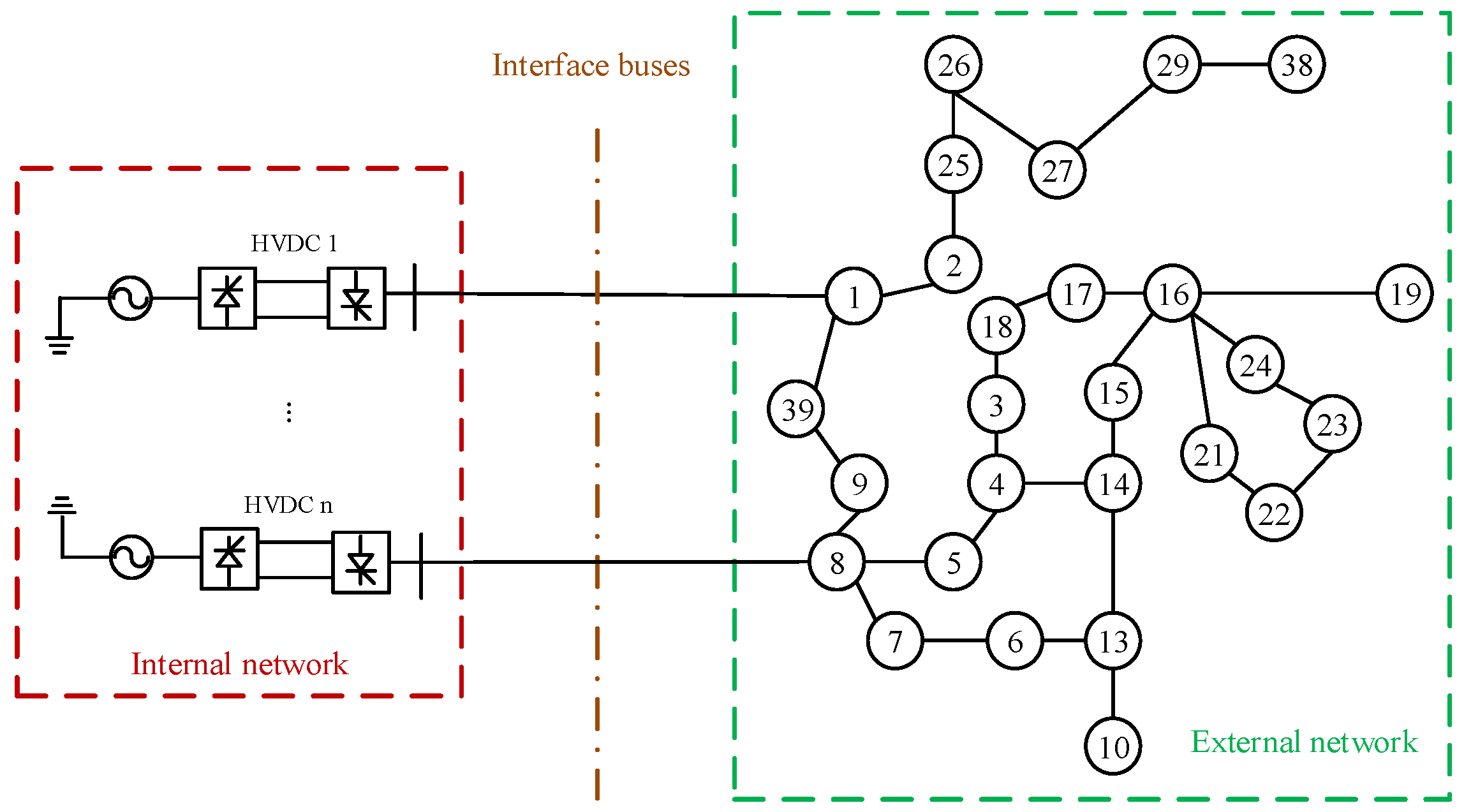
- (1)
- Interface location. As shown in Figure 2, the power system will be divided into two parts: The internal network and the external network. The internal network is comprised of HVDCs and the nearby AC buses, and it is modeled in the EMT simulator EMTDC/PSCAD. The rest of the system is the external network and is represented in the TS simulator PSS/E. To guarantee the accuracy and efficiency of the hybrid simulation, a proper interface location should be identified.
- (2)
- Equivalent models of the external and internal networks. For the model in EMTDC/PSCAD, in addition to the detailed model of the internal network, an equivalent model of the external network needs to be constructed to ensure the integrity of the system. Similarly, an equivalent model of the internal network in PSS/E is also indispensable.
- (3)
- Interaction protocol and data. During the hybrid simulation, the two simulators will exchange data through a certain interaction protocol to update the states of the equivalent models in time.
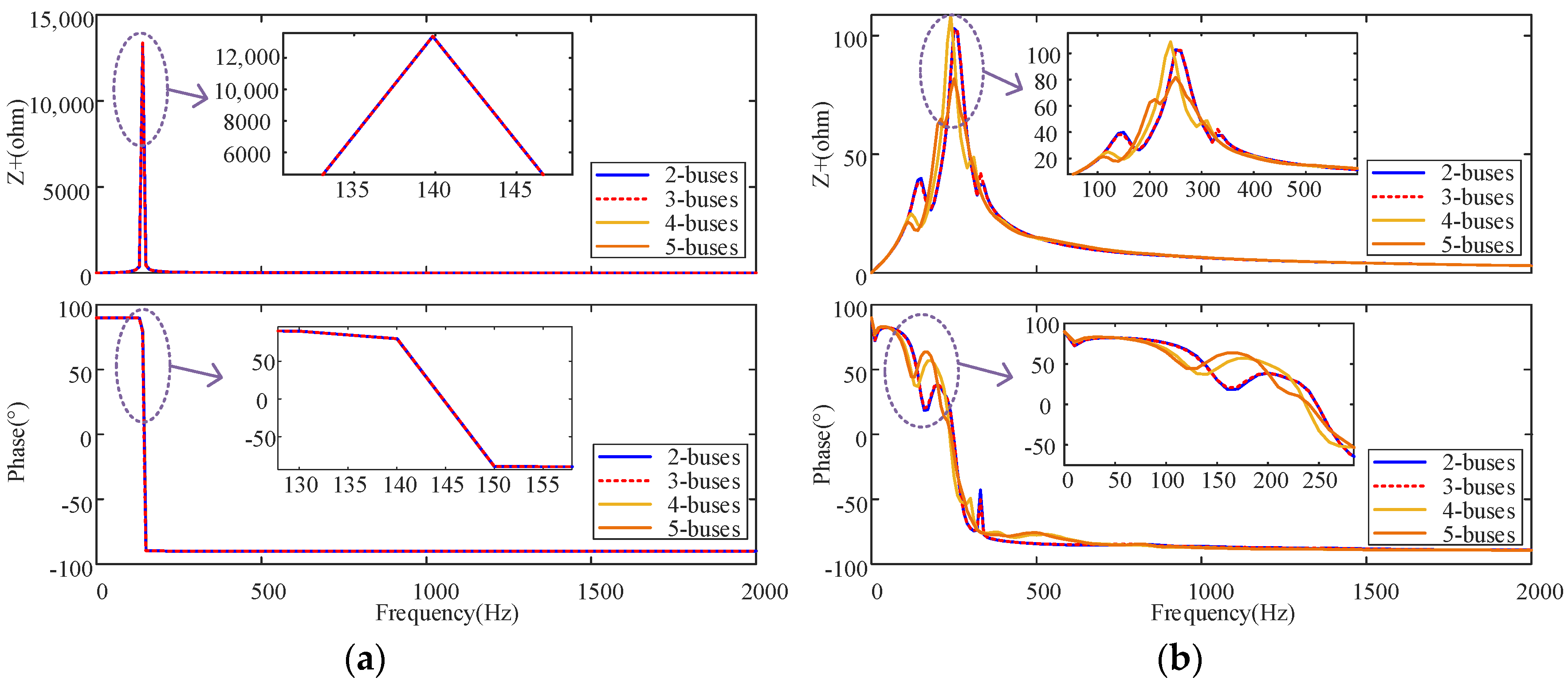
3.2.1. Identify the Interface Location
3.2.2. Equivalent Models of the External and Internal Networks
3.2.3. Interaction Protocol and Data
3.3. Security Assessment Index System
4. Emergency Control Strategy Decision-Making Based on BAS
4.1. Mathematical Decision-Making Model
4.1.1. Objective Function
4.1.2. Adjustment Amount Constraints
4.1.3. Steady-State Constraints
4.1.4. Transient-State Constraints
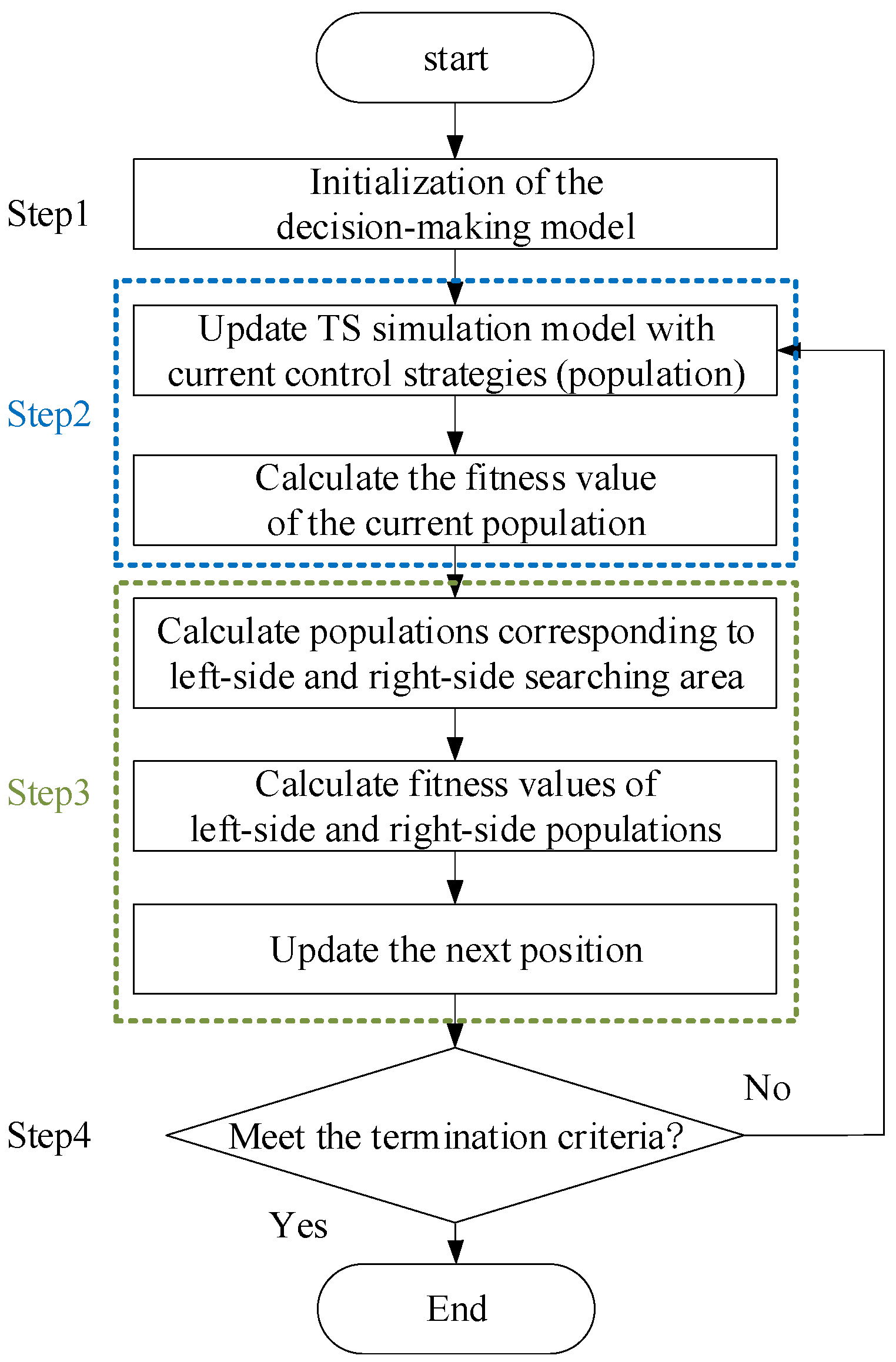
4.2. Decision-Making Procedure of the Emergency Control Strategy
5. Case Studies
5.1. Test System 1
5.1.1. Construction of the Hybrid Simulation
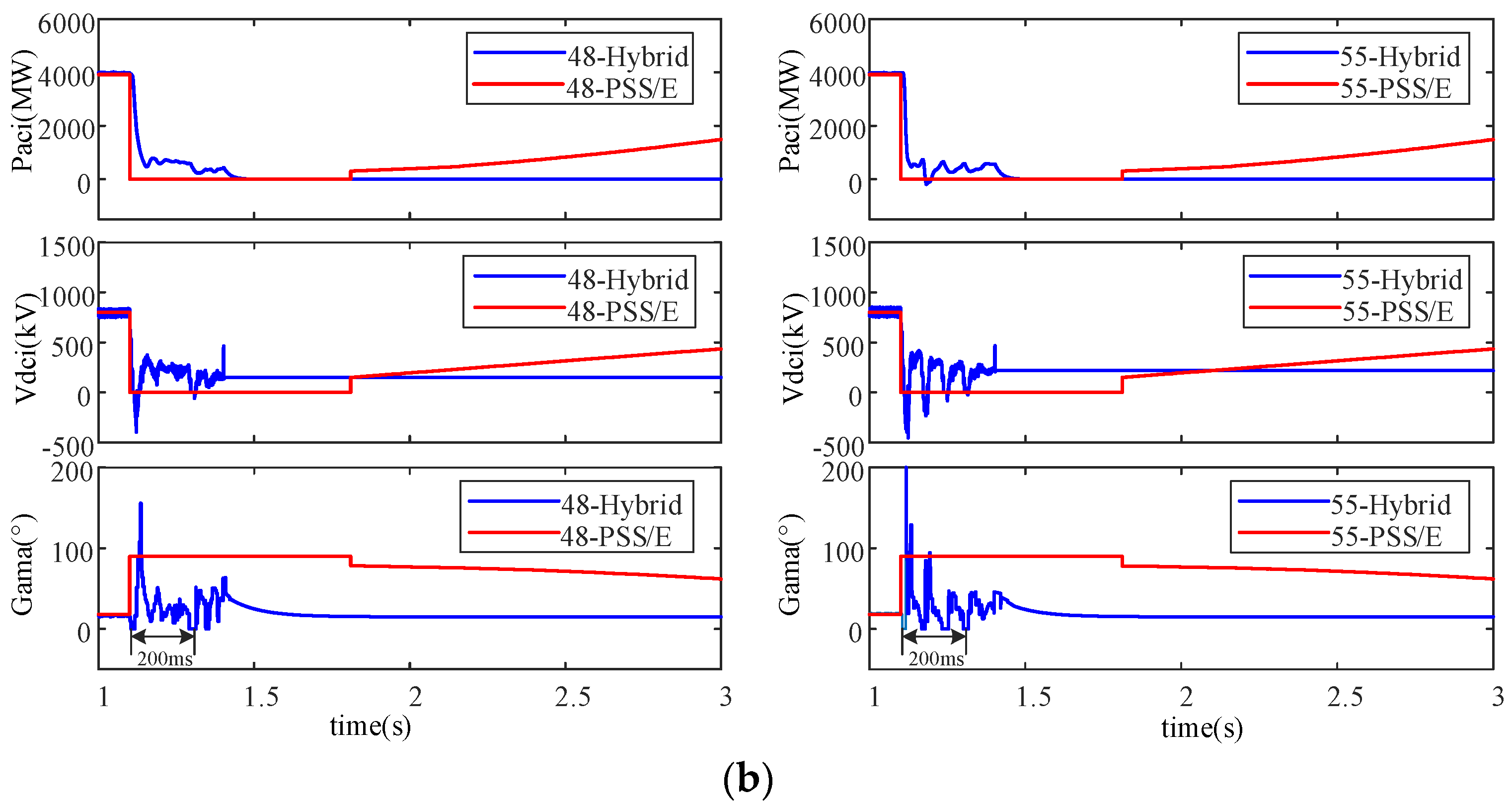
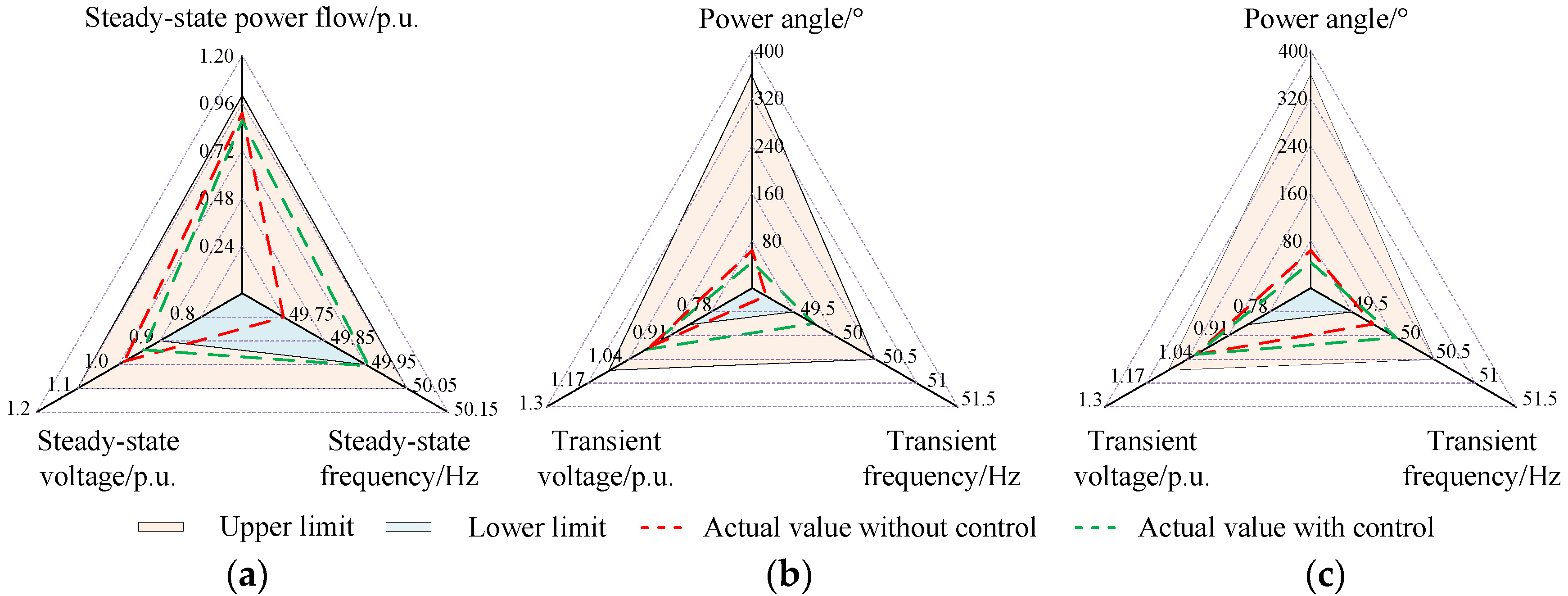
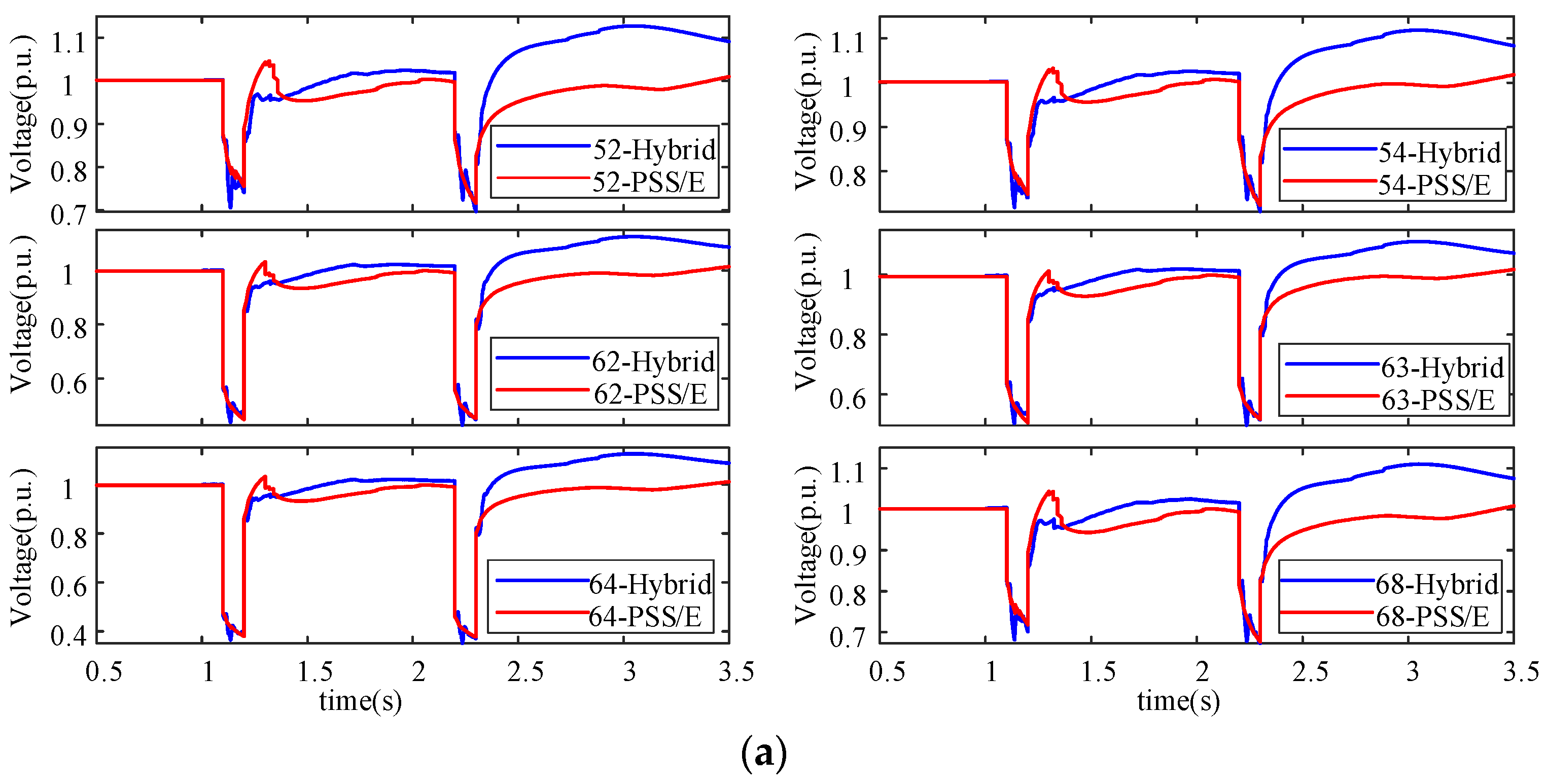
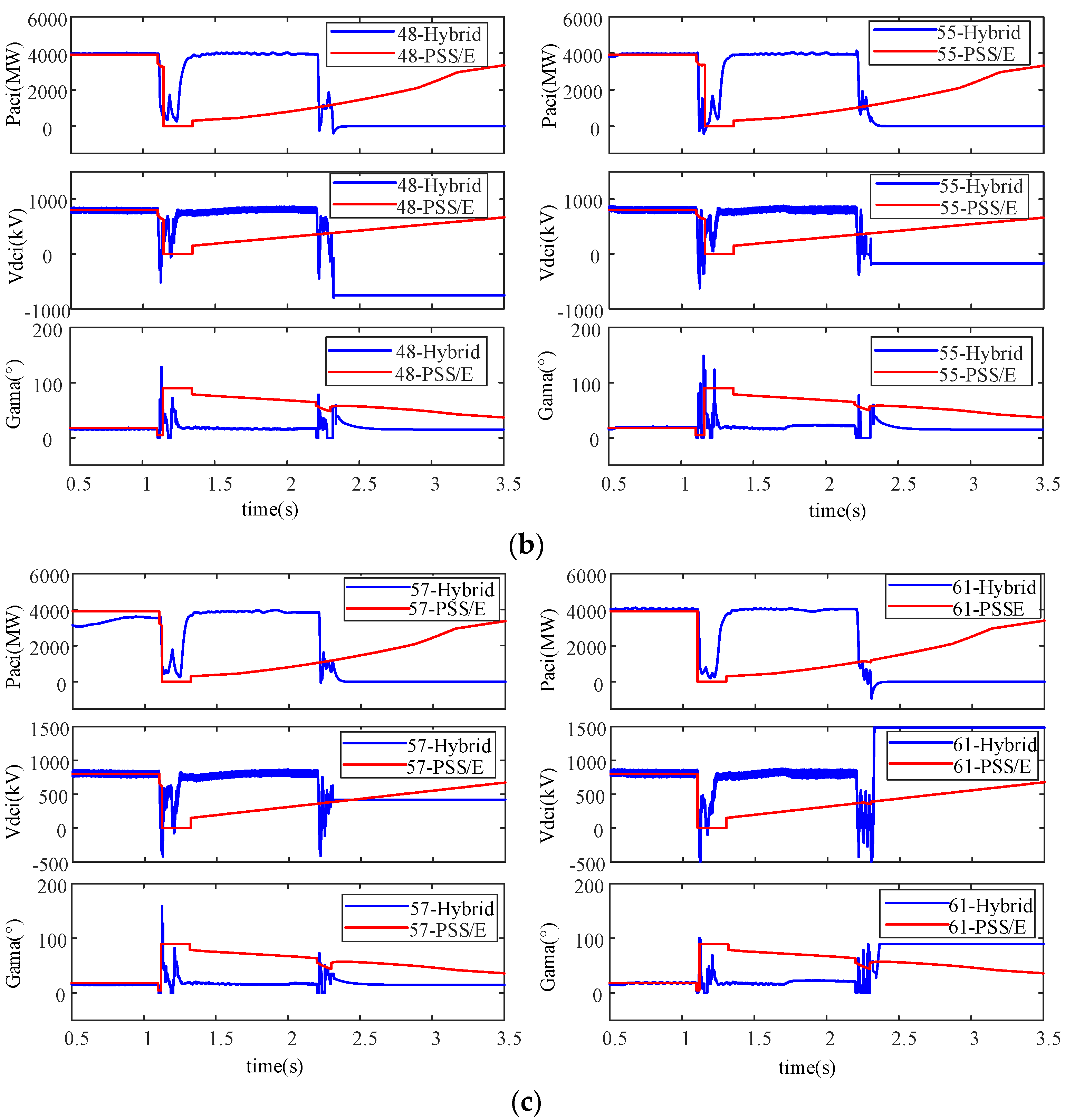
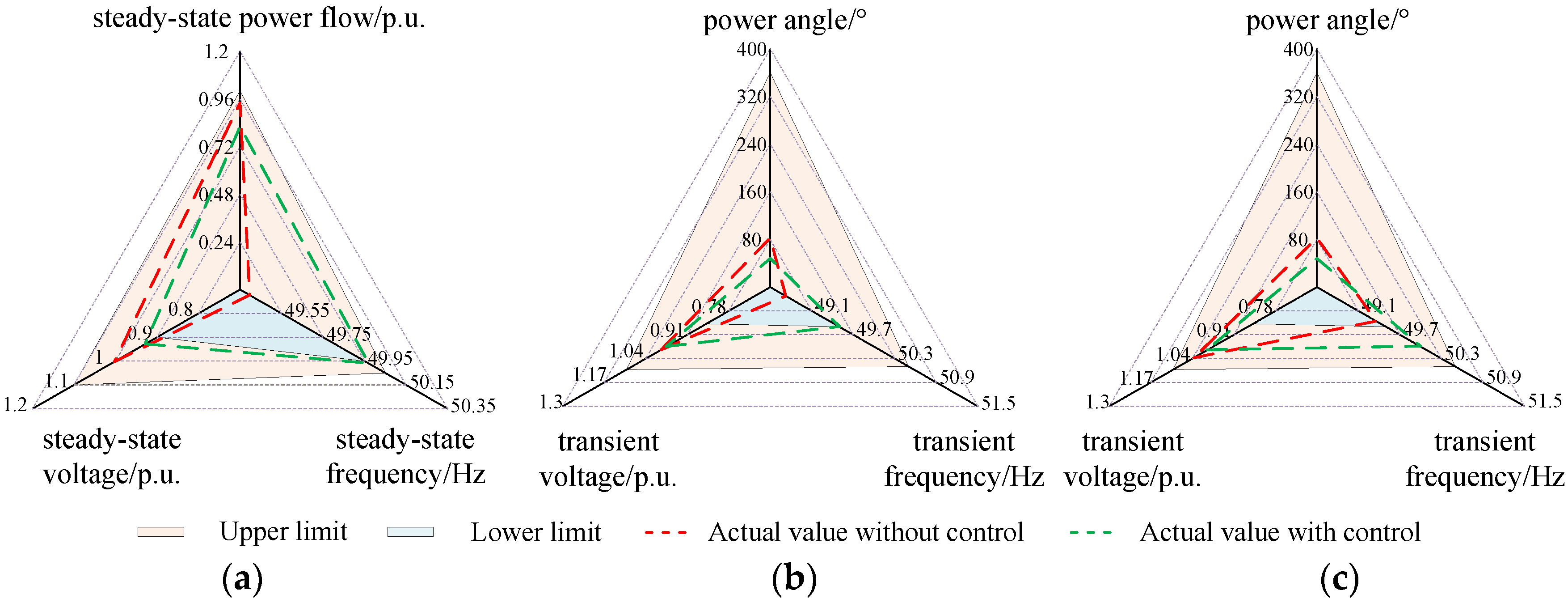
5.1.2. Implementation of Security Assessment and Emergency Control Strategy Decision-Making
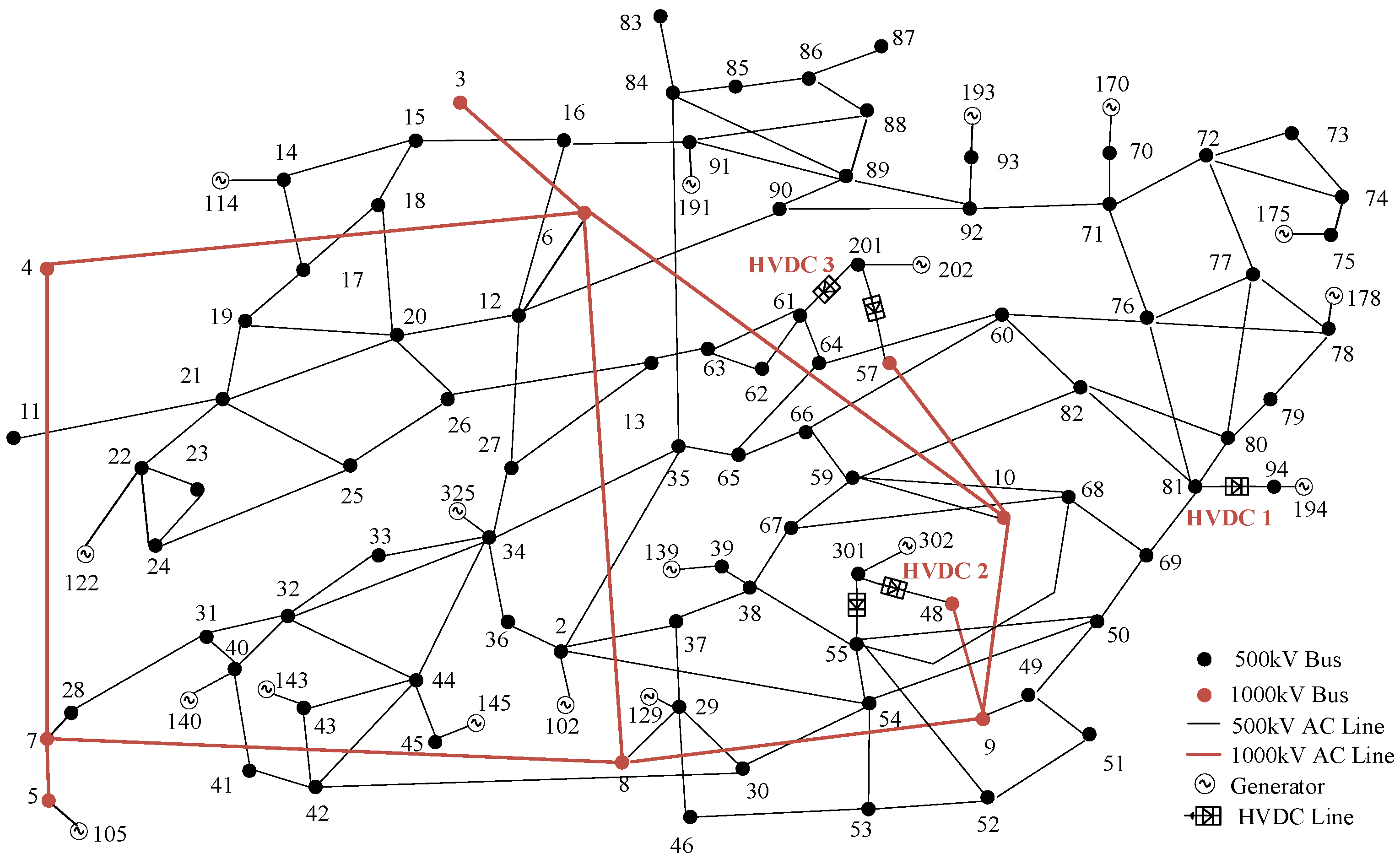
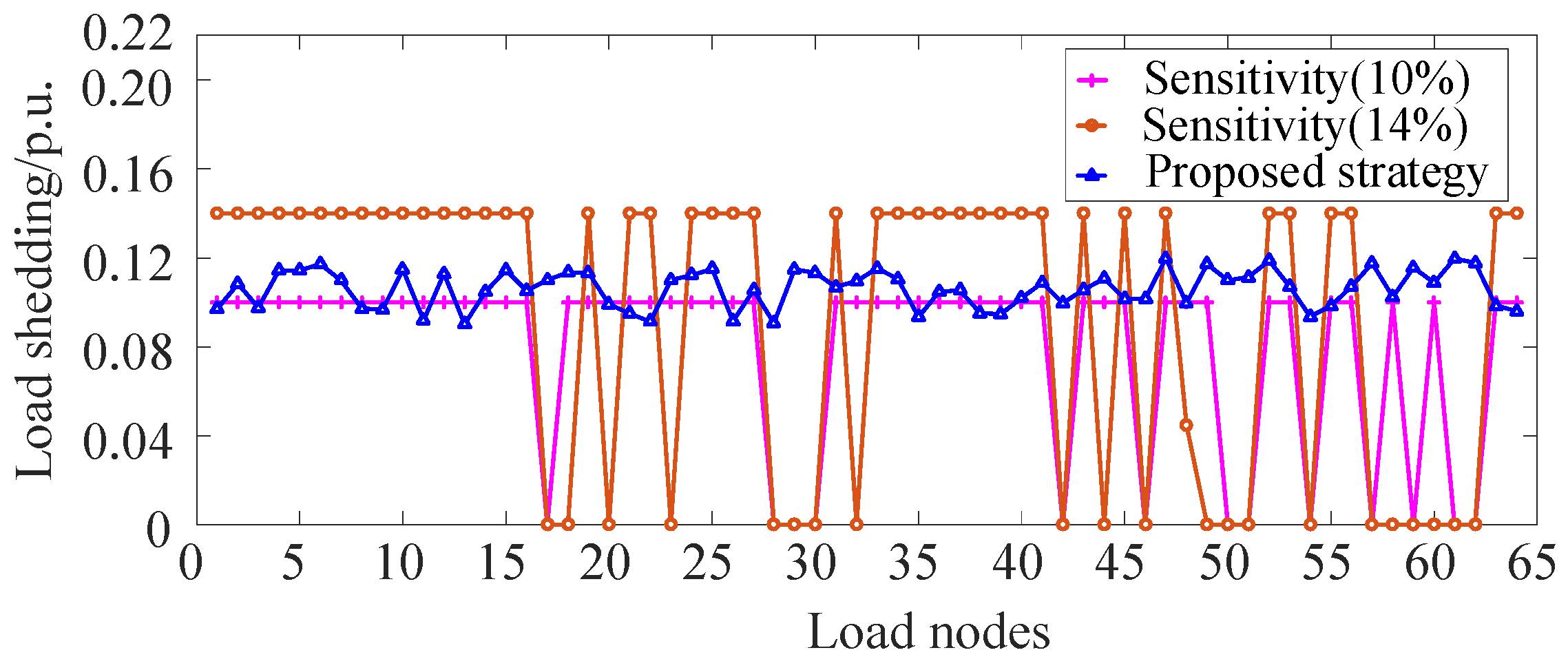
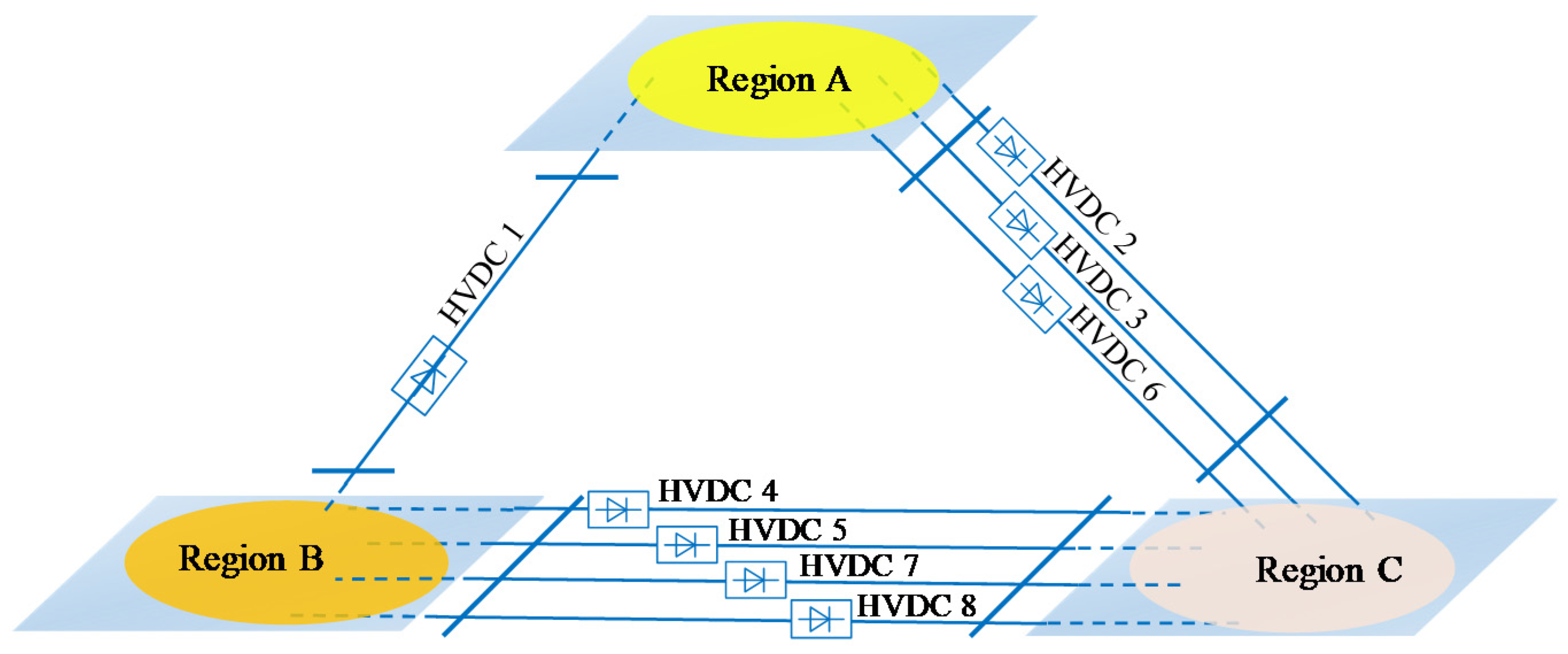
5.2. Test System 2
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pedroso, F.R.V.A.; Bassini, M.T.; Horita, M.A.B.; Jardini, J.A.; Graham, J.F.; Liu, G. HVDC multi-infeed analysis of the Brazilian transmission system and possible mitigation methods. CSEE J. Power Energy Syst. 2018, 4, 487–494. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Liu, L.; Wang, W.; Li, Y.; Cao, Y. Latin hypercube sampling method for location selection of multi-infeed HVDC system terminal. Energies 2020, 13, 1646. [Google Scholar] [CrossRef]
- Li, H.C.; Yuan, Y.B.; Bian, Z.D.; Xu, W. Analysis of frequency emergency control characteristics of UHV AC/DC large receiving end power grid. J. Eng. 2017, 36, 27–31. [Google Scholar] [CrossRef]
- Zhou, B.R.; Rao, H.; Wu, W.; Wang, T.; Hong, C.; Huang, D.Q.; Yao, W.F.; Su, X.R.; Mao, T. Principle and application of asynchronous operation of china southern power grid. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1032–1040. [Google Scholar] [CrossRef]
- Aik, D.L.H.; Andersson, G. Impact of renewable energy sources on steady-state stability of weak AC/DC systems. CSEE J. Power Energy Syst. 2017, 3, 419–430. [Google Scholar] [CrossRef]
- Zhang, F.; Xin, H.H.; Wu, D.; Wang, Z.; Gan, D.Q. Assessing strength of multi-infeed LCC-HVDC systems using generalized short-circuit ratio. IEEE Trans. Power Syst. 2019, 34, 467–480. [Google Scholar] [CrossRef]
- Shao, Y.; Tang, Y. Fast Evaluation of commutation failure risk in multi-infeed HVDC systems. IEEE Trans. Power Syst. 2017, 33, 646–653. [Google Scholar] [CrossRef]
- Wu, P.; Zhao, B.; Guo, J.B.; Bu, G.Q. Coordinated control method of interconnected grid to solve cascading faults of UHVDC valve groups. Power Syst. Technol. 2017, 41, 1460–1467. [Google Scholar]
- Luo, J.; Gong, Y.; Li, H.C. Online emergency control and corrective control coordination strategy for UHVDC blocking faults. In Proceedings of the International Conference on Electronics Technology, Chengdu, China, 23–27 May 2018; pp. 5–10. [Google Scholar]
- Tian, F.; Zhang, X.; Yu, Z.H.; Qiu, W.J.; Shi, D.Y.; Qiu, J.; Liu, M.; Li, Y.L.; Zhou, X.X. On-line decision-making and control of power system stability based on super-real-time simulation. CSEE J. Power Energy Syst. 2016, 2, 95–103. [Google Scholar] [CrossRef]
- Bao, Y.H.; Xu, T.S.; Zhou, H.; Ren, X.C.; Lou, B.L.; Wu, F. An online pre-decision method for security and stability emergency regulation. Electr. Power 2019, 52, 91–97. [Google Scholar]
- Lin, L.; Zhang, K.; Sun, F.; Li, Q.J. Comparison and conversion of dynamic models of speed governor for transient stability analysis in BPA and PSS/E. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Cui, Y.; Feng, N.; Feng, Y.Y.; Yu, Y.H.; Wang, W.H. Evaluation of security and stability risk of AC/DC grid under extreme contingencies. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Xi’an, China, 25–28 October 2016; pp. 1284–1290. [Google Scholar]
- Li, H.; Diao, R.; Zhang, X.; Lin, X.; Lu, X.; Shi, D.; Wang, Z.W.; Wang, L. An integrated online dynamic security assessment system for improved situational awareness and economic operation. IEEE Access 2019, 7, 162571–162582. [Google Scholar] [CrossRef]
- Wang, Y.; Li, K.; Zhang, G.H.; Su, J.J.; Xie, J.P.; Li, J.L. Online dynamic voltage stability assessment method of AC/DC power systems. J. Eng. 2019, 16, 1356–1360. [Google Scholar] [CrossRef]
- Zadkhast, S.; Jatskevich, J.; Vaahedi, E. A multi-decomposition approach for accelerated time-domain simulation of transient stability problems. IEEE Trans. Power Syst. 2015, 30, 2301–2311. [Google Scholar] [CrossRef]
- Kim, S.; Overbye, T.J. Optimal subinterval selection approach for power system transient stability simulation. Energies 2015, 8, 11871–11882. [Google Scholar] [CrossRef]
- Zhan, F.J.; Du, Z.B.; Zhao, F.; Zhang, Y. Analysis of the transient voltage stability of AC/DC system based on numerical energy function method. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Xi’an, China, 25–28 October 2016; pp. 2204–2208. [Google Scholar]
- Chen, X.; Xu, Y.; He, J.H. Transient stability analysis of AC-DC hybrid power systems using direct method. In Proceedings of the 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–6 November 2018; pp. 76–81. [Google Scholar]
- Xu, Y.; Dong, Z.Y.; Zhang, R.; Xue, Y.; Hill, D.J. A decomposition-based practical approach to transient stability-constrained unit commitment. IEEE Trans. Power Syst. 2015, 30, 1455–1464. [Google Scholar] [CrossRef]
- Bhui, P.; Senroy, N. Real-time prediction and control of transient stability using transient energy function. IEEE Trans. Power Syst. 2017, 32, 923–934. [Google Scholar] [CrossRef]
- Xu, T.; Li, G.; Yu, Z.; Zhang, J.; Wang, L.; Li, Y.; Zhang, Y.; Zhuang, K.; Luo, J.; Li, D. Design and Application of emergency coordination control system for multi-infeed HVDC receiving-end system coping with frequency stability problem. Autom. Electr. Power Syst. 2017, 41, 98–104. [Google Scholar]
- Yin, J.J. Research on load friendly interactive technology for safe operation of UHV interconnected power grid. Proc. CSEE 2016, 36, 5715–5723. [Google Scholar]
- Ren, C.; Xu, Y. A fully data-driven method based on generative adversarial networks for power system dynamic security assessment with missing data. IEEE Trans. Power Syst. 2019, 34, 5044–5052. [Google Scholar] [CrossRef]
- Zhang, R.Y.; Wu, J.Y.; Xu, Y.; Li, B.Q.; Shao, M.Y. A hierarchical self-adaptive method for post-disturbance transient stability assessment of power systems using an integrated CNN-based ensemble classifier. Energies 2019, 12, 3217. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Q.; Zhang, B. Transient stability assessment combined model framework based on cost-sensitive method. IET Gener. Transm. Distrib. 2020, 14, 2256–2262. [Google Scholar] [CrossRef]
- Szechtman, M.; Ximenes, M.J.; Saavedra, A.R. Comparative analysis of stability and electromagnetic transient studies for HVDC multi-infeed systems. CSEE J. Power Energy Syst. 2017, 3, 253–259. [Google Scholar] [CrossRef]
- Shekari, T.; Aminifar, F.; Sanaye-Pasand, M. An analytical adaptive load shedding scheme against severe combinational disturbances. IEEE Trans. Power Syst. 2016, 31, 4135–4143. [Google Scholar] [CrossRef]
- Sun, D.; Zhou, H.; Ju, P.; Zhou, R.; Su, D.; Xu, C. Optimization method for emergency load control of receiving-end system considering coordination of economy and voltage stability. Autom. Electr. Power Syst. 2017, 41, 106–112. [Google Scholar]
- Xu, X.; Zhang, H.; Li, C.; Liu, Y.; Li, W.; Terzija, V. Optimization of event-driven emergency load-shedding considering transient security and stability constraints. IEEE Trans. Power Syst. 2017, 32, 2581–2592. [Google Scholar] [CrossRef]
- Zhang, C.L.; Chu, X.D.; Zhang, B.; Ma, L.L.; Li, X.; Wang, X.B.; Wang, L.; Wu, C. A coordinated DC power support strategy for multi-infeed HVDC systems. Energies 2018, 11, 1637. [Google Scholar] [CrossRef]
- Zhang, N.Y.; Zhou, Q.; Hu, H.M. Minimum frequency and voltage stability constrained unit commitment for AC/DC transmission systems. Appl. Sci. 2019, 9, 3412. [Google Scholar] [CrossRef]
- Song, Y.Z.; Meng, J. Optimization strategy of under-frequency load shedding for pumped storage units in power system. Meas. Control Technol. 2017, 36, 52–56. [Google Scholar]
- Li, H.; Yuan, Y.; Zhang, X.; Su, C. The frequency emergency control characteristic analysis for UHV AC/DC large receiving end power grid. Electr. Power Eng. Technol. 2017, 36, 27–31. [Google Scholar] [CrossRef]
- Dong, X.J.; Luo, J.B.; Li, X.M.; Li, B.; Wan, F.; Xue, F.; Wang, Z.; Li, Z. Research and application of frequency emergency coordination and control technology in hybrid AC/DC power grids. Power Syst. Prot. Control 2018, 46, 59–66. [Google Scholar]
- Yuan, S.; Chen, D.Z.; Luo, Y.Z.; Ren, J.; Song, Y.; Jia, L.; Zi, P.; Wang, Q.; Li, Z.; Zhang, C.; et al. Stability characteristics and coordinated control measures of multi-resource for DC blocking fault impacting weak AC channel. Electr. Power Autom. Equip. 2018, 38, 203–210. [Google Scholar]
- Shu, Y.B.; Tang, Y.; Sun, H.D. Research on power system security and stability standards. Proc. CSEE 2013, 33, 1–8. [Google Scholar]
- Jing, L.M.; Wang, B.; Dong, X.Z. Review of consecutive commutation failure research for HVDC transmission system. Electr. Power Autom. Equip. 2019, 39, 116–123. [Google Scholar]
- Pipelzadeh, Y.; Moreno, R.; Chaudhuri, B.; Strbac, G.; Green, T.C. Corrective control with transient assistive measures: Value assessment for Great Britain transmission system. IEEE Trans. Power Syst. 2017, 32, 1638–1650. [Google Scholar]
- Jiang, X.; Li, S. BAS: Beetle antennae search algorithm for optimization problems. Int. J. Robot. Control 2018, 1, 1–5. [Google Scholar] [CrossRef]
- Sauer, P.W.; Tomsovic, K.L.; Vittal, V. Power System Stability and Control, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1985; Chapter 15. [Google Scholar]
- Thio, C.V.; Davies, J.B. Commutation failures in HVDC transmission systems. IEEE Trans. Power Deliv. 1996, 11, 946–957. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Z.; He, H. HVDC Models of PSS/E and their applicability in simulations. Power Syst. Technol. 2004, 28, 25–29. [Google Scholar]
- Li, W.; Niu, S.B.; Lv, Y.Z.; Ke, X.Y.; Huo, C.; Yu, Y.; Xu, Z.; Wen, Y.; Liu, N. HVDC electromechanical transient model and comparison with HVDC electromagnetic transient model. High Volt. Appar. 2018, 54, 155–160. [Google Scholar]
- PSS/E-High-Performance Transmission Planning and Analysis Software. Available online: https://new.siemens.com/global/en/products/energy/services/transmission-distribution-smart-grid/consulting-and-planning/pss-software/pss-e.html (accessed on 10 May 2019).
- PSCAD. Available online: https://hvdc.ca/pscad/ (accessed on 5 March 2019).
- E-Tran. Available online: http://www.electranix.com/software/ (accessed on 15 May 2019).
- Heffernan, M.D.; Tunrer, K.S.; Arrillaga, J.; Arnold, C.P. Computation of AC-DC system disturbances-Parts I: Interactive coordination of generator and convertor transient models. IEEE Trans. Power Appar. Syst. 1981, 100, 4341–4348. [Google Scholar] [CrossRef]
- Tuner, K.S.; Heffernan, M.D.; Arnold, C.P.; Arrillaga, J. Computation of AC-DC system disturbances-Parts II: Derivation of power frequency variables from convertor transient response. IEEE Trans. Power Appar. Syst. 1981, 100, 4349–4355. [Google Scholar] [CrossRef]
- Reeve, J.; Adapa, R. A new approach to dynamic analysis of ac networks incorporating detailed modeling of DC systems. Part I: Principles and implementation. IEEE Trans. Power Deliv. 1988, 3, 2005–2011. [Google Scholar] [CrossRef]
- Zhang, H.; Li, R.; Song, Y.T.; Liu, W.Z. Research on the interface algorithm of power system electromechanical-electromagnetic hybrid simulation. In Proceedings of the 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 296–300. [Google Scholar]
- Shi, Z.; Xu, Y.; Wu, X.Y.; He, J.H.; Yang, R.; Yang, M. Assessment of system protection strategy and aided decision scheme for AC/DC hybrid power systems. Electr. Power Autom. Equip. 2020, 40, 25–31. [Google Scholar]
- Chen, G.P.; Li, M.J.; Xu, T. System protection and its key technologies of UHV AC and DC power grid. Autom. Electr. Power Syst. 2018, 42, 8–16. [Google Scholar]
- Li, G.; Liang, J.; Ma, F.; Ugalde-Loo, C.E.; Liang, H.F. Analysis of single-phase-to-ground faults at the valve-side of HB-MMCs in HVDC systems. IEEE Trans. Ind. Electron. 2019, 66, 2444–2453. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, H.X.; Li, C.G.; Liu, Y.K.; Li, W. Emergency load shedding optimization algorithm based on trajectory sensitivity. Autom. Electr. Power Syst. 2016, 40, 143–148. [Google Scholar]


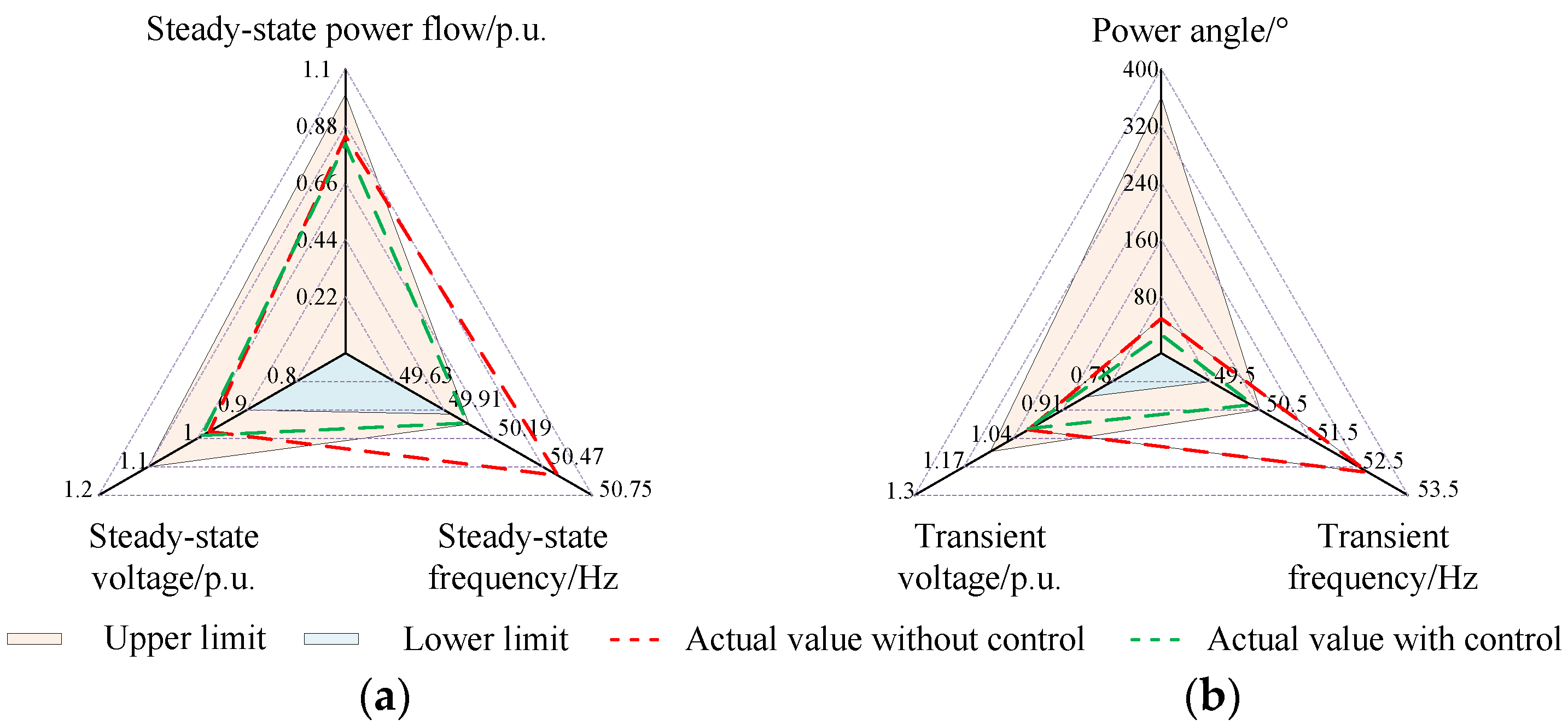
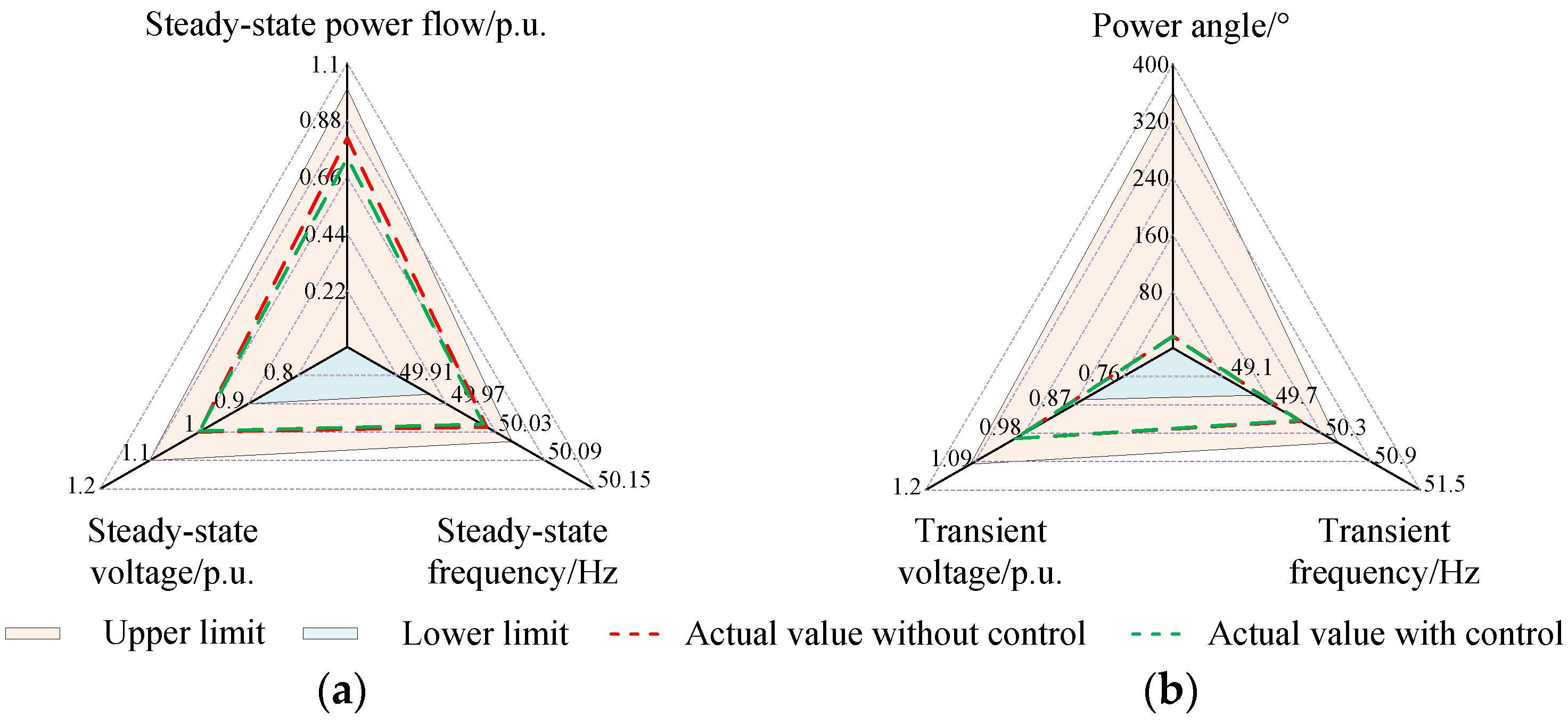
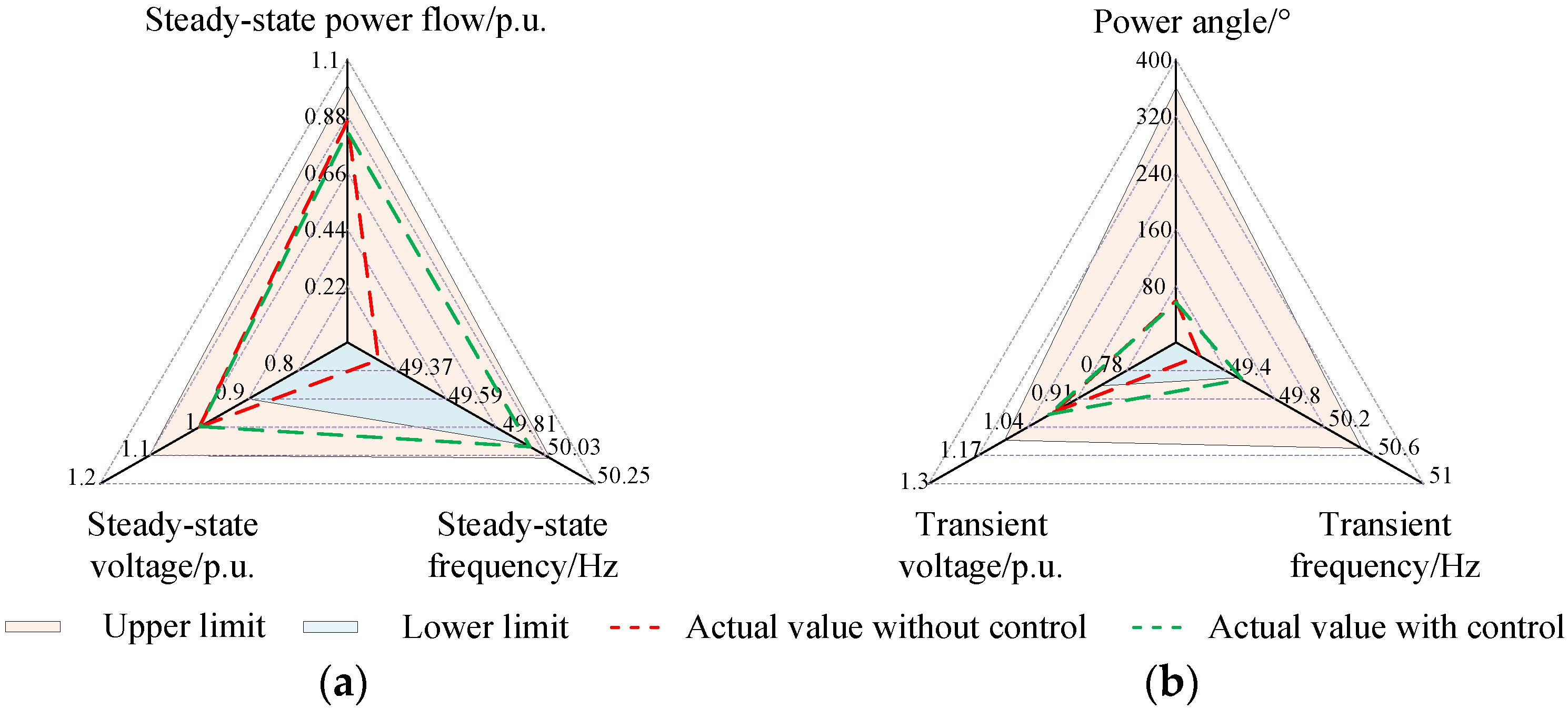
| Simulation Methods | Commutation Failures | Blocking Events |
|---|---|---|
| Pure TS simulation | AC voltage at the inverter side (e.g., 0.785 p.u.) | AC voltage at the rectifier side (e.g., 0.6 p.u.) |
| EMT-TS simulation | Extinction angle (7.2° [44]) | Interval between two commutation failures (200 ms [38]) |
| Static Security Indices | Preset Range | Dynamic Security Indices | Preset Range |
|---|---|---|---|
| steady-state frequency deviation (Hz) | |Δf| < 0.05 | maximum/minimum transient frequency (Hz) | 49.5 < f < 50.5 |
| steady-state voltage deviation (p.u.) | |ΔV| < 0.1 | maximum/minimum transient voltage (p.u.) | 0.85 < V < 1.1 |
| steady-state power flow of lines (p.u.) | p < pmax | maximum transient relative power angle (°) | Δδ < 360° |
| Regions | Capacity of Generators (MW) | Capacity of Loads (MW) | Sending HVDC (MW) | Feeding HVDC (MW) |
|---|---|---|---|---|
| Region A | 8100 | 6363 | 3200 | 800 |
| Region B | 10,000 | 5653 | 4000 | 0 |
| Region C | 9450 | 14,862 | 0 | 5600 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shi, Z.; Wang, Y.; He, J.; Xu, Y.; Li, M. Security Assessment and Coordinated Emergency Control Strategy for Power Systems with Multi-Infeed HVDCs. Energies 2020, 13, 3174. https://doi.org/10.3390/en13123174
Zhang Q, Shi Z, Wang Y, He J, Xu Y, Li M. Security Assessment and Coordinated Emergency Control Strategy for Power Systems with Multi-Infeed HVDCs. Energies. 2020; 13(12):3174. https://doi.org/10.3390/en13123174
Chicago/Turabian StyleZhang, Qiufang, Zheng Shi, Ying Wang, Jinghan He, Yin Xu, and Meng Li. 2020. "Security Assessment and Coordinated Emergency Control Strategy for Power Systems with Multi-Infeed HVDCs" Energies 13, no. 12: 3174. https://doi.org/10.3390/en13123174
APA StyleZhang, Q., Shi, Z., Wang, Y., He, J., Xu, Y., & Li, M. (2020). Security Assessment and Coordinated Emergency Control Strategy for Power Systems with Multi-Infeed HVDCs. Energies, 13(12), 3174. https://doi.org/10.3390/en13123174





