Calculating the Energy Yield of Si-Based Solar Cells for Belgium and Vietnam Regions at Arbitrary Tilt and Orientation under Actual Weather Conditions
Abstract
:1. Introduction
2. Study Objectives
- Develop a model to calculate the total daily, monthly and annual energy yield of arbitrarily oriented PV system based on minimum input parameters of the local weather conditions.
- The model can be transferred easily from one location to another.
- Combine the results of this research with previous studies to analyze the potential application of tandem solar cells in a specific location.
3. Methodology
- Collection of solar irradiance and weather data for study regions;
- Calculation of the solar irradiation incident on the earth and tilt surface;
- Calculation of electric energy yield of Si-based PV panel and tandem solar cells.
3.1. Input Data
3.1.1. Database
3.1.2. Solar Angles Equations
3.1.3. Calculate Solar Radiation on Horizontal and Tilted Surface
3.2. Calculate Solar Energy Yield for Si-Based Tandem Cell and Commercial Panel
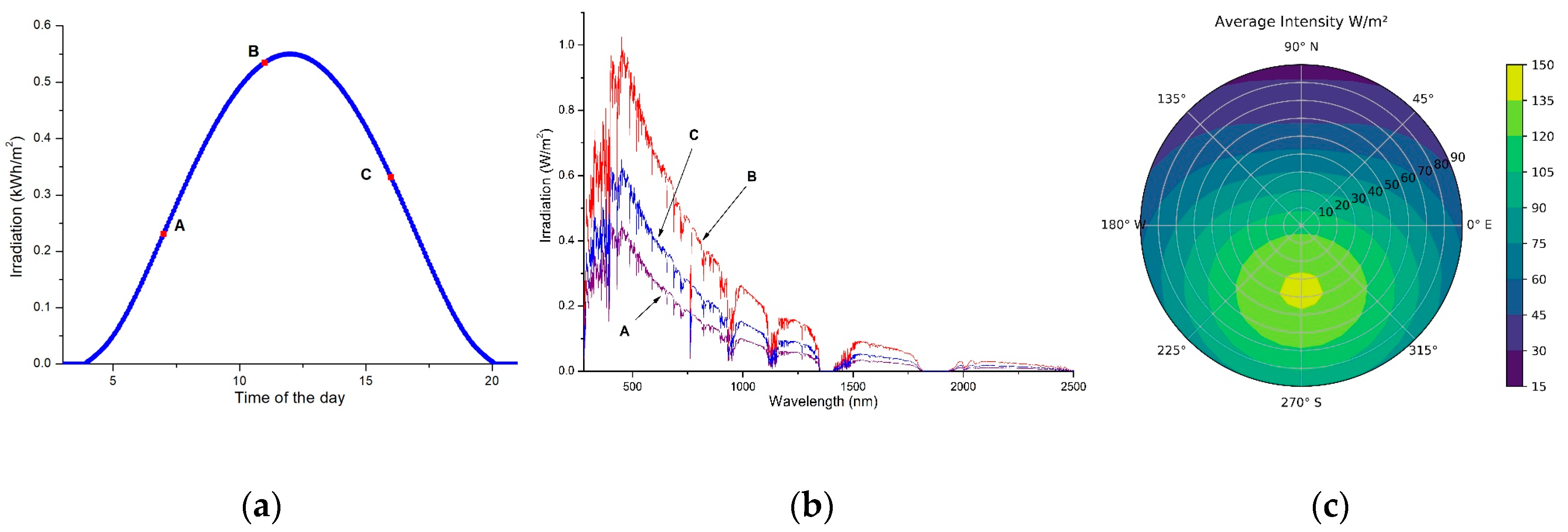
3.3. Estimating Daily Solar Irradiation from Databases
4. Result and Discussion
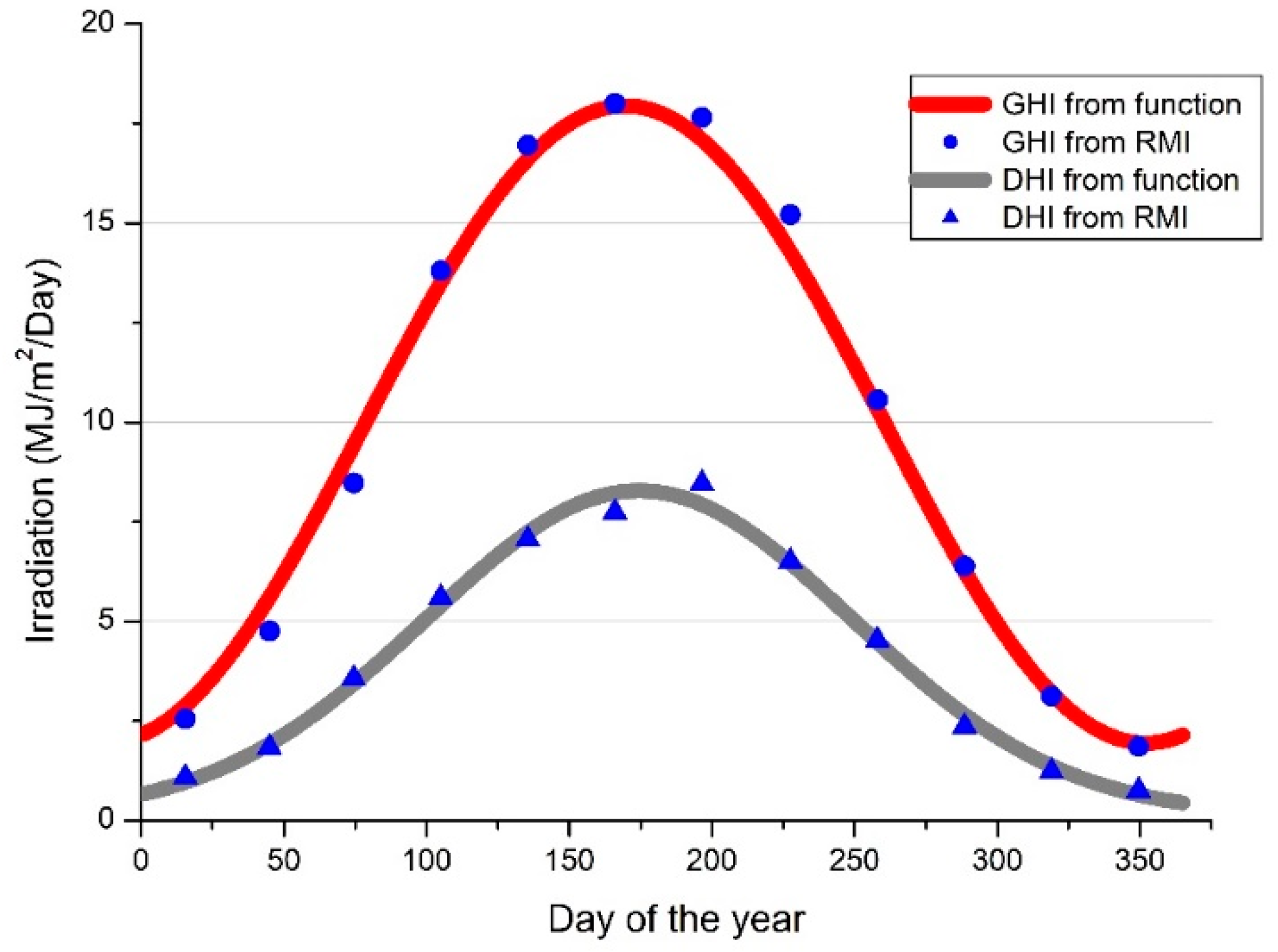
4.1. Daily, Monthly and Annual GHI on the Flat and Tilted Surface
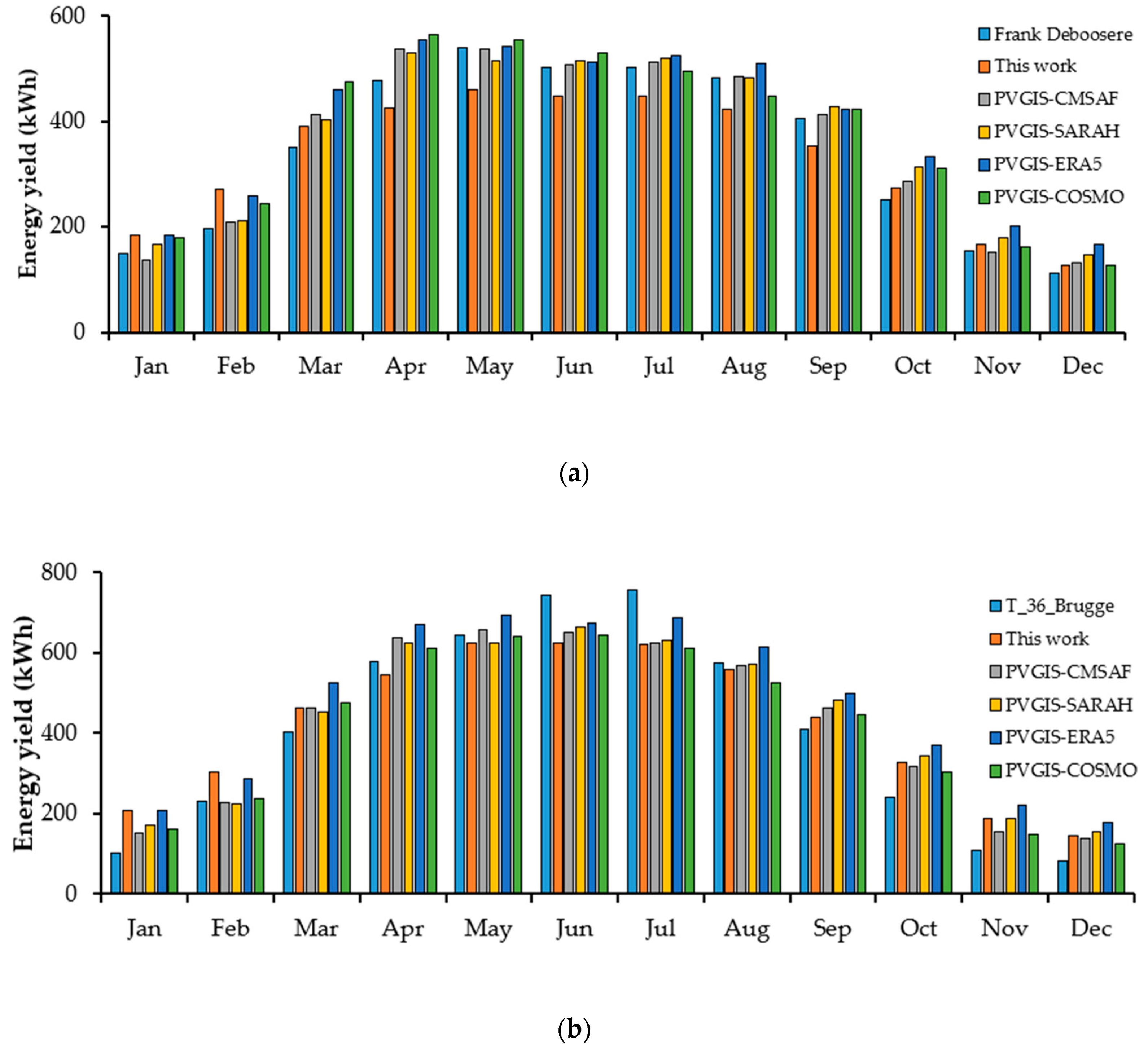
4.2. Energy Yield Calculation for Silicon Solar Panel with Arbitrary Tilt and Orientation in Flanders, Belgium
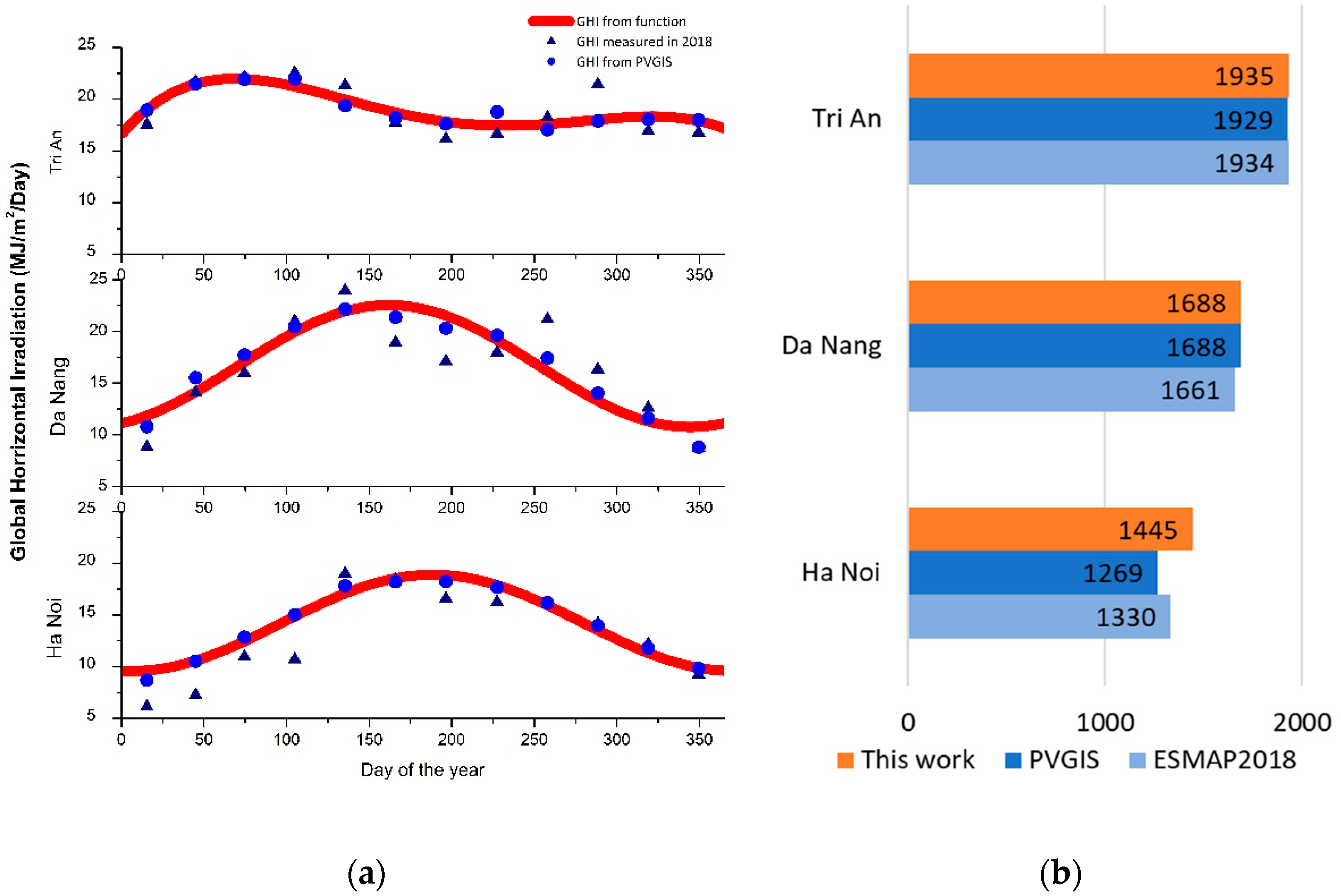
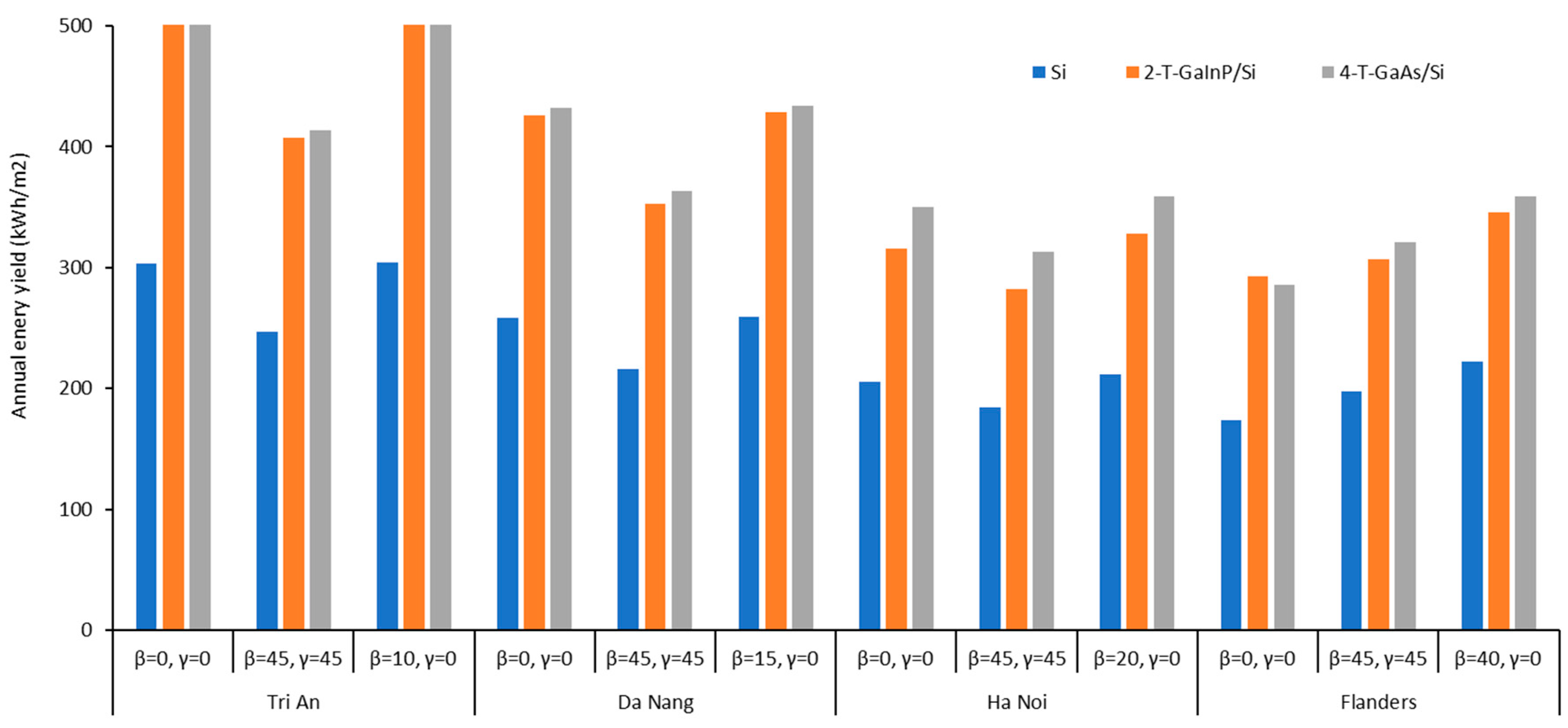
4.3. Transferring the Model to Vietnam Conditions
4.4. Estimation Using EQE of State-of-the Art Solar Cells
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Philips, D.S.; Warmuth, W. Fraunhofer ISE: Photovoltaics Report. Available online: https://www.ise.fraunhofer.de/en/publications/studies/photovoltaics-report.html (accessed on 19 April 2020).
- Battaglia, C.; Cuevas, A.; De Wolf, S. High-efficiency crystalline silicon solar cells: Status and perspectives. Energy Environ. Sci. 2016, 9, 1552–1576. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Yoshikawa, K.; Uzu, H.; Adachi, D. High-efficiency heterojunction crystalline Si solar cells. Jpn. J. Appl. Phys. 2018, 57. [Google Scholar] [CrossRef]
- Andreani, L.C.; Bozzola, A.; Kowalczewski, P.; Liscidini, M.; Redorici, L. Silicon solar cells: Toward the efficiency limits. Adv. Phys. X 2019, 4. [Google Scholar] [CrossRef] [Green Version]
- Richter, A.; Hermle, M.; Glunz, S.W. Reassessment of the limiting efficiency for crystalline silicon solar cells. IEEE J. Photovolt. 2013, 3, 1184–1191. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Lee, K.H.; Araki, K.; Kojima, N. A review of recent progress in heterogeneous silicon tandem solar cells. J. Phys. D. Appl. Phys. 2018, 51. [Google Scholar] [CrossRef]
- Essig, S.; Allebé, C.; Remo, T.; Geisz, J.F.; Steiner, M.A.; Horowitz, K.; Barraud, L.; Ward, J.S.; Schnabel, M.; Descoeudres, A.; et al. Raising the one-sun conversion efficiency of III-V/Si solar cells to 32.8% for two junctions and 35.9% for three junctions. Nat. Energy 2017, 2. [Google Scholar] [CrossRef]
- Mathews, I.; O’Mahony, D.; Corbett, B.; Morrison, A.P. Theoretical performance of multi-junction solar cells combining III-V and Si materials. Opt. Express 2012, 20, A754. [Google Scholar] [CrossRef]
- Faine, P.; Kurtz, S.R.; Riordan, C.; Olson, J.M. The influence of spectral solar irradiance variations on the performance of selected single-junction and multijunction solar cells. Sol. Cells 1991, 31, 259–278. [Google Scholar] [CrossRef]
- Eke, R.; Betts, T.R.; Gottschalg, R. Spectral irradiance effects on the outdoor performance of photovoltaic modules. Renew. Sustain. Energy Rev. 2017, 69, 429–434. [Google Scholar] [CrossRef] [Green Version]
- Pérez-López, J.J.; Fabero, F.; Chenlo, F. Experimental solar spectral irradiance until 2500 nm: Results and influence on the PV conversion of different materials. Prog. Photovolt. Res. Appl. 2007, 15, 303–315. [Google Scholar] [CrossRef]
- Gulkowski, S.; Zdyb, A.; Dragan, P. Experimental efficiency analysis of a photovoltaic system with different module technologies under temperate climate conditions. Appl. Sci. 2019, 9. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Ren, Z.; Liu, Z.; Aberle, A.G.; Buonassisi, T.; Peters, I.M. Predicting the outdoor performance of flat-plate III–V/Si tandem solar cells. Sol. Energy 2017, 149, 77–84. [Google Scholar] [CrossRef]
- Al Garni, H.Z.; Awasthi, A.; Wright, D. Optimal orientation angles for maximizing energy yield for solar PV in Saudi Arabia. Renew. Energy 2019, 133, 538–550. [Google Scholar] [CrossRef]
- Abdallah, R.; Juaidi, A.; Abdel-Fattah, S.; Manzano-Agugliaro, F. Estimating the optimum tilt angles for south-facing surfaces in Palestine. Energies 2020, 13. [Google Scholar] [CrossRef] [Green Version]
- Mubarak, R.; Luiz, E.W.; Seckmeyer, G. Why PV modules should preferably no longer be oriented to the south in the near future. Energies 2019, 12. [Google Scholar] [CrossRef] [Green Version]
- Ustun, T.S.; Nakamura, Y.; Hashimoto, J.; Otani, K. Performance analysis of PV panels based on different technologies after two years of outdoor exposure in Fukushima, Japan. Renew. Energy 2019, 136, 159–178. [Google Scholar] [CrossRef]
- Bora, B.; Kumar, R.; Sastry, O.S.; Prasad, B.; Mondal, S.; Tripathi, A.K. Energy rating estimation of PV module technologies for different climatic conditions. Sol. Energy 2018, 174, 901–911. [Google Scholar] [CrossRef]
- Schulte-Huxel, H.; Silverman, T.J.; Deceglie, M.G.; Friedman, D.J.; Tamboli, A.C. Energy Yield Analysis of Multiterminal Si-Based Tandem Solar Cells. IEEE J. Photovolt. 2018, 8, 1376–1383. [Google Scholar] [CrossRef]
- Müller, B.; Hardt, L.; Armbruster, A.; Kiefer, K.; Reise, C. Yield predictions for photovoltaic power plants: Empirical validation, recent advances and remaining uncertainties. Prog. Photovolt. Res. Appl. 2016, 24, 570–583. [Google Scholar] [CrossRef]
- Virtuani, A.; Strepparava, D. Modelling the performance of amorphous and crystalline silicon in different typologies of building-integrated photovoltaic (BIPV) conditions. Sol. Energy 2017, 146, 113–118. [Google Scholar] [CrossRef]
- Muñoz, J.; Perpiñán, O. A simple model for the prediction of yearly energy yields for grid-connected PV systems starting from monthly meteorological data. Renew. Energy 2016, 97, 680–688. [Google Scholar] [CrossRef] [Green Version]
- Royal Meteorological Institute of Belgium. Available online: https://www.meteo.be/resources/climatology/climateCity/pdf/climate_INS44021_nl.pdf (accessed on 19 April 2020).
- Amillo, A.G.; Huld, T.; Müller, R. A new database of global and direct solar radiation using the eastern meteosat satellite, models and validation. Remote Sens. 2014, 6, 8165–8189. [Google Scholar] [CrossRef] [Green Version]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- PVGIS. Available online: http://re.jrc.ec.europa.eu/pvgis/ (accessed on 19 April 2020).
- Polo, J.; Gastón, M.; Vindel, J.M.; Pagola, I. Spatial variability and clustering of global solar irradiation in Vietnam from sunshine duration measurements. Renew. Sustain. Energy Rev. 2015, 42, 1326–1334. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems; Elsevier Inc.: Amsterdam, The Netherlands, 2009; ISBN 9780123745019. [Google Scholar]
- Strubble, F.; Beekman, J. Solar Cells; Ghent University: Ghent, Belgium, 2016; pp. 22–27. [Google Scholar]
- Demoulias, C. A new simple analytical method for calculating the optimum inverter size in grid-connected PV plants. Electr. Power Syst. Res. 2010, 80, 1197–1204. [Google Scholar] [CrossRef]
- Faranda, R.S.; Hafezi, H.; Leva, S.; Mussetta, M.; Ogliari, E. The optimum PV plant for a given solar DC/AC converter. Energies 2015, 8, 4853–4870. [Google Scholar] [CrossRef]
- Nann, S.; Riordan, C. Solar spectral irradiance under clear and cloudy skies: Measurements and a semiempirical model. J. Appl. Meteorol. 1991, 30, 447–462. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, P.; Schüttauf, J.W.A.; van der Werf, C.H.M.; Houshyani Hassanzadeh, B.; van Sark, W.G.J.H.M.; Schropp, R.E.I. Response to simulated typical daily outdoor irradiation conditions of thin-film silicon-based triple-band-gap, triple-junction solar cells. Sol. Energy Mater. Sol. Cells 2009, 93, 691–697. [Google Scholar] [CrossRef] [Green Version]
- Reference Solar Spectral Irradiance: Air Mass 1.5. Available online: https://rredc.nrel.gov/solar//spectra/am1.5/ (accessed on 20 February 2020).
- International Electro-Technical Commission. Standard IEC 60904-3: Photovoltaic Devices. Part 3: Measurement Principles for Terrestrial Photovoltaic (PV) Solar Devices with Reference Spectral Irradiance; International Electro-Technical Commission: Geneva, Switzerland, 2008. [Google Scholar]
- Abdul Jalil, M.A.; Abdul Karim, S.A.; Baharuddin, Z.; Abdullah, M.F.; Othman, M. Forecasting Solar Radiation Data Using Gaussian and Polynomial Fitting Methods; Springer: Singapore, 2018; pp. 11–24. ISBN 978-981-13-0434-7. [Google Scholar]
- Frankdeboosere. Available online: https://www.frankdeboosere.be/zonnepanelen/zonnepanelen.php (accessed on 30 March 2020).
- T_36_Brugge_Belgium. Available online: https://pvoutput.org/ (accessed on 20 April 2020).
- Polo, J.; Bernardos, A.; Navarro, A.A.; Fernandez-Peruchena, C.M.; Ramírez, L.; Guisado, M.V.; Martínez, S. Solar resources and power potential mapping in Vietnam using satellite-derived and GIS-based information. Energy Convers. Manag. 2015, 98, 348–358. [Google Scholar] [CrossRef]
- Nguyen, B.T.; Pryor, T.L. The relationship between global solar radiation and sunshine duration in Vietnam. Renew. Energy 1997, 11, 47–60. [Google Scholar] [CrossRef]
- PVWatts Calculator. Available online: https://pvwatts.nrel.gov/index.php (accessed on 20 April 2020).
- Almansouri, I.; Ho-Baillie, A.; Bremner, S.P.; Green, M.A. Supercharging Silicon Solar Cell Performance by Means of Multijunction Concept. IEEE J. Photovolt. 2015, 5, 968–976. [Google Scholar] [CrossRef]





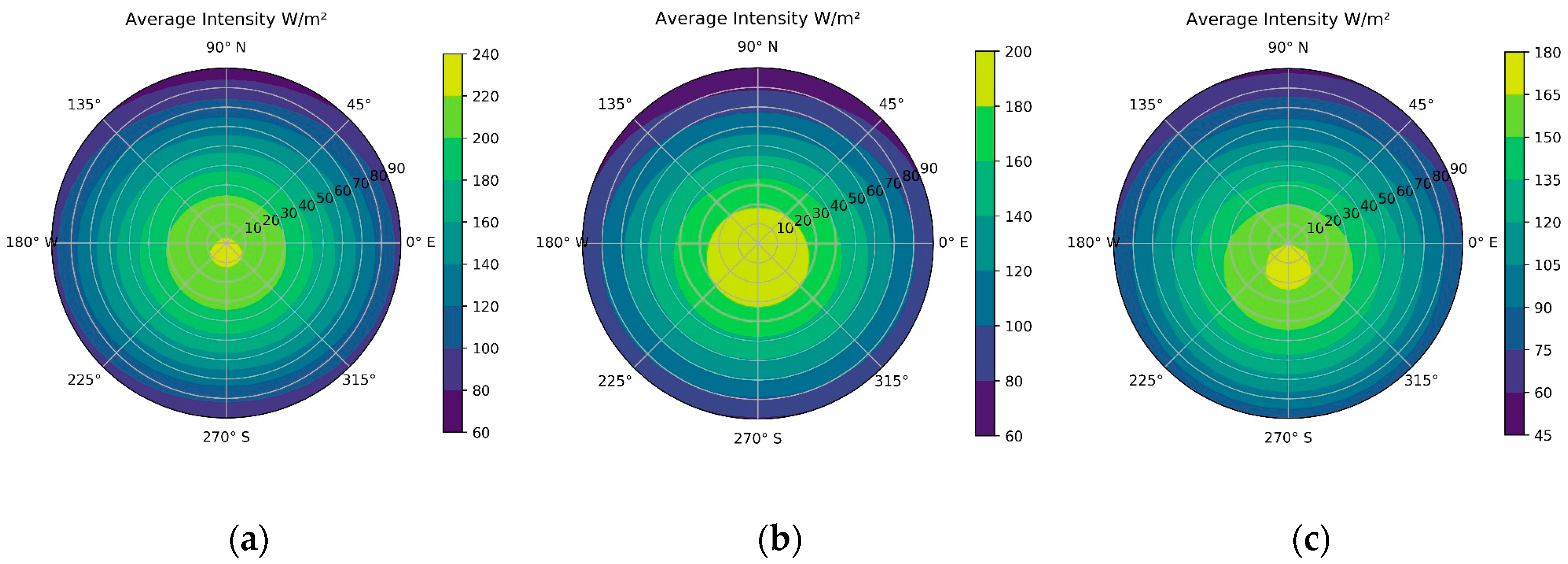
| Location | Latitude | Longitude | Average Temperature | Years (Database) |
|---|---|---|---|---|
| (deg) | (deg) | |||
| Flanders, Belgium | 51 | 003 | 15 °C | 1984–2013 (RMI) |
| Tri An, Vietnam | 11 | 107 | 28 °C | 2005–2016 (PVGIS), 2018 (ESMAP) |
| Da Nang, Vietnam | 16 | 108 | 26 °C | 2005–2016 (PVGIS), 2018 (ESMAP) |
| Ha Noi, Vietnam | 21 | 106 | 25 °C | 2005–2016 (PVGIS), 2018 (ESMAP) |
| Installation | Latitude | Temperature | γ | Power | |
|---|---|---|---|---|---|
| (deg) | (deg) | (deg) | (deg) | (panels × Wp = kWp) | |
| Frank Deboosere | 51 | 15 | 45 | 292.5 (SSE) | 25 × 175 = 4.35 |
| T_36_Brugge | 51 | 15 | 45 | 225 (SW) | 22 × 240 = 5.280 |
| System | Frank Deboosere | T_36_Brugge | ||
|---|---|---|---|---|
| Yield (kWh) | Deviation (%) | Yield (kWh) | Deviation (%) | |
| Actual Installation | 4123 | 4869 | ||
| This work | 3972 | 3.67 | 5042 | 3.54 |
| PVGIS-CMSAF | 4323 | 4.85 | 5846 | 3.51 |
| PVGIS-SARAH | 4415 | 7.08 | 5858 | 5.24 |
| PVGIS-ERA5 | 4678 | 13.46 | 6587 | 15.53 |
| PVGIS-COSMO | 4512 | 9.43 | 5619 | 1.27 |
| Unit: kWh/kWp | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Annual | ||
| Tri An | This work | 149 | 154 | 174 | 162 | 156 | 141 | 138 | 135 | 132 | 141 | 139 | 140 | 1760 |
| PVGIS-SARAH | 140 | 145 | 160 | 149 | 146 | 134 | 138 | 144 | 126 | 133 | 131 | 134 | 1680 | |
| PVWATTS | 147 | 143 | 165 | 166 | 128 | 115 | 113 | 118 | 114 | 134 | 139 | 141 | 1622 | |
| Da Nang | This work | 88 | 97 | 132 | 152 | 173 | 172 | 169 | 150 | 120 | 100 | 81 | 79 | 1513 |
| PVGIS-SARAH | 83 | 108 | 134 | 148 | 162 | 151 | 148 | 145 | 126 | 107 | 86 | 67 | 1466 | |
| PVWATTS | 86 | 82 | 102 | 120 | 135 | 125 | 133 | 129 | 117 | 107 | 94 | 80 | 1308 | |
| Ha Noi | This work | 70 | 70 | 93 | 109 | 131 | 138 | 146 | 138 | 118 | 103 | 81 | 72 | 1269 |
| PVGIS-SARAH | 75 | 82 | 111 | 125 | 153 | 152 | 157 | 152 | 135 | 120 | 98 | 85 | 1445 | |
| PVWATTS | 62 | 52 | 72 | 104 | 142 | 139 | 143 | 132 | 135 | 118 | 102 | 88 | 1288 | |
| Unit: kWh/m2 | ||||
|---|---|---|---|---|
| Tri An | Da Nang | Ha Noi | Flanders | |
| Si | 304.3 | 260.3 | 260.1 | 219.6 |
| 2-T-GaInP/Si | 506.7 | 430.1 | 429.9 | 346.2 |
| 4-T-GaInP/Si | 551.7 | 476.8 | 476.1 | 372.2 |
| 2-T-GaAs/Si | 187.6 | 155.4 | 115.3 | 155.7 |
| 4-T-GaAs/Si | 507.3 | 435.1 | 358.9 | 355.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.P.N.; Lauwaert, J. Calculating the Energy Yield of Si-Based Solar Cells for Belgium and Vietnam Regions at Arbitrary Tilt and Orientation under Actual Weather Conditions. Energies 2020, 13, 3180. https://doi.org/10.3390/en13123180
Nguyen DPN, Lauwaert J. Calculating the Energy Yield of Si-Based Solar Cells for Belgium and Vietnam Regions at Arbitrary Tilt and Orientation under Actual Weather Conditions. Energies. 2020; 13(12):3180. https://doi.org/10.3390/en13123180
Chicago/Turabian StyleNguyen, D. P. N., and Johan Lauwaert. 2020. "Calculating the Energy Yield of Si-Based Solar Cells for Belgium and Vietnam Regions at Arbitrary Tilt and Orientation under Actual Weather Conditions" Energies 13, no. 12: 3180. https://doi.org/10.3390/en13123180
APA StyleNguyen, D. P. N., & Lauwaert, J. (2020). Calculating the Energy Yield of Si-Based Solar Cells for Belgium and Vietnam Regions at Arbitrary Tilt and Orientation under Actual Weather Conditions. Energies, 13(12), 3180. https://doi.org/10.3390/en13123180





