Experimental Investigation of the Prestrike Characteristics of a Double-Break Vacuum Circuit Breaker under DC Voltages
Abstract
1. Introduction
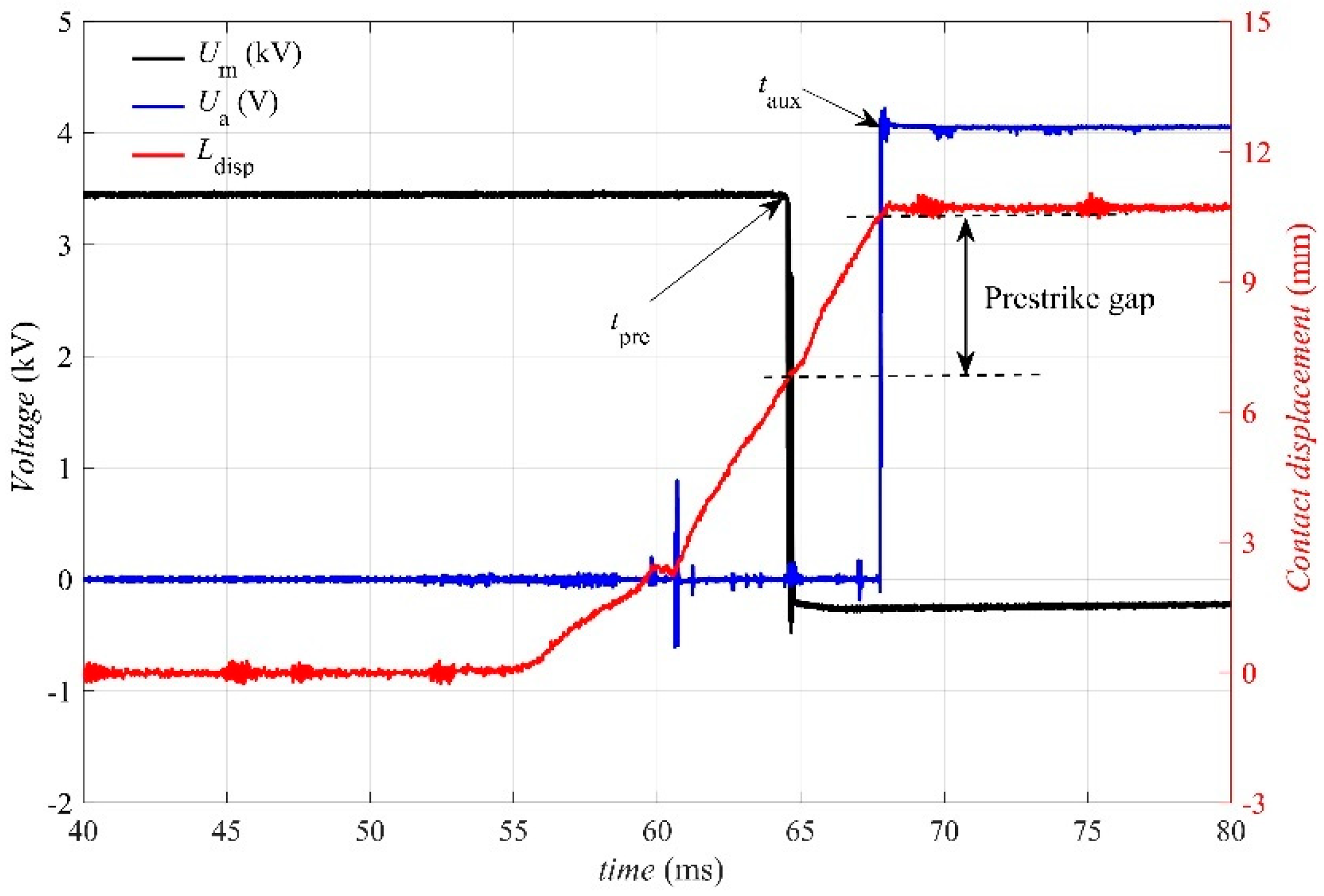
2. Experimental Setup
3. Experimental Results
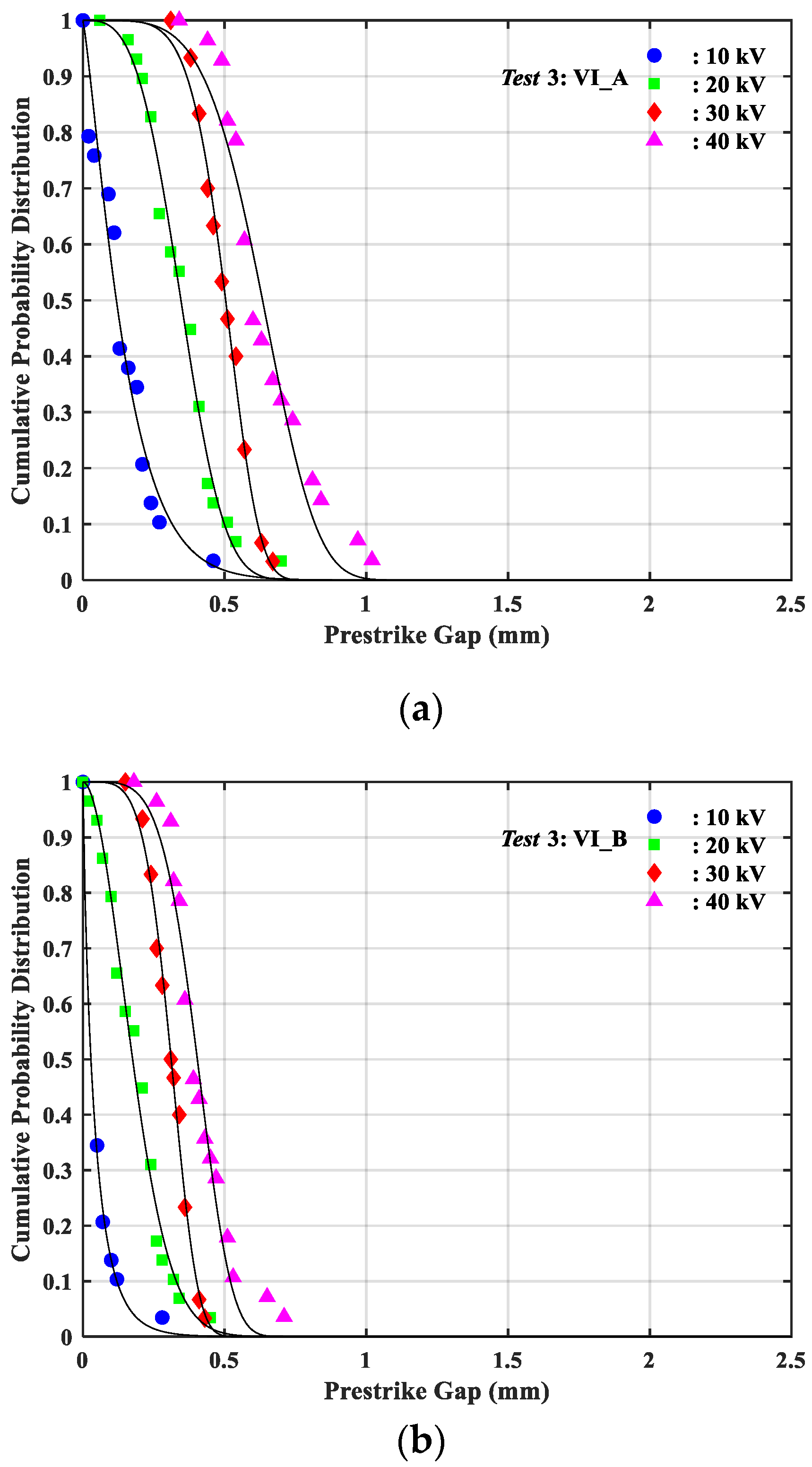
3.1. Probabilistic Characteristics of the Pestrike Gap
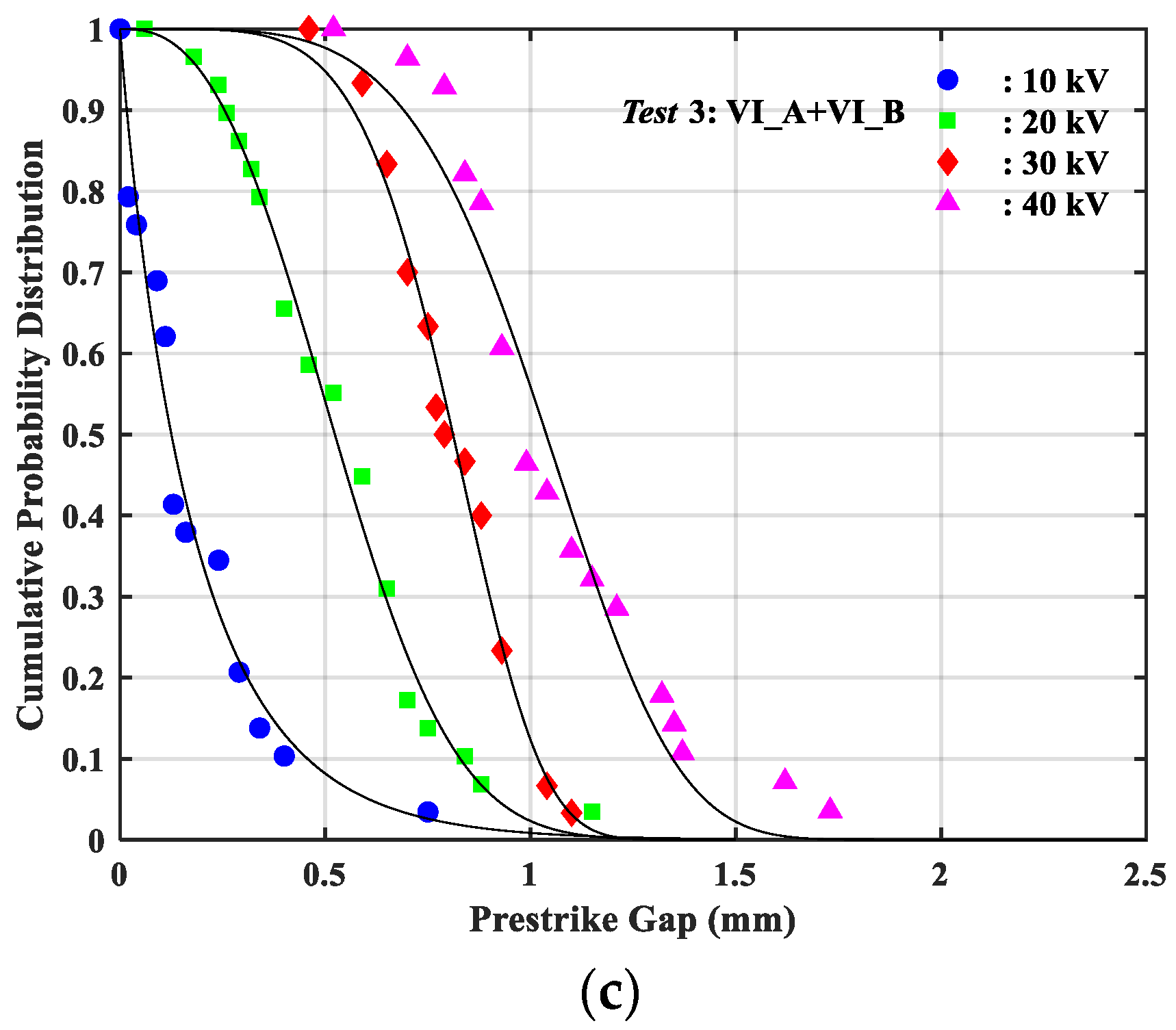
3.2. Scatters in the Prestrike Gap
4. Discussion
4.1. Positive Effects of the Double-Break Vacuum Circuit Breaker
4.2. Negative Effects of the Double-Break Vacuum Circuit Breaker
5. Conclusions
- (1)
- With the increment of the applied DC voltage, the 10% prestrike gap d10, 50% prestrike gap d50 and 90% prestrike gap d90 were all increasing significantly, whereas the scatters in the prestrike gaps were not changing too much. Specifically, the value of d50 was approximately proportional to the applied voltage.
- (2)
- With a given applied DC voltage, the positive effect of the double-break VCBs on the prestrike characteristics can be observed, i.e., the prestrike gaps of the vacuum interrupters in the double-break tests can be significantly reduced in comparison with that in the single-break tests due to the voltage-sharing effect in double-break VCBs. Moreover, fewer scatters in the prestrike gaps during the double-break tests can be found.
- (3)
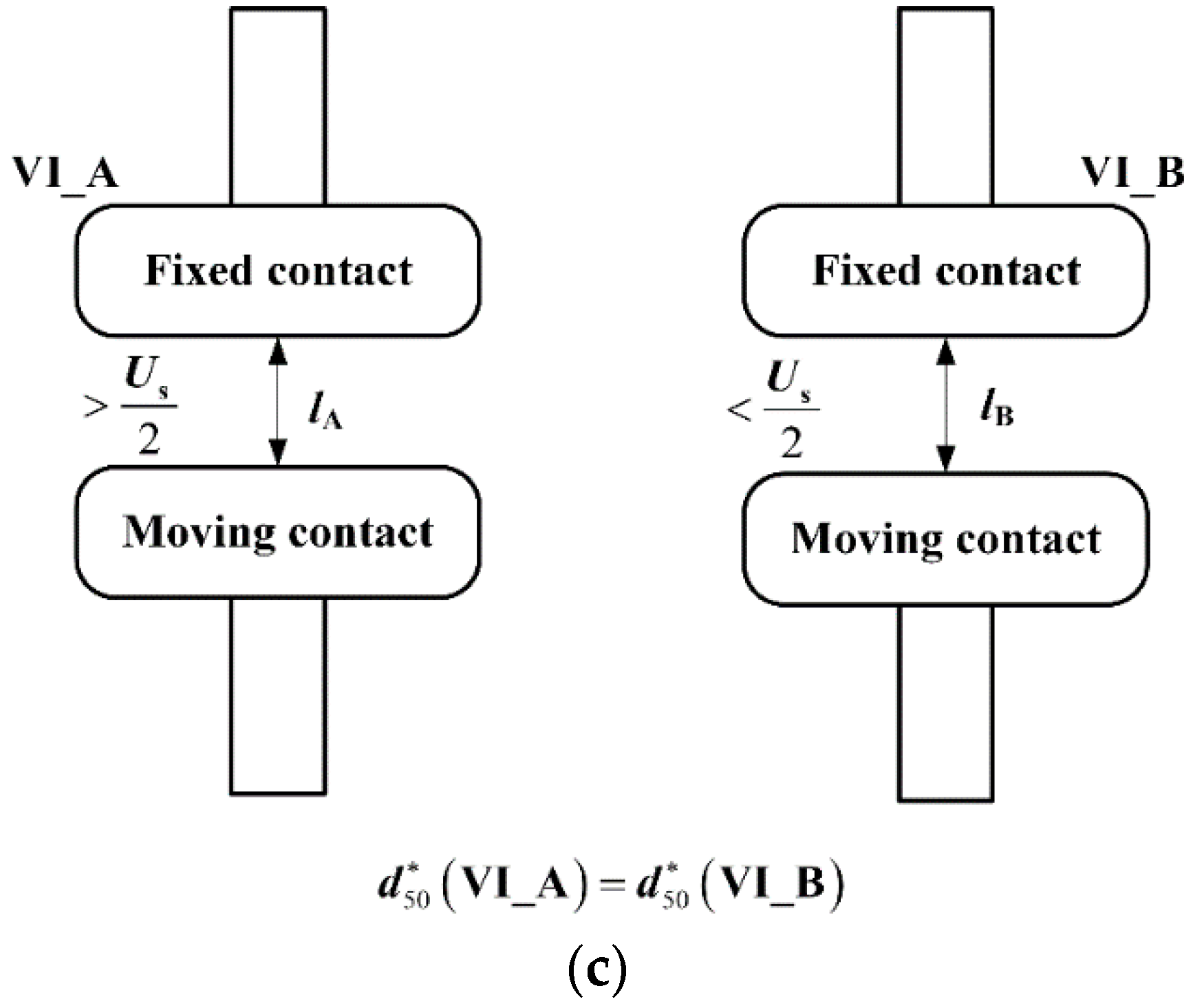
- The double-break VCB with two vacuum interrupters in series did not take full advantage of the dielectric strength of the vacuum gap on the low-voltage side, i.e., the negative effect of a double-break VCB on the prestrike characteristics, which may be caused by the asynchronous property of the mechanical actuators, the inhomogeneity of the inherent prestrike characteristics and the unequal voltage-sharing ratio of VIs in a double-break VCB.
Author Contributions
Funding
Conflicts of Interest
References
- Ide, N.; Tanaka, O.; Yanabu, S.; Kaneko, S.; Okabe, S.; Matsui, Y. Interruption characteristics of double-break vacuum circuit breakers. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1065–1072. [Google Scholar] [CrossRef]
- Ge, G.; Liao, M.; Duan, X.; Cheng, X.; Zhao, Y.; Liu, Z.; Zou, J. Experimental Investigation into the Synergy of Vacuum Circuit Breaker with Double-Break. IEEE Trans. Plasma Sci. 2016, 44, 79–84. [Google Scholar] [CrossRef]
- Giere, S.; Karner, H.C.; Knobloch, H. Dielectric strength of double and single-break vacuum interrupters: Experiments with real HV demonstration bottles. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 43–47. [Google Scholar] [CrossRef]
- Fugel, T.; Koenig, D. Switching performance of two 24 kV vacuum interrupters in series. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 164–168. [Google Scholar] [CrossRef]
- Delachaux, T.; Rager, F.; Gentsch, D. Study of vacuum circuit breaker performance and weld formation for different drive closing speeds for switching capacitive current. In Proceedings of the 24th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV2010), Braunschweig, Germany, 30 August–3 September 2010; pp. 241–244. [Google Scholar]
- Zhang, Y.; Xu, X.; Jin, L.; An, Z.; Zhang, Y. Fractal-based electric field enhancement modeling of vacuum gap electrodes. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1957–1964. [Google Scholar] [CrossRef]
- Slade, P.G. The Vacuum Interrupter Theory, Design and Application; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Descoeudres, A.; Ramsvik, T.; Calatroni, S.; Taborelli, M.; Wuensch, W. DC breakdown conditioning and breakdown rate of metals and metallic alloys under ultrahigh vacuum. Phys. Rev. Spec. Top. Accel. Beams 2009, 12. [Google Scholar] [CrossRef]
- Latham, R.V. High Voltage and Vacuum Insulation: Basic Concepts and Technological Practice; Academic Press: London, UK, 1995. [Google Scholar]
- Slade, P.G.; Taylor, E.D.; Haskins, R.E. Effect of short circuit current duration on the welding of closed contacts in vacuum. In Proceedings of the 51th IEEE Holm Conference on Electrical Contacts, Chicago, IL, USA, 26–28 September 2005; pp. 69–74. [Google Scholar]
- Slade, P.G.; Smith, R.K.; Taylor, E.D. The effect of contact closure in vacuum with fault current on prestrike arcing time, contact welding and the field enhancement factor. In Proceedings of the 2007 53rd IEEE Holm Conference on Electrical Contacts, Pittsburgh, PA, USA, 16–19 September 2007; pp. 32–36. [Google Scholar]
- Dullni, E.; Shang, W.; Gentsch, D.; Kleberg, I.; Niayesh, K. Switching of Capacitive Currents and the Correlation of Restrike and Pre-ignition Behavior. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 65–71. [Google Scholar] [CrossRef]
- Körner, F.; Lindmayer, M.; Kurrat, M.; Gentsch, D. Contact Behavior in vacuum under capacitive switching duty. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 643–648. [Google Scholar] [CrossRef]
- Körner, F.; Lindmayer, M.; Kurrat, M.; Gentsch, D. Switching behavior of different contacts materials under capacitive switching conditions. In Proceedings of the 23rd International Symposium on Discharges Electrical Insulation in Vacuum, Braunschweig, Germany, 15–19 September 2008; pp. 202–205. [Google Scholar]
- Kumichev, G.A.; Poluyanova, I.N. Investigation of welding characteristics and NSDD probabilities of different contact materials under capacitive load conditions. In Proceedings of the 27th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV), Suzhou, China, 18–23 September 2016; pp. 1–4. [Google Scholar]
- Yu, Y.; Li, G.; Geng, Y.; Wang, J.; Liu, Z. Prestrike inrush current arc behaviors in vacuum interrupters subjected to a transverse magnetic field and an axial magnetic field. IEEE Trans. Plasma Sci. 2018, 46, 3075–3082. [Google Scholar] [CrossRef]
- Yu, Y.; Geng, Y.; Geng, Y.; Wang, J.; Liu, Z. Inrush current prestrike arc behaviours of contact materials CuCr50/50 and CuW10/90. IEEE Trans. Plasma Sci. 2017, 45, 266–274. [Google Scholar] [CrossRef]
- Geng, Y.; Yu, Y.; Geng, Y.; Wang, J.; Liu, Z. Inrush current arc characteristics in vacuum interrupters with axial magnetic field contact and butt-type contact. In Proceedings of the 3rd International Conference on Electric Power Equipment—Switching Technology (ICEPE-ST2015), Busan, Korea, 25–28 October 2015; pp. 512–515. [Google Scholar]
- Razi-Kazemi, A.A.; Fallah, M.R.; Rostami, M.; Malekipour, F. A new realistic transient model for restrike/prestrike phenomena in vacuum circuit breaker. Int. J. Electr. Power Energy Syst. 2020, 117. [Google Scholar] [CrossRef]
- Ma, X.; McLester, M.; Sudarshan, T.S. Prebreakdown and breakdown characteristics of micrometric vacuum gaps between broad area electrodes. In Proceedings of the IEEE 1997 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Minneapolis, MN, USA, 19–22 October 1997; pp. 583–586. [Google Scholar]
- Kharin, S.N.; Nouri, H.; Amft, D. Dynamics of electrical contact floating in vacuum. In Proceedings of the 48th IEEE Holm Conference on Electrical Contacts, Orlando, FL, USA, 22–23 October 2002; pp. 197–205. [Google Scholar]
- Kharin, S.N.; Ghori, Q.K. Influence of the pre-arcing bridging on the duration of vacuum arc. In Proceedings of the 19th International Symposium on Discharges and Electrical Insulation in Vacuum, Xi’an, China, 18–22 September 2000; pp. 278–285. [Google Scholar]
- Sima, W.; Zou, M.; Yang, Q.; Yang, M.; Li, L. Field experiments on 10 kV switching shunt capacitor banks using ordinary and phase-controlled vacuum circuit breakers. Energies 2016, 9, 88. [Google Scholar] [CrossRef]
- Mccool, J.I. Using the Weibull Distribution Reliability: Modeling, and Inference; Wiley & Sons Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zhang, Y.; Yang, H.; Wang, J.; Geng, Y.; Liu, Z.; Jin, L.; Yu, L. Influence of high-frequency high-voltage impulse conditioning on back-to-back capacitor bank switching performance of vacuum interrupters. IEEE Trans. Plasma Sci. 2016, 44, 321–330. [Google Scholar] [CrossRef]
- Yang, H.; Geng, Y.; Liu, Z.; Zhang, Y.; Wang, J. Capacitive switching of vacuum interrupters and inrush currents. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 159–170. [Google Scholar] [CrossRef]
- Cheng, X.; Liao, M.; Duan, X.; Zou, J. Experimental research on dynamic dielectric recovery characteristics for vacuum switch with double-break. In Proceedings of the 2011 IEEE Pulsed Power Conference, Chicago, IL, USA, 19–23 June 2011; pp. 291–296. [Google Scholar]
- Shiba, Y.; Ide, N.; Ichikawa, H.; Matsui, Y.; Sakaki, M.; Yanabu, S. Withstand Voltage Characteristics of Two Series Vacuum Interrupters. IEEE Trans. Plasma Sci. 2007, 35, 879–884. [Google Scholar] [CrossRef]
- Liao, M.; Duan, X.; Cheng, X.; Zou, J. Dynamic dielectric recovery property for vacuum circuit-breakers with double breaks. In Proceedings of the 24th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV2010), Braunschweig, Germany, 30 August–3 September 2010; pp. 225–228. [Google Scholar]
- Fugel, T.; Koenig, D. Breaking performance of a capacitive-graded series design of two 24-kV vacuum circuit breakers. In Proceedings of the 20th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV2002), Tours, France, 1–5 July 2002; pp. 360–363. [Google Scholar]
- Betz, T.; Konig, D. Influence of grading capacitors on the breaking capacity of two vacuum interrupters in series. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 405–409. [Google Scholar] [CrossRef]
- Li, S.; Geng, Y.; Liu, Z.; Wang, J. A breakdown mechanism transition with increasing vacuum gaps. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3340–3346. [Google Scholar]
- Wei, L.; Chun-En, F.; Bi-De, Z.; Pian, X.; Xiao, R.; Yan, L. Research on controlled switching in reducing unloaded power transformer inrush current considering circuit breaker’s prestrike characteristics. In Proceedings of the 27th International Symposium on Discharges and Electrical Insulation in Vacuum (ISDEIV 2016), Suzhou, China, 18–23 September 2016; pp. 1–4. [Google Scholar]










| Test Group | Applied Voltage (kV) | Experimental Condition | Making Operation |
|---|---|---|---|
| Test 1 | Us | Single-break test with VI_A | 30 |
| Test 2 | Us | Single-break test with VI_B | 30 |
| Test 3 | Us | Double-break test with VI_A and VI_B in series | 30 |
| Test Group | Us (kV) | β | η (mm) | R-Square | |
|---|---|---|---|---|---|
| Test 1 (VI_A) | 10 | 2.2 | 0.3 | 0.99 | |
| 20 | 4.9 | 0.5 | 0.98 | ||
| 30 | 6.7 | 0.7 | 0.99 | ||
| 40 | 10.3 | 1.0 | 0.95 | ||
| Test 2 (VI_B) | 10 | 1.8 | 0.1 | 0.99 | |
| 20 | 3.2 | 0.3 | 0.99 | ||
| 30 | 3.7 | 0.7 | 0.97 | ||
| 40 | 3.4 | 1.1 | 0.99 | ||
| Test 3 | VI_A and VI_B | 10 | 0.9 | 0.2 | 0.97 |
| 20 | 2.6 | 0.6 | 0.99 | ||
| 30 | 5.3 | 0.9 | 0.99 | ||
| 40 | 4.6 | 1.1 | 0.97 | ||
| VI_A | 10 | 1.2 | 0.2 | 0.95 | |
| 20 | 3.3 | 0.4 | 0.99 | ||
| 30 | 5.9 | 0.5 | 0.99 | ||
| 40 | 4.7 | 0.7 | 0.96 | ||
| VI_B | 10 | 0.8 | 0.04 | 0.99 | |
| 20 | 1.9 | 0.2 | 0.99 | ||
| 30 | 4.7 | 0.3 | 0.99 | ||
| 40 | 4.7 | 0.4 | 0.97 | ||
| Test Group | Us (kV) | d10 (mm) | d50 (mm) | d90 (mm) | σ (mm) | |
|---|---|---|---|---|---|---|
| Test 1 (VI_A) | 10 | 0.39 | 0.23 | 0.10 | 0.11 | |
| 20 | 0.62 | 0.48 | 0.33 | 0.16 | ||
| 30 | 0.82 | 0.69 | 0.52 | 0.12 | ||
| 40 | 1.09 | 0.97 | 0.81 | 0.15 | ||
| Test 2 (VI_B) | 10 | 0.20 | 0.11 | 0.04 | 0.06 | |
| 20 | 0.35 | 0.24 | 0.13 | 0.16 | ||
| 30 | 0.82 | 0.60 | 0.36 | 0.17 | ||
| 40 | 1.38 | 0.96 | 0.55 | 0.41 | ||
| Test 3 | VI_A and VI_B | 10 | 0.46 | 0.13 | 0.02 | 0.16 |
| 20 | 0.83 | 0.52 | 0.25 | 0.23 | ||
| 30 | 1.02 | 0.81 | 0.57 | 0.16 | ||
| 40 | 1.35 | 1.04 | 0.69 | 0.27 | ||
| VI_A | 10 | 0.32 | 0.12 | 0.03 | 0.11 | |
| 20 | 0.50 | 0.35 | 0.19 | 0.13 | ||
| 30 | 0.62 | 0.50 | 0.37 | 0.09 | ||
| 40 | 0.82 | 0.63 | 0.42 | 0.16 | ||
| VI_B | 10 | 0.12 | 0.03 | 0.00 | 0.06 | |
| 20 | 0.33 | 0.18 | 0.07 | 0.10 | ||
| 30 | 0.40 | 0.31 | 0.21 | 0.07 | ||
| 40 | 0.52 | 0.40 | 0.27 | 0.11 | ||
| Us (kV) | 10 | 20 | 30 | 40 | |
|---|---|---|---|---|---|
| VI_A | δ (d10) | −17.9% | −19.4% | −24.4% | −24.8% |
| δ (d50) | −47.8% | −27.1% | −27.5% | −35.1% | |
| δ (d90) | −70% | −42.4% | −28.8% | −48.1% | |
| VI_B | δ (d10) | −40% | −5.7% | −51.2% | −62.3% |
| δ (d50) | −72.7% | −25.0% | −48.3% | −58.3% | |
| δ (d90) | −100% | −46.2% | −41.7% | −50.9% | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, Y.; Yao, X.; Dong, J.; Liu, X.; Geng, Y.; Liu, Z.; Peng, J.; Wang, K. Experimental Investigation of the Prestrike Characteristics of a Double-Break Vacuum Circuit Breaker under DC Voltages. Energies 2020, 13, 3217. https://doi.org/10.3390/en13123217
Geng Y, Yao X, Dong J, Liu X, Geng Y, Liu Z, Peng J, Wang K. Experimental Investigation of the Prestrike Characteristics of a Double-Break Vacuum Circuit Breaker under DC Voltages. Energies. 2020; 13(12):3217. https://doi.org/10.3390/en13123217
Chicago/Turabian StyleGeng, Yun, Xiaofei Yao, Jinlong Dong, Xue Liu, Yingsan Geng, Zhiyuan Liu, Jing Peng, and Ke Wang. 2020. "Experimental Investigation of the Prestrike Characteristics of a Double-Break Vacuum Circuit Breaker under DC Voltages" Energies 13, no. 12: 3217. https://doi.org/10.3390/en13123217
APA StyleGeng, Y., Yao, X., Dong, J., Liu, X., Geng, Y., Liu, Z., Peng, J., & Wang, K. (2020). Experimental Investigation of the Prestrike Characteristics of a Double-Break Vacuum Circuit Breaker under DC Voltages. Energies, 13(12), 3217. https://doi.org/10.3390/en13123217






