1. Introduction
Wind speed forecasting is an extremely relevant metric for wind resource assessment (WRA) for wind parks in renewable sector. With environmental pollution becoming increasingly more serious, the development of green and environmentally safe renewable energy has become a research hotspot. As one form of green renewable energy, wind energy has been widely used around the world in recent years. The accurate prediction of wind speeds is an important component of effectively utilizing wind energy to generate electricity. However, due to the stochasticity and intermittence of wind speed [
1,
2,
3,
4], it is difficult to accurately predict the wind speed estimation errors and meet the actual requirements of wind power generation. Therefore, the accurate prediction of wind speed is of great significance.
Wind speed predictions can be divided into short, medium and long term predictions according to the sample time interval [
5]. There are also various prediction models: physical models, statistical models and artificial intelligence models and hybrid methods [
6]. Each model has its specialty: for example, physical models are suitable for long-term predictions, and statistical methods are applicable to short-term predictions [
5]. With the development of artificial intelligence methods in recent years, machine learning methods have also been applied to wind speed prediction. The feedforward neural network is the most commonly used neural network, which due to its fast learning speed and good generalization performance. Various feedforward neural networks have been used in various scientific fields. Authors in [
6] proposed training the support vector machine (SVR) and artificial neural network (ANN) models with different training sets for short-term wind speed prediction and compared their prediction results. Authors in [
7] proposed the use of feedforward neural networks to predict stock index and sunspot movements. The results show that the method is effective at predicting stock and sunspot activity by improving the training set of the neural network. However, whether this method is suitable for short-term wind speed prediction is a topic for further research. In addition, the main problem with these models was that utilizing a single neural network to model and predict wind-speed data did not provide sufficient results [
8,
9,
10,
11,
12].
As for hybrid methods, Authors in [
13] the idea of combining predictions, which combines different prediction methods in an appropriate way. In recent decades, different models such as linear/nonlinear, supervised/unsupervised and statistical/intelligent have been combined to form various hybrid models, including the following: ARIMA–ANN [
8,
9] ARIMA–LSSVM [
10], EMD–ANN [
11], ARIAM–BP [
12], ARIMA-Kalman [
14], ARIMA–MLP and ARIMA–SVR [
15]. Aasim [
16] proposed an RWT–ARIMA model based on the continuous wavelet transform, which improved the accuracy of very-short-term wind speed predictions. Wang et.al [
5] proposed a nonlinear combination model based on data feature extraction and multi-objective optimization for short-term wind speed predictions. The results show that the model has higher prediction accuracy and stability than the comparison model. The hybrid models proposed in the above literature [
17,
18,
19,
20,
21,
22,
23,
24] combine the single models through different methods, and the results verify that the combined prediction effect is better than that of the single model.
In recent years, the idea of a fuzzy set has been introduced into time-series prediction algorithms. Through the fuzzy preprocessing of original time-series, fuzzy relation are established and defuzzification is applied to improve the prediction accuracy. A large number of definitions and applications of fuzzy-time series are proposed in [
25,
26,
27,
28,
29,
30,
31]. Jiang et.al [
32] developed a mixed prediction system consisting of a data pretreatment module, an optimization module and a prediction module. The multi-objective differential evolutionary algorithm is used to optimize the fuzzy-time series to balance the prediction accuracy and stability. Although the fuzzy-time-series (FTS) methods has been widely used in other scientific fields, to the best of our knowledge, it is rarely used to predict wind speed. Therefore, we apply the fuzzy set idea to wind-speed data prediction, which is a great contribution to the application of fuzzy-time series to meteorology.
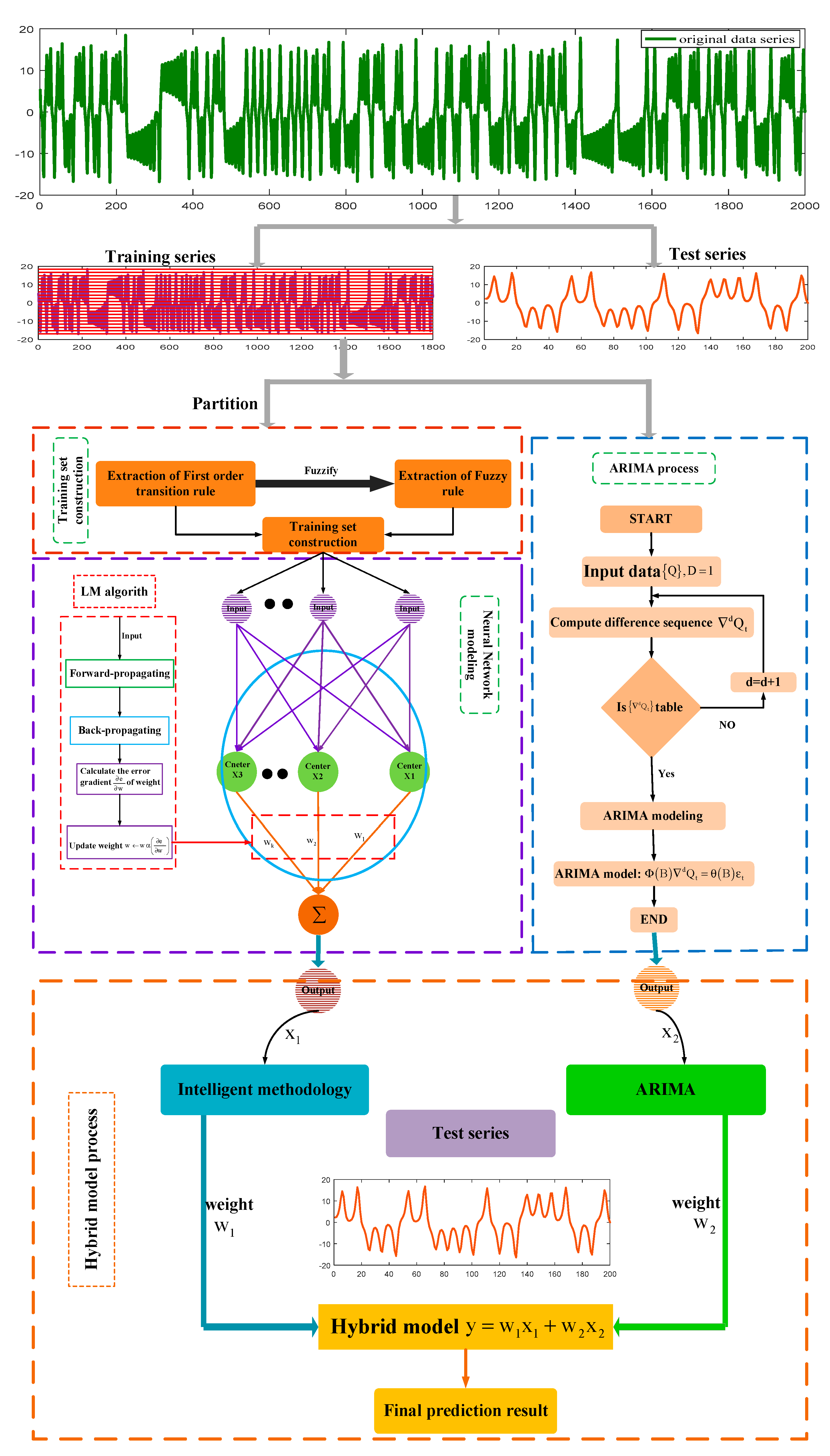
Therefore, in order to solve the above problems to improve the accuracy of time-series prediction, we propose a new hybrid model in this study, which is indicated to enhance the forecast accuracy. It combines the ARIMA model, the three-layer feedforward neural network and fuzzy sets. This hybrid system uses the ARIMA and feedforward neural network to predict the original series and utilizes the dominance matrix to optimize the weight of the single model to maximize the accuracy of the hybrid model prediction. Additionally, we evaluate it with a set of Lorenz-63 and two sets of actual wind-speed data and analyze the results by using three evaluation indices. All of these approaches confirm that the novel hybrid model can be used to predict time series. The innovations of our study are as following:
First, the overwhelming majority of existing studies used ARIMA methods to preprocess the original time-series, and they then used other intelligent models to model and predict the residuals of the original time-series. In this study, the ARIMA is employed to model and predict the original time-series, and then the neural network is employed to process the original time-series, forming a parallel linear-nonlinear hybrid model. Additionally, the neural network model in this study can be used as a preprocessing method for the original time-series and can also be used as a postprocessing method to deal with the errors.
Second, to validate the effectiveness of the framework of the proposed ARIMA–NN–FFOTR model, another hybrid model is proposed based on the framework: the ARIMA–NN–FOTR. Furthermore, this study reports the results of a comparative study on single models and the proposed model, including the following: the ARIMA, the NN–FOTR and the NN–FFOTR. Additionally, the three-layer feedforward neural network is employed, which has many advantages over other neural networks, the most important of which are its extremely short training time and fast convergence speed.
Third, in existing studies, most fuzzy-time series are mainly used for enrollment rate or stock index predictions. In this article, the fuzzy-time-series method is applied to wind speed predictions, which is a great contribution to the application of fuzzy-time series to meteorology. Structure of our proposed hybrid forecasting system is described in
Figure 1.
The rest of this study is organized as follows:
Section 2 describes the methods of the proposed hybrid system.
Section 3 shows the experimental set up and the results of the proposed system.
Section 4 presents relevant aspects of the proposed system. Finally,
Section 5 contains the concluding remarks and the future work.
2. Background Theories
In this section, we summarize some background theories which are relative to our hybrid method in detail.
2.1. Fuzzy Sets
A fuzzy set is different from a regular set, in that the elements of the fuzzy set belong to a certain membership value in the range of the closed interval
. The definition of the fuzzy set is defined as follows
Section 2.1.1.
2.1.1. Definition
Given a set
that is the “universe of discourse”, a fuzzy set in the universe
is defined as a set of 2-tuples [
7], as show below
where x is an element of universe
and
denotes the membership value of element
in fuzzy set
. If the universe of discourse
is continuous and infinite, it is not possible to define a set of discrete 2-tuples as given in Equation (1) for fuzzy set
. In such cases, a fuzzy membership function
is defined to map each element in the universe of discourse to its corresponding membership value in fuzzy set
.
2.2. Time-Series of Partition
2.2.1. Definition
Given a time series
, let c
max and c
min represent the maximum and minimum values of the time-series, respectively. We define partitioning as the act of dividing the range into
non-overlapping contiguous Intervals such that the following two conditions jointly hold [
7]:
Let a partition be defined as a bounded set, where and represent the lower and upper bounds of the partition, respectively. Clearly, a time-series data point belongs to the partition if and only if .
2.2.2. Definition
Let
and
denote two consecutive data points in a time-series
and let
and
be the partitions to which these data points belong. Then, we denote
as a first-order [
7].
2.3. Basis Function (RBF) Networks
The radial basis function (RBF) network is a three-layer (input, hidden layer and output) feedforward neural network, and its input consists of a source node that connects the network to the outside world. Its hidden layer uses a nonlinear radial basis function as the activation function. The output of the network is typically a linear combination of hidden layer functional values. Let the network output be a vector
. There are n hidden layer neurons in the network, and the output of the RBF network is as follows:
represents the center vector of the jth hidden layer neuron,
is the Euclidean norm,
is the activation function, and
is the number of hidden layer unit activation functions. There are a variety of hidden layer activation functions and the most commonly used radial basis function is the Gaussian function [
33]. It is defined as follows:
where
is a positive integer. Since the activation function depends on the distance between the input vector and the center vector of the hidden-layer neuron, the function is radially symmetric with the central vector of the neuron. RBF neurons are used as pre-selectors to determine when the neural network triggers based on the pre-trained neural network transition rules. The linear weighted sum is used to convert the weighted sum of the output layers to the output of the neural network and the activity of the ith unit in the output layer can be calculated according to the following formula:
where w
0 is the bias term, w
pr is the connecting weight between the pth hidden unit and the rth output unit, w
pr is calculated by using the Levenberg–Marquardt (LM) back-propagation algorithm [
34], Y is the response of the qth hidden unit resulting from all input data and N is the number of output units.
2.4. First-Order Transition Rules Based on the Neural Network Model
In this section, the neural networks are trained by using first-order transition rules [
7] for a given time series.
is a set of all first-order transition rules and
indicates the probability that the next partition is
when the current partition is
. Then the formula for
is as follows:
where count
is the sum of the number of occurrences of the transition rule
. The set
can be expressed as follows:
Given the current partition, in order to predict the next partition, consider the weighted contributions of all transition rules with as an antecedent, which can be achieved by designing a neural network model. This model allows all rules in the set to be triggered at the same time. To implement the model, a set of neural networks is used that satisfy the following conditions.
Condition 1: Given the current input partition , each neural network in the ensemble can trigger at most one transition rule with in the antecedent.
Condition 2: All transition rules with partitions in the antecedent must be triggered by the ensemble. In other words, all rules contained in ensemble must be triggered.
Condition 3: There are no two neural networks in ensemble that can trigger the same transition rules, such as: and simultaneously triggering .
The above conditions can be satisfied by constraining the training set of the neural network. See the relevant theorems from these conditions [
7].
The steps of grouping the set transition rules into training sets are as follows:
Step 1: Partition. Divide set
into a subset or group of transition rules. All rules in a group have the same partition in the antecedent, and the antecedent contains partition
. The number of these subsets is equal to the total number of different partitions that occurred before the transition rules. The choice of the number of partitions will affect prediction accuracy [
25], and the number of partitions of the model is set to 20 (multiple trials). The partition diagram of Lorenz-63 is shown in
Figure 2.
Step 2: Construct a training set. The transition rules in each subset are ordered. By collecting the transition rules of the position in each subset, the training set of the ith neural network in the set is constructed. By repeating this process, multiple training sets are constructed. These training sets contain transition rules, and the antecedent and consequence of each rule represent a partition label. The regression neural network model is used to obtain the time-series data points that are input as the current time-series data points and output as the future time-series data points. Therefore, the label of each partition is replaced by the corresponding partition median value to get the modified training set . The Levenberg–Marquardt (LM) back propagation algorithm is used to train the neural network.
Step 3: Neural network training. The first-order transition rules training set constructed in step 2 is used to train the neural network.
Step 4: Predicting the next data point. In the prediction phase, assuming that the partition containing the current time-series data points (system inputs) is
, it may happen that the neural network in the ensemble has not been trained according to the rules containing
in the antecedent, which will lead to an approximation error. Therefore, the RBF is used as the pre-selector to trigger the appropriate neural network in the given input set. The output
of the ith hidden layer neuron is as follows:
where
is the input to the RBF neuron,
is the median of the
partition and
. If the current partition
exists in the antecedent of any training set rules of neural network
, neural network
is enabled. The enable signal of
is obtained by the logical OR operation of the RBF neuron output.
Given the current data point
, the final prediction
is calculated using the weighted sum of the single output of the neural network triggered by the pre-selector RBF neurons. Suppose there are
elected neurons whose outputs
are located in partitions
, respectively, and the final output is as follows:
2.5. Fuzzy First-Order Transition Rules Based on the Neural Network Model
In this section, the first-order transition rules are fuzzified to get the fuzzy first- order transition rules to build the training set and then train the neural network [
7]. It should be noted that the best way to represent a time-series partition is by using the center of the partition, but the data points of time series cannot be completely represented by the partition. Therefore, by approximating the data points in the partition and their corresponding midpoints, some approximate errors that increase with the width of the partition itself can be deliberately studied [
10]. One way to avoid this error is to treat each partition as a fuzzy set. Obviously, each partition is associated with a fuzzy membership function, and each time-series data point will have some membership values in the set
. The classical Gaussian function is chosen as the membership function, and its peak corresponds to the center of the partition. Near the boundary of the partition, both sides of the peak have values that gradually decrease and approach 0. The membership value at the partition boundary is not necessarily 0. These membership values can be used to train the neural network in the model. The advantage of this approach is that it takes advantage of the inherent fuzziness involved in assigning partitions to time-series data points and uses partitions to obtain better results. The membership function corresponding to the
partition is as calculated as follows:
Then, we train the neural network using the improved fuzzy-first-order-transition rules, as follows.
Step 1: Partition. Set the number of partitions to 40 (multiple trials) to get the best prediction results.
Step 2: Construct the first-order transition rules and training set. The training set constructed by the fuzzified first-order transition rules is where and are the median values corresponding to the partitions and , respectively and is the membership value of in the fuzzy set.
Step 3: Neural network training. The fuzzy-first-order-transition-rules training set constructed in step 2 is used to train the neural network.
Step 4: Predicting the next data point. This is the same as the first-order-transition-rules-based model discussed in
Section 2.4.
2.6. Proposed Model
2.6.1. Determination of the Weights of the Proposed Model
The general form of a hybrid model uses the weighted sum of each single prediction model. Therefore, the key point of the hybrid model is to determine the weight coefficients. If the weight coefficients of each single prediction model are properly assigned, the prediction accuracy of the whole hybrid model will be improved accordingly. However, when using the hybrid model, how to determine the weight coefficients of the single models is a big problem. In this regard, many scholars have proposed their own methods for determining the weights. The current commonly used methods are the arithmetic average method, the optimal weight method, the variance reciprocal method, etc. In this study, we use the dominance matrix method to determine the prediction weights of two single models. Let the ARIMA model be model 1 and the neural network model be model 2. By calculating the relative errors of two single-model predictions, we determine the size of the relative error of two single models. For example, when the relative error of the predicted value at a certain point in model 1 is less than the relative error of the predicted value at the same point in model 2. It shows that the prediction effect of model 1 is better than model 2. We judge the relative error of 200 predicted values of two single models by analogy, it can be obtained that the prediction effect of model 1 is better than model 2 times, the prediction effect of model 2 is better than model 1 times, and the total number of predicted steps is . Then, the weights are and respectively.
2.6.2. Proposed Model Prediction
After determining the weights, the predicted value of the hybrid model can be obtained by the formula
.
is the weight of the ARIMA model,
is the weight of the neural network model,
is the predicted value of the ARIMA model and
is the predicted value of the neural network model. The weights of the new proposed model for the three time-series data sets are shown in
Table 1 below.
4. Discussion
Aiming at the problems and shortcomings of the existing time-series prediction models, this study proposes a comparative study of two hybrid prediction models based on the ARIMA and a neural network. Each model obtains a better prediction with respect to the Lorenz theoretical value and wind-speed data. Based on the existing work, we can conduct in-depth discussions from the following aspects.
(1) Effectiveness of the new algorithm
This study proposes a new linear-nonlinear parallel combination model. For the theoretical and actual wind-speed data, the combined ARIMA–NN–FFOTR model proposed in this study has higher prediction accuracy than any single model. This study uses a three-layer feedforward neural network with a single input and a single output. The resulting training time is short, and the convergence rate of the whole prediction system is effectively improved. The effectiveness of the new algorithm is verified by comparative experiments. The results show that the hybrid model effectively combines the advantages of a single model to make up for the shortcomings of a single model prediction, and it improves the prediction accuracy and convergence speed of the hybrid model.
(2) Robustness of the fuzzy-time series
This study applies fuzzy-time series to wind-speed data. The original wind-speed data are partitioned and then fuzzified, which will describe the distribution of the membership values of the data points in the partition, and the comparison experiment verifies the robustness of the neural network prediction by using fuzzy set training. Based on the existing research work, the robustness of the fuzzy-time series in real-time-series predictions is further proved.
(3) Applicability in real-time series
In this study, the proposed model is verified by using the Lorenz-63 theoretical value and actual wind-speed data, which shows the validity of this model. The model can be applied to any real-time-series prediction.
5. Conclusions
This work proposes a hybrid system that performs time-series forecasting in three steps: The linear component of time-series modeling using ARIMA model; the nonlinear component of time-series forecasting with feedforward neural network model; and linear combination of the forecasts of ARIMA and feedforward neural network using the dominant matrix theory. To maximize the accuracy, the feedforward neural network is trained by first-order transition rules and fuzzy first-order transition rules. Generating two hybrid systems: ARIMA–NN–FOTR and ARIMA–NN–FFOTR.
Using three evaluation metrics to evaluate experiments, the results show that the ARIMA–NN–FFOTR attains a better performance than single models and ARIMA–NN–FOTR model. The ARIMA–NN–FFOTR reaches a higher accuracy because it is able to forecast separately the linear and nonlinear patterns of the series through ARIMA and NN–FFOTR model; compare with the ARIMA–NN–FOTR model, after the input partition Gaussian of the feedforward neural network is fuzzified, the contribution of the weighted data points in the partition is effectively improved.
In future work, we aim to develop a method to calculate the optimal weight. Additionally, this study considers only short-term wind-speed predictions. Therefore, future studies should evaluate the performance of the developed method for mid-term and long-term wind speed predictions.