Investigative Coupled Thermo-Hydro-Mechanical Modelling Approach for Geothermal Heat Extraction through Multistage Hydraulic Fracturing from Hot Geothermal Sedimentary Systems
Abstract
:1. Introduction
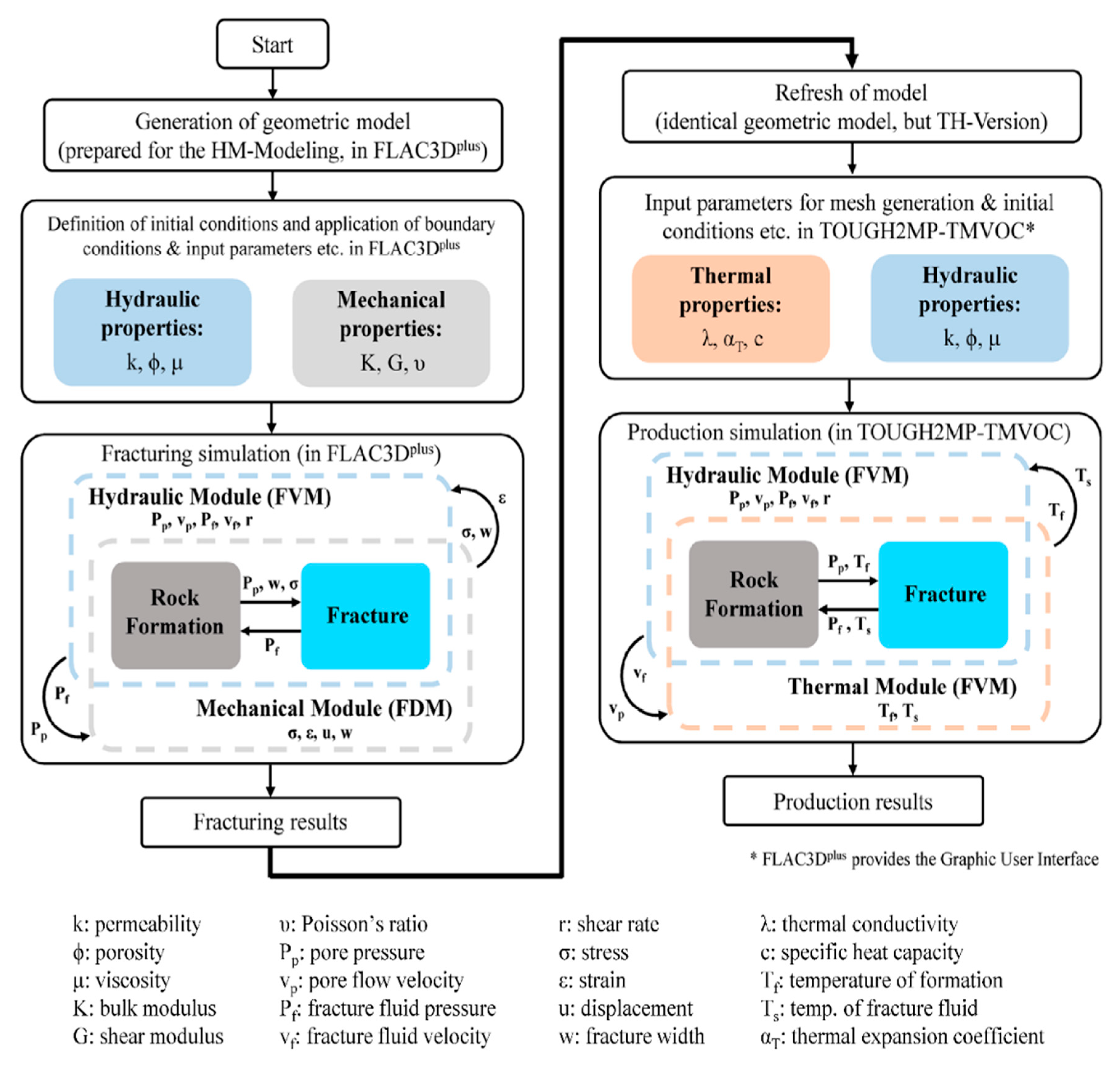
2. Simulation Concept
3. Numerical Simulation
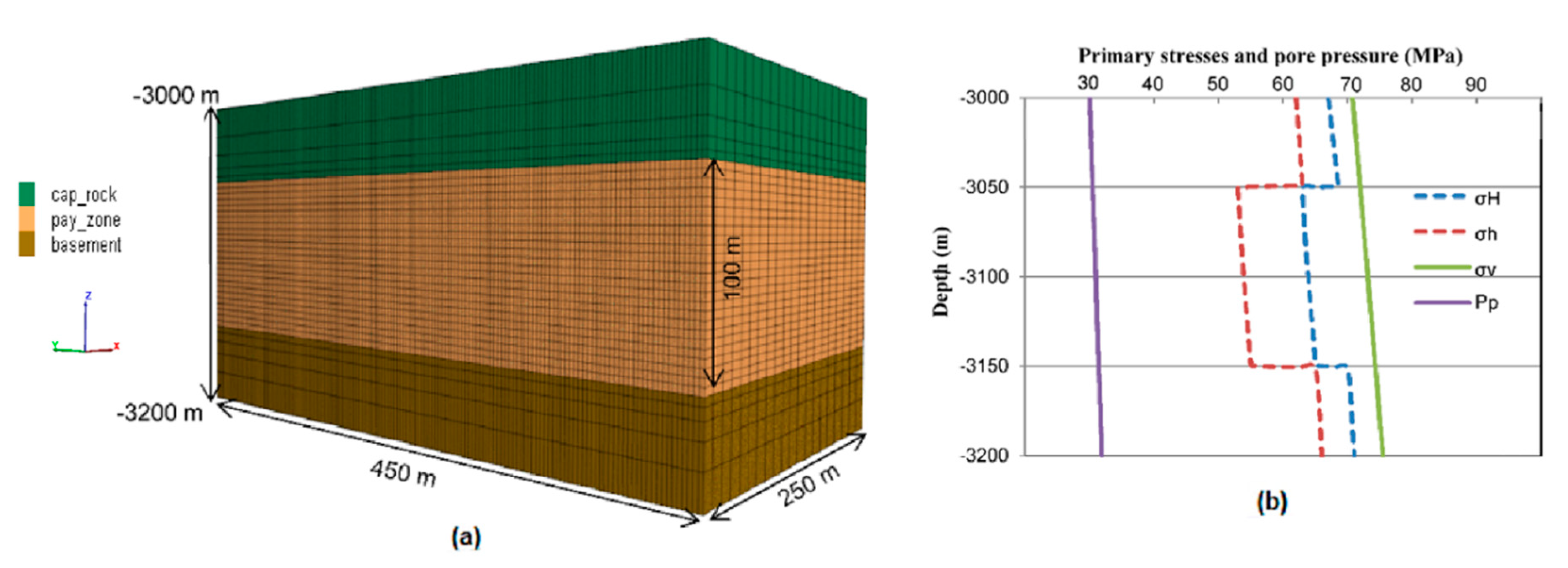
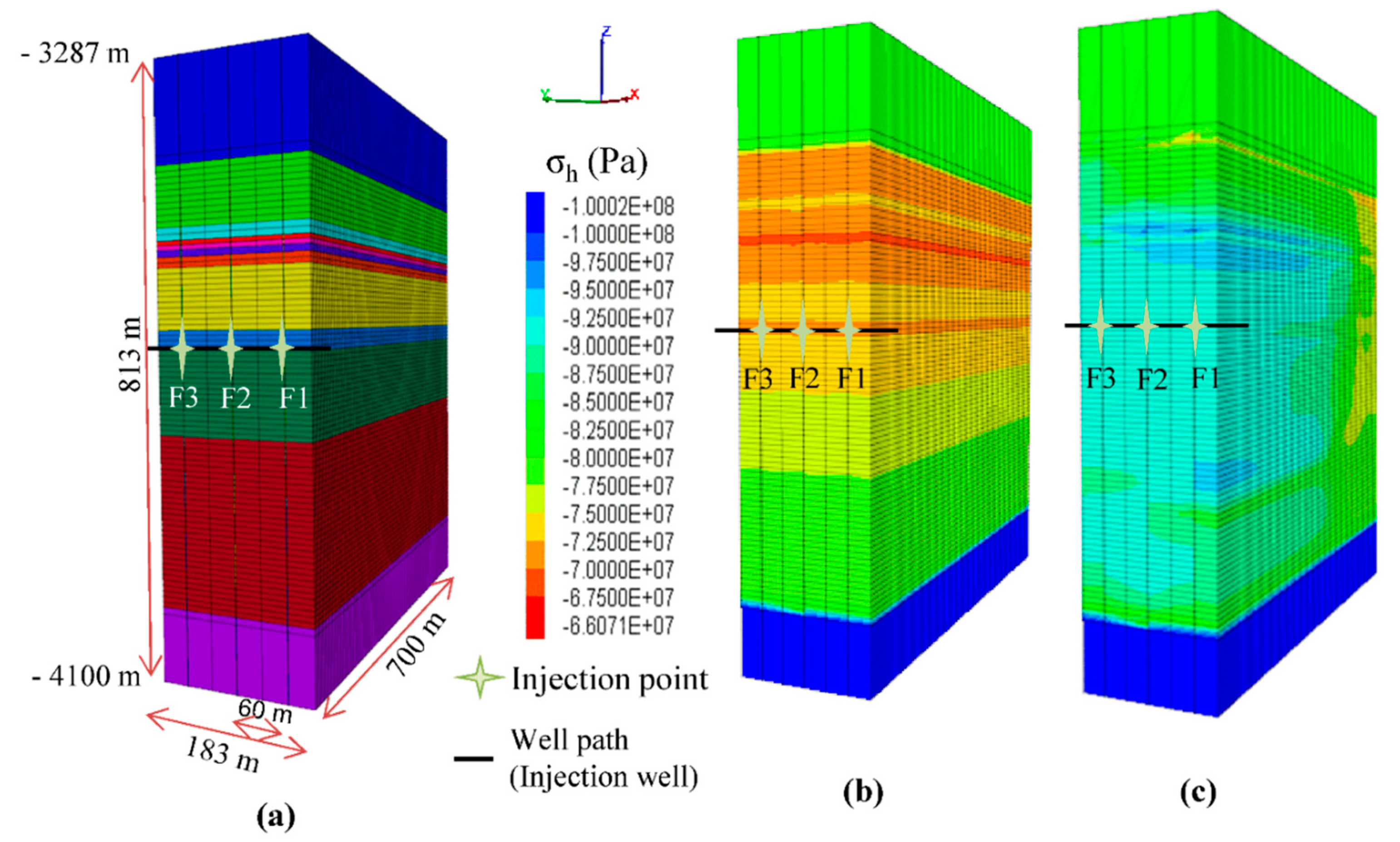
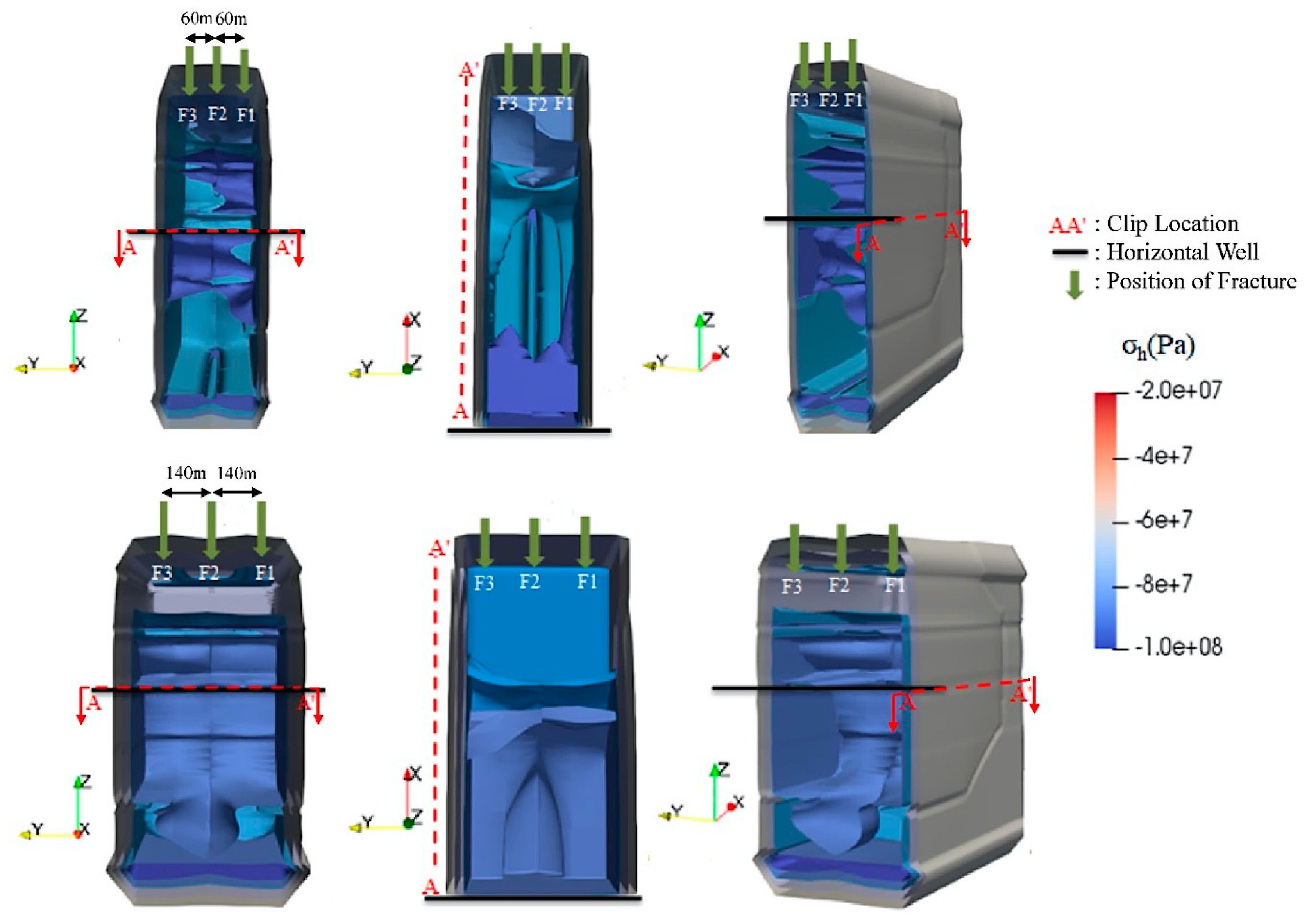
3.1. Fictive Model Generation
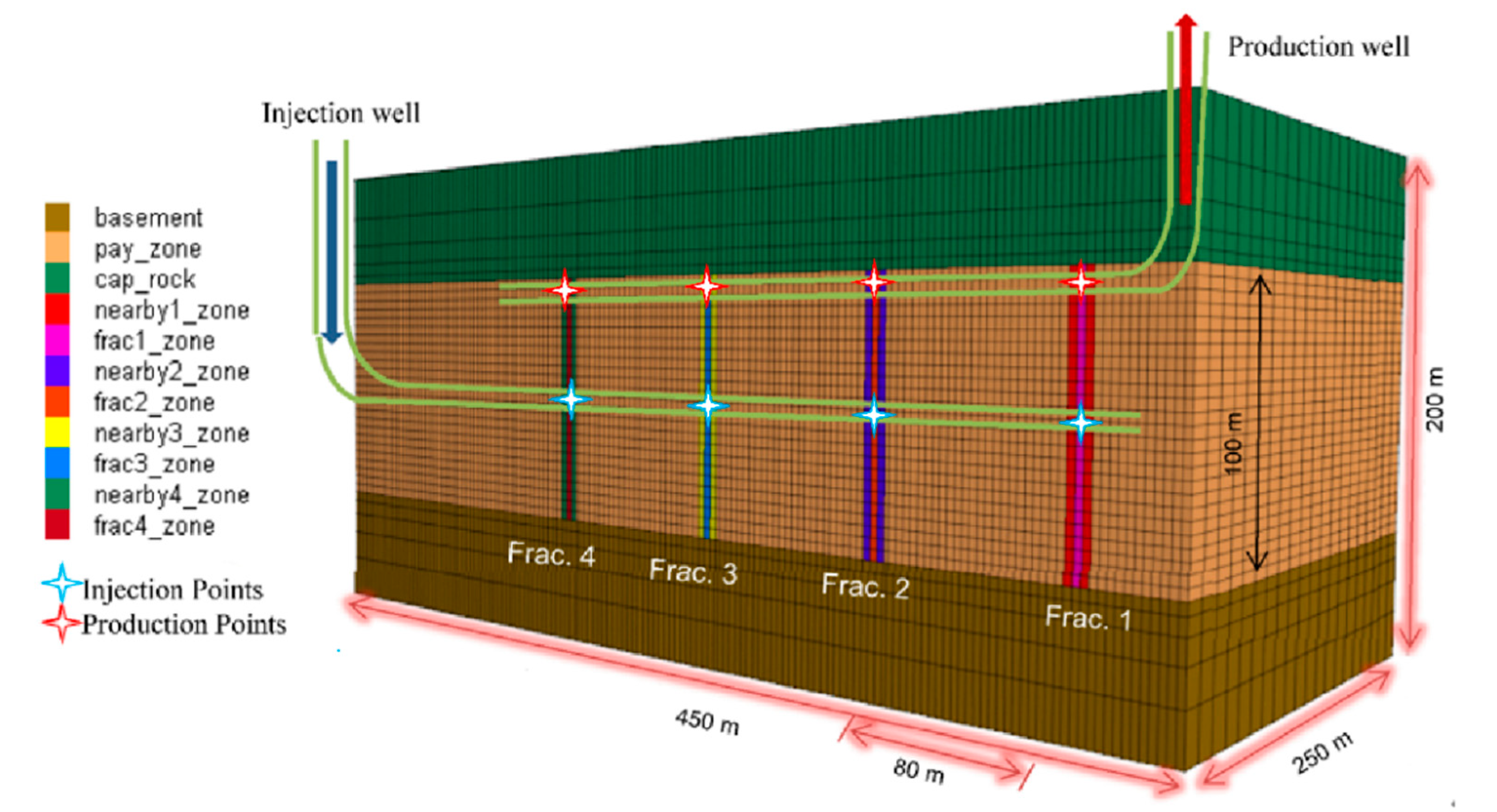
3.2. Equivalent Model for Geothermal Exploitation
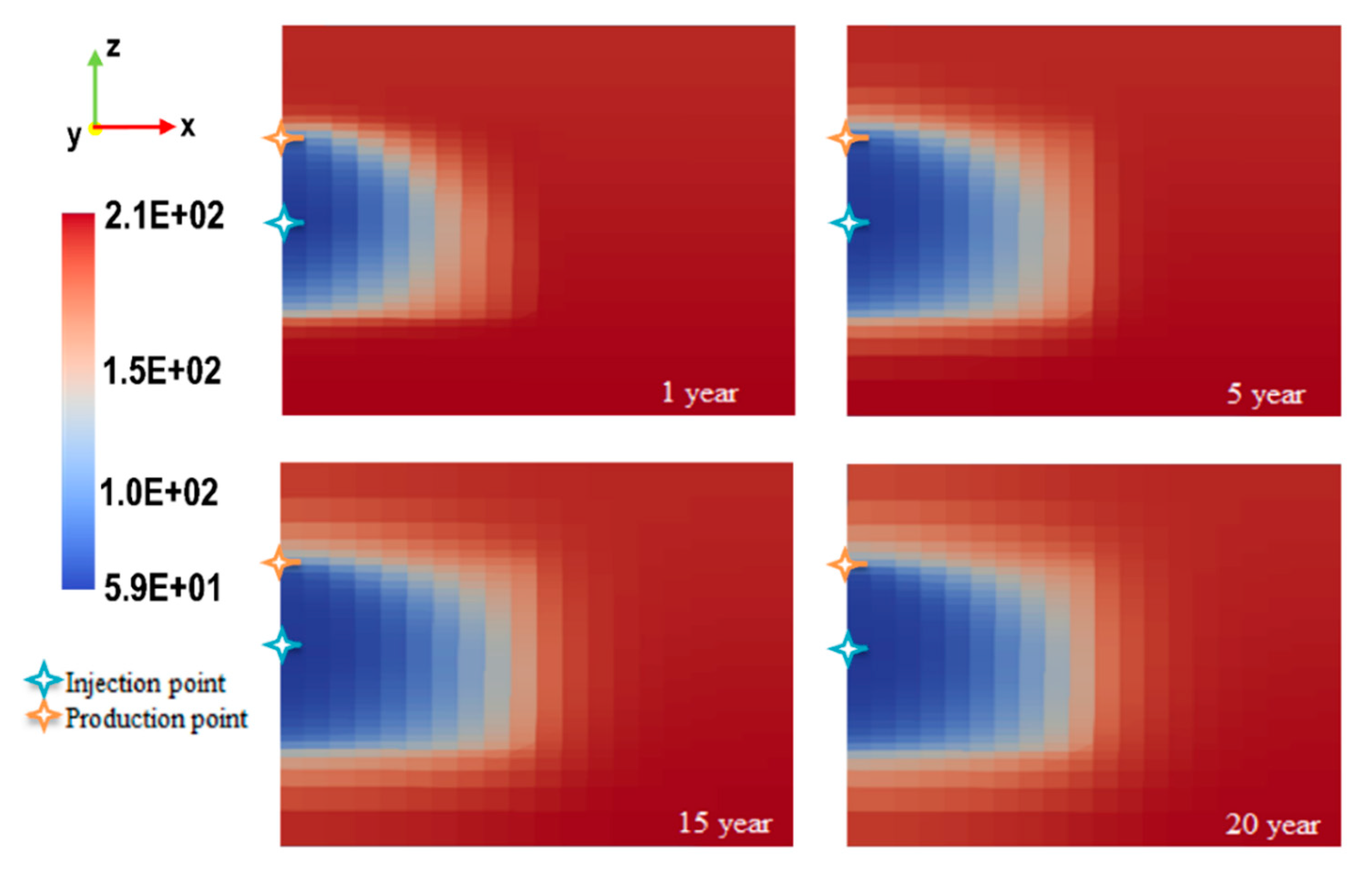
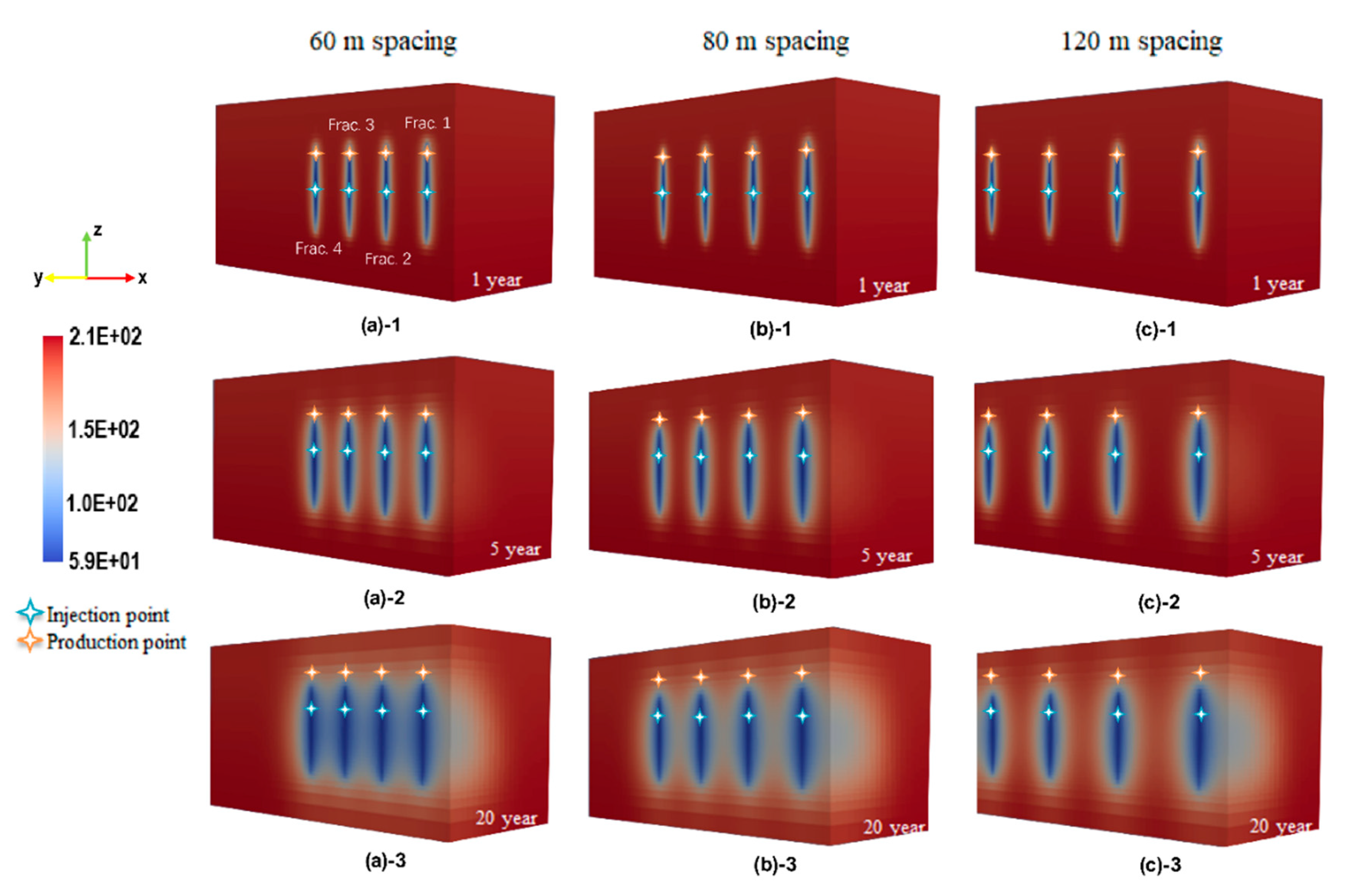
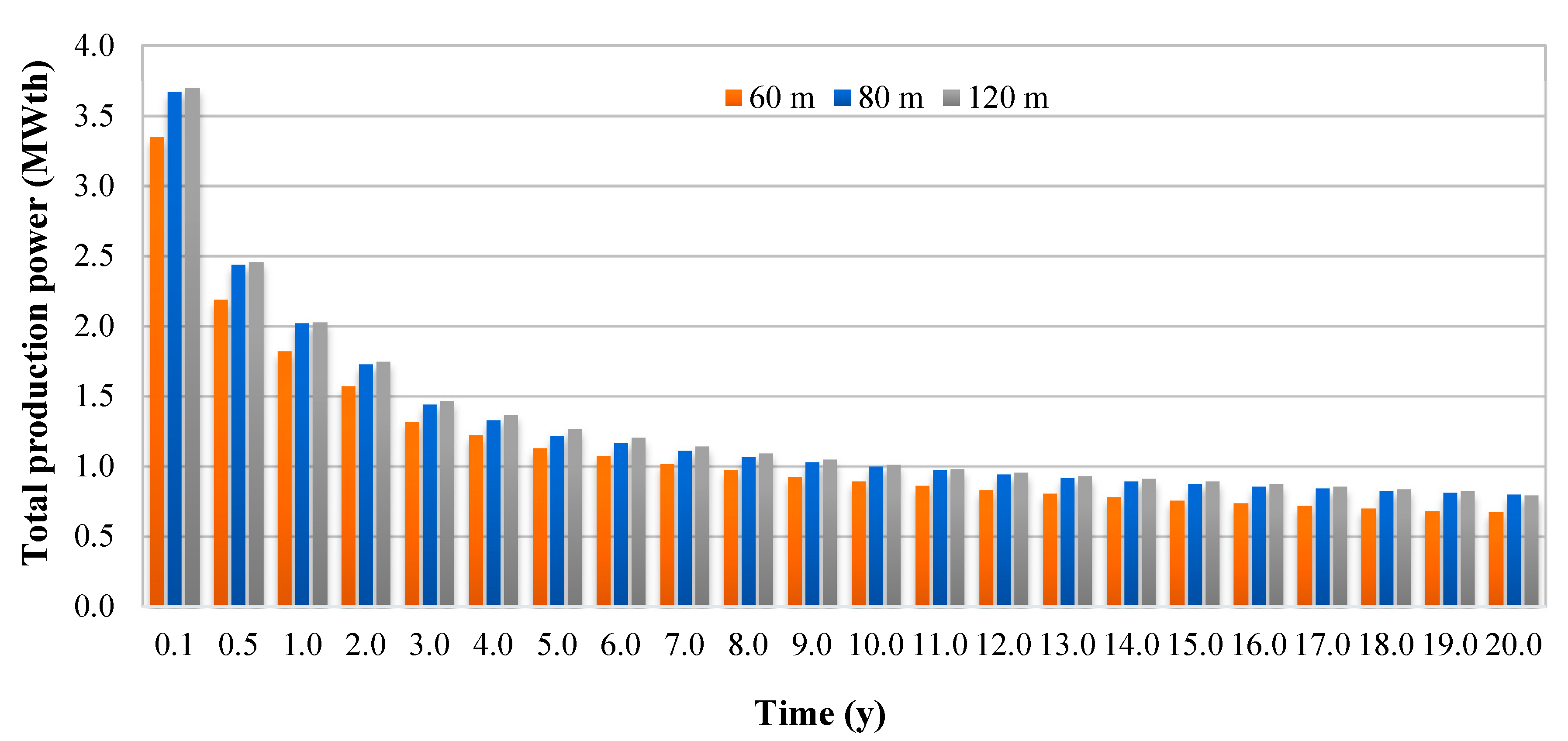
3.3. Spatial Distribution of Temperature Decline Results during Production
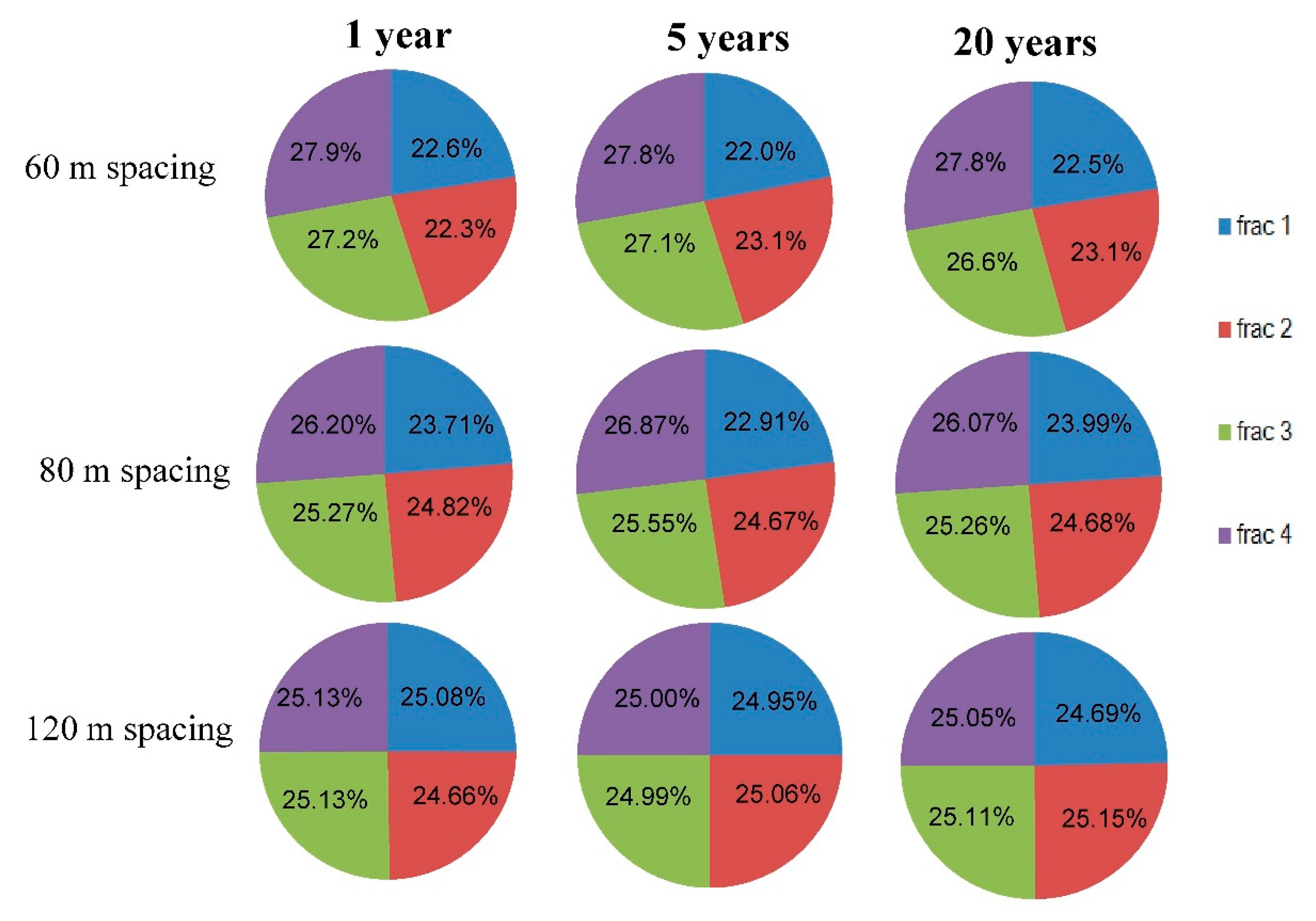
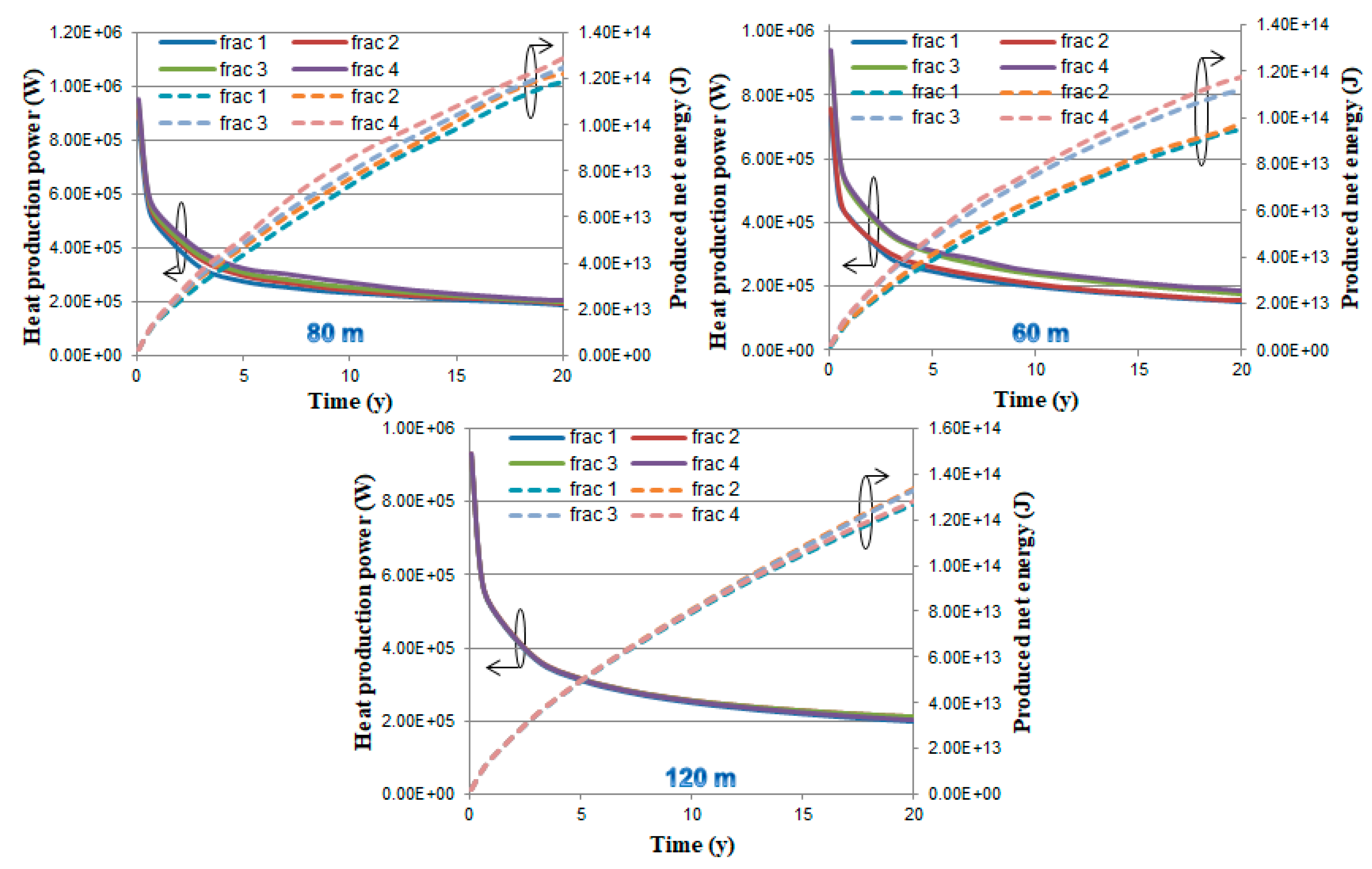
3.4. Heat Production Results and Discussion
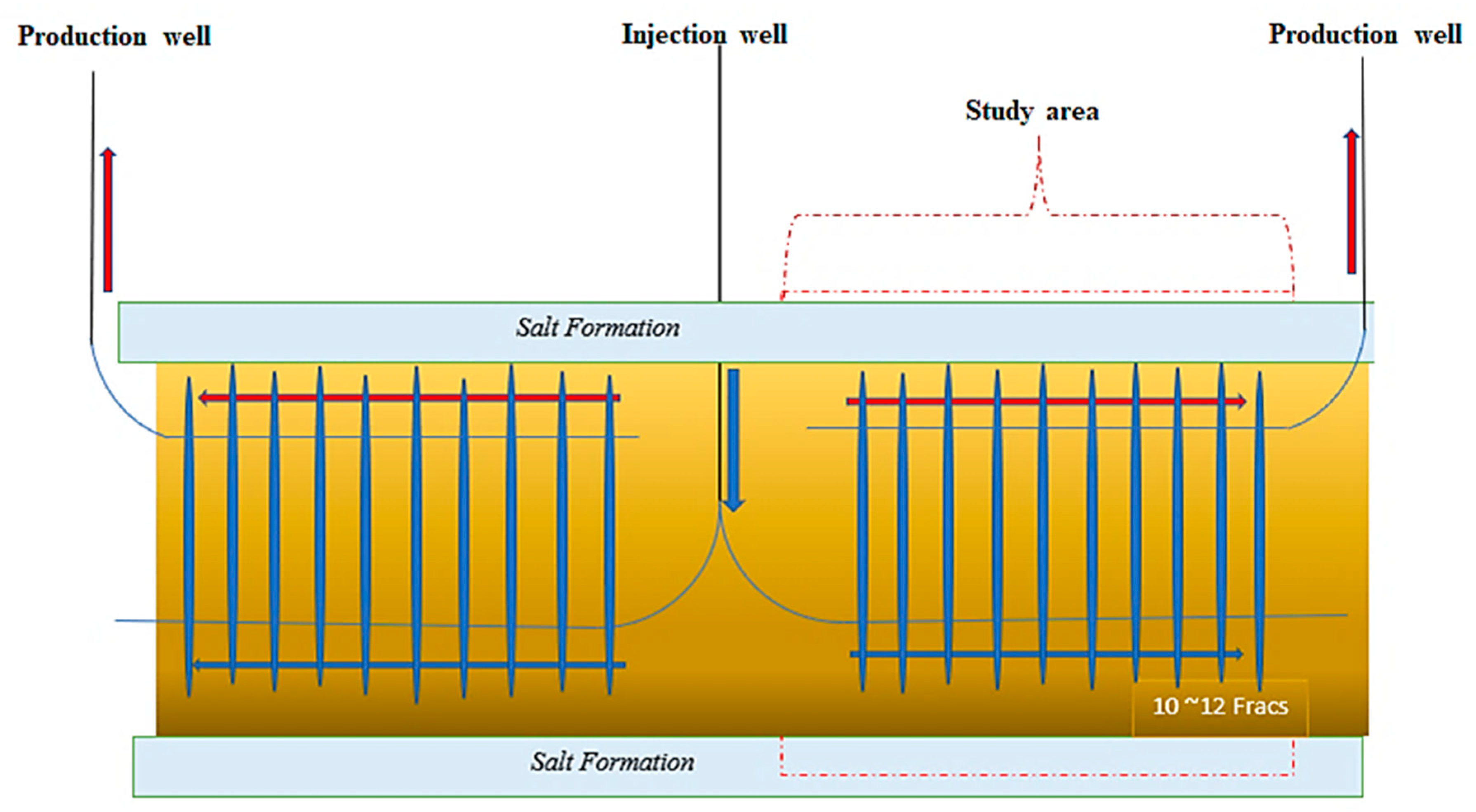
4. Field Case Study
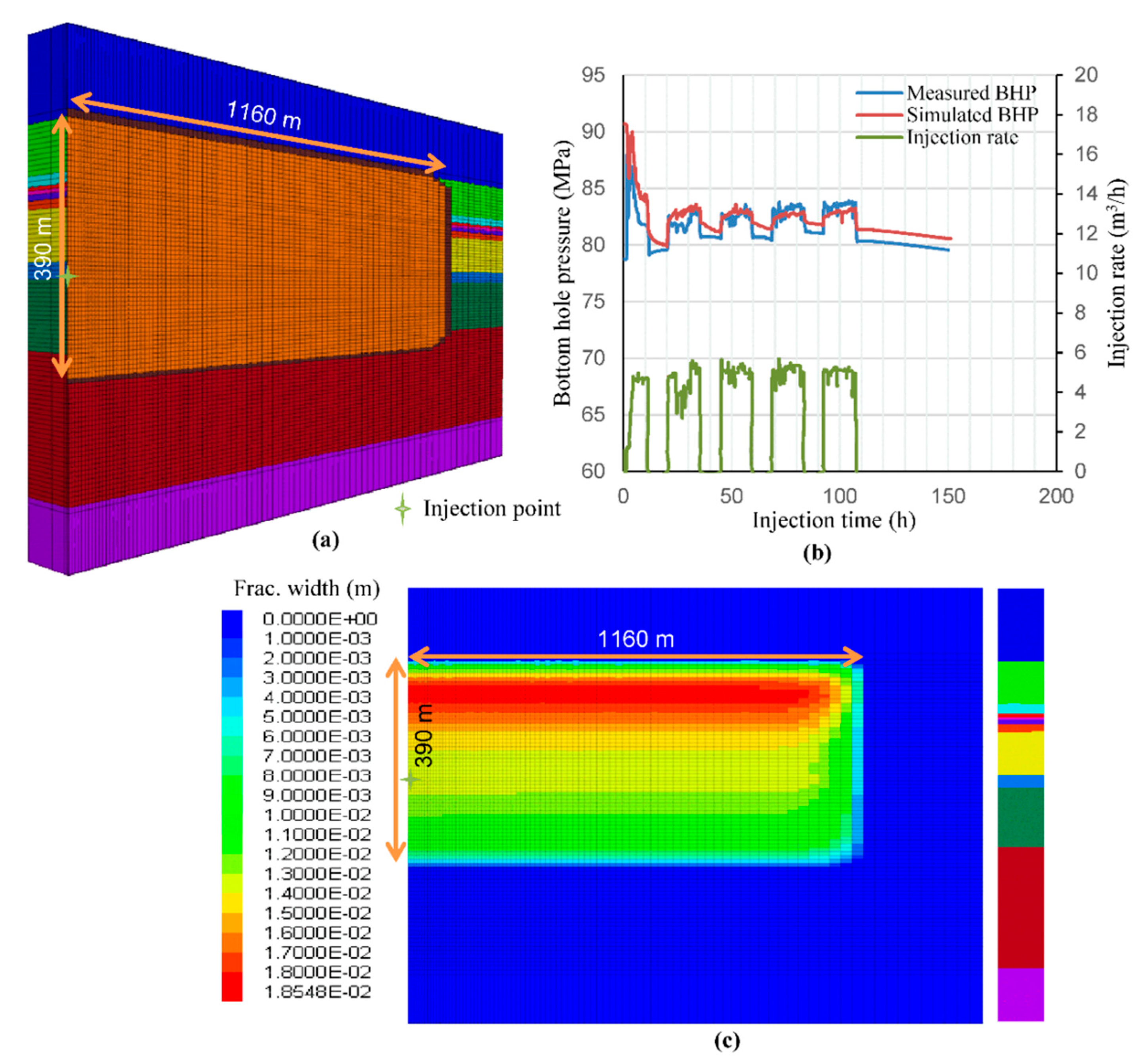
4.1. Numerical Simulation Model of Well GB X1
4.2. Verification of Simulation Model
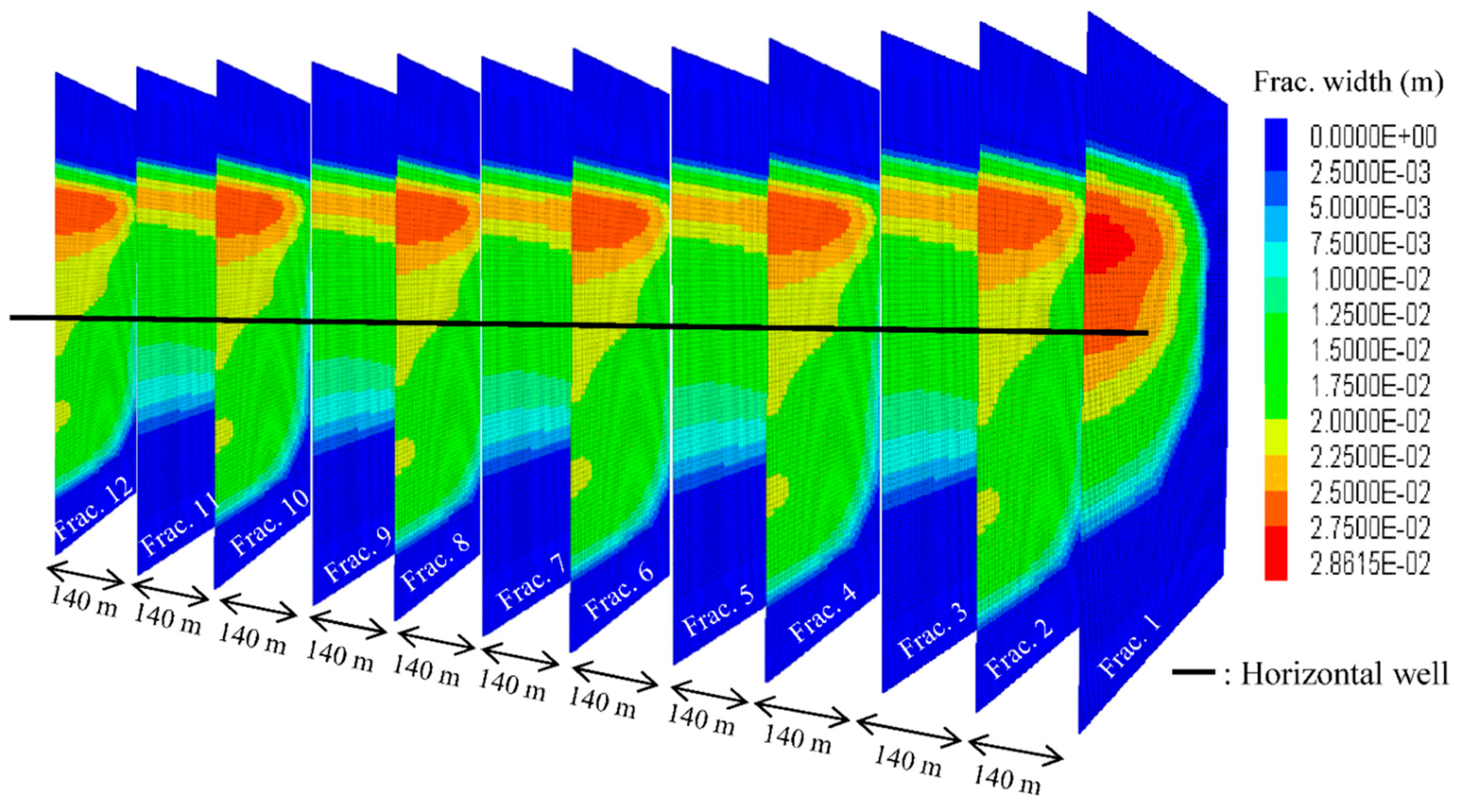
4.3. Results and Discussion of Multiple Fracturing Operation at Well GB X1
5. Conclusions
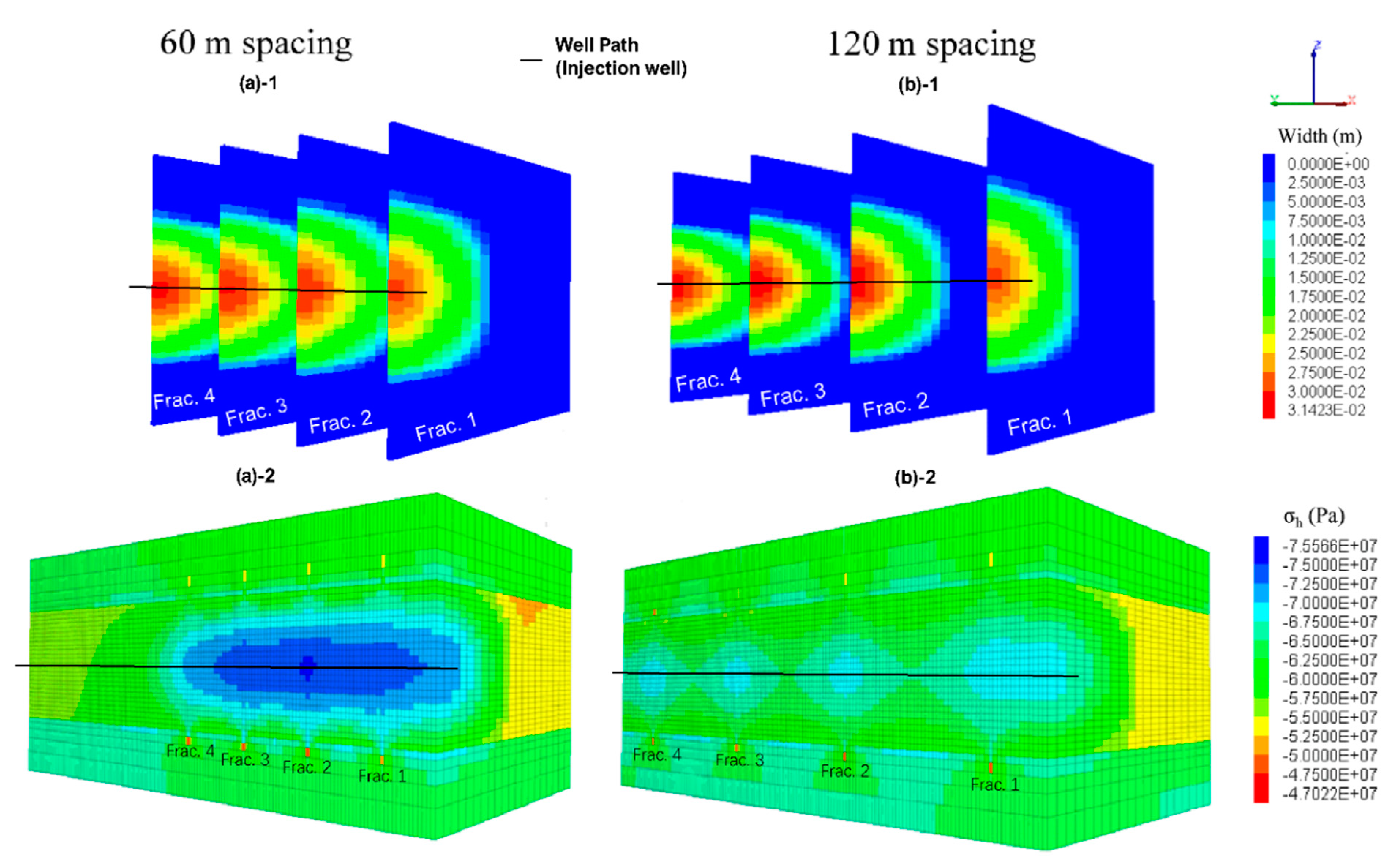
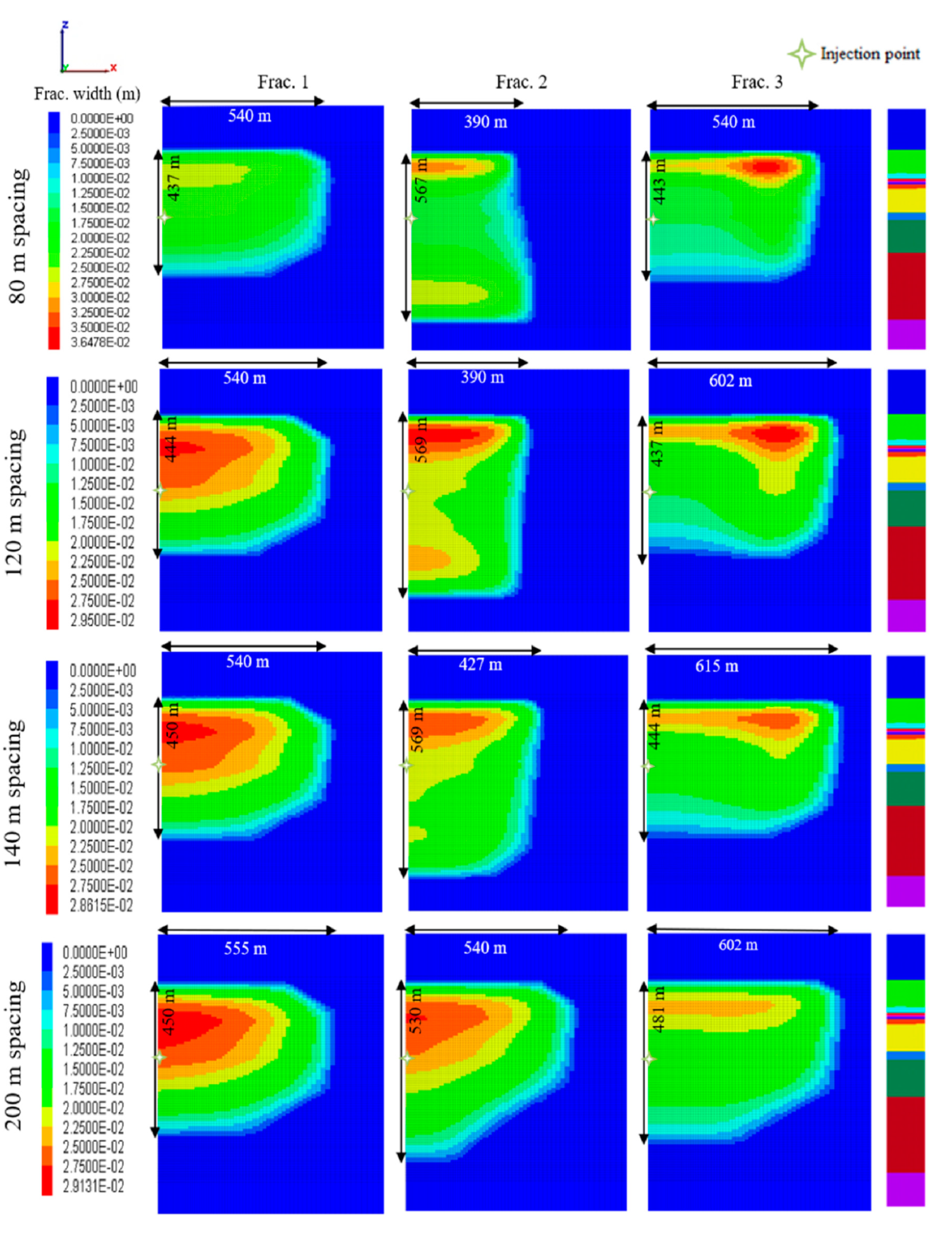
- Through fictive model study outcomes, it is evident that stress shadow superposition affects the subsequent fracture width, which ultimately plays a vital role in geothermal energy production. The assumption of similar fracture width may lead to erroneous results.
- Stress shadow superposition enlarges in massive multiple fracturing operations, which eventually distort the fracture propagation as depicted from the results of well GB X1 in the North German basin.
- Regardless of initial minimum horizontal stress conditions, the shape of the newly created fracture is highly dependent on the previous fracture configuration and attenuation in successive fracture shape becomes more prominent in the case of massive fracturing operations with lower fracture spacing.
- In order to predict the precise estimations of geothermal energy exploitation, proper multiple fracture configuration becomes imperative and should be studied with reference to fracture spacing under the influence of stress shadow impact.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, M.; Gou, Y.; Hou, Z.; Were, P. Investigation of a new HDR system with horizontal wells and multiple fractures using the coupled wellbore–reservoir simulator TOUGH2MP-WELL/EOS3. Environ. Earth Sci. 2015, 73, 6047–6058. [Google Scholar] [CrossRef]
- Pandey, S.N.; Chaudhuri, A.; Kelkar, S. A coupled thermo-hydro-mechanical modeling of fracture aperture alteration and reservoir deformation during heat extraction from a geothermal reservoir. Geothermics 2017, 65, 17–31. [Google Scholar] [CrossRef]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. Impact of enhanced geothermal systems on US energy supply in the twenty-first century. Philos. Transact. A Math. Phys. Eng. Sci. 2007, 365, 1057–1094. [Google Scholar] [CrossRef] [PubMed]
- Chamorro, C.R.; Mondéjar, M.E.; Ramos, R.; Segovia, J.J.; Martín, M.C.; Villamañán, M.A. World geothermal power production status: Energy, environmental and economic study of high enthalpy technologies. Energy 2012, 42, 10–18. [Google Scholar] [CrossRef]
- Will, J.; Eckardt, S.; Ranjan, A. Numerical Simulation of Hydraulic Fracturing Process in an Enhanced Geothermal Reservoir Using a Continuum Homogenized Approach. Procedia Eng. 2017, 191, 821–828. [Google Scholar] [CrossRef]
- World Energy Resources: 2013 Survey; World Energy Council: London, UK, 2013; Available online: https://www.worldenergy.org/publications/entry/world-energy-resources-2013-survey (accessed on 8 May 2020).
- Twidell, J.; Weir, T. Renewable Energy Resources; CRC Press: Boca Raton, FL, USA, 2015; Available online: https://www.routledge.com/Renewable-Energy-Resources-3rd-Edition/Twidell-Weir/p/book/9780415584388 (accessed on 15 May 2020).
- Johnston, I.W.; Narsilio, G.A.; Colls, S. Emerging geothermal energy technologies. KSCE J. Civ. Eng. 2011, 15, 643–653. [Google Scholar] [CrossRef]
- Olasolo, P.; Juárez, M.C.; Morales, M.P.; D’Amico, S.; Liarte, I.A. Enhanced geothermal systems (EGS): A review. Renew. Sustain. Energy Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Barbier, E. Geothermal energy technology and current status: An overview. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Ogino, F.; Yamamura, M.; Fukuda, T. Heat transfer from hot dry rock to waterflowingthrough a circular fracture. Geothermics 1999, 28, 21–44. [Google Scholar] [CrossRef]
- Mortensen, J.J. Hot dry rock: A new geothermal energy source. Energy 1978, 3, 639–644. [Google Scholar] [CrossRef]
- Brown, D.W.; Duchane, D.V. Scientific progress on the Fenton Hill HDR project since 1983. Geothermics 1999, 28, 591–601. [Google Scholar] [CrossRef] [Green Version]
- Economides, M.J.; Nolte, K.G. Reservoir Stimulation, 3rd ed.; Wiley: Chichester, UK; New York, NY, USA, 2000. [Google Scholar]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Li, T.; Shiozawa, S.; McClure, M.W. Thermal breakthrough calculations to optimize design of a multiple-stage Enhanced Geothermal System. Geothermics 2016, 64, 455–465. [Google Scholar] [CrossRef] [Green Version]
- Evans, K.F. Permeability creation and damage due to massive fluid injections into granite at 3.5 km at Soultz: 2. Critical stress and fracture strength. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef]
- Parker, R. The Rosemanowes HDR project 1983–1991. Geothermics 1999, 28, 603–615. [Google Scholar] [CrossRef]
- Genter, A.; Evans, K.; Cuenot, N.; Fritsch, D.; Sanjuan, B. Contribution of the exploration of deep crystalline fractured reservoir of Soultz to the knowledge of enhanced geothermal systems (EGS). Comptes Rendus Geosci. 2010, 342, 502–516. [Google Scholar] [CrossRef]
- Hayashi, K.; Willis-Richards, J.; Hopkirk, R.J.; Niibori, Y. Numerical models of HDR geothermal reservoirs—A review of current thinking and progress. Geothermics 1999, 28, 507–518. [Google Scholar] [CrossRef]
- O’Sullivan, M.J.; Pruess, K.; Lippmann, M.J. State of the art of geothermal reservoir simulation. Geothermics 2001, 30, 395–429. [Google Scholar] [CrossRef]
- Tsang, C.-F. Coupled hydromechanical-thermochemical processes in rock fractures. Rev. Geophys. 1991, 29, 537–551. [Google Scholar] [CrossRef]
- McDermott, C.I.; Randriamanjatosoa, A.R.L.; Tenzer, H.; Kolditz, O. Simulation of heat extraction from crystalline rocks: The influence of coupled processes on differential reservoir cooling. Geothermics 2006, 35, 321–344. [Google Scholar] [CrossRef]
- Hou, Z.; Şen, O.; Gou, Y.; Eker, A.M.; Li, M.; Yal, G.P.; Cambazoğlu, S.; Were, P. Preliminary geological, geochemical and numerical study on the first EGS project in Turkey. Environ. Earth Sci. 2015, 73, 6747–6767. [Google Scholar] [CrossRef]
- Legarth, B.; Huenges, E.; Zimmermann, G. Hydraulic fracturing in a sedimentary geothermal reservoir: Results and implications. Int. J. Rock Mech. Min. Sci. 2005, 42, 1028–1041. [Google Scholar] [CrossRef]
- Cao, W.; Huang, W.; Jiang, F. A novel thermal–hydraulic–mechanical model for the enhanced geothermal system heat extraction. Int. J. Heat Mass Transf. 2016, 100, 661–671. [Google Scholar] [CrossRef] [Green Version]
- Salimzadeh, S.; Paluszny, A.; Nick, H.M.; Zimmerman, R.W. A three-dimensional coupled thermo-hydro-mechanical model for deformable fractured geothermal systems. Geothermics 2018, 71, 212–224. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Z.; Feng, Z.; Yang, D.; Liang, W. THM (Thermo-hydro-mechanical) coupled mathematical model of fractured media and numerical simulation of a 3D enhanced geothermal system at 573 K and buried depth 6000–7000 M. Energy 2015, 82, 193–205. [Google Scholar] [CrossRef]
- Jiang, F.; Luo, L.; Chen, J. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems. Int. Commun. Heat Mass Transf. 2013, 41, 57–62. [Google Scholar] [CrossRef]
- Xu, C.; Dowd, P.A.; Tian, Z.F. A simplified coupled hydro-thermal model for enhanced geothermal systems. Appl. Energy 2015, 140, 135–145. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhan, J.; Wu, N.; Luo, Y.; Cai, W. Numerical investigation of electricity generation potential from fractured granite reservoir by water circulating through three horizontal wells at Yangbajing geothermal field. Appl. Therm. Eng. 2016, 104, 1–15. [Google Scholar] [CrossRef]
- Roussel, N.P.; Sharma, M.M. Optimizing Fracture Spacing and Sequencing in Horizontal-Well Fracturing. SPE Prod. Oper. 2011, 26, 173–184. [Google Scholar] [CrossRef]
- Fisher, M.K.; Heinze, J.R.; Harris, C.D.; Davidson, B.M.; Wright, C.A.; Dunn, K.P. Optimizing Horizontal Completion Techniques in the Barnett Shale Using Microseismic Fracture Mapping. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar] [CrossRef]
- Shin, D.H.; Sharma, M.M. Factors Controlling the Simultaneous Propagation of Multiple Competing Fractures in a Horizontal Well. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2014. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.; Li, Y.; Fu, B. Simulation of simultaneous propagation of multiple hydraulic fractures in horizontal wells. J. Pet. Sci. Eng. 2016, 147, 788–800. [Google Scholar] [CrossRef]
- Zhou, L.; Hou, M.Z.; Gou, Y.; Li, M. Numerical investigation of a low-efficient hydraulic fracturing operation in a tight gas reservoir in the North German Basin. J. Pet. Sci. Eng. 2014, 120, 119–129. [Google Scholar] [CrossRef]
- Feng, W.; Were, P.; Li, M.; Hou, Z.; Zhou, L. Numerical study on hydraulic fracturing in tight gas formation in consideration of thermal effects and THM coupled processes. J. Pet. Sci. Eng. 2016, 146, 241–254. [Google Scholar] [CrossRef]
- Zhou, L.; Hou, M.Z. A new numerical 3D-model for simulation of hydraulic fracturing in consideration of hydro-mechanical coupling effects. Int. J. Rock Mech. Min. Sci. 2013, 60, 370–380. [Google Scholar] [CrossRef]
- TMVOC, a Numerical Simulator for Three-Phase Non-Isothermal Flows of Multicomponent Hydrocarbon Mixtures in Saturated-Unsaturated Heterogeneous Media. ResearchGate. Available online: https://www.researchgate.net/publication/255274015_TMVOC_a_numerical_simulator_for_three-phase_non-isothermal_flows_of_multicomponent_hydrocarbon_mixtures_in_saturated-unsaturated_heterogeneous_media (accessed on 28 May 2020).
- Randolph, J.B.; Saar, M.O. Coupling carbon dioxide sequestration with geothermal energy capture in naturally permeable, porous geologic formations: Implications for CO2 sequestration. Energy Procedia 2011, 4, 2206–2213. [Google Scholar] [CrossRef] [Green Version]
- Tischner, T.; Krug, S.; Pechan, E.; Hesshaus, A.; Jatho, R.; Bischoff, M.; Wonik, T. Massive Hydraulic Fracturing in Low Permeable Sedimentary Rock in the GeneSys Project. In Proceedings of the Thirty-Eighth Workshop on Geothermal Reservoir Engineering, SGP-TR-198, Stanford University, Stanford, CA, USA, 11–13 February 2013; p. 11. [Google Scholar]
- Pechan, E.; Tischner, T.; Renner, J. Fracture Properties after Hydraulic Stimulation in Low-Permeability Sediments (Genesys-Project). In Proceedings of the ISRM Regional Symposium—EUROCK 2014, Vigo, Spain, 27–29 May 2014; Available online: https://www.onepetro.org/conference-paper/ISRM-EUROCK-2014-232 (accessed on 28 May 2020).
- Hou, M.Z.; Kracke, T.; Zhou, L.; Wang, X. Rock Mechanical Influences of Hydraulic Fracturing Deep Underground the North German Basin: Geological Integrity of the Cap Rock Salt and Maximum Magnitude of Induced Microseismicity Based on the GeneSys Stimulation in May 2011. Erdoel Erdgas Kohle 2012, 128, 454–460. [Google Scholar]
- Zhou, L. New Numerical Approaches to Model Hydraulic Fracturing in Tight Reservoirs with Consideration of Hydro-Mechanical Coupling Effects, 1st ed.; Cuvillier Verlag: Göttingen, Germany, 2014. [Google Scholar]
- Zhang, Y.-J.; Li, Z.-W.; Guo, L.-L.; Gao, P.; Jin, X.-P.; Xu, T.-F. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: A case study in Xujiaweizi area in Daqing Oilfield, China. Energy 2014, 78, 788–805. [Google Scholar] [CrossRef]





| Zones | Porosity (-) | Permeability (m2) | Density (kg/m3) | Poisson’s Ratio (-) | Young’s Modulus (Pa) |
|---|---|---|---|---|---|
| Cap rock | 0.025 | 1 × 10−18 | 2650 | 0.3 | 2.5 × 1010 |
| Pay-zone | 0.1 | 1 × 10−15 | 2600 | 0.25 | 3.5 × 1010 |
| Basement | 0.025 | 1 × 10−18 | 2650 | 0.3 | 2.5 × 1010 |
| Parameter | Value |
|---|---|
| Injected fluid | Water |
| Injected fluid volume per half fracture | 3600 m3 |
| Injection rate per half fracture | 5.4 m3/min. |
| Specific heat of formations | 1200 J/kg °C |
| Thermal conductivity of rock formations | 2.5 W/m °C |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haris, M.; Hou, M.Z.; Feng, W.; Luo, J.; Zahoor, M.K.; Liao, J. Investigative Coupled Thermo-Hydro-Mechanical Modelling Approach for Geothermal Heat Extraction through Multistage Hydraulic Fracturing from Hot Geothermal Sedimentary Systems. Energies 2020, 13, 3504. https://doi.org/10.3390/en13133504
Haris M, Hou MZ, Feng W, Luo J, Zahoor MK, Liao J. Investigative Coupled Thermo-Hydro-Mechanical Modelling Approach for Geothermal Heat Extraction through Multistage Hydraulic Fracturing from Hot Geothermal Sedimentary Systems. Energies. 2020; 13(13):3504. https://doi.org/10.3390/en13133504
Chicago/Turabian StyleHaris, Muhammad, Michael Z. Hou, Wentao Feng, Jiashun Luo, Muhammad Khurram Zahoor, and Jianxing Liao. 2020. "Investigative Coupled Thermo-Hydro-Mechanical Modelling Approach for Geothermal Heat Extraction through Multistage Hydraulic Fracturing from Hot Geothermal Sedimentary Systems" Energies 13, no. 13: 3504. https://doi.org/10.3390/en13133504
APA StyleHaris, M., Hou, M. Z., Feng, W., Luo, J., Zahoor, M. K., & Liao, J. (2020). Investigative Coupled Thermo-Hydro-Mechanical Modelling Approach for Geothermal Heat Extraction through Multistage Hydraulic Fracturing from Hot Geothermal Sedimentary Systems. Energies, 13(13), 3504. https://doi.org/10.3390/en13133504






