Design of Nanomaterials for Hydrogen Storage †
Abstract
:1. Introduction
- Gravimetric H density in the range 5–10 wt % H2, corresponding to an energy density of 1.6–3.2 kWh/kg.
- Volumetric H density kg H2 m−3, corresponding to an energy density kWh/L.
- Thermodynamics: °C (transport applications) or °C (stationary applications).
- Kinetics (tank level): fill time 3–5 min; H2 release flow 1.6 g/s.
- Durability: 1500 cycles (1/4 tank to full).
2. Hydrogen in Nanomaterials
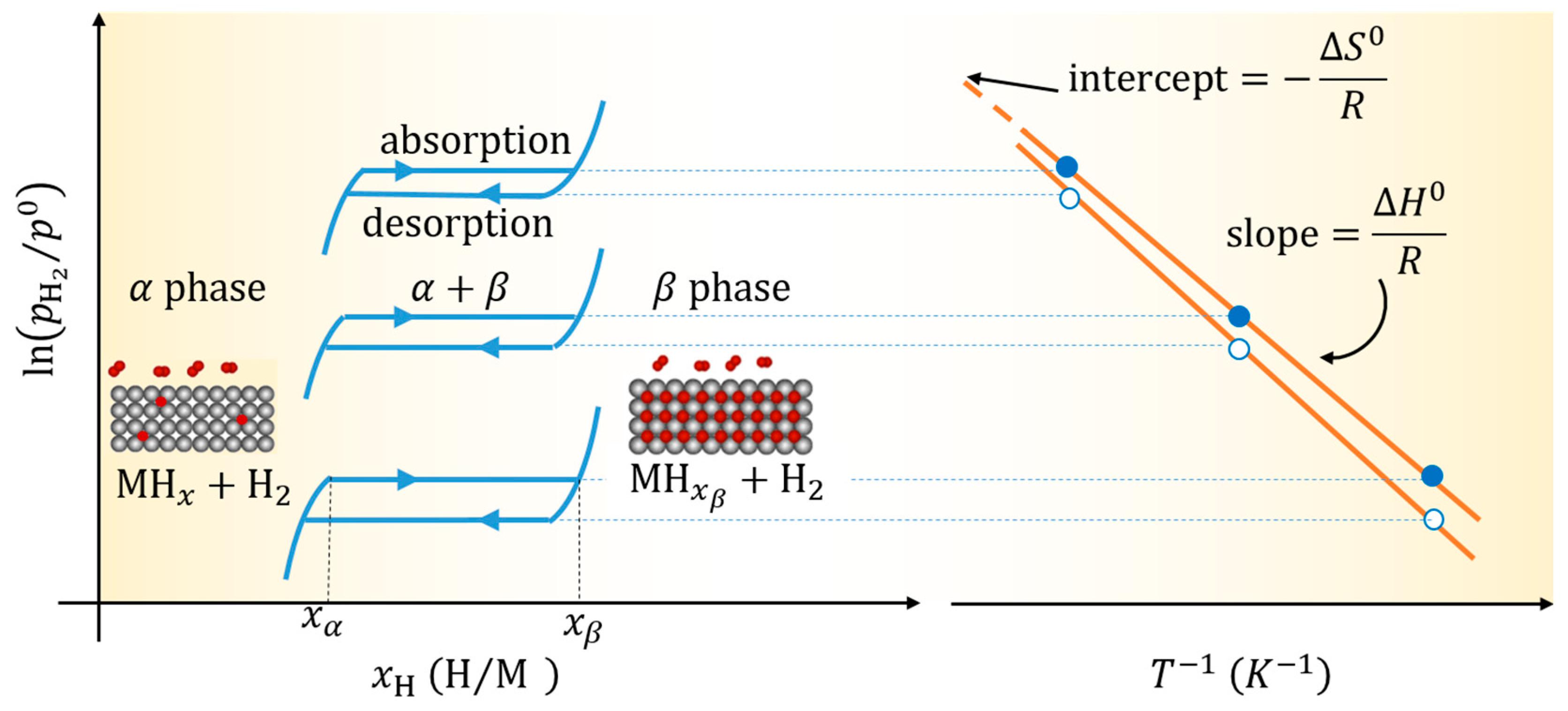
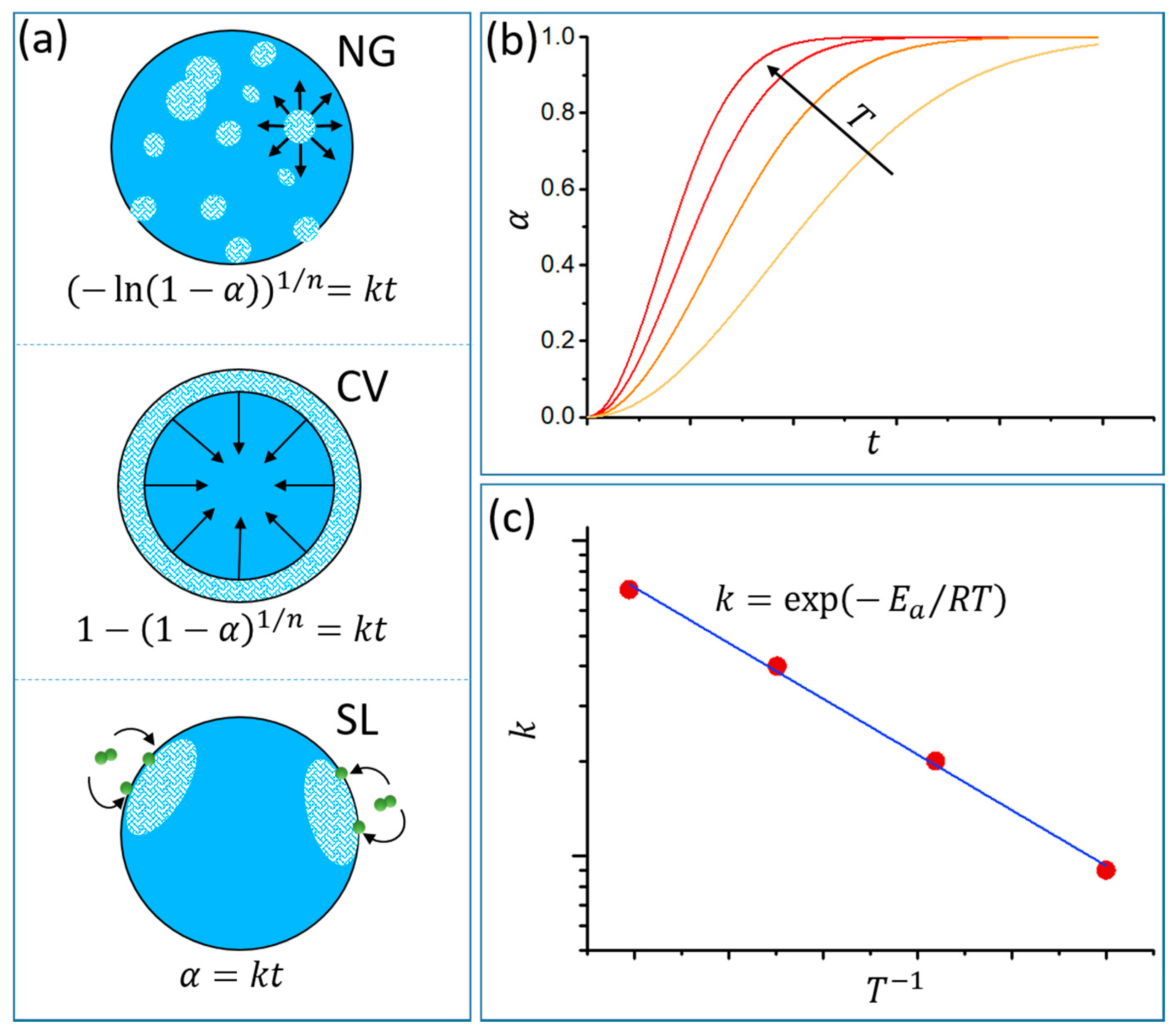
2.1. Thermodynamics and Kinetics of Hydride Formation and Decomposition
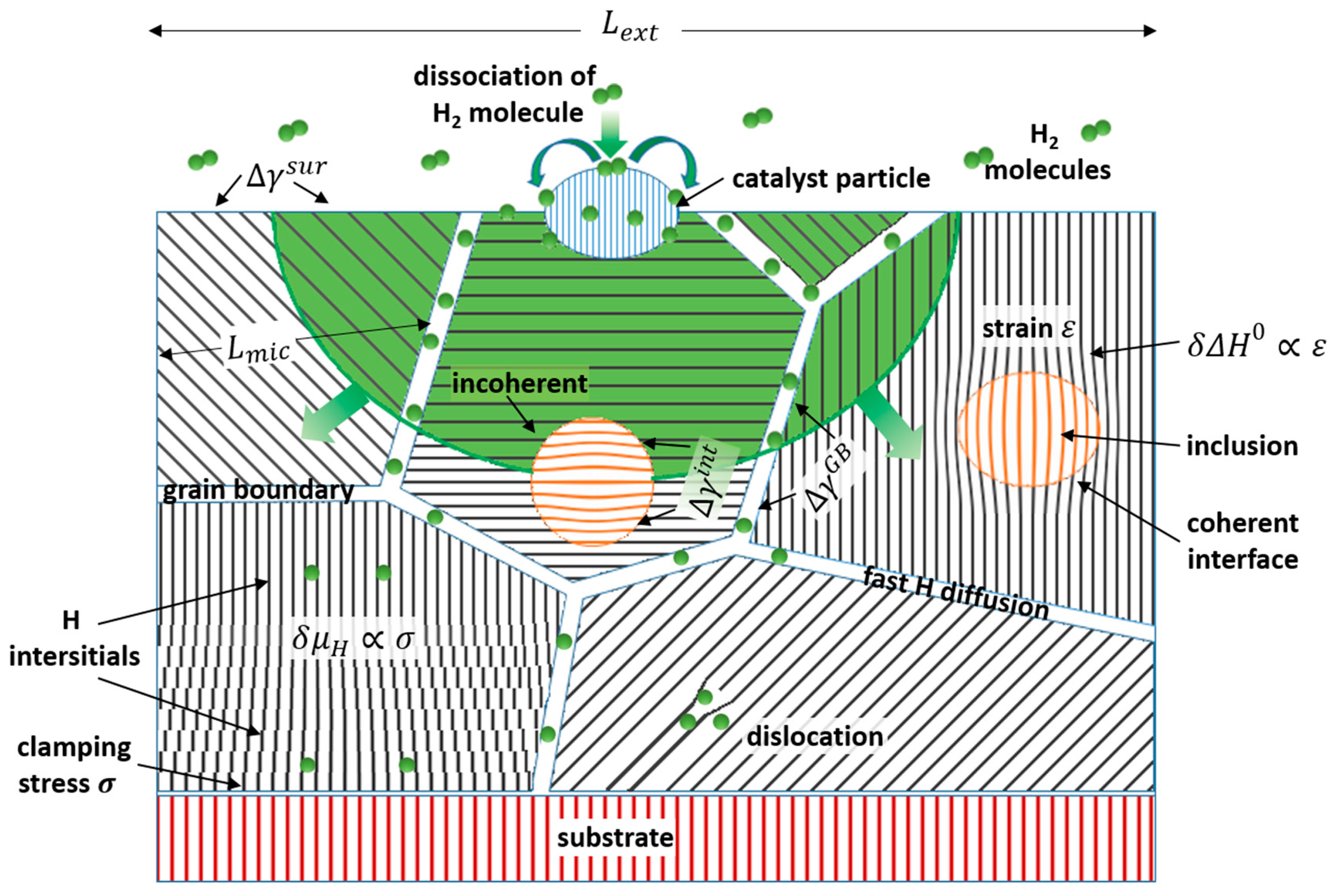
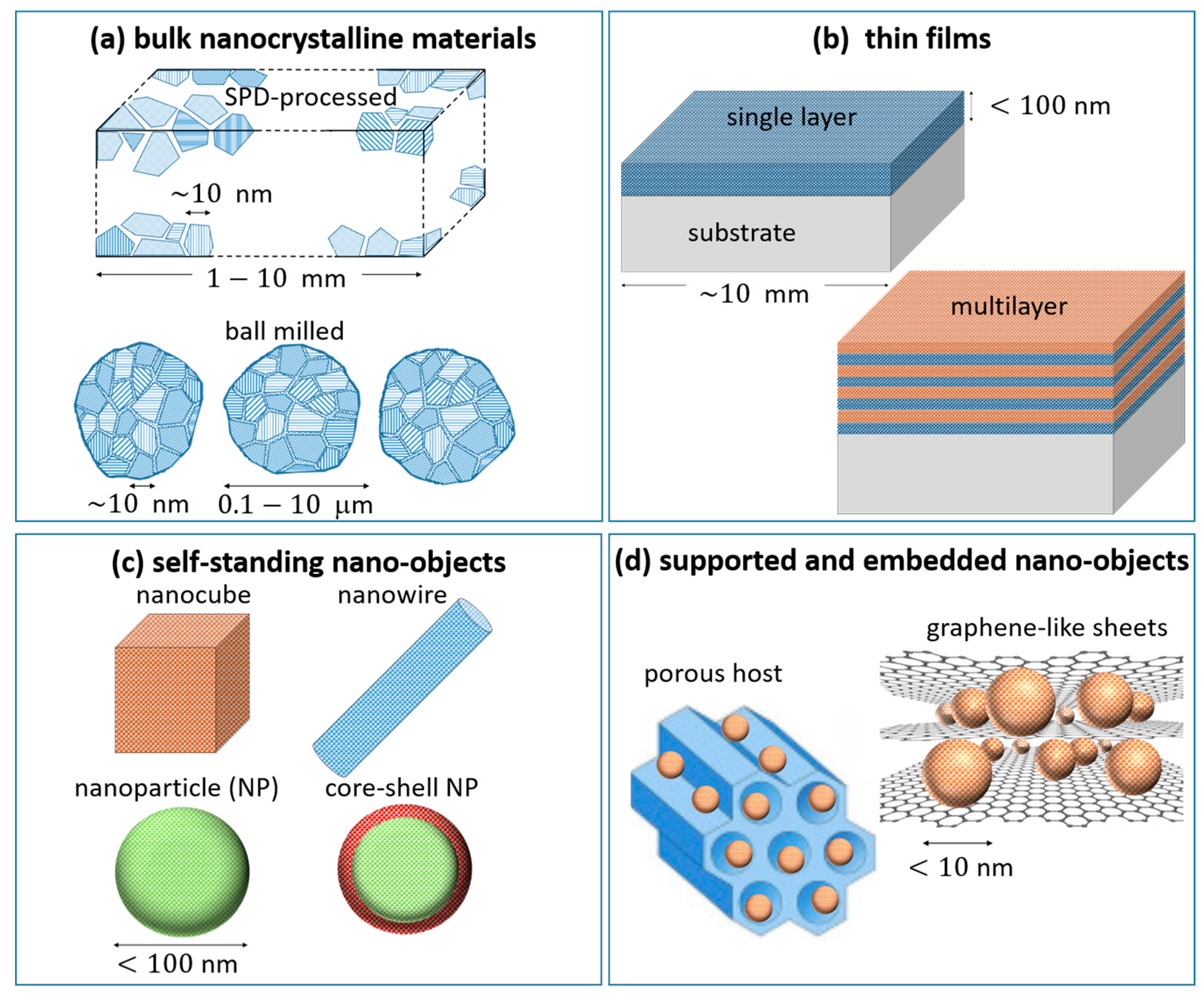
2.2. Influence of Nanomaterials Structure on H Sorption Properties
- Bulk nanocrystalline materials (Figure 4a) have nm in all directions and a fine microstructure nm. They are prepared by top-down mechanical deformation methods such as severe plastic deformation (SPD) and ball milling.
- Thin films (Figure 4b) are characterized by having nm along one direction, and can be stacked to build multilayers with several heterophasic interfaces. Metal hydride thin films are usually prepared by physical vapor deposition techniques under high vacuum, such as magnetron sputtering or e-beam evaporation, followed by exposure to H2. The layer–substrate and layer–layer interactions have a measurable impact on the H sorption properties.
- In self-standing nano-objects such as nanoparticles (NPs) and nanowires (NWs; Figure 4c), mutual interactions are negligible and do not influence the metal–hydride transformation. These objects have nm along two (NWs) or three (NPs) directions and can be fabricated both by physical and chemical synthesis techniques.
- Composite architectures, such as supported and embedded nano-objects (Figure 4d), combine several features of the other categories. Most of the time the H-storage units consist in very small NPs (<10 nm). The analysis of H sorption must encompass both the properties of single NPs and their interaction with the surrounding medium.
3. Bulk Nanostructured Materials
3.1. Ball Milling
3.2. Severe Plastic Deformation
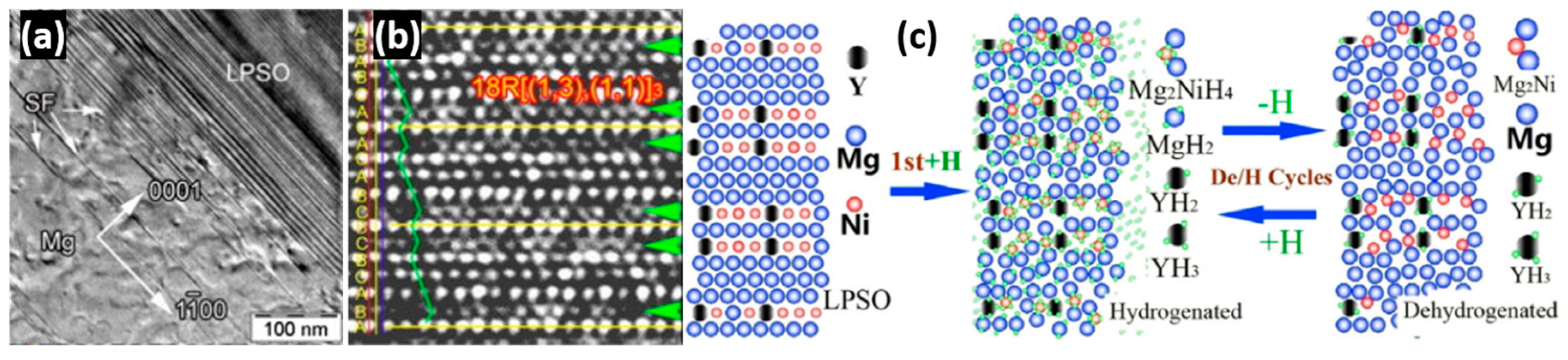
3.3. Long-Period Stacking Ordered Structures
4. Thin Films
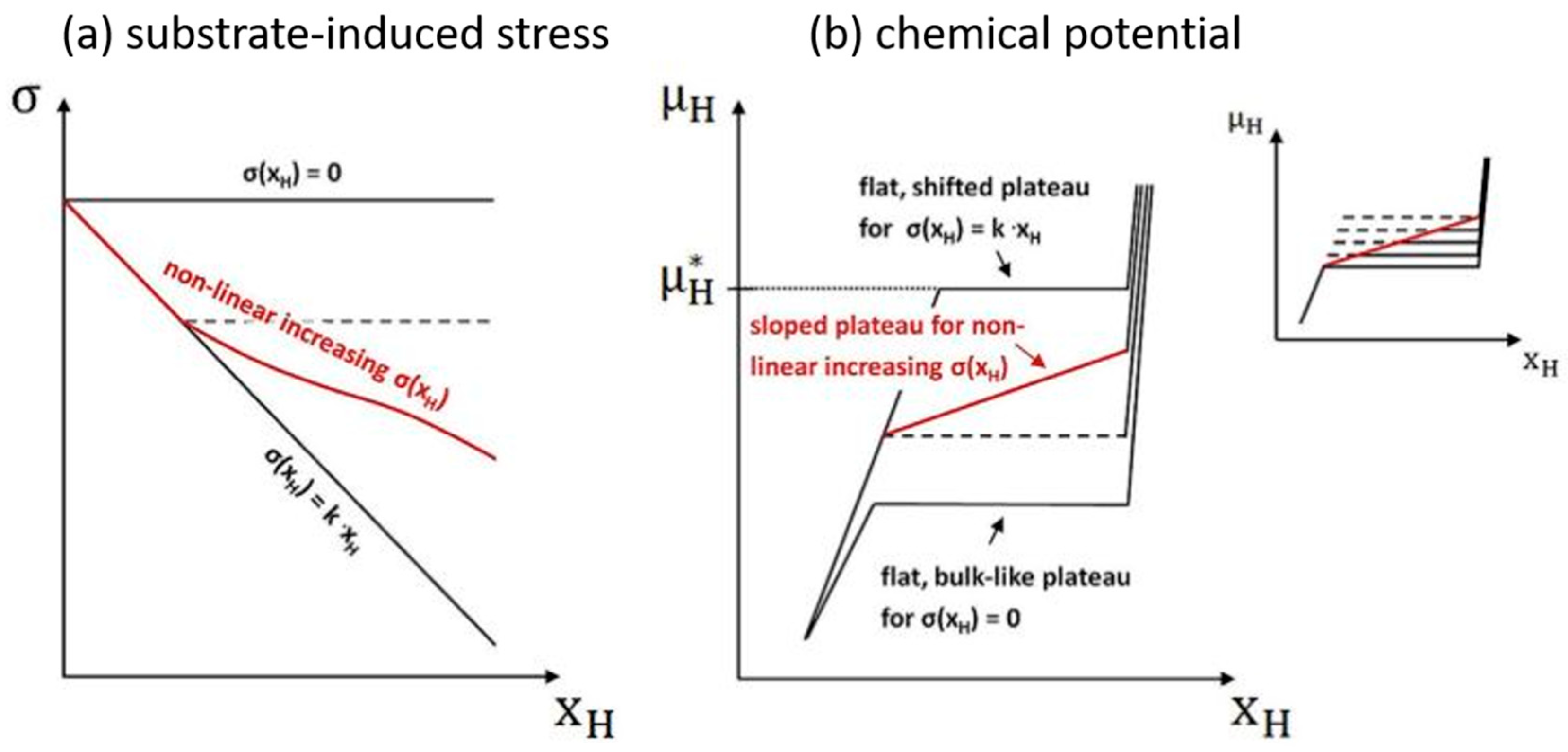
4.1. Elastic Strains in Thin Films
4.2. Interface Free Energy in Thin Films
5. Nano-Objects with a Composite Architecture
5.1. Core–Shell Nanoparticles
5.2. Thin Films Decorated with Nanoparticles
5.3. Composite Nanoparticles
5.4. Nanoconfined Hydrides in Porous Scaffolds and Graphene-Based Materials
6. In Situ Observations of the Metal–Hydride Transformation
7. Summary and Outlook
Funding
Acknowledgments
Conflicts of Interest
References
- US DOE Hydrogen & Fuel Cells Program. Available online: https://www.hydrogen.energy.gov/ (accessed on 30 June 2020).
- EERA-JP Fuel Cells and Hydrogen Implementation Plan. Available online: https://www.eera-set.eu/news-resources/78:eera-jp-fuel-cells-and-hydrogen-publishes-its-implementation-plan-up-to-2030.html (accessed on 30 June 2020).
- van de Krol, R.; Grätzel, M. Photoelectrochemical Hydrogen Production; van de Krol, R., Grätzel, M., Eds.; Springer: Boston, MA, USA, 2012. [Google Scholar]
- SUNERGY-Unlocking the Renewable Energy Future. Available online: https://www.sunergy-initiative.eu/ (accessed on 30 June 2020).
- Carrette, L.; Friedrich, K.A.; Stimming, U. Fuel cells-fundamentals and applications. Fuel Cells 2001, 1, 5–39. [Google Scholar] [CrossRef]
- Steele, B.C.H.; Heinzel, A. Materials for fuel-cell technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Schlapbach, L.; Züttel, A. Hydrogen-storage materials for mobile applications. Nature 2001, 414, 353–358. [Google Scholar] [CrossRef] [PubMed]
- Eberle, U.; Felderhoff, M.; Schüth, F. Chemical and physical solutions for hydrogen storage. Angew. Chem. Int. Ed. 2009, 48, 6608–6630. [Google Scholar] [CrossRef]
- Møller, K.T.; Jensen, T.R.; Akiba, E.; Li, H. Hydrogen-A sustainable energy carrier. Prog. Nat. Sci. Mater. Int. 2017, 27, 34–40. [Google Scholar] [CrossRef]
- Züttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Hirscher, M.; Yartys, V.A.; Baricco, M.; Bellosta von Colbe, J.; Blanchard, D.; Bowman, R.C.; Broom, D.P.; Buckley, C.E.; Chang, F.; Chen, P.; et al. Materials for hydrogen-based energy storage—Past, recent progress and future outlook. J. Alloy. Compd. 2020, 827, 153548. [Google Scholar] [CrossRef]
- Yartys, V.A.; Lototskyy, M.V.; Akiba, E.; Albert, R.; Antonov, V.E.; Ares, J.R.; Baricco, M.; Bourgeois, N.; Buckley, C.E.; Bellosta von Colbe, J.M.; et al. Magnesium based materials for hydrogen based energy storage: Past, present and future. Int. J. Hydrogen Energy 2019, 44, 7809–7859. [Google Scholar] [CrossRef]
- Chen, P.; Zhu, M. Recent progress in hydrogen storage. Mater. Today 2008, 11, 36–43. [Google Scholar] [CrossRef]
- Sandrock, G. Panoramic overview of hydrogen storage alloys from a gas reaction point of view. J. Alloy. Compd. 1999, 293, 877–888. [Google Scholar] [CrossRef]
- US DOE Target Explanation Document: Onboard Hydrogen Storage for Light-Duty Fuel Cell Vehicles. Available online: www.energy.gov/eere/fuelcells/downloads/target-explanation-document-onboard-hydrogen-storage-light-duty-fuel-cell (accessed on 30 June 2020).
- Callini, E.; Aguey-Zinsou, K.-F.; Ahuja, R.; Ares, J.R.; Bals, S.; Biliškov, N.; Chakraborty, S.; Charalambopoulou, G.; Chaudhary, A.-L.; Cuevas, F.; et al. Nanostructured materials for solid-state hydrogen storage: A review of the achievement of COST Action MP1103. Int. J. Hydrogen Energy 2016, 41, 14404–14428. [Google Scholar] [CrossRef]
- Gleiter, H. Nanostructured materials: Basic concepts and microstructure. Acta Mater. 2000, 48, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Dosch, H. Some general aspects of confinement in nanomaterials. Appl. Surf. Sci. 2001, 182, 192–195. [Google Scholar] [CrossRef]
- Pundt, A. Hydrogen in Nano-sized Metals. Adv. Eng. Mater. 2004, 6, 11–21. [Google Scholar] [CrossRef]
- Bérubé, V.; Radtke, G.; Dresselhaus, M.; Chen, G. Size effects on the hydrogen storage properties of nanostructured metal hydrides: A review. Int. J. Energy Res. 2007, 31, 637–663. [Google Scholar] [CrossRef]
- de Jongh, P.E.; Allendorf, M.; Vajo, J.J.; Zlotea, C. Nanoconfined light metal hydrides for reversible hydrogen storage. MRS Bull. 2013, 38, 488–494. [Google Scholar] [CrossRef]
- Sachs, C.; Pundt, A.; Kirchheim, R.; Winter, M.; Reetz, M.; Fritsch, D. Solubility of hydrogen in single-sized palladium clusters. Phys. Rev. B 2001, 64, 075408. [Google Scholar] [CrossRef]
- Mooij, L.P.A.; Baldi, A.; Boelsma, C.; Shen, K.; Wagemaker, M.; Pivak, Y.; Schreuders, H.; Griessen, R.; Dam, B. Interface energy controlled thermodynamics of nanoscale metal hydrides. Adv. Energy Mater. 2011, 1, 754–758. [Google Scholar] [CrossRef]
- Patelli, N.; Migliori, A.; Morandi, V.; Pasquini, L. Interfaces within biphasic nanoparticles give a boost to magnesium-based hydrogen storage. Nano Energy 2020, 72, 104654. [Google Scholar] [CrossRef]
- Barkhordarian, G.; Klassen, T.; Bormann, R. Catalytic mechanism of transition-metal compounds on Mg hydrogen sorption reaction. J. Phys. Chem. B 2006, 110, 11020–11024. [Google Scholar] [CrossRef]
- Rizo-Acosta, P.; Cuevas, F.; Latroche, M. Hydrides of early transition metals as catalysts and grain growth inhibitors for enhanced reversible hydrogen storage in nanostructured magnesium. J. Mater. Chem. A 2019, 7, 23064. [Google Scholar] [CrossRef]
- Baldi, A.; Gonzalez-Silveira, M.; Palmisano, V.; Dam, B.; Griessen, R. Destabilization of the Mg-H system through elastic constraints. Phys. Rev. Lett. 2009, 102, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Pasquini, L.; Sacchi, M.; Brighi, M.; Boelsma, C.; Bals, S.; Perkisas, T.; Dam, B. Hydride destabilization in core-shell nanoparticles. Int. J. Hydrogen Energy 2014, 39. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. Enthalpy-entropy compensation: A phantom phenomenon. J. Biosci. 2002, 27, 121–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griessen, R.; Strohfeldt, N.; Giessen, H. Thermodynamics of the hybrid interaction of hydrogen with palladium nanoparticles. Nat. Mater. 2016, 15, 311–317. [Google Scholar] [CrossRef]
- Huot, J.; Ravnsbæk, D.B.; Zhang, J.; Cuevas, F.; Latroche, M.; Jensen, T.R. Mechanochemical synthesis of hydrogen storage materials. Prog. Mater. Sci. 2013, 58, 30–75. [Google Scholar] [CrossRef]
- Kumar, S.; Pavloudis, T.; Singh, V.; Nguyen, H.; Steinhauer, S.; Pursell, C.; Clemens, B.; Kioseoglou, J.; Grammatikopoulos, P.; Sowwan, M. Hydrogen Flux through Size Selected Pd Nanoparticles into Underlying Mg Nanofilms. Adv. Energy Mater. 2018, 8, 1701326. [Google Scholar] [CrossRef]
- Patelli, N.; Migliori, A.; Pasquini, L. Reversible metal-hydride transformation in Mg-Ti-H nanoparticles at remarkably low temperatures. Chem. Phys. Chem. 2019, 20, 1325–1333. [Google Scholar] [CrossRef] [Green Version]
- Baldi, A.; Narayan, T.C.; Koh, A.L.; Dionne, J. A in situ detection of hydrogen-induced phase transitions in individual palladium nanocrystals. Nat. Mater. 2014, 13. [Google Scholar] [CrossRef]
- Syrenova, S.; Wadell, C.; Nugroho, F.A.A.; Gschneidtner, T.A.; Diaz Fernandez, Y.A.; Nalin, G.; Świtlik, D.; Westerlund, F.; Antosiewicz, T.J.; Zhdanov, V.P.; et al. Hydride formation thermodynamics and hysteresis in individual Pd nanocrystals with different size and shape. Nat. Mater. 2015, 14, 1236–1244. [Google Scholar] [CrossRef]
- Ulvestad, A.; Welland, M.J.; Cha, W.; Liu, Y.; Kim, J.W.; Harder, R.; Maxey, E.; Clark, J.N.; Highland, M.J.; You, H.; et al. Three-dimensional imaging of dislocation dynamics during the hydriding phase transformation. Nat. Mater. 2017, 16, 565–571. [Google Scholar] [CrossRef] [PubMed]
- Pundt, A.; Kirchheim, R. Hydrogen in metals: Microstructural Aspects. Annu. Rev. Mater. Res. 2006, 36, 555–608. [Google Scholar] [CrossRef]
- Pasquini, L. The effects of nanostructure on the hydrogen sorption properties of magnesium-based metallic compounds: A review. Crystals 2018, 8, 106. [Google Scholar] [CrossRef] [Green Version]
- Schneemann, A.; White, J.L.; Kang, S.; Jeong, S.; Wan, L.F.; Cho, E.S.; Heo, T.W.; Prendergast, D.; Urban, J.J.; Wood, B.C.; et al. Nanostructured metal hydrides for hydrogen Storage. Chem. Rev. 2018, 118, 10775–10839. [Google Scholar] [CrossRef]
- De Jongh, P.E.; Adelhelm, P. Nanosizing and nanoconfinement: New strategies towards meeting hydrogen storage goals. ChemSusChem 2010, 3, 1332–1348. [Google Scholar] [CrossRef]
- Zou, J.; Sun, H.; Zeng, X.; Ji, G.; Ding, W. Preparation and hydrogen storage properties of MG-rich Mg-Ni ultrafine particles. J. Nanomater. 2012, 2012, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, R.B.; Khachaturyan, A.G. Thermodynamics of open two-phase systems with coherent interfaces: Application to metal-hydrogen systems. Acta Mater. 2006, 54, 313–323. [Google Scholar] [CrossRef]
- Mooij, L.; Dam, B. Hysteresis and the role of nucleation and growth in the hydrogenation of Mg nanolayers. Phys. Chem. Chem. Phys. 2013, 15, 2782–2792. [Google Scholar] [CrossRef]
- Fukai, Y. The Metal-Hydrogen System: Basic Bulk Properties; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Uchida, H.T.; Wagner, S.; Hamm, M.; Kürschner, J.; Kirchheim, R.; Hjörvarsson, B.; Pundt, A. Absorption kinetics and hydride formation in magnesium films: Effect of driving force revisited. Acta Mater. 2015, 85, 279–289. [Google Scholar] [CrossRef]
- Mintz, M.H.; Zeiri, Y. Hydriding kinetics of powders. J. Alloys Compd. 1995, 216, 159–175. [Google Scholar] [CrossRef]
- Borgschulte, A.; Gremaud, R.; Griessen, R. Interplay of diffusion and dissociation mechanisms during hydrogen absorption in metals. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 78, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Rudman, P.S. Hydrogen-diffusion-rate-limited hydriding and dehydring kinetics. J. Appl. Phys. 1979, 50, 7195–7199. [Google Scholar] [CrossRef]
- Ron, M. The normalized pressure dependence method for the evaluation of kinetic rates of metal hydride formation/decomposition. J. Alloys Compd. 1999, 283, 178–191. [Google Scholar] [CrossRef]
- Berube, V.; Chen, G.; Dresselhaus, M.S. Impact of nanostructuring on the enthalpy of formation of metal hydrides. Int. J. Hydrogen Energy 2008, 33, 4122–4131. [Google Scholar] [CrossRef]
- Hao, S.Q.; Sholl, D.S. Effect of TiH2-induced strain on thermodynamics of hydrogen release from MgH2. J. Phys. Chem. C 2012, 116, 2045–2050. [Google Scholar] [CrossRef]
- Molinari, A.; D’Amico, F.; Calizzi, M.; Zheng, Y.; Boelsma, C.; Mooij, L.; Lei, Y.; Hahn, H.; Dam, B.; Pasquini, L. Interface and strain effects on the H-sorption thermodynamics of size-selected Mg nanodots. Int. J. Hydrogen Energy 2016, 41, 9841–9851. [Google Scholar] [CrossRef]
- Sun, Y.; Shen, C.; Lai, Q.; Liu, W.; Wang, D.-W.; Aguey-Zinsou, K.-F. Tailoring magnesium based materials for hydrogen storage through synthesis: Current state of the art. Energy Storage Mater. 2018, 10, 168–198. [Google Scholar] [CrossRef]
- Asano, K.; Enoki, H.; Akiba, E. Synthesis of HCP, FCC and BCC structure alloys in the Mg-Ti binary system by means of ball milling. J. Alloys Compd. 2009, 480, 558–563. [Google Scholar] [CrossRef]
- Zaluska, A.; Zaluski, L.; Ström-Olsen, J.O. Structure, catalysis and atomic reactions on the nano-scale: A systematic approach to metal hydrides for hydrogen storage. Appl. Phys. A Mater. Sci. Process. 2001, 72, 157–165. [Google Scholar] [CrossRef]
- Barkhordarian, G.; Klassen, T.; Bormann, R. Kinetic investigation of the effect of milling time on the hydrogen sorption reaction of magnesium catalyzed with different Nb2O 5 contents. J. Alloys Compd. 2006, 407, 249–255. [Google Scholar] [CrossRef]
- Lu, J.; Choi, Y.J.; Fang, Z.Z.; Sohn, H.Y.; Rönnebro, E. Hydrogen storage properties of nanosized MgH2-0.1TiH2 prepared by ultrahigh-energy-high-pressure milling. J. Am. Chem. Soc. 2009, 131, 15843–15852. [Google Scholar] [CrossRef] [PubMed]
- Ravnsbœk, D.; Filinchuk, Y.; Cerenius, Y.; Jakobsen, H.J.; Besenbacher, F.; Skibsted, J.; Jensen, T.R. A series of mixed-metal borohydrides. Angew. Chem. Int. Ed. 2009, 48, 6659–6663. [Google Scholar] [CrossRef]
- Huot, J.; Cuevas, F.; Deledda, S.; Edalati, K.; Filinchuk, Y.; Grosdidier, T.; Hauback, B.C.; Heere, M.; Jensen, T.R.; Latroche, M.; et al. Mechanochemistry of metal hydrides: Recent advances. Materials 2019, 12, 2778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Webb, C.J. A review of catalyst-enhanced magnesium hydride as a hydrogen storage material. J. Phys. Chem. Solids 2015, 84. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Fernández, J.F.; Sánchez, C.R. Rate determining step in the absorption and desorption of hydrogen by magnesium. J. Alloys Compd. 2002, 340, 189–198. [Google Scholar] [CrossRef]
- Paskevicius, M.; Sheppard, D.A.; Buckley, C.E. Thermodynamic changes in mechanochemically synthesized magnesium hydride nanoparticles. J. Am. Chem. Soc. 2010, 6, 469–472. [Google Scholar] [CrossRef]
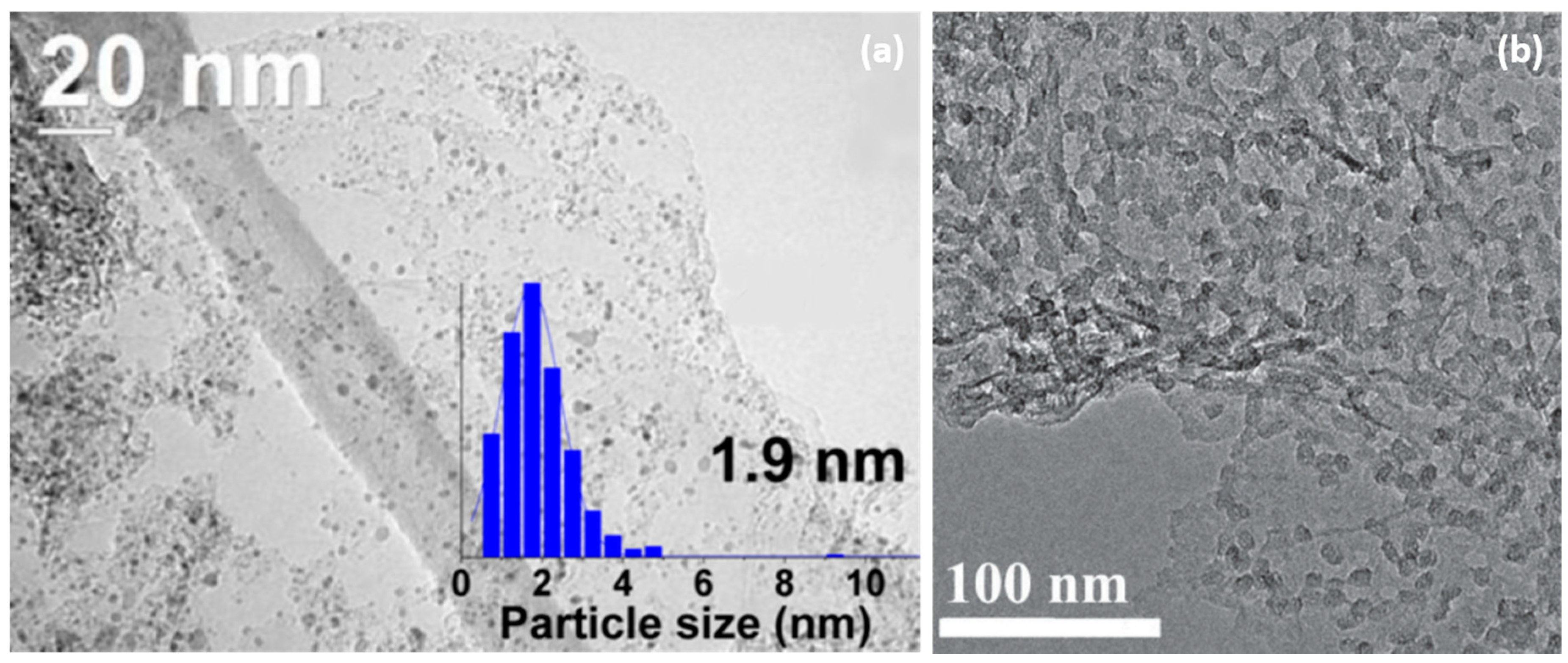
- Norberg, N.S.; Arthur, T.S.; Fredrick, S.J.; Prieto, A.L. Size-dependent hydrogen storage properties of Mg nanocrystals prepared from solution. J. Am. Chem. Soc. 2011, 133, 10679–10681. [Google Scholar] [CrossRef]
- Li, W.; Li, C.; Ma, H.; Chen, J. Magnesium nanowires: Enhanced kinetics for hydrogen absorption and desorption. J. Am. Chem. Soc. 2007, 129, 6710–6711. [Google Scholar] [CrossRef]
- Cho, E.S.; Ruminski, A.M.; Aloni, S.; Liu, Y.-S.; Guo, J.; Urban, J.J. Graphene oxide/metal nanocrystal multilaminates as the atomic limit for safe and selective hydrogen storage. Nat. Commun. 2016, 7, 10804. [Google Scholar] [CrossRef] [Green Version]
- Xia, G.; Tan, Y.; Chen, X.; Sun, D.; Guo, Z.; Liu, H.; Ouyang, L.; Zhu, M.; Yu, X. Monodisperse magnesium hydride nanoparticles uniformly self-assembled on graphene. Adv. Mater. 2015, 27, 5981–5988. [Google Scholar] [CrossRef] [PubMed]
- Shinde, S.S.; Kim, D.H.; Yu, J.Y.; Lee, J.H. Self-assembled air-stable magnesium hydride embedded in 3-D activated carbon for reversible hydrogen storage. Nanoscale 2017, 9, 7094–7103. [Google Scholar] [CrossRef] [PubMed]
- Fry, C.M.P.; Grant, D.M.; Walker, G.S. Catalysis and evolution on cycling of nano-structured magnesium multilayer thin films. Int. J. Hydrogen Energy 2014, 39, 1173–1184. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Wang, H.; Liu, J.; Ouyang, L.; Zhang, Q.; Sun, D.; Yao, X.; Zhu, M. Remarkable enhancement in dehydrogenation of MgH2 by a nano-coating of multi-valence Ti-based catalysts. J. Mater. Chem. A 2013, 1, 5603. [Google Scholar] [CrossRef]
- Liu, J.W.; Zou, C.C.; Wang, H.; Ouyang, L.Z.; Zhu, M. Facilitating de/hydrogenation by long-period stacking ordered structure in Mg based alloys. Int. J. Hydrogen Energy 2013, 38, 10438–10445. [Google Scholar] [CrossRef]
- Yamauchi, M.; Ikeda, R.; Kitagawa, H.; Takata, M. Nanosize effects on hydrogen storage in palladium. J. Phys. Chem. C 2008, 112, 3294–3299. [Google Scholar] [CrossRef]
- Bardhan, R.; Hedges, L.O.; Pint, C.L.; Javey, A.; Whitelam, S.; Urban, J.J. Uncovering the intrinsic size dependence of hydriding phase transformations in nanocrystals. Nat. Mater. 2013, 12. [Google Scholar] [CrossRef] [Green Version]
- Edalati, K.; Matsuda, J.; Iwaoka, H.; Toh, S.; Akiba, E.; Horita, Z. High-pressure torsion of TiFe intermetallics for activation of hydrogen storage at room temperature with heterogeneous nanostructure. Int. J. Hydrogen Energy 2013, 38, 4622–4627. [Google Scholar] [CrossRef]
- Révész, Á.; Gajdics, M.; Schafler, E.; Calizzi, M.; Pasquini, L. Dehydrogenation-hydrogenation characteristics of nanocrystalline Mg2Ni powders compacted by high-pressure torsion. J. Alloys Compd. 2017, 702, 84–91. [Google Scholar] [CrossRef]
- Edalati, K.; Shao, H.; Emami, H.; Iwaoka, H.; Akiba, E.; Horita, Z. Activation of titanium-vanadium alloy for hydrogen storage by introduction of nanograins and edge dislocations using high-pressure torsion. Int. J. Hydrogen Energy 2016, 41, 8917–8924. [Google Scholar] [CrossRef]
- Huot, J. Nanocrystalline metal hydrides obtained by severe plastic deformations. Metals (Basel) 2012, 2, 22–40. [Google Scholar] [CrossRef] [Green Version]
- Révész, A.; Kánya, Z.; Verebélyi, T.; Szabó, P.J.; Zhilyaev, A.P.; Spassov, T. The effect of high-pressure torsion on the microstructure and hydrogen absorption kinetics of ball-milled Mg70Ni30. J. Alloys Compd. 2010, 504, 83–88. [Google Scholar] [CrossRef]
- Gajdics, M.; Calizzi, M.; Pasquini, L.; Schafler, E.; Révész, A. Characterization of a nanocrystalline Mg-Ni alloy processed by high-pressure torsion during hydrogenation and dehydrogenation. Int. J. Hydrogen Energy 2016, 41, 9803–9809. [Google Scholar] [CrossRef]
- Emami, H.; Edalati, K.; Matsuda, J.; Akiba, E.; Horita, Z. Hydrogen storage performance of TiFe after processing by ball milling. Acta Mater. 2015, 88, 190–195. [Google Scholar] [CrossRef]
- Hongo, T.; Edalati, K.; Arita, M.; Matsuda, J.; Akiba, E.; Horita, Z. Significance of grain boundaries and stacking faults on hydrogen storage properties of Mg2Ni intermetallics processed by high-pressure torsion. Acta Mater. 2015, 92, 46–54. [Google Scholar] [CrossRef]
- Edalati, K.; Akiba, E.; Horita, Z. High-pressure torsion for new hydrogen storage materials. Sci. Technol. Adv. Mater. 2018, 19, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Edalati, K.; Matsuda, J.; Arita, M.; Daio, T.; Akiba, E.; Horita, Z. Mechanism of activation of TiFe intermetallics for hydrogen storage by severe plastic deformation using high-pressure torsion. Appl. Phys. Lett. 2013, 103, 143902. [Google Scholar] [CrossRef]
- Okuda, H.; Yamasaki, M.; Kawamura, Y.; Tabuchi, M.; Kimizuka, H. Nanoclusters first: A hierarchical phase transformation in a novel Mg alloy. Sci. Rep. 2015, 5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Abe, E.; Kawamura, Y.; Hayashi, K.; Inoue, A. Long-period ordered structure in a high-strength nanocrystalline Mg-1 at% Zn-2 at% Y alloy studied by atomic-resolution Z-contrast STEM. Acta Mater. 2002, 50, 3845–3857. [Google Scholar] [CrossRef]
- Itoi, T.; Seimiya, T.; Kawamura, Y.; Hirohashi, M. Long period stacking structures observed in Mg97Zn 1Y2 alloy. Scr. Mater. 2004, 51, 107–111. [Google Scholar] [CrossRef]
- Zhang, Q.A.; Liu, D.D.; Wang, Q.Q.; Fang, F.; Sun, D.L.; Ouyang, L.Z.; Zhu, M. Superior hydrogen storage kinetics of Mg12YNi alloy with a long-period stacking ordered phase. Scr. Mater. 2011, 65, 233–236. [Google Scholar] [CrossRef]
- Cermak, J.; Kral, L.; Roupcova, P. Significantly decreased stability of MgH2 in the Mg-In-C alloy system: Long-period-stacking-ordering as a new way how to improve performance of hydrogen storage alloys? Renew. Energy 2020, 150, 204–212. [Google Scholar] [CrossRef]
- Yoshimura, K.; Langhammer, C.; Dam, B. Metal hydrides for smart window and sensor applications. MRS Bull. 2013, 38, 495–503. [Google Scholar] [CrossRef] [Green Version]
- Nugroho, F.A.A.; Darmadi, I.; Cusinato, L.; Susarrey-Arce, A.; Schreuders, H.; Bannenberg, L.J.; da Silva Fanta, A.B.; Kadkhodazadeh, S.; Wagner, J.B.; Antosiewicz, T.J.; et al. Metal–polymer hybrid nanomaterials for plasmonic ultrafast hydrogen detection. Nat. Mater. 2019, 18, 489–495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagner, S.; Pundt, A. Quasi-thermodynamic model on hydride formation in palladium–hydrogen thin films: Impact of elastic and microstructural constraints. Int. J. Hydrogen Energy 2016, 41, 2727–2738. [Google Scholar] [CrossRef]
- Chung, C.J.; Lee, S.C.; Groves, J.R.; Brower, E.N.; Sinclair, R.; Clemens, B.M. Interfacial alloy hydride destabilization in Mg/Pd thin films. Phys. Rev. Lett. 2012, 108, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Baldi, A.; Mooij, L.; Palmisano, V.; Schreuders, H.; Krishnan, G.; Kooi, B.J.; Dam, B.; Griessen, R. Elastic versus Alloying effects in Mg-based hydride films. Phys. Rev. Lett. 2018, 121, 255503. [Google Scholar] [CrossRef] [Green Version]
- Pivak, Y.; Schreuders, H.; Dam, B. Thermodynamic properties, hysteresis behavior and stress-strain analysis of MgH2 thin films, studied over a wide temperature range. Crystals 2012, 2, 710–729. [Google Scholar] [CrossRef]
- Ngene, P.; Longo, A.; Mooij, L.; Bras, W.; Dam, B. Metal-hydrogen systems with an exceptionally large and tunable thermodynamic destabilization. Nat. Commun. 2017, 8, 1846. [Google Scholar] [CrossRef]
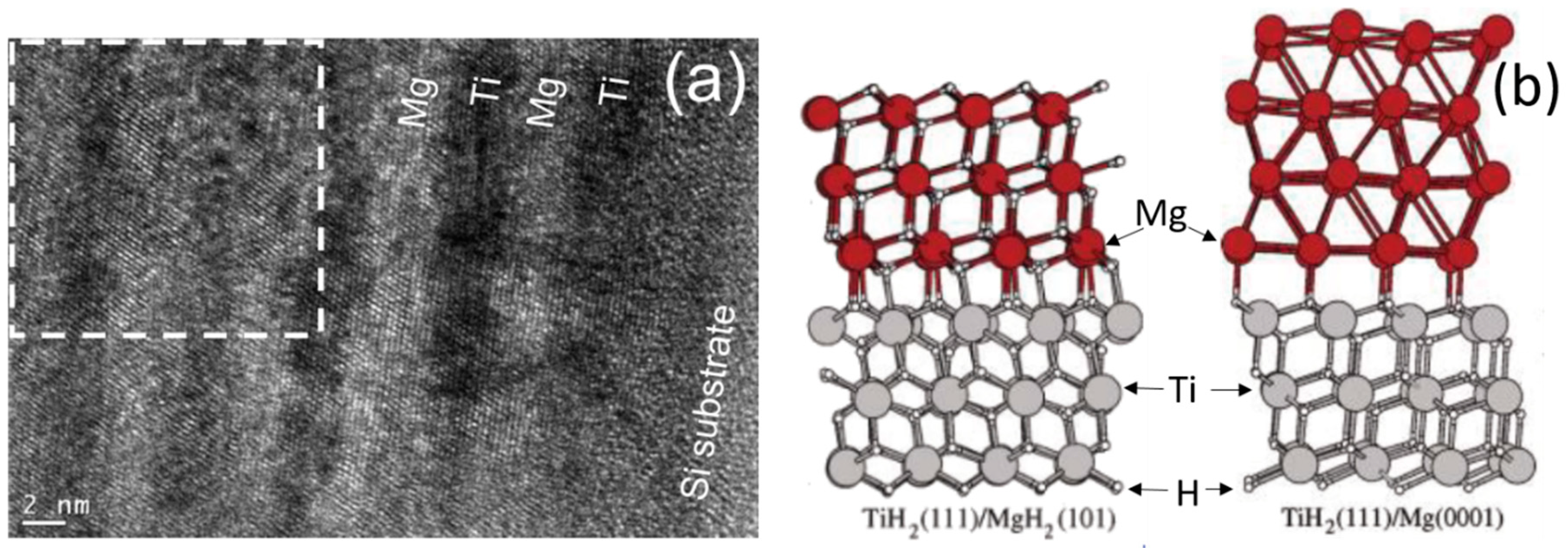
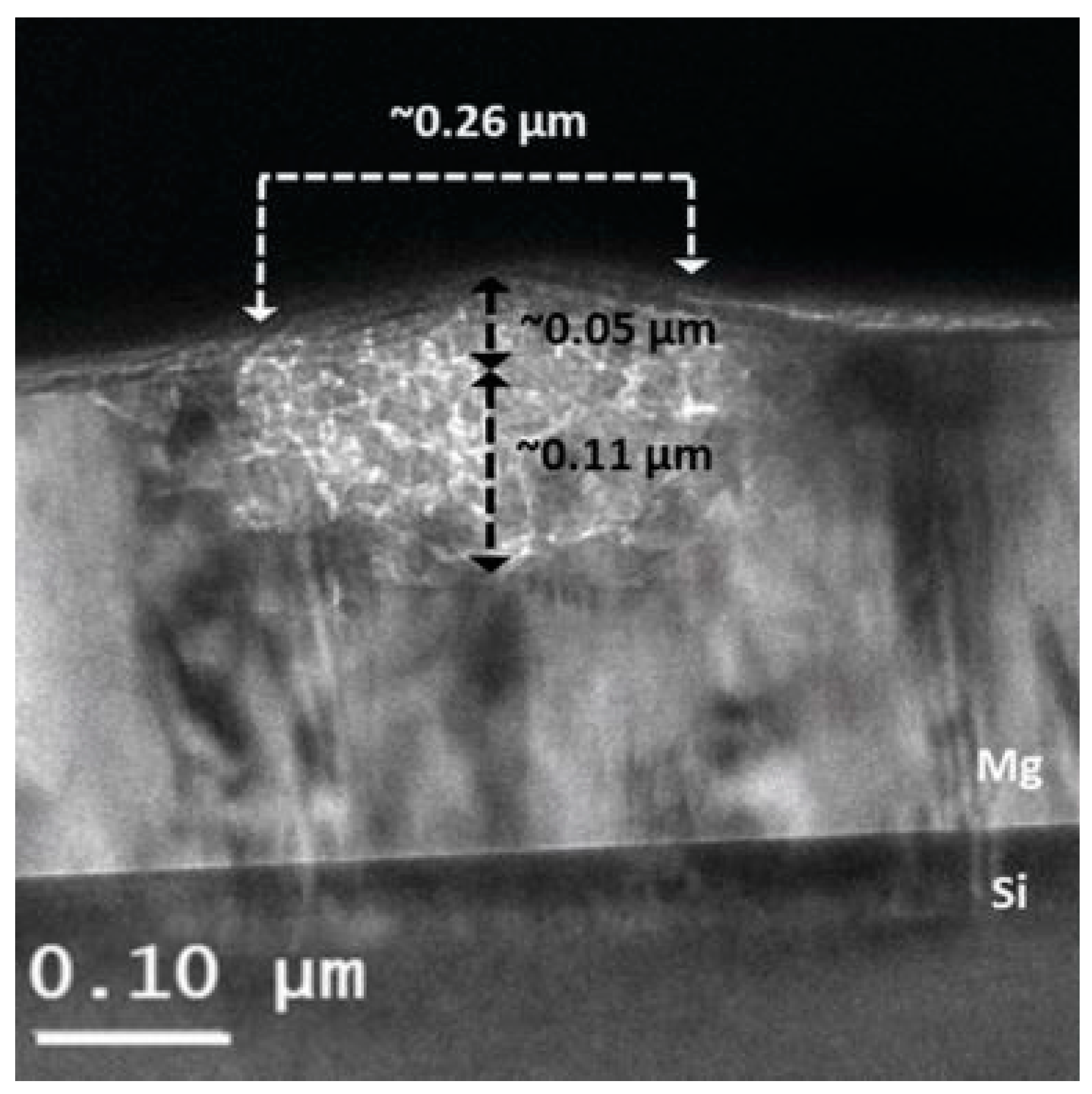
- Baldi, A.; Pálsson, G.K.; Gonzalez-Silveira, M.; Schreuders, H.; Slaman, M.; Rector, J.H.; Krishnan, G.; Kooi, B.J.; Walker, G.S.; Fay, M.W.; et al. Mg/Ti multilayers: Structural and hydrogen absorption properties. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 81, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kalisvaart, P.; Shalchi-Amirkhiz, B.; Zahiri, R.; Zahiri, B.; Tan, X.; Danaie, M.; Botton, G.; Mitlin, D. Thermodynamically destabilized hydride formation in “bulk” Mg–AlTi multilayers for hydrogen storage. Phys. Chem. Chem. Phys. 2013, 15, 16432–16436. [Google Scholar] [CrossRef]
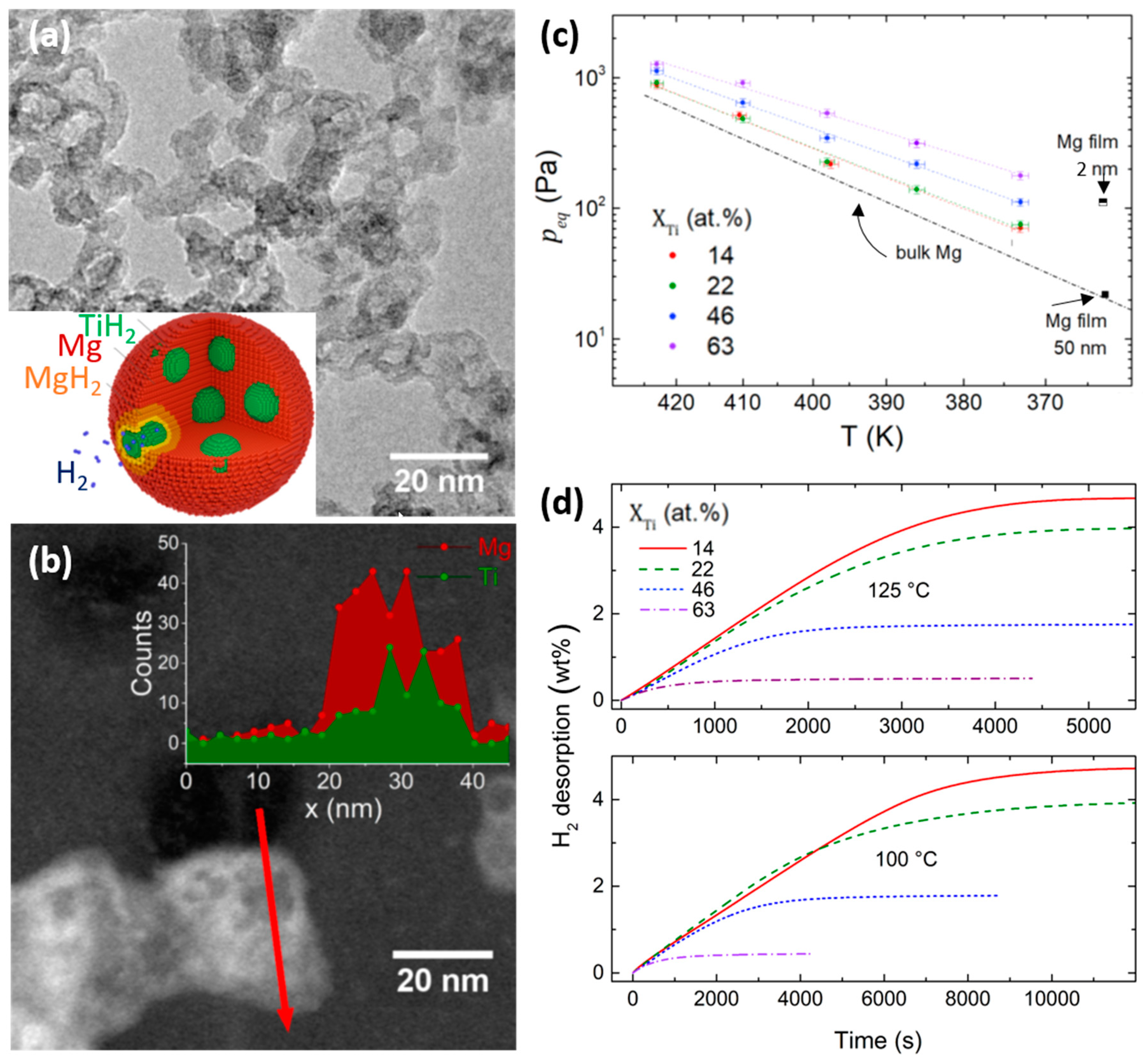
- Asano, K.; Westerwaal, R.J.; Anastasopol, A.; Mooij, L.P.A.; Boelsma, C.; Ngene, P.; Schreuders, H.; Eijt, S.W.H.; Dam, B. Destabilization of Mg hydride by self-organized nanoclusters in the immiscible Mg–Ti system. J. Phys. Chem. C 2015, 119, 12157–12164. [Google Scholar] [CrossRef]
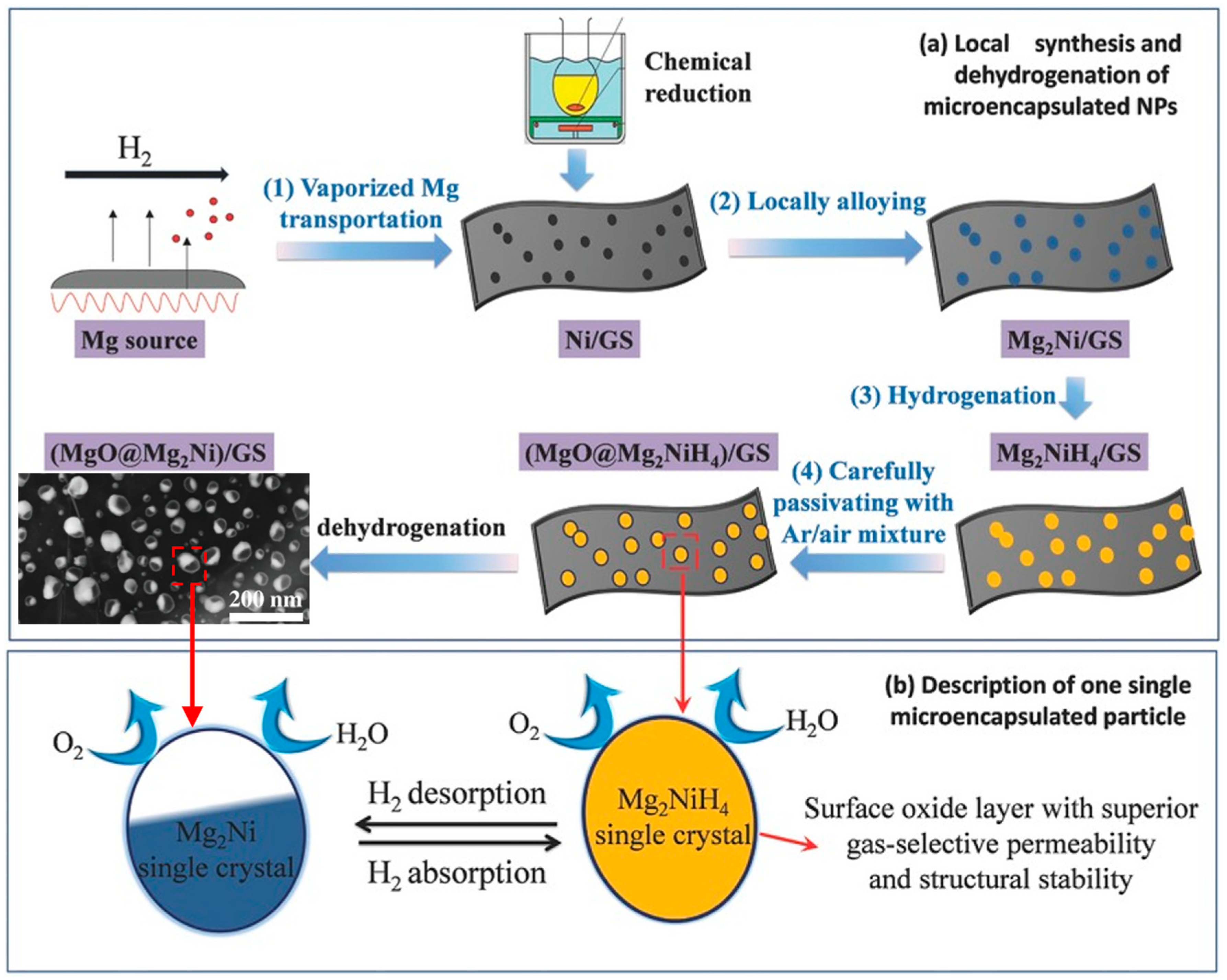
- Zhang, J.; Zhu, Y.; Lin, H.; Liu, Y.; Zhang, Y.; Li, S.; Ma, Z.; Li, L. Metal hydride nanoparticles with ultrahigh structural stability and hydrogen storage activity derived from microencapsulated nanoconfinement. Adv. Mater. 2017, 29, 1700760. [Google Scholar] [CrossRef] [PubMed]
- Pasquini, L.; Callini, E.; Piscopiello, E.; Montone, A.; Antisari, M.V.; Bonetti, E. Metal-hydride transformation kinetics in Mg nanoparticles. Appl. Phys. Lett. 2009, 94, 041918. [Google Scholar] [CrossRef]
- Callini, E.; Pasquini, L.; Piscopiello, E.; Montone, A.; Antisari, M.V.; Bonetti, E. Hydrogen sorption in Pd-decorated Mg-MgO core-shell nanoparticles. Appl. Phys. Lett. 2009, 94, 221905. [Google Scholar] [CrossRef]
- Pasquini, L.; Montone, A.; Callini, E.; Antisari, M.V.; Bonetti, E. Formation of hollow structures through diffusive phase transition across a membrane. Appl. Phys. Lett. 2011, 99, 021911. [Google Scholar] [CrossRef]
- Landuzzi, F.; Pasquini, L.; Giusepponi, S.; Celino, M.; Montone, A.; Palla, P.L.; Cleri, F. Molecular dynamics of ionic self-diffusion at an MgO grain boundary. J. Mater. Sci. 2015, 50, 2502–2509. [Google Scholar] [CrossRef]
- Duan, X.; Griessen, R.; Wijngaarden, R.J.; Kamin, S.; Liu, N. Self-recording and manipulation of fast long-range hydrogen diffusion in quasifree magnesium. Phys. Rev. Mater. 2018, 2, 085802. [Google Scholar] [CrossRef]
- Liu, W.; Setijadi, E.J.; Aguey-Zinsou, K.-F. Tuning the thermodynamic properties of MgH2 at the nanoscale via a catalyst or destabilizing element coating strategy. J. Phys. Chem. C 2014, 118, 27781–27792. [Google Scholar] [CrossRef]
- Nielsen, T.K.; Besenbacher, F.; Jensen, T.R. Nanoconfined hydrides for energy storage. Nanoscale 2011, 3, 2086–2098. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, T.K.; Manickam, K.; Hirscher, M.; Besenbacher, F.; Jensen, T.R. Confinement of MgH2 Nanoclusters within nanoporous aerogel scaffold materials. ACS Nano 2009, 3, 3521–3528. [Google Scholar] [CrossRef] [PubMed]
- Zlotea, C.; Oumellal, Y.; Hwang, S.-J.; Ghimbeu, C.M.; de Jongh, P.E.; Latroche, M. Ultrasmall MgH2 nanoparticles embedded in an ordered microporous carbon exhibiting rapid hydrogen Sorption Kinetics. J. Phys. Chem. C 2015, 119, 18091–18098. [Google Scholar] [CrossRef]
- Jeon, K.-J.; Moon, H.R.; Ruminski, A.M.; Jiang, B.; Kisielowski, C.; Bardhan, R.; Urban, J.J. Air-stable magnesium nanocomposites provide rapid and high-capacity hydrogen storage without using heavy-metal catalysts. Nat. Mater. 2011, 10, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Zlotea, C.; Oumellal, Y.; Msakni, M.; Bourgon, J.; Bastide, S.; Cachet-Vivier, C.; Latroche, M. First evidence of rh nano-hydride formation at low pressure. Nano Lett. 2015, 15, 4752–4757. [Google Scholar] [CrossRef] [PubMed]
- Berseth, P.A.; Harter, A.G.; Zidan, R.; Blomqvist, A.; Araújo, C.M.; Scheicher, R.H.; Ahuja, R.; Jena, P. Carbon nanomaterials as catalysts for hydrogen uptake and release in NaAIH 4. Nano Lett. 2009, 9, 1501–1505. [Google Scholar] [CrossRef] [Green Version]
- Shegai, T.; Langhammer, C. Hydride formation in single palladium and magnesium nanoparticles studied by nanoplasmonic dark-field scattering spectroscopy. Adv. Mater. 2011, 23, 4409–4414. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, R.B.; Khachaturyan, A.G. Thermodynamics of open two-phase systems with coherent interfaces. Phys. Rev. Lett. 1995, 74, 2523–2526. [Google Scholar] [CrossRef]
- Narayan, T.C.; Hayee, F.; Baldi, A.; Koh, A.L.; Sinclair, R.; Dionne, J.A. Direct visualization of hydrogen absorption dynamics in individual palladium nanoparticles. Nat. Commun. 2017, 8, 14020. [Google Scholar] [CrossRef] [Green Version]
- Narayan, T.C.; Baldi, A.; Koh, A.L.; Sinclair, R.; Dionne, J.A. Reconstructing solute-induced phase transformations within individual nanocrystals. Nat. Mater. 2016, 15, 768–774. [Google Scholar] [CrossRef]
- Surrey, A.; Nielsch, K.; Rellinghaus, B. Comments on “Evidence of the hydrogen release mechanism in bulk MgH2”. Sci. Rep. 2017, 7, 44216. [Google Scholar] [CrossRef] [Green Version]
- Hamm, M.; Bongers, M.D.; Roddatis, V.; Dietrich, S.; Lang, K.H.; Pundt, A. In situ observation of hydride nucleation and selective growth in magnesium thin-films with environmental transmission electron microscopy. Int. J. Hydrogen Energy 2019, 44, 32112–32123. [Google Scholar] [CrossRef]
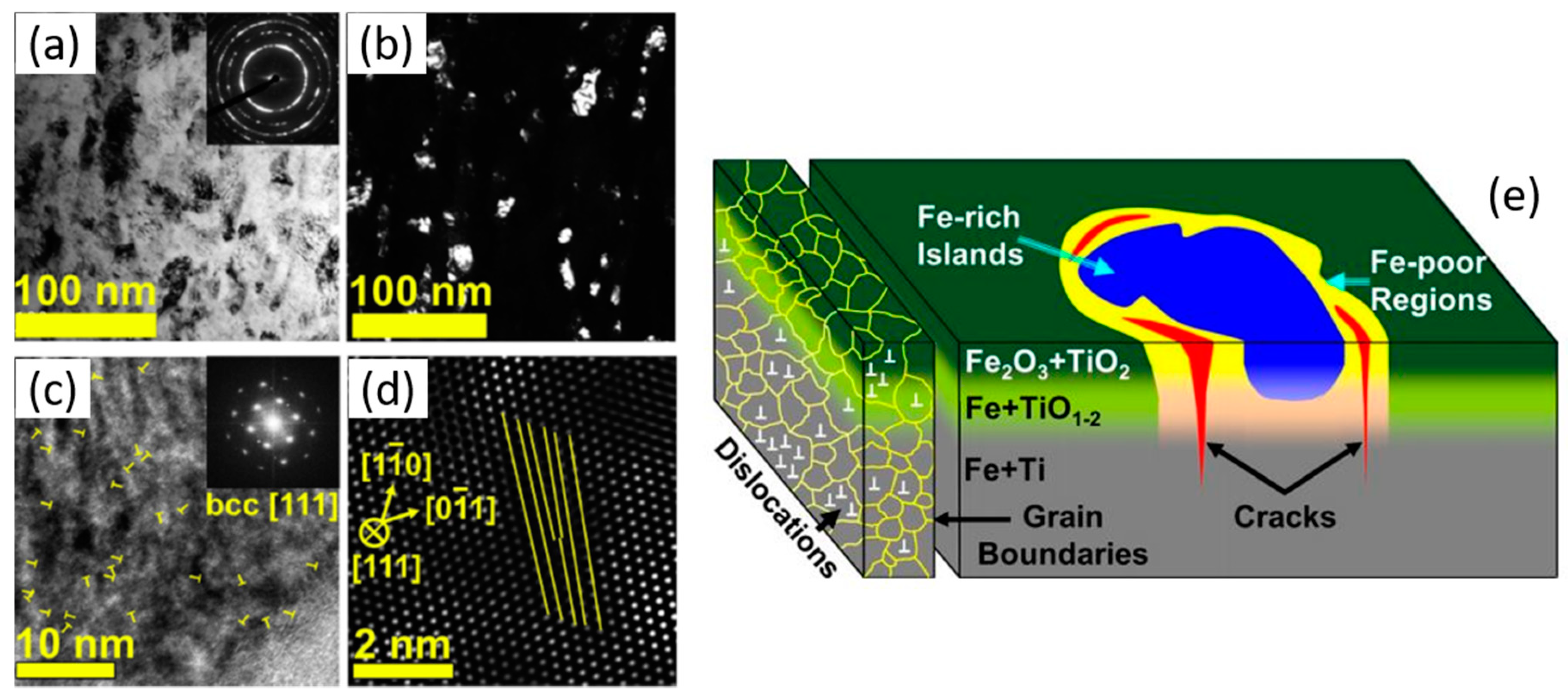

| Material | L (nm) | Preparation Method | (wt %) | Ea (kJ/mol) | |ΔH0| (kJ/molH2) | |ΔS0| (J/K·molH2) | Ref |
|---|---|---|---|---|---|---|---|
| bulk Mg | >104 | commercial powders | 7 | 95–130 a 120–160 b | 74 | 133 | [62,63] |
| Mg NPs | 25–38 | Cp2Mg reduction with potassium | ~6 | 115–122 a 126–160 b | [64] | ||
| Mg NWs | 30–50 | vapor transport | 6.8 | 33.5 a 38.8 b | 65.3 b | [65] | |
| Mg-Ti NPs | 20 | gas phase condensation of Mg-Ti vapors | 4.8 | 52 a 35 b | 67 c | 119 c | [24,33] |
| Mg-rGO § composite | 3–4 | co-reduction of Mg2+ and GO by C10H7Li | 6.5 | 61 a 93 b | [66] | ||
| Ni-doped Mg NPs | 6.5 | MgBu2 Hydrogenation on graphene | 5.4 | 22.7 a 64.7 b | 62.1 a | [67] | |
| Mg | 3.4 | infiltration of MgBu2 in Ni-doped 3-D carbon | 6.6 | 31 a 43 b | 46.9 a 49.1 b | [68] | |
| Mg/Cr multilayers | 18 | magnetron sputtering | 6.1 | 65.7 b | 73.6 b | 134 b | [69] |
| Mg-TiH2 | 5–10 | ball milling (BM) | 6.1 | 58.4 b | 68.2 b | 127 b | [57] |
| Mg-Nb2O5 | ~20 | BM | 6.5 | 62 b | [56] | ||
| Ti-coated Mg | ~50 | BM followed by reaction withTiCl3 | 6.3 | 30.8 b | 75.2 b | 136 b | [70] |
| Mg-Ni-Y LPSO alloy | 5–10 | induction melting + pulverization + BM | 5.8 | [71] | |||
| bulk Pd | >104 | black Pd | 0.6 | 36.4 a | 90 a | [72] | |
| Pd NPs | 2.6 | solution chemistry/PVP | ~0.4 | 31 a | 67 a | [72] | |
| Pd NPs | 7.0 | solution chemistry/PVP | ~0.4 | 35 a | 83 a | [72] | |
| Pd cube | 14 | solution chemistry/CTAB | 18 a 47 b | 27 a | 61 a | [73] | |
| Pd cube | 18 | solution chemistry | 32 a | 78 a | [35] | ||
| bulk TiFe | >104 | precursors melting | 1.9 | activation issues | 28.1 b | 106 b | [14] |
| TiFe | ~10 | high pressure torsion | 1.7 | reversible H-sorption at RT without activation | [74] | ||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasquini, L. Design of Nanomaterials for Hydrogen Storage. Energies 2020, 13, 3503. https://doi.org/10.3390/en13133503
Pasquini L. Design of Nanomaterials for Hydrogen Storage. Energies. 2020; 13(13):3503. https://doi.org/10.3390/en13133503
Chicago/Turabian StylePasquini, Luca. 2020. "Design of Nanomaterials for Hydrogen Storage" Energies 13, no. 13: 3503. https://doi.org/10.3390/en13133503
APA StylePasquini, L. (2020). Design of Nanomaterials for Hydrogen Storage. Energies, 13(13), 3503. https://doi.org/10.3390/en13133503






