Analysis of Torque Ripples of an Induction Motor Taking into Account a Inter-Turn Short-Circuit in a Stator Winding
Abstract
:1. Introduction
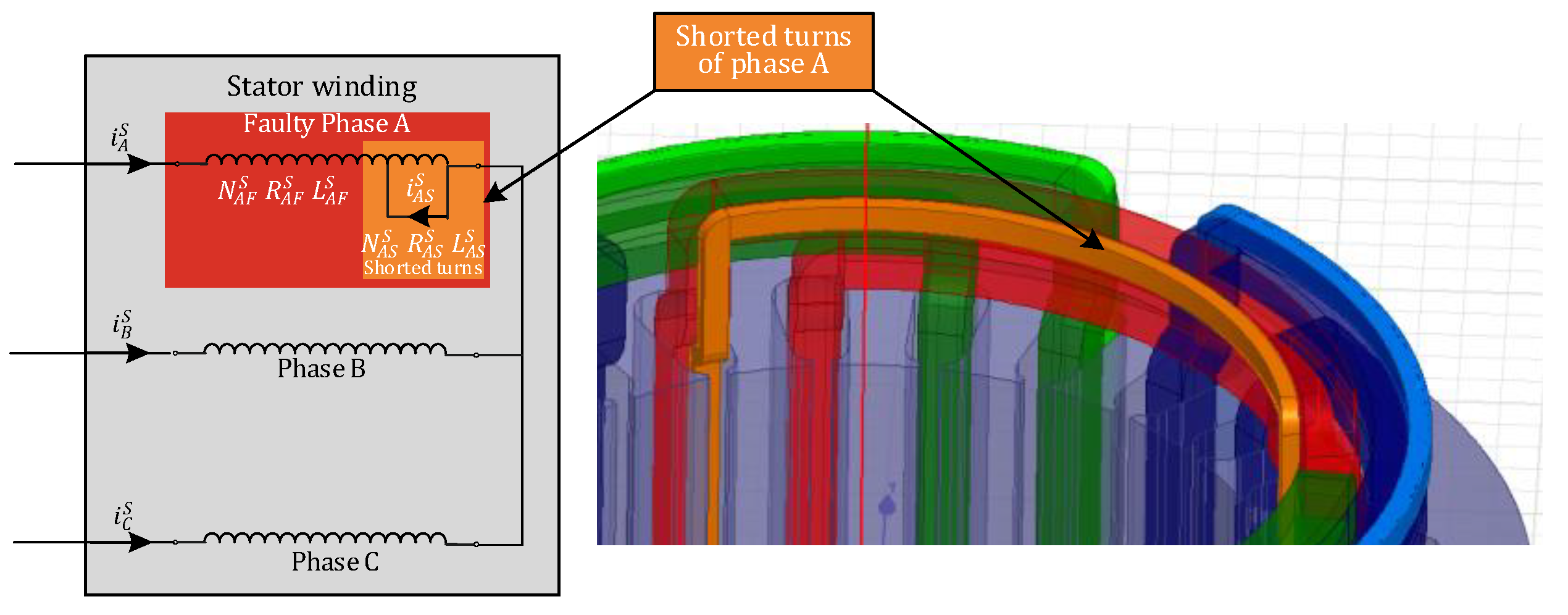
2. Stator Winding Failure—Inter-Turn Short-Circuit Modeling
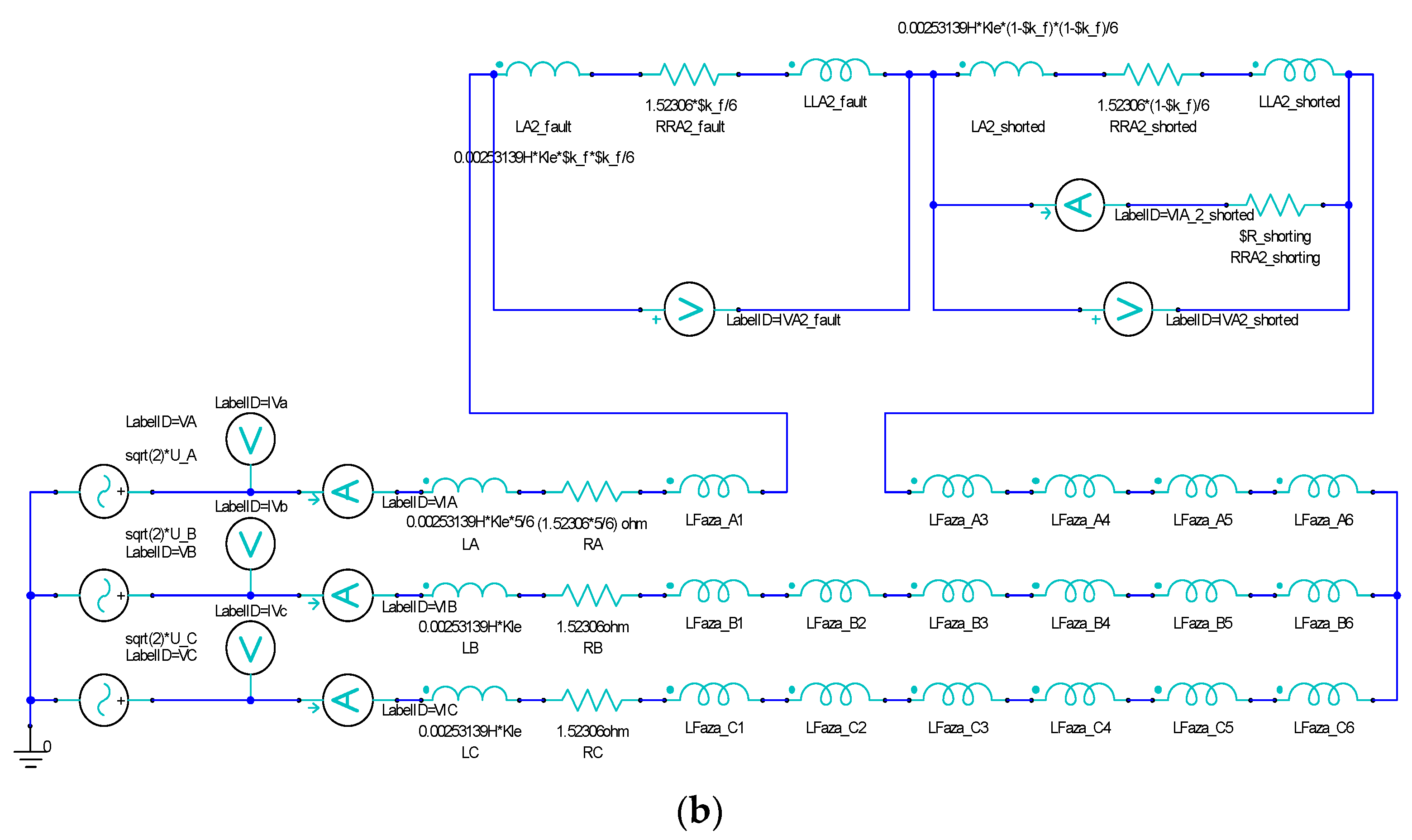
2.1. Method of Modeling Inter-Turn Short-Circuit
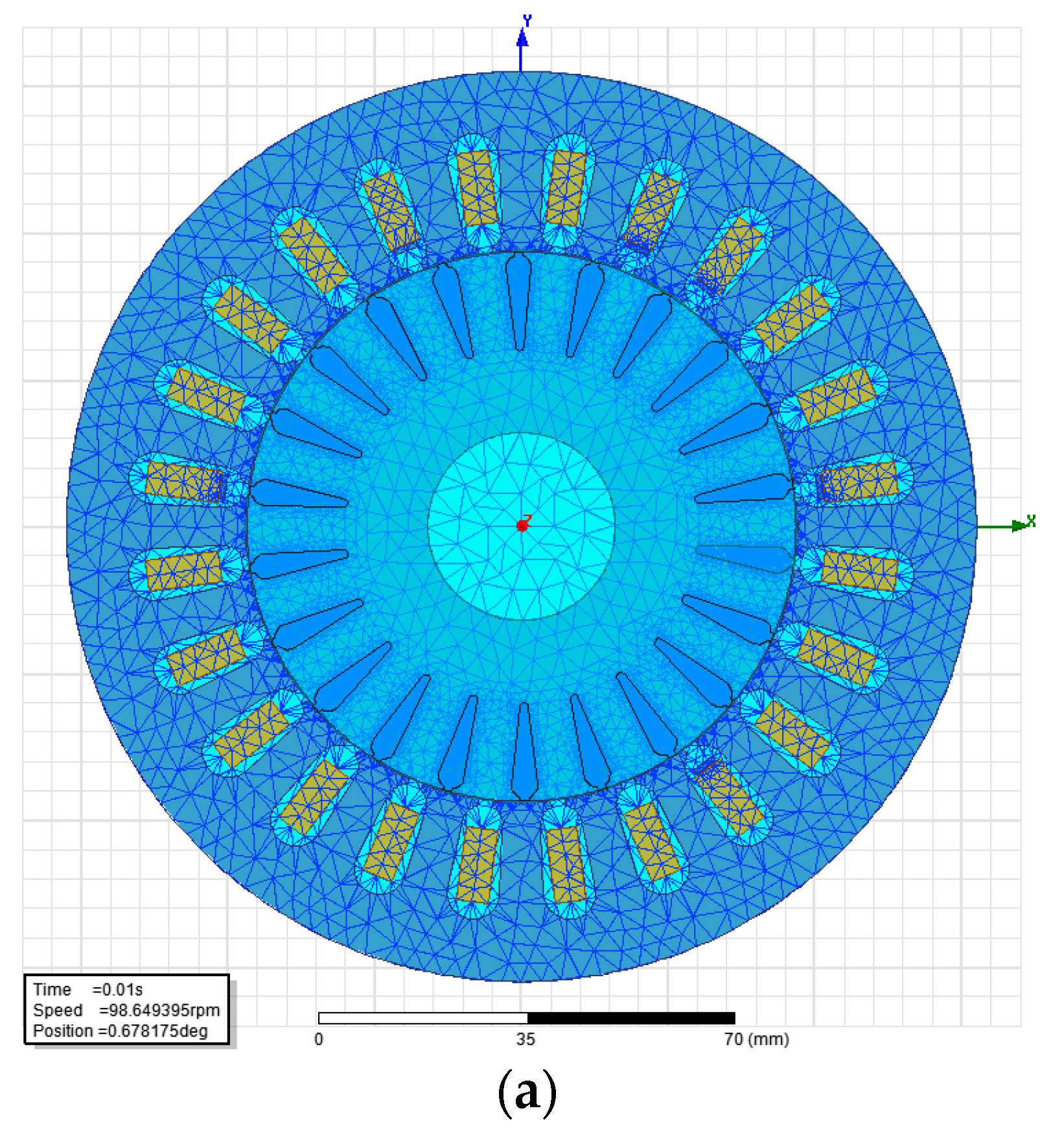
2.2. Field–Circuit Model of the Induction Motor
3. Selected Results of the Torque Calculation
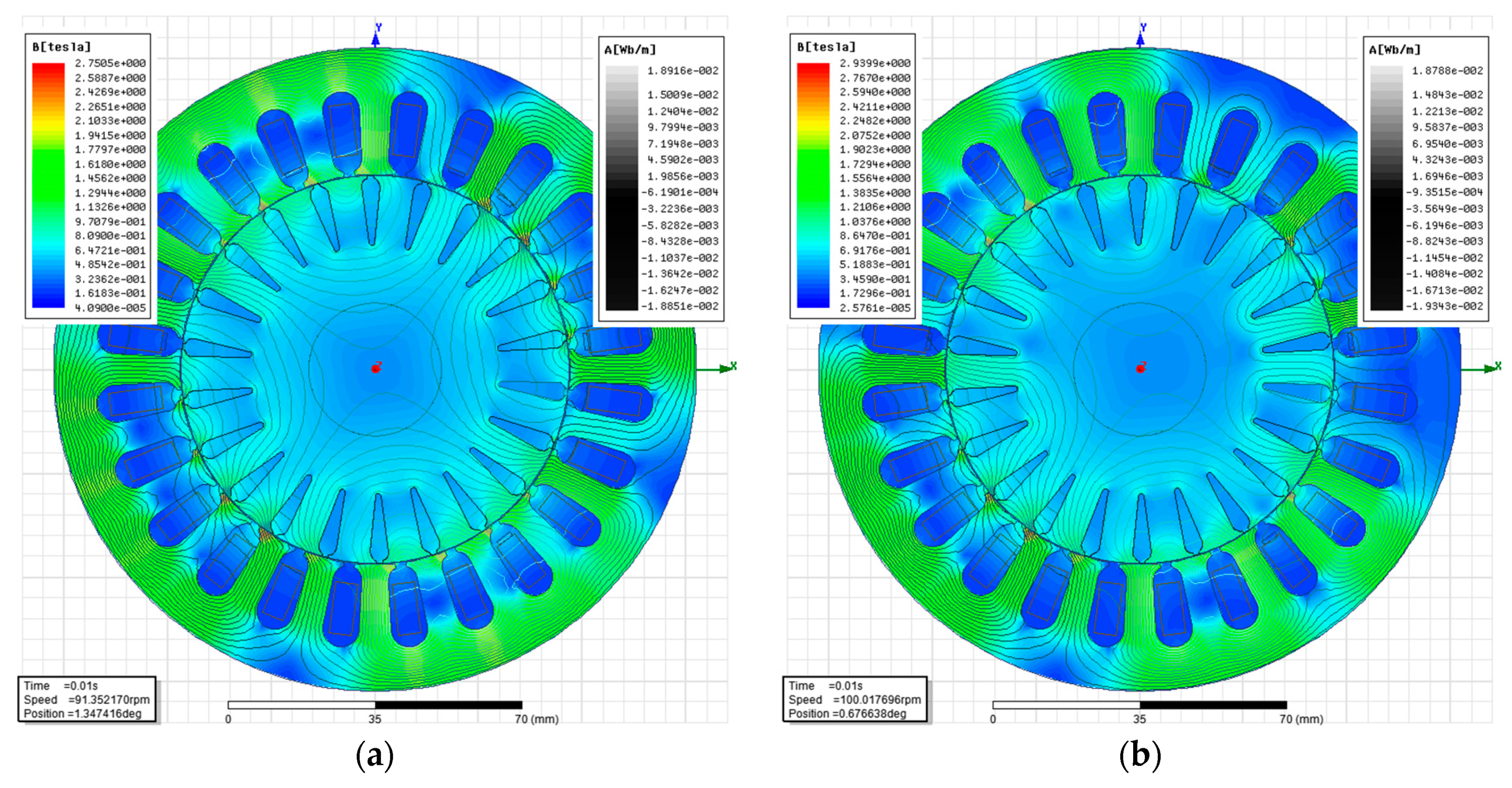
3.1. Magnetic Field Distribution
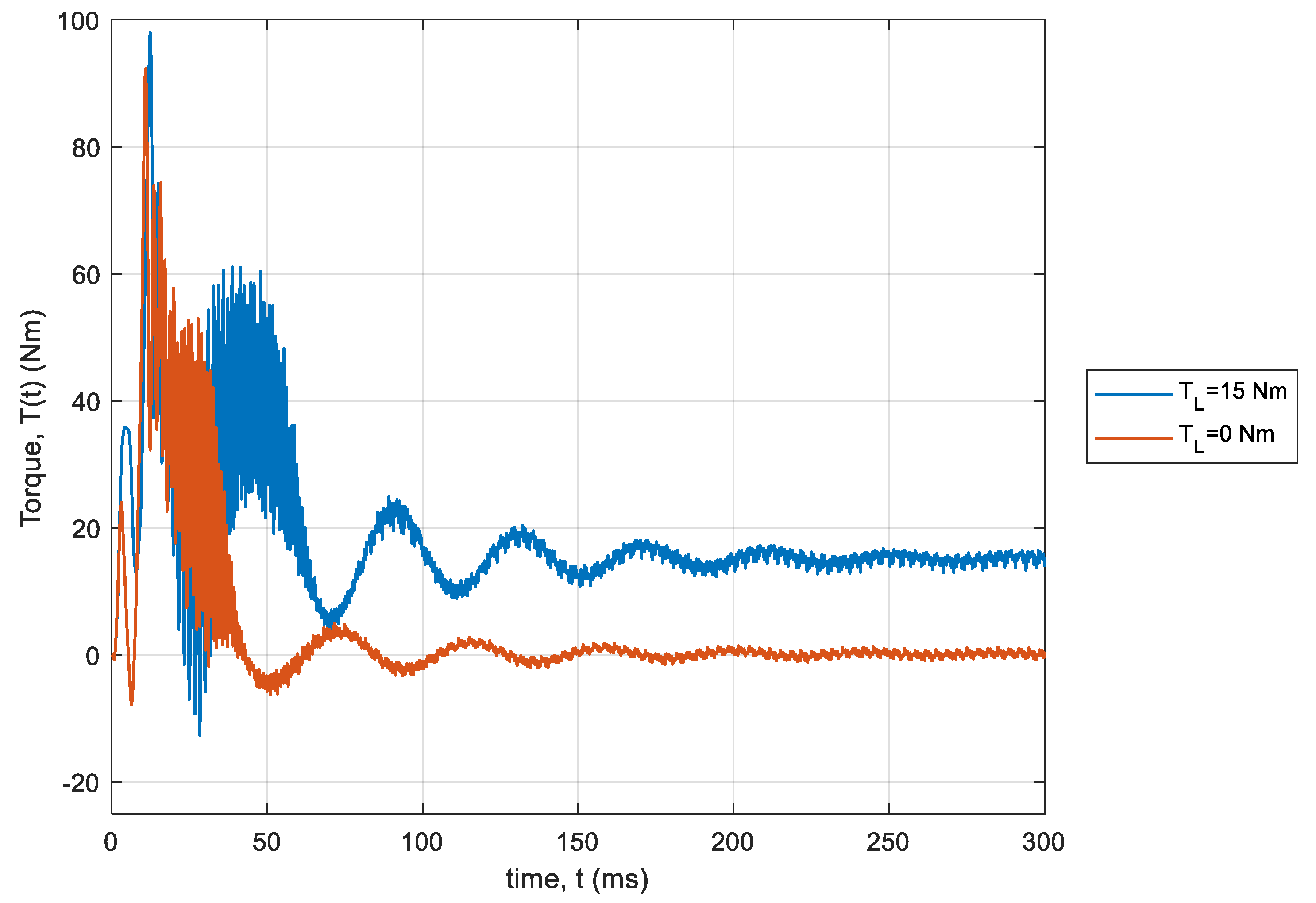
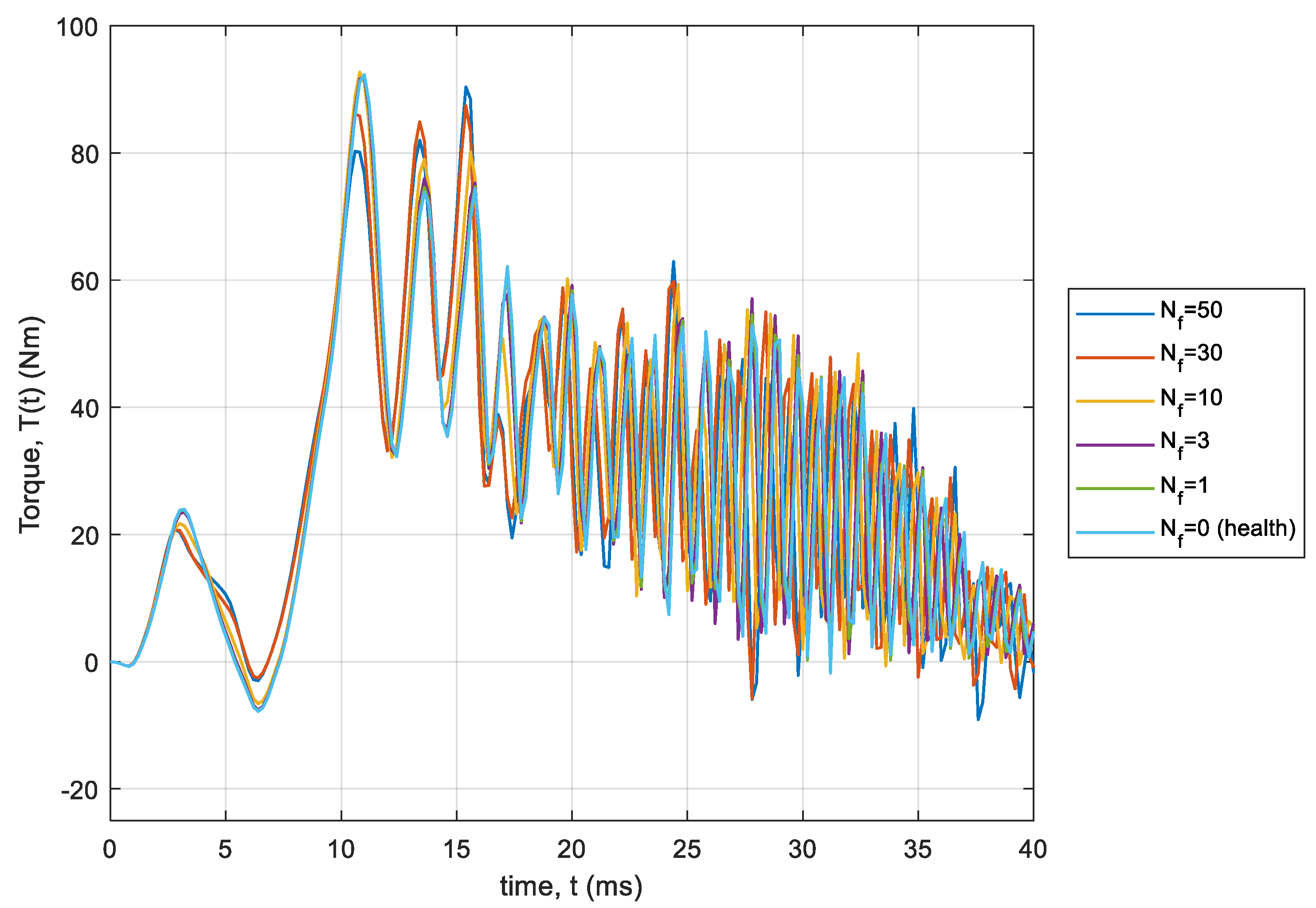
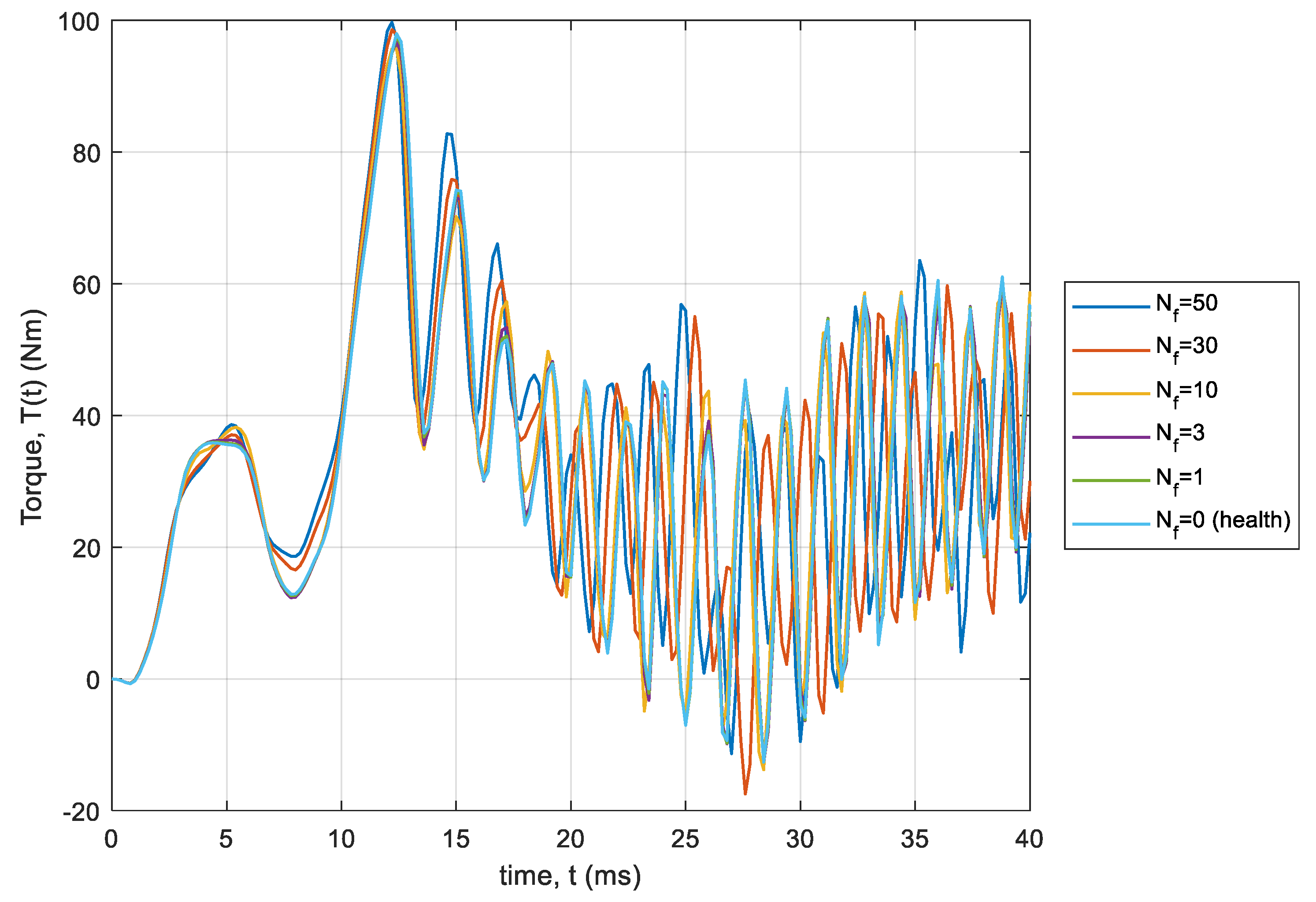
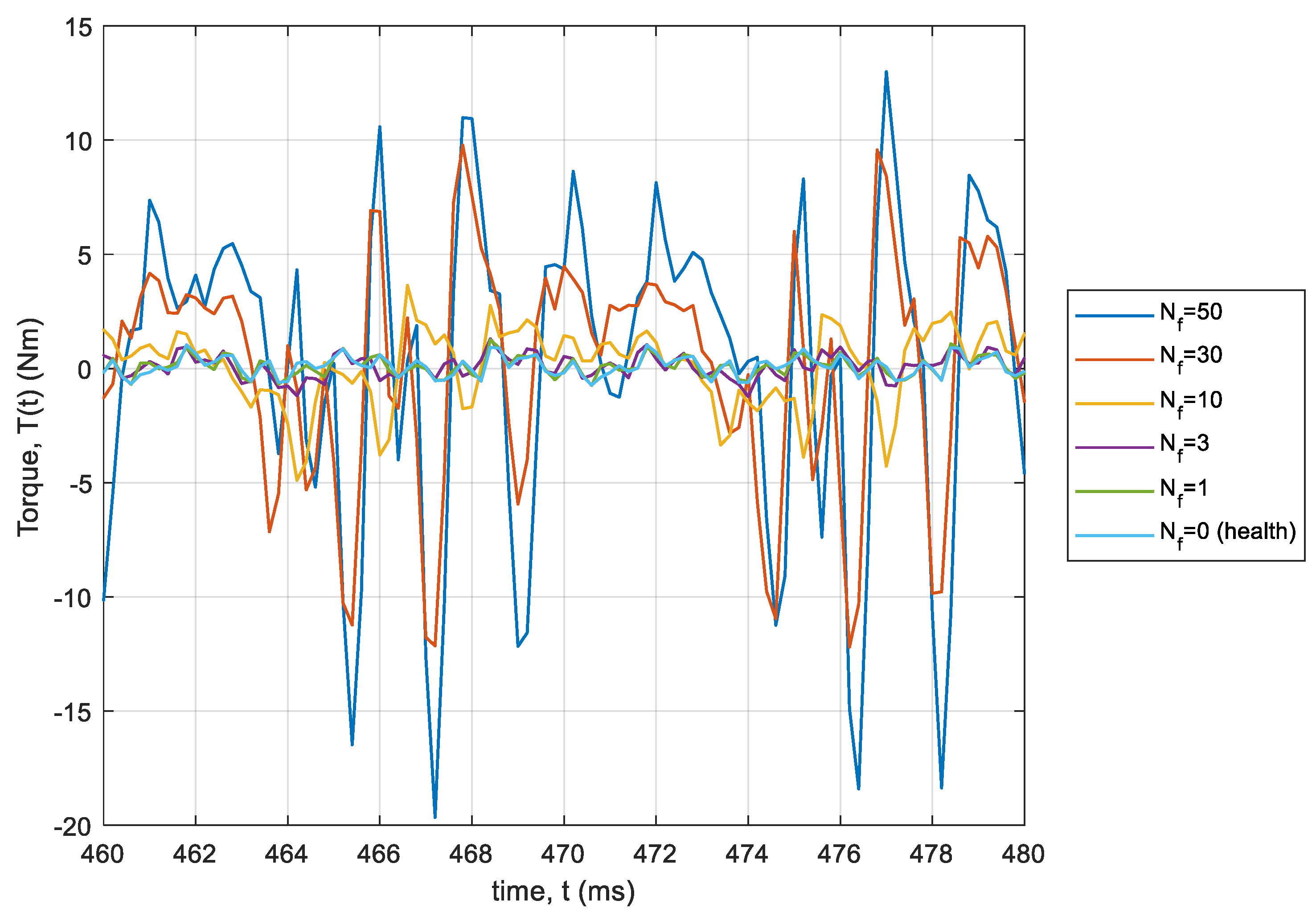
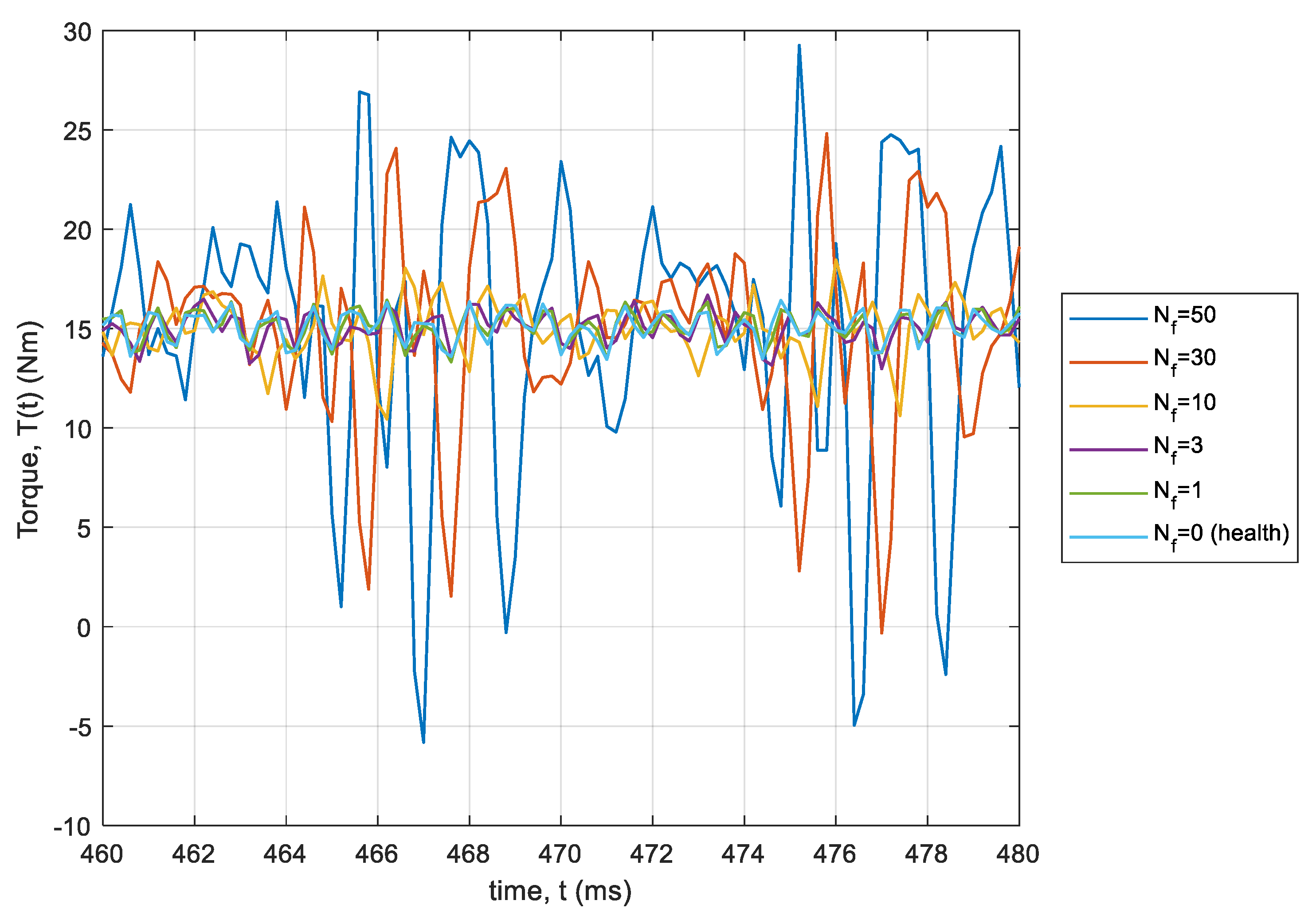
3.2. The Torque Waveforms at Steady State of the Machine
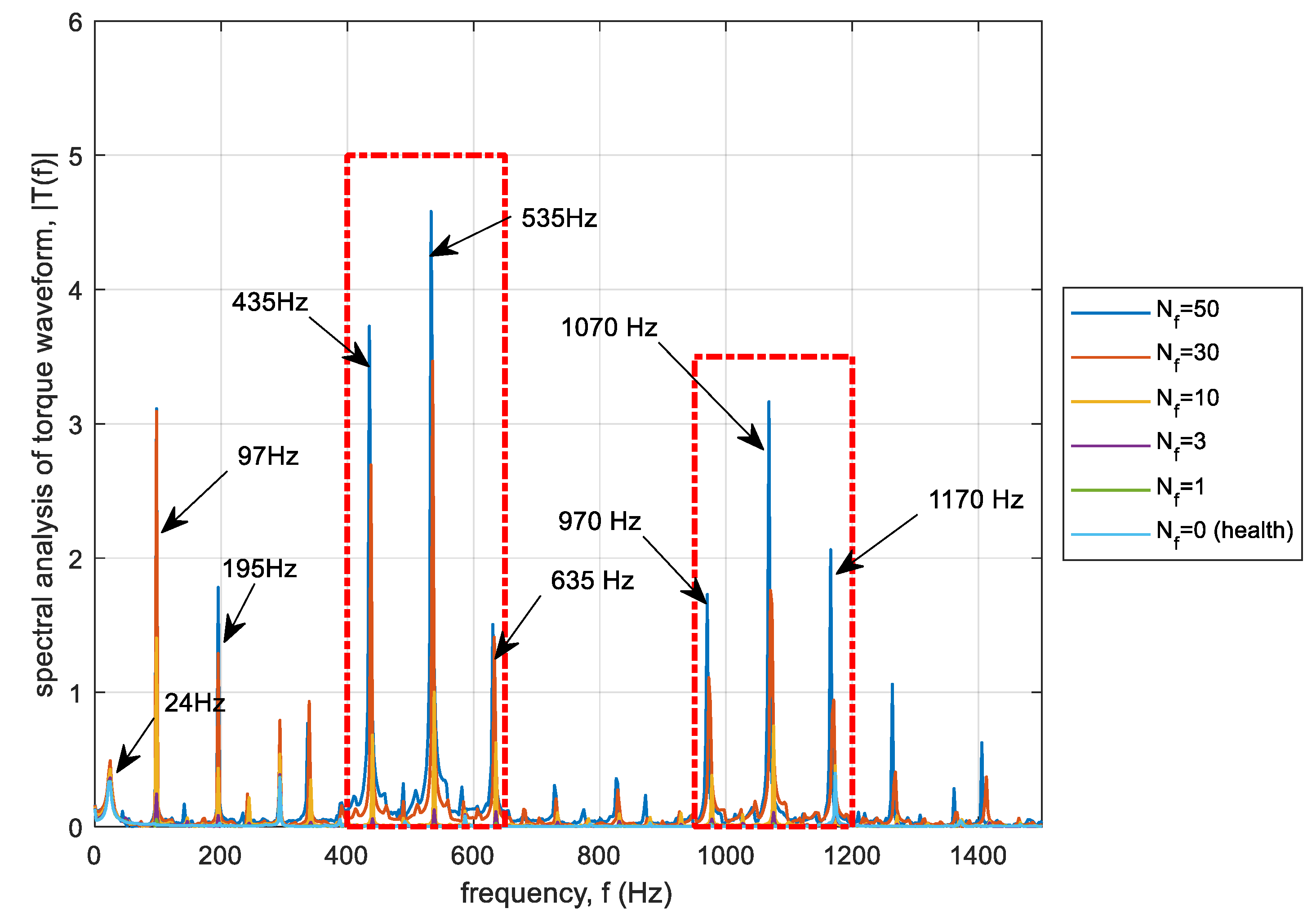
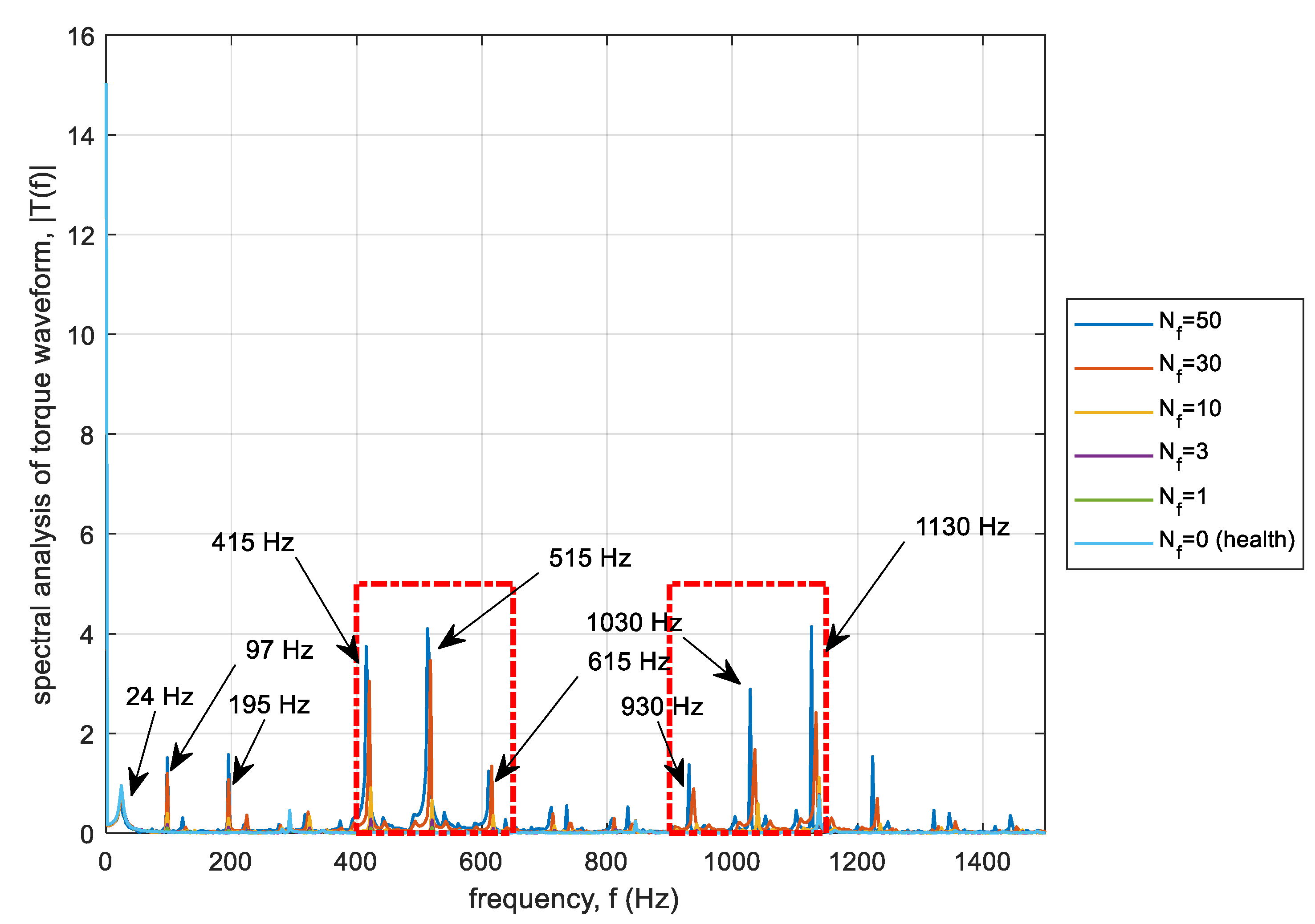
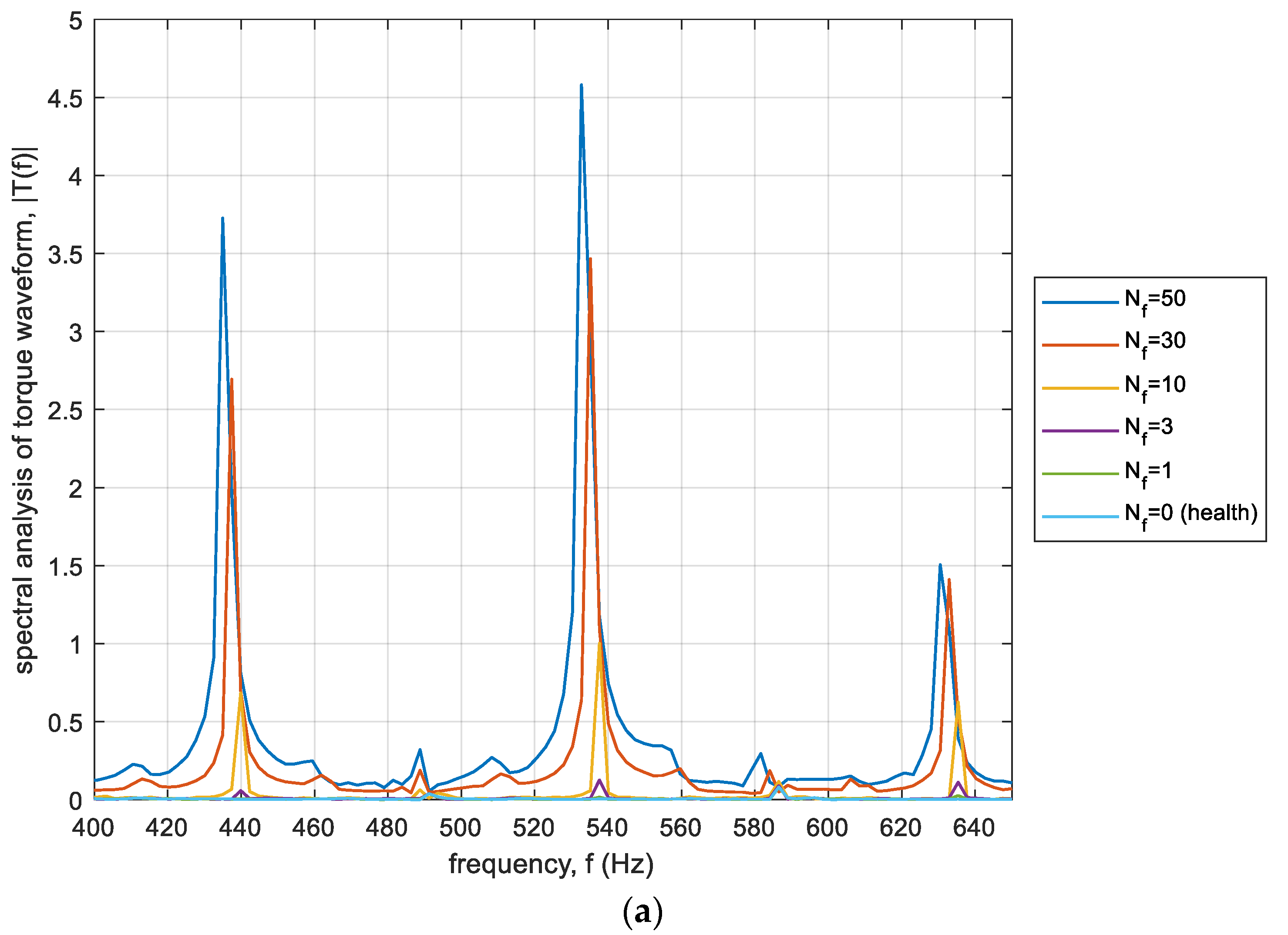
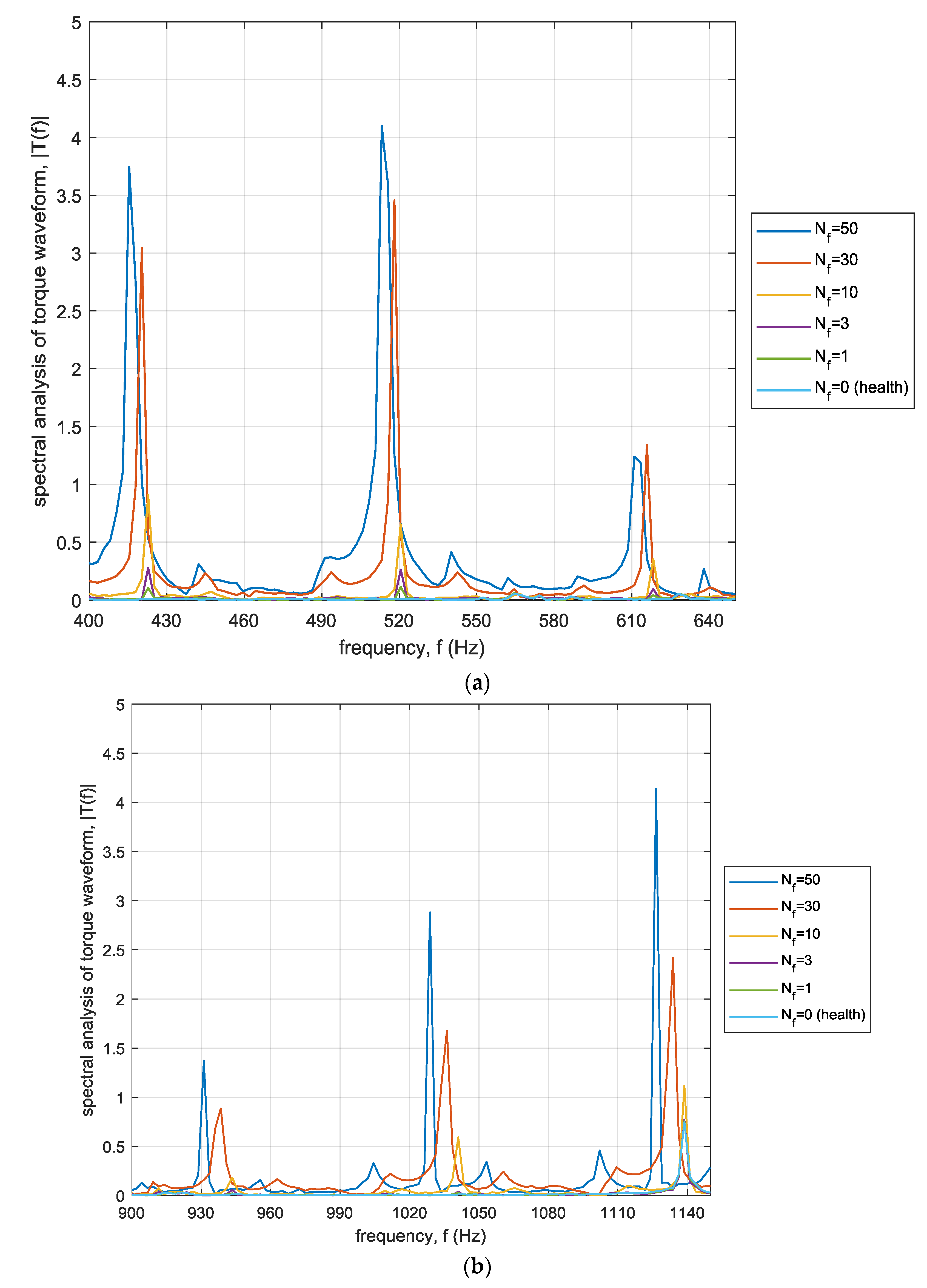
3.3. Torque Analysis—Signal Spectrum
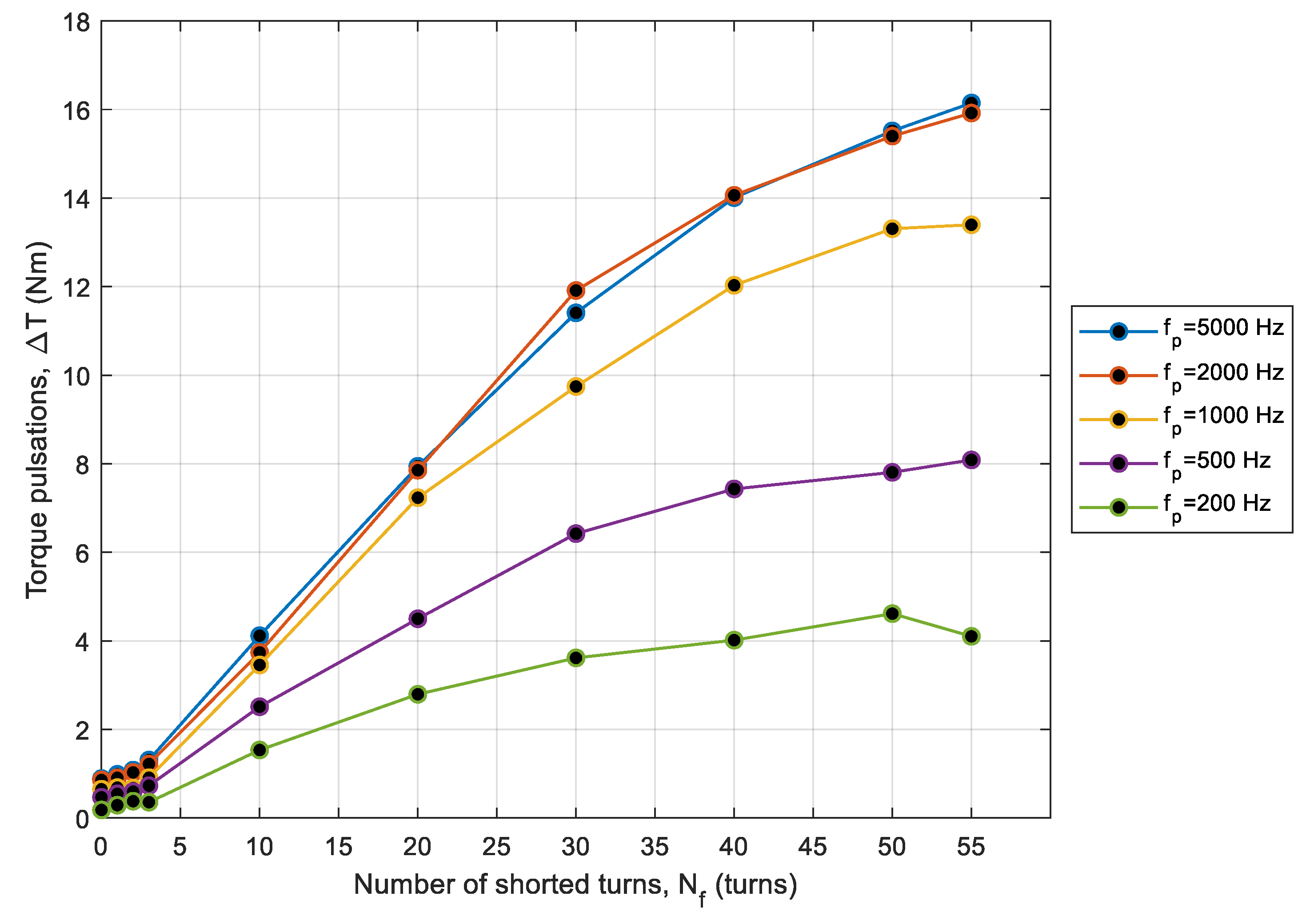
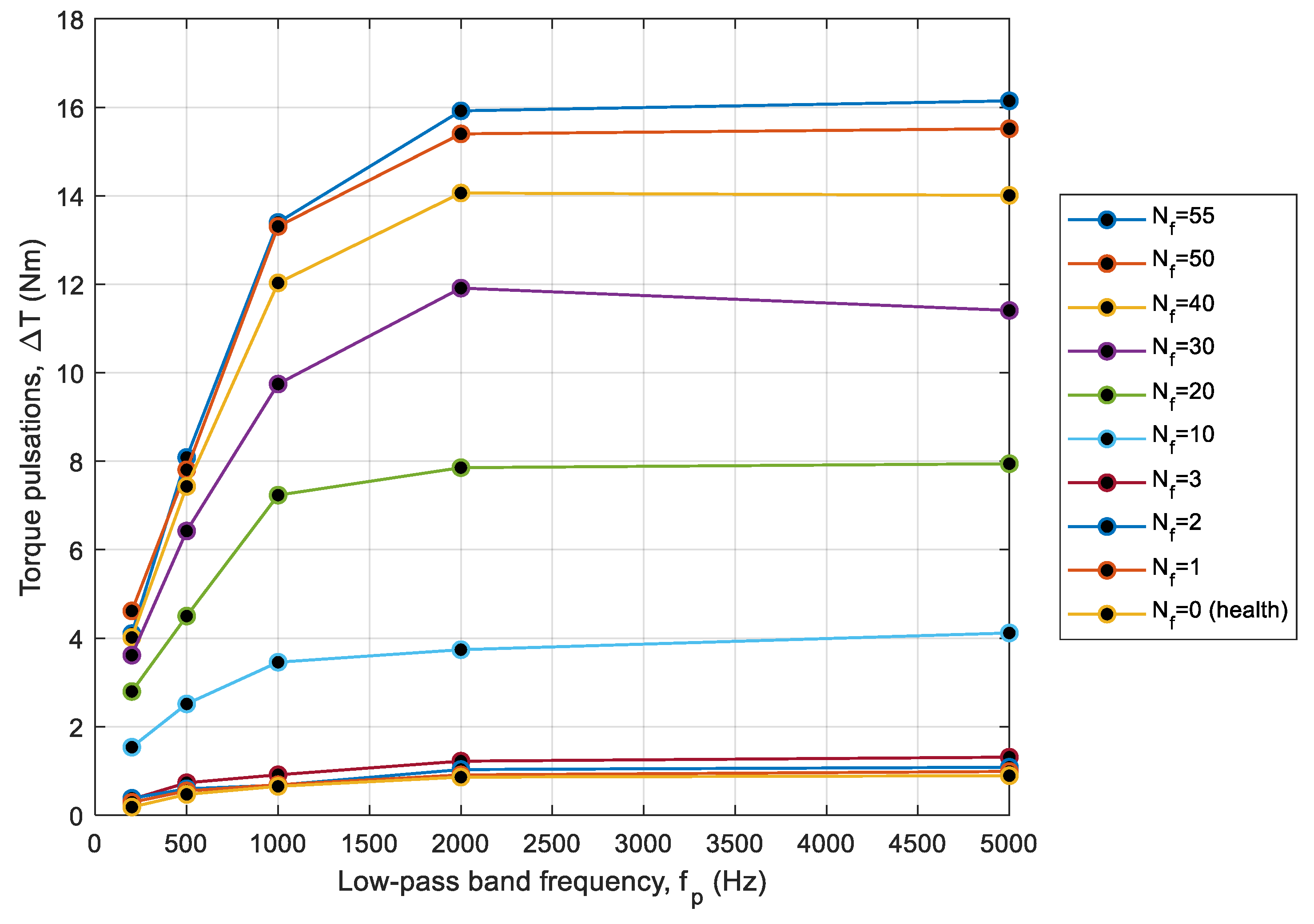
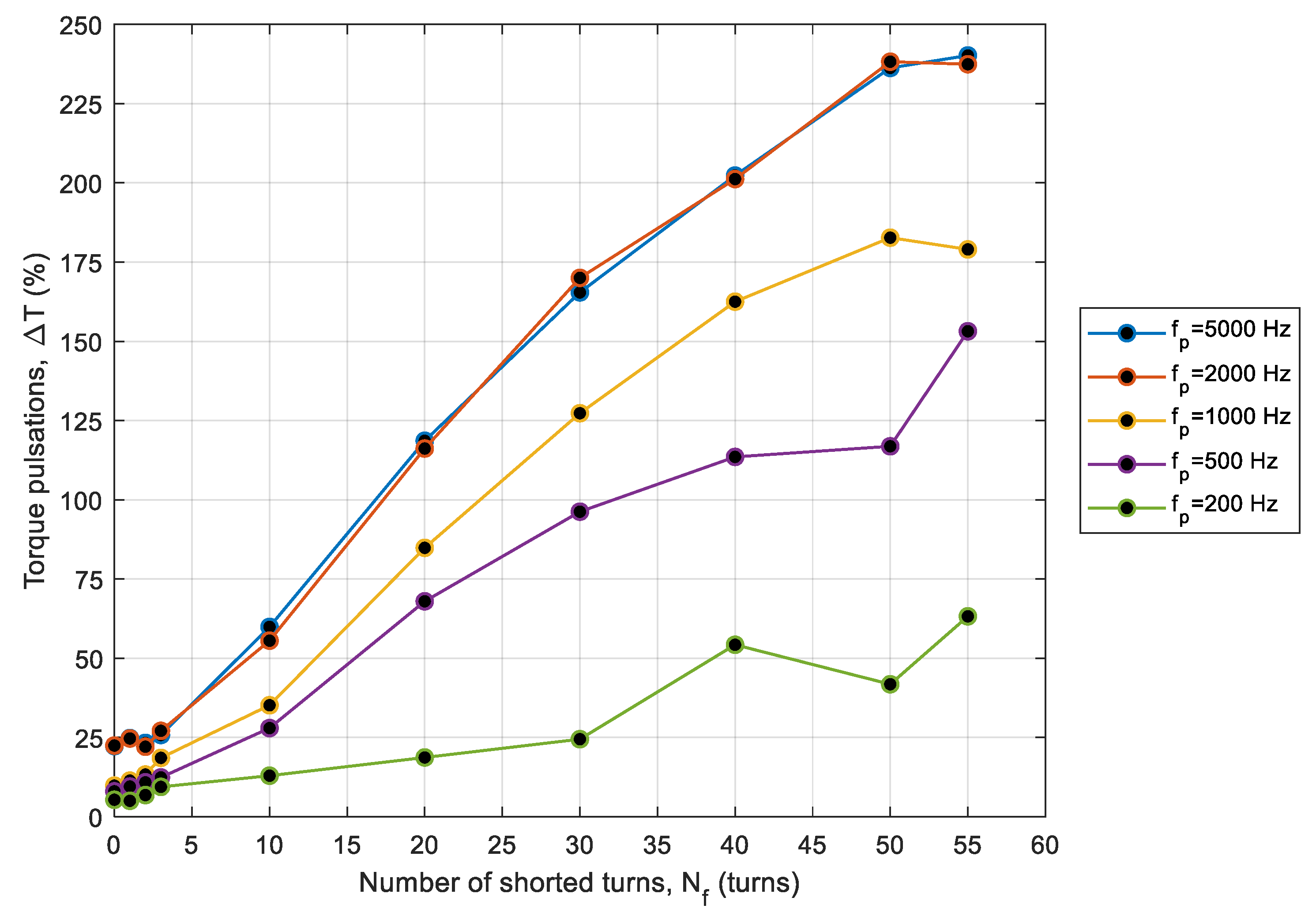
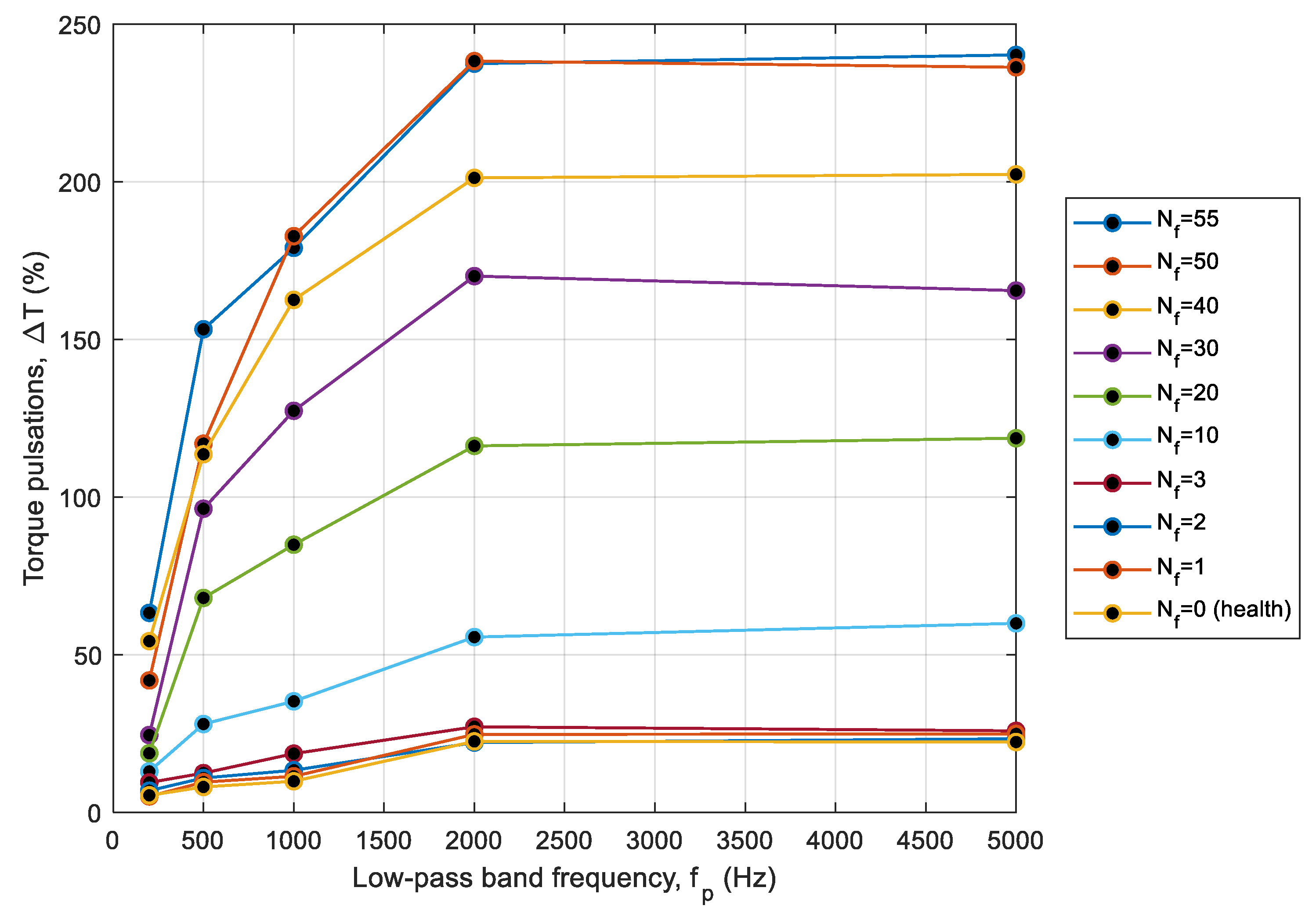
3.4. Torque Ripple Factor
4. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Rajput, S.; Bender, E.; Averbukh, M. Simplified algorithm for assessment equivalent circuit parameters of induction motors. IET Electr. Power Appl. 2020, 14, 426–432. [Google Scholar] [CrossRef]
- Morsalin, S.; Mahmud, K.; Mohiuddin, H.; Halim, M.R.; Saha, P. Induction Motor Inter-turn Fault Detection Using Heuristic Noninvasive Approach by Artificial Neural Network with Levenberg Marquardt Algorithm. In Proceedings of the Informatics, Electronics & Vision (ICIEV), International Conference, Dhaka, Bangladesh, 23–24 May 2014; pp. 1–6. [Google Scholar]
- Patel, R.K.; Giri, V.K. Condition monitoring of induction motor bearing based on bearing damage index. Arch. Electr. Eng. 2017, 66, 105–119. [Google Scholar] [CrossRef] [Green Version]
- Sobański, P.; Orłowska-Kowalska, T. Detection of single and multiple IGBTs open-circuit faults in a field-oriented controlled induction motor drive. Arch. Electr. Eng. 2017, 66, 89–104. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Yang, Y.; Shi, Y. Online Diagnosis of Inter-turn Short Circuit for Dual-Redundancy Permanent Magnet Synchronous Motor Based on Reactive Power Difference. Energies 2019, 12, 510. [Google Scholar] [CrossRef] [Green Version]
- He, Y.L.; Ke, M.Q.; Tang, G.J.; Jiang, H.C.; Yuan, X.H. Analysis and simulation on the effect of rotor interturn short circuit on magnetic flux density of turbo-generator. J. Electr. Eng. Elektrotech. Cas 2016, 67, 323–333. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.C.; Li, Y.G. Diagnosis of Rotor Winding Inter-turn Short-Circuit in Turbine Generators Using Virtual Power. IEEE Trans. Energy Convers. 2015, 30, 183–188. [Google Scholar]
- Broniera, P.J.; Gongora, W.S.; Goedtel, A.; Godoy, W.F. Diagnosis of Stator Winding Inter-turn Short Circuit in Three-Phase Induction Motors by Using Artificial Neural Networks, Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED). In Proceedings of the 9th IEEE International Symposium, Valencia, Spain, 27–30 August 2013; pp. 281–287. [Google Scholar]
- Pietrowski, W.; Górny, K. Detection of inter-turn short-circuit at start-up of induction machine based on torque analysis. Open Phys. 2017, 15, 851–856. [Google Scholar] [CrossRef] [Green Version]
- Pietrowski, W.; Górny, K. Wavelet analysis of torque at start-up of an induction machine under inter-turn short-circuit. In Proceedings of the 2017 International Symposium on Electrical Machines (SME 2017), Nałęczów, Poland, 18–21 June 2017; pp. 1–4. [Google Scholar]
- Wolkiewicz, M.; Tarchała, G.J.; Orłowska-Kowalska, T.; Kowalski, C.T. Online stator interturn short ciruits monitoring in the DFOC induction-motor drive. IEEE Trans. Ind. Electron. 2016, 63, 2517–2528. [Google Scholar] [CrossRef]
- Huang, B.; Feng, G.; Tang, X.; Xi Gu, J.; Xu, G.; Cattley, R.; Gu, F.; Ball, A.D. A Performance Evaluation of Two Bispectrum Analysis Methods Applied to Electrical Current Signals for Monitoring Induction Motor-Driven Systems. Energies 2019, 12, 1438. [Google Scholar] [CrossRef] [Green Version]
- Zoeller, C.; Wolbank, T.M.; Vogelsberger, M.A. Influence of Voltage Excitation and Current Sensors on Monitoring of Stator Winding Insulation based on Transient Current Step Response. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 2854–2861. [Google Scholar]
- Bouzid, M.B.; Champenois, G. Neural Network Based Method for the Automatic Detection of the Stator Faults of the Induction Motor. In Proceedings of the Electrical Engineering and Software Applications (ICEESA), International Conference, Hammamet, Tunisia, 21–23 March 2013; pp. 1–7. [Google Scholar]
- Sellami, T.; Berriri, H.; Jelassi, S.; Darcherif, A.M.; Mimouni, M.F. Short-Circuit Fault Tolerant Control of a Wind Turbine Driven Induction Generator Based on Sliding Mode Observers. Energies 2017, 10, 1611. [Google Scholar] [CrossRef] [Green Version]
- Zoeller, C.; Wolbank, T.M.; Vogelsberger, M.A. Online Insulation Condition Monitoring of Traction Machines using Inverter Induced Voltage Injection. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 2456–2462. [Google Scholar]
- Williamson, S.J.; Wrobel, R.; Yon, J.; Booker, J.D.; Mellor, P.H. Investigation of Equivalent Stator-Winding Thermal Resistance during Insulation System Ageing. In Proceedings of the IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 550–556. [Google Scholar]
- Zoeller, C.; Vogelsberger, M.A.; Fasching, R.; Grubelnik, W.; Wolbank, T.M. Evaluation and Current-Response-Based Identification of Insulation Degradation for High Utilized Electrical Machines in Railway Application. IEEE Trans. Ind. Appl. 2017, 53, 2679–2689. [Google Scholar] [CrossRef]
- Cabanas, M.F.; Norniella, J.G.; Melero, M.G.; Rojas, C.H.; Cano, J.M.; Pedrayes, F.; Orcajo, G.A. Detection of stator winding insulation failures: On-line and off-line tests. In Proceedings of the 2013 IEEE Workshop on Electrical Machines Design Control and Diagnosis (WEMDCD), Paris, France, 11–12 March 2013; pp. 210–219. [Google Scholar]
- Maraaba, L.; Al-Hamouz, Z.; Abido, M. An Efficient Stator Inter-Turn Fault Diagnosis Tool for Induction Montors. Energies 2018, 11, 653. [Google Scholar] [CrossRef] [Green Version]
- Leite, V.C.M.N.; Borges da Silva, J.G.; Veloso, G.F.C.; Borges da Silva, L.E.; Lambert-Torres, G.; Bonaldi, E.L.; de Oliveira, L.E.D.L. Detection of Localized Bearing Faults in Induction Machines by Spectral Kurtosis and Envelope Analysis of Stator Current. IEEE Trans. Ind. Electron. 2015, 62, 1855–1865. [Google Scholar] [CrossRef]
- Glowacz, A.; Głowacz, Z.; Glowacz, W.; Carletti, E.; Kozik, J.; Korenciak, D.; Gutten, M.; Khan, F.; Irfant, M. Fault Diagnosis of Three Phase Induction Motor Using Current Signal, MSAF-Ratio15 and Selected Classifiers. Arch. Metall. Mater. 2017, 62, 2413–2419. [Google Scholar] [CrossRef]
- da Silva, A.M.; Povinelli, R.J.; Demerdash, N.A.O. Rotor Bar Fault Monitoring Method Based on Analysis of Air-Gap Torques of Induction Motors. IEEE Trans. Ind. Inform. 2013, 9, 2274–2283. [Google Scholar] [CrossRef] [Green Version]
- Arkan, M.; Kostic-Perovic, D.; Unsworth, P.J. Modelling and simulation of induction motors with inter-turn faults for diagnostics. Electr. Power Syst. Res. 2005, 75, 57–66. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Mechanical power | 2.2 kW |
| Supply voltage | 380 V |
| Efficiency | 82% |
| Speed | 1410 rpm |
| Torque | 15 Nm |
| Frequency | 50 Hz |
| Core loss | 37 W |
| Stator slots | 36 |
| Rotor slots | 24 |
| Num Elements | Min Edge Length | Max Edge Length | RMS Edge Length | Min Elem. Area | Max Elem. Area | Mean Elem. Area | |
|---|---|---|---|---|---|---|---|
| Band | 627 | 0.000125 | 0.0019747 | 0.000854215 | 1.48933 × 10−8 | 1.59494 × 10−7 | 6.82612 × 10−8 |
| Shaft | 96 | 0.00312145 | 0.00613875 | 0.00458931 | 5.9426 × 10−6 | 1.46274 × 10−5 | 8.32385 × 10−6 |
| Outer Region | 1737 | 0.000125 | 0.00589417 | 0.00216509 | 2.24777 × 10−8 | 4.85527 × 10−6 | 1.0943 × 10−6 |
| Stator | 2161 | 0.000408465 | 0.00614834 | 0.00327034 | 2.03949 × 10−7 | 1.50488 × 10−5 | 3.89616 × 10−6 |
| Coil | 33 | 0.000897214 | 0.00340384 | 0.00239494 | 9.34699 × 10−7 | 3.15461 × 10−6 | 2.03934 × 10−6 |
| Rotor | 6300 | 0.000273126 | 0.00582202 | 0.00140777 | 4.81107 × 10−8 | 1.03163 × 10−5 | 7.93901 × 10−7 |
| Bar | 453 | 0.000273126 | 0.000699128 | 0.000498602 | 4.60133 × 10−8 | 1.81518 × 10−7 | 1.06182 × 10−7 |
| Bar_Separate | 499 | 0.000273126 | 0.000699128 | 0.000473352 | 4.60133 × 10−8 | 1.81518 × 10−7 | 9.6394 × 10−8 |
| Coil Shorted | 7 | 0.0008 | 0.002 | 0.00118964 | 4 × 10−7 | 1 × 10−6 | 5.71429 × 10−7 |
| Nf | TL = 0 Nm | TL = 15 Nm |
|---|---|---|
| 55 | 90.589 | 99.471 |
| 50 | 90.365 | 99.702 |
| 40 | 89.148 | 99.567 |
| 30 | 87.410 | 98.583 |
| 20 | 91.727 | 96.986 |
| 10 | 92.689 | 95.689 |
| 3 | 91.938 | 97.009 |
| 2 | 92.076 | 97.286 |
| 1 | 92.220 | 97.599 |
| 0 | 92.305 | 97.974 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrowski, W.; Górny, K. Analysis of Torque Ripples of an Induction Motor Taking into Account a Inter-Turn Short-Circuit in a Stator Winding. Energies 2020, 13, 3626. https://doi.org/10.3390/en13143626
Pietrowski W, Górny K. Analysis of Torque Ripples of an Induction Motor Taking into Account a Inter-Turn Short-Circuit in a Stator Winding. Energies. 2020; 13(14):3626. https://doi.org/10.3390/en13143626
Chicago/Turabian StylePietrowski, Wojciech, and Konrad Górny. 2020. "Analysis of Torque Ripples of an Induction Motor Taking into Account a Inter-Turn Short-Circuit in a Stator Winding" Energies 13, no. 14: 3626. https://doi.org/10.3390/en13143626
APA StylePietrowski, W., & Górny, K. (2020). Analysis of Torque Ripples of an Induction Motor Taking into Account a Inter-Turn Short-Circuit in a Stator Winding. Energies, 13(14), 3626. https://doi.org/10.3390/en13143626






