Modeling of Electric Energy Consumption during Dairy Wastewater Treatment Plant Operation

Abstract

The intensification of biological wastewater treatment requires the high usage of electric energy, mainly for aeration processes. Publications on energy consumption have been mostly related to municipal wastewater treatment plants (WWTPs). The aim of the research was to elaborate on models for the estimation of energy consumption during dairy WWTP operation. These models can be used for the optimization of electric energy consumption. The research was conducted in a dairy WWTP, operating with dissolved air flotation (DAF) and an activated sludge system. Energy consumption was measured with the help of three-phase network parameter transducers and a supervisory control and data acquisition (SCADA) system. The obtained models provided accurate predictions of DAF, biological treatment, and the overall WWTP energy consumption using chemical oxygen demand (COD), sewage flow, and air temperature. Using the energy consumption of the biological treatment as an independent variable, as well as air temperature, it is possible to estimate the variability of the total electric energy consumption. During the summer period, an increase in the organic load (expressed as COD) discharged into the biological treatment causes higher electric energy consumption in the whole dairy WWTP. Hence, it is recommended to increase the efficiency of the removal of organic pollutants in the DAF process. An application for the estimation of energy consumption was created.

1. Introduction

Sewage and sludge treatment processes are inextricably linked to electric energy consumption. The intensification of biological wastewater treatment has a positive impact on the natural environment, but requires the high usage of electric energy, mainly for aeration processes. The increased production in dairy plants, observed since Poland’s accession to the European Union, has resulted in an increase in the quantity of dairy sewage and pollutant load. A steady increase in the volume of processed milk has also been observed. Between 2000 and 2016, annual milk production increased from 11,552 hm³ to 12,867 hm³, while the global amount of sewage from the dairy sector reached 28.1 hm³ in 2016 [1].

The characteristics of dairy sewage differ significantly from typical municipal wastewater. The values of pollution indicators, measured by biochemical oxygen demand (BOD₅) and chemical oxygen demand (COD), range from 4 to as much as 10 times higher than in municipal wastewater [2,3]. Dairy wastewater is also characterized by a high concentration of phosphorus. Due to the high concentration of pollutants and strict requirements regarding the quality of treated wastewater, the amount of energy used is much higher in comparison with municipal sewage. Energy consumption is also influenced by the high variability of sewage composition and quantity over time [4,5]. Both the volume flow rate and the pollutant load from dairy wastewater treatment plants (WWTPs) depend on the production profile, which may often change daily [6]. About 90% of organic contaminants in dairy wastewater come from residual products washed out during the operation of cleaning-in-place (CIP) stations [7].

In Polish dairy WWTPs, the dominant method of biological wastewater treatment is the aerobic process with activated sludge. The technology of anaerobic treatment is rarely used, however, many food industries use this process for wastewater pre-treatment, before discharging it into municipal WWTPs [8]. According to Dębowski et al. [9], the most commonly used anaerobic reactors are upflow anaerobic sludge blankets (UASBs) and expanded granular sludge beds (EGSBs). Their advantage is the possibility of obtaining biogas and producing heat and electricity. However, the investment costs are high, and maintenance requires highly qualified staff. These technologies are cost-efficient for large WWTPs. Most dairy WWTPs in Poland, including the one analyzed, operate with aerobic systems.

Previous research by the authors has confirmed that the consumption of electric energy in dairy WWTPs is mainly caused by the aeration processes in activated sludge chambers, averaging tanks, and excess sludge stabilization chambers [10,11]. The same is observed in municipal WWTPs [12,13]. Publications on the energy intensity of wastewater treatment are mostly related to municipal WWTPs [14,15]. The given indicators concern entire WWTPs, without division into individual processes. The amount of energy per unit of wastewater volume is the most common indicator given as a result of analysis [16]. Large differences in energy consumption are caused by applying technologically different facilities, hydraulics, and pollutant loads. There is a clear downward trend in unit energy consumption as the capacity of the WWTPs increases. The highest values are characterized by objects operating with classical activated sludge technology, with intensive aeration. Municipal WWTPs in most cases consume less than 1 kWh per m³ of treated wastewater [17].

It is important to state that although there are many publications describing energy consumption, only a few of them go so far as to state the actual equations for energy usage, based on online measurement [18,19,20,21]. Yu et al. [18] modeled the energy intensity of municipal WWTPs, using semi-parametric quantum regression in Bayesian terms. The data were used to develop a model of electric energy consumption and to formulate conclusions allowing for optimization. It was shown that electric energy consumption, in relation to the unit of removed load, is closely correlated to sewage temperature. Models proposed by [13,22] require online measurements of COD and air temperature to obtain predicted values of energy consumption.

Analyzing the state of the art, it was found that it is necessary to use advanced real-time electric energy measuring systems to determine and improve energy efficiency. There is a lack of uniform and widely accepted procedures for determining the energy efficiency of municipal and industrial WWTPs. The need to optimize the electric energy consumption in dairy WWTPs has become a prerequisite for carrying out research and modeling processes.

The aim of the research was to elaborate on models for energy consumption estimation during the operation of dairy WWTPs, which could then be used by operators and designers for the optimization of electric energy consumption during particular processes.

2. Materials and Methods

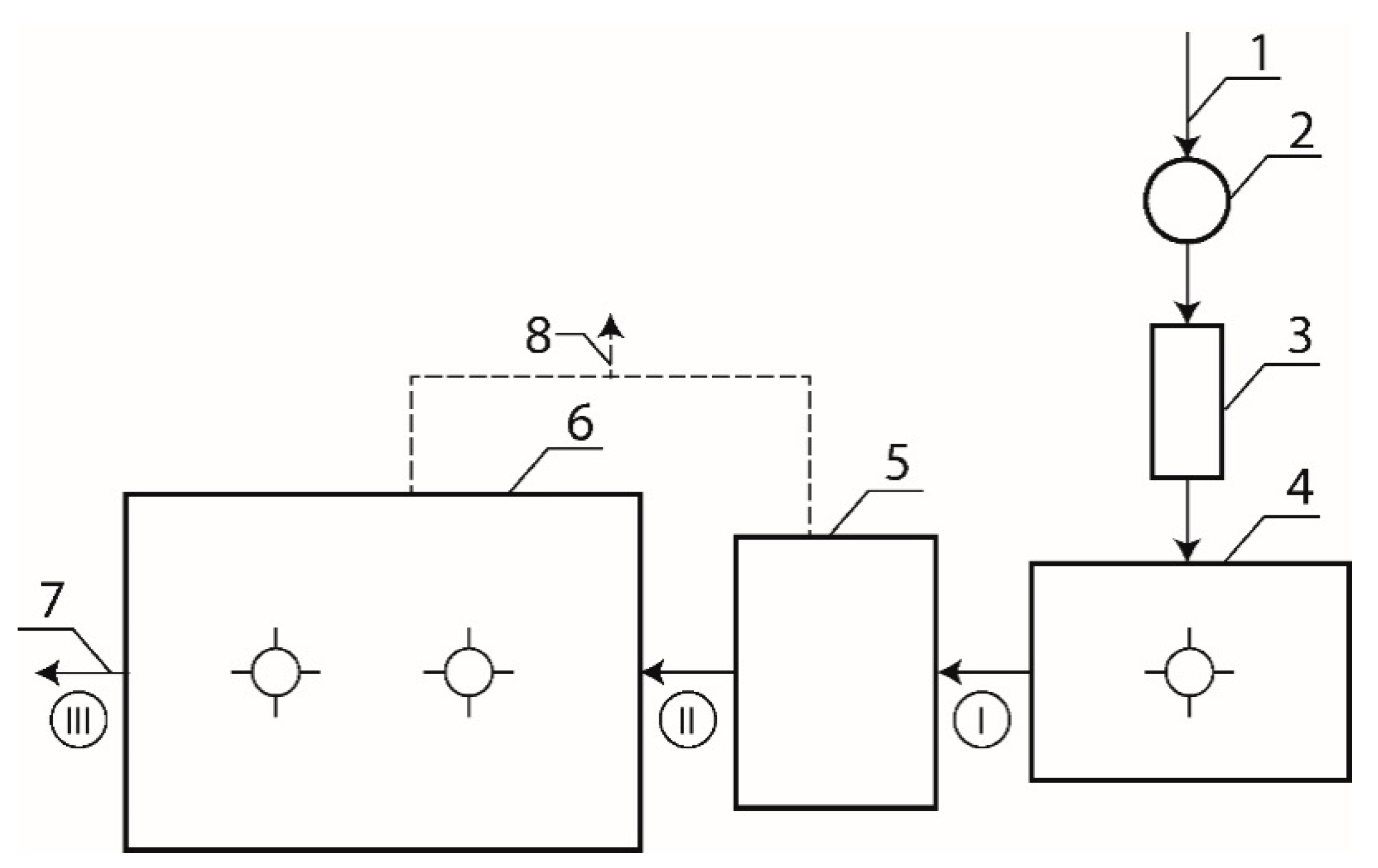
2.1. Study Site

The Bielmlek dairy WWTP (52.756199 N, 23.173387 E) has applied sequence batch reactors (SBRs) during biological treatment since 2012. The project parameters were an average sewage flow of 750 m³d⁻¹ and a 11,500 person equivalent (PE). The average daily flow during the research period was 653 m³d⁻¹ (301 ÷ 1154 m³d⁻¹). The value of BOD₅ changed from 1067 to 2240 mgO₂ dm⁻³, while that of COD varied from 1429 to 2945 mg O₂ dm⁻³. The concentration of total nitrogen (N_tot) fluctuated within the range of 32 ÷ 64 mg N dm⁻³, while the concentration of total phosphorus (P_tot) was from 5 to 24 mg P dm⁻³.

The sewage treatment process has two phases: physical and biological. After the sieve and grit chamber, wastewater is discharged into an averaging tank. The next step is dissolved air flotation (DAF), supported by adding coagulants and flocculant. After biological treatment with two SBRs, sewage is discharged into the Biała river. Excess sewage sludge generated in the process is subjected to aerobic stabilization and mechanical dewatering and is finally used as fertilizer. The total installed power of the dairy WWTP is 234.7 kW while the DAF treatment is 19.3 kW and the biological treatment is 104.5 kW. Figure 1 shows a diagram of the Bielmlek dairy WWTP and sampling points.

2.2. Electric Energy Measuring Methods

Three-phase network parameter transducers installed within the plant were used to measure energy consumption. The current transformers sent signals, which were then received by the transducers. Precise measurement was possible thanks to current transformers connected to every single electric device within the plant. A supervisory control and data acquisition system (SCADA) collected the information from the current transformers and showed the results online; it also archived and processed the data.

2.3. Sampling of Sewage and Analytical Procedures

Measurements of 95 series were performed. Each series included measurements of sewage parameters from sampling points I, II, and III (Figure 1). The measurements were taken over 30 months. The following basic parameters of wastewater were monitored: BOD₅, COD, N_tot, and P_tot. Sewage quantity and meteorological conditions were also monitored. The performed analysis allowed for the creation of a database containing the following parameters:

• $T$—air temperature,
• $L_{BOD5}$, $L_{COD}$, $L_{Ntot}$, $L_{Ptot}$—pollutant (BOD₅, COD, N_tot, and P_tot) loads after the averaging tank (point I),
• $L_{DAF.BOD5}$, $L_{DAF.COD}$, $L_{DAF.Ntot}$, $L_{DAF.Ptot}$—pollutant loads after DAF treatment (point II),
• $L_{BIO.BOD5}$, $L_{BIO.COD}$, $L_{BIO.Ntot}$, $L_{BIO.Ptot}$—pollutant loads after biological treatment in SBRs (point III).

Determinations were conducted in a certified laboratory (Hamilton, Poland) in accordance with the procedures set out by the Polish Maritime Economy and Inland Navigation Minister [23] and the American Public Health Association [24].

2.4. Modeling of Electric Energy Consumption

It was found that the total electric energy consumption ($E_{TOT}$) was significantly affected by the electric energy consumption during biological treatment $(E_{BIO}$), and the electric energy consumption during the DAF process ($E_{DAF})$.

Statistical inference, regarding energy consumption during various treatment stages, was based on regression methods. For all modeling procedures, residual analysis was performed to confirm the validity of linear fits. The inference was conducted according to the following scheme (the selected method of analysis is given in brackets):

• modeling of $E_{TOT}$ was carried out based on $E_{BIO}$ and $T$ (the least squares linear regression);
• a qualitative analysis of $L_{DAF.BOD5}$, $L_{DAF.Ntot}$, $L_{DAF.Ptot}$, and $Q$ was carried out. $L_{DAF.COD}$ was used as an independent variable (quantile and quantile segmented regression methods);
• modeling of $E_{BIO}$ was carried out based on the $L_{DAF.COD}$ and $T$ (the least squares linear regression method);
• a qualitative analysis of $L_{DAF.COD}$ was carried out based on $L_{COD}$ (quantile regression and segmented quantile regression methods);
• modeling of $E_{DAF}$ was carried out based on $Q$ (the least squares linear regression method).

The qualitative analysis was performed using quantile regression [25]. This method is recommended for the analysis of data from biological systems with complex interactions [26]. Based on nonlinear quantile regression [27], a segmented quantile regression was performed to better fit the data:

$$y=a+b\times x+c\times \mathit{max}\left(x-d,0\right)$$

(1)

where $y$—dependent variable;$x$—independent variable; $a$—intercept;$b$—slope; $c$—slope modifier; and $d$—value of $x$, where slope changes by the modifier.

A nonlinear model of the form (1) can be rewritten for different values of an independent variable:

$$y=\{\begin{array}{cc}a+b\times x& x<d\\ \left(a-cd\right)+\left(b+c\right)\times x& x\ge d\end{array}.$$

(2)

Numerical analysis was performed in the R environment [28], version 3.5.2. The following additional packages were used in the analysis besides the basic ones supplied with the environment: quantreg version 5.38 for quantile regression [29]; RColorBrewer version 1.1.2 for graphical presentation of the obtained models [30]; and lattice version 0.20.38 for graphical presentation of the obtained models [31].

3. Results

3.1. Total Electric Energy Consumption

$E_{TOT}$ depends on $E_{BIO}$ and $T$. The standard least squares regression analysis revealed the following model:

$$E_{TOT}=681.084+0.993\times E_{BIO}-24.036\times T+0.024\times E_{BIO}\times T.$$

(3)

A graphical representation of model (3) is presented in Figure 2.

The obtained model, presented in Figure 2 as a surface in three dimensions, is characterized by: a very good linear fit with a high coefficient of determination (adjusted for multiplicity) $R^2=0.912$, a proper residual structure (no significant deviation from normality and homoscedasticity), overall statistical significance ($p\text{-}value<{10}^{-15}$), and statistically significant coefficients ($p\text{-}value<{10}^{-4}$). A characteristic element of the model (3) is the interaction term $E_{BIO}\times T$, which can be interpreted as an element changing the ratio of $E_{TOT}$ depending on $E_{BIO}$ and $T$. This interpretation is presented in Equations (4) and (5).

$$E_{TOT}=681.084+\left(0.993+0.024\times T\right)\times E_{BIO}-24.036\times T$$

(4)

$$E_{TOT}=681.084+0.993\times E_{BIO}+\left(-24.036+0.024\times E_{BIO}\right)\times T$$

(5)

A graphical representation of model (4) is presented in Figure 3.

Figure 3 is a two-dimensional representation of the three-dimensional Figure 2, so it does not show temperature fluctuations. The green lines were obtained by inserting the value of $T$ into the Equation (3). The points and lines should follow themselves in order to follow the plane in Figure 2. The energy consumption was measured at a variable outside temperature, which slightly distorted Figure 3. The plane shown in Figure 3 is twisted as coded in the Equation (3). Temperature lines intersect at $E_{BIO}=1001.5kWh·d^{-1}$. This specific value presents the value of $E_{BIO}$, which, for this twisted plane, is parallel to the temperature axis. It means that $E_{TOT}$ is constant there. If we skip the temperature axis, like in Figure 3, then this point presents the intersection of temperature lines.

The model clearly shows that as the temperature increased, the share of the biological part ($E_{BIO}$) in total electric energy consumption ($E_{TOT})$ rose. This was due to a decrease in oxygen solubility in wastewater as the air temperature increases. During the summer months, while a reduction in oxygen solubility can be observed, the energy requirement for wastewater aeration is higher when compared with $E_{TOT}$. After exceeding the limit amount of energy taken for biological treatment ($E_{BIO}=1001.5kWh·d^{-1}$), the opposite phenomenon occurs. The same conclusion can be drawn directly from Figure 2. The twisting of the plane representing Equation (3) means that if the temperature increases, so does the linear coefficient of $E_{BIO}$, and total energy usage is more sensitive to changes in $E_{BIO}$.

3.2. Electric Energy Consumption during Biological Treatment

The amount of energy used in the process of biological treatment with activated sludge should be dependent on the input of pollutant loads and the air temperature T. However, when examining the relationships between these parameters, only T and $L_{DAF.COD}$ are completely independent of each other. This can be explained by the operation of the averaging tank and DAF process. It results in the averaging of sewage parameters discharged for biological treatment. Using quantile regression, a description of the sewage parameters correlation was made in the form of appropriate models for the quantiles $\tau =0.9$ and $\tau =0.1$. $L_{DAF.COD}$ was the independent variable in all models. This variable was chosen because of measurement simplicity. To ensure that every dependent variable was greater than 0, the segmented model for $\tau =0.1$ was used. The obtained models are presented in Figure 4.

The equations describing the obtained models are presented in

Table 1. The obtained models.

Parameter	Equations	Conditions
$Q$	$\{\begin{array}{c}222.337+0.331\times L_{DAF.COD}\\ 507.627+0.409\times L_{DAF.COD}\end{array}$	$\begin{array}{c}\tau =0.1\\ \tau =0.9\end{array}$
$L_{DAF.BOD}$	$\{\begin{array}{c}25.415+0.431\times L_{DAF.COD}\\ 46.046+0.757\times L_{DAF.COD}\end{array}$	$\begin{array}{c}\tau =0.1\\ \tau =0.9\end{array}$
$L_{DAF.Ntot}$	$\{\begin{array}{c}1.031+0.009\times L_{DAF.COD}\\ -159.964+1.135\times L_{DAF.COD}\\ 4.507+0.094\times L_{DAF.COD}\end{array}$	$\begin{array}{c}\tau =0.1;L_{DAF.COD}<1544.635\\ \tau =0.1;L_{DAF.COD}<1544.635\\ \tau =0.9\end{array}$
$L_{DAF.Ptot}$	$\{\begin{array}{c}0.633+0.002\times L_{DAF.COD}\\ -9.319+0.011\times L_{DAF.COD}\\ 5.060+0.011\times L_{DAF.COD}\end{array}$	$\begin{array}{c}\tau =0.1;L_{DAF.COD}<1060.207\\ \tau =0.1;L_{DAF.COD}\ge 1060.207\\ \tau =0.9\end{array}$

.

$E_{BIO}$ should depend on sewage parameters and $T$. Taking into account the information presented in Table 1, $L_{DAF.COD}$ and $T$ were the independent parameters used for describing $E_{BIO}$. The following model was estimated by a linear least squares analysis:

$$E_{BIO}=370.521+0.345\times L_{DAF.COD}-7.744\times T+0.018\times L_{DAF.COD}\times T.$$

(6)

Equation (6) is presented in Figure 5.

The obtained model, presented graphically as a surface in three-dimensions in Figure 5, is characterized by: a good linear fit, with an acceptable coefficient of determination (adjusted for multiplicity) $R^2=0.723;$ a proper residual structure (no significant deviation from normality and homoscedasticity); overall statistical significance ($p\text{-}value<{10}^{-15}$); and statistically significant coefficients ($p\text{-}value<{10}^{-4}$), except the one for $T$ ($p\text{-}value=0.04$), which is at the border of significance. The coefficient was retained in the model due to the presence and significance of the interaction term $L_{DAF.COD}\times T$. Using the interaction term, as temperature-based change of COD, we obtained the load coefficient Equation (7).

$$E_{BIO}=370.521+\left(0.345+0.018\times T\right)\times L_{DAF.COD}-7.744\times T$$

(7)

Equation (7) is presented in Figure 6.

Figure 6 is a two-dimensional representation of the three-dimensional Figure 5, so it does not show temperature fluctuations (as Figure 2 and Figure 3 do). Temperature lines intersect at $L_{DAF.COD}=430.222\mathrm{kg}·{\mathrm{d}}^{-1}$. For this specific load value, $E_{BIO}$ is constant and does not vary with temperature. Changing $L_{DAF.COD}$ around this value changes the nature of sensitivity of $E_{BIO}$ to temperature variations.

As T increases, the impact of $L_{DAF.COD}$ on the electric energy consumption of the biological part ($E_{BIO}$) in a treatment plant increases. Exceeding the load value, $L_{DAF.COD}=430.222$ kgd⁻¹, results in a reversal of the nature of $E_{BIO}$’s dependence on $L_{DAF.COD}$ in relation to T. For loads smaller than $L_{DAF.COD}=430.222$ kgd⁻¹, a decreasing temperature results in an increase in electric energy consumption; for larger loads, it results in a reduction of electric energy consumption.

$L_{DAF.COD}$ should depend on $L_{COD}$. Using the quantile regression, a description of this dependence was made in the form of appropriate models for the quantiles $\tau =0.9$ and $\tau =0.1$. The obtained models are presented in a set of Equations (8).

$$L_{DAF.COD}=\{\begin{array}{cc}\begin{array}{c}59.955+0.246\times L_{COD}\\ -197.414+0.543\times L_{COD}\\ 11.490+0.802\times L_{COD}\end{array}& \begin{array}{c}\tau =0.1;L_{COD}<866.855\\ \tau =0.1;L_{COD}\ge 866.855\\ \tau =0.9\end{array}\end{array}$$

(8)

Equation (8) is presented in Figure 7.

Energy consumption during the DAF process depends on sewage flow $\left(Q\right)$. The standard least squares regression analysis revealed the following model (9):

$$E_{DAF}=13.969+0.030\times Q.$$

(9)

The obtained model, presented graphically in Figure 8, is characterized by: a relatively good linear fit with a coefficient of determination (adjusted for multiplicity) $R^2=0.559;$ a proper residual structure; no significant deviation from normality and homoscedasticity; overall statistical significance ($p\text{-}value<{10}^{-15}$); and statistically significant coefficients ($p\text{-}value<{10}^{-4}$). Equation (9) is presented in Figure 8.

4. Final Modeling Scheme and Discussion

The obtained database made it possible to present energy consumption models during the DAF process and biological treatment. Despite the fact that biological treatment is only one part of the entire wastewater treatment process, it was possible to describe the variability of the total electric energy consumption on its basis. This is due to the fact that the activated sludge technology generates the highest energy consumption [17]. According to Bisak et al. [32] and Panaitescu et al. [33], the share of aeration systems in total electric energy consumption in sewage treatment plants ranges from 46 to 69 percent. In the case of industrial WWTPs, this share is even higher [17].

The obtained models describe the variability of energy consumption, in selected steps of dairy WWTP operation, depending on chosen parameters ($L_{DAF.COD}$, $Q$, and $T$). The influence of these parameters on unit energy consumption has been confirmed by Longo et al. [12]. A clear downward trend in unit energy consumption has been observed with an increase in the plant capacity [34]. $L_{DAF.COD}$ is the parameter most reflecting energy consumption, as it contains information on wastewater flow and pollutant concentration. The values of this parameter are comparable in WWTPs with different capacities and design parameters. Yu et al. [18] have shown that the electric energy consumption per unit of removed substance is strongly correlated to the sewage temperature. It was shown that with an increasing content of organic substances, expressed as COD, in raw sewage, the unit energy consumption of the process decreases.

The main modeling scheme based on the obtained results is presented in Figure 9.

The interpretation of the results presented in Figure 9A–C leads to the following conclusions:

• The increased electric energy consumption in the biological treatment process causes a decrease in the temperature dependence of the total electric energy consumption. After exceeding the value of $E_{BIO}=1001.5kWh·d^{-1}$, the reverse dependence can be observed, i.e., with increasing temperature, total energy consumption grows. Mamais et al. [19] have also reported an increase in the electric energy consumption during summer periods. This is due to an increase of endogenous respiration when the temperature rises.
• Quantile regression models confirm the interdependence of wastewater parameters after the DAF process. Due to the ease of measurement, $L_{DAF.COD}$ can be used to qualitatively describe other wastewater parameters. Along with the increase in $T$, the influence of $L_{DAF.COD}$ on electric energy consumption during biological treatment increases. When exceeding the load $L_{DAF.COD}=430.2kg·d^{-1}$, the relationship between $E_{BIO}$ and $L_{DAF.COD}$ with respect to temperature reverses. Lowering the air temperature increases energy consumption for smaller loads, and decreases electric energy consumption for larger pollutant loads. According to Niu et. al. [20], in order to reduce electric energy consumption, the pollutant load in the wastewater discharged into biological treatment should be increased. The authors point out that a properly loaded WWTP is characterized by lower energy consumption than an underloaded one. Therefore, it is important to control the pollutant load discharged into the biological treatment, depending on the air temperature. This can be realized by controlling the flotation efficiency.
• The results of the qualitative analysis make it possible to predict the range of variability of the $L_{DAF.COD}$ by measuring the COD parameter in the wastewater before the DAF process. Parameters such as $L_{COD}$ and $L_{DAF.COD}$ can be easily monitored during all of the treatment processes. The COD parameter in raw sewage was also mentioned by Huang et al. [21] as being important to the modeling of electric energy consumption. It is used to predict not only the electric energy consumption but also the parameters of treated wastewater.

An application for simulation of electric energy consumption during dairy sewage treatment was prepared on the basis of the presented modeling scheme (Figure 10).

The initial parameters are COD in raw sewage, $Q$, and $T$. The application calculates $E_{TOT}$, and the share of $E_{BIO}$ and $E_{DAF}$ for the example’s data. The personal computer (PC) application can be used for other dairy WWTPs applying DAF and activated sludge systems. However, the obtained results would be less precise than in the case of the original object [35].

5. Conclusions

On the basis of the obtained research results, mathematical models have been developed. They can be used to optimize electric energy consumption during dairy WWTP operation. The obtained models describe the variability of electric energy consumption of a WWTP with high accuracy. The main parameter determining the consumption of electric energy in the analyzed dairy WWTP is the load of organic substances expressed as COD. The significant influence of air temperature was observed. Using the parameter of electric energy consumption in the biological treatment as an independent variable, together with air temperature, it is possible to estimate the variability of the total electric energy consumption. During summer periods, an increase in the load of organic substances expressed as COD, during biological treatment, causes higher electric energy consumption in the whole dairy WWTP. It is recommended to increase the efficiency of the removal of organic pollutants in the DAF process, which will reduce the total electric energy consumption.