Numerical Study on the Influence Mechanism of Crosswind on Frozen Phenomena in a Direct Air-Cooled System
Abstract
:1. Introduction
2. Mathematical Model
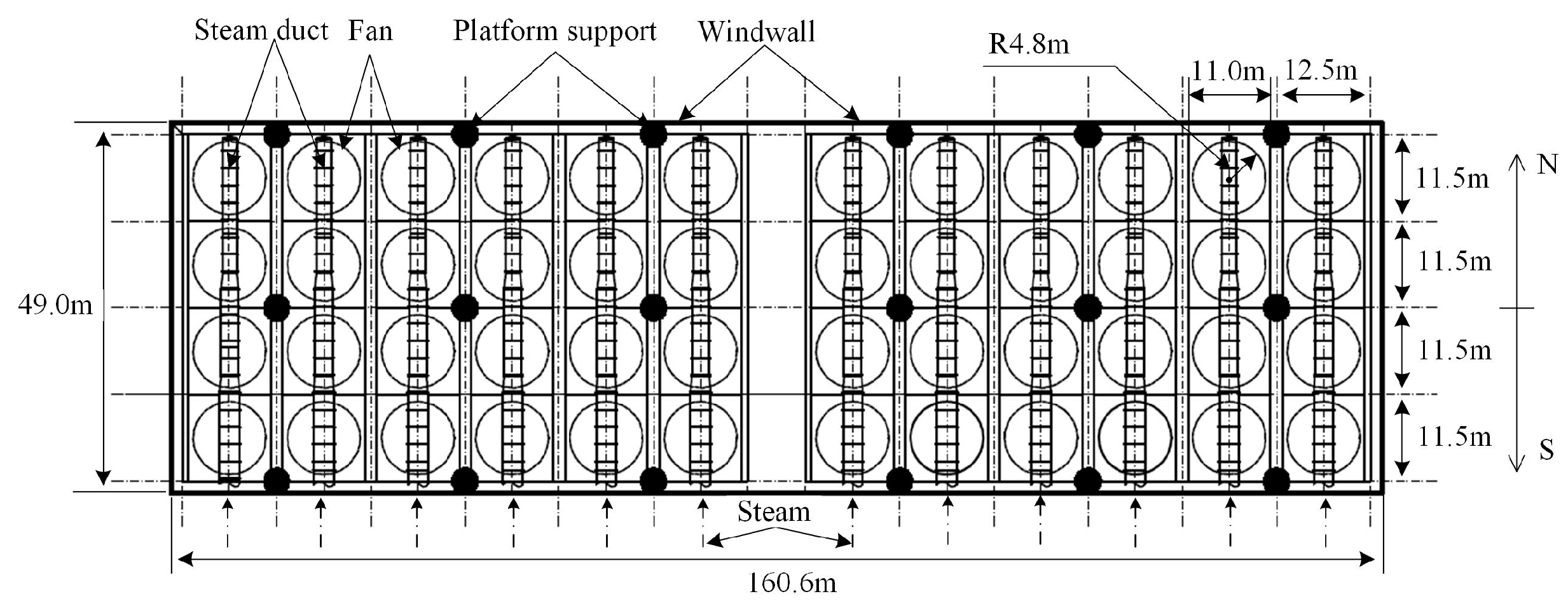
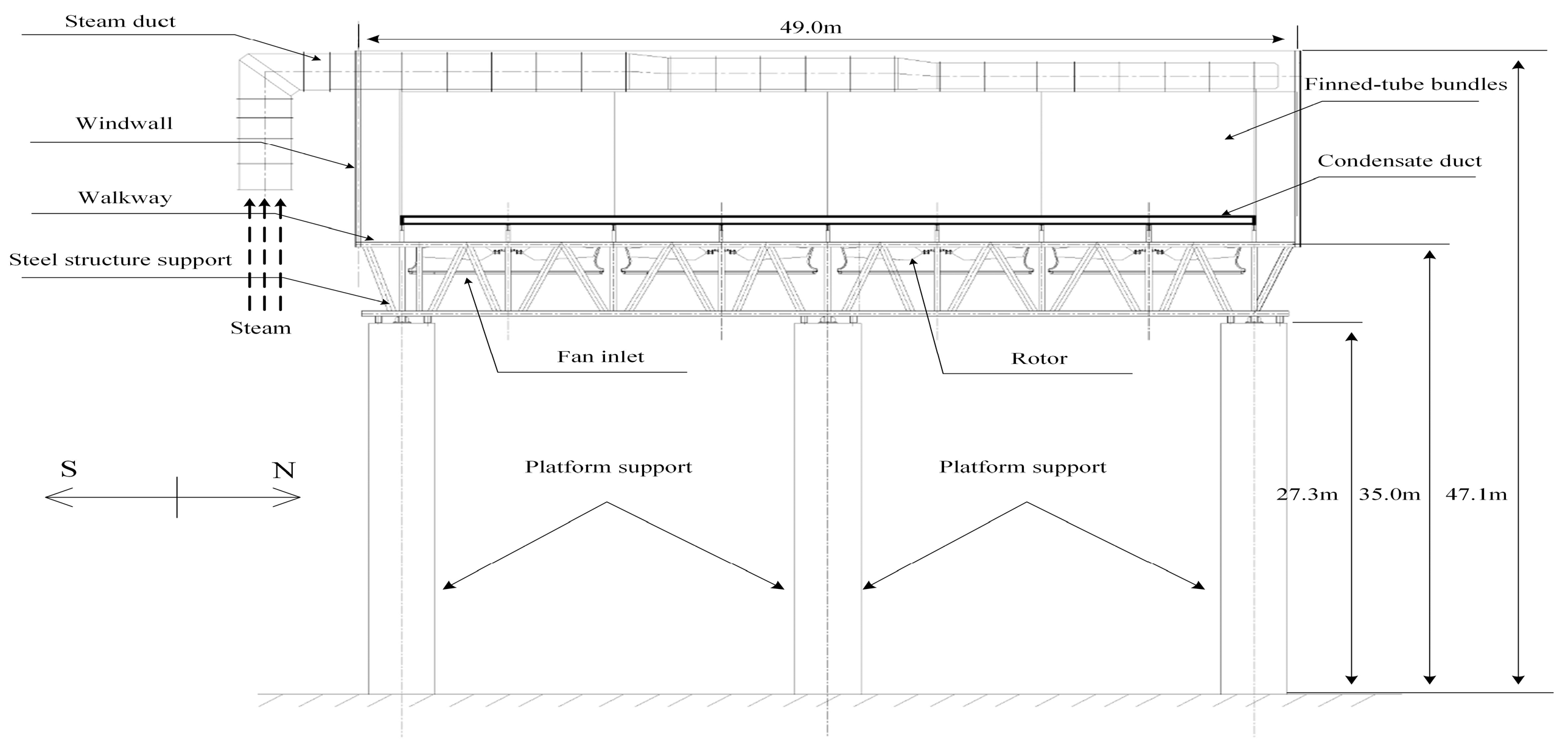
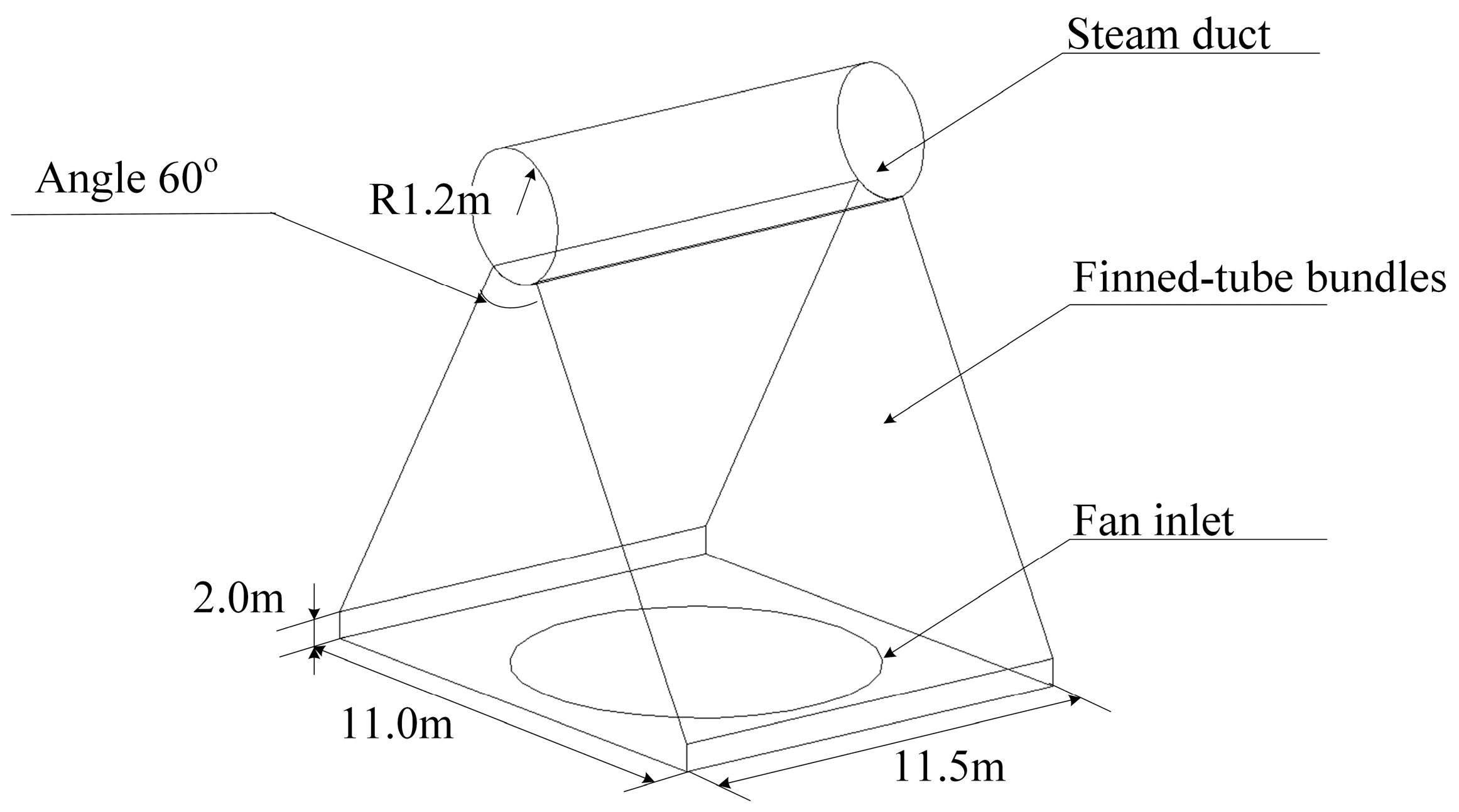
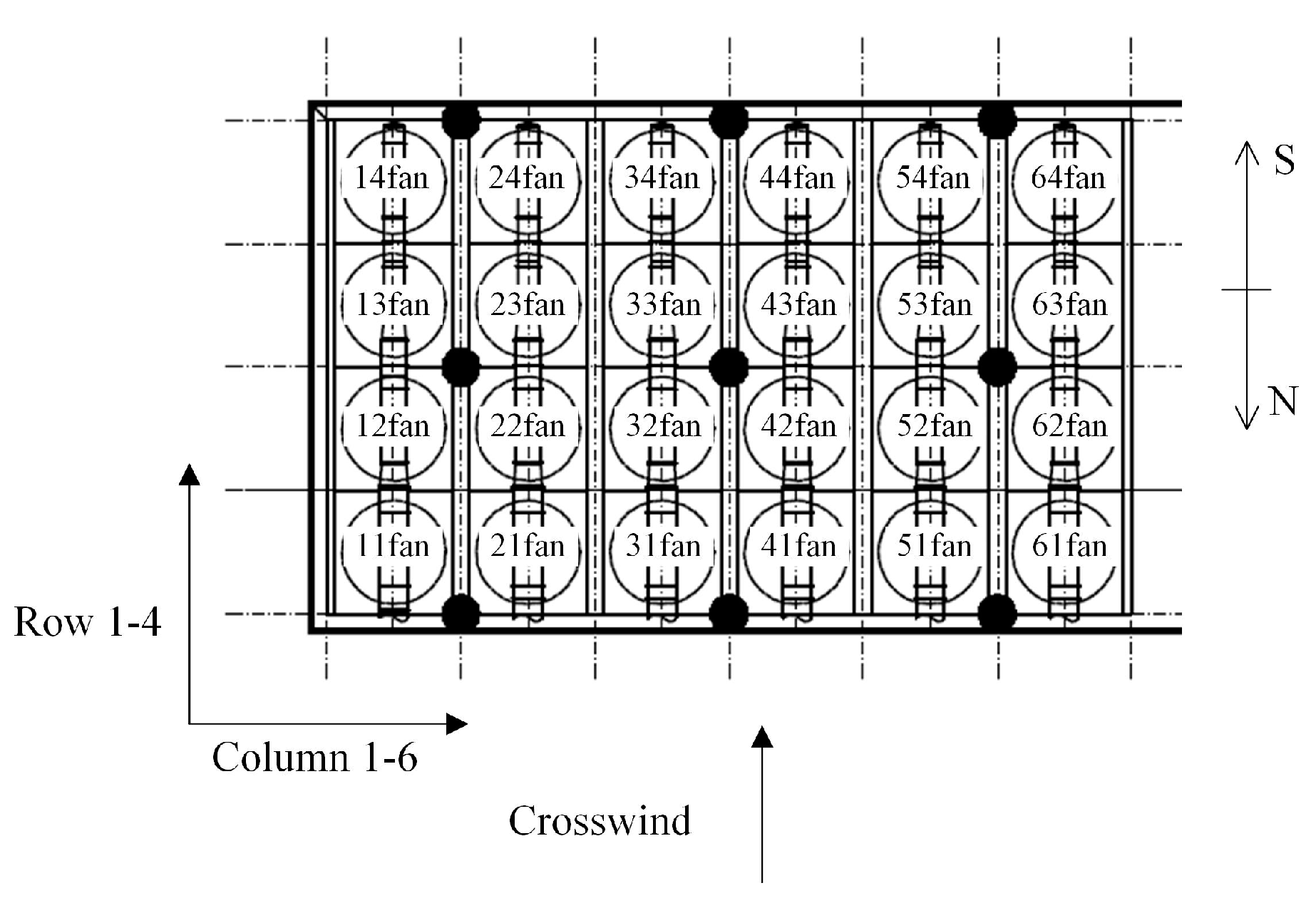
2.1. Geometric Model
2.2. Governing Equations
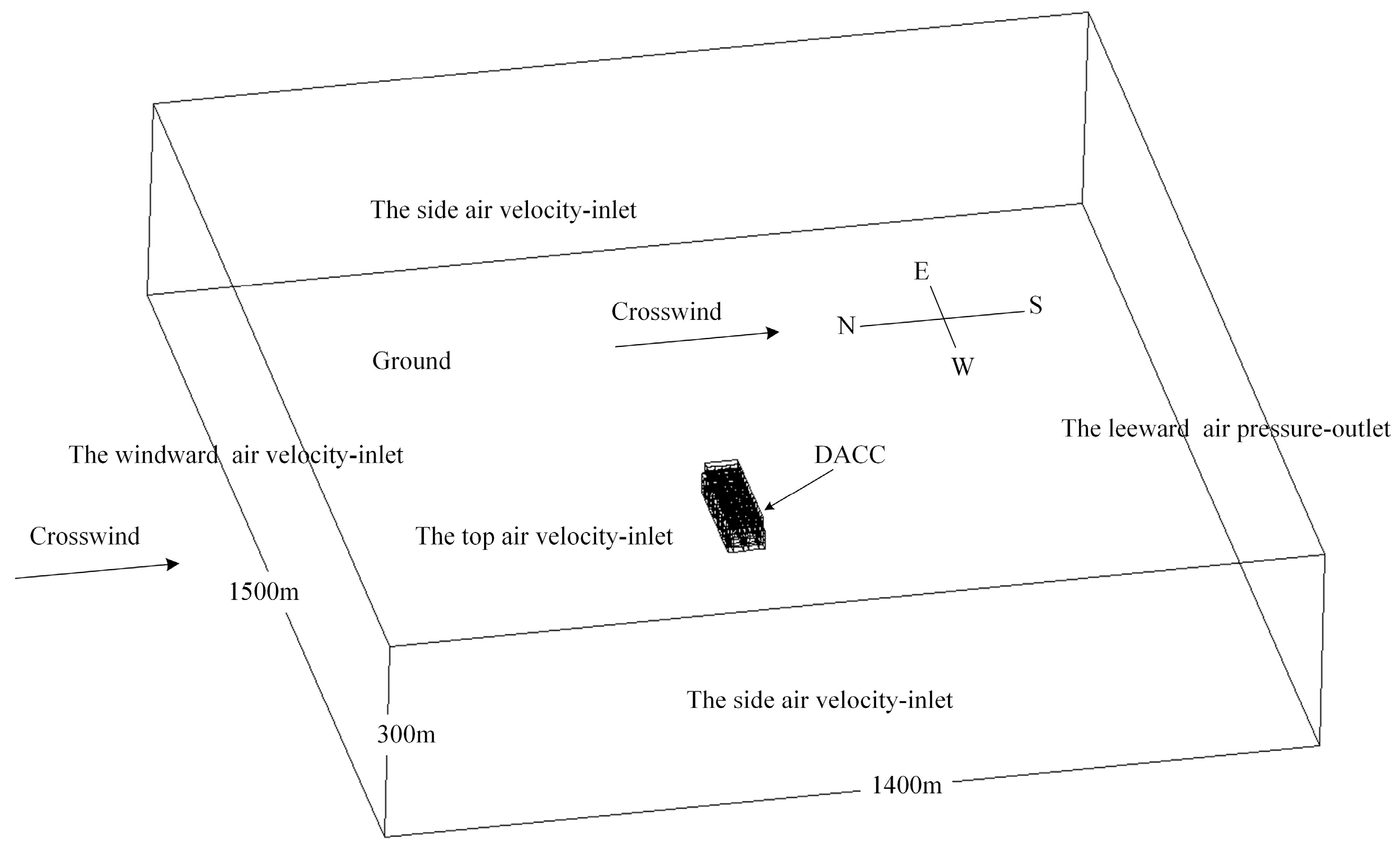
2.3. Boundary Conditions
2.4. Grid Independence Verification and Check of the Convergence
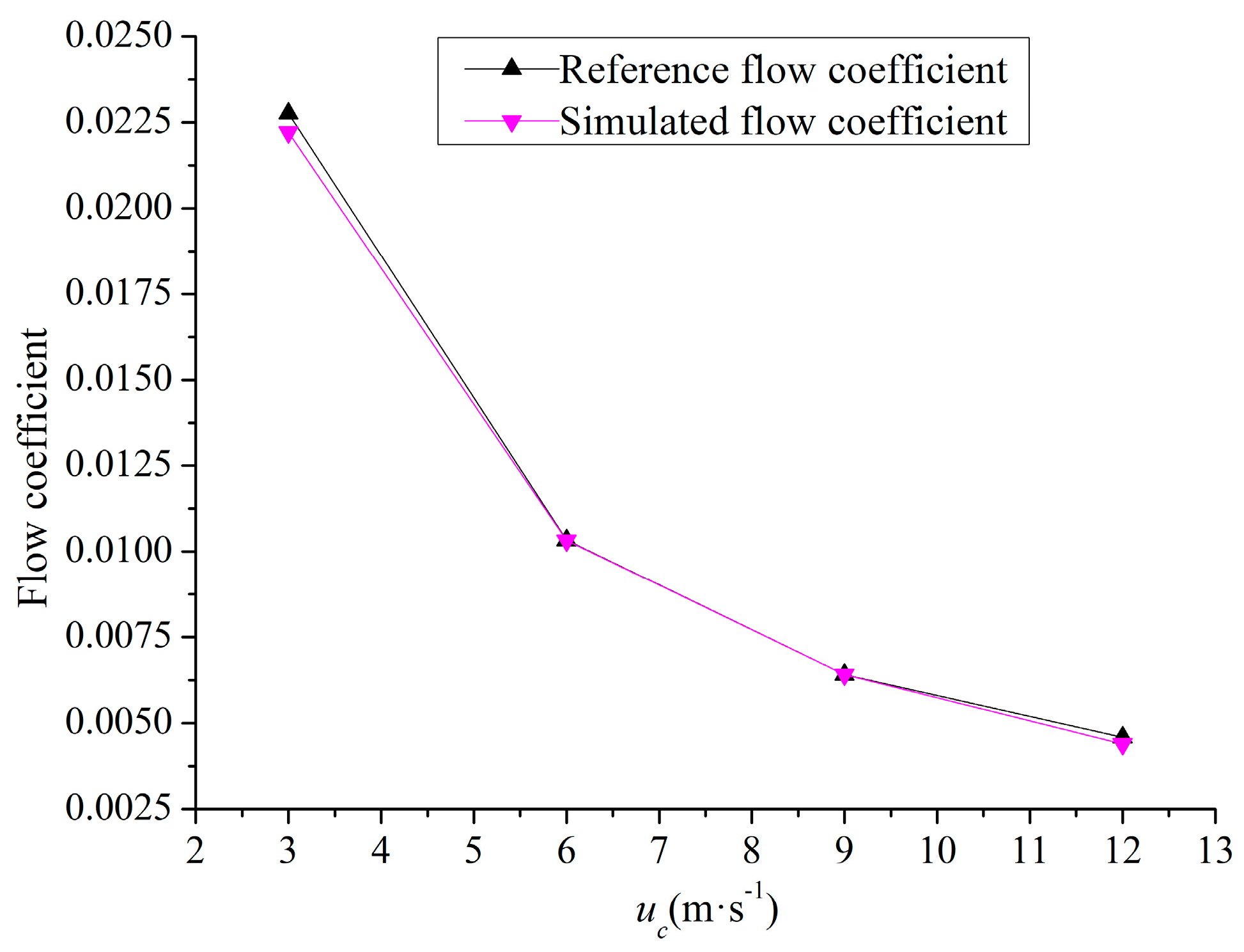
2.5. Validation
3. Results and Discussion
3.1. Variation of Airflow Rate under Crosswind Conditions
3.2. Variation of Inlet Air Temperature under Crosswind Conditions
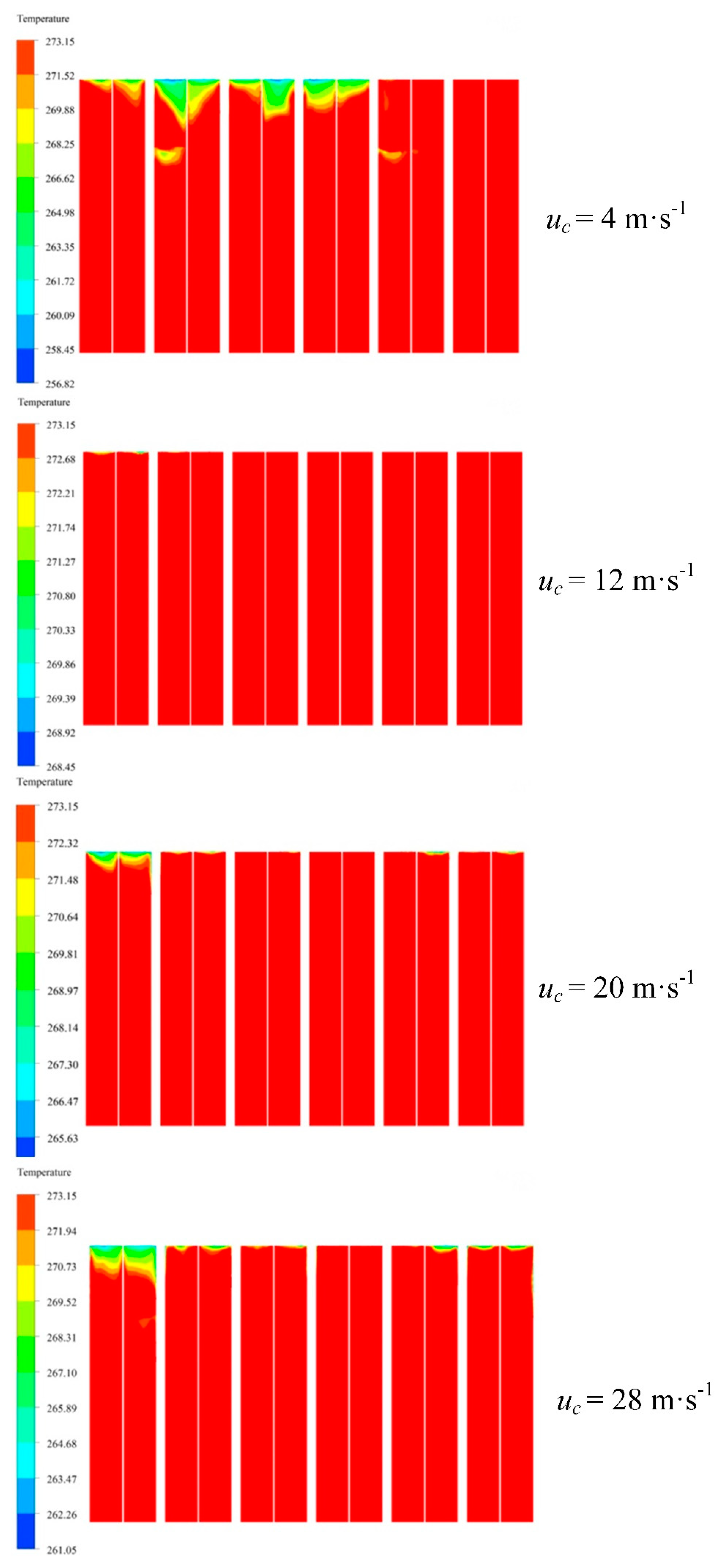
3.3. Temperature Contours of Finned-Tube Radiators
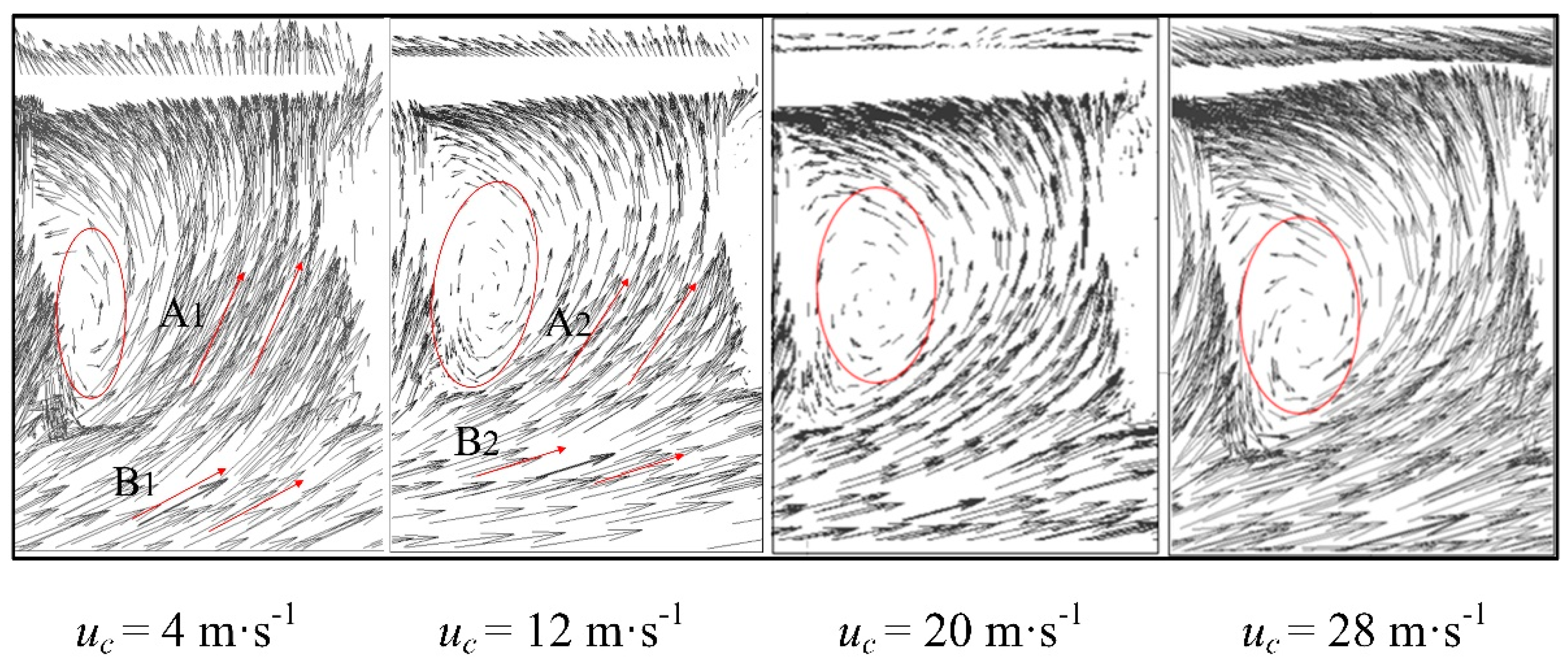
3.4. Flow Field Characteristics of Frozen Regions
4. Conclusions
- (a)
- The frozen phenomena are most likely to appear in row 4 under different crosswind conditions. The airflow rate increases and the inlet air temperature decreases along the direction of the crosswind. When the crosswind velocity is lower than 12 m·s−1, the maximum value of airflow rate remains unchanged. When the crosswind velocity is greater than 12 m·s−1, and the maximum value of airflow rate and minimum value of inlet air temperature appear in column 1 row 4, the maximum value of airflow rate gradually increases and the minimum value of inlet air temperature decreases along with the increasing of crosswind velocity.
- (b)
- The number of frozen air-cooled units gradually shrinks to zero and then increases along the increase of crosswind velocity. The frozen phenomena in the DACC disappears when the crosswind velocity is 12 m·s−1. The frozen region mainly appears in column 1 row 4, and the area of the frozen region increases from one-third of the air-cooled unit surface to half when the crosswind velocity increases from 20 m·s−1 to 28 m·s−1. At a crosswind velocity of 4 m·s−1, the number and area of frozen regions reach the maximum of six.
- (c)
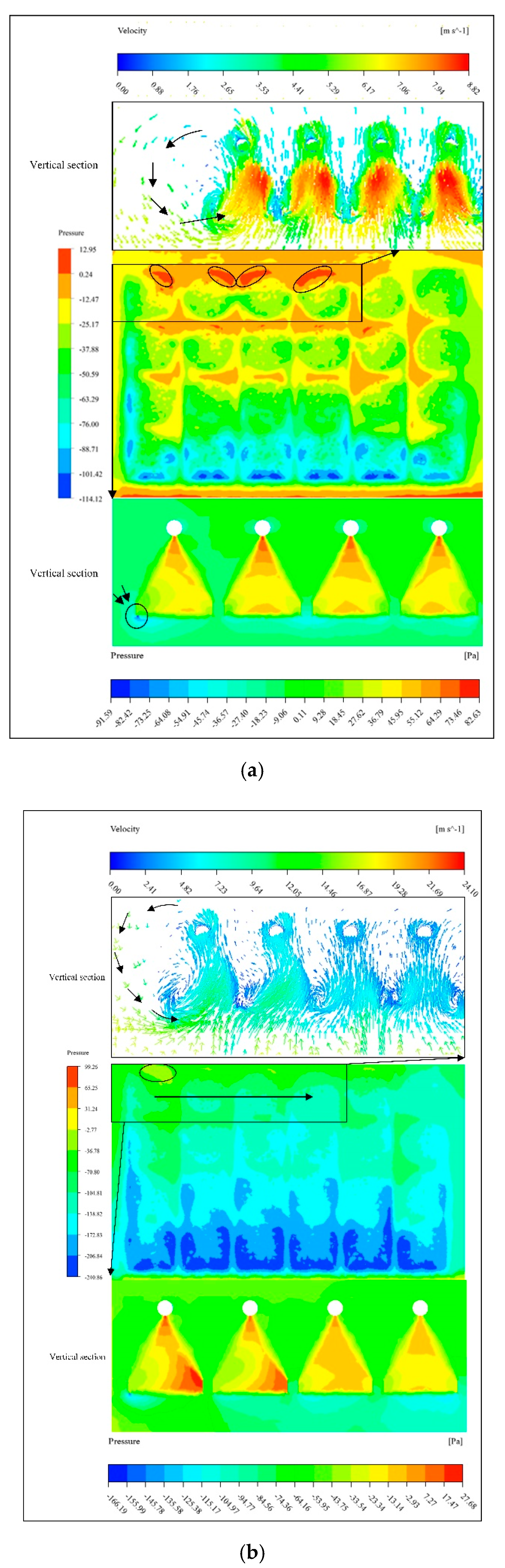
- One vortex will be formed on the upwind side of the air-cooled unit under different crosswind velocities and it is not easy to form a frozen region where the vortex is formed. The increase of vortex can availably reduce the area of the frozen regions at a crosswind velocity of not more than 12 m·s−1. When the crosswind velocity is greater than 20 m·s−1, the vortices in the air-cooled unit are the same size.
- (d)
- There exists hot air recirculation under a crosswind velocity of not more than 12 m·s−1, which may be one of the reasons to restrain the formation of the frozen zone. The hot air recirculation disappears when the crosswind velocity exceeds 20 m·s−1. With the increase of crosswind velocity, the negative pressure region gradually increases along the direction of the crosswind velocity, and a relatively high-pressure zone appears below each frozen region.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| e | specific internal energy (J·kg−1) |
| keff | air thermal conductivity (W·m−1·K−1) |
| d | the distance to the wall (m) |
| C2 | pressure-jump coefficient (m−1) |
| Cb1, etc | empirical constants in the turbulence model |
| modified vorticity | |
| S | magnitude of the vorticity |
| Gv | turbulent viscous generation term |
| Sh | heat source (W·m−3) |
| q | heat flux (W·m−2) |
| h | specific enthalpy (kJ·kg−1) |
| hλ | convective heat transfer coefficient (W·m−1·K−1) |
| T | temperature (K) |
| ui | air velocity in the xi direction |
| uc | ambient natural crosswind velocity (m·s−1) |
| p | pressure (Pa) |
| v | kinematic viscosity (m2·s−1) |
| xi | cartesian coordinate (m) |
| kL | nondimensional loss coefficient |
| Greek Letters | |
| ρ | air density (kg·m−3) |
| μ | effective dynamic viscosity (kg·m−1·s−1) |
| χ | intermediate variable |
| σ | turbulent Prandtl number |
| α | profile index |
| Subscripts | |
| eff | effective |
| a | air |
References
- Zhang, L.; Zhang, L.; Zhang, Q.; Jiang, K.; Tie, Y.; Wang, S. Effects of the Second-Stage of Rotor with Single Abnormal Blade Angle on Rotating Stall of a Two-Stage Variable Pitch Axial Fan. Energies 2018, 11, 3293. [Google Scholar] [CrossRef] [Green Version]
- Meyer, C.J. Numerical investigation of the effect of inlet flow distortions on forced draught air-cooled heat exchanger performance. Appl. Therm. Eng. 2005, 25, 1634–1649. [Google Scholar] [CrossRef]
- Wang, Q.W.; Zhang, D.J.; Zeng, M.; Lin, M.; Tang, L.H. CFD simulation on a thermal power plant with air-cooled heat exchanger system in north China. Eng. Comput. 2008, 25, 342–365. [Google Scholar] [CrossRef]
- Liu, P.; Duan, H.; Zhao, W. Numerical investigation of hot air recirculation of air-cooled condensers at a large power plant. Appl. Therm. Eng. 2009, 29, 1927–1934. [Google Scholar] [CrossRef]
- Gu, H.; Zhe, Z.; Wang, H.; Qi, C. A numerical study on the effect of roof windbreak structures in an air-cooled system. Appl. Therm. Eng. 2015, 90, 684–693. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Li, Z.; Lv, J.; Ni, W.; Li, W. Adoption of enclosure and windbreaks to prevent the degradation of the cooling performance for a natural draft dry cooling tower under crosswind conditions. Energy 2016, 116, 1360–1369. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H.; Lv, J.; Liu, Q.; Yue, G.; Ni, W. Ventilation enhancement for a natural draft dry cooling tower in crosswind via windbox installation. Appl. Therm. Eng. 2018, 137, 93–100. [Google Scholar] [CrossRef]
- Bustamante, J.G.; Rattner, A.S.; Garimella, S. Achieving near-water-cooled power plant performance with air-cooled condensers. Appl. Therm. Eng. 2016, 105, 362–371. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Du, X.; Xi, X.; Yang, L.; Yang, Y. Experimental analysis of parameter influences on the performances of direct air cooled power generating unit. Energy 2013, 56, 117–123. [Google Scholar] [CrossRef]
- Owen, M.T.F.; Kröger, D.G. An investigation of air-cooled steam condenser performance under windy conditions using computational fluid dynamics. J. Eng. Gas Turbines Power 2011, 133, 064502. [Google Scholar] [CrossRef]
- Al-Waked, R.; Behnia, M. The performance of natural draft dry cooling towers under crosswind: CFD study. Int. J. Energy Res. 2004, 28, 147–161. [Google Scholar] [CrossRef]
- Al-Waked, R.; Behnia, M. The effect of windbreak walls on the thermal performance of natural draft dry cooling towers. Heat Transf. Eng. 2005, 26, 50–62. [Google Scholar] [CrossRef]
- Yang, L.J.; Du, X.Z.; Yang, Y.P. Measures against the adverse impact of natural wind on air-cooled condensers in power plant. Sci. China Technol. Sci. 2010, 53, 1320–1327. [Google Scholar] [CrossRef]
- Yang, L.J.; Du, X.Z.; Yang, Y.P. Wind effect on the thermo-flow performances and its decay characteristics for air-cooled condensers in a power plant. Int. J. Therm. Sci. 2012, 53, 175–187. [Google Scholar] [CrossRef]
- Butler, C.; Grimes, R. The effect of wind on the optimal design and performance of a modular air-cooled condenser for a concentrated solar power plant. Energy 2014, 68, 886–895. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, T. Effects of diffuser orifice plate on the performance of air-cooled steam condenser. Appl. Therm. Eng. 2016, 98, 179–188. [Google Scholar] [CrossRef]
- Fabbri, G. Analysis of vapor back flow in single-pass air-cooled condensers. Int. J. Heat Mass Transf. 1997, 40, 3969–3979. [Google Scholar] [CrossRef]
- O’Brien, J.E.; Sohal, M.S. Heat transfer enhancement for finned-tube heat exchangers with winglets. Trans. Asme-C-J. Heat Transf. 2005, 127, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Causes of freezing in direct air cooling system for large-scale air cooling units and freeze-preventing measures thereof. Therm. Power Gener. 2008, 37, 58–60. [Google Scholar]
- Klimeš, L.; Pospíšil, J.; Štětina, J.; Kracik, P. Semi-empirical balance-based computational model of air-cooled condensers with the A-frame layout. Energy 2019, 182, 1013–1027. [Google Scholar] [CrossRef]
- Moore, J.; Grimes, R.; Walsh, E.; O’Donovan, A. Modelling the thermodynamic performance of a concentrated solar power plant with a novel modular air-cooled condenser. Energy 2014, 69, 378–391. [Google Scholar] [CrossRef]
- He, W.F.; Dai, Y.P.; Wang, J.F.; Li, M.Q.; Ma, Q.Z. Performance prediction of an air-cooled steam condenser using UDF method. Appl. Therm. Eng. 2013, 50, 1339–1350. [Google Scholar] [CrossRef]
- Xue, X.; Feng, X.; Wang, J.; Liu, F. Modeling and simulation of an air-cooling condenser under transient conditions. Procedia Eng. 2012, 31, 817–822. [Google Scholar] [CrossRef] [Green Version]
- Medina, Y.C.; Khandy, N.H.; Carlson, K.M.; Fonticiella, O.M.C.; Morales, O.F.C. Mathematical modeling of two-phase media heat transfer coefficient in air cooled condenser systems. Int. J. Heat Technol. 2018, 36, 319–324. [Google Scholar] [CrossRef]
- ANSYS Fluent 16.2: Fluent Theory Guide. In ANSYS Help Viewer; ANSYS Software Company: Canonsburg, PA, USA, 2015.







| f1 | f2 | f3 |
|---|---|---|
| 144.8 | −5.86 | 0.81 |
| r1 | r2 | r3 |
|---|---|---|
| 71.689 | −31.707 | 4.798 |
| h1 | h2 | h3 |
|---|---|---|
| 71.689 | −31.707 | 4.798 |
| Working Conditions | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| The value of uc (m·s−1) | 4 | 12 | 20 | 28 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, W.; Sun, F.; Zhao, Y.; Chen, X.; Li, Y.; Lyu, X. Numerical Study on the Influence Mechanism of Crosswind on Frozen Phenomena in a Direct Air-Cooled System. Energies 2020, 13, 3831. https://doi.org/10.3390/en13153831
Yuan W, Sun F, Zhao Y, Chen X, Li Y, Lyu X. Numerical Study on the Influence Mechanism of Crosswind on Frozen Phenomena in a Direct Air-Cooled System. Energies. 2020; 13(15):3831. https://doi.org/10.3390/en13153831
Chicago/Turabian StyleYuan, Wei, Fengzhong Sun, Yuanbin Zhao, Xuehong Chen, Ying Li, and Xiaolei Lyu. 2020. "Numerical Study on the Influence Mechanism of Crosswind on Frozen Phenomena in a Direct Air-Cooled System" Energies 13, no. 15: 3831. https://doi.org/10.3390/en13153831
APA StyleYuan, W., Sun, F., Zhao, Y., Chen, X., Li, Y., & Lyu, X. (2020). Numerical Study on the Influence Mechanism of Crosswind on Frozen Phenomena in a Direct Air-Cooled System. Energies, 13(15), 3831. https://doi.org/10.3390/en13153831




