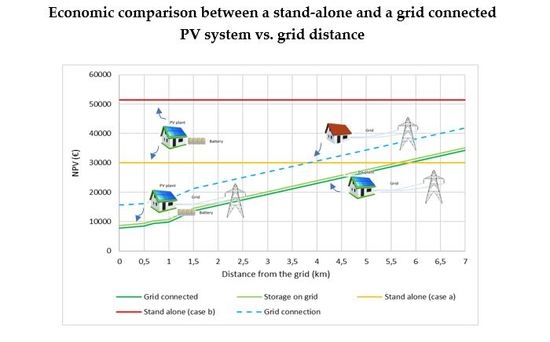
Economic Comparison Between a Stand-Alone and a Grid Connected PV System vs. Grid Distance
Abstract
:1. Introduction
2. PV System Sizing
2.1. Daily Load Assessment
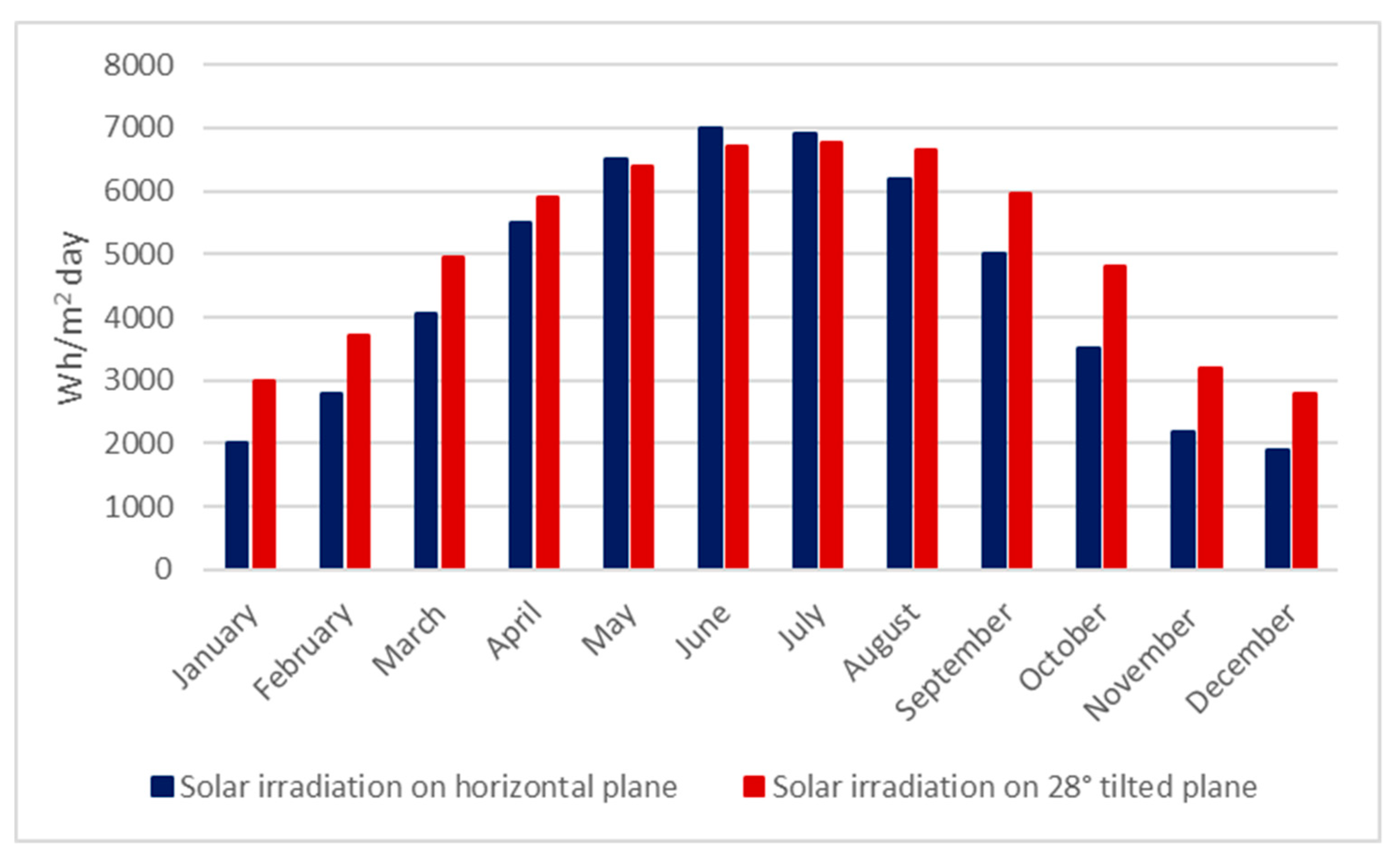
2.2. Solar Irradiance on the Panels
2.3. Nominal Power Assessment–Grid-Connected and Storage-on-Grid PV plant
2.4. Nominal Power Assessment–Stand-Alone PV Plant
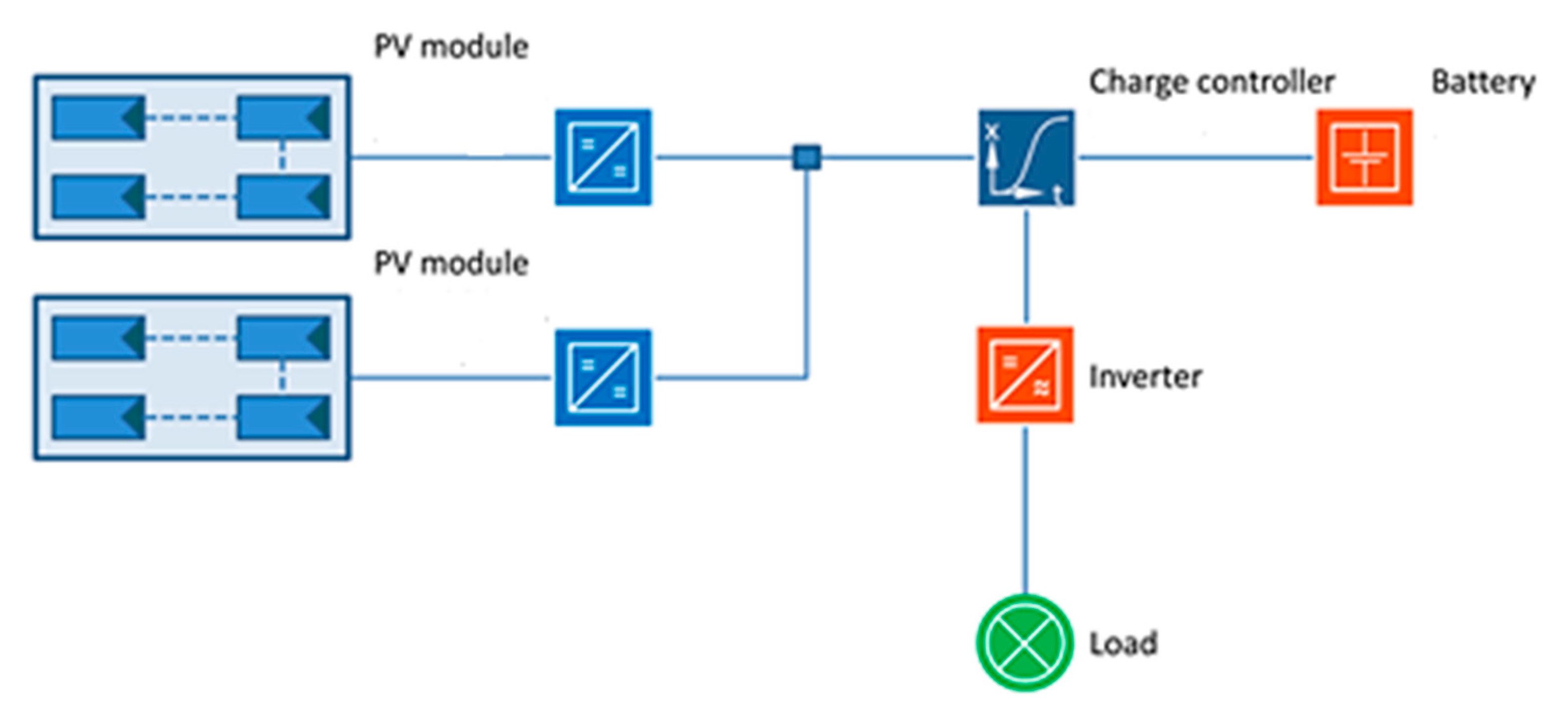
2.5. Battery Sizing
- Dd is the design load,
- V is the rated voltage of the array (V),
- Lc is the minimum allowed depth of the battery discharge (%).
2.6. Charge Controller Dimensioning
2.7. Shadows Pattern
- L module installation height (m),
- δ module tilt (°),
- α sun altitude at 12 a.m. on 21 December (°).
3. Energy Production
- η panel efficiency,
- S panels surface (m2),
- I solar irradiance on the panel (kWh/m2),
- η is a function of the temperature (it decreases as the temperature increases):
- ηr panel efficiency at reference temperature,
- β panel temperature coefficient (%/°C),
- tc cell temperature (°C),
- tr reference temperature (25 °C).
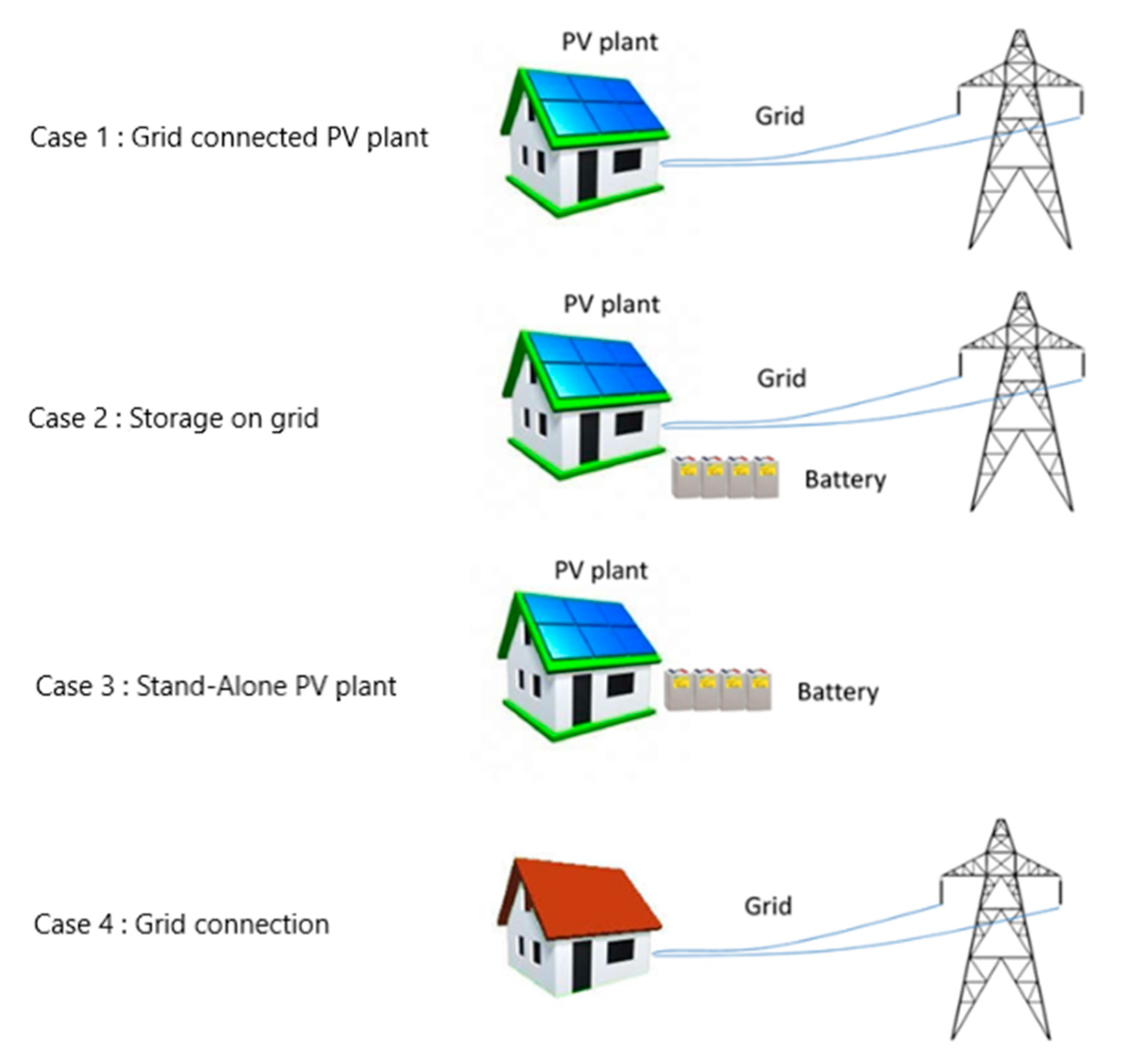
4. Case Study
4.1. PV System Sizing
4.1.1. Case 1: Grid-Connected PV System
4.1.2. Case 2: Storage-on-Grid PV System
4.1.3. Case 3: Stand-Alone System
4.1.4. Case 4: Connection to the Grid
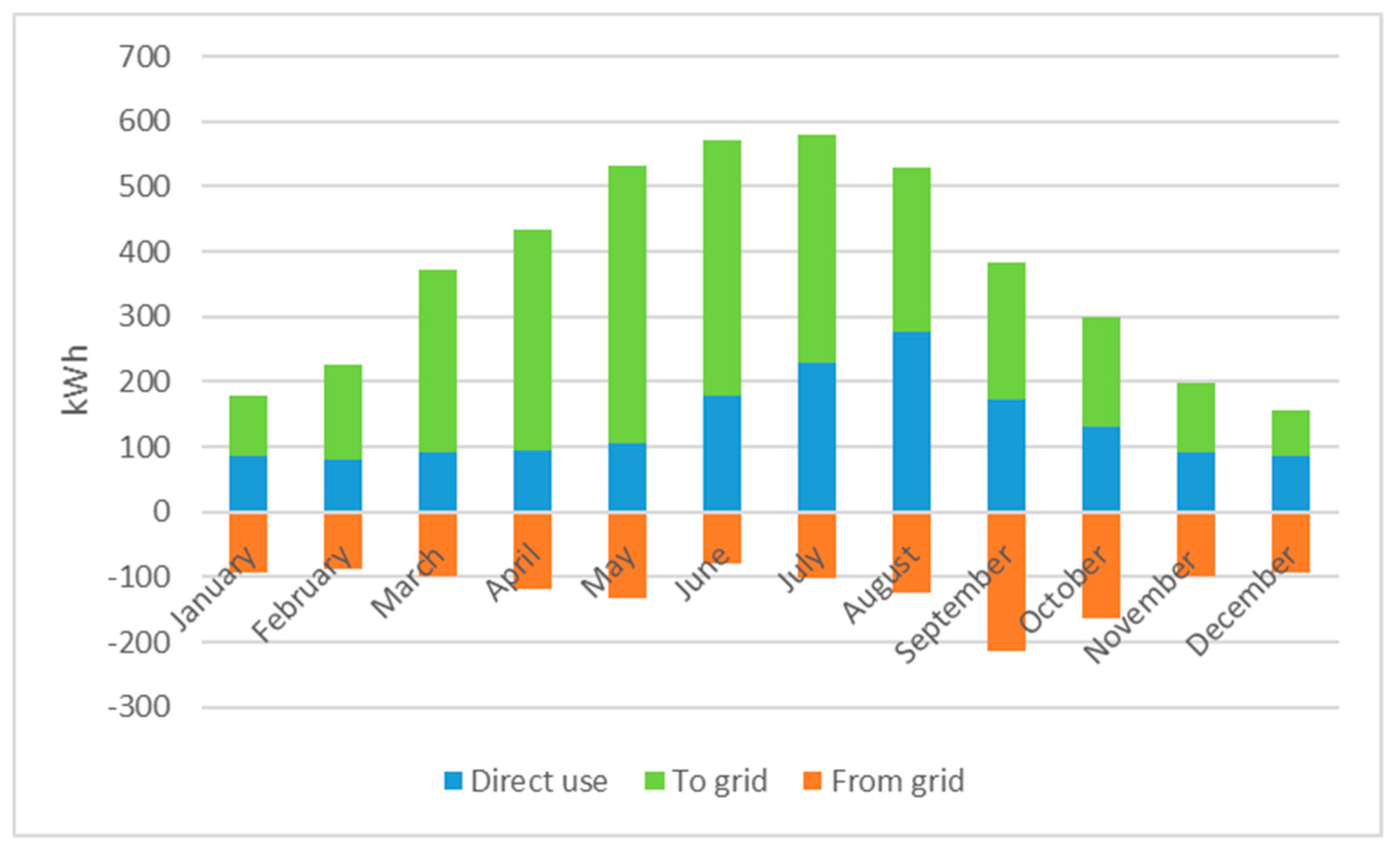
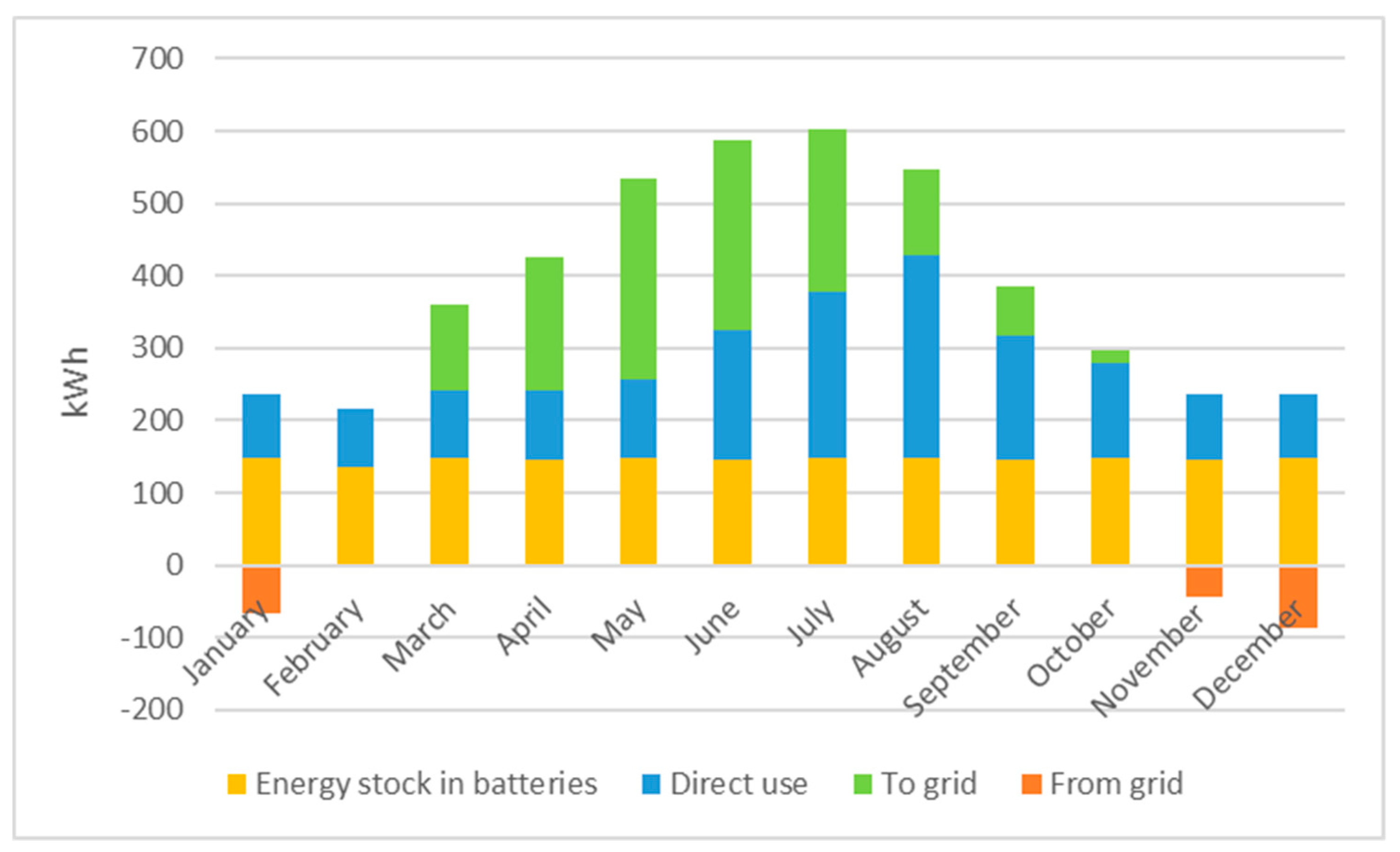
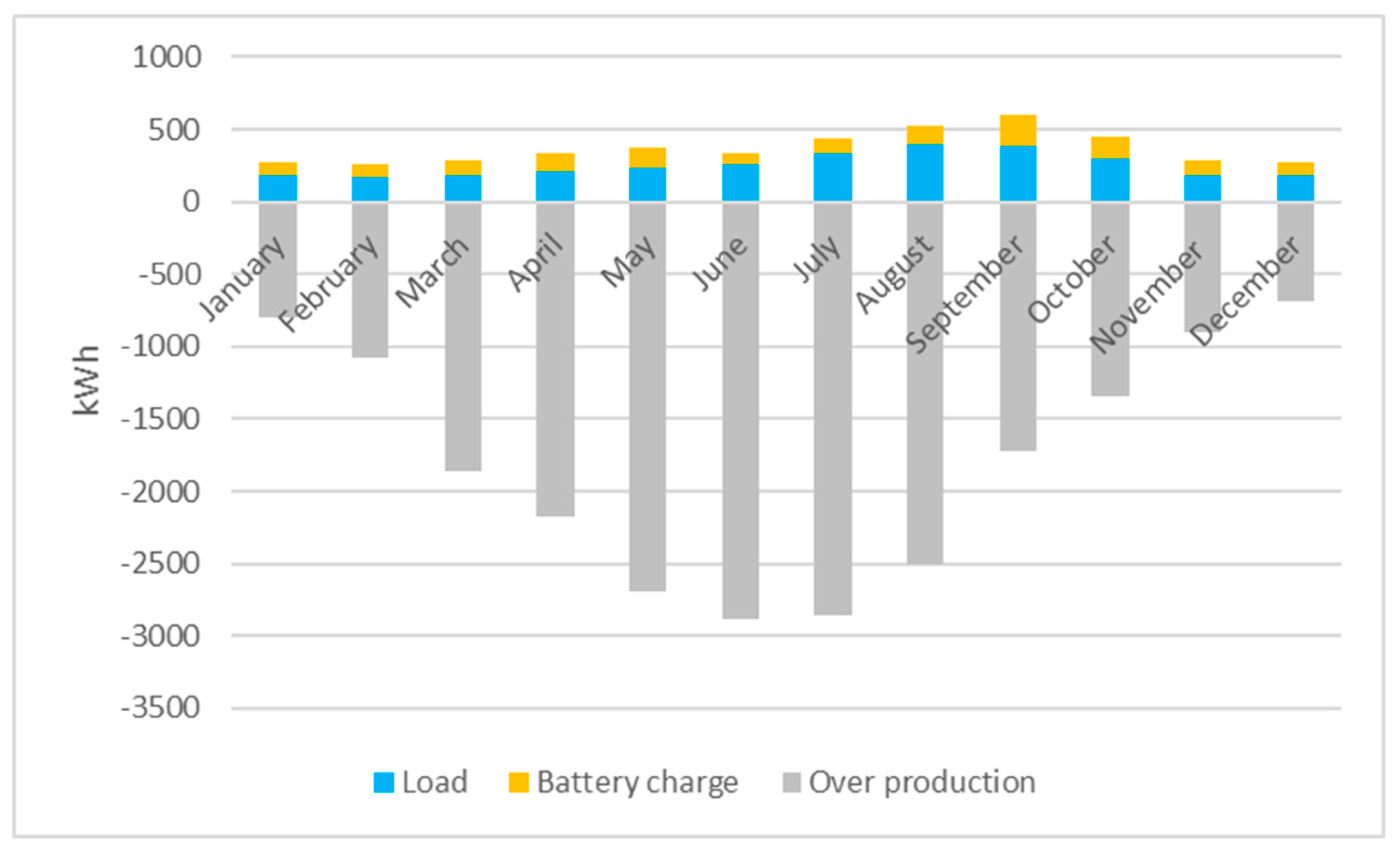
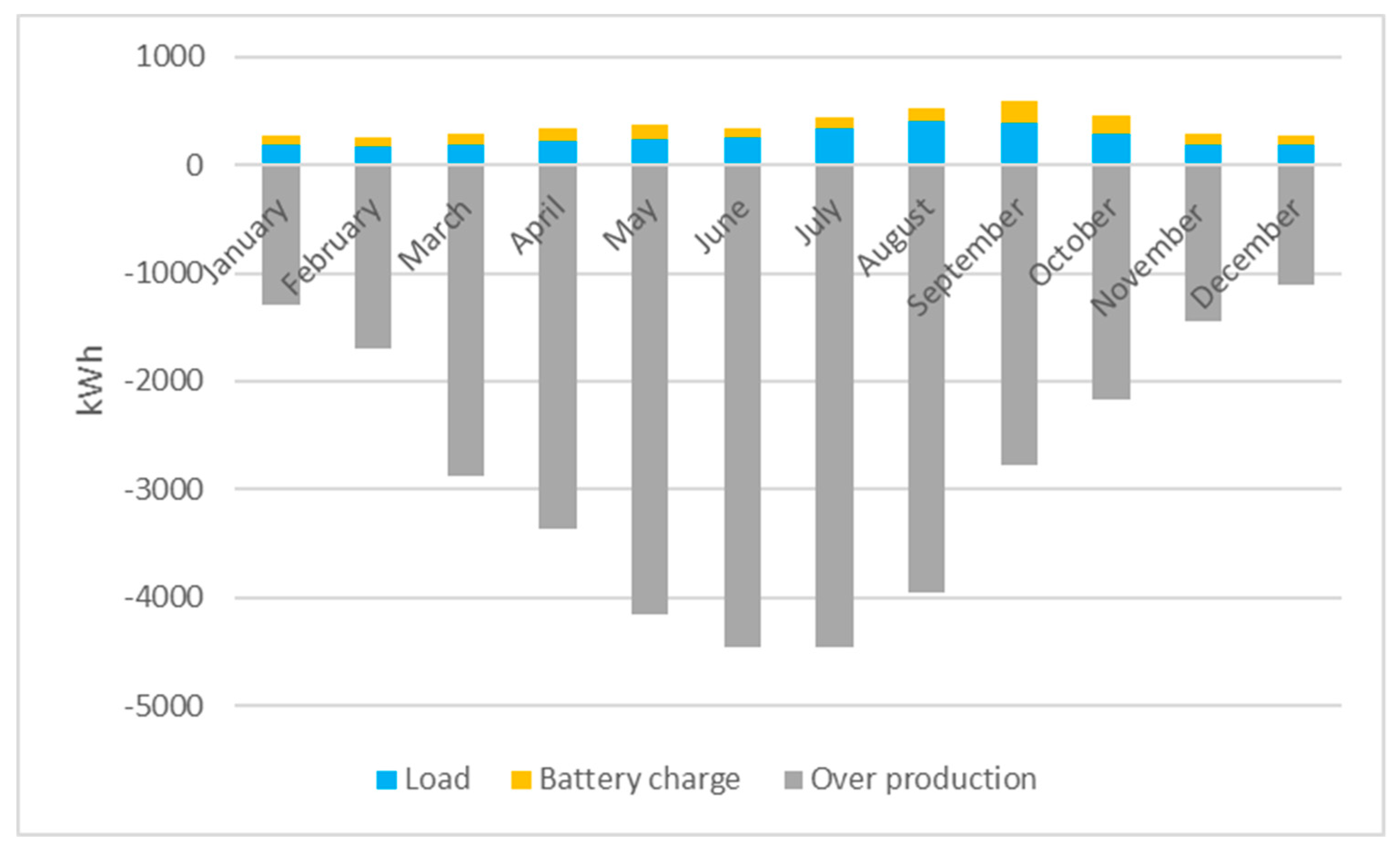
5. Energetic Analysis
- load = direct use + from grid
- produced energy = direct use + to grid
- load = direct use + battery withdrawal + from grid
- produced energy = direct use + battery income + to grid
- produced energy = load + battery charge + over production
6. Economic Analysis
- k year,
- C annual operating costs,
- B annual benefits,
- I investment costs,
- r annual return rate.
7. Environmental Analysis
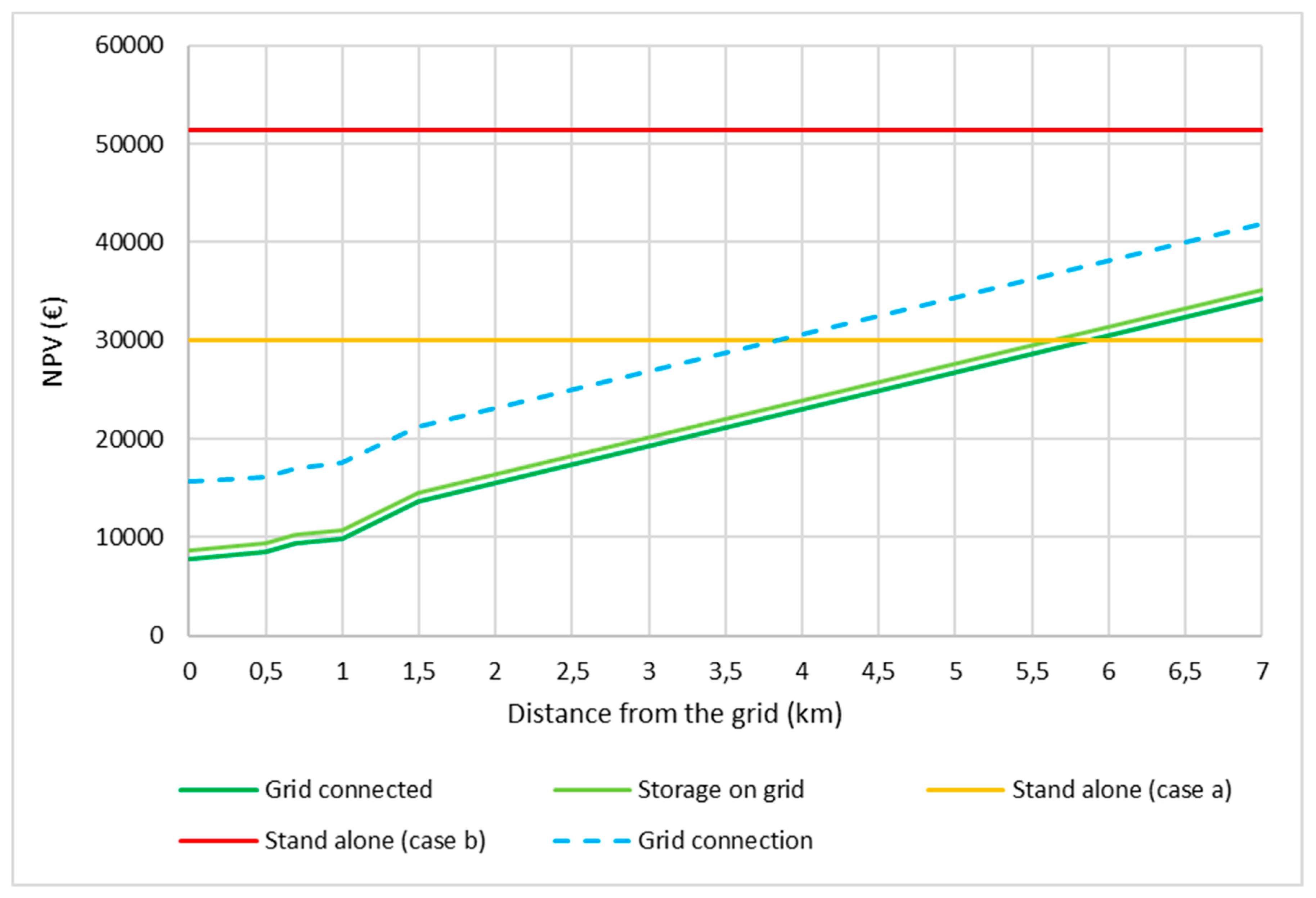
8. Discussion of Main Results and Achievements
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| teq | equivalent period of time with constant irradiance |
| I | irradiance |
| Is | solar radiation power on the panel |
| Pid | nominal power delivered by the PV array in the absence of power losses |
| D | yearly energy demand |
| P | nominal power under real condition |
| η | system overall efficiency |
| Dmax | maximum daily load |
| N | autonomy days of the system |
| t*eq | equivalent hours of the minimum irradiance day |
| D’max | maximum evening load |
| C | battery capacity |
| V | rated voltage of the array |
| Lc | minimum allowed depth of battery discharge |
| Imax | maximum producible current from the PV field |
| n | number of modules |
| Icc,module max | short circuit current |
| d | string distance minimizing reciprocal shadows |
| L | module installation height |
| δ | module tilt |
| α | sun altitude at 12 a.m. on 21 December |
| E | energy production |
| S | panels surface |
| ηr | panel efficiency at reference temperature |
| β | panel temperature coefficient |
| tc | cell temperature |
| tr | reference temperature |
| ta | air temperature |
| NOCT | Nominal Operating Cell Temperature |
| Pm | module power |
| NPV | Net Present Value |
| k | year |
| C | annual operating costs |
| B | annual benefits |
| I | investment costs |
| r | an |
References
- Apergis, N.; Payne, J.E. CO2 emissions, energy usage, and output in Central America. Energy Policy 2009, 35, 4772–4778. [Google Scholar] [CrossRef]
- Birge, D.; Bergera, A.M. Transitioning to low-carbon suburbs in hot-arid regions: A case-study of Emirati villas in Abu Dhabi. Build. Env. 2018, 147, 77–96. [Google Scholar] [CrossRef]
- Arsalis, A.; Alexandrou, A.N.; Georghiou, G.E. Thermoeconomic modelling of a completely autonomous, zero-emission photovoltaic system with hydrogen storage for residential applications. Renew. Energy 2018, 126, 354–369. [Google Scholar] [CrossRef]
- Official Journal of European Union. Directive 2009/28/EC of the European Parliament and of the Council of 23 April 2009, On the promotion of the use of energy from renewable sources and amending and subsequently repealing Directives 2001/77/EC and 2003/30/EC. Off. J. Eur. Union 2009, 11, 39–85. [Google Scholar]
- Official Journal of European Union. Directive 2010/31/EC of the European Parliament and of the Council of 19 May 2010, Energy performance of buildings. Off. J. Eur. Union 2010, 3, 124–146. [Google Scholar]
- Narayanan, A.; Mets, K.; Strobbe, M.; Develder, C. Feasibility of 100% renewable energy-based electricity production for cities with storage and flexibility. Renew. Energy 2019, 134, 698–709. [Google Scholar] [CrossRef]
- Foley, A.; Olabi, A.G. Renewable energy technology developments, trends and policy implications that can underpin the drive for global climate change. Renew. Sustain. Energy Rev. 2017, 68, 1112–1114. [Google Scholar] [CrossRef] [Green Version]
- Gonçalves da Silva, C. Renewable energies: Choosing the best options. Energy 2010, 35, 3179–3193. [Google Scholar] [CrossRef]
- Hvelplund, F. Renewable energy and the need for local energy markets. Energy 2006, 31, 2293–2302. [Google Scholar] [CrossRef] [Green Version]
- Official Journal of European Union. Directive 2006/32/EC of the European Parliament and of the Council of 5 April 2006, Efficiency in the final use of energy and energy systems. Off. J. Eur. Union 2006, 2, 222–243. [Google Scholar]
- Official Journal of European Union. Directive 2012/27/EC of the European Parliament and of the Council of 25 October 2012, Energy efficiency. Off. J. Eur. Union 2012, 2, 202–257. [Google Scholar]
- D’Agostino, D.; Cuniberti, B.; Bertoldi, P. Energy consumption and efficiency technology measures in European non-residential buildings. Energy Build. 2017, 153, 72–86. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Pietrafesa, M. Does window-to-wall ratio have a significant effect on the energy consumption of buildings? A parametric analysis in Italian climate conditions. J. Build. Eng. 2017, 13, 169–183. [Google Scholar] [CrossRef]
- Murano, G.; Corgnati, S.P.; Cotana, F.; D’Oca, S.; Pisello, A.L.; Rossi, F. A Cost-Effective Human-Based Energy-Retrofitting Approach, Cost-Effective Energy Efficient Building Retrofitting. Mater. Technol. Optim. Case Stud. 2017, 219–255. [Google Scholar] [CrossRef]
- Parida, B.; Iniyan, S.; Goic, R. A review of solar photovoltaic technologies. Renew. Sustain. Energy Rev. 2011, 15, 1625–1636. [Google Scholar] [CrossRef]
- Razykov, T.M.; Ferekides, C.S.; Morel, D.; Stefanakos, E.; Ullal, H.S.; Upadhyaya, H.M. Solar photovoltaic electricity: Current status and future prospects. Solar Energy 2011, 85, 1580–1608. [Google Scholar] [CrossRef]
- Cotana, F.; Rossi, F.; Nicolini, A. Evaluation and optimization of an innovative Low-Cost photovoltaic solar concentrator. Int. J. Photoenergy 2011. [Google Scholar] [CrossRef] [Green Version]
- Malara, A.; Marino, C.; Nucara, A.; Pietrafesa, M.; Scopelliti, F.; Streva, G. Energetic and economic analysis of shading effects on PV panels energy production. Int. J. Heat Technol. 2016, 34, 465–472. [Google Scholar] [CrossRef]
- Vad Mathiesen, B.; Duić, N.; Stadler, I.; Rizzo, G.; Guzović, Z. The interaction between intermittent renewable energy and the electricity, heating and transport sectors. Energy 2012, 48, 406–414. [Google Scholar] [CrossRef]
- Kyriakopoulos, G.; Arabatzis, G.; Tsialis, P.; Ioannou, K. Electricity consumption and RES plants in Greece: Typologies of regional units. Renew. Energy 2018, 127, 134–144. [Google Scholar] [CrossRef]
- Lund, H. The implementation of renewable energy systems. Lessons learned from the Danish case. Energy 2010, 35, 4003–4009. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Pietrafesa, M. Proposal of comfort classification indexes suitable for both single environments and whole buildings. Build. Environ. 2012, 57, 58–67. [Google Scholar] [CrossRef]
- Kotopouleas, A.; Nikolopoulou, M. Evaluation of comfort conditions in airport terminal buildings. Build. Environ. 2017, 130, 162–178. [Google Scholar] [CrossRef]
- Luoa, M.; Cao, B.; Zouy, X.; Li, M.; Zhang, J.; Ouyang, Q.; Zhu, Y. Can personal control influence human thermal comfort? A field study in residential buildings in China in winter. Energy Build. 2013, 72, 411–418. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Pietrafesa, M. Thermal comfort in indoor environment: Effect of the solar radiation on the radiant temperature asymmetry. Solar Energy 2017, 144, 295–309. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Peri, G.; Pietrafesa, M.; Pudano, A.; Rizzo, G. A MAS-based subjective model for indoor adaptive thermal comfort. Sci. Technol. Built Environ. 2015, 21, 114–125. [Google Scholar] [CrossRef]
- Guazzi, G.; Bellazzi, A.; Meroni, I.; Magrini, A. Refurbishment design through cost-optimal methodology: The case study of a social housing in the northern Italy. Int. J. Heat Technol. 2017, 35, S336–S344. [Google Scholar] [CrossRef]
- Piccolo, A.; Marino, C.; Nucara, A.; Pietrafesa, M. Energy performance of an electrochromic switchable glazing: Experimental and computational assessments. Energy Build. 2018, 165, 390–398. [Google Scholar] [CrossRef]
- Marszal, A.J.; Heiselberg, P.; Bourrelle, J.S.; Musall, E.; Voss, K.; Sartori, I.; Napolitano, A. Zero Energy Building—A review of definitions and calculation methodologies. Energy Build. 2011, 43, 971–979. [Google Scholar] [CrossRef]
- Sartori, I.; Napolitano, A.; Voss, K. Net zero energy buildings: A consistent definition framework. Energy Build. 2012, 48, 220–232. [Google Scholar] [CrossRef] [Green Version]
- Kapsalaki, M.; Leal, V. Recent progress on net zero energy buildings. Adv. Build. Energy Res. 2011, 5, 129–162. [Google Scholar] [CrossRef]
- Attia, S.; Eleftheriou, P.; Xeni, F.; Morlot, R.; Ménézo, C.; Kostopoulos, V.; Betsi, M.; Kalaitzoglou, I.; Pagliano, L.; Cellura, M.; et al. Overview and future challenges of nearly Zero Energy Buildings (nZEB) design in Southern Europe. Energy Build. 2017, 155, 439–458. [Google Scholar] [CrossRef]
- Kolokotsa, D.; Rovas, D.; Kosmatopoulos, E.; Kalaitzakis, K. A roadmap towards intelligent net zero-and positive-energy buildings. Solar Energy 2011, 85, 3067–3084. [Google Scholar] [CrossRef]
- AbuGrain, M.Y.; Alibaba, H.Z. Optimizing existing multistory building designs towards net-zero energy. Sustainability 2017, 9, 399. [Google Scholar] [CrossRef] [Green Version]
- Lund, H.; Marszal, A.; Heiselberg, P. Zero energy buildings and mismatch compensation factors. Energy Build. 2011, 43, 1646–1654. [Google Scholar] [CrossRef]
- Ballarini, I.; Dirutigliano, D.; Primo, E.; Corrado, V. The significant imbalance of nZEB energy need for heating and cooling in Italian climatic zones. Energy Procedia 2017, 126, 258–265. [Google Scholar] [CrossRef] [Green Version]
- Romano, R.; Gallo, P. The SELFIE Project Smart and efficient envelope’ system for nearly zero energy buildings in the Mediterranean Area. GSTF J. Eng. Technol. 2018, 4, 562–569. [Google Scholar] [CrossRef] [Green Version]
- Trombetta, C.; Milardi, M. Building future Lab: A great infrastructure for testing. Energy Procedia 2015, 78, 657–662. [Google Scholar] [CrossRef] [Green Version]
- Ministero dello Sviluppo Economico e Ministero dell’Ambiente, della Tutela del territorio e del Mare – Strategia Energetica Nazionale (SEN). 2017. Available online: https://www.mise.gov.it/images/stories/documenti/Testo-integrale-SEN-2017.pdf (accessed on 10 July 2020).
- Ministero dello Sviluppo Economico, Ministero dell’Ambiente, della Tutela del territorio e del Mare e Ministero delle Infrastrutture e dei Trasporti–Piano Nazionale Integrato per l’Energia e per il Clima. 2019. Available online: https://www.mise.gov.it/images/stories/documenti/PNIEC_finale_17012020.pdf (accessed on 10 July 2020).
- Beaudin, M.; Zareipour, H.; Schellenberglabe, A.; Rosehart, W. Energy storage for mitigating the variability of renewable electricity sources: An updated review. Energy Sustain. Dev. 2010, 14, 302–314. [Google Scholar] [CrossRef]
- Pearre, N.S.; Swan, L.G. Renewable electricity and energy storage to permit retirement of coal-fired generators in Nova Scotia. Sustain. Energy Technol. Assess. 2013, 1, 44–53. [Google Scholar] [CrossRef]
- Lorestani, A.; Ardehali, M.M. Optimization of autonomous combined heat and power system including PVT, WT, storages, and electric heat utilizing novel evolutionary particle swarm optimization algorithm. Renew. Energy 2018, 119, 490–503. [Google Scholar] [CrossRef]
- Cammarata, G.; Monaco, L.; Cammarata, L.; Petrone, G. A numerical procedure for PCM thermal storage design in solar plants. In Proceedings of the 7th AIGE Conference, Cosenza, Italy, 10–11 June 2013. [Google Scholar]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Lopez-Sabiron, A.M.; Royo, P.; Ferreira, V.J.; Aranda-Uson, A.; Ferreira, G. Carbon footprint of a thermal energy storage system using phase change materials for industrial energy recovery to reduce the fossil fuel consumption. Appl. Energy 2014, 135, 616–624. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Pietrafesa, M.; Pudano, A. An energy self-sufficient public building using integrated renewable sources and hydrogen storage. Energy 2013, 57, 95–105. [Google Scholar] [CrossRef]
- Avril, S.; Arnaud, G.; Florentin, A.; Vinard, M. Multi-objective optimization of batteries and hydrogen storage technologies for remote photovoltaic systems. Energy 2010, 35, 5300–5308. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Pietrafesa, M. Electrolytic hydrogen production from renewable source, storage and reconversion in fuel cells: The system of the Mediterranea University of Reggio Calabria. Energy Procedia 2015, 78, 818–823. [Google Scholar] [CrossRef] [Green Version]
- Krajacic, G.; Loncar, D.; Duic, N.; Zeljko, M.; Arantegui, R.L.; Loisel, R.; Raguzin, I. Analysis of financial mechanisms in support to new pumped hydropower storage projects in Croatia. Appl. Energy 2013, 101, 161–171. [Google Scholar] [CrossRef] [Green Version]
- Foley, A.; Lobera, D. Impacts of compressed air energy storage plant on an electricity market with a large renewable energy portfolio. Energy 2013, 57, 85–94. [Google Scholar] [CrossRef]
- Al-akayshee, A.S.; Kuznetsov, O.N.; Sultan, H.M. Viability Analysis of Large Photovoltaic Power Plants as a Solution of Power Shortage in Iraq. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 27–30 January 2020. [Google Scholar] [CrossRef]
- Yang, Y.; Lian, C.; Ma, C.; Zhang, Y. Research on Energy Storage Optimization for Large-Scale PV Power Stations under Given Long-Distance Delivery Mode. Energies 2020, 13, 27. [Google Scholar] [CrossRef] [Green Version]
- Bernal, E.A.; Lopez, M.B.; Ardila, A. Solar Microgrids to Enhance Electricity Access in Remote Rural Areas. 2019. Available online: https://www.researchgate.net/publication/335430858_Solar_Microgrids_to_Enhance_Electricity_Access_in_Remote_Rural_Areas (accessed on 10 July 2020).
- Nwaigwe, K.N.; Mutabilwa, P.; Dintwa, E. An overview of solar power (PV systems) integration into electricity grids. Mater. Sci. Energy Technol. 2019, 629–633. [Google Scholar] [CrossRef]
- Kaviani, A.K.; Baghaee, H.R. Gholam Hossein Riahy, Optimal Sizing of a Stand-alone Wind/Photovoltaic Generation Unit using Particle Swarm Optimization. Soc. Modeling Simul. Int. 2009, 85. [Google Scholar] [CrossRef]
- Barbaro, G.; Foti, G.; Labarbera, F.; Pietrafesa, M. Energetic and economic comparison between systems for the production of electricity from renewable energy sources (hydroelectric, wind generator, photovoltaic). Accad. Peloritana Pericolanti Cl. Phys. Math. Nat. Sci. 2019, 97. [Google Scholar] [CrossRef]
- Bruno, R.; Bevilacqua, P.; Longo, L.; Arcuri, N. Small Size Single-axis PV Trackers: Control Strategies and System Layout for Energy Optimization. Energy Procedia 2015, 82, 737–743. [Google Scholar] [CrossRef] [Green Version]
- Bevilacqua, P.; Bruno, R.; Arcuri, N. Comparing the performances of different cooling strategies to increase photovoltaic electric performance in different meteorological conditions. Energy 2020, 195. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Taleb, H.A. Reliability/cost-based multi-objective Pareto optimal design of stand-alone wind/PV/FC generation microgrid system. Energy 2016, 115, 1022–1041. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Multi-objective optimal power management and sizing of a reliable wind/PV microgrid with hydrogen energy storage using MOPSO. J. Intell. Fuzzy Syst. 2017, 32, 1753–1773. [Google Scholar] [CrossRef]
- Nikolovski, S.; Baghaee, H.R.; Mlakić, D. ANFIS-Based Peak Power Shaving/Curtailment in Microgrids Including PV Units and BESSs. Energies 2018, 11, 2953. [Google Scholar] [CrossRef] [Green Version]
- Gattuso, D.; Greco, A.; Marino, C.; Nucara, A.; Pietrafesa, M.; Scopelliti, F. Sustainable Mobility: Environmental and Economic Analysis of a Cable Railway, Powered by Photovoltaic System. Int. J. Heat Technol. 2016, 34, 7–14. [Google Scholar] [CrossRef]
- Sinigaglia, T.; Lewiski, F.; Martins, M.E.S.; Siluk, J.C.M. Production, storage, fuel stations of hydrogen and its utilization in automotive applications-a review. Int. J. Hydrog. Energy 2017, 42, 24597–24611. [Google Scholar] [CrossRef]
- Marino, C.; Nucara, A.; Panzera, M.F.; Pietrafesa, M. Towards the nearly zero and the plus energy building: Primary energy balances and economic evaluations. Therm. Sci. Eng. Prog. 2019, 13. [Google Scholar] [CrossRef]
- UNI 10349. Riscaldamento e Raffrescamento Degli Edifici: Dati Climatici, Ente Italiano per L’unificazione; UNI 10349: Milano, Italy, 1994. [Google Scholar]
- Vart, T.M.; Castaner, L. Practical Handbook of Photovoltaic: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kreider, J.F.; Kreith, F. Solar Energy Handbook; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Allegrezza, M.; Giuliani, G.; Mileto, G.; Pietrafesa, M.; Summonte, C. Impact of increased efficiency on cost of WP. In Proceedings of the 27th EU PVSEC European Photovoltaic Solar Energy Conference, Messe Frankfurt, Germany, 24–28 September 2012. [Google Scholar] [CrossRef]
- Deliberazione dell’Autorità Per L’energia Elettrica E Il Gas ARG/elt 74/08, Testo Integrato per lo Scambio sul Posto. Available online: https://www.arera.it/allegati/docs/08/074-08argall2.pdf (accessed on 26 July 2012).
- Allegato, C.; ARERA, Authority for the Regulation of Energy, Grid and Enrivonment. Testo Integrato Delle Condizioni Economiche per l’erogazione del Servizio di Connessione (TIC) (2020–2023). Available online: https://www.arera.it/allegati/docs/19/568-19allc.pdf (accessed on 15 January 2020).
- Italian Regulatory Authority for Electricity and Gas, Electric Energy Prices. 2013. Available online: http://www.autorita.energia.it/it/dati/eep35.htm (accessed on 15 January 2020).
- Italian National Institute of Statistics, Consumer prices. 2013. Available online: http://www.istat.it/it/archivio/14413. (accessed on 15 January 2020).
- Bank of Italy, Interest Rates. 2013. Available online: http://www.bancaditalia.it/statistiche/SDDS/stat_fin/tassi_int/ (accessed on 15 January 2020).
- Ministero dello Sviluppo Economico—Decreto ministeriale 20 dicembre 2019—Tasso da Applicare per le Operazioni di Attualizzazione e Rivalutazione ai Fini della Concessione ed Erogazione delle Agevolazioni in Favore delle imprese. Available online: https://www.mise.gov.it/index.php/it/incentivi/impresa/strumenti-e-programmi/tasso-di-attualizzazione-e-rivalutazione. (accessed on 15 January 2020).
- Istituto Superiore per la Protezione e la Ricerca Ambientale (ISPRA). Fattori di Emissione Atmosferica di Gas a Effetto Serra e Altri Gas Nel Settore Elettrico; Rapporto; ISPRA: Roma, Italy, 2018. [Google Scholar]



| Design Configuration | Investment Costs | Annual Operating Costs |
|---|---|---|
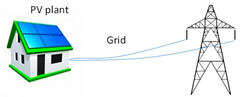 | Photovoltaic panels Inverters and accessories Connection to the grid | Energy purchases Maintenance facility |
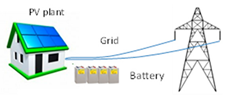 | Photovoltaic panels Inverters and accessories Batteries Charge Controller Connection to the grid | Energy purchases Maintenance facility |
 | Photovoltaic panels Inverters and accessories Batteries Charge Controllers | Maintenance facility |
 | Connection to the grid | Energy purchases |
| Design Configuration | Investment Benefit | Energy Benefit |
|---|---|---|
 | Income tax deduction | On-site energy exchange mechanism |
 | Income tax deduction | On-site energy exchange mechanism |
 | Income tax deduction |
| Configuration | Investment Item | Unit | Quantity | Unit Cost (€/unit) | Total Cost (€) |
|---|---|---|---|---|---|
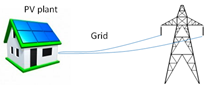 | Photovoltaic panels | each | 8 | 195 | 1560 |
| Inverters | each | 1 | 1000 | 1000 | |
| Cables, installation, support structures, etc. | 2000 | ||||
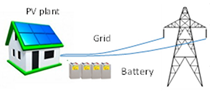 | Photovoltaic panels | each | 8 | 195 | 1560 |
| Inverters | each | 1 | 1000 | 1000 | |
| Cables, installation, support structures, etc. | 2000 | ||||
| Battery and charge controller | each | 1 | 3500 | 3500 | |
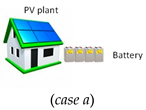 | Photovoltaic panels | each | 44 | 195 | 8580 |
| Inverters | each | 4 | 1000 | 4000 | |
| Batteries | each | 2 | 5000 | 10,000 | |
| Charge controllers | each | 4 | 200 | 800 | |
| Cables, installation support structures, etc. | 3000 | ||||
 | Photovoltaic panels | each | 66 | 195 | 12,870 |
| Inverters | each | 6 | 1000 | 6000 | |
| Batteries | each | 4 | 5000 | 20,000 | |
| Charge controllers | each | 6 | 300 | 1800 | |
| Cables, installation support structures, etc. | 4000 | ||||
 | Connection to grid: | ||||
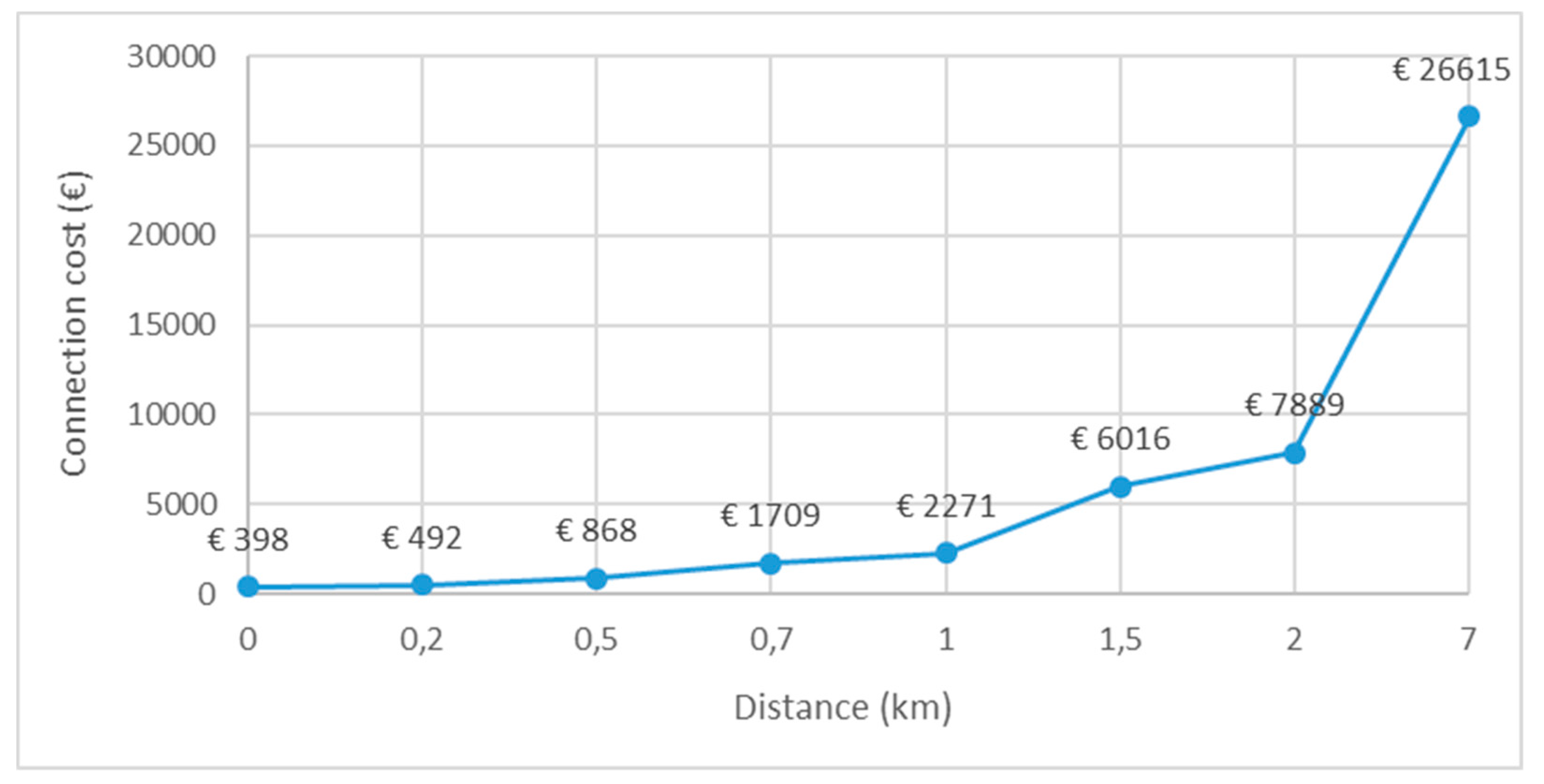
| a) power rate b) distance rate | km | Figure 11 | |||
| Configuration | Annual Cost Item | Unit | Quantity | Unit Cost (€/unit) | Total Cost (€) |
|---|---|---|---|---|---|
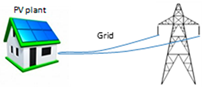 | Maintenance Energy purchase | kWh | 1 1406 | 100 0.22 | 100 309.3 |
 | Maintenance Energy purchase | kWh | 1 197 | 100 0.22 | 100 43.4 |
 | Maintenance | € | 1 | 100 | 100 |
 | Energy purchase | kWh | 3035 | 0.22 | 667.7 |
| Design Configuration | Benefit Item | Unit Benefit (€/year) | Total Benefit (€/year) |
|---|---|---|---|
 | Income tax deduction On-site energy exchange mechanism | 228 (years 1–10) 226.8 | 454.8 |
 | Income tax deduction On-site energy exchange mechanism | 403 (years 1–10) 50.8 | 453.8 |
 | Income tax deduction (case a) Income tax deduction (case b) | 1319 2233.5 | 1319 2233.5 |
| Pollutant | Emission Factor (g/kWh) |
|---|---|
| CO2 | 303.5 |
| NOx | 0.2376 |
| SO2 | 0.0716 |
| PM10 | 0.0057 |
| Design Configuration | PV Energy (kWh/year) | Avoided Emission (kg/year) | |||
|---|---|---|---|---|---|
| CO2 | NOx | SO2 | PM | ||
 | 4468 (produced energy) | 1356 | 1.1 | 0.3 | 0.03 |
 | 4468 (produced energy) | 1356 | 1.1 | 0.3 | 0.03 |
 | 3035 (load) | 921 | 0.7 | 0.2 | 0.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marino, C.; Nucara, A.; Panzera, M.F.; Pietrafesa, M.; Pudano, A. Economic Comparison Between a Stand-Alone and a Grid Connected PV System vs. Grid Distance. Energies 2020, 13, 3846. https://doi.org/10.3390/en13153846
Marino C, Nucara A, Panzera MF, Pietrafesa M, Pudano A. Economic Comparison Between a Stand-Alone and a Grid Connected PV System vs. Grid Distance. Energies. 2020; 13(15):3846. https://doi.org/10.3390/en13153846
Chicago/Turabian StyleMarino, Concettina, Antonino Nucara, Maria Francesca Panzera, Matilde Pietrafesa, and Alfredo Pudano. 2020. "Economic Comparison Between a Stand-Alone and a Grid Connected PV System vs. Grid Distance" Energies 13, no. 15: 3846. https://doi.org/10.3390/en13153846
APA StyleMarino, C., Nucara, A., Panzera, M. F., Pietrafesa, M., & Pudano, A. (2020). Economic Comparison Between a Stand-Alone and a Grid Connected PV System vs. Grid Distance. Energies, 13(15), 3846. https://doi.org/10.3390/en13153846