Pull-Out Capacity and Failure Mechanisms of Strip Anchors in Clay
Abstract
:1. Introduction
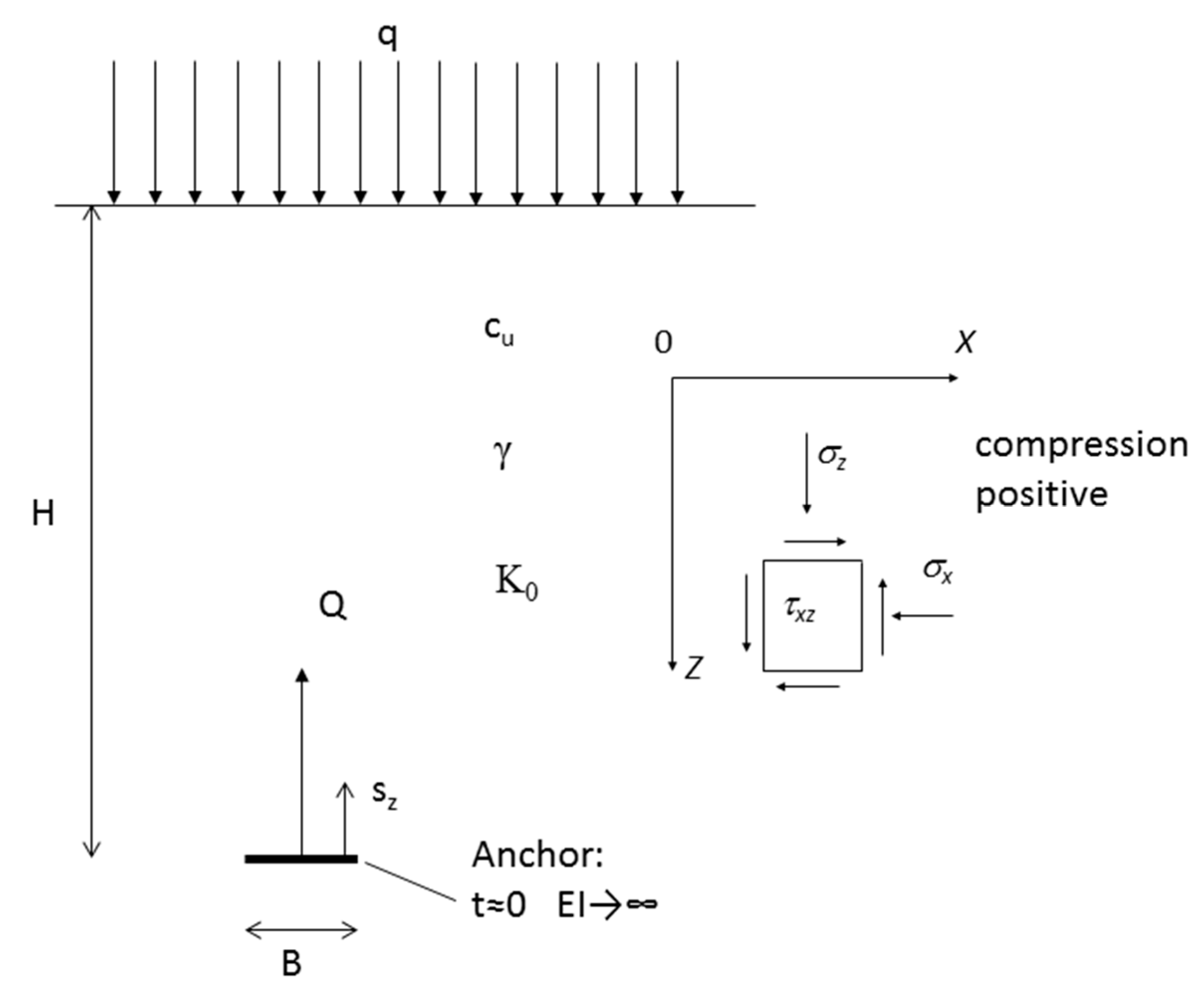
2. Dimensional Analysis
- (a)
- Geometrical variables: Anchor width, B; Anchor embedment, H; anchor thickness, t, assumed as null here (t ≈ 0).
- (b)
- Initial stress state: Unit weight of the soil (γ), coefficient of lateral earth pressure at rest K0.
- (c)
- Surface surcharge at the seabed: q.
- (d)
- Soil properties: Stiffness and strength (e.g., undrained shear strength, cu).
- (e)
- Anchor properties: Assumed as infinitely stiff and as infinitely rough or smooth.
- (f)
- Results, e.g., pull-out capacity (Q) and anchor vertical displacement, sz.
3. Review of Analytical Exact Solutions for Limit Cases
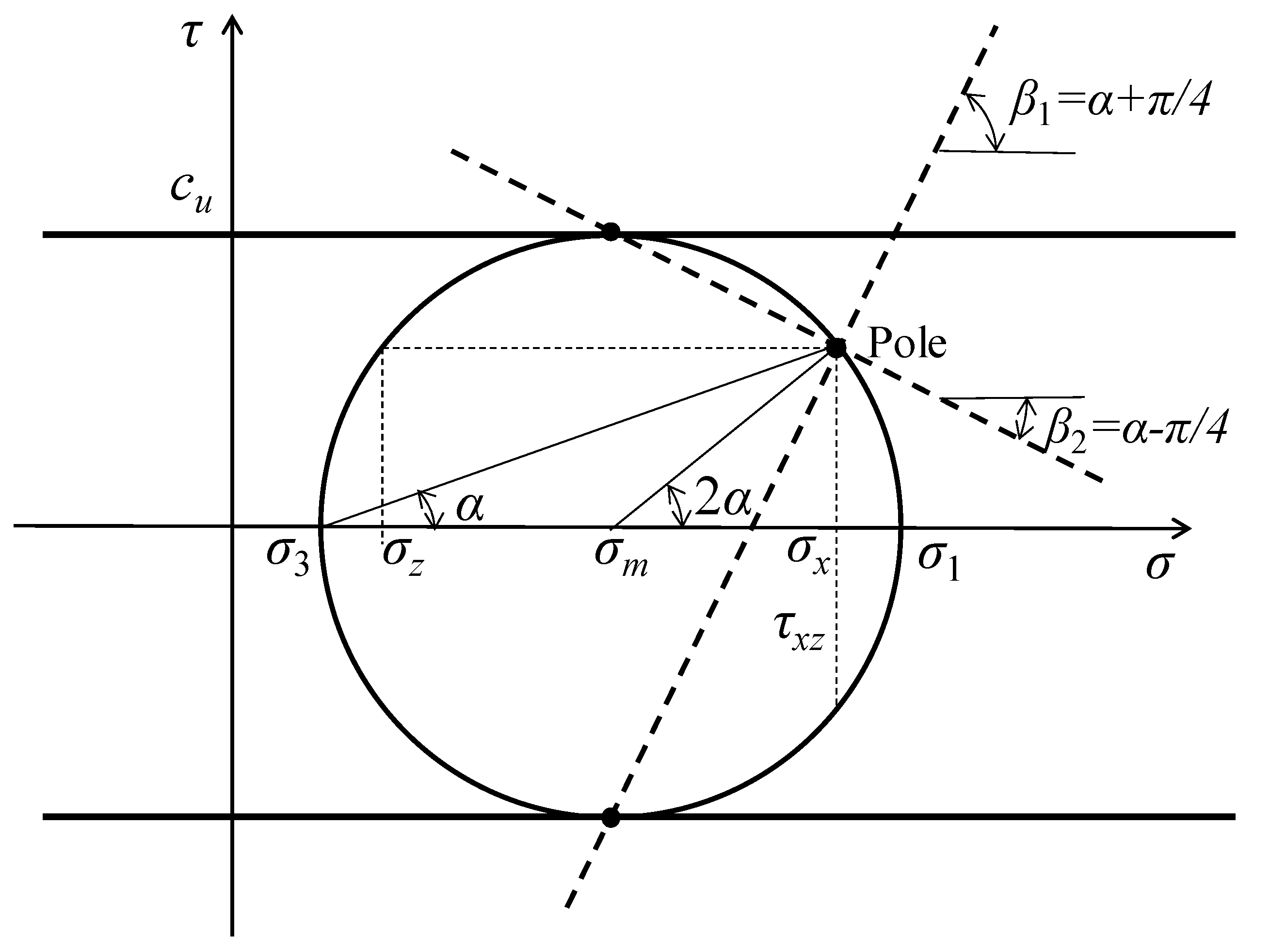
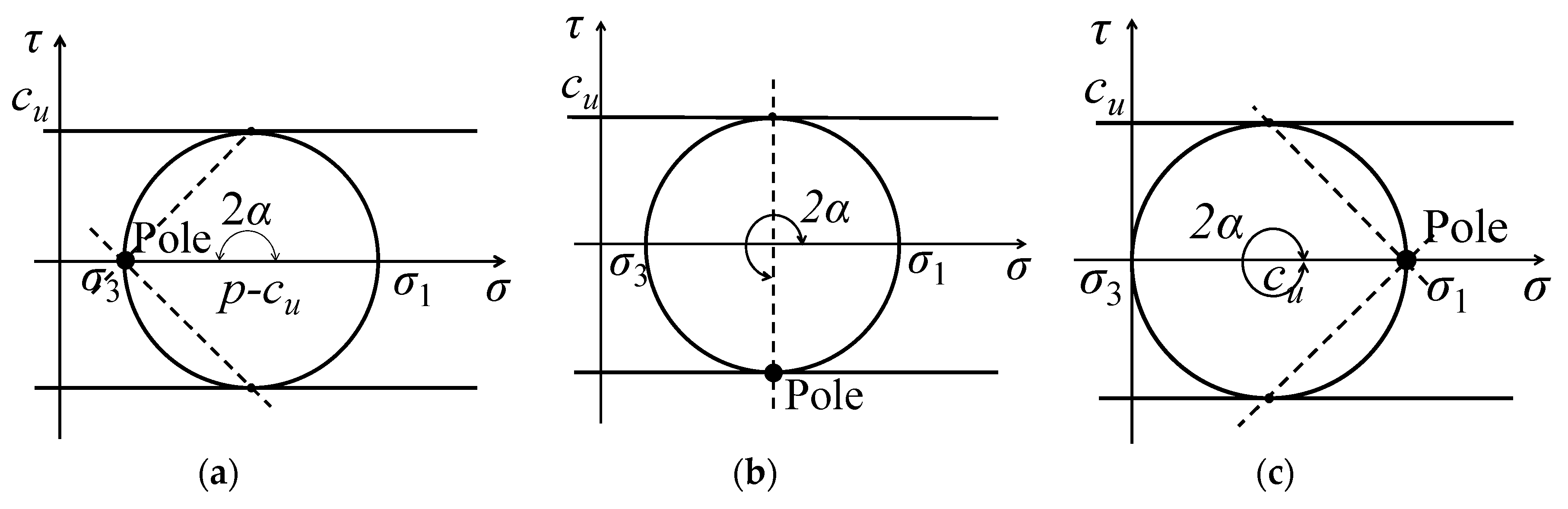
3.1. Methods of Characteristics in a Rigid-Plastic Tresca Material
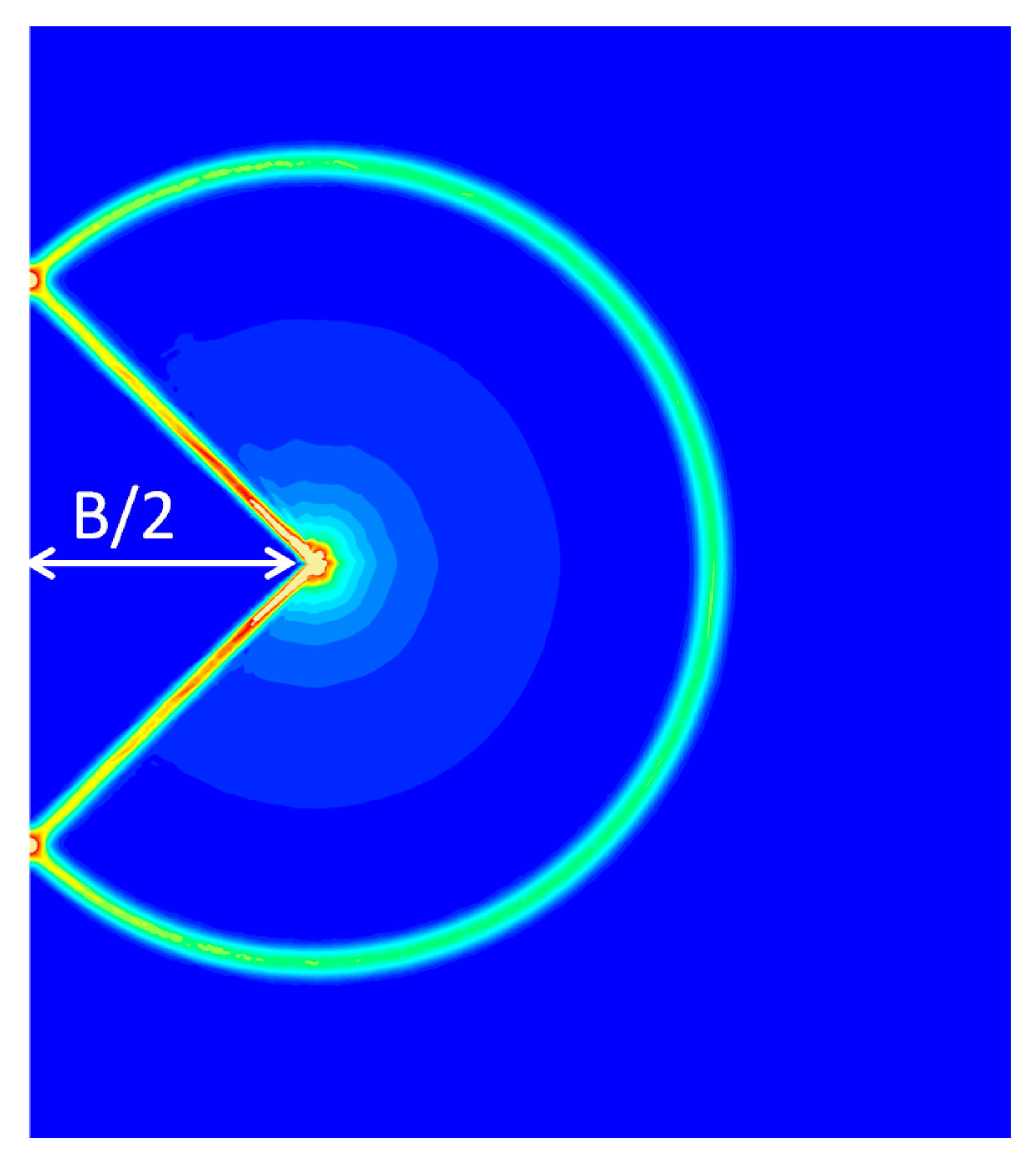
3.2. Deep Failure
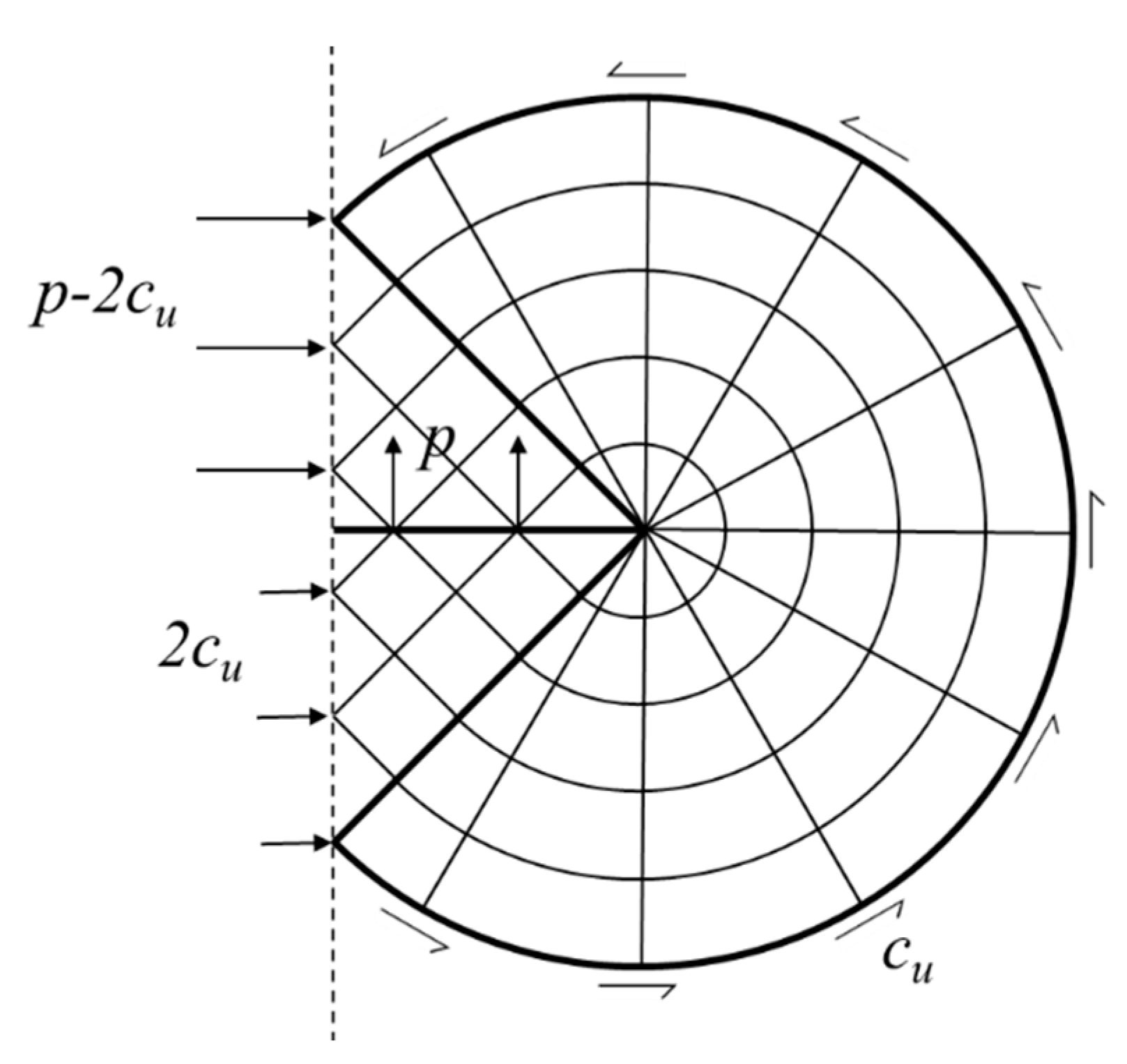
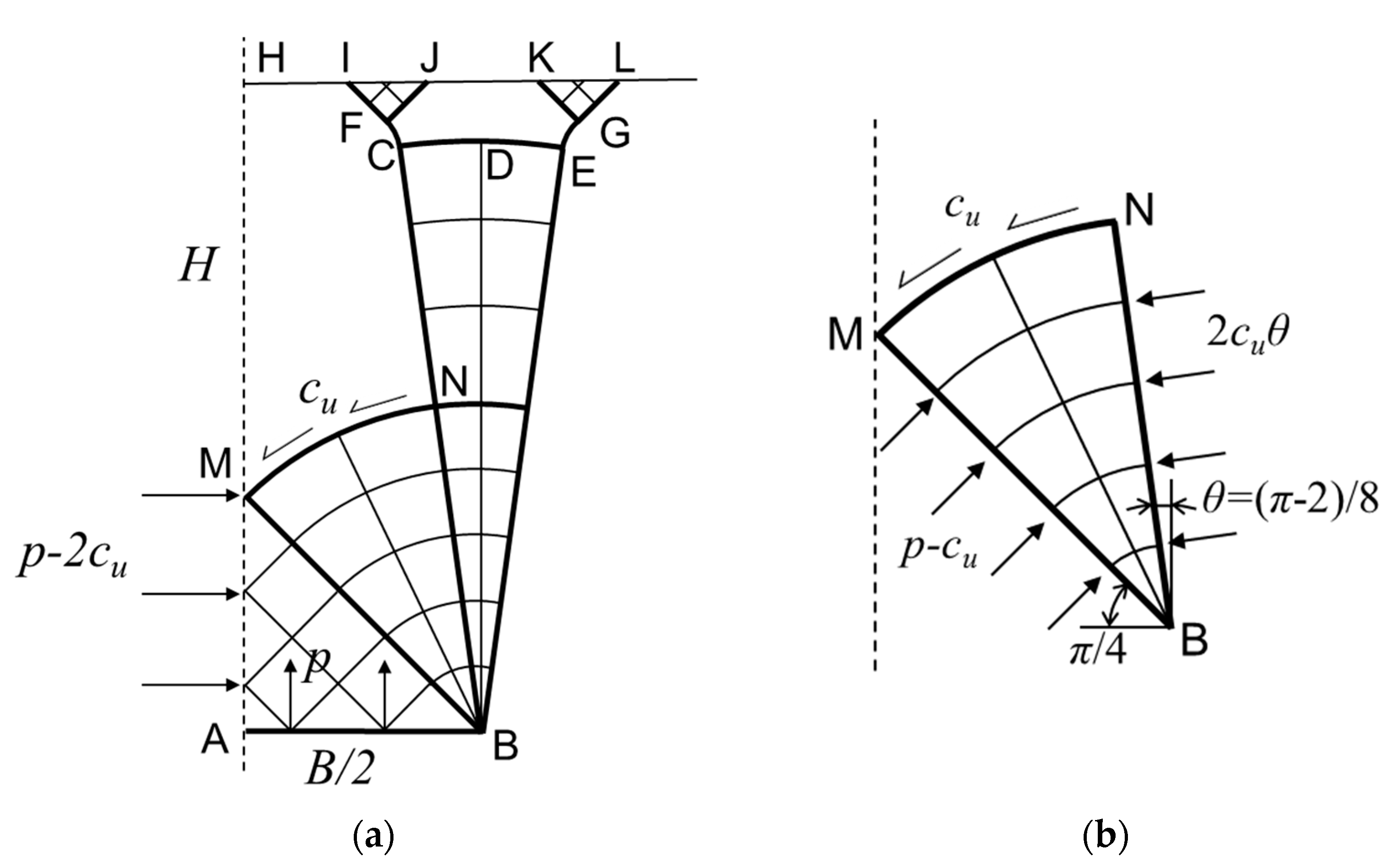
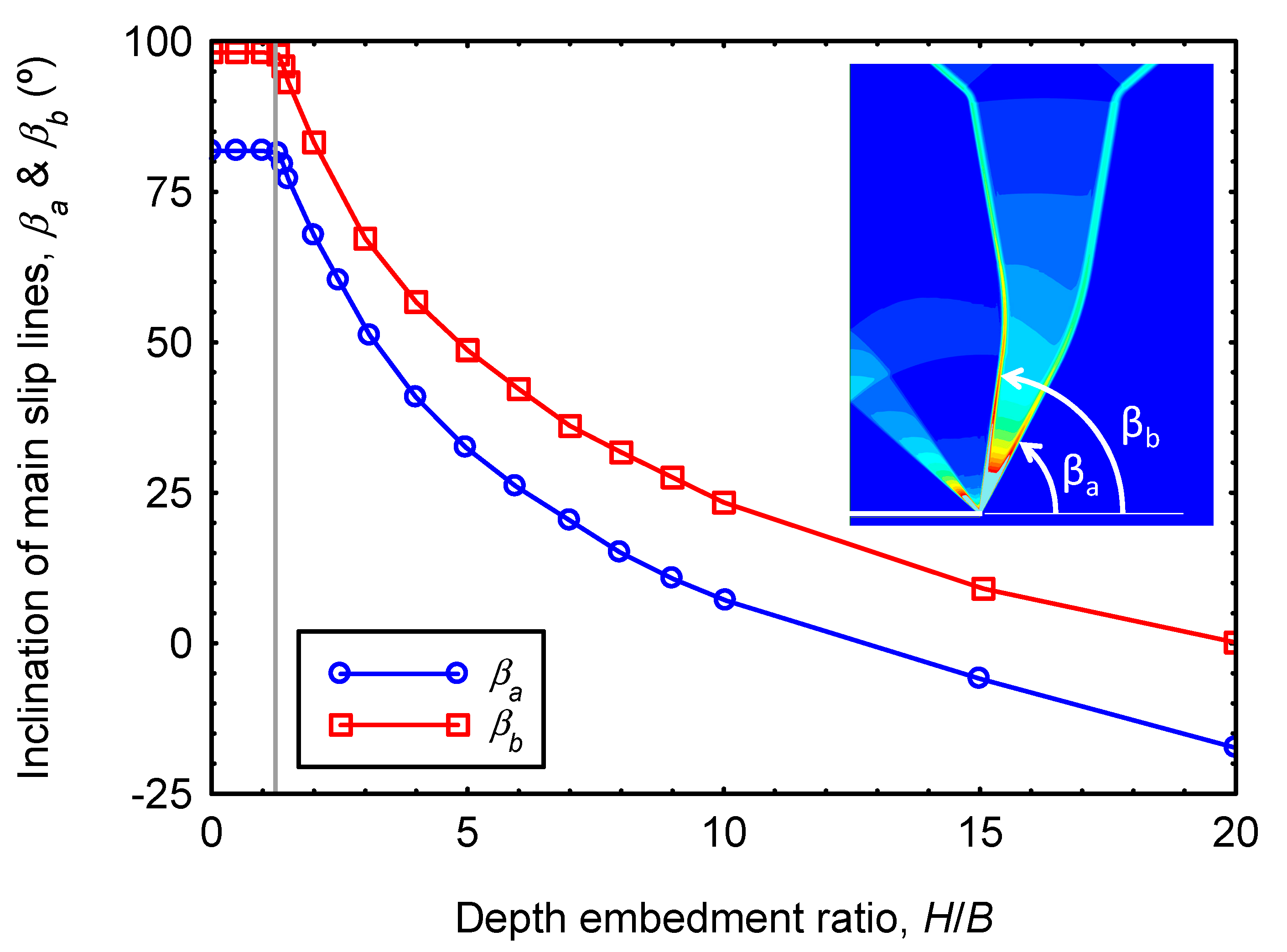
3.3. Very Shallow Failure
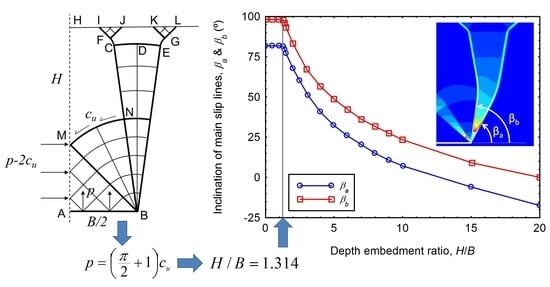
4. Proposed Analytical Limit for Very Shallow Failure
5. Finite Element Analyses
5.1. Numerical Models
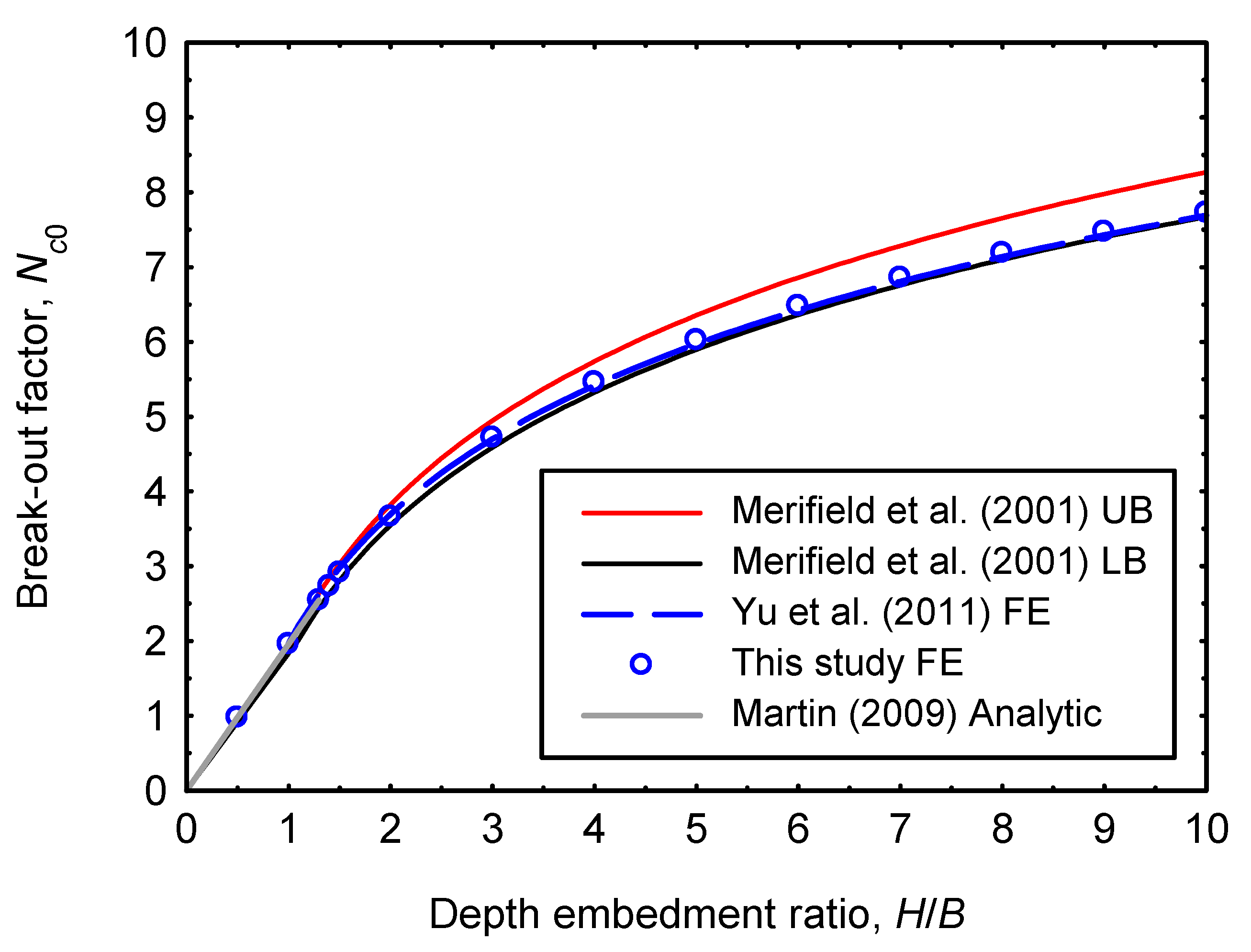
5.2. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Methods of Characteristics in a Rigid-Plastic Tresca Material
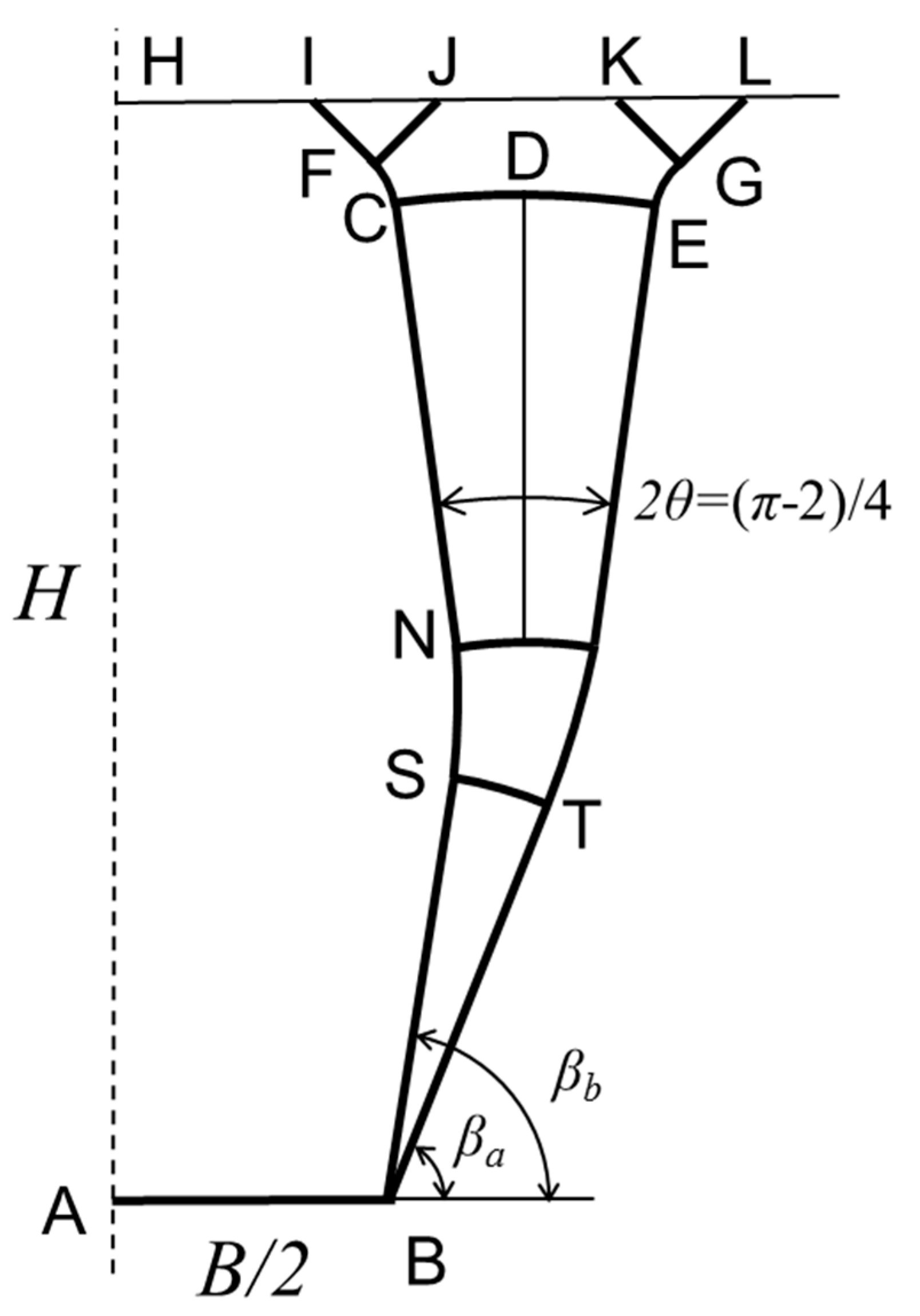
Appendix B. Conservation of the Angle between Main Slip Lines for Shallow Failure Mechanisms
References
- Randolph, M.; Gourvenec, S. Offshore Geotechnical Engineering; Spon Press: New York, NY, USA, 2011. [Google Scholar]
- Giampa, J.R.; Bradshaw, A.S.; Gerkus, H.; Gilbert, R.B.; Gavin, K.G.; Sivakumar, V. The effect of shape on the pull-out capacity of shallow plate anchors in sand. Géotechnique 2019, 69, 355–363. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Hu, Y.; Randolph, M.F. Three-dimensional large deformation finite-element analysis of plate anchors in uniform clay. J. Geotech. Geoenviron. Eng. 2010, 136, 355–365. [Google Scholar] [CrossRef]
- Terzaghi, K. Stress distribution in dry and in saturated sand above a yielding trap-door. In Proceedings of the International Conference on Soil Mechanics and Foundation Engineering, Harvard, MA, USA, 22–26 June 1936; Volume 1, pp. 307–311. [Google Scholar]
- Vesic, A.S. Breakout resistance of objects embedded in ocean bottom. J. Soil Mech. Found. Div. 1971, 97, 1183–1205. [Google Scholar]
- Das, B.M. A procedure for estimation of ultimate capacity of foundations in clay. Soil Found. 1980, 20, 77–82. [Google Scholar] [CrossRef] [Green Version]
- Das, B.M. Model tests for uplift capacity of foundations in clay. Soil Found. 1978, 18, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Gunn, M.J. Limit analysis of undrained stability problems using a very small computer. In Symposium on Computer Applications to Geotechnical Problems in Highway Engineering; Engineering Department, Cambridge University: Cambridge, UK, 1980; p. 530. [Google Scholar]
- Rowe, R.K.; Davis, E.H. The behaviour of anchor plates in clay. Géotechnique 1982, 32, 9–23. [Google Scholar] [CrossRef] [Green Version]
- Sloan, S.W.; Assadi, A.; Purushothaman, N. Undrained stability of a trapdoor. Géotechnique 1990, 40, 45–62. [Google Scholar] [CrossRef]
- Merifield, R.S.; Sloan, S.W.; Yu, H.S. Stability of plate anchors in undrained clay. Géotechnique 2001, 51, 141–153. [Google Scholar] [CrossRef]
- Yu, L.; Liu, J.; Kong, X.-J.; Hu, Y. Numerical study on plate anchor stability in clay. Géotechnique 2011, 61, 235–246. [Google Scholar] [CrossRef]
- Yu, L.; Zhou, Q.; Liu, J. Experimental study on the stability of plate anchors in clay under cyclic loading. Theor. App. Mech. Lett. 2015, 5, 93–96. [Google Scholar] [CrossRef] [Green Version]
- Elkhatib, S.; Randolph, M.F. The effect of interface friction on the performance of drag-in plate anchors. In Proceedings of the 5th International Symposium on Frontiers in Offshore Geotechnics, Perth, Australia, 19–21 September 2005; pp. 171–177. [Google Scholar]
- Maitra, S.; White, D.; Chatterjee, S.; Choudhury, D. Numerical modelling of seepage and tension beneath plate anchors. Comput. Geotech. 2019, 108, 131–142. [Google Scholar] [CrossRef]
- Cassidy, M.; Gaudin, C.; Randolph, M.; Wong, P.C.; Wang, D.; Tian, Y. A plasticity model to assess the keying of plate anchors. Géotechnique 2012, 62, 825–836. [Google Scholar] [CrossRef]
- Song, Z.; Hu, Y.; Randolph, M.F. Numerical simulation of vertical pullout of plate anchors in clay. J. Geotech. Geoenviron. Eng. 2008, 134, 866–875. [Google Scholar] [CrossRef]
- Liu, J.; Tan, M.; Hu, Y. New analytical formulas to estimate the pullout capacity factor for rectangular plate anchors in NC clay. Appl. Ocean Res. 2018, 75, 234–247. [Google Scholar] [CrossRef]
- Singh, V.; Maitra, S.; Chatterjee, S. Generalized design approach for inclined strip anchors in clay. Int. J. Geomech. 2017, 17, 04016148. [Google Scholar] [CrossRef]
- Martin, C.M. Undrained collapse of a shallow plane-strain trapdoor. Géotechnique 2009, 59, 855–863. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity; Developments in Geotechnical Engineering; Elsevier: New York, NY, USA, 1975; Volume 7. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1950. [Google Scholar]
- Meyerhof, G.G. The ultimate bearing capacity of foundations. Géotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- Martin, C.M.; Randolph, M.F. Applications of the lower and upper bound theorems of plasticity to collapse of circular foundations. In Proceedings of the 10th International Conferecne on Computer Methods and Advances in Geomechanics, Tucson, AZ, USA, 7–12 January 2001; International Association of Computer Methods and Advances in Geomechnics: Tucson, AZ, USA, 2001; Volume 2, pp. 1417–1428. [Google Scholar]
- Rowe, R.K. Soil Structure Interaction Analysis and Its Application to the Prediction of Anchor Behavior. Ph.D. Thesis, University of Sidney, Sidney, Australia, 1978. [Google Scholar]
- Merifield, R.S.; Sloan, S.W.; Yu, H.S. Rigorous plasticity solutions for the bearing capacity of two-layered clays. Géotechnique 1999, 49, 471–490. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.B.; Hambleton, J.P.; Sloan, S.W. Undrained uplift capacity of deeply embedded strip anchors in non-uniform soil. Comput. Geotech. 2015, 70, 41–49. [Google Scholar] [CrossRef]
- Merifield, R.S.; Smith, C.C. The ultimate uplift capacity of multi-plate strip anchors in undrained clay. Comput. Geotech. 2010, 37, 504–514. [Google Scholar] [CrossRef]
- Charlton, T.S.; Rouainia, M.; Gens, A. Numerical analysis of suction embedded plate anchors in structured clay. Appl. Ocean Res. 2016, 61, 156–166. [Google Scholar] [CrossRef]
- Ardebili, Z.A.; Gabr, M.A.; Rahman, M.S. Uplift capacity of plate anchors in saturated clays: Analyses with different constitutive models. Int. J. Geomech. 2015, 04015053. [Google Scholar] [CrossRef]
- Merifield, R.S.; Lyamin, A.V.; Sloan, S.W.; Yu, H.S. Three-dimensional lower bound solutions for stability of plate anchors in clay. J. Geotech. Geoenviron. Eng. 2003, 129, 243–253. [Google Scholar] [CrossRef] [Green Version]
- Brinkgreve, R.B.J.; Kumarswamy, S.; Swolfs, W.M. Plaxis 2015; Plaxis bv: Delft, The Netherlands, 2015. [Google Scholar]
- Smith, C.C.; Gilbert, M. Identification of rotational failure mechanisms in cohesive media using discontinuity layout optimization. Géotechnique 2013, 63, 1194–1208. [Google Scholar] [CrossRef] [Green Version]
- Blake, A.P.; O’Loughlin, C.D.; Gaudin, C. Capacity of dynamically embedded plate anchors as assessed through field tests. Can. Geotech. J. 2015, 52, 87–95. [Google Scholar] [CrossRef]
- Gaudin, C.; O’Loughlin, C.D.; Randolph, M.F.; Lowmass, A.C. Influence of the installation process on the performance of suction embedded plate anchors. Géotechnique 2006, 56, 381–391. [Google Scholar] [CrossRef]
- Davis, E.H. Theories of plasticity and the failure of soil masses. In Soil Mechanics-Selected Topics; Lee, I.K., Ed.; Butterworths: London, UK, 1968; pp. 341–380. [Google Scholar]


| I/B(%) | Nc0 |
|---|---|
| 0.33 | 0.9779 |
| 0.67 | 0.9768 |
| 1.00 | 0.9760 |
| 1.33 | 0.9749 |
| (a) | |
|---|---|
| NOE 1 | Nc0 |
| 15,177 | 0.97752 |
| 6792 | 0.97765 |
| 3264 | 0.97787 |
| (b) | |
| 70,123 | 7.7270 |
| 33,553 | 7.7273 |
| 19,547 | 7.7276 |
| 12,735 | 7.7289 |
| H/B | Nc0 |
|---|---|
| 0.5 | 0.978 |
| 1 | 1.957 |
| 1.3 | 2.543 |
| 1.4 | 2.734 |
| 1.5 | 2.913 |
| 2 | 3.662 |
| 3 | 4.720 |
| 4 | 5.459 |
| 5 | 6.022 |
| 6 | 6.477 |
| 7 | 6.858 |
| 8 | 7.189 |
| 9 | 7.473 |
| 10 | 7.728 |
| 15 | 8.70 |
| 20 | 9.38 |
| 30 | 10.30 |
| 50 | 11.42 |
| H/B | FEA This Study | LB (FELA) [20] | UB (FELA) [20] | Average [20] | Analytical [20] |
|---|---|---|---|---|---|
| 0.5 | 0.978 | 0.976 | 0.980 | 0.978 | 0.978 |
| 1 | 1.957 | 1.953 | 1.960 | 1.957 | 1.956 |
| 1.3 | 2.543 | 2.539 | 2.548 | 2.544 | 2.543 |
| 1.4 | 2.734 | 2.728 | 2.739 | 2.734 | 2.739 |
| 1.5 | 2.913 | 2.907 | 2.918 | 2.912 | 2.934 |
| 2 | 3.662 | 3.654 | 3.668 | 3.661 | 3.912 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cañizal, F.; Castro, J.; Cañizal, J.; Sagaseta, C. Pull-Out Capacity and Failure Mechanisms of Strip Anchors in Clay. Energies 2020, 13, 3853. https://doi.org/10.3390/en13153853
Cañizal F, Castro J, Cañizal J, Sagaseta C. Pull-Out Capacity and Failure Mechanisms of Strip Anchors in Clay. Energies. 2020; 13(15):3853. https://doi.org/10.3390/en13153853
Chicago/Turabian StyleCañizal, Fernando, Jorge Castro, Jorge Cañizal, and César Sagaseta. 2020. "Pull-Out Capacity and Failure Mechanisms of Strip Anchors in Clay" Energies 13, no. 15: 3853. https://doi.org/10.3390/en13153853