Modelling Grid Constraints in a Multi-Energy Municipal Energy System Using Cumulative Exergy Consumption Minimisation
Abstract
:1. Introduction
2. State of Research and Research Objective
2.1. Cumulative Exergy Consumption
2.2. Multi-Energy-Systems
2.3. Load Flow Calculations
2.4. Research Objective and Paper Outline
- System design: How can the optimum capacity of storages and conversion units be determined?
- System operation: How can such a system be operated while always meeting the demand?
- What is the impact of maximum grid capacities on installed RES, storage and conversion unit capacities and their operation?
- What is the impact of different load flow representations (network flow vs. power flow)?
- What influence do the spatially unevenly distributed RE potentials have? High potentials typically exist in thinly populated rural regions, low potentials in densely populated cities.
3. Methodology
3.1. Formulation of the Optimisation Problem
3.2. Cumulative Exergy Consumption Minimisation
3.3. Energy System Components
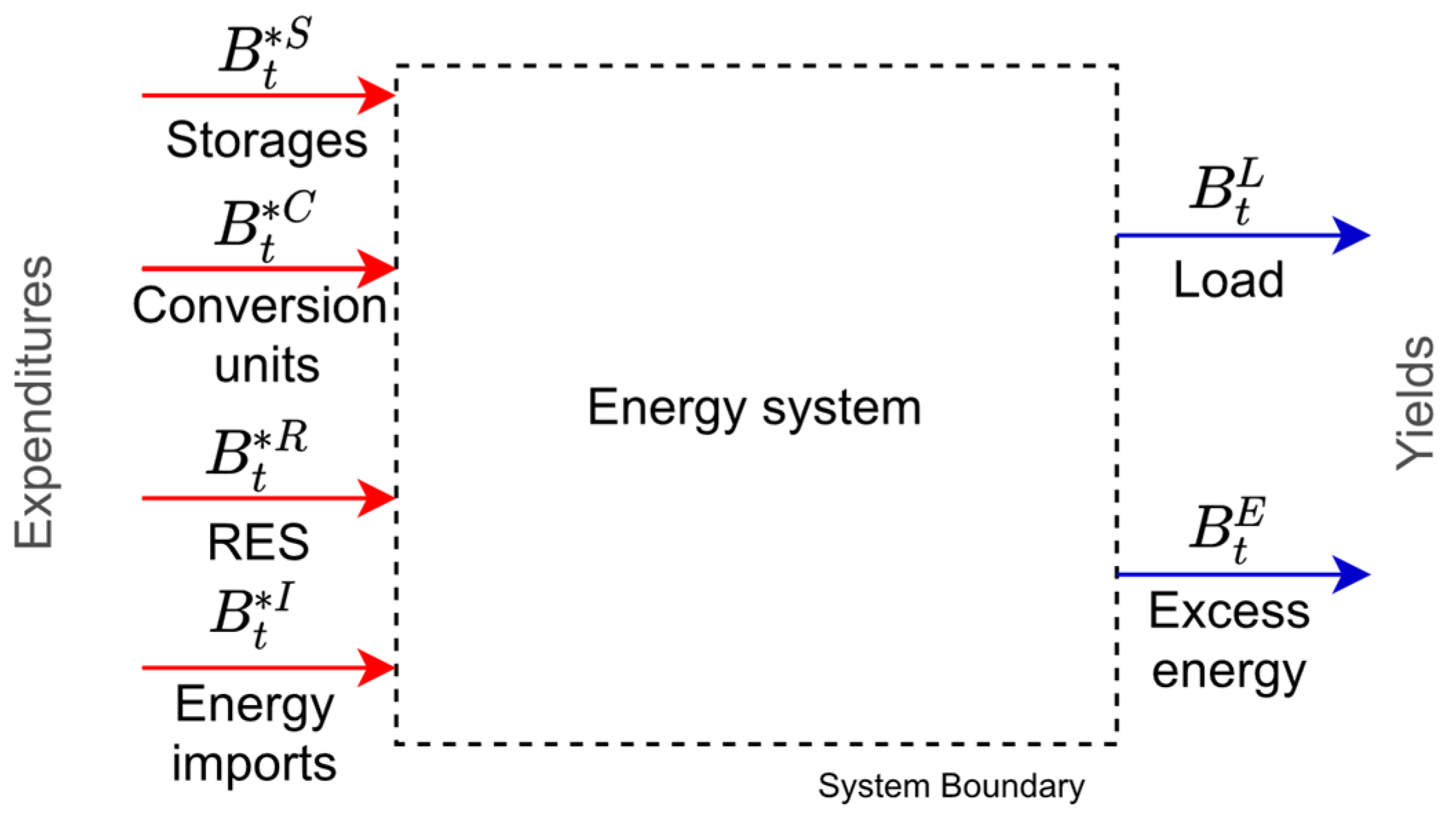
3.3.1. Energy Imports, Loads and Excess Energy
3.3.2. RES
3.3.3. Conversion Units
3.3.4. Storages
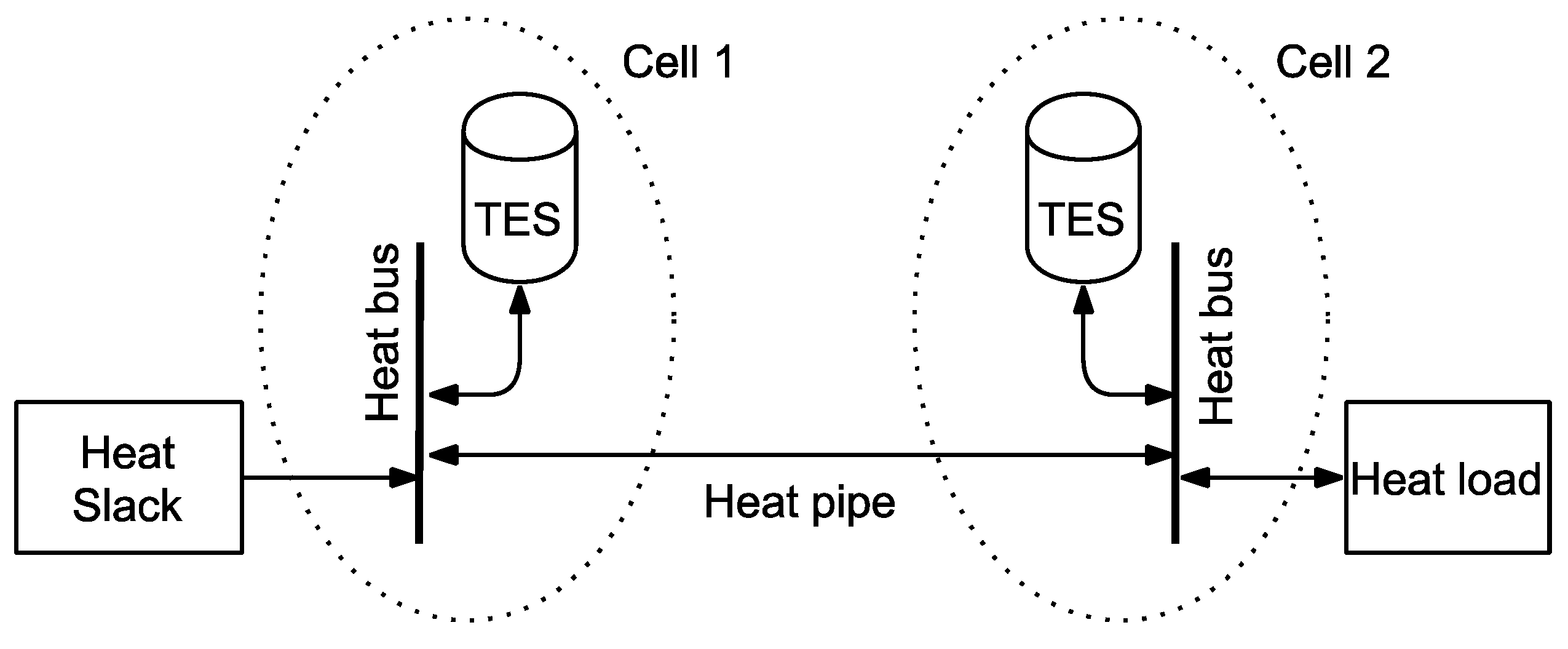
3.3.5. Energy Transmission
3.3.6. Busses
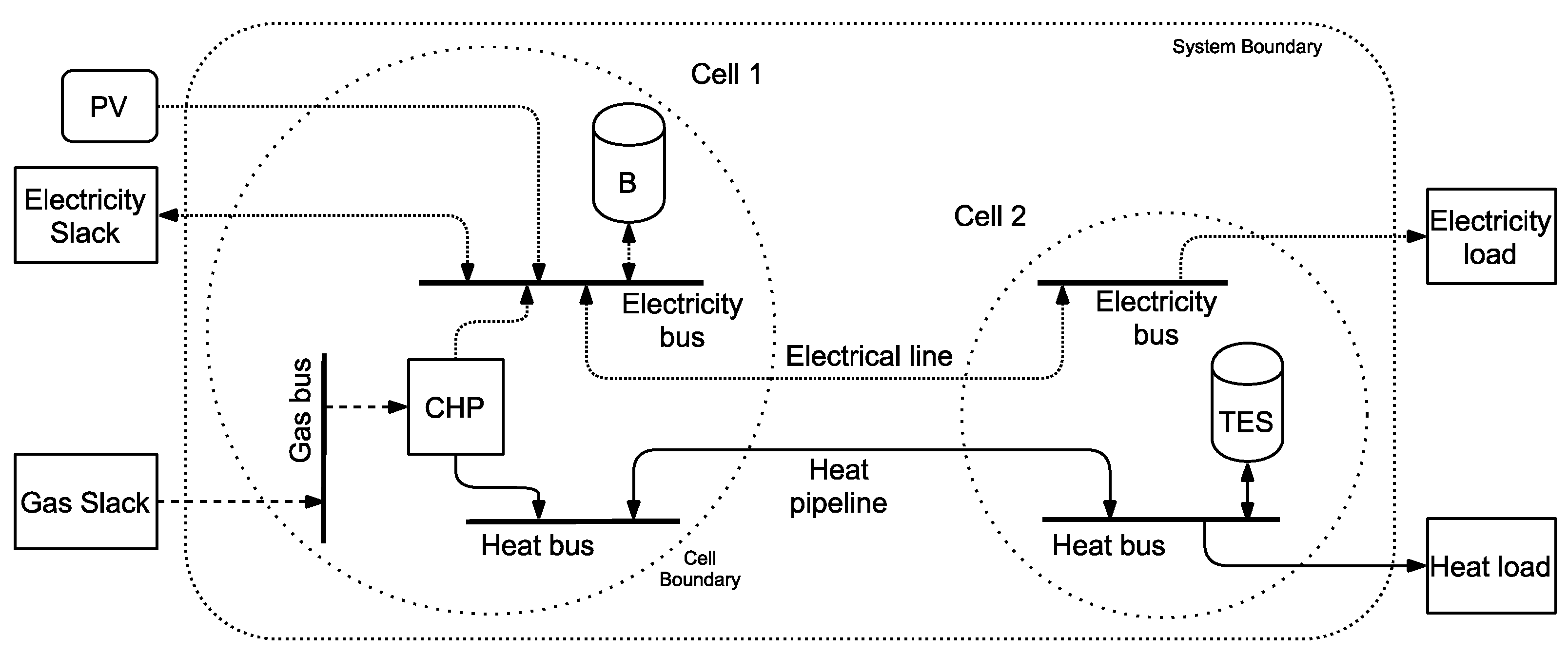
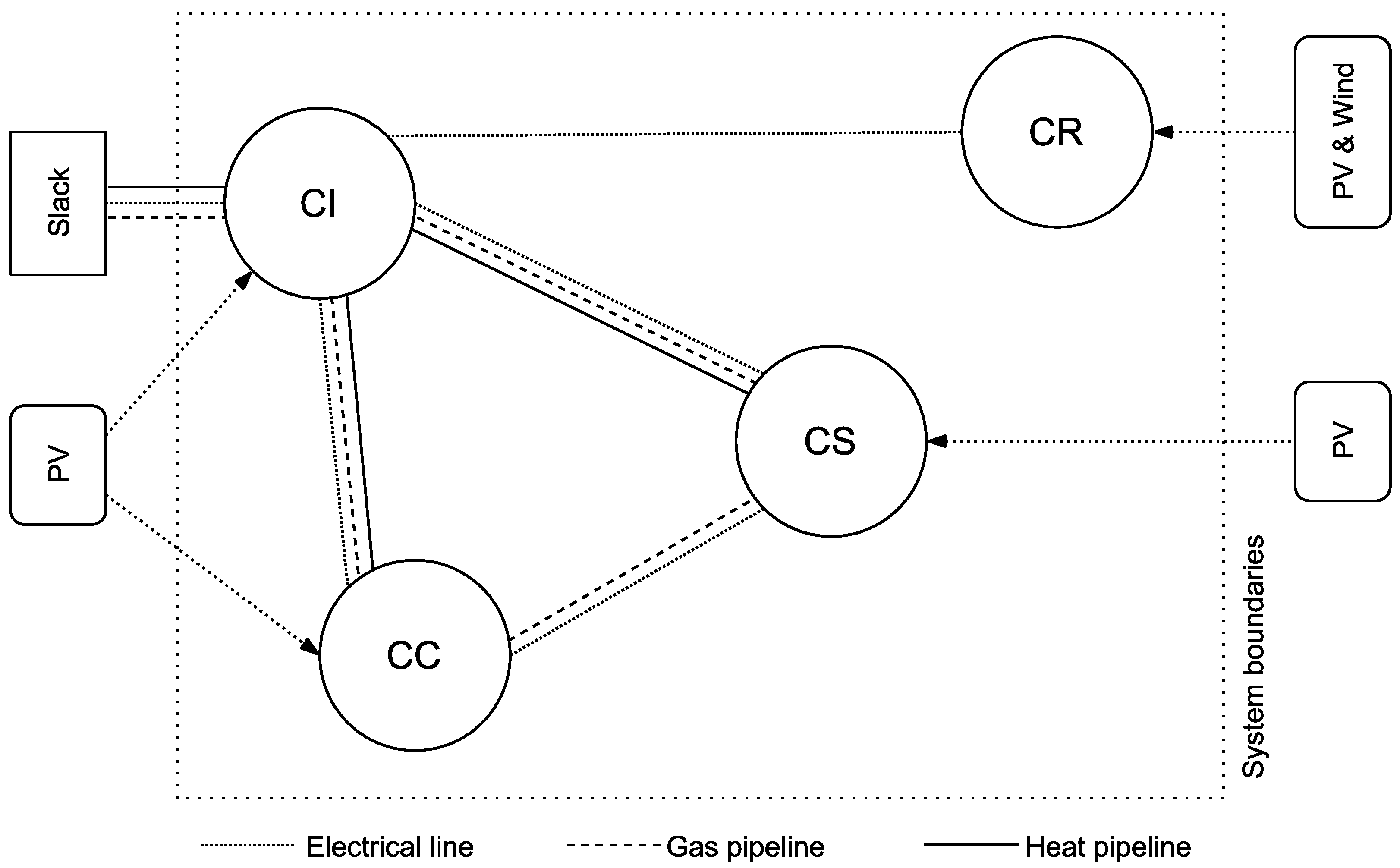
4. Case Study
4.1. System Description
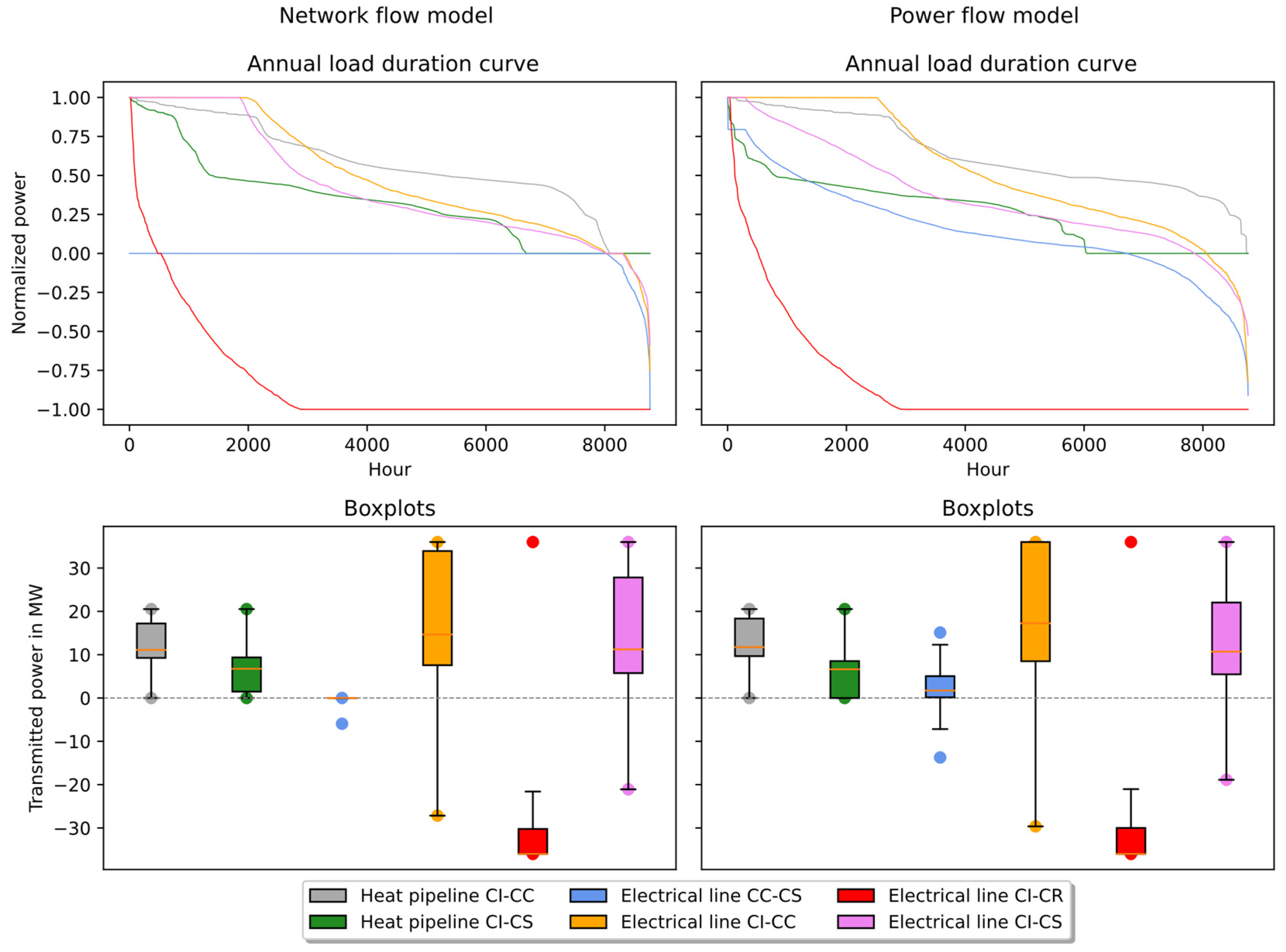
4.2. Results
5. Discussion and Conclusions
5.1. Model Discussion and Comparison
5.2. Conclusion and Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AC | alternating current |
| CExC | cumulative exergy consumption |
| CHP | combined heat and power |
| DC | direct current |
| EU | European Union |
| HP | heat pump |
| MES | multi energy system |
| MILP | mixed integer linear programming |
| NF | network flow |
| OECD | Organisation for Economic Co-operation and Development |
| OPF | optimal power flow |
| PF | power flow |
| RES | renewable energy sources |
| TES | thermal energy storage |
Nomenclature
| cross section | exergy factor | ||
| CExC-yield | CExC-factor | ||
| CExC-expenditures | equivalent periodic CExC-factor | ||
| storage capacity | state of energy | ||
| diameter | time period | ||
| specific energy | time series | ||
| length | reactance | ||
| mass | density | ||
| power | efficiency | ||
| pressure | voltage angle | ||
| resistance | friction factor | ||
| Reynolds number | time step |
Appendix A. Linearisation of the Heat and Gas Flows and Pressure Losses
| Heat Pipe | Gas Pipe | |
|---|---|---|
| Diameter | 350 mm | 300 mm |
| Length | 1000 m | 1000 m |
| Temperature difference Supply/return | 50 °C | |
| Gross calorific value | 11 kWh/Nm3 | |
| Pipe roughness | 1 mm | 0.3 mm |
| Max. power | 50 MW | 163 MW |
| Natural Gas | District Heat | ||
|---|---|---|---|
| 1 | 0.0 | 0.000 | 0.000 |
| 2 | 0.2 | 0.062 | 0.040 |
| 3 | 0.4 | 0.158 | 0.160 |
| 4 | 0.6 | 0.358 | 0.360 |
| 5 | 0.8 | 0.637 | 0.640 |
| 6 | 1.0 | 1.000 | 1.000 |
Appendix B. Component Properties and Equivalent Periodic CExC-Factors
| Technology | Inflow Efficiency | Outflow Efficiency | Capacity Loss | Equivalent Periodic CExC-Factor |
|---|---|---|---|---|
| - | - | |||
| Battery | ||||
| TES | ||||
| H2-Storage |
| Type | Efficiency | Equivalent Periodic CExC-Factor |
|---|---|---|
| - | ||
| Biomass boiler | ||
| Gas boiler | ||
| Heat pump | ||
| PEM electrolyser | ||
| PEM fuel cell | ||
| Resistance heater | ||
| Biomass CHP | ||
| Gas CHP |
| Type | CExC-Factor | Equivalent Periodic CExC-Factor |
|---|---|---|
| PV | ||
| Wind |
Appendix C. PF Equations, Multi-Cell Models and Result Quality
References
- European Commission. Energy Roadmap 2050. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions; 885 Brussels, Belgium, 2011; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Eurostat. Energy Balances. Available online: https://ec.europa.eu/eurostat/web/energy/data/energy-balances (accessed on 6 November 2019).
- Sejkora, C.; Kienberger, T. Dekarbonisierung der Industrie mithilfe elektrischer Energie? In 15. Symposium Energieinnovation; Technische Universität Graz: Graz, Austria, 2018. [Google Scholar]
- Geyer, R.; Knöttner, S.; Diendorfer, C.; Drexler-Schmid, G. IndustRiES. Energieinfrastruktur Für 100% Erneuerbare Energie in der Industrie; Klima-und Energiefonds der österreichischen Bundesregierung: Wien, Austria, 2019. [Google Scholar]
- Wall, G. Exergy. A Useful Concept; TH: Göteborg, Sweden, 1986; ISBN 9170322694. [Google Scholar]
- International Energy Agency. Key World Energy Statistics. Also Available on Smartphones and Tablets; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Statistik Austria. Nutzenergieanalyse (NEA). 2017. Available online: http://www.statistik.at/web_de/statistiken/energie_umwelt_innovation_mobilitaet/energie_und_umwelt/energie/nutzenergieanalyse/index.html (accessed on 18 January 2018).
- Haas, R.; Panzer, C.; Resch, G.; Ragwitz, M.; Reece, G.; Held, A. A historical review of promotion strategies for electricity from renewable energy sources in EU countries. Renew. Sustain. Energy Rev. 2011, 15, 1003–1034. [Google Scholar] [CrossRef]
- Kriechbaum, L.; Scheiber, G.; Kienberger, T. Grid-based multi-energy systems—modelling, assessment, open source modelling frameworks and challenges. Energ. Sustain. Soc. 2018, 8, 244. [Google Scholar] [CrossRef] [Green Version]
- Sejkora, C.; Kühberger, L.; Radner, F.; Trattner, A.; Kienberger, T. Exergy as Criteria for Efficient Energy Systems—A Spatially Resolved Comparison of the Current Exergy Consumption, the Current Useful Exergy Demand and Renewable Exergy Potential. Energies 2020, 13, 843. [Google Scholar] [CrossRef] [Green Version]
- Böckl, B.; Greiml, M.; Leitner, L.; Pichler, P.; Kriechbaum, L.; Kienberger, T. HyFlow—A Hybrid Load Flow-Modelling Framework to Evaluate the Effects of Energy Storage and Sector Coupling on the Electrical Load Flows. Energies 2019, 12, 956. [Google Scholar] [CrossRef] [Green Version]
- Krause, T.; Kienzle, F.; Art, S.; Andersson, G. Maximizing exergy efficiency in multi-carrier energy systems. In Proceedings of the Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- Wall, G. Exergy tools. Proc. Inst. Mech. Eng. A J. Power Energy 2003, 217, 125–136. [Google Scholar] [CrossRef]
- Dewulf, J.; van Langenhove, H.; Muys, B.; Bruers, S.; Bakshi, B.R.; Grubb, G.F.; Paulus, D.M.; Sciubba, E. Exergy: Its Potential and Limitations in Environmental Science and Technology. Environ. Sci. Technol. 2008, 42, 2221–2232. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Thermoeconomic analysis and optimization of energy systems. Prog. Energy Combust. Sci. 1993, 19, 227–257. [Google Scholar] [CrossRef]
- Szargut, J.; Morris, D.R. Cumulative exergy consumption and cumulative degree of perfection of chemical processes. Int. J. Energy Res. 1987, 11, 245–261. [Google Scholar] [CrossRef]
- Valero, A.; Lozano, M.A.; Munoz, M. A general theory of exergy saving: I. On the exergetic cost. In Computer-Aided Engineering of Energy Systems: Vol 3. Second Law Analysis and Modelling, Proceedings of the Winter Annual Meeting of the American Society Mechan. Engin., Anaheim, CA, USA, 7–12 December 1986; Gaggioli, R.A., Ed.; ASME: New York, NY, USA, 1986. [Google Scholar]
- Lozano, M.A.; Valero, A. Theory of the exergetic cost. Energy 1993, 18, 939–960. [Google Scholar] [CrossRef]
- Sciubba, E.; Bastianoni, S.; Tiezzi, E. Exergy and extended exergy accounting of very large complex systems with an application to the province of Siena, Italy. J. Environ. Manag. 2008, 86, 372–382. [Google Scholar] [CrossRef]
- Sciubba, E. Beyond thermoeconomics? The concept of Extended Exergy Accounting and its application to the analysis and design of thermal systems. Exergy, Int. J. 2001, 1, 68–84. [Google Scholar] [CrossRef]
- Ziębik, A.; Gładysz, P. Analysis of the cumulative exergy consumption of an integrated oxy-fuel combustion power plant. Arch. Thermodyn. 2013, 34, 105–122. [Google Scholar] [CrossRef]
- Wang, S.; Liu, C.; Liu, L.; Xu, X.; Zhang, C. Ecological cumulative exergy consumption analysis of organic Rankine cycle for waste heat power generation. J. Clean. Prod. 2019, 218, 543–554. [Google Scholar] [CrossRef]
- Ertesvåg, I.S. Society exergy analysis: A comparison of different societies. Energy 2001, 26, 253–270. [Google Scholar] [CrossRef]
- Sun, B.; Nie, Z.; Gao, F. Cumulative exergy consumption (CExC) analysis of energy carriers in China. IJEX 2014, 15, 196. [Google Scholar] [CrossRef]
- Ukidwe, N.U.; Bakshi, B.R. Industrial and ecological cumulative exergy consumption of the United States via the 1997 input-output benchmark model. Energy 2007, 32, 1560–1592. [Google Scholar] [CrossRef]
- Causone, F.; Sangalli, A.; Pagliano, L.; Carlucci, S. An Exergy Analysis for Milano Smart City. Energy Procedia 2017, 111, 867–876. [Google Scholar] [CrossRef] [Green Version]
- Kriechbaum, L.; Kienberger, T. Optimal Municipal Energy System Design and Operation Using Cumulative Exergy Consumption Minimisation. Energies 2020, 13, 182. [Google Scholar] [CrossRef] [Green Version]
- Mancarella, P. MES (multi-energy systems): An overview of concepts and evaluation models. Energy 2014, 65, 1–17. [Google Scholar] [CrossRef]
- Böckl, B.; Kriechbaum, L.; Kienberger, T. Analysemethode für kommunale Energiesysteme unter Anwendung des zellularen Ansatzes. In 14. Symposium Energieinnovation, Proceedings of the Energie für unser Europa. 14. Symposium Energieinnovation, Graz, Austria, 10–12 February 2016; Institut für Elektrizitätswirtschaft und Energieinnovation, Ed.; TU Graz: Graz, Austria, 2016; ISBN 978-3-85125-448-8. [Google Scholar]
- Geidl, M.; Koeppel, G.; Perrod, P.F.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2007, 5, 24–30. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Optimal Power Flow of Multiple Energy Carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept—A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Geidl, M.; Andersson, G. Operational and topological optimization of multi-carrier energy systems. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 16–18 November 2005; p. 6. [Google Scholar]
- Koeppel, G. Reliability Considerations of Future Energy Systems: Multi-Carrier Systemsand the Effect of Energy Storage. Ph.D. Dissertation, ETH Zürich, Zürich, Sweden, 2007. [Google Scholar]
- Morvaj, B.; Evins, R.; Carmeliet, J. Comparison of individual and microgrid approaches for a distributed multi energy system with different renewable shares in the grid electricity supply. Energy Procedia 2017, 122, 349–354. [Google Scholar] [CrossRef]
- Asmus, P. Microgrids, virtual Power Plants and Our Distributed Energy Future. Electr. J. 2010, 23, 72–82. [Google Scholar] [CrossRef]
- Bracco, S.; Delfino, F.; Pampararo, F.; Robba, M.; Rossi, M. A mathematical model for the optimal operation of the University of Genoa Smart Polygeneration Microgrid: Evaluation of technical, economic and environmental performance indicators. Energy 2014, 64, 912–922. [Google Scholar] [CrossRef]
- Kusch, W.; Schmidla, T.; Stadler, I. Consequences for district heating and natural gas grids when aiming towards 100% electricity supply with renewables. Energy 2012, 48, 153–159. [Google Scholar] [CrossRef]
- Glavitsch, H.; Bacher, R. Optimal Power Flow Algorithms. In Control and Dynamic Systems V41: Advances in Theory and Applications; Leonides, C.T., Ed.; Elsevier Science: Burlington, NJ, USA, 1991; pp. 135–205. ISBN 9780120127412. [Google Scholar]
- Frank, S.; Rebennack, S. An introduction to optimal power flow: Theory, formulation, and examples. IIE Trans. 2016, 48, 1172–1197. [Google Scholar] [CrossRef]
- Biskas, P.N.; Ziogos, N.P.; Tellidou, A.; Zoumas, C.E.; Bakirtzis, A.G.; Petridis, V. Comparison of two metaheuristics with mathematical programming methods for the solution of OPF. IEE Proc. Gener. Transm. Distrib. 2006, 153, 16. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey I. Energy Syst. 2012, 3, 221–258. [Google Scholar] [CrossRef]
- Geidl, M. Integrated Modeling and Optimization of Multi-Carrier Energy Systems. Ph.D. Thesis, ETH Zürich, Zürich, Sweden, 2007. [Google Scholar]
- Purchala, K.; Meeus, L.; van Dommelen, D.; Belmans, R. Usefulness of DC power flow for active power flow analysis. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; pp. 2457–2462, ISBN 0-7803-9157-8. [Google Scholar]
- Geidl, M.; Andersson, G. Optimal power dispatch and conversion in systems with multiple energy carriers. In Proceedings of the 15th Power System Computation Conference (PSSC), Liege, Belgium, 22–26 August 2005. [Google Scholar]
- Shao, C.; Wang, X.; Shahidehpour, M.; Wang, X.; Wang, B. An MILP-Based Optimal Power Flow in Multicarrier Energy Systems. IEEE Trans. Sustain. Energy 2017, 8, 239–248. [Google Scholar] [CrossRef]
- Xu, X.; Li, K.; Liu, Y.; Jia, H. Integrated optimal power flow for distribution networks in local and urban scales. In Proceedings of the 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, UK, 31 August–2 September 2016; pp. 1–6, ISBN 978-1-4673-9891-6. [Google Scholar]
- Unsihuay, C.; Lima, J.W.M.; de Souza, A.Z. Modeling the Integrated Natural Gas and Electricity Optimal Power Flow. In Proceedings of the IEEE Power Engineering Society General meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–7, ISBN 1-4244-1296-X. [Google Scholar]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Qiu, Z.; Deconinck, G.; Belmans, R. A literature survey of Optimal Power Flow problems in the electricity market context. In Proceedings of the PES’09, IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–6, ISBN 978-1-4244-3810-5. [Google Scholar]
- Oemof Developer Group. Open Energy Modelling Framework (Oemof)—A Modular Open Source Framework to Model Energy Supply Systems. Version V0.1.4; Zenodo: Berlin, Germany, 2017. [Google Scholar]
- Hilpert, S.; Kaldemeyer, C.; Krien, U.; Günther, S.; Wingenbach, C.; Plessmann, G. The Open Energy Modelling Framework (oemof)—A new approach to facilitate open science in energy system modelling. Energy Strategy Rev. 2018, 22, 16–25. [Google Scholar] [CrossRef] [Green Version]
- United Nations (Ed.) International Recommendations for Energy Statistics (IRES); United Nations: New York, NY, USA, 2017; ISBN 9789211615845. [Google Scholar]
- Oemof Developer Group. The Oemof Demandlib (Oemof.Demandlib); Zenodo: Berlin, Germany, 2016. [Google Scholar]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef] [Green Version]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Fuller, J.D. Nodal, Uniform, or Zonal Pricing: Distribution of Economic Surplus. IEEE Trans. Power Syst. 2005, 20, 875–882. [Google Scholar] [CrossRef]
- Frederiksen, S.; Werner, S. District Heating and Cooling; Studentliteratur: Lund, Sweden, 2013; ISBN 9789144085302. [Google Scholar]
- Handbuch der Gasversorgungstechnik. Logistik—Infrastruktur-Lösungen, 1. Auflage; Homann, K., Hüwener, T., Klocke, B., Wernekinck, U., Eds.; DIV Deutscher Industrieverlag: München, Germany, 2017; ISBN 9783835672994. [Google Scholar]
- Pfenninger, S.; Keirstead, J. Renewables, nuclear, or fossil fuels? Scenarios for Great Britain’s power system considering costs, emissions and energy security. Appl. Energy 2015, 152, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Willi, D.; Chokani, N.; Abhari, R.S. Optimal power flow analysis of a Switzerland’s transmission system for long-term capacity planning. Renew. Sustain. Energy Rev. 2014, 34, 596–607. [Google Scholar] [CrossRef]
- ProBas; Umwelbundesamt: Dessau-Roßlau, Germany, 2015.
- Ecoinvent. Ecoinvent; Ecoinvent: Zurich, Sweden, 2020.
- Pavić, Z. Convex combinations, barycenters and convex functions. J. Inequal. Appl. 2013, 2013. [Google Scholar] [CrossRef] [Green Version]
- Siemens, A.G. PSS®SINCAL; Siemens AG: Munich, Germany, 2016. [Google Scholar]
- Kriechbaum, L.; Heinrich, D.; Kienberger, T. Werkzeug zur Ermittlung der Exergieeffizienz von Fernwärmesystemen. In Proceedings of the 10. Internationale Energiewirtschaftstagung, Wien, Austria, 15–17 February 2017. [Google Scholar]
- Gurobi Optimization. Gurobi; Gurobi Optimization: Beaverton, OR, USA, 2020. [Google Scholar]
| Electricity | Natural Gas | Waste Heat | Biomass | |
|---|---|---|---|---|
| CExC-factor in | 2.0 | 1.21 | 0.21 | 1.1 |
| Electricity | Natural Gas | Heat | ||
|---|---|---|---|---|
| CI-Slack | Max. cap. | 600 MW | 1000 MW | 20 MW |
| CI-CC | Max. cap. | 36 MW | 163 MW | 30 MW |
| Efficiency | 99.9% | 99.9% | 85% | |
| CI-CS | Max. cap. | 36 MW | 141 MW | 30 MW |
| Efficiency | 99.9% | 99.9% | 85% | |
| CC-CS | Max. cap. | 36 MW | 100 MW | |
| Efficiency | 99.9% | 99.9% | ||
| CI-CR | Max. cap. | 36 MW | ||
| Efficiency | 99.9% |
| CI-CC | 2.5 | 0.0729 | 40.5 | 119.1 |
| CI-CS | 5.0 | 0.0729 | 40.5 | 119.1 |
| CC-CS | 7.5 | 0.0729 | 40.5 | |
| CI-CR | 10.0 | 0.0729 |
| Cell | Electricity | Domestic Heat | Process Heat | PV | Wind | ||
|---|---|---|---|---|---|---|---|
| CC | Ann. Demand | GWh | 137.5 | 405.0 | 31.8 | ||
| Max. Power | MW | 26.1 | 162.2 | 62.5 | |||
| CS | Ann. Demand | GWh | 110.0 | 315.0 | 65.5 | ||
| Max. Power | MW | 20.9 | 140.4 | 50 | |||
| CI | Ann. Demand | GWh | 220.0 | 72.0 | 130.9 | ||
| Max. Power | MW | 52.8 | 22.1 | 100 | |||
| CR | Ann. Demand | GWh | 82.5 | 180.0 | 49.1 | 697.1 | |
| Max. Power | MW | 17.6 | 92.5 | 37.5 | 330 |
| CI | CC | CS | CR | Total | Gap | ||
|---|---|---|---|---|---|---|---|
| MW | MW | MW | MW | MW | MW | ||
| Gas boiler PH | NF | 22.1 | 22.1 | 0.0 | |||
| PF | 22.1 | 22.1 | |||||
| Resistance heater PH | NF | 20.8 | 20.8 | 0.0 | |||
| PF | 20.8 | 20.8 | |||||
| Heat pump | NF | 163.0 | 145.4 | 240.2 | 548.6 | +1.8 | |
| PF | 138.8 | 171.6 | 240.0 | 550.4 | |||
| Biomass CHP | NF | 7.1 | 7.1 | +3.9 | |||
| PF | 11.0 | 11.0 | |||||
| Fuel Cell | NF | 20.0 | 20.0 | 0.0 | |||
| PF | 20.0 | 20.0 | |||||
| Electrolyser | NF | 66.3 | 66.3 | −0.2 | |||
| PF | 66.1 | 66.1 | |||||
| Wind | NF | 214.9 | 214.9 | +0.1 | |||
| PF | 215.0 | 215.0 | |||||
| PV | NF | 100 | 62.5 | 50 | 212.5 | 0.0 | |
| PF | 100 | 62.5 | 50 | 212.5 | |||
| CI | CC | CS | CR | Total | Gap | ||
|---|---|---|---|---|---|---|---|
| MWh | MWh | MWh | MWh | MWh | MWh | ||
| Battery | NF | 22.0 | 96.3 | 73.1 | 443.3 | 634.7 | +1.5 |
| PF | 22.0 | 162.5 | 6.9 | 444.8 | 636.2 | ||
| TES | NF | 1340.0 | 1625.2 | 8614.2 | 11579.4 | −15.8 | |
| PF | 1728.8 | 1219.7 | 8614.2 | 11,563.6 | |||
| H2 storage | NF | 13,474.0 | 13,474.0 | −12.8 | |||
| PF | 13,461.2 | 13,461.2 | |||||
| - | |||||||
|---|---|---|---|---|---|---|---|
| CI | Gas boiler PH | NF | 0.39 | 8.6 | 0.0 | 22.1 | 8.4 |
| PF | 0.39 | 8.6 | 0.0 | 22.1 | 8.4 | ||
| Resistance heater PH | NF | 0.08 | 1.7 | 0.0 | 20.8 | 0.0 | |
| PF | 0.08 | 1.7 | 0.0 | 20.8 | 0.0 | ||
| PV | NF | 0.15 | 14.9 | 0.0 | 85.0 | 0.5 | |
| PF | 0.15 | 14.9 | 0.0 | 85.0 | 0.5 | ||
| CC | Heat Pump | NF | 0.21 | 34.2 | 0.0 | 163.0 | 0.3 |
| PF | 0.23 | 31.9 | 0.0 | 138.8 | 3.7 | ||
| Biomass CHP | NF | 0.05 | 0.4 | 0.0 | 7.1 | 0.0 | |
| PF | 0.10 | 1.1 | 0.0 | 11.0 | 0.0 | ||
| PV | NF | 0.15 | 9.3 | 0.0 | 53.1 | 0.3 | |
| PF | 0.15 | 9.3 | 0.0 | 53.1 | 0.3 | ||
| CS | Heat Pump | NF | 0.20 | 29.4 | 0.0 | 145.4 | 0.0 |
| PF | 0.18 | 30.7 | 0.0 | 171.6 | 0.0 | ||
| PV | NF | 0.15 | 7.5 | 0.0 | 42.5 | 0.3 | |
| PF | 0.15 | 7.5 | 0.0 | 42.5 | 0.3 | ||
| CR | Heat Pump | NF | 0.09 | 21.8 | 0.0 | 240.2 | 0.0 |
| PF | 0.09 | 21.8 | 0.0 | 240.0 | 0.0 | ||
| Fuel Cell | NF | 0.26 | 6.9 | 0.0 | 26.7 | 0.0 | |
| PF | 0.26 | 6.9 | 0.0 | 26.7 | 0.0 | ||
| Electrolyser | NF | 0.11 | 5.1 | 0.0 | 20.0 | 0.0 | |
| PF | 0.11 | 5.1 | 0.0 | 20.0 | 0.0 | ||
| Wind | NF | 0.24 | 51.8 | 0.1 | 212.9 | 39.6 | |
| PF | 0.24 | 51.8 | 0.1 | 212.9 | 39.6 |
| - | |||||||
|---|---|---|---|---|---|---|---|
| CI | Battery | NF | 108.1 | 3.9 | 0 | 22.0 | 0.0 |
| PF | 135.4 | 4.7 | 0 | 22.0 | 0.0 | ||
| CC | Battery | NF | 131.8 | 50.6 | 0 | 96.3 | 51.7 |
| PF | 129.2 | 82.5 | 0 | 162.5 | 79.1 | ||
| TES | NF | 55.6 | 285.5 | 0 | 1339.8 | 138.7 | |
| PF | 50.9 | 327.8 | 0 | 1728.8 | 153.8 | ||
| CS | Battery | NF | 137.1 | 38.8 | 0 | 73.1 | 39.4 |
| PF | 128.7 | 3.4 | 0 | 6.9 | 2.9 | ||
| TES | NF | 40.0 | 297.3 | 0 | 1625.2 | 125.1 | |
| PF | 38.9 | 204.3 | 0 | 1219.7 | 32.3 | ||
| CR | Battery | NF | 72.4 | 221.9 | 0 | 443.3 | 212.2 |
| PF | 72.8 | 277.9 | 0 | 444.8 | 303.0 | ||
| TES | NF | 13.2 | 1583.5 | 0 | 8614.2 | 692.7 | |
| PF | 13.2 | 1577.5 | 0 | 8614.2 | 684.7 | ||
| H2-storage | NF | 4.5 | 8738.7 | 0 | 13,474.0 | 9881.4 | |
| PF | 4.5 | 8698.5 | 0 | 13,461.2 | 9823.1 |
| CI-CC Heat | NF | 11.8 | 0.0 | 20.8 | 13.4 |
| PF | 13.1 | 0.0 | 20.8 | 10.7 | |
| CI-CS Heat | NF | 6.8 | 0.0 | 20.5 | 6.8 |
| PF | 5.4 | 0.0 | 20.8 | 6.4 | |
| CC-CS Electricity | NF | −0.1 | −5.9 | 0.0 | 0.0 |
| PF | 2.3 | −16.6 | 18.4 | 1.7 | |
| CI-CC Electricity | NF | 17.8 | −27.2 | 36.0 | 14.7 |
| PF | 19.1 | −31.7 | 36.0 | 18.9 | |
| CI-CR Electricity | NF | −29.6 | −36.0 | 36.0 | −36.0 |
| PF | −29.6 | −36.0 | 36.0 | −36.0 | |
| CI-CS Electricity | NF | 15.4 | −21.1 | 36.0 | 11.2 |
| PF | 13.0 | −20.2 | 36.0 | 10.7 | |
| Expenditures in GWh | Yields in GWh | ||||||
|---|---|---|---|---|---|---|---|
| RES | Import | Infrastructure | Total | Load | Excess | Total | |
| NW | 732.1 | 454.8 | 133.3 | 1320.2 | 766.0 | 19.9 | 785.9 |
| PF | 732.2 | 455.7 | 133.6 | 1321.5 | 766.0 | 19.9 | 785.9 |
| Electricity | Gas | Heat | Biomass | |
|---|---|---|---|---|
| GWh | GWh | GWh | GWh | |
| NF | 312.6 | 95.9 | 36.4 | 9.9 |
| PF | 294.5 | 95.9 | 36.4 | 28.9 |
| NF | PF | ||
|---|---|---|---|
| Electricity grids | High voltage/transmission | X | |
| Medium voltage/distribution | X | ||
| Low voltage/distribution | X | ||
| District heating networks | Large scale | X | |
| Small scale | X | ||
| Gas networks | High pressure/transmission | X | |
| Low pressure/distribution | X | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kriechbaum, L.; Gradl, P.; Reichenhauser, R.; Kienberger, T. Modelling Grid Constraints in a Multi-Energy Municipal Energy System Using Cumulative Exergy Consumption Minimisation. Energies 2020, 13, 3900. https://doi.org/10.3390/en13153900
Kriechbaum L, Gradl P, Reichenhauser R, Kienberger T. Modelling Grid Constraints in a Multi-Energy Municipal Energy System Using Cumulative Exergy Consumption Minimisation. Energies. 2020; 13(15):3900. https://doi.org/10.3390/en13153900
Chicago/Turabian StyleKriechbaum, Lukas, Philipp Gradl, Romeo Reichenhauser, and Thomas Kienberger. 2020. "Modelling Grid Constraints in a Multi-Energy Municipal Energy System Using Cumulative Exergy Consumption Minimisation" Energies 13, no. 15: 3900. https://doi.org/10.3390/en13153900





