Energy Intensity and Long- and Short-Term Efficiency in US Manufacturing Industry
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Models
3.2. Stochastic Frontier Approach with Panel Data
4. Data
5. Empirical Results
5.1. Change in Energy Intensity of Industries
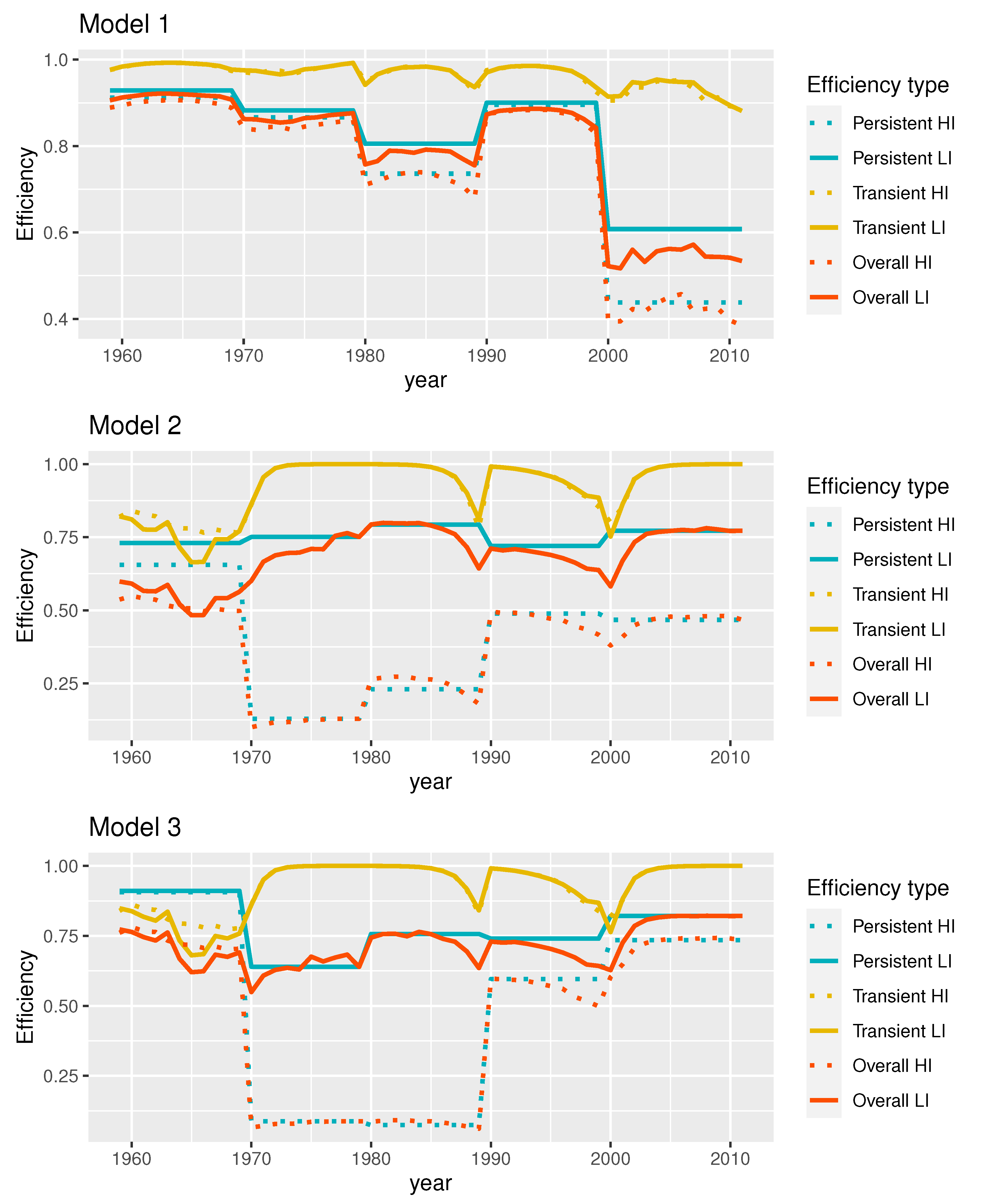
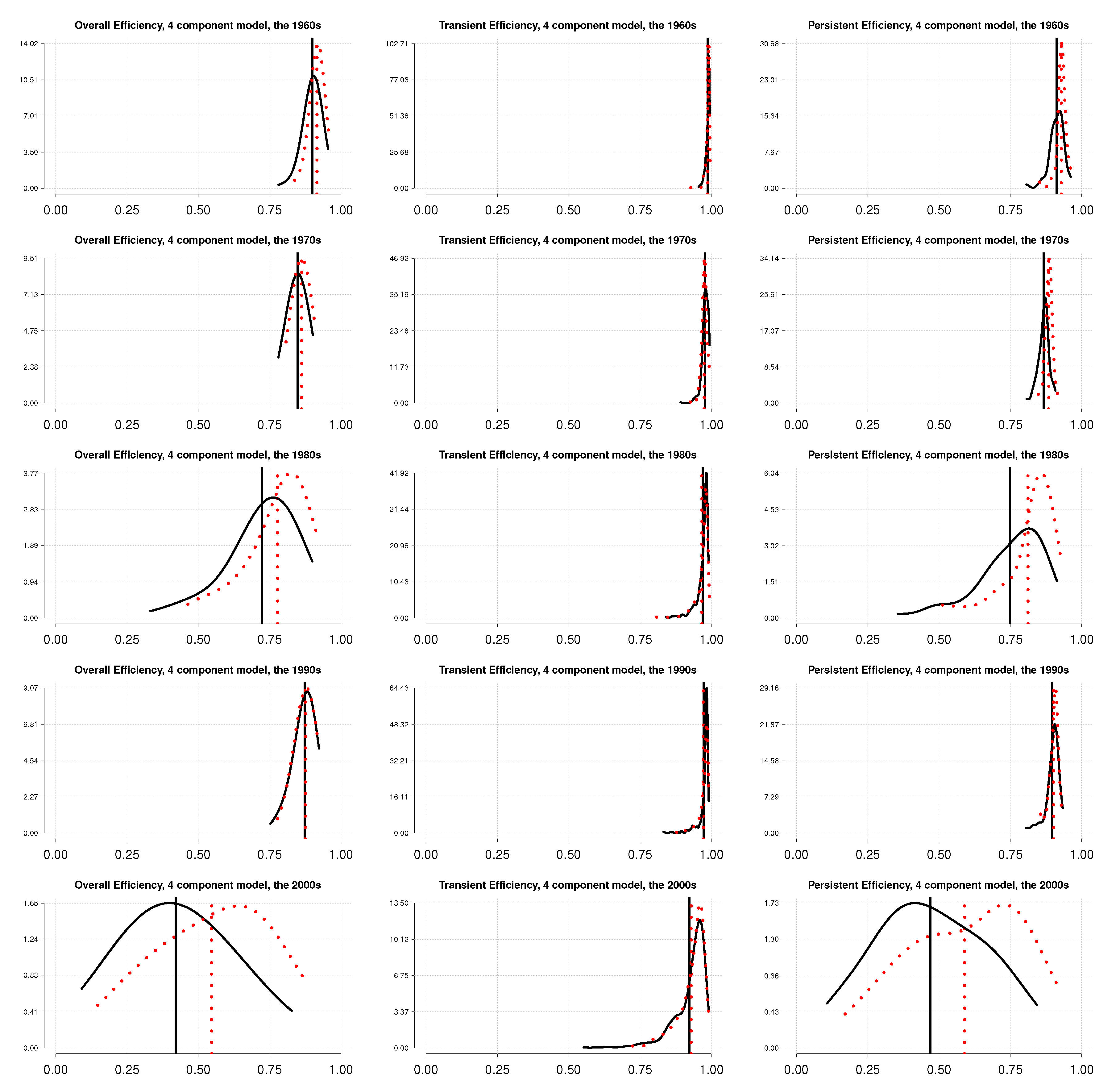
5.2. Energy Use Efficiency
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Time Period | Industries | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|---|
| Y | ||||||
| The 1960s | Least energy-intensive | 832.95 | 1509.60 | 2214.52 | 27.10 | 17,931.30 |
| The 1960s | Most energy-intensive | 546.85 | 1251.66 | 2780.79 | 79.70 | 21,983.20 |
| The 1970s | Least energy-intensive | 1438.45 | 3796.49 | 7199.52 | 150.30 | 43,128.30 |
| The 1970s | Most energy-intensive | 1128.70 | 3024.25 | 6117.26 | 111.60 | 54,446.30 |
| The 1980s | Least energy-intensive | 3639.00 | 8997.84 | 14,000.49 | 286.80 | 73,925.10 |
| The 1980s | Most energy-intensive | 2222.15 | 4855.71 | 8216.35 | 136.60 | 56,738.40 |
| The 1990s | Least energy-intensive | 6168.60 | 16,492.67 | 23,594.40 | 219.30 | 145,256.20 |
| The 1990s | Most energy-intensive | 3312.50 | 6678.93 | 10,571.67 | 116.30 | 56,895.00 |
| The 2000s | Least energy-intensive | 7992.90 | 19,773.51 | 30,016.89 | 149.10 | 16,2181.80 |
| The 2000s | Most energy-intensive | 4243.00 | 9790.06 | 17,328.47 | 130.80 | 123,129.80 |
| K | ||||||
| The 1960s | Least energy-intensive | 400.85 | 1131.83 | 1841.05 | 6.20 | 9507.70 |
| The 1960s | Most energy-intensive | 1548.30 | 4670.45 | 12,180.26 | 111.10 | 90,867.10 |
| The 1970s | Least energy-intensive | 631.45 | 2049.62 | 3965.95 | 27.60 | 20,595.00 |
| The 1970s | Most energy-intensive | 2646.90 | 6482.31 | 14,042.12 | 257.70 | 92,312.80 |
| The 1980s | Least energy-intensive | 960.60 | 3075.50 | 5135.97 | 52.80 | 25,549.50 |
| The 1980s | Most energy-intensive | 2475.65 | 6780.63 | 13,499.10 | 236.70 | 91,786.60 |
| The 1990s | Least energy-intensive | 1338.90 | 4242.53 | 6078.23 | 39.40 | 27,170.30 |
| The 1990s | Most energy-intensive | 2933.30 | 6867.77 | 12,257.56 | 172.20 | 70,528.90 |
| The 2000s | Least energy-intensive | 1605.60 | 5526.12 | 8706.73 | 57.30 | 53,612.40 |
| The 2000s | Most energy-intensive | 3162.85 | 7044.35 | 11,075.66 | 165.70 | 58,371.10 |
| L | ||||||
| The 1960s | Least energy-intensive | 72.40 | 127.50 | 147.79 | 1.35 | 1018.47 |
| The 1960s | Most energy-intensive | 31.66 | 83.17 | 164.73 | 3.75 | 1145.57 |
| The 1970s | Least energy-intensive | 76.74 | 121.04 | 122.07 | 9.94 | 727.97 |
| The 1970s | Most energy-intensive | 30.70 | 80.51 | 150.27 | 3.90 | 1070.72 |
| The 1980s | Least energy-intensive | 69.93 | 116.73 | 125.13 | 6.91 | 686.44 |
| The 1980s | Most energy-intensive | 28.38 | 59.72 | 92.65 | 2.98 | 762.71 |
| The 1990s | Least energy-intensive | 64.72 | 113.52 | 117.39 | 4.49 | 659.60 |
| The 1990s | Most energy-intensive | 26.66 | 55.92 | 74.33 | 2.09 | 423.21 |
| The 2000s | Least energy-intensive | 55.18 | 92.35 | 96.65 | 2.29 | 487.05 |
| The 2000s | Most energy-intensive | 20.63 | 39.73 | 53.02 | 2.48 | 380.14 |
| NEM | ||||||
| The 1960s | Least energy-intensive | 432.60 | 917.37 | 1687.38 | 16.90 | 15,436.70 |
| The 1960s | Most energy-intensive | 193.25 | 555.57 | 1414.46 | 6.50 | 11,553.60 |
| The 1970s | Least energy-intensive | 787.60 | 2501.26 | 5759.85 | 65.80 | 37,855.40 |
| The 1970s | Most energy-intensive | 485.10 | 1460.07 | 3318.96 | 14.70 | 29,737.30 |
| The 1980s | Least energy-intensive | 1832.10 | 5568.41 | 10,423.51 | 129.60 | 50,316.50 |
| The 1980s | Most energy-intensive | 873.20 | 2306.36 | 4384.77 | 27.70 | 31,836.00 |
| The 1990s | Least energy-intensive | 2950.90 | 9604.14 | 16,286.32 | 80.50 | 102,924.30 |
| The 1990s | Most energy-intensive | 1276.85 | 3034.87 | 5404.51 | 25.30 | 29,446.20 |
| The 2000s | Least energy-intensive | 3954.40 | 10,175.94 | 18,271.44 | 63.80 | 110,074.70 |
| The 2000s | Most energy-intensive | 1602.30 | 4847.67 | 10,339.06 | 24.80 | 75,089.60 |
| E | ||||||
| The 1960s | Least energy-intensive | 2.50 | 4.83 | 8.95 | 0.10 | 75.70 |
| The 1960s | Most energy-intensive | 29.00 | 70.23 | 135.82 | 2.60 | 1056.00 |
| The 1970s | Least energy-intensive | 7.00 | 18.22 | 35.64 | 0.40 | 225.20 |
| The 1970s | Most energy-intensive | 96.30 | 248.52 | 513.12 | 7.10 | 5325.20 |
| The 1980s | Least energy-intensive | 23.70 | 56.56 | 84.23 | 1.50 | 348.40 |
| The 1980s | Most energy-intensive | 202.60 | 494.83 | 782.74 | 20.30 | 5858.60 |
| The 1990s | Least energy-intensive | 29.30 | 66.00 | 86.92 | 1.00 | 350.40 |
| The 1990s | Most energy-intensive | 219.90 | 486.65 | 689.62 | 8.90 | 3570.80 |
| The 2000s | Least energy-intensive | 35.00 | 78.93 | 126.08 | 0.70 | 858.00 |
| The 2000s | Most energy-intensive | 355.60 | 777.17 | 1158.60 | 12.00 | 6775.10 |
Appendix B
References
- Menghi, R.; Papetti, A.; Germani, M.; Marconi, M. Energy efficiency of manufacturing systems: A review of energy assessment methods and tools. J. Clean. Prod. 2019, 240, 118276. [Google Scholar] [CrossRef]
- Kanellakis, M.; Martinopoulos, G.; Zachariadis, T. European energy policy-A review. Energy Policy 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Wang, C.N.; Ho, H.X.T.; Hsueh, M.H. An integrated approach for estimating the energy efficiency of seventeen countries. Energies 2017, 10, 1597. [Google Scholar] [CrossRef]
- Gerarden, T.D.; Newell, R.G.; Stavins, R.N. Assessing the Energy-Efficiency Gap. J. Econ. Lit. 2017, 55, 1486–1525. [Google Scholar] [CrossRef]
- Blass, V.; Corbett, C.J.; Delmas, M.A.; Muthulingam, S. Top management and the adoption of energy efficiency practices: Evidence from small and medium-sized manufacturing firms in the US. Energy 2014, 65, 560–571. [Google Scholar] [CrossRef]
- Boyd, G.A.; Lee, J.M. Measuring plant level energy efficiency and technical change in the U.S. metal-based durable manufacturing sector using stochastic frontier analysis. Energy Econ. 2019, 81, 159–174. [Google Scholar] [CrossRef]
- Filipović, S.; Verbič, M.; Radovanović, M. Determinants of energy intensity in the European Union: A panel data analysis. Energy 2015, 92, 547–555. [Google Scholar] [CrossRef]
- Bentzen, J. Estimating the rebound effect in US manufacturing energy consumption. Energy Econ. 2004, 26, 123–134. [Google Scholar] [CrossRef]
- Bartelsman, E.J.; Gray, W. The NBER Manufacturing Productivity Database; Working Paper 205; National Bureau of Economic Research: Cambridge, MA, USA, 1996. [Google Scholar] [CrossRef]
- Parker, S.; Liddle, B. Energy efficiency in the manufacturing sector of the OECD: Analysis of price elasticities. Energy Econ. 2016, 58, 38–45. [Google Scholar] [CrossRef]
- Badunenko, O.; Kumbhakar, S.C. Economies of scale, technical change and persistent and time-varying cost efficiency in Indian banking: Do ownership, regulation and heterogeneity matter? Eur. J. Oper. Res. 2017, 260, 789–803. [Google Scholar] [CrossRef]
- Wei, T. Impact of energy efficiency gains on output and energy use with Cobb-Douglas production function. Energy Policy 2007, 35, 2023–2030. [Google Scholar] [CrossRef]
- Saunders, H.D. Historical evidence for energy efficiency rebound in 30 US sectors and a toolkit for rebound analysts. Technol. Forecast. Soc. Chang. 2013, 80, 1317–1330. [Google Scholar] [CrossRef]
- Allcott, H.; Knittel, C.; Taubinsky, D. Tagging and Targeting of Energy Efficiency Subsidies. Am. Econ. Rev. 2015, 105, 187–191. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lovell, C.A.K. Stochastic Frontier Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lovell, C.A.K. Production Frontiers; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar] [CrossRef]
- Kumbhakar, S.C. The Measurement and Decomposition of Cost-Inefficiency: The Translog Cost System. Oxf. Econ. Pap. New Ser. 1991, 43, 667–683. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Heshmati, A. Efficiency Measurement in Swedish Dariy Farms: An Application of Rotating Panel Data. Am. J. Agric. Econ. 1995, 77, 660–674. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Hjalmarsson, L. Technical Efficiency and Technical Progress in Swedish Dairy Farms. In The Measurement of Productive Efficiency. Techniques and Applications; Fried, H.O., Lovell, C.A.K., Schmidt, S.S., Eds.; Oxford University Press: Oxford, UK, 1993; pp. 256–270. [Google Scholar]
- Kumbhakar, S.C.; Hjalmarsson, L. Labour-Use Efficiency in Swedish Social Insurance Offices. J. Appl. Econ. 1995, 10, 33–47. [Google Scholar] [CrossRef]
- Greene, H.W. Reconsidering Heterogeneity in Panel Data Estimators of the Stochastic Frontier Model. J. Econ. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lien, G.; Hardaker, J.B. Technical Efficiency in Competing Panel Data Models: A Study of Norwegian Grain Farming. J. Product. Anal. 2014, 41, 321–337. [Google Scholar] [CrossRef]
- Mukherjee, K. Energy use efficiency in U.S. manufacturing: A nonparametric analysis. Energy Econ. 2008, 30, 76–96. [Google Scholar] [CrossRef]
- Mukherjee, K. Energy use efficiency in the Indian manufacturing sector: An interstate analysis. Energy Policy 2008, 36, 662–672. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Linear programming models for measuring economy-wide energy efficiency performance. Energy Policy 2008, 36, 2911–2916. [Google Scholar] [CrossRef]
- Mousavi-Avval, S.H.; Rafiee, S.; Jafari, A.; Mohammadi, A. Improving energy use efficiency of canola production using data envelopment analysis (DEA) approach. Energy 2011, 36, 2765–2772. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Boyd, G.A. A Method for Measuring the Efficiency Gap between Average and Best Practice Energy Use: The ENERGY STAR Industrial Energy Performance Indicator. J. Ind. Ecol. 2005, 9, 51–65. [Google Scholar] [CrossRef][Green Version]
- Boyd, G.A. Estimating Plant Level Energy Efficiency with a Stochastic Frontier. Energy J. 2008, 29, 23–43. [Google Scholar] [CrossRef]
- Filippini, M.; Hunt, L.C. US residential energy demand and energy efficiency: A stochastic demand frontier approach. Energy Econ. 2012, 34, 1484–1491. [Google Scholar] [CrossRef]
- Shui, H.; Jin, X.; Ni, J. Manufacturing productivity and energy efficiency: A stochastic efficiency frontier analysis. Int. J. Energy Res. 2015, 39, 1649–1663. [Google Scholar] [CrossRef]
- Farsi, M.; Filippini, M.; Greene, W. Application of Panel Data Models in Benchmarking Analysis of the Electricity Distribution Sector. Ann. Public Coop. Econ. 2006, 77, 271–290. [Google Scholar] [CrossRef]
- Filippini, M.; Hunt, L.C. Measuring persistent and transient energy efficiency in the US. Energy Effic. 2016, 9, 663–675. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lien, G. Yardstick Regulation of Electricity Distribution – Disentangling Short-run and Long-run Inefficiencies. Energy J. 2017, 38, 1944–9089. [Google Scholar] [CrossRef]
- Kumbhakar, S.C. Specification and estimation of multiple output technologies: A primal approach. Eur. J. Oper. Res. 2013, 231, 465–473. [Google Scholar] [CrossRef]
- Diewert, W.E. Functional Forms for Revenue and Factor Requirements Functions. Int. Econ. Rev. 1974, 15, 119–130. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.A.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econ. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; van den Broeck, J. Efficiency estimation from {C}obb-{D}ouglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Colombi, R.; Kumbhakar, S.C.; Martini, G.; Vittadini, G. Closed-skew normality in stochastic frontiers with individual effects and long/short-run efficiency. J. Product. Anal. 2014, 42, 123–136. [Google Scholar] [CrossRef]
- Tsionas, E.G.; Kumbhakar, S.C. Firm Heterogeneity, Persistent And Transient Technical Inefficiency: A Generalized True Random Effects model. J. Appl. Econ. 2014, 29, 110–132. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Product. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Cornwell, C.; Schmidt, P.; Sickles, R.C. Production frontiers with cross-sectional and time-series variation in efficiencylevels. J. Econ. 1990, 46, 185–200. [Google Scholar] [CrossRef]
- Kumbhakar, S.C. Production frontiers, panel data, and time-varying technical inefficiency. J. Econ. 1990, 46, 201–211. [Google Scholar] [CrossRef]
- Hsiao, W.L.; Hu, J.L.; Hsiao, C.; Chang, M.C. Energy Efficiency of the Baltic Sea Countries: An Application of Stochastic Frontier Analysis. Energies 2019, 12, 104. [Google Scholar] [CrossRef]
- Thollander, P.; Danestig, M.; Rohdin, P. Energy policies for increased industrial energy efficiency: Evaluation of a local energy programme for manufacturing SMEs. Energy Policy 2007, 35, 5774–5783. [Google Scholar] [CrossRef]
- Thollander, P.; Backlund, S.; Trianni, A.; Cagno, E. Beyond barriers—A case study on driving forces for improved energy efficiency in the foundry industries in Finland, France, Germany, Italy, Poland, Spain, and Sweden. Appl. Energy 2013, 111, 636–643. [Google Scholar] [CrossRef]
- Brunke, J.C.; Johansson, M.; Thollander, P. Empirical investigation of barriers and drivers to the adoption of energy conservation measures, energy management practices and energy services in the Swedish iron and steel industry. J. Clean. Prod. 2014, 84, 509–525. [Google Scholar] [CrossRef]
- Trianni, A.; Cagno, E.; Worrell, E.; Pugliese, G. Empirical investigation of energy efficiency barriers in Italian manufacturing SMEs. Energy 2013, 49, 444–458. [Google Scholar] [CrossRef]
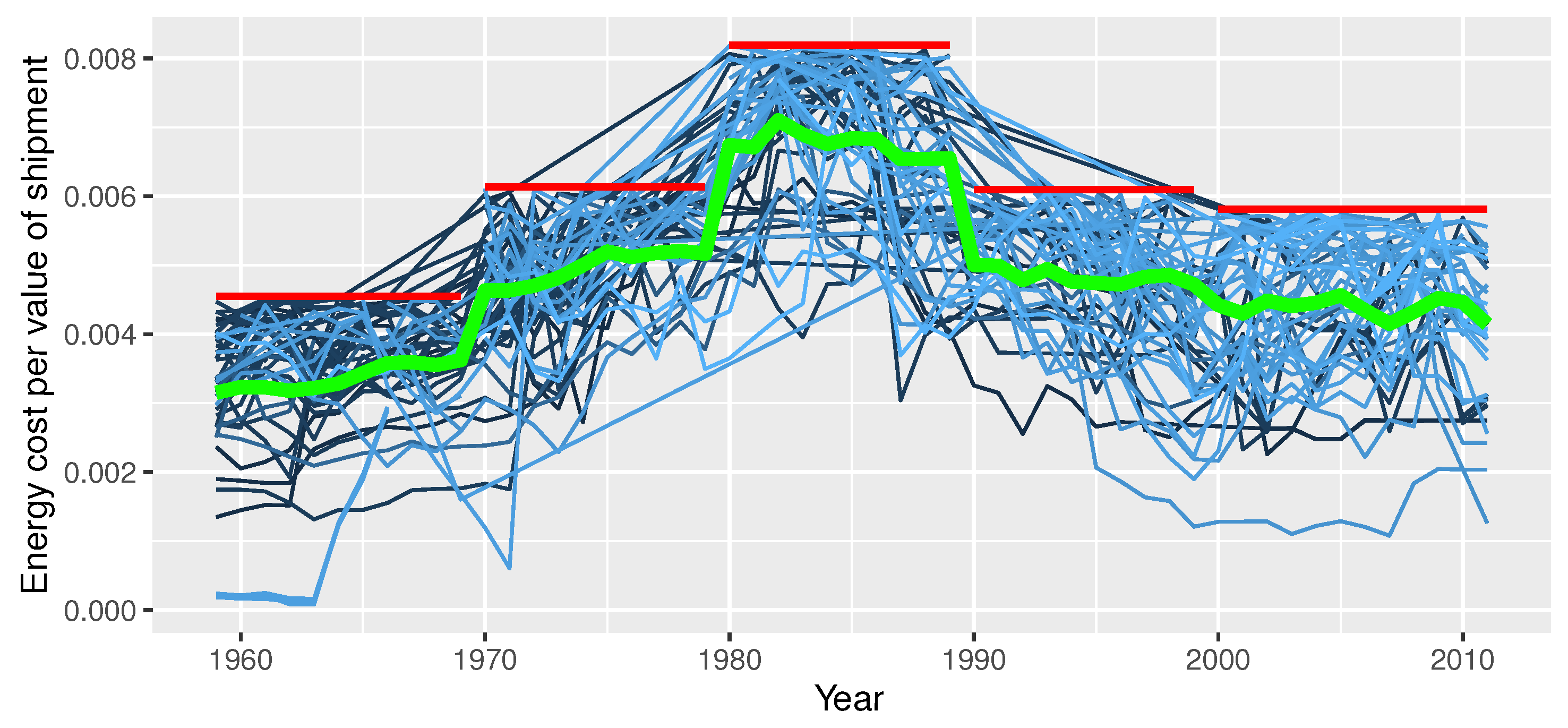
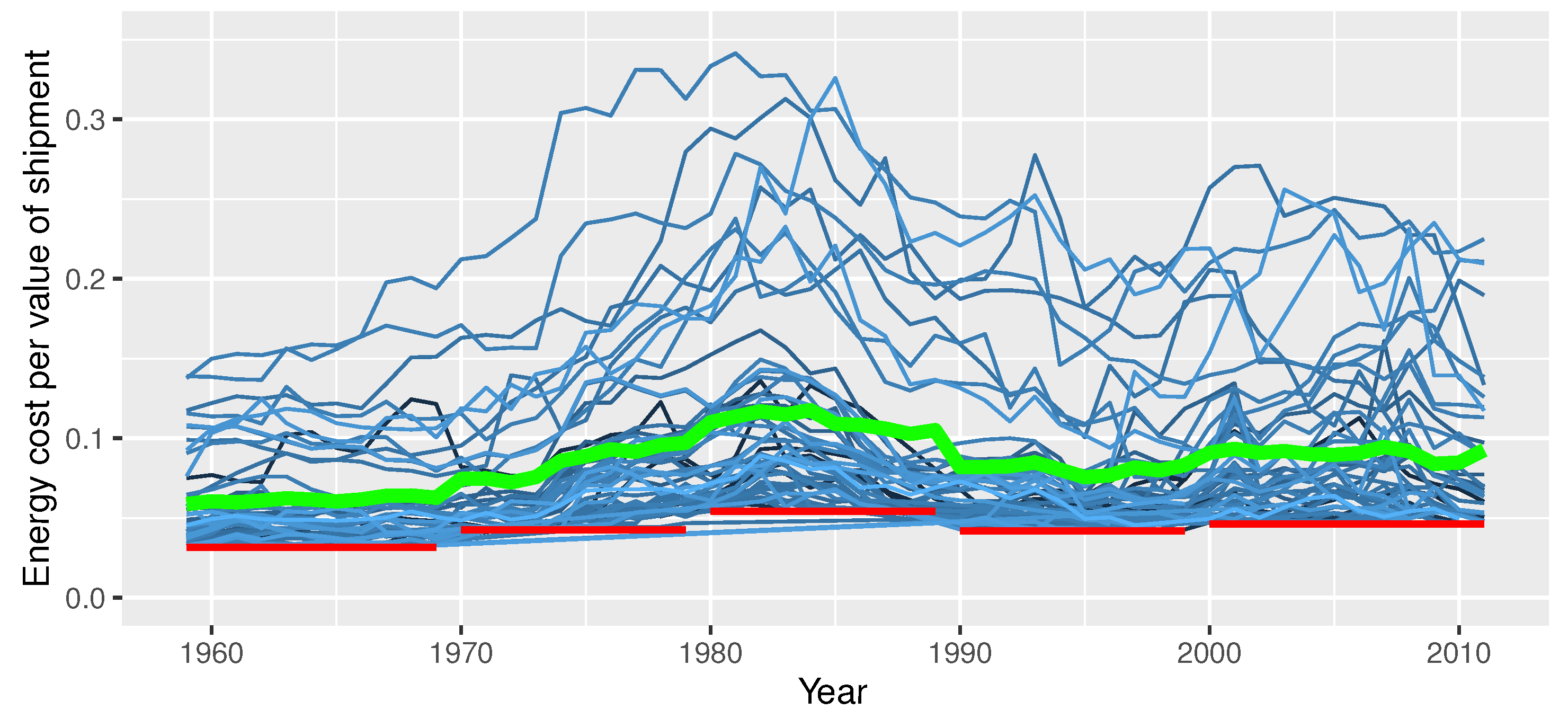
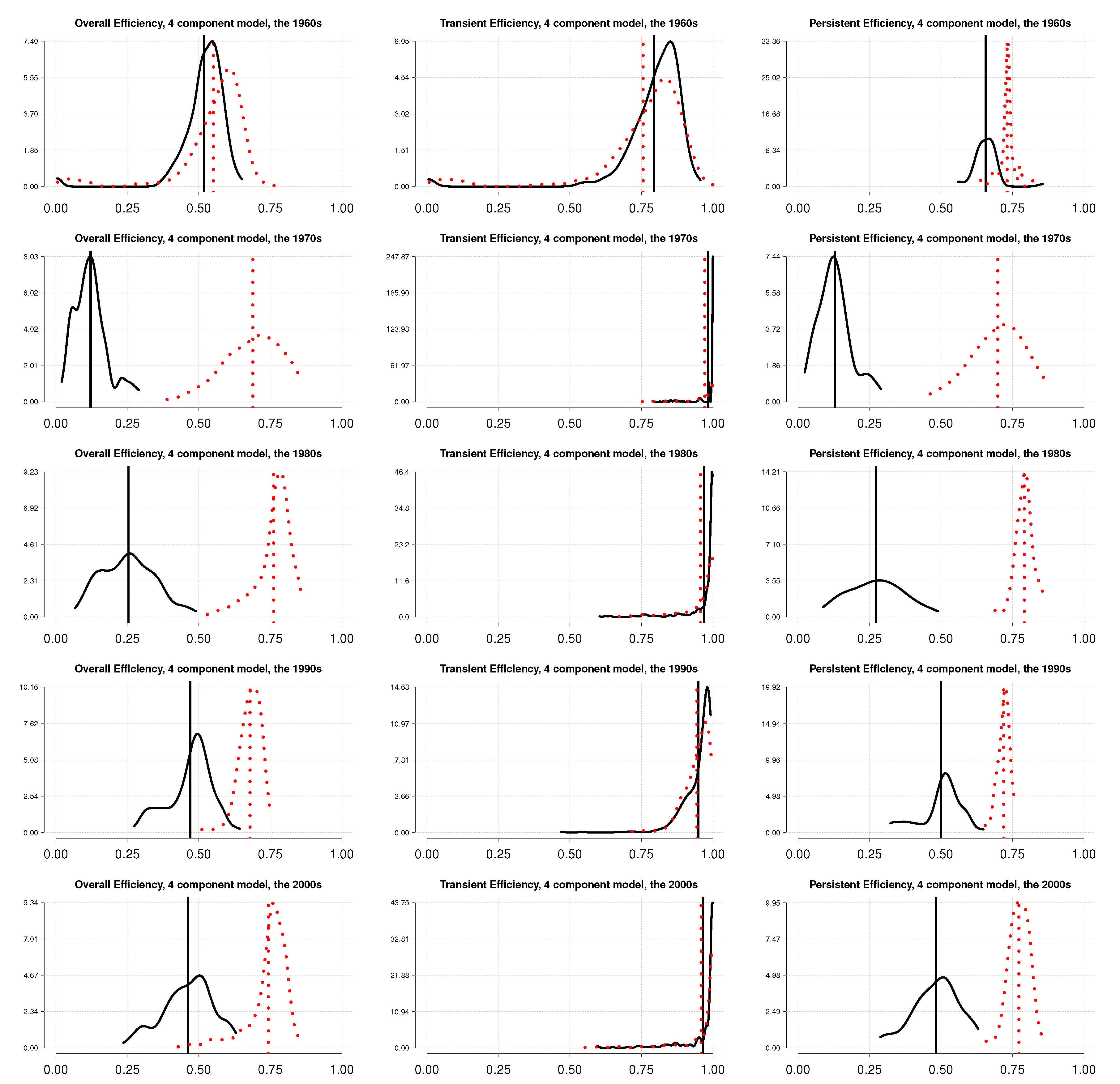
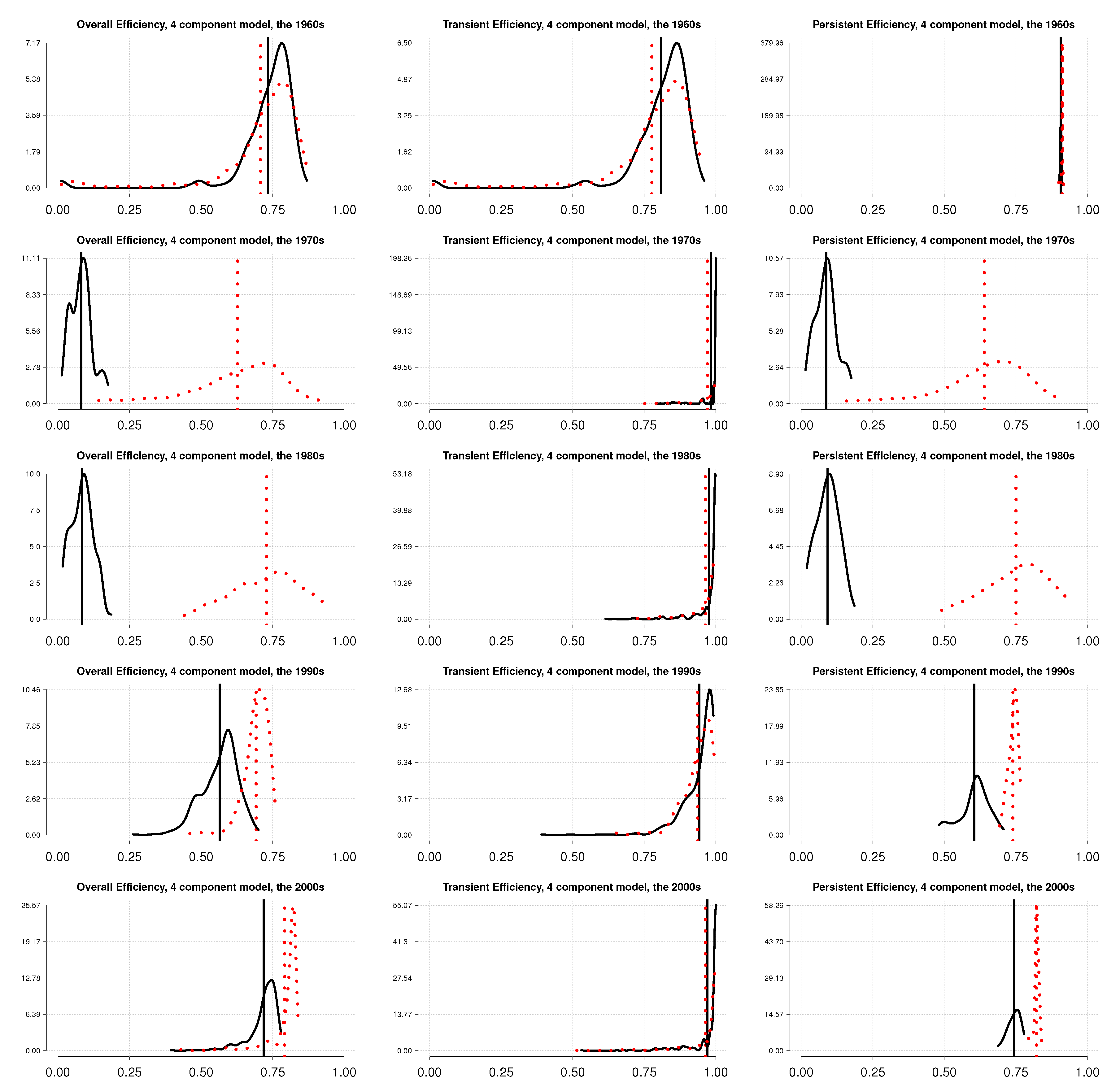
| Time Period | Industries | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|---|
| All | Both most and least energy-intensive | 0.0417 | 0.0489 | 0.0565 | 0.00008 | 0.3414 |
| All | Least energy-intensive | 0.0045 | 0.0046 | 0.0015 | 0.00008 | 0.0082 |
| All | Most energy-intensive | 0.0690 | 0.0873 | 0.0527 | 0.03169 | 0.3414 |
| The 1960s | Least energy-intensive | 0.0035 | 0.0033 | 0.0011 | 0.00008 | 0.0046 |
| The 1960s | Most energy-intensive | 0.0489 | 0.0627 | 0.0333 | 0.03169 | 0.2006 |
| The 1970s | Least energy-intensive | 0.0049 | 0.0048 | 0.0009 | 0.00061 | 0.0061 |
| The 1970s | Most energy-intensive | 0.0706 | 0.0881 | 0.0513 | 0.04258 | 0.3311 |
| The 1980s | Least energy-intensive | 0.0068 | 0.0065 | 0.0012 | 0.00304 | 0.0082 |
| The 1980s | Most energy-intensive | 0.0850 | 0.1128 | 0.0639 | 0.05426 | 0.3414 |
| The 1990s | Least energy-intensive | 0.0047 | 0.0046 | 0.0010 | 0.00121 | 0.0061 |
| The 1990s | Most energy-intensive | 0.0645 | 0.0819 | 0.0477 | 0.04202 | 0.2775 |
| The 2000s | Least energy-intensive | 0.0042 | 0.0042 | 0.0011 | 0.00108 | 0.0058 |
| The 2000s | Most energy-intensive | 0.0711 | 0.0921 | 0.0513 | 0.04630 | 0.2709 |
| Parameter | The 1960s | The 1970s | The 1980s | The 1990s | The 2000s | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | 1.430 | (24.95) | 1.094 | (6.44) | 1.635 | (7.17) | 1.109 | (6.55) | 2.459 | (16.77) |
| 0.5 * log(K/E) | 0.020 | (1.51) | 0.019 | (0.39) | 0.028 | (0.24) | 0.091 | (3.14) | −0.031 | (−1.37) |
| 0.5 * log(L/E) | 0.107 | (9.48) | −0.041 | (−3.25) | 0.092 | (4.83) | −0.031 | (−1.77) | 0.072 | (2.69) |
| 0.5 * log(NEM/E) | 0.189 | (17.96) | 0.124 | (6.50) | 0.187 | (6.92) | 0.160 | (6.52) | 0.071 | (2.56) |
| 0.5 * log(Y) | 0.002 | (0.41) | −0.017 | (−0.95) | 0.044 | (14.23) | 0.043 | (21.12) | 0.054 | (29.65) |
| 0.5 * Trend | 0.003 | (4.33) | (−0.45) | 0.004 | (3.40) | 0.003 | (2.72) | 0.003 | (4.58) | |
| log(K/E) | −0.082 | (−2.68) | 0.118 | (0.92) | −0.142 | (−1.21) | 0.026 | (0.32) | 0.023 | (0.32) |
| log(K/E) * log(L/E) | 0.039 | (4.53) | 0.061 | (6.54) | 0.002 | (0.08) | −0.031 | (−2.72) | −0.052 | (−2.78) |
| log(K/E) * log(NEM/E) | −0.037 | (−3.89) | −0.057 | (−2.24) | −0.006 | (−0.10) | −0.064 | (−2.88) | 0.058 | (2.45) |
| log(K/E) * log(Y) | 0.020 | (3.53) | 0.002 | (0.29) | 0.042 | (2.29) | 0.016 | (3.78) | 0.023 | (2.52) |
| log(K/E) * Trend | 0.005 | (2.83) | 0.006 | (1.12) | 0.005 | (1.59) | 0.004 | (1.93) | 0.002 | (1.32) |
| log(L/E) | 0.493 | (17.03) | 0.418 | (4.42) | 0.501 | (6.96) | 0.862 | (11.33) | 0.903 | (10.50) |
| log(L/E) * log(NEM/E) | −0.148 | (−10.56) | −0.032 | (−2.54) | −0.137 | (−4.89) | −0.016 | (−1.08) | −0.059 | (−2.67) |
| log(L/E) * log(Y) | −0.011 | (−1.26) | −0.030 | (−1.42) | 0.024 | (1.63) | −0.051 | (−6.52) | −0.032 | (−7.93) |
| log(L/E) * Trend | 0.006 | (5.75) | −0.002 | (−0.42) | −0.001 | (−0.84) | 0.002 | (0.98) | −0.006 | (−2.65) |
| log(NEM/E) | 0.431 | (23.41) | 0.242 | (8.68) | 0.363 | (4.87) | 0.331 | (5.19) | 0.061 | (1.06) |
| log(NEM/E) * log(Y) | −0.018 | (−2.14) | 0.018 | (1.00) | −0.063 | (−3.79) | −0.028 | (−6.73) | −0.023 | (−2.72) |
| log(NEM/E) * Trend | −0.007 | (−6.50) | −0.005 | (−1.01) | −0.005 | (−2.51) | −0.007 | (−3.93) | 0.003 | (1.62) |
| log(Y) | −0.932 | (−76.70) | −0.772 | (−10.27) | −1.014 | (−37.43) | −0.991 | (−65.69) | −1.059 | (−60.64) |
| log(Y) * Trend | (−0.16) | −0.001 | (−0.70) | −0.001 | (−0.50) | −0.001 | (−1.49) | −0.005 | (−4.01) | |
| Trend | −0.017 | (−2.39) | 0.017 | (1.14) | 0.006 | (0.28) | 0.020 | (2.40) | 0.012 | (0.81) |
| Random effects component: | ||||||||||
| lnVARv0iIntercept | −3.820 | (−95.00) | −2.548 | (−15.71) | −2.978 | (−12.85) | −2.066 | (−65.46) | −3.204 | (−67.88) |
| Persistent inefficiency component: | ||||||||||
| lnVARu0iIntercept | −4.570 | (−56.15) | −3.936 | (−5.12) | −2.197 | (−21.74) | −3.943 | (−44.12) | -0.764 | (−23.66) |
| Random noise component: | ||||||||||
| lnVARvitIntercept | −6.571 | (−97.67) | −6.445 | (−49.51) | −6.455 | (−47.84) | −6.379 | (−44.86) | −7.431 | (−44.92) |
| Transient inefficiency component: | ||||||||||
| lnVARuitIntercept | −4.548 | (−4.04) | −7.251 | (−4.62) | −3.859 | (−8.03) | −5.909 | (−3.74) | −3.658 | (−13.88) |
| lnVARuitTrend | −1.372 | (−3.10) | 0.462 | (0.80) | −1.469 | (−5.51) | −0.931 | (−2.12) | −0.634 | (−6.76) |
| lnVARuitTrend | 0.098 | (2.91) | −0.067 | (−1.17) | 0.139 | (5.54) | 0.104 | (3.09) | 0.056 | (7.84) |
| Sample Size | ||||||||||
| N | 105 | 113 | 104 | 98 | 109 | |||||
| 968 | 850 | 835 | 817 | 1005 | ||||||
| Sim. logL | 1497.73 | 1144.89 | 1055.05 | 1021.78 | 1067.50 | |||||
| Parameter | The 1960s | The 1970s | The 1980s | The 1990s | The 2000s | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | −8.488 | (−21.97) | −4.999 | (−8.78) | −4.001 | (−42.61) | −7.573 | (−33.18) | −7.973 | (−26.42) |
| 0.5 * log(K) | 0.019 | (0.70) | 0.131 | (1.90) | 0.057 | (2.29) | −0.038 | (−1.79) | −0.130 | (−5.22) |
| 0.5 * log(L) | −0.782 | (−15.67) | −0.087 | (−3.52) | 0.106 | (6.43) | 0.047 | (1.26) | −0.049 | (−1.44) |
| 0.5 * log(NEM) | −0.486 | (−5.73) | 0.258 | (6.97) | 0.127 | (4.43) | 0.791 | (10.17) | −0.256 | (−15.50) |
| 0.5 * log(Y) | 0.849 | (6.90) | 0.353 | (7.99) | −0.310 | (−6.63) | 0.300 | (5.12) | −0.678 | (−24.19) |
| 0.5 * Trend | (−0.30) | −0.009 | (−3.52) | −0.027 | (−15.93) | −0.006 | (−3.63) | −0.017 | (−11.00) | |
| log(K) | 1.504 | (26.62) | −0.552 | (−2.51) | −0.270 | (−3.07) | −0.014 | (−0.20) | 0.129 | (1.03) |
| log(K) * log(L) | 0.349 | (9.52) | −0.038 | (−0.97) | −0.130 | (−4.60) | −0.055 | (−1.17) | −0.007 | (−0.16) |
| log(K) * log(NEM) | −0.344 | (−10.11) | 0.198 | (2.41) | −0.149 | (−10.31) | 0.068 | (1.75) | −0.124 | (−3.52) |
| log(K) * log(Y) | −0.158 | (−9.43) | −0.150 | (−4.94) | 0.257 | (21.41) | 0.056 | (2.08) | 0.275 | (16.63) |
| log(K) * Trend | 0.023 | (7.19) | 0.008 | (1.50) | −0.020 | (−6.35) | 0.004 | (1.15) | 0.006 | (1.55) |
| log(L) | 1.022 | (11.95) | −0.138 | (−1.37) | 0.464 | (7.54) | 0.448 | (4.34) | −0.114 | (−2.11) |
| log(L) * log(NEM) | 0.982 | (9.05) | −0.080 | (−1.22) | 0.007 | (0.19) | −0.413 | (−4.51) | () | |
| log(L) * log(Y) | −0.758 | (−7.77) | 0.167 | (1.90) | 0.017 | (0.36) | 0.400 | (4.23) | 0.065 | (1.25) |
| log(L) * Trend | −0.023 | (−2.89) | −0.006 | (−0.73) | 0.003 | (0.76) | −0.007 | (−1.45) | (−0.04) | |
| log(NEM) | 0.763 | (5.20) | 0.148 | (0.64) | 0.527 | (4.98) | 0.792 | (8.17) | 0.005 | (0.04) |
| log(NEM) * log(Y) | −0.052 | (−1.69) | −0.405 | (−8.70) | 0.007 | (1.01) | −0.684 | (−66.10) | 0.339 | (29.12) |
| log(NEM) * Trend | 0.039 | (3.99) | 0.001 | (0.11) | −0.019 | (−2.58) | 0.002 | (0.26) | −0.005 | (−0.94) |
| log(Y) | −0.432 | (−1.28) | 1.182 | (5.33) | 0.393 | (2.43) | 0.954 | (12.19) | 1.475 | (6.87) |
| log(Y) * Trend | −0.030 | (−1.75) | 0.004 | (0.20) | 0.036 | (2.78) | −0.002 | (−0.13) | 0.005 | (0.43) |
| Trend | −0.044 | (−2.14) | 0.061 | (2.18) | 0.105 | (4.91) | 0.018 | (0.78) | 0.085 | (3.62) |
| Random effects component: | ||||||||||
| lnVARv0iIntercept | 0.567 | (25.03) | −2.153 | (−24.98) | −1.542 | (−37.01) | −0.367 | (−5.24) | −0.643 | (−26.28) |
| Persistent inefficiency component: | ||||||||||
| lnVARu0iIntercept | −1.363 | (−23.33) | 0.459 | (10.69) | −0.469 | (−15.46) | −0.730 | (−9.23) | −1.022 | (−19.82) |
| Random noise component: | ||||||||||
| lnVARvitIntercept | −6.180 | (−25.73) | −4.043 | (−66.60) | −4.723 | (−63.28) | −4.185 | (−57.02) | −4.079 | (−74.23) |
| Transient inefficiency component: | ||||||||||
| lnVARuitIntercept | −3.195 | (−14.71) | −1.013 | (−1.92) | −17.732 | (−5.89) | −9.850 | (−8.06) | −0.320 | (−0.88) |
| lnVARuitTrend | 0.214 | (7.36) | −2.225 | (−4.11) | 1.531 | (5.13) | 0.673 | (5.07) | −1.666 | (−8.42) |
| Sample Size | ||||||||||
| N | 105 | 113 | 104 | 98 | 109 | |||||
| 968 | 850 | 835 | 817 | 1005 | ||||||
| Sim. logL | −274.84 | 155.72 | 328.12 | 163.25 | 136.60 | |||||
| Parameter | The 1960s | The 1970s | The 1980s | The 1990s | The 2000s | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | −5.788 | (−27.29) | −4.111 | (−13.84) | −4.328 | (−19.92) | −6.833 | (−27.68) | −6.349 | (−19.86) |
| 0.5 * log(K) | −0.055 | (−1.54) | 0.091 | (3.74) | 0.011 | (0.67) | −0.046 | (−1.66) | −0.109 | (−5.19) |
| 0.5 * log(L) | −0.480 | (−13.99) | −0.036 | (−1.30) | 0.246 | (19.91) | 0.183 | (8.27) | 0.186 | (7.85) |
| 0.5 * log(NEM) | −0.203 | (−1.30) | −0.010 | (−0.50) | 0.047 | (1.19) | 0.176 | (5.53) | 0.069 | (3.56) |
| 0.5 * log(wE/wY) | −0.340 | (−7.45) | −0.005 | (−0.24) | −0.071 | (−1.55) | −0.067 | (−0.23) | −0.105 | (−2.50) |
| 0.5 * Trend | (0.13) | −0.011 | (−4.85) | −0.021 | (−12.95) | −0.007 | (−4.07) | −0.018 | (−12.46) | |
| log(K) | 1.180 | (8.92) | −0.377 | (−3.85) | 0.275 | (5.94) | 0.852 | (18.24) | 1.061 | (14.19) |
| log(K) * log(L) | 0.207 | (6.18) | 0.020 | (0.64) | 0.029 | (1.27) | 0.060 | (1.30) | 0.065 | (2.07) |
| log(K) * log(NEM) | −0.264 | (−108.79) | −0.005 | (−0.72) | −0.003 | (−1.84) | −0.035 | (−12.27) | −0.012 | (−3.90) |
| log(K) * log(wE/wY) | 0.088 | (0.93) | −0.003 | (−0.10) | 0.113 | (3.90) | −0.075 | (−0.87) | −0.070 | (−1.43) |
| log(K) * Trend | 0.016 | (5.66) | 0.019 | (5.67) | −0.006 | (−3.55) | 0.009 | (3.87) | 0.006 | (2.00) |
| log(L) | −0.426 | (−1.15) | 0.675 | (8.24) | 0.095 | (1.04) | 1.736 | (26.02) | 0.452 | (5.57) |
| log(L) * log(NEM) | 0.336 | (3.92) | −0.057 | (−1.93) | −0.146 | (−4.47) | −0.311 | (−6.62) | −0.163 | (−4.85) |
| log(L) * log(wE/wY) | 0.050 | (0.47) | 0.151 | (3.91) | −0.031 | (−0.71) | 0.034 | (0.28) | 0.055 | (1.06) |
| log(L) * Trend | −0.027 | (−6.74) | −0.010 | (−1.85) | 0.019 | (7.95) | 0.001 | (0.40) | 0.010 | (2.29) |
| log(NEM) | 1.128 | (2.28) | 0.706 | (11.62) | 0.636 | (4.38) | 0.292 | (3.91) | 0.561 | (14.16) |
| log(NEM) * log(wE/wY) | −0.053 | (−0.39) | −0.090 | (−2.58) | −0.079 | (−1.62) | −0.111 | (−1.01) | −0.019 | (−0.49) |
| log(NEM) * Trend | 0.023 | (4.45) | −0.004 | (−0.83) | −0.006 | (−2.29) | −0.013 | (−3.77) | −0.006 | (−1.55) |
| log(wE/wY) | −0.542 | (−2.10) | 0.114 | (0.76) | −0.094 | (−0.54) | 1.371 | (2.97) | 0.533 | (1.91) |
| log(wE/wY) * Trend | −0.005 | (−0.62) | 0.024 | (5.10) | 0.021 | (4.38) | 0.013 | (0.65) | 0.011 | (1.43) |
| Trend | −0.093 | (−2.22) | 0.092 | (4.71) | 0.113 | (8.89) | 0.056 | (3.85) | 0.111 | (6.40) |
| Random effects component: | ||||||||||
| lnVARv0iIntercept | 0.769 | (20.77) | −3.036 | (−20.12) | −3.841 | (−37.08) | −0.039 | (−0.93) | −0.071 | (−3.18) |
| Persistent inefficiency component: | ||||||||||
| lnVARu0iIntercept | −4.199 | (−9.11) | 1.390 | (29.23) | 0.433 | (15.01) | −0.981 | (−13.94) | −2.428 | (−18.20) |
| Random noise component: | ||||||||||
| lnVARvitIntercept | −5.714 | (−8.29) | −4.004 | (−70.89) | −4.749 | (−71.78) | −4.218 | (−57.99) | −3.912 | (−74.27) |
| Transient inefficiency component: | ||||||||||
| lnVARuitIntercept | −3.459 | (−13.87) | −1.055 | (−1.88) | −18.646 | (−6.10) | −9.658 | (−9.10) | −0.409 | (−1.06) |
| lnVARuitTrend | 0.248 | (7.63) | −2.300 | (−4.16) | 1.572 | (5.21) | 0.688 | (5.86) | −1.765 | (−7.76) |
| Sample Size | ||||||||||
| N | 105 | 113 | 104 | 98 | 109 | |||||
| 968 | 850 | 835 | 817 | 1005 | ||||||
| Sim. logL | −290.77 | 144.77 | 376.35 | 151.07 | 84.05 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badunenko, O.; Kumbhakar, S.C. Energy Intensity and Long- and Short-Term Efficiency in US Manufacturing Industry. Energies 2020, 13, 3954. https://doi.org/10.3390/en13153954
Badunenko O, Kumbhakar SC. Energy Intensity and Long- and Short-Term Efficiency in US Manufacturing Industry. Energies. 2020; 13(15):3954. https://doi.org/10.3390/en13153954
Chicago/Turabian StyleBadunenko, Oleg, and Subal C. Kumbhakar. 2020. "Energy Intensity and Long- and Short-Term Efficiency in US Manufacturing Industry" Energies 13, no. 15: 3954. https://doi.org/10.3390/en13153954
APA StyleBadunenko, O., & Kumbhakar, S. C. (2020). Energy Intensity and Long- and Short-Term Efficiency in US Manufacturing Industry. Energies, 13(15), 3954. https://doi.org/10.3390/en13153954





