Estimation of Radioactivity Release Activity Using Non-Linear Kalman Filter-Based Estimation Techniques

Abstract

The estimation of radioactivity release following an accident in a nuclear power plant is crucial due to its short and long-term impacts on the surrounding population and the environment. In the case of any accidental release, the activity needs to be estimated quickly and reliably to effectively plan a rapid emergency response and design an appropriate evacuation strategy. The accurate prediction of incurred dose rate during normal or accident scenario is another important aspect. In this article, three different non-linear estimation techniques, extended Kalman filter, unscented Kalman filter, and cubature Kalman filter are proposed in order to estimate release activity and to improve the prediction of dose rates. Radionuclide release rate, average wind speed, and height of release are estimated using the dose rate monitors data collected in proximity of the release point. Further, the estimates are employed to improve the prediction of dose rates. The atmospheric dispersion phenomenon of radioactivity release is modelled using the Gaussian plume model. The Gaussian plume model is then employed for the calculation of dose rates. A variety of atmospheric and accident related scenarios for single source and multiple sources are studied in order to assess the efficacy of the proposed filters. Statistical measures have been used in order to validate the performance of the proposed approaches.

1. Introduction

Nuclear power plants (NPP) and installations are potential sources of release of radionuclides into the atmosphere. Some radionuclides may release routinely and others may arise out of accidental situations. Radionuclides release estimation in the vicinity of a nuclear power plant is thus a crucial and regular activity. It plays a deciding role while performing various important tasks, such as emergency planning, sheltering, evacuation management, and in measuring environmental impact during normal or accidental scenarios [1]. Particularly, at the initial release stage, a good estimate of the radionuclide spread is of paramount importance. These requirements make radionuclide release estimation a key regulatory problem.

The early release of radionuclides from nuclear installations forms radioactive plume in the atmosphere. These plumes are transported and dispersed by the winds and turbulence in the surroundings. The release of radioactivity can cause significant doses in the surroundings [2]. For instance, these radionuclides may get deposited on vegetation and find their way to human metabolism [3]. Environmental radiation monitoring detectors or dose rate monitors are placed in the vicinity of an NPP to measure the dose rates. These monitors provide on-line data, which can be used to estimate the source term and other relevant parameters [4]. During radiological emergency, it is sometimes difficult to exactly know the amount of release or plume rise. Moreover, the data received from such measurements usually contain noise and affect their use in estimating the exact source of release [5]. The accurate and timely prediction of radioactivity release is essential to evaluate the adequacy of emergency response measures, and to know its short-term or long-term environmental impact [6].

The environmental monitors placed around a nuclear installation employ radionuclide release information to measure dose rates [7]. The calculation of dose rate is dependent on the plume shape and the distribution of radionuclide concentration. The dispersion and transport of radionuclides in the atmosphere is governed by the atmospheric dispersion modelling [8,9,10]. At the early release stage, a rapid evaluation of the imminent radionuclide spread is required [11]. Thus, the dispersion model should be fast, reliable, and easy-to-use, such as Gaussian models. The Gaussian plume dispersion (GPD) model has been widely used in the literature with different simplifications [12]. The GPD model is suitable for modelling radionuclide release from point sources. It only requires a limited amount of input information and are usually time efficient during setting up and execution. The rendered results are trustworthy for near-field dispersion cases. Based on this rationale, the GPD model has been considered in this work to model radionuclide release in atmosphere and for the calculation of dose rates.

In the literature, different estimation techniques have been applied in order to solve problems of dispersion parameter estimation, such as predication improvement or data assimilation [13,14,15,16,17,18,19,20,21,22,23] and source term estimation or source inversion [24,25,26,27,28,29,30,31,32,33,34]. A data assimilation technique based on Kalman filter has been proposed by Rojas-Palma et al. to improve the prediction capability of a real-time on-line decision support system [13]. The work has been extended by Astrup et al. for off-site nuclear emergency management for the mesoscale atmospheric dispersion program [14]. An Extended Kalman Filter (EKF) based approach has been suggested by Drews et al. for source term estimation in the case of short-range radionuclide release utilizing the offline recorded radiation monitoring data [24]. However, their work did not consider improvement of gamma dose rates. Drews et al. further extended the application of the Kalman filter while using experimental online radiation monitoring data from ${}^{41}Ar$ releases [25]. Santhosh et al. applied the Kalman filter technique to design part of a diagnostic system for accident management during radioactivity release [26]. Ensemble Kalman filters (EnKF) [15,16] have been proposed by Zheng et al. to develop data assimilation techniques combining model predictions and measurements for the design of emergency response system using the Monte Carlo atmospheric dispersion model. EnKF [27] is further employed by for source estimation using multi-direction wind tunnel experiments. Modified EnKF have been proposed by Zhang et al. to improve predictions during nuclear accidents [17,18]. However, the measurements considered are tracer concentration, which is different from the actual nuclear accident scenario. In some recent studies, particle filter based techniques have been proposed by Hiemstra et al. for model prediction and in forecasting the contamination [19,20]. A preliminary study based on Unscented Kalman Filter (UKF) has been done in [28]. An adaptive neuro-fuzzy inference system and linear regression filter are proposed for data assimilation [22]. Application of other source estimation methods in real nuclear accident scenarios, such as the Chernobyl and Fukushima accidents [29,30,31,32], have been demonstrated.

Most of the work reported in literature employs estimation techniques for radionuclide release problem while a few studies attempted nonlinear estimation techniques. Particle filters generally encounter difficulties to generate meaningful samples in high-dimensional spaces. The EnKF belongs to a broader category of particle filters. In the case of EnKF, the accuracy of the state estimates is dependent on ensemble size which is heuristically chosen. The EnKF requires several equally weighted ensembles, which increases the computational time. On the contrary, the unscented and cubature Kalman filters (CKF) are computationally efficient filters in which the sample points are chosen deterministically and the number of sample points required is of the same order as the dimension of the system. The performance of unscented and cubature Kalman filters can be enhanced by careful tuning of their parameters. In this work, different nonlinear Kalman filter-based approaches are proposed in order to estimate radionuclide release activity. Particularly, EKF, UKF, and CKF techniques are proposed to estimate concentration of release, height of release, and wind speed from the measured dose rates obtained from radiation monitors. In addition, the estimation algorithms work to improve prediction of dose rates. The proposed algorithms are tested in a variety of atmospheric and beyond design basis scenarios. The efficacy of the proposed techniques has been validated using simulations in Matlab/Simulink. The performance of proposed algorithms are compared while using statistical measures of root mean squared error and sample correlation coefficients. The main contributions of the paper are listed below:

• formulation of three nonlinear estimation approaches, EKF, UKF, and CKF for radionuclide release estimation;
• estimation of source parameters like release rate, wind speed, and release height;
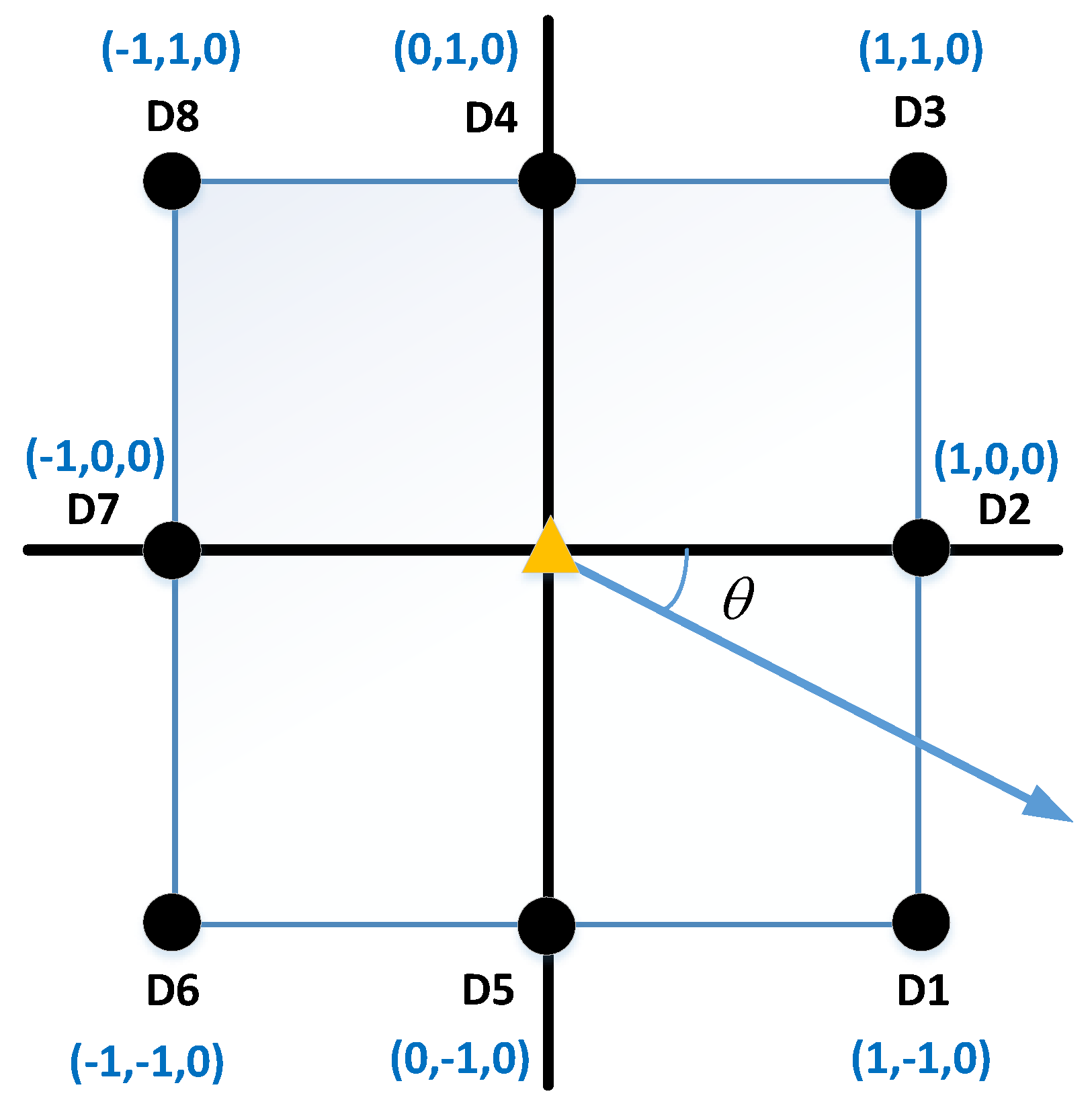
• prediction improvement of dose rate measurements at different detectors;
• simulation analysis of different beyond design basis scenarios; and,
• statistical performance analysis and comparison of the proposed estimation algorithms.

The rest of the paper is organized, as follows: Section 2 describes dynamical models of atmospheric dispersion and dose rate calculation. Section 3 presents different nonlinear estimation techniques. Section 4 demonstrates the application of estimation techniques in radionuclide release estimation. Finally, conclusions are given in Section 5.

2. Modelling of Radioactivity Release

Radioactivity releases travel and disperse in the atmosphere and they are diffused with the wind in its direction. The movement of release is governed by the physical properties of radionuclide and the ambient atmosphere. Generally, the initial values of speed, momentum, and temperature of release are different from the ambient conditions. Due to the combination of these factors and buoyancy, the radionuclides release rise in the vertical direction until their effect get dissipated by mixing with the ambient atmosphere. This vertical rise of release is called plume rise and it can change the effective height of release, which denotes the summation of plume rise and stack height. Once the release enters the atmosphere, it is transported by wind and diffused by turbulent eddies, both during the plume rise and subsequently. Moreover, the turbulent motion of the atmosphere causes random movement of the release resulting in its progressive lateral and vertical spread by mixing with air. The combination of this transport and diffusion phenomena is called atmospheric dispersion [3,8,9,10].

2.1. Atmospheric Dispersion Model

Accident management of an NPP is decided by the atmospheric dispersion model, which predicts the spatio-temporal diffusion of a radionuclide containment in the atmosphere. Atmospheric dispersion phenomenon in the case of release can be represented using different models. The GPD model [8] is adopted in this work due to its suitability for point sources in the case of plain and homogeneous terrain conditions, and due to its feasibility in modelling both short and long term impacts effectively. The GPD model is based on the assumptions that meteorological conditions are homogeneous and stationary with constant source and the radionuclide concentration is normally dispersed along the centreline [9].

The concentration of radionuclide activity is represented, as

$$\begin{array}{c}\hfill \zeta \left(x,y,z\right)=\frac{q}{2\pi {\sigma }_y\left(x\right){\sigma }_z\left(x\right)u}exp\left(-\frac{y^2}{2{\sigma }_y{\left(x\right)}^2}\right)\left\{exp\left(-\frac{{\left(z-h\right)}^2}{2{\sigma }_z{\left(x\right)}^2}\right)+exp\left(-\frac{{\left(z+h\right)}^2}{2{\sigma }_z{\left(x\right)}^2}\right)\right\}\end{array}$$

(1)

where x, y, and z denote downwind distance from the release point, crosswind distance from centreline of plume, and height above the ground, respectively. q, u, and h are release rate, wind speed, and height of radionuclide release respectively. ${\sigma }_y\left(x\right)$ and ${\sigma }_z\left(x\right)$ are plume dispersion parameters in y and z direction, respectively. They can be derived from observed wind speed fluctuations through similarity theory, or they can be inferred from Pasquill-Gifford type atmospheric stability classification [9]. The Pasquill-Gifford stability categorisation is done while using wind speed together with the incoming solar radiation during daytime and cloudiness during night time. The stability of the atmosphere is a property that depends upon temperature profile and determines the vertical acceleration of atmospheric motions [10]. The Pasquill–Gifford stability are derived using the Eimutis–Konicek relations of the form

$$\begin{array}{c}{\sigma }_y\left(x\right)=a_y{x}^{b_y}\hfill \\ {\sigma }_z\left(x\right)=a_z{x}^{b_z}+c_z\hfill \end{array}$$

(2)

where the parameters $a_y,a_z,b_y,b_z$, and $c_z$ depend on the Pasquill–Gifford stability class which classify the amount of atmospheric turbulence present [8].

2.2. Dose Rate Model

The evaluation of dose rate for an atmospheric release of radioactivity is carried out at various stages of nuclear fuel cycle. It starts from the design phase of a nuclear facility and it continues to its operational phase for ascertaining compliance during normal operation and for emergency planning during accidents [3].

Dose rate computation from radionuclide release is related to meteorological parameters and the release itself [10]. The dose rate absorbed at a receptor position is given by:

$$\begin{array}{c}\hfill D\left(x_0,y_0,z_0\right)=\frac{E_{\gamma }{\mu }_a}{4\pi \rho }\underset{0}{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}\frac{B\left(\mu r\right)exp\left(-\mu r\right)\zeta \left(x,y,z\right)}{r^2}dxdydz\end{array}$$

(3)

where $E_{\gamma }$ is photon energy, $\rho$ is mass density of air, and $\zeta \left(x,y,z\right)$ is radionuclide activity concentration at point $\left(x,y,z\right)$ in the plume. The linear mass attenuation factor and energy absorption factor for photons in air are represented by $\mu$ and ${\mu }_a$, respectively. The photon yield or the number of photons per disintegration is assumed to be equal to one. The distance between plume point and receptor point is given by

$$r=\sqrt{{\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2+{\left(z-z_0\right)}^2}.$$

(4)

The dose build-up factor for Compton scattered radiation is

$$B\left(\mu r\right)=1+k\mu r,\mathrm{where}k=\frac{\mu -{\mu }_a}{{\mu }_a}$$

(5)

3. Nonlinear Estimation Techniques

A general non-linear discrete-time system is given by

$$\begin{array}{ccc}\hfill x_{k+1}& =& f\left(x_k,u_k\right)+w_k\hfill \\ \hfill y_k& =& h\left(x_k,u_k\right)+v_k\hfill \end{array}$$

(6)

where $u\in {\mathbb{R}}^{n_u}$, $x\in {\mathbb{R}}^{n_x}$, and $y\in {\mathbb{R}}^{n_y}$ denote input, state, and output vector, respectively; $f\left(.\right)$ and $h\left(.\right)$ are known nonlinear vector functions; The covariance of process noise $w\in {\mathbb{R}}^{n_w}$ and measurement noise $v\in {\mathbb{R}}^{n_v}$ are assumed to be uncorrelated white with zero mean and covariances $Q_k=E\left[w_k{w}_k^T\right]$ and $R_k=E\left[v_k{v}_k^T\right]$, respectively.

3.1. Extended Kalman Filter

EKF is a well-known approach for nonlinear stochastic state estimation. It works by performing the first-order Taylor series expansion of the model. The implementation of the EKF is based on the computation of Jacobian matrices at each time step in order to determine the local linearized model of the system for which the Kalman filter equations can be employed [35].

The main steps of the EKF algorithm are described, as follows:

• Initialization
  The EKF is initialized using an initial estimate of state vector and error covariance matrix as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_0& =& E\left[x_0\right]\hfill \end{array}$$

  (7)

  $$\begin{array}{ccc}\hfill {\widehat{P}}_0& =& E\left[\left(x_0-{\widehat{x}}_0\right){\left(x_0-{\widehat{x}}_0\right)}^T\right]\hfill \end{array}$$

  (8)
  For $k\in 1,2,\dots ,N$
• Time Update

  (a)

  For the given nonlinear system (6), the Jacobian matrices are calculated as

  $$F_{k-1}={\left.\frac{\partial f\left(x\right)}{\partial x_{k-1}}\right|}_{{\widehat{x}}_{k-1}},H_k={\left.\frac{\partial h\left(x\right)}{\partial x_k}\right|}_{{\widehat{x}}_{k|k-1}}$$

  (9)

  (b)

  Prediction Transformation: The a priori state and covariance are computed as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_{\left.k\right|k-1}& =& f\left({\widehat{x}}_{k-1},u_{k-1}\right)\hfill \end{array}$$

  (10)

  $$\begin{array}{ccc}\hfill P_{\left.k\right|k-1}& =& Q_{k-1}+F_{k-1}{P}_{k-1}{F}_{k-1}^T\hfill \end{array}$$

  (11)

  (c)

  Observation Transformation: The mean and covariance of predicted output and cross-covariance between state and output are given as

  $$\begin{array}{ccc}\hfill {\widehat{y}}_{\left.k\right|k-1}& =& h\left({\widehat{x}}_{\left.k\right|k-1}\right)\hfill \end{array}$$

  (12)

  $$\begin{array}{ccc}\hfill P_k^{yy}& =& R_k+H_k{P}_{k|k-1}{H}_k^T\hfill \end{array}$$

  (13)

  $$\begin{array}{ccc}\hfill P_k^{xy}& =& P_{k|k-1}{H}_k^T\hfill \end{array}$$

  (14)

• Measurement Update

  (a)

  The Kalman gain is calculated while using the covariance matrices as

  $$K_k=P_k^{xy}{\left(P_k^{yy}\right)}^{-1}$$

  (15)

  (b)

  The state vector and error covariance matrix are updated as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_k& =& {\widehat{x}}_{\left.k\right|k-1}+K_k\left(y_k-{\widehat{y}}_{\left.k\right|k-1}\right)\hfill \end{array}$$

  (16)

  $$\begin{array}{ccc}\hfill P_k& =& P_{\left.k\right|k-1}-K_k{P}_k^{yy}{K}_k^T\hfill \end{array}$$

  (17)

3.2. Unscented Kalman Filter

The UKF is a derivative-free nonlinear Kalman Filter algorithm to avoid the analytic linearisation that is required by the EKF [36]. The implementation of UKF is based on unscented transformation (UT), which is used to handle the nonlinearity in the transformation. The UT provides a statistical alternative to the analytical linearisation approach using Jacobian matrices, which is used in the EKF. The UT uses a small set of deterministically selected points, called sigma-points, in order to capture the probability distribution and generalizes to nonlinear system without the burdensome analytic derivation as in the EKF. The confidence level of these points from the assumed prior distribution is determined based on the selected scaling parameters for the UT. The scaling parameters affect the spread of the sigma points as well as the weight vectors that are used in reconstructing the a posteriori statistics.

The UT-based UKF algorithm is described, as follows:

• Initialization
  The UKF is initialized using the initial estimate of state vector and error covariance matrix, as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_0& =& E\left[x_0\right]\hfill \end{array}$$

  (18)

  $$\begin{array}{ccc}\hfill {\widehat{P}}_0& =& E\left[\left(x_0-{\widehat{x}}_0\right){\left(x_0-{\widehat{x}}_0\right)}^T\right]\hfill \end{array}$$

  (19)
  For $k\in 1,2,\dots ,N$
• Time Update

  (a)

  The UT transformation employs primary, secondary, and tertiary scaling parameters, in which the primary scaling parameter $\alpha$ determines the spread of the sigma-points around the mean, the secondary scaling parameter $\beta$ includes information regarding the prior distribution, and the tertiary parameter $\kappa$ minimizes the higher order errors of mean and covariance approximations. Using these three scaling parameters, an additional scaling parameter $\lambda$ and weight vectors, ${\eta }^m$ and ${\eta }^c$ are defined as

  $$\lambda ={\alpha }^2\left(n_x+\kappa \right)-n_x$$

  (20)

  and

  $$\begin{array}{ccc}\hfill {\eta }_0^m& =& \lambda /\phantom{\lambda \lambda \left(n_x+\lambda \right)}\lambda \left(n_x+\lambda \right)\hfill \end{array}$$

  (21)

  $$\begin{array}{ccc}\hfill {\eta }_0^c& =& \lambda /\phantom{\lambda \lambda \left(n_x+\lambda \right)}\lambda \left(n_x+\lambda \right)+\left(1-{\alpha }^2+\beta \right)\hfill \end{array}$$

  (22)

  $$\begin{array}{ccc}\hfill {\eta }_i^m& =& {\eta }_i^c=1/\phantom{1\left(2\left(n_x+\lambda \right)\right)}\left(2\left(n_x+\lambda \right)\right),i=1,2,\dots ,2n_x\hfill \end{array}$$

  (23)

  (b)

  The Sigma points are computed using the initial state estimate (${\widehat{x}}_{k-1}$) and covariance ($P_{k-1}$) as

  $${\chi }_{k-1}=\left[\begin{array}{ccc}{\widehat{x}}_{k-1}& {\widehat{x}}_{k-1}\Gamma +\sqrt{P_{k-1}\left(n_x+\lambda \right)}& {\widehat{x}}_{k-1}\Gamma -\sqrt{P_{k-1}\left(n_x+\lambda \right)}\end{array}\right]$$

  (24)

  where $\Gamma$ is a $1\times n_x$ vector of ones.

  (c)

  Prediction Transformation: Sigma points are fed to the non-linear state prediction as

  $${\chi }_{\left.k\right|k-1}^{\left(i\right)}=f\left({\chi }_{k-1}^{\left(i\right)},u_{k-1}\right),i=0,1,\dots ,2n_x$$

  (25)

  The a priori state and covariance are computed based on weighted averages of the transformed sigma-points as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_{\left.k\right|k-1}& =& \sum _{i=0}^{2n_x}{\eta }_i^m{\chi }_{\left.k\right|k-1}^{\left(i\right)}\hfill \end{array}$$

  (26)

  $$\begin{array}{ccc}\hfill P_{\left.k\right|k-1}& =& Q_{k-1}+\sum _{i=0}^{2n_x}{\eta }_i^c\left(\left({\chi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{x}}_{\left.k\right|k-1}\right)\right.\left.{\left({\chi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{x}}_{\left.k\right|k-1}\right)}^T\right)\hfill \end{array}$$

  (27)

  (d)

  Observation Transformation: Sigma-points are transformed while using observation function as

  $${\psi }_{\left.k\right|k-1}^{\left(i\right)}=h\left({\chi }_{\left.k\right|k-1}^{\left(i\right)},u_k\right),i=0,1,\dots 2n_x$$

  (28)

  The mean and covariance of predicted output and cross-covariance between state and output are given as

  $$\begin{array}{ccc}\hfill {\widehat{y}}_{\left.k\right|k-1}& =& \sum _{i=0}^{2n_x}{\eta }_i^m{\psi }_{\left.k\right|k-1}^{\left(i\right)}\hfill \end{array}$$

  (29)

  $$\begin{array}{ccc}\hfill P_k^{yy}& =& R_k+\sum _{i=0}^{2n_x}{\eta }_i^c\left(\left({\psi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{y}}_{\left.k\right|k-1}\right)\right.\left.{\left({\psi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{y}}_{\left.k\right|k-1}\right)}^T\right)\hfill \end{array}$$

  (30)

  $$\begin{array}{ccc}\hfill P_k^{xy}& =& \sum _{i=0}^{2n_x}{\eta }_i^c\left(\left({\chi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{x}}_{\left.k\right|k-1}\right)\right.\left.{\left({\psi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{y}}_{\left.k\right|k-1}\right)}^T\right)\hfill \end{array}$$

  (31)

• Measurement Update

  (a)

  The Kalman gain is calculated using the covariance matrices as

  $$K_k=P_k^{xy}{\left(P_k^{yy}\right)}^{-1}$$

  (32)

  (b)

  The state vector and error covariance matrix are updated as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_k& =& {\widehat{x}}_{\left.k\right|k-1}+K_k\left(y_k-{\widehat{y}}_{\left.k\right|k-1}\right)\hfill \end{array}$$

  (33)

  $$\begin{array}{ccc}\hfill P_k& =& P_{\left.k\right|k-1}-K_k{P}_k^{yy}{K}_k^T\hfill \end{array}$$

  (34)

  (c)

  Sigma points are updated while using the a prior state estimate (${\widehat{x}}_k$) and covariance ($P_k$) as

  $${\chi }_k=\left[\begin{array}{ccc}{\widehat{x}}_k& {\widehat{x}}_k\Gamma +\sqrt{P_k\left(n_x+\lambda \right)}& {\widehat{x}}_k\Gamma -\sqrt{P_k\left(n_x+\lambda \right)}\end{array}\right]$$

  (35)

3.3. Cubature Kalman Filter

The CKF is a recently developed derivative-free nonlinear Kalman filtering algorithm. The performance of the CKF gives nonlinear optimal approximation, filtering accuracy, and numerical stability. The CKF builds on the numerical-integration perspective of Gaussian filters [37]. It uses spherical-radial cubature rules of third degree in order to evaluate Gaussian-weighted integrals encountered in the nonlinear Bayesian filter. The CKF calculates the means and covariances of state variables at a set of cubature points.

The CKF algorithm is described, as follows:

• Initialization
  The CKF is initialized using an estimate of state vector and error covariance matrix, as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_0& =& E\left[x_0\right]\hfill \end{array}$$

  (36)

  $$\begin{array}{ccc}\hfill {\widehat{P}}_0& =& E\left[\left(x_0-{\widehat{x}}_0\right){\left(x_0-{\widehat{x}}_0\right)}^T\right]\hfill \end{array}$$

  (37)
  For $k\in 1,2,\dots ,N$
• Time Update

  (a)

  Cubature points are computed using the initial state estimate (${\widehat{x}}_{k-1}$) and covariance ($P_{k-1}$) as

  $${\zeta }_{k-1}=\left[\begin{array}{cc}{\widehat{x}}_{k-1}\Gamma +\sqrt{P_{k-1}{n}_x}& {\widehat{x}}_{k-1}\Gamma -\sqrt{P_{k-1}{n}_x}\end{array}\right]$$

  (38)

  (b)

  Prediction Transformation: Cubature points are fed to the non-linear state prediction, as

  $${\zeta }_{\left.k\right|k-1}^{\left(i\right)}=f\left({\zeta }_{k-1}^{\left(i\right)},u_{k-1}\right),i=1,2,\dots ,2n_x$$

  (39)

  The a priori state and covariance are computed based on weighted averages of the transformed cubature-points as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_{\left.k\right|k-1}& =& \frac{1}{2n_x}\sum _{i=1}^{2n_x}{\zeta }_{\left.k\right|k-1}^{\left(i\right)}\hfill \end{array}$$

  (40)

  $$\begin{array}{ccc}\hfill P_{\left.k\right|k-1}& =& Q_{k-1}+\frac{1}{2n_x}\sum _{i=1}^{2n_x}\left(\left({\zeta }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{x}}_{\left.k\right|k-1}\right)\right.\left.{\left({\zeta }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{x}}_{\left.k\right|k-1}\right)}^T\right)\hfill \end{array}$$

  (41)

  (c)

  Observation Transformation: Cubature-points are transformed using observation function as

  $${\xi }_{\left.k\right|k-1}^{\left(i\right)}=h\left({\zeta }_{\left.k\right|k-1}^{\left(i\right)},u_{k-1}\right),i=1,2,\dots 2n_x$$

  (42)

  The mean and covariance of predicted output and cross-covariance between state and output are given as

  $$\begin{array}{ccc}\hfill {\widehat{y}}_{\left.k\right|k-1}& =& \frac{1}{2n_x}\sum _{i=1}^{2n_x}{\xi }_{\left.k\right|k-1}^{\left(i\right)}\hfill \end{array}$$

  (43)

  $$\begin{array}{ccc}\hfill P_k^{yy}& =& R_k+\frac{1}{2n_x}\sum _{i=1}^{2n_x}\left(\left({\xi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{y}}_{\left.k\right|k-1}\right)\right.\left.{\left({\xi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{y}}_{\left.k\right|k-1}\right)}^T\right)\hfill \end{array}$$

  (44)

  $$\begin{array}{ccc}\hfill P_k^{xy}& =& \frac{1}{2n_x}\sum _{i=1}^{2n_x}\left(\left({\zeta }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{x}}_{\left.k\right|k-1}\right)\right.\left.{\left({\xi }_{\left.k\right|k-1}^{\left(i\right)}-{\widehat{y}}_{\left.k\right|k-1}\right)}^T\right)\hfill \end{array}$$

  (45)

• Measurement Update

  (a)

  The Kalman gain is calculated while using the covariance matrices, as

  $$K_k=P_k^{xy}{\left(P_k^{yy}\right)}^{-1}$$

  (46)

  (b)

  The state vector and error covariance matrix are updated as

  $$\begin{array}{ccc}\hfill {\widehat{x}}_k& =& {\widehat{x}}_{\left.k\right|k-1}+K_k\left(y_k-{\widehat{y}}_{\left.k\right|k-1}\right)\hfill \end{array}$$

  (47)

  $$\begin{array}{ccc}\hfill P_k& =& P_{\left.k\right|k-1}-K_k{P}_k^{yy}{K}_k^T\hfill \end{array}$$

  (48)

  (c)

  Cubature points are updated using the a prior state estimate (${\widehat{x}}_k$) and covariance ($P_k$) as

  $${\zeta }_k=\left[\begin{array}{cc}{\widehat{x}}_k\Gamma +\sqrt{P_k{n}_x}& {\widehat{x}}_k\Gamma -\sqrt{P_k{n}_x}\end{array}\right]$$

  (49)

4. Application to Radionuclide Release Estimation

The nonlinear estimation techniques proposed in Section 3 are applied to estimate radionuclides release rate, wind speed, and effective height of release. Eight radiation detectors (D1 to D8), placed 1 km away from the source at the ground level, as shown in Figure 1. The source is placed at the origin indicated with a triangle. The mean wind direction is assumed to be constant at 30 degrees to x-axis in a counter-clockwise direction. The measurement data comprise of a set of dose rates from D1 to D8 detectors is generated using the GPD model discussed in Section II. The initial value of release rate, mean wind speed, and release height are assumed as $1\times {10}^7$ Bq/s, 4 m/s, and 100 m, respectively [28]. Once the release has occurred and the dose rate have been recorded, the model can be used in its inverse mode to estimate the system states and input parameters. This task is performed by coupling the model to the measurements. For the purpose of estimation, the GPD model can be represented in state space form using a random walk model. It is suitable if the unknown parameters are time-varying. The random walk model is given by,

$$\begin{array}{c}{s}_k=\left[\begin{array}{c}{q}_k\\ u_k\\ h_k\end{array}\right]=\left[\begin{array}{c}{q}_{k-1}\\ u_{k-1}\\ h_{k-1}\end{array}\right]+\left[\begin{array}{c}{w}_{q,k-1}\\ w_{u,k-1}\\ w_{h,k-1}\end{array}\right]\hfill \\ \begin{array}{c}{o}_k={\left[\begin{array}{ccc}{D}_{1,k}& \cdots & D_{8,k}\end{array}\right]}^T+{\left[\begin{array}{ccc}{v}_{d_1,k}& \cdots & v_{d_8,k}\end{array}\right]}^T\hfill \end{array}\hfill \end{array}$$

(50)

where $s_k$ and $o_k$ denote system states and measurement, respectively. The vectors w and v represent process noise and measurement noise, respectively. q, u, and h denote the release rate, mean wind speed, and effective height of release, respectively. $D_1$ to $D_8$ respectively represent dose rates measured at detectors. The proposed algorithms are then applied to estimate different states using environmental radiation monitoring data collected close to the release point.

4.1. Case Studies of Different Scenarios

4.1.1. Variation in Radionuclides Release Rate

A simulation analysis is performed in order to study the effectiveness of proposed techniques during an explosion scenario [17]. To represent an explosion, it is considered that the release rate is step changed to two times of its initial value at 100 s and maintained there for the next 200 s. Countermeasures are applied at 300 s, which gradually brings back the release rate to its initial value in the next 500 s. The release is then kept constant afterwards. The dose rate detectors measure the amount of release in terms of doses and they are assumed to be added with white Gaussian noise. These noisy measurements are then used in designing estimation algorithms. The estimated dose rates using EKF, UKF, and CKF are shown with measurements at eight different detector locations in Figure 2. The estimates of radionuclides release rate, mean wind speed, and effective height of release with true values are shown in Figure 3. All of the estimation algorithms able sufficiently to estimate the true values of the dose rates. The UKF and CKF clearly outperform the EKF during state estimation. The EKF shows perturbations during tracking the state variation. The UKF and CKF algorithms are able to track the step and ramp variations change in release rate in addition to other states and measurements. The estimated states from UKF and CKF are found to be in good agreement with the true values.

4.1.2. Variation in Mean Wind Speed

The efficacy of the proposed approaches is validated by testing another beyond design basis scenario of a wind storm [28]. The wind is regarded to be time-dependent, in which the speed varies with time while the direction remains fixed. The wind speed is considered to be 4 m/s for the first 200 s. It is then linearly changed to 24 m/s in 500 s and maintained there for the rest of the duration. The noisy measurements of dose rates at different detectors are collected and then used in estimation algorithms. The dose rates estimated using EKF, UKF, and CKF are shown with measurements at eight different detector locations in Figure 4. Estimates of release rate, wind speed, and height of release are shown in Figure 5. All three techniques are able to estimate the dose rates close to their true values. The UKF and CKF perform better than the EKF during state estimation. The EKF shows comparatively more perturbations in the estimation of mean speed and height of release than the UKF and CKF. All of the algorithms are able to track the ramp variation in wind speed. The estimates are in good agreement with the true measurements.

4.1.3. Variation in Effective Height of Release

The effective height of release is a sum of the physical stack height and the plume rise. The physical stack height remains constant, while the plume rise can vary, which can alter the effective height of release [3]. During radionuclides release generally the plume is of non-buoyant nature, in which the radionuclide discharge temperature is near ambient. During an accident, the discharge temperature can increase and it will affect the plume rise, which, in turn, change the effective height of release. Here, a scenario is considered, in which the effective release height is step changed by 25 m from its initial value at 100 s. It then linearly decreased to its initial value during 300 to 800 s and maintained at its initial value for rest of the duration [17]. The noisy measurements of dose rates at different detectors are collected and used in estimation algorithms. The estimated dose rates using EKF, UKF, and CKF are shown with measurements at eight different detector locations in Figure 6. Figure 7 shows the estimates of radionuclides release rate, mean wind speed, and height of release with true values. The UKF and CKF are effectively able to predict the dose rates at D1, D2, D3, and D5 detectors, while the predictions at detectors placed away from plume dispersion contain perturbations. The UKF and CKF show initial variation in the estimation and takes some time before tracking the true values. The state estimates from EKF contain perturbations. It can be observed that all the three techniques are able to track states, except some initial variation. The algorithms are able to handle the step and ramp variation in release height in while tracking other states and measurements.

4.1.4. Variation in Atmospheric Condition

This simulation studies the effectiveness of estimation techniques during variation in atmospheric condition. The atmospheric condition changes due to variation in incoming solar radiation, night time cloud cover, and surface wind speed [10]. For instance, solar radiation increases atmospheric instability through warming of the Earth’s surface, whereas clear nights push conditions toward stability [3]. Here, the atmospheric condition are considered to change due to atmospheric turbulence in random fashion. Figure 8 shows the variation in atmospheric turbulence parameters. Because of the variation in atmospheric condition, the wind speed is also assumed to vary in a random fashion from its initial value. The noisy measurements of dose rates at different detectors are collected and then used in estimation algorithms. Dose rates estimated using EKF, UKF, and CKF are shown with measurements at eight different detector locations in Figure 9. Estimates of release rate, wind speed, and height of release are shown in Figure 10. The UKF and CKF techniques perform better than the EKF during prediction as well as during estimation. The EKF shows comparatively more perturbations in the estimation of mean speed and height of release than the UKF and CKF. Further, the dose rates estimated by UKF and CKF are in close agreement with the true value than the EKF.

4.1.5. Multiple Release Points

To analyse the effectiveness of the estimation techniques when there are multiple sources of radionuclide release estimation, a case study that comprised of three release sources has been considered. These three sources represent three different units with locations $\left(x_s,y_s,z_s\right)$ and release concentrations ${\zeta }_s\left(x_s,y_s,z_s\right)$ for $s=1,2,3$ and their placement is shown in Figure 11 by the points labelled S1 to S3. The initial values of release rates from sources S1 to S3 are considered as $1\times {10}^7$ Bq/s, $1.2\times {10}^7$ Bq/s, and $1.3\times {10}^7$ Bq/s, respectively. In a worst case scenario, where an earthquake affects all three units simultaneously, there would be radionuclides release from all three sources. The total concentration that results from all three sources is given by the sum of individual concentration. For simulation purposes, here, the total release rate variation is considered, as follows. The total release rate is varied to two times of its initial value from 50 s to 150 s and maintained there for the next 200 s. Countermeasures are applied at 350 s, which gradually bring back the total release rate to its initial value in the next 500 s. The release is then kept constant afterwards. The noisy measurements of dose rates at different detectors are collected and then used in estimation algorithms. Estimates of dose rates using EKF, UKF, and CKF are shown with corresponding measurements in Figure 12. Figure 13 shows estimates of release rate, wind speed, and height of release. The estimation algorithms estimate the dose rates and states with variations in tracking. It is to be noted that the measurements comprised of multiple sources while the estimation algorithms modelled only a single source. All three techniques predict the dose rate with some overshoot and take some time in predicting the measurements. The UKF and CKF are found to be perform better than the EKF during state estimation.

4.2. Statistical Performance Assessment

The performance of the estimation algorithms is quantitatively assessed using different statistical measures. The root mean squared error (RMSE) is calculated between the reference value and estimated value. The RSME is given by

$$\begin{array}{ccc}\hfill RMSE& =& \sqrt{\frac{1}{N}\sum _{k=1}^N{\left(r_k-{\widehat{p}}_k\right)}^2}\hfill \end{array}$$

(51)

where N is the length of data. $r_k$ and ${\widehat{p}}_k$, respectively denote the reference and estimated values. The RMSE for different scenarios is calculated for measurements and states and are listed in

Table 1. Root mean squared error between true and estimated dose rates for EKF, UKF, and CKF.

Scenario	Parameter	EKF	UKF	CKF
Release Rate Variation	Dose Rate, $D1$	$\mathbf{5.1515}\times {\mathbf{10}}^{-\mathbf{2}}$	$5.1526\times {10}^{-2}$	$5.1527\times {10}^{-2}$
	Dose Rate, $D2$	$\mathbf{9.0130}\times {\mathbf{10}}^{-\mathbf{3}}$	$9.0285\times {10}^{-3}$	$9.0286\times {10}^{-3}$
	Dose Rate, $D3$	$9.2147\times {10}^{-6}$	$\mathbf{9.1710}\times {\mathbf{10}}^{-\mathbf{6}}$	$9.1711\times {10}^{-6}$
	Dose Rate, $D4$	$6.3466\times {10}^{-5}$	$\mathbf{6.0327}\times {\mathbf{10}}^{-\mathbf{5}}$	$6.0330\times {10}^{-5}$
	Dose Rate, $D5$	$4.3348\times {10}^{-4}$	$\mathbf{4.3297}\times {\mathbf{10}}^{-\mathbf{4}}$	$4.3299\times {10}^{-4}$
	Dose Rate, $D6$	$3.2434\times {10}^{-6}$	$\mathbf{3.1516}\times {\mathbf{10}}^{-\mathbf{6}}$	$3.1517\times {10}^{-6}$
	Dose Rate, $D7$	$4.7821\times {10}^{-5}$	$\mathbf{4.3786}\times {\mathbf{10}}^{-\mathbf{5}}$	$4.3788\times {10}^{-5}$
	Dose Rate, $D8$	$1.7251\times {10}^{-6}$	$\mathbf{1.5677}\times {\mathbf{10}}^{-\mathbf{6}}$	$1.5678\times {10}^{-6}$
Wind Speed Variation	Dose Rate, $D1$	$\mathbf{7.2559}\times {\mathbf{10}}^{-\mathbf{3}}$	$7.2721\times {10}^{-3}$	$7.2725\times {10}^{-3}$
	Dose Rate, $D2$	$2.1059\times {10}^{-3}$	$2.1042\times {10}^{-3}$	$\mathbf{2.1040}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D3$	$3.5540\times {10}^{-6}$	$3.5293\times {10}^{-6}$	$\mathbf{3.5284}\times {\mathbf{10}}^{-\mathbf{6}}$
	Dose Rate, $D4$	$2.8018\times {10}^{-5}$	$2.7578\times {10}^{-5}$	$\mathbf{2.7504}\times {\mathbf{10}}^{-\mathbf{5}}$
	Dose Rate, $D5$	$1.6268\times {10}^{-4}$	$1.6187\times {10}^{-4}$	$\mathbf{1.6183}\times {\mathbf{10}}^{-\mathbf{4}}$
	Dose Rate, $D6$	$1.4232\times {10}^{-6}$	$1.4061\times {10}^{-6}$	$\mathbf{1.4035}\times {\mathbf{10}}^{-\mathbf{6}}$
	Dose Rate, $D7$	$2.0839\times {10}^{-5}$	$2.0396\times {10}^{-5}$	$\mathbf{2.0327}\times {\mathbf{10}}^{-\mathbf{5}}$
	Dose Rate, $D8$	$7.4886\times {10}^{-6}$	$7.3210\times {10}^{-6}$	$\mathbf{7.2953}\times {\mathbf{10}}^{-\mathbf{7}}$
Release Height Variation	Dose Rate, $D1$	$4.1322\times {10}^{-2}$	$1.4958\times {10}^{-1}$	$\mathbf{4.0454}\times {\mathbf{10}}^{-\mathbf{2}}$
	Dose Rate, $D2$	$\mathbf{6.3177}\times {\mathbf{10}}^{-\mathbf{3}}$	$2.4084\times {10}^{-2}$	$6.5735\times {10}^{-3}$
	Dose Rate, $D3$	$5.7564\times {10}^{-6}$	$1.9472\times {10}^{-5}$	$\mathbf{5.6332}\times {\mathbf{10}}^{-\mathbf{6}}$
	Dose Rate, $D4$	$\mathbf{7.0099}\times {\mathbf{10}}^{-\mathbf{5}}$	$1.2377\times {10}^{-4}$	$7.4222\times {10}^{-5}$
	Dose Rate, $D5$	$\mathbf{2.5523}\times {\mathbf{10}}^{-\mathbf{4}}$	$9.6189\times {10}^{-4}$	$2.7058\times {10}^{-4}$
	Dose Rate, $D6$	$3.0462\times {10}^{-6}$	$5.9013\times {10}^{-6}$	$\mathbf{3.0183}\times {\mathbf{10}}^{-\mathbf{6}}$
	Dose Rate, $D7$	$\mathbf{5.9094}\times {\mathbf{10}}^{-\mathbf{5}}$	$1.0259\times {10}^{-4}$	$6.3784\times {10}^{-5}$
	Dose Rate, $D8$	$\mathbf{2.1546}\times {\mathbf{10}}^{-\mathbf{6}}$	$3.7491\times {10}^{-6}$	$2.3164\times {10}^{-6}$
Atmospheric Condition Variation	Dose Rate, $D1$	$\mathbf{4.7629}\times {\mathbf{10}}^{-\mathbf{2}}$	$4.7665\times {10}^{-2}$	$4.7665\times {10}^{-2}$
	Dose Rate, $D2$	$\mathbf{9.3726}\times {\mathbf{10}}^{-\mathbf{3}}$	$9.8950\times {10}^{-3}$	$9.8951\times {10}^{-3}$
	Dose Rate, $D3$	$1.5512\times {10}^{-5}$	$\mathbf{9.0330}\times {\mathbf{10}}^{-\mathbf{6}}$	$9.0333\times {10}^{-6}$
	Dose Rate, $D4$	$2.0458\times {10}^{-4}$	$\mathbf{3.6280}\times {\mathbf{10}}^{-\mathbf{5}}$	$3.6281\times {10}^{-5}$
	Dose Rate, $D5$	$5.9008\times {10}^{-4}$	$\mathbf{4.5455}\times {\mathbf{10}}^{-\mathbf{4}}$	$4.5449\times {10}^{-4}$
	Dose Rate, $D6$	$8.6542\times {10}^{-6}$	$\mathbf{2.2331}\times {\mathbf{10}}^{-\mathbf{6}}$	$2.2333\times {10}^{-6}$
	Dose Rate, $D7$	$1.8127\times {10}^{-4}$	$\mathbf{2.4203}\times {\mathbf{10}}^{-\mathbf{5}}$	$2.4207\times {10}^{-5}$
	Dose Rate, $D8$	$6.6942\times {10}^{-6}$	$\mathbf{8.6014}\times {\mathbf{10}}^{-\mathbf{7}}$	$8.6016\times {10}^{-7}$
Multiple Release Sources	Dose Rate, $D1$	$\mathbf{1.8879}\times {\mathbf{10}}^{-\mathbf{1}}$	$1.9067\times {10}^{-1}$	$1.9067\times {10}^{-1}$
	Dose Rate, $D2$	$\mathbf{4.1812}\times {\mathbf{10}}^{-\mathbf{1}}$	$4.3772\times {10}^{-1}$	$4.3772\times {10}^{-1}$
	Dose Rate, $D3$	$\mathbf{4.0458}\times {\mathbf{10}}^{-\mathbf{4}}$	$4.1799\times {10}^{-4}$	$4.1799\times {10}^{-4}$
	Dose Rate, $D4$	$2.4125\times {10}^{-3}$	$\mathbf{2.2319}\times {\mathbf{10}}^{-\mathbf{3}}$	$2.2321\times {10}^{-3}$
	Dose Rate, $D5$	$\mathbf{2.4407}\times {\mathbf{10}}^{-\mathbf{2}}$	$2.4622\times {10}^{-2}$	$2.4622\times {10}^{-2}$
	Dose Rate, $D6$	$\mathbf{1.4315}\times {\mathbf{10}}^{-\mathbf{4}}$	$1.5184\times {10}^{-4}$	$1.5184\times {10}^{-4}$
	Dose Rate, $D7$	$2.1210\times {10}^{-3}$	$\mathbf{1.3728}\times {\mathbf{10}}^{-\mathbf{3}}$	$1.3729\times {10}^{-3}$
	Dose Rate, $D8$	$8.6166\times {10}^{-5}$	$\mathbf{5.4653}\times {\mathbf{10}}^{-\mathbf{5}}$	$5.4655\times {10}^{-5}$

and

Table 2. Root mean squared error between true and estimated states for Extended Kalman Filter (EKF), Unscented Kalman Filter (UKF), and cubature Kalman filters (CKF).

Scenario	Parameter	EKF	UKF	CKF
Release Rate Variation	Release Rate, q	$1.1807\times {10}^6$	$\mathbf{7.8613}\times {\mathbf{10}}^{\mathbf{5}}$	$7.8615\times {10}^5$
	Wind speed, u	$2.9620\times {10}^{-1}$	$\mathbf{4.4865}\times {\mathbf{10}}^{-\mathbf{2}}$	$4.4868\times {10}^{-2}$
	Release Height, h	$9.1955\times {10}^{-1}$	$\mathbf{2.0810}\times {\mathbf{10}}^{-\mathbf{2}}$	$2.0814\times {10}^{-2}$
Wind Speed Variation	Release Rate, q	$\mathbf{1.7415}\times {\mathbf{10}}^{-\mathbf{3}}$	$5.9361\times {10}^{-3}$	$5.9237\times {10}^{-3}$
	Wind speed, u	$4.335\times {10}^{-1}$	$3.950\times {10}^{-1}$	$\mathbf{3.943}\times {\mathbf{10}}^{-\mathbf{1}}$
	Release Height, h	$1.1538\times {10}^0$	$4.705\times {10}^{-1}$	$\mathbf{4.701}\times {\mathbf{10}}^{-\mathbf{1}}$
Release Height Variation	Release Rate, q	$\mathbf{5.0994}\times {\mathbf{10}}^{-\mathbf{3}}$	$8.0262\times {10}^0$	$3.5156\times {10}^0$
	Wind speed, u	$\mathbf{7.0717}\times {\mathbf{10}}^{-\mathbf{2}}$	$3.1281\times {10}^0$	$7.9367\times {10}^{-1}$
	Release Height, h	$4.7822\times {10}^0$	$\mathbf{4.7149}\times {\mathbf{10}}^{\mathbf{0}}$	$1.5546\times {10}^1$
Atmospheric Condition Variation	Release Rate, q	$\mathbf{3.7557}\times {\mathbf{10}}^{-\mathbf{5}}$	$9.9270\times {10}^{-5}$	$9.9253\times {10}^{-5}$
	Wind speed, u	$1.5112\times {10}^{-1}$	$\mathbf{1.2070}\times {\mathbf{10}}^{-\mathbf{1}}$	$1.2075\times {10}^{-1}$
	Release Height, h	$8.4462\times {10}^0$	$\mathbf{4.8311}\times {\mathbf{10}}^{-\mathbf{1}}$	$4.8314\times {10}^{-1}$
Multiple Release Sources	Release Rate, q	$1.7596\times {10}^7$	$\mathbf{6.4765}\times {\mathbf{10}}^{\mathbf{6}}$	$6.4767\times {10}^6$
	Wind speed, u	$2.3402\times {10}^0$	$\mathbf{1.4179}\times {\mathbf{10}}^{\mathbf{0}}$	$1.4182\times {10}^0$
	Release Height, h	$1.6789\times {10}^1$	$\mathbf{4.4444}\times {\mathbf{10}}^{-\mathbf{1}}$	$4.4554\times {10}^{-1}$

, respectively. The bold values represent the best estimate among all. It can be noted that the RMSE values by the UKF and CKF techniques are much lower than that obtained by the EKF approach. From the Table 1 and Table 2, it can be noticed that the estimation accuracy for the algorithms is similar for cases 4.1.2, 4.1.3, and 4.1.4. The non-linear estimation algorithms that are based on statistical linearisation track the variation in release rate, effective release height, and mean wind speed better than the analytical linearisation technique.

The estimation and prediction capabilities can be assessed by calculating the fraction bias (FB). It is given by

$$FB=\frac{1}{2}\left(\frac{{\overline{r}}_k-{\overline{p}}_k}{{\overline{r}}_k+{\overline{p}}_k}\right)$$

(52)

where ${\overline{r}}_k$ and ${\overline{p}}_k$ denote the mean values of $r_k$ and $p_k$, respectively. The FB for different scenarios is calculated for states and measurements and they are listed in

Table 3. Fractional Bias between true and estimated states for EKF, UKF, and CKF.

Scenario	Parameter	EKF	UKF	CKF
Release Rate Variation	Release Rate, q	$-1.2290\times {10}^{-2}$	$\mathbf{1.3038}\times {\mathbf{10}}^{-\mathbf{3}}$	$1.3040\times {10}^{-3}$
	Wind speed, u	$-1.4542\times {10}^{-2}$	$\mathbf{2.9502}\times {\mathbf{10}}^{-\mathbf{4}}$	$2.9505\times {10}^{-4}$
	Release Height, h	$-8.4870\times {10}^{-7}$	$\mathbf{3.8890}\times {\mathbf{10}}^{-\mathbf{5}}$	$3.8899\times {10}^{-5}$
Wind Speed Variation	Release Rate, q	0	0	0
	Wind speed, u	$-2.0903\times {10}^{-3}$	$-1.1644\times {10}^{-3}$	$-\mathbf{1.1573}\times {\mathbf{10}}^{-\mathbf{3}}$
	Release Height, h	$1.7878\times {10}^{-3}$	$\mathbf{9.5695}\times {\mathbf{10}}^{-\mathbf{4}}$	$9.5731\times {10}^{-4}$
Release Height Variation	Release Rate, q	0	0	0
	Wind speed, u	$-\mathbf{2.7877}\times {\mathbf{10}}^{-\mathbf{3}}$	$-3.9980\times {10}^{-2}$	$-8.9383\times {10}^{-3}$
	Release Height, h	$4.7606\times {10}^{-3}$	$\mathbf{2.4833}\times {\mathbf{10}}^{-\mathbf{3}}$	$1.4368\times {10}^{-2}$
Atmospheric Condition Variation	Release Rate, q	0	0	0
	Wind speed, u	$-5.5498\times {10}^{-3}$	$\mathbf{2.7754}\times {\mathbf{10}}^{-\mathbf{3}}$	$2.7755\times {10}^{-3}$
	Release Height, h	$1.7182\times {10}^{-2}$	$\mathbf{8.1338}\times {\mathbf{10}}^{-\mathbf{4}}$	$8.1344\times {10}^{-4}$
Multiple Release Sources	Release Rate, q	$7.2928\times {10}^{-2}$	$-\mathbf{8.5414}\times {\mathbf{10}}^{-\mathbf{3}}$	$-8.5415\times {10}^{-3}$
	Wind speed, u	$1.8665\times {10}^{-1}$	$\mathbf{9.3525}\times {\mathbf{10}}^{-\mathbf{2}}$	$9.3528\times {10}^{-2}$
	Release Height, h	$-2.6260\times {10}^{-2}$	$\mathbf{8.3504}\times {\mathbf{10}}^{-\mathbf{4}}$	$8.3506\times {10}^{-4}$

and

Table 4. Fractional bias between true and estimated dose rates for EKF, UKF, and CKF.

Scenario	Parameter	EKF	UKF	CKF
Release Rate Variation	Dose Rate, $D1$	$-\mathbf{2.7873}\times {\mathbf{10}}^{-\mathbf{4}}$	$-2.8087\times {10}^{-4}$	$-2.8086\times {10}^{-4}$
	Dose Rate, $D2$	$-\mathbf{1.5748}\times {\mathbf{10}}^{-\mathbf{4}}$	$-1.9856\times {10}^{-4}$	$-1.9856\times {10}^{-4}$
	Dose Rate, $D3$	$7.5515\times {10}^{-4}$	$\mathbf{1.7548}\times {\mathbf{10}}^{-\mathbf{4}}$	$1.7548\times {10}^{-4}$
	Dose Rate, $D4$	$3.5323\times {10}^{-3}$	$\mathbf{4.1807}\times {\mathbf{10}}^{-\mathbf{4}}$	$4.1808\times {10}^{-4}$
	Dose Rate, $D5$	$4.7299\times {10}^{-4}$	$\mathbf{1.2235}\times {\mathbf{10}}^{-\mathbf{4}}$	$1.2237\times {10}^{-4}$
	Dose Rate, $D6$	$2.4883\times {10}^{-3}$	$\mathbf{4.2748}\times {\mathbf{10}}^{-\mathbf{4}}$	$4.2751\times {10}^{-4}$
	Dose Rate, $D7$	$4.7950\times {10}^{-3}$	$\mathbf{3.3025}\times {\mathbf{10}}^{-\mathbf{4}}$	$3.3026\times {10}^{-4}$
	Dose Rate, $D8$	$5.0009\times {10}^{-3}$	$\mathbf{3.1502}\times {\mathbf{10}}^{-\mathbf{4}}$	$3.1505\times {10}^{-4}$
Wind Speed Variation	Dose Rate, $D1$	$-\mathbf{4.0608}\times {\mathbf{10}}^{-\mathbf{4}}$	$-4.0649\times {10}^{-4}$	$-4.0642\times {10}^{-4}$
	Dose Rate, $D2$	$-\mathbf{6.1211}\times {\mathbf{10}}^{-\mathbf{4}}$	$-6.4648\times {10}^{-4}$	$-6.4632\times {10}^{-4}$
	Dose Rate, $D3$	$6.7956\times {10}^{-4}$	$4.2180\times {10}^{-4}$	$\mathbf{4.1588}\times {\mathbf{10}}^{-\mathbf{4}}$
	Dose Rate, $D4$	$3.1642\times {10}^{-3}$	$2.4336\times {10}^{-3}$	$\mathbf{2.4104}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D5$	$2.8057\times {10}^{-4}$	$9.2435\times {10}^{-5}$	$\mathbf{8.8979}\times {\mathbf{10}}^{-\mathbf{5}}$
	Dose Rate, $D6$	$2.3606\times {10}^{-3}$	$1.8046\times {10}^{-3}$	$\mathbf{1.7871}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D7$	$3.9689\times {10}^{-3}$	$3.0314\times {10}^{-3}$	$\mathbf{3.0035}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D8$	$4.1034\times {10}^{-3}$	$3.1294\times {10}^{-3}$	$\mathbf{3.1010}\times {\mathbf{10}}^{-\mathbf{3}}$
Release Height Variation	Dose Rate, $D1$	$\mathbf{3.9049}\times {\mathbf{10}}^{-\mathbf{5}}$	$-2.0707\times {10}^{-3}$	$-6.8006\times {10}^{-5}$
	Dose Rate, $D2$	$\mathbf{2.7270}\times {\mathbf{10}}^{-\mathbf{4}}$	$-1.9502\times {10}^{-3}$	$-8.6245\times {10}^{-5}$
	Dose Rate, $D3$	$-\mathbf{1.3714}\times {\mathbf{10}}^{-\mathbf{5}}$	$-1.1677\times {10}^{-3}$	$3.3945\times {10}^{-4}$
	Dose Rate, $D4$	$-4.2531\times {10}^{-3}$	$\mathbf{2.9566}\times {\mathbf{10}}^{-\mathbf{3}}$	$-3.8136\times {10}^{-3}$
	Dose Rate, $D5$	$\mathbf{3.2063}\times {\mathbf{10}}^{-\mathbf{4}}$	$-1.4707\times {10}^{-3}$	$4.8002\times {10}^{-4}$
	Dose Rate, $D6$	$-2.8939\times {10}^{-3}$	$\mathbf{1.1653}\times {\mathbf{10}}^{-\mathbf{3}}$	$-2.1439\times {10}^{-3}$
	Dose Rate, $D7$	$-\mathbf{4.6874}\times {\mathbf{10}}^{-\mathbf{3}}$	$5.3485\times {10}^{-3}$	$-4.6173\times {10}^{-3}$
	Dose Rate, $D8$	$-\mathbf{4.6190}\times {\mathbf{10}}^{-\mathbf{3}}$	$5.7571\times {10}^{-3}$	$-4.4494\times {10}^{-3}$
Atmospheric Condition Variation	Dose Rate, $D1$	$-2.4751\times {10}^{-5}$	$4.0318\times {10}^{-6}$	$\mathbf{4.0316}\times {\mathbf{10}}^{-\mathbf{6}}$
	Dose Rate, $D2$	$-\mathbf{4.6815}\times {\mathbf{10}}^{-\mathbf{4}}$	$-1.7304\times {10}^{-3}$	$-1.7305\times {10}^{-3}$
	Dose Rate, $D3$	$1.0294\times {10}^{-2}$	$-2.8680\times {10}^{-3}$	$-\mathbf{2.8679}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D4$	$4.4446\times {10}^{-2}$	$-2.2647\times {10}^{-3}$	$-\mathbf{2.2646}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D5$	$6.4633\times {10}^{-3}$	$-3.0025\times {10}^{-3}$	$-\mathbf{3.0023}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D6$	$3.0587\times {10}^{-2}$	$-3.4323\times {10}^{-3}$	$-\mathbf{3.4322}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D7$	$6.0159\times {10}^{-2}$	$-1.2138\times {10}^{-3}$	$-\mathbf{1.2135}\times {\mathbf{10}}^{-\mathbf{3}}$
	Dose Rate, $D8$	$6.2857\times {10}^{-2}$	$-1.0359\times {10}^{-3}$	$-\mathbf{1.0356}\times {\mathbf{10}}^{-\mathbf{3}}$
Multiple Release Sources	Dose Rate, $D1$	$-\mathbf{6.7244}\times {\mathbf{10}}^{-\mathbf{4}}$	$-7.5957\times {10}^{-4}$	$-7.5958\times {10}^{-4}$
	Dose Rate, $D2$	$\mathbf{1.9101}\times {\mathbf{10}}^{-\mathbf{2}}$	$2.1844\times {10}^{-2}$	$2.1846\times {10}^{-2}$
	Dose Rate, $D3$	$-1.2789\times {10}^{-2}$	$-\mathbf{1.2655}\times {\mathbf{10}}^{-\mathbf{2}}$	$-1.2656\times {10}^{-2}$
	Dose Rate, $D4$	$\mathbf{8.8186}\times {\mathbf{10}}^{-\mathbf{3}}$	$-2.7563\times {10}^{-2}$	$-2.7563\times {10}^{-2}$
	Dose Rate, $D5$	$-3.3659\times {10}^{-2}$	$-\mathbf{3.1000}\times {\mathbf{10}}^{-\mathbf{2}}$	$-3.1101\times {10}^{-2}$
	Dose Rate, $D6$	$-\mathbf{2.9651}\times {\mathbf{10}}^{-\mathbf{2}}$	$-5.1488\times {10}^{-2}$	$-5.1493\times {10}^{-2}$
	Dose Rate, $D7$	$7.0950\times {10}^{-2}$	$\mathbf{2.0353}\times {\mathbf{10}}^{-\mathbf{2}}$	$2.0355\times {10}^{-2}$
	Dose Rate, $D8$	$9.0966\times {10}^{-2}$	$\mathbf{3.8934}\times {\mathbf{10}}^{-\mathbf{2}}$	$3.8935\times {10}^{-2}$

, respectively. The positive and negative values of FB denote underestimation and overestimation, respectively, whereas the zero value denotes correct estimation. It can be noted that the value of FB is lowest in the case of UKF during state estimation, while all of the algorithms perform similarly during prediction.

Further, the prediction capability of the estimation algorithms in predicting the true value from the noisy measurements can be assessed by estimating the sample correlation coefficient. It is given by

$$\begin{array}{ccc}\hfill r_{rp}& =& \frac{\sum _{k=1}^N\left(r_k-{\overline{r}}_k\right)\left(p_k-{\overline{p}}_k\right)}{\sqrt{\sum _{k=1}^N{\left(r_k-{\overline{r}}_k\right)}^2}\sqrt{\sum _{k=1}^N{\left(p_k-{\overline{p}}_k\right)}^2}}\hfill \end{array}$$

(53)

The sample correlation coefficient is calculated between the reference value and predicted values.

Table 5. Sample correlation coefficients between true and estimated dose rates for EKF, UKF, and CKF.

Scenario	Parameter	EKF	UKF	CKF
Release Rate Variation	Dose Rate, $D1$	0.99929	0.99929	0.99929
	Dose Rate, $D2$	0.99890	0.99890	0.99890
	Dose Rate, $D3$	0.99709	0.99713	0.99712
	Dose Rate, $D4$	0.98924	0.98951	0.98949
	Dose Rate, $D5$	0.99769	0.99771	0.99669
	Dose Rate, $D6$	0.99208	0.99218	0.99216
	Dose Rate, $D7$	0.98655	0.98730	0.98727
	Dose Rate, $D8$	0.98615	0.98702	0.98700
Wind Speed Variation	Dose Rate, $D1$	0.99946	0.99946	0.99946
	Dose Rate, $D2$	0.99863	0.99863	0.99863
	Dose Rate, $D3$	0.99622	0.99622	0.99622
	Dose Rate, $D4$	0.99375	0.99384	0.99387
	Dose Rate, $D5$	0.99697	0.99697	0.99697
	Dose Rate, $D6$	0.99449	0.99453	0.99455
	Dose Rate, $D7$	0.99315	0.99331	0.99335
	Dose Rate, $D8$	0.99308	0.99325	0.99329
Release Height Variation	Dose Rate, $D1$	0.99911	0.99837	0.99915
	Dose Rate, $D2$	0.99871	0.99737	0.99860
	Dose Rate, $D3$	0.99669	0.99454	0.99680
	Dose Rate, $D4$	0.92929	0.96793	0.91879
	Dose Rate, $D5$	0.99766	0.99522	0.99735
	Dose Rate, $D6$	0.96016	0.97869	0.96033
	Dose Rate, $D7$	0.91439	0.96228	0.89660
	Dose Rate, $D8$	0.91297	0.96161	0.89561
Atmospheric Condition Variation	Dose Rate, $D1$	0.99927	0.99927	0.99927
	Dose Rate, $D2$	0.99829	0.99823	0.99823
	Dose Rate, $D3$	0.99307	0.99599	0.99598
	Dose Rate, $D4$	0.72922	0.98483	0.98482
	Dose Rate, $D5$	0.99508	0.99635	0.99634
	Dose Rate, $D6$	0.90956	0.98914	0.98913
	Dose Rate, $D7$	0.40531	0.98011	0.98010
	Dose Rate, $D8$	0.34802	0.97933	0.97932
Multiple Release Sources	Dose Rate, $D1$	0.99974	0.99974	0.99974
	Dose Rate, $D2$	0.95793	0.95600	0.95600
	Dose Rate, $D3$	0.92437	0.92071	0.92071
	Dose Rate, $D4$	0.89899	0.89064	0.89064
	Dose Rate, $D5$	0.92954	0.92524	0.92524
	Dose Rate, $D6$	0.90521	0.90115	0.90115
	Dose Rate, $D7$	0.89292	0.88066	0.88066
	Dose Rate, $D8$	0.89263	0.87926	0.87926

shows the value of correlation coefficient for different estimation algorithms in predicting dose rates. It can be noted that all of the estimation algorithms predict the measurement accurately. The sample correlation using UKF and CKF are closer to one as compared to that obtained by EKF.

4.3. Tuning of Covariance Matrices

The process noise covariance matrix $Q_k$ and the measurement noise covariance matrix $R_k$ are constants and they do not depend on k. In the literature, various noise covariances matrix estimation approaches, such as the maximum-likelihood methods, correlation methods, covariance matching methods, and Bayesian methods are proposed. The various methods differ in assumptions related to the system model, underlying ideas and principles, properties of the estimates, and number and essence of the design parameters. Any of the above-mentioned methods can be employed to estimate the covariance matrices $Q_k$ and $R_k$ [38]. Selecting the optimum value of $Q_k$ and $R_k$ is crucial for the successful application of estimation algorithms however, the optimal selection is arduous. If $Q_k$ is chosen less than the actual value, the estimation algorithm will weigh the model more over the measurements. This can affect the performance during the correction of system states. In contrast, if $Q_k$ is chosen more than the actual value, then the increased values of the state covariance matrix will give noisy and uncertain estimates. A tuning approach that is based on computing the variance of innovations has been adopted here. The values of $Q_K$ are varied for a fixed value of $R_k$ and the variance of innovation is calculated. The values of $Q_k$ and $R_k$ are selected, such that there is no significant variation in the variance of innovations on further reducing $Q_k$ for a fixed value of $R_k$.

4.4. Discussion

The proposed nonlinear Kalman filter techniques simultaneously estimate different parameters related to radioactivity release and improve the forecast of dose rate measurement. The unscented and cubature Kalman filters are found to have higher accuracy and robustness for non-linear models than the extended Kalman filter. Instead of linearising the functions as is done by the extended Kalman filter, the unscented and the cubature Kalman filters use a set of points and propagate these points through the actual non-linear function. These points are chosen, such that the lower and possibly the higher-order moments match those of the Gaussian random variable. The mean and the covariance can be recalculated from the propagated points, yielding more accurate results when compared to the ordinary function linearisation. Different scenarios have been studied to analyse the performance of the proposed estimation techniques. In case of increment in release rate, the dose rate monitors suddenly detect large dose rates. This sudden increment in dose can also be due to a reduction in wind speed. Thus, the estimation algorithm initially estimate a reduction in wind speed. However, due to the prediction and correction nature of Kalman filters, they are able to figure out the exact reason of increased dose rate and, thus, are able to estimate estimate the correct states. Then, due to countermeasure the release rate decreases, which leads to a decrement in the dose rates. This decrement in dose can also be due to an increment in wind speed which take away the plume. After prediction and correction, the estimation algorithms are able to estimate the correct states which leads to increment in the estimate of wind speed. In the case of increment in wind speed, the dose rate monitors suddenly detect low dose rates. This low dose rates can also be due to a reduction in release. Thus, the estimation algorithm initially estimate a reduction in release rate. Now, when the wind is strong, the released plume will quickly leave the monitored area, and the dose rate monitors fail to capture the plume. Moreover, the estimate of release heights are slightly different than the steady state condition due to poor measurements. In case of increment in plume rise, it becomes difficult for the plume to reach the ground, which leads to the insufficiency of the measurements. This will lead to sudden increment in wind speed. However, after prediction and correction steps with more dose rate data, the Kalman filter will converge to its steady state value. Thus, the accuracy of the nonlinear Kalman filter-based techniques is dependent on the accuracy of the model and the measurements. The employed Gaussian plume dispersion model is suitable in the range of tens of km for plain and homogeneous terrain conditions. If the measurements are sufficiently clean then the accuracy of the proposed technique does not differ much in between these characteristic lengths. However, if the measurements are heavily noisy then the performance of the algorithms will be affected. The selection of process and measurement noise covariance matrices further affect the performance. Thus, a careful selection of $Q_k$ and $R_k$ matrices is important. In addition, the considered Gaussian plume dispersion model implies some limitations on model’s applicability for detailed studies. The presented model does not try to represent wind direction, which is assumed as constant. Any variation in the wind direction will act as modelling uncertainty and it will affect the accuracy of the state estimation. For a better prediction, the wind direction can be considered as another state of the model. For the detection of source location, the estimation algorithm can be combined with any backtracking algorithm to locate the centre of the source by extrapolating the states backwards [39]. This will further increase the accuracy of the release rate. For locating multiple release sources, the nonlinear estimation algorithm can be combined with other techniques, such as the optimization methods that are used in the field of collective robotics [40,41].

5. Conclusions

Radioactivity release estimation is an important task during normal or accident scenarios. In this work, nonlinear Kalman filter-based approaches have been proposed for radionuclide release activity estimation. Specifically, Extended Kalman Filter, Unscented Kalman Filter, and Cubature Kalman Filter algorithms have been proposed in order to estimate radionuclides release rate, mean wind speed, and effective height of release. The algorithms are further employed to predict dose rates at different detectors. The estimation algorithms are found to reliably estimate the source information. It has been found that the UKF and CKF give better estimates than the EKF algorithm. The technique employed the Gaussian plume model of atmospheric dispersion for the computation of doses. The effectiveness of the estimation algorithms has been validated for different simulated scenarios. It has been observed from the simulation results that the estimation algorithms perform satisfactorily. Different statistical measures have been computed for analysing the performance of the proposed approaches. In the future, the nonlinear estimation algorithms will be designed in order to incorporate mobile sensors placed on autonomous vehicles in addition to the fixed sensor arrangement to further enhance the estimates.