Adaptive Higher-Order Sliding Mode Control of Series-Compensated DFIG-Based Wind Farm for Sub-Synchronous Control Interaction Mitigation
Abstract
:1. Introduction
2. System Modeling and SSCI Analysis
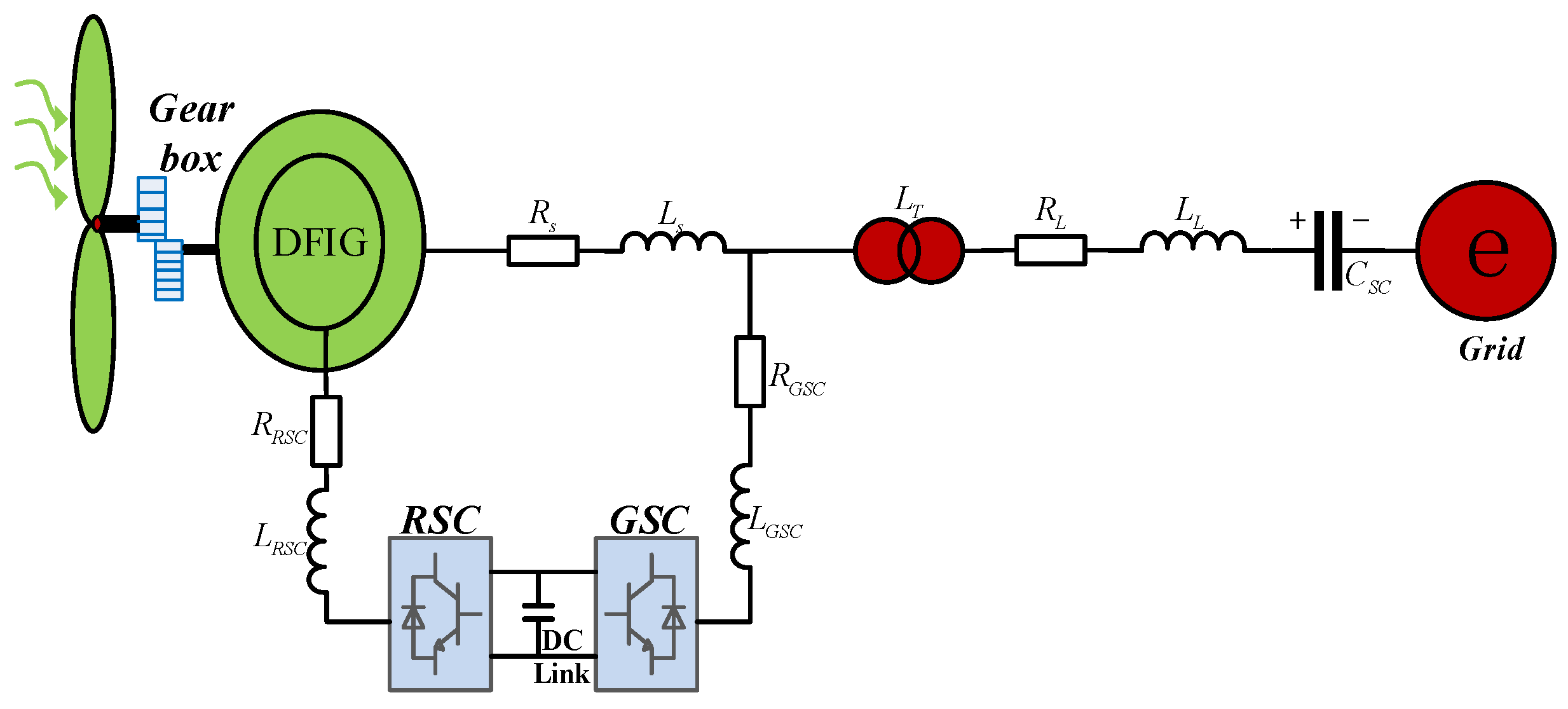
2.1. Series-Compensated DFIG-Based Wind Farm Grid-Connected System Modeling
2.2. SSCI Analysis
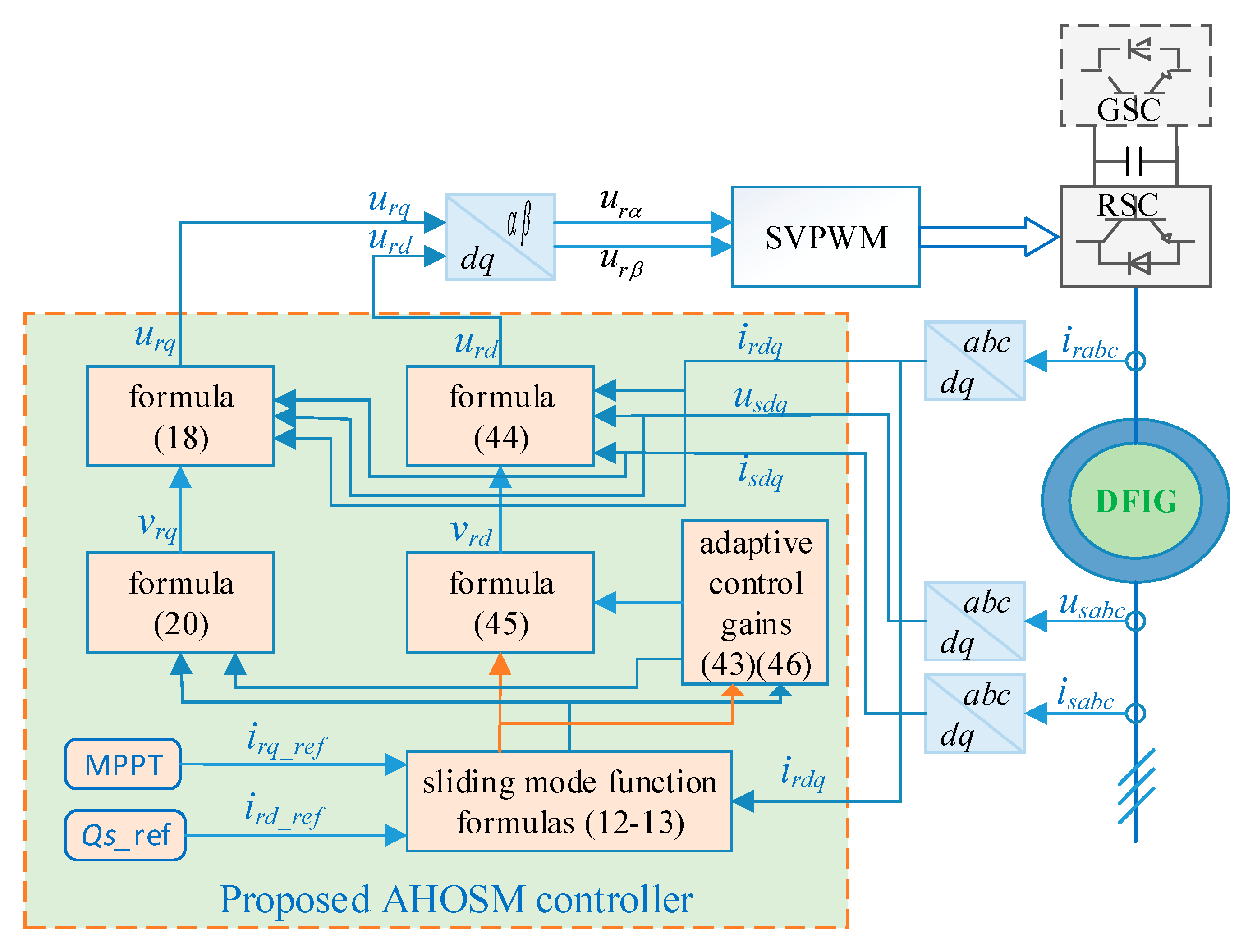
3. AHOSM Control Design
4. Time-Domain Simulation
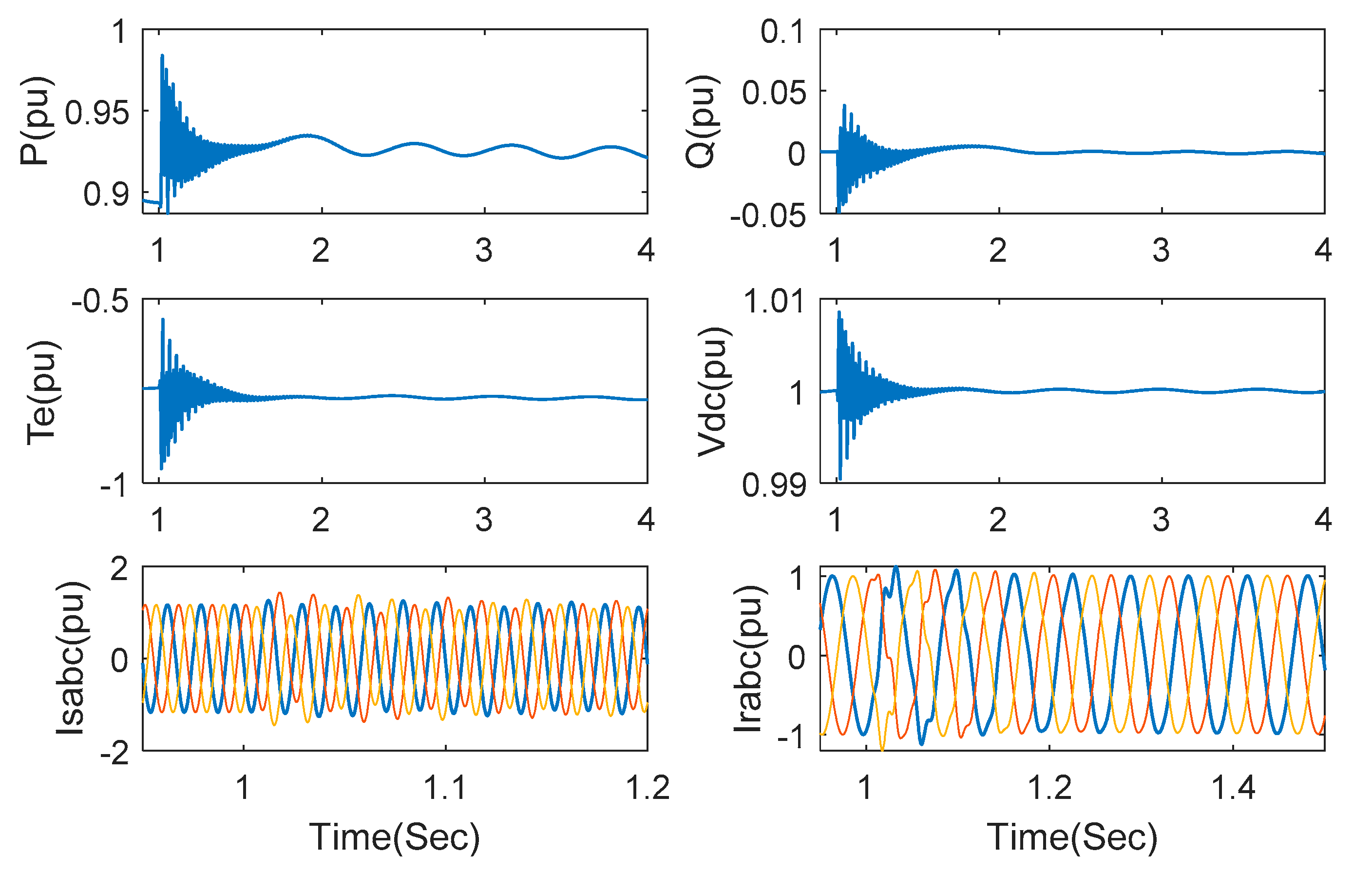
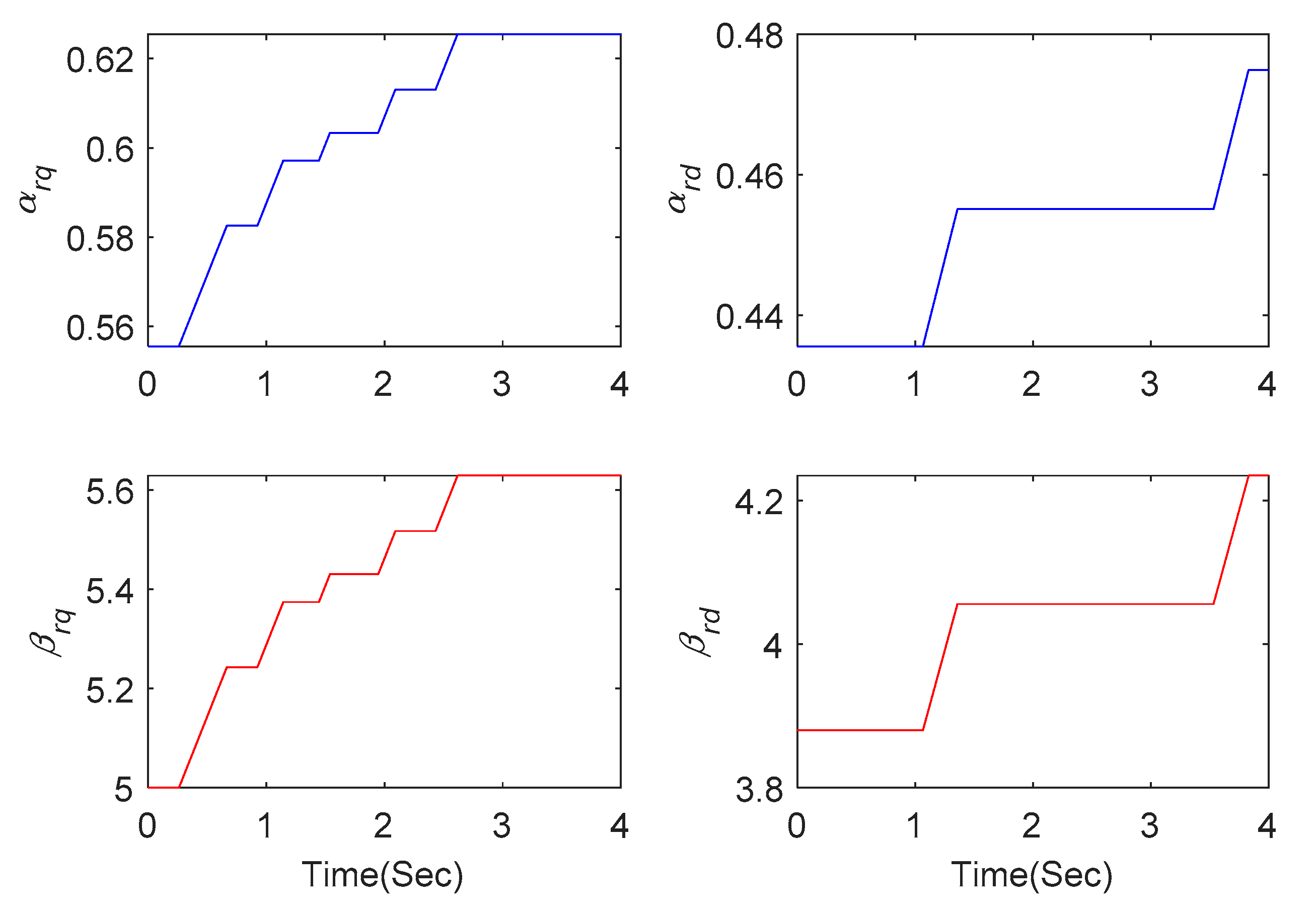
4.1. Control Performance Demonstration
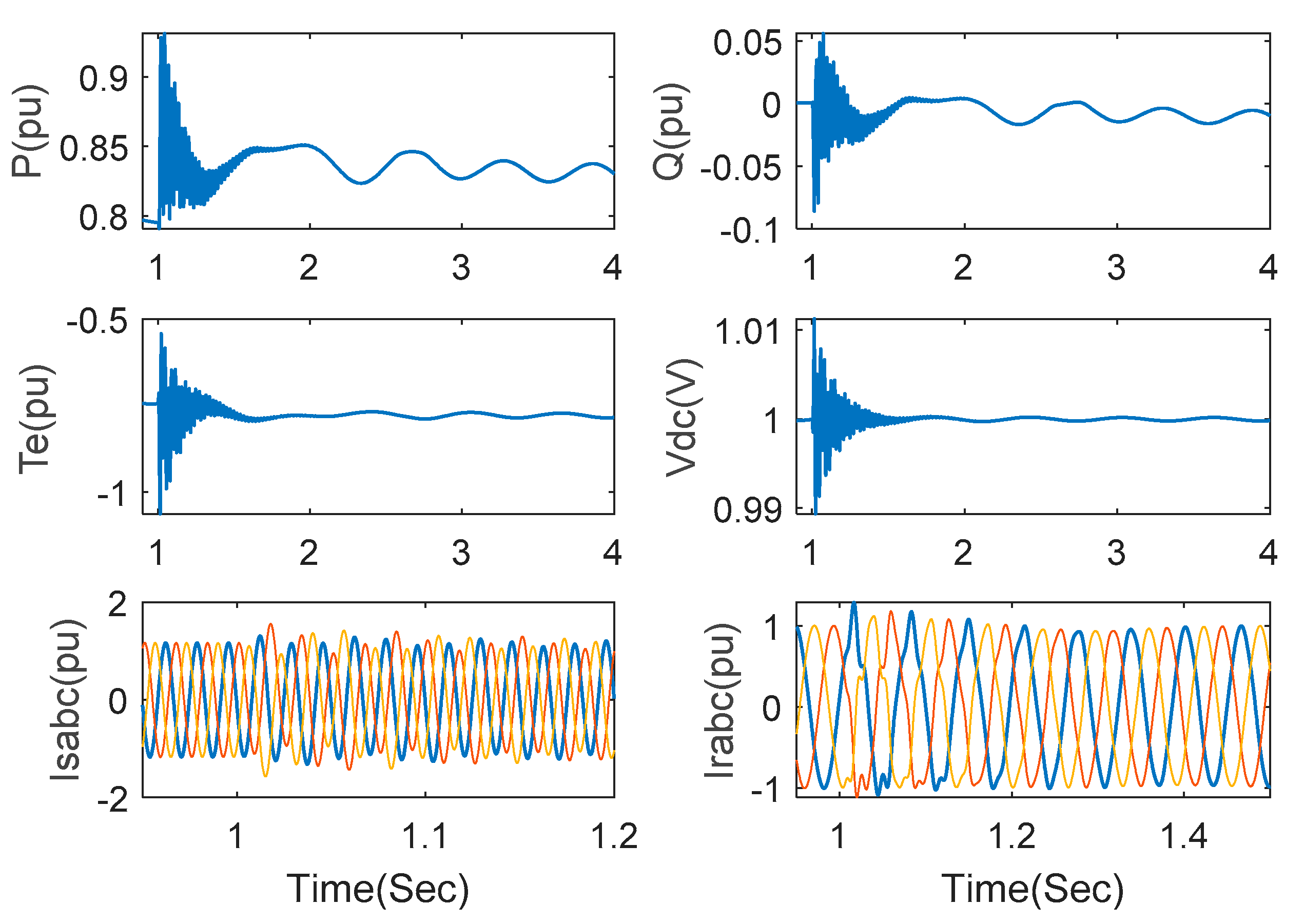
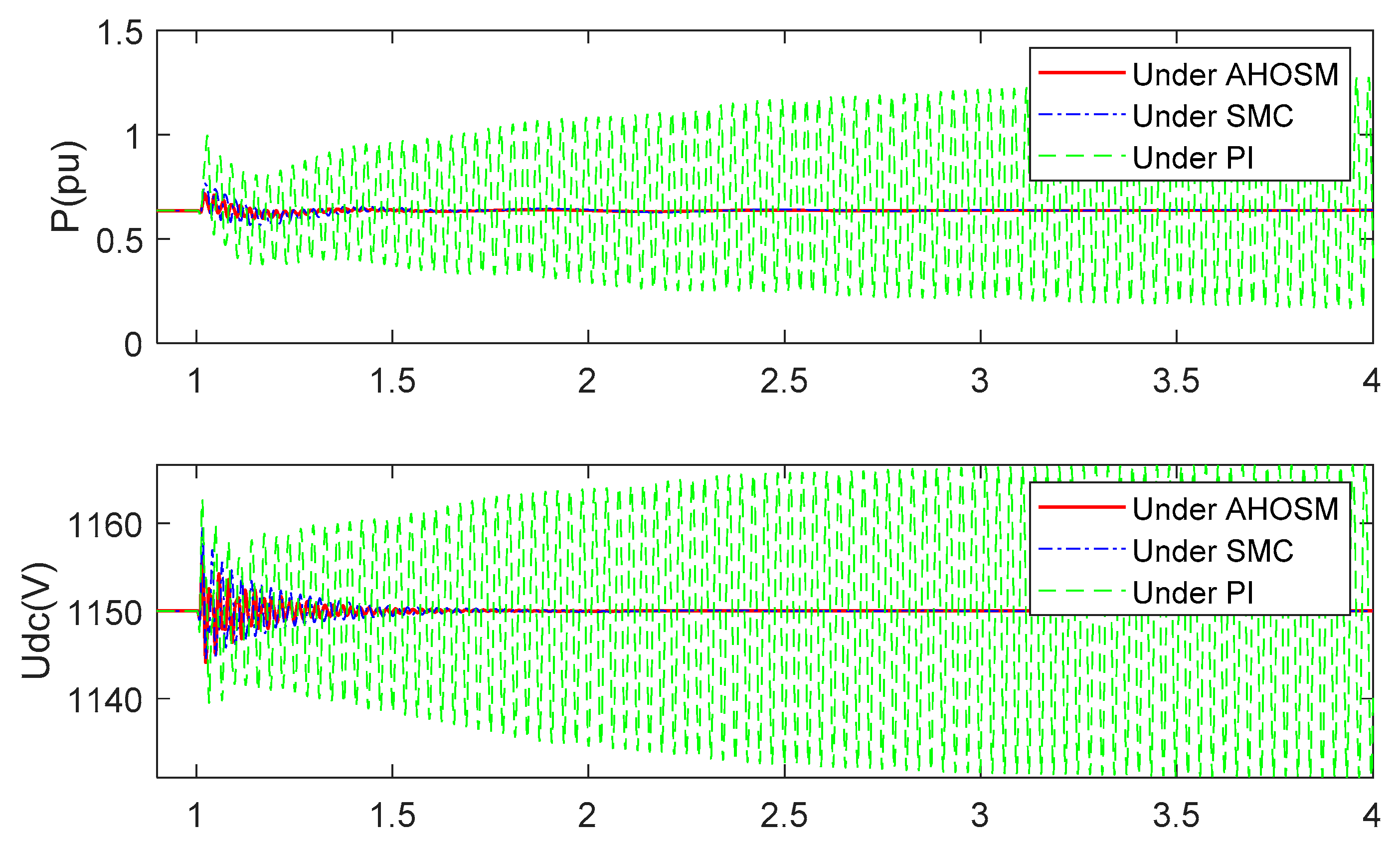
4.2. Comparison with PI and SMC Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bounar, N.; Labdai, S.; Boulkroune, A. PSO–GSA based fuzzy sliding mode controller for DFIG-based wind turbine. ISA Trans. 2019, 85, 177–188. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Fu, Q.; Wang, H. Power System Small-Signal Angular Stability Affected by Virtual Synchronous Generators. IEEE Trans. Power Syst. 2019, 34, 3209–3219. [Google Scholar] [CrossRef]
- Chernet, S.; Beza, M.B.; Bongiorno, M. Investigation of subsynchronous control interaction in DFIG-based wind farms connected to a series compensated transmission line. Int. J. Electr. Power Energy Syst. 2019, 105, 765–774. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, X.; Shair, J.; Liu, H.; Li, Y.; Li, Y. A Grid-Side Subsynchronous Damping Controller to Mitigate Unstable SSCI and Its Hardware-in-the-loop Tests. IEEE Trans. Sustain. Energy 2019, 11, 1548–1558. [Google Scholar] [CrossRef]
- Ghafouri, M.; Karaagac, U.; Karimi, H.; Mahseredjian, J. Robust subsynchronous interaction damping controller for DFIG-based wind farms. J. Mod. Power Syst. Clean Energy 2019, 7, 1663–1674. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Zhang, X.; Liu, H.; Liu, H.; Li, Y.; Zhang, C. Characteristic Analysis of Subsynchronous Resonance in Practical Wind Farms Connected to Series-Compensated Transmissions. IEEE Trans. Energy Convers. 2017, 32, 1117–1126. [Google Scholar] [CrossRef]
- Revel, G.; Alonso, D.M. Subsynchronous interactions in power networks with multiple DFIG-based wind farms. Electr. Power Syst. Res. 2018, 165, 179–190. [Google Scholar] [CrossRef]
- Fan, L.; Zhu, C.; Miao, Z.; Hu, M. Modal Analysis of a DFIG-Based Wind Farm Interfaced With a Series Compensated Network. IEEE Trans. Energy Convers. 2011, 26, 1010–1020. [Google Scholar] [CrossRef]
- He, C.; Sun, D.; Song, L.; Ma, L. Analysis of Subsynchronous Resonance Characteristics and Influence Factors in a Series Compensated Transmission System. Energies 2019, 12, 3282. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Miao, Z. Mitigating SSR Using DFIG-Based Wind Generation. IEEE Trans. Sustain. Energy 2012, 3, 349–358. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.; Miao, Z. Replicating Real-World Wind Farm SSR Events. IEEE Trans. Power Deliv. 2020, 35, 339–348. [Google Scholar] [CrossRef]
- Ghaffarzadeh, H.; Mehrizi-Sani, A. Mitigation of Subsynchronous Resonance Induced by a Type III Wind System. IEEE Trans. Sustain. Energy 2019, 11, 1717–1727. [Google Scholar] [CrossRef]
- Yao, J.; Wang, X.; Li, J.; Liu, R.; Zhang, H. Sub-Synchronous Resonance Damping Control for Series-Compensated DFIG-Based Wind Farm with Improved Particle Swarm Optimization Algorithm. IEEE Trans. Energy Convers. 2019, 34, 849–859. [Google Scholar] [CrossRef]
- Ghafouri, M.; Karaagac, U.; Karimi, H.; Jensen, S.; Mahseredjian, J.; Faried, S.O. An LQR Controller for Damping of Subsynchronous Interaction in DFIG-Based Wind Farms. IEEE Trans. Power Syst. 2017, 32, 1. [Google Scholar] [CrossRef]
- Yang, J.-W.; Sun, X.-F.; Chen, F.-H.; Liao, K.; He, Z.-Y. Subsynchronous resonance suppression strategy for doubly fed induction generators based on phase-shift average of rotor current. Int. Trans. Electr. Energy Syst. 2019, 29, e2831. [Google Scholar] [CrossRef]
- Chen, A.; Xie, D.; Zhang, D.; Gu, C.; Wang, K. PI Parameter Tuning of Converters for Sub-Synchronous Interactions Existing in Grid-Connected DFIG Wind Turbines. IEEE Trans. Power Electron. 2018, 34, 6345–6355. [Google Scholar] [CrossRef]
- Chowdhury, A.; Mahmud, A.; Shen, W.; Pota, H.R. Nonlinear Controller Design for Series-Compensated DFIG-Based Wind Farms to Mitigate Subsynchronous Control Interaction. IEEE Trans. Energy Convers. 2017, 32, 707–719. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Shafiullah, G. SSR Mitigation of Series-Compensated DFIG Wind Farms by a Nonlinear Damping Controller Using Partial Feedback Linearization. IEEE Trans. Power Syst. 2017, 33, 2528–2538. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Wu, F.; Li, H. Nonlinear controller based on state feedback linearization for series-compensated DFIG-based wind power plants to mitigate sub-synchronous control interaction. Int. Trans. Electr. Energy Syst. 2018, 29, e2682. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wu, Q.; Yang, R.; Tao, G.; Liu, Z. H∞ current damping control of DFIG based wind farm for sub-synchronous control interaction mitigation. Int. J. Electr. Power Energy Syst. 2018, 98, 509–519. [Google Scholar] [CrossRef]
- Xu, Y.; Zhao, S. Mitigation of Subsynchronous Resonance in Series-Compensated DFIG Wind Farm Using Active Disturbance Rejection Control. IEEE Access 2019, 7, 68812–68822. [Google Scholar] [CrossRef]
- Ding, S.; Park, J.H.; Chen, C.-C. Second-order sliding mode controller design with output constraint. Automatica 2020, 112, 108704. [Google Scholar] [CrossRef]
- Vidal, P.V.N.M.; Nunes, E.V.L.; Hsu, L. Output-Feedback Multivariable Global Variable Gain Super-Twisting Algorithm. IEEE Trans. Autom. Control. 2016, 62, 2999–3005. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Xiong, L.; Wang, J.; Jiang, X.; Bai, G.; Li, R.; Liu, S. DFIG wind turbine sliding mode control with exponential reaching law under variable wind speed. Int. J. Electr. Power Energy Syst. 2018, 96, 253–260. [Google Scholar] [CrossRef]
- Han, Y.; Ma, R. Adaptive-Gain Second-Order Sliding Mode Direct Power Control for Wind-Turbine-Driven DFIG under Balanced and Unbalanced Grid Voltage. Energies 2019, 12, 3886. [Google Scholar] [CrossRef] [Green Version]
- Merabet, A.; Eshaft, H.; Tanvir, A.A. Power-current controller based sliding mode control for DFIG-wind energy conversion system. IET Renew. Power Gener. 2018, 12, 1155–1163. [Google Scholar] [CrossRef]
- Li, P.; Xiong, L.; Wu, F.; Ma, M.; Wang, J. Sliding mode controller based on feedback linearization for damping of sub-synchronous control interaction in DFIG-based wind power plants. Int. J. Electr. Power Energy Syst. 2019, 107, 239–250. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Xiong, L.; Ma, M. Robust Nonlinear Controller Design for Damping of Sub-Synchronous Control Interaction in DFIG-Based Wind Farms. IEEE Access 2019, 7, 16626–16637. [Google Scholar] [CrossRef]
- Karunanayake, C.; Ravishankar, J.; Dong, Z.Y. Nonlinear SSR Damping Controller for DFIG Based Wind Generators Interfaced to Series Compensated Transmission Systems. IEEE Trans. Power Syst. 2020, 35, 1156–1165. [Google Scholar] [CrossRef]
- Utkin, V. Discussion Aspects of High-Order Sliding Mode Control. IEEE Trans. Autom. Control. 2015, 61, 829–833. [Google Scholar] [CrossRef]
- Levant, A.; Shustin, B. Quasi-Continuous MIMO Sliding-Mode Control. IEEE Trans. Autom. Control. 2018, 63, 3068–3074. [Google Scholar] [CrossRef]
- Sadeghi, R.; Madani, S.M.; Ataei, M.; Kashkooli, M.R.A.; Ademi, S. Super-Twisting Sliding Mode Direct Power Control of a Brushless Doubly Fed Induction Generator. IEEE Trans. Ind. Electron. 2018, 65, 9147–9156. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, P.; Zhang, F.; Meng, Z. Contact Dynamics and Control for Tethered Space Net Robot. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 918–929. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ali, Z.; Ullah, N.; Ro, J.-S. A Super Twisting Fractional Order Terminal Sliding Mode Control for DFIG-Based Wind Energy Conversion System. Energies 2020, 13, 2158. [Google Scholar] [CrossRef]












| Quantity | Value |
|---|---|
| Nominal power (MW) | 100 |
| Rater voltage (V) | 690 |
| Rs (pu) | 0.0084 |
| Ls (pu) | 0.167 |
| HT (pu) | 2.5 |
| HG (pu) | 0.5 |
| Ks (pu) | 0.15 |
| RRSC (pu) | 0.0083 |
| LRSC (pu) | 0.1323 |
| RGSC (pu) | 0.0015 |
| LGSC (pu) | 0.151 |
| DC link capacitance (mF) | 10 |
| Nominal DC link voltage (V) | 1150 |
| RL (pu) | 0.02 |
| LL (pu) | 0.0016 |
| CSC(at 45% compensation) (uF) | 42.61 |
| RMSurq | RMSurd | RMSeirq | RMSeird | |
|---|---|---|---|---|
| PI | 0.9857 | 0.9172 | 0.0672 | 0.0712 |
| SMC | 0.7719 | 0.7183 | 0.0533 | 0.0602 |
| AHOSM | 0.5316 | 0.5029 | 0.0371 | 0.0392 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Li, S.; Du, C. Adaptive Higher-Order Sliding Mode Control of Series-Compensated DFIG-Based Wind Farm for Sub-Synchronous Control Interaction Mitigation. Energies 2020, 13, 5421. https://doi.org/10.3390/en13205421
Han Y, Li S, Du C. Adaptive Higher-Order Sliding Mode Control of Series-Compensated DFIG-Based Wind Farm for Sub-Synchronous Control Interaction Mitigation. Energies. 2020; 13(20):5421. https://doi.org/10.3390/en13205421
Chicago/Turabian StyleHan, Yaozhen, Shuzhen Li, and Cuiqi Du. 2020. "Adaptive Higher-Order Sliding Mode Control of Series-Compensated DFIG-Based Wind Farm for Sub-Synchronous Control Interaction Mitigation" Energies 13, no. 20: 5421. https://doi.org/10.3390/en13205421
APA StyleHan, Y., Li, S., & Du, C. (2020). Adaptive Higher-Order Sliding Mode Control of Series-Compensated DFIG-Based Wind Farm for Sub-Synchronous Control Interaction Mitigation. Energies, 13(20), 5421. https://doi.org/10.3390/en13205421




