Insights into the Aeroacoustic Noise Generation for Vertical Axis Turbines in Close Proximity
Abstract
:1. Introduction
- We provide validation for Large Eddy Simulations of airfoils and VAWTs.
- We propose physics-based theoretical estimates for tonal frequencies appearing in VAWTs.
- We identify tonal frequencies in VAWT and group of four turbines in close proximity (or farm).
- We analyse the spectra and directivities of the isolated VAWT and the farm of four VAWTs, and identify the main physical mechanisms of noise generation.
2. Methodology
2.1. Solver Details
2.2. Configurations and Meshes
3. Numerical Simulations
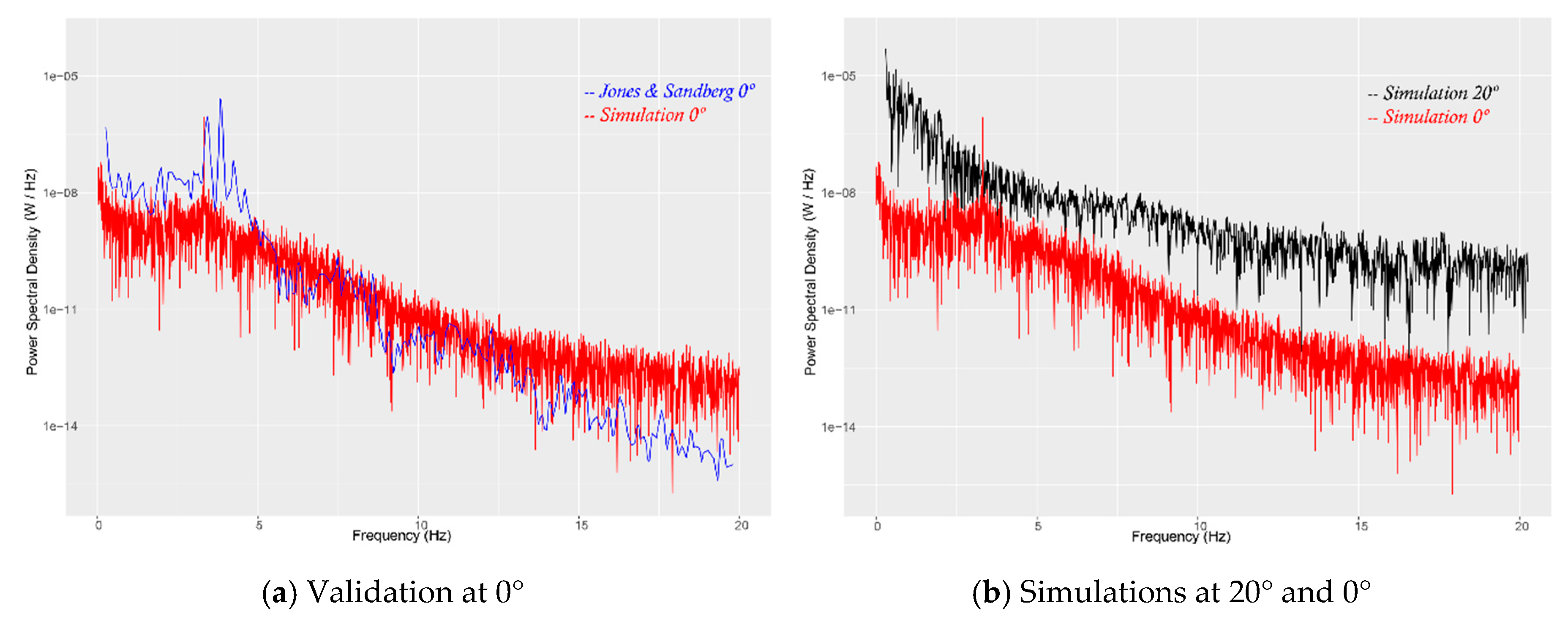
3.1. Aeroacoustic Sources for an Isolated NACA0012 Airfoil
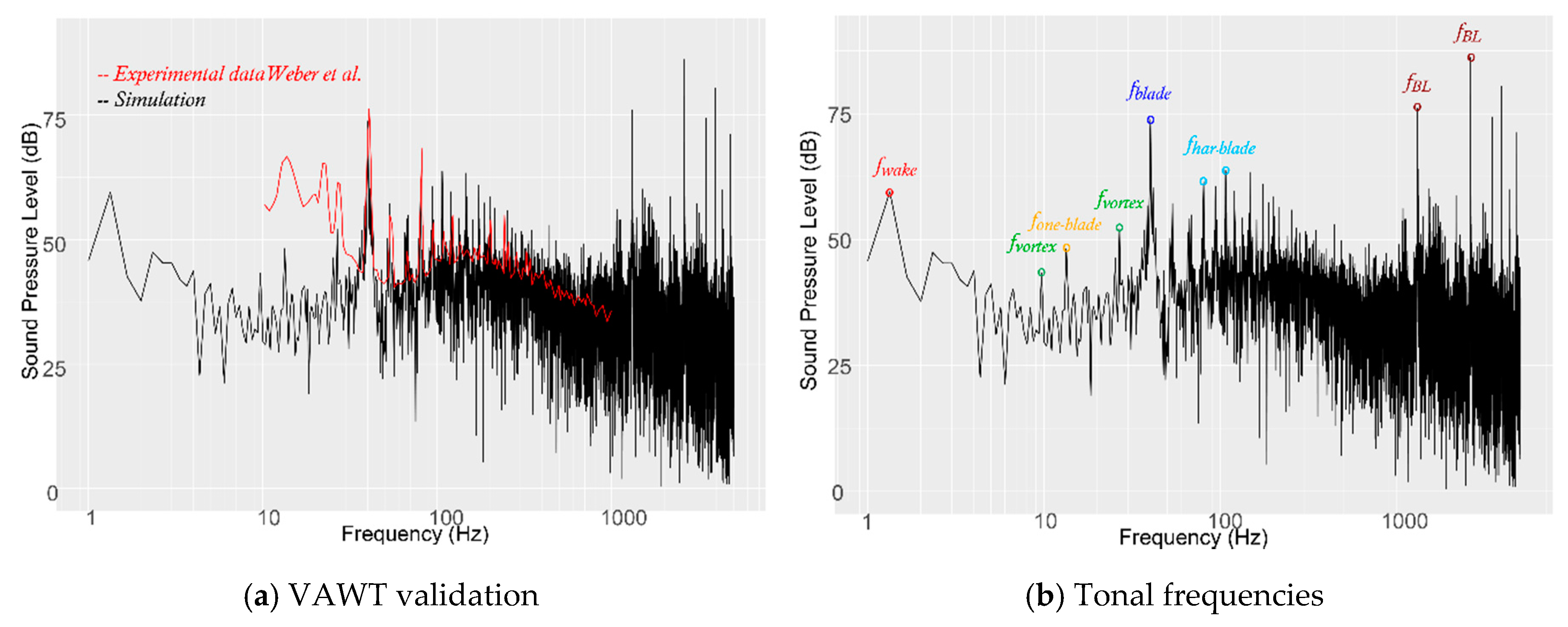
3.2. Aeroacoustic Sources for a Vertical Axis Wind Turbine
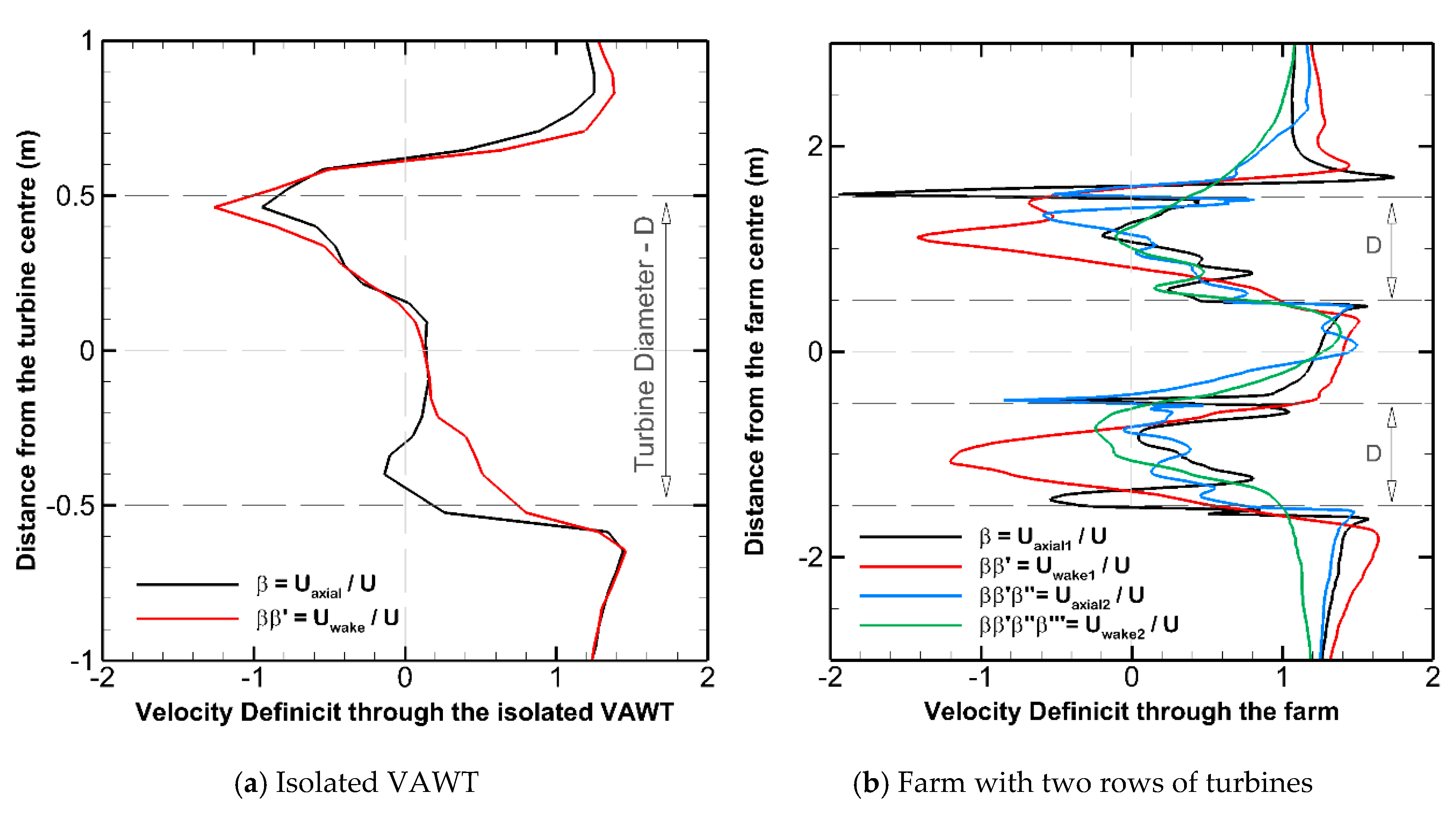
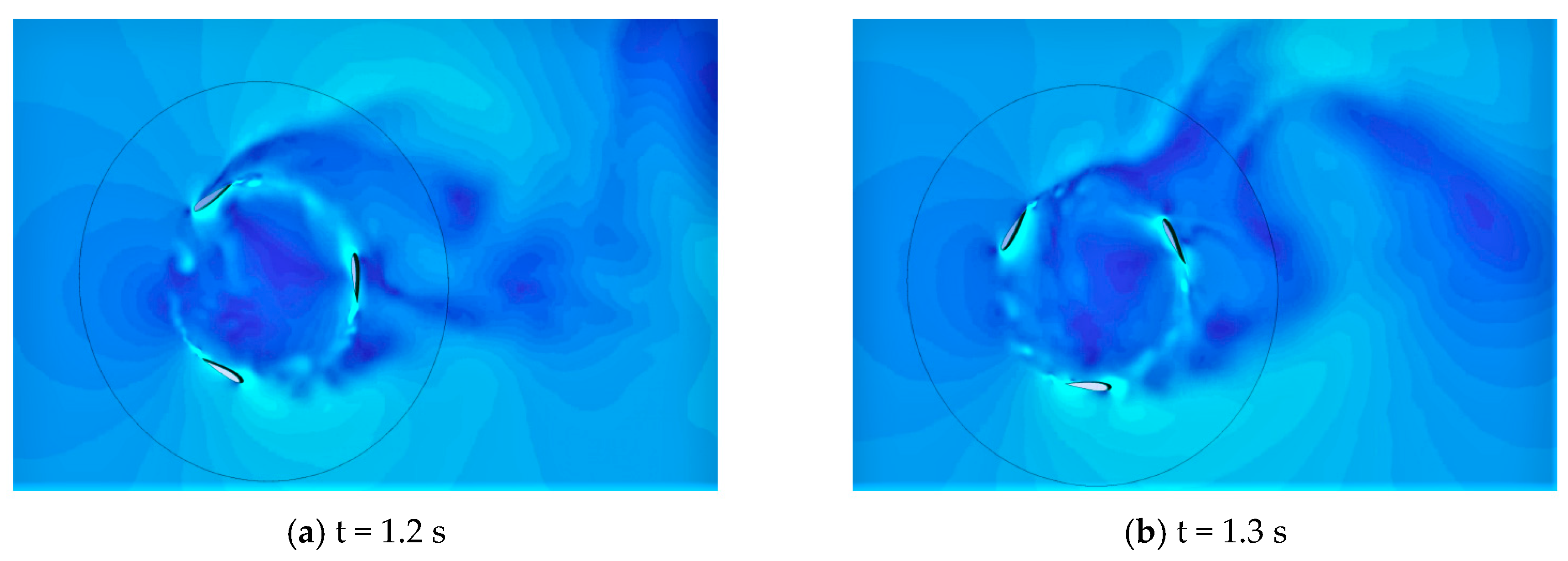
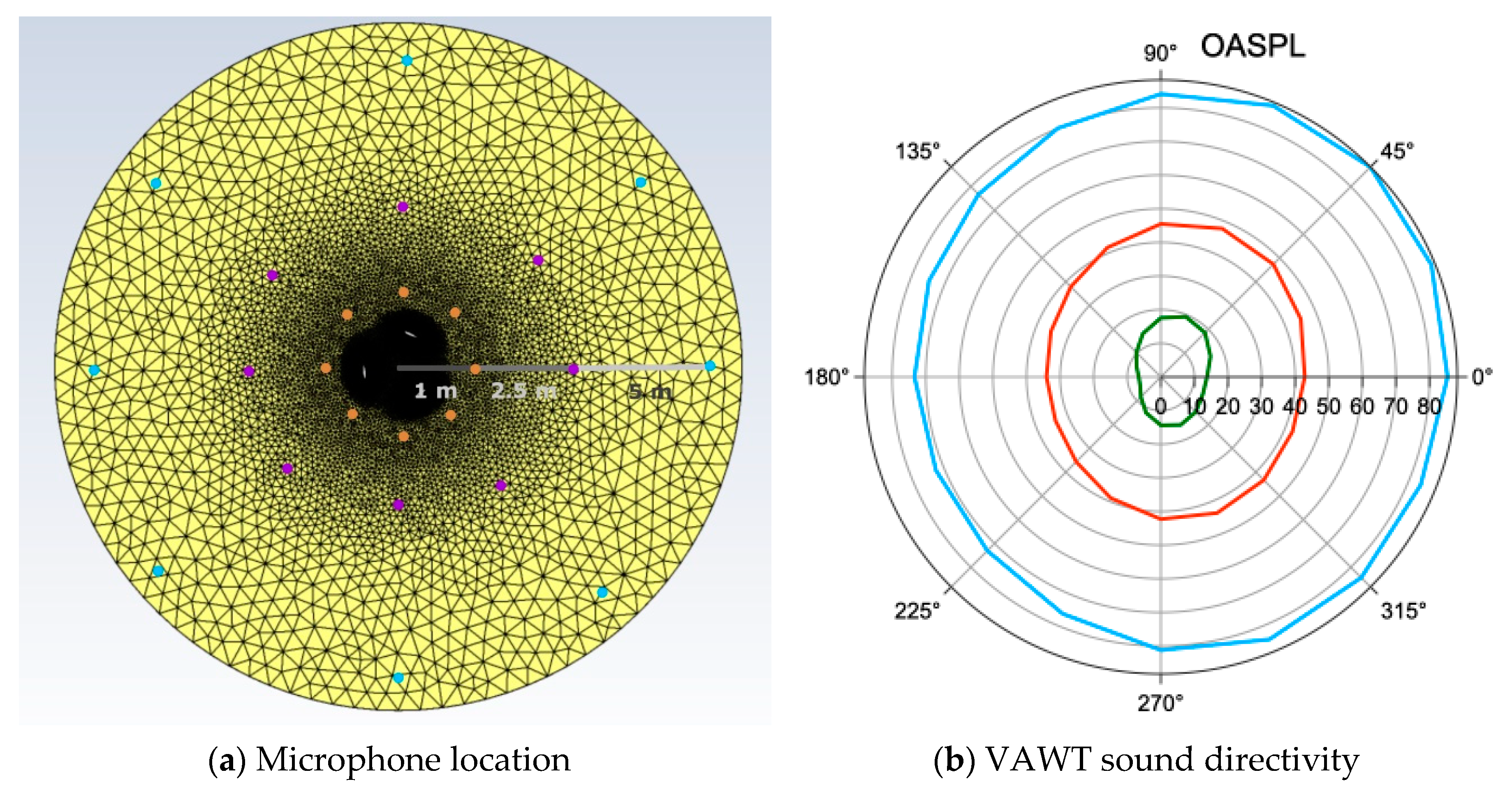
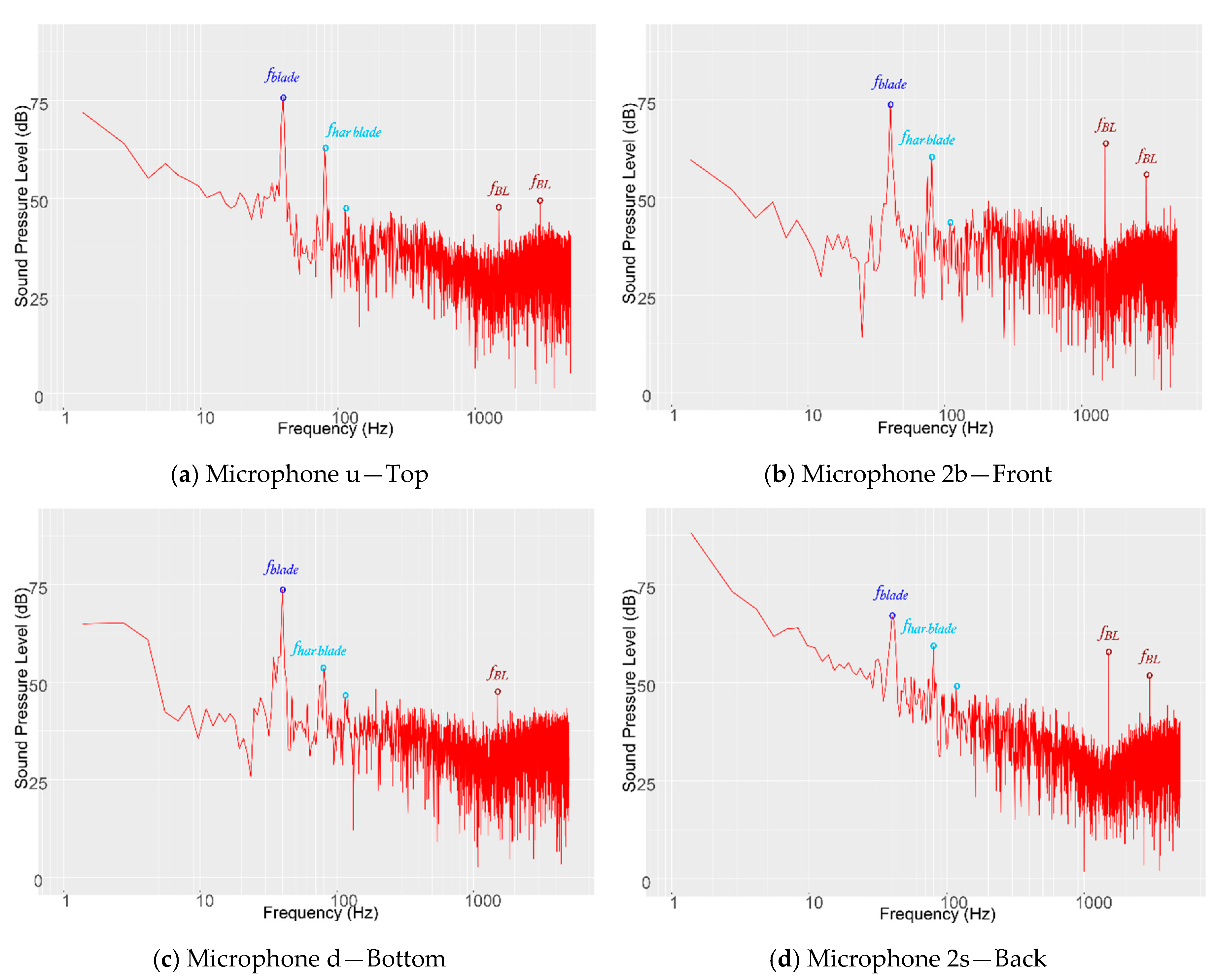
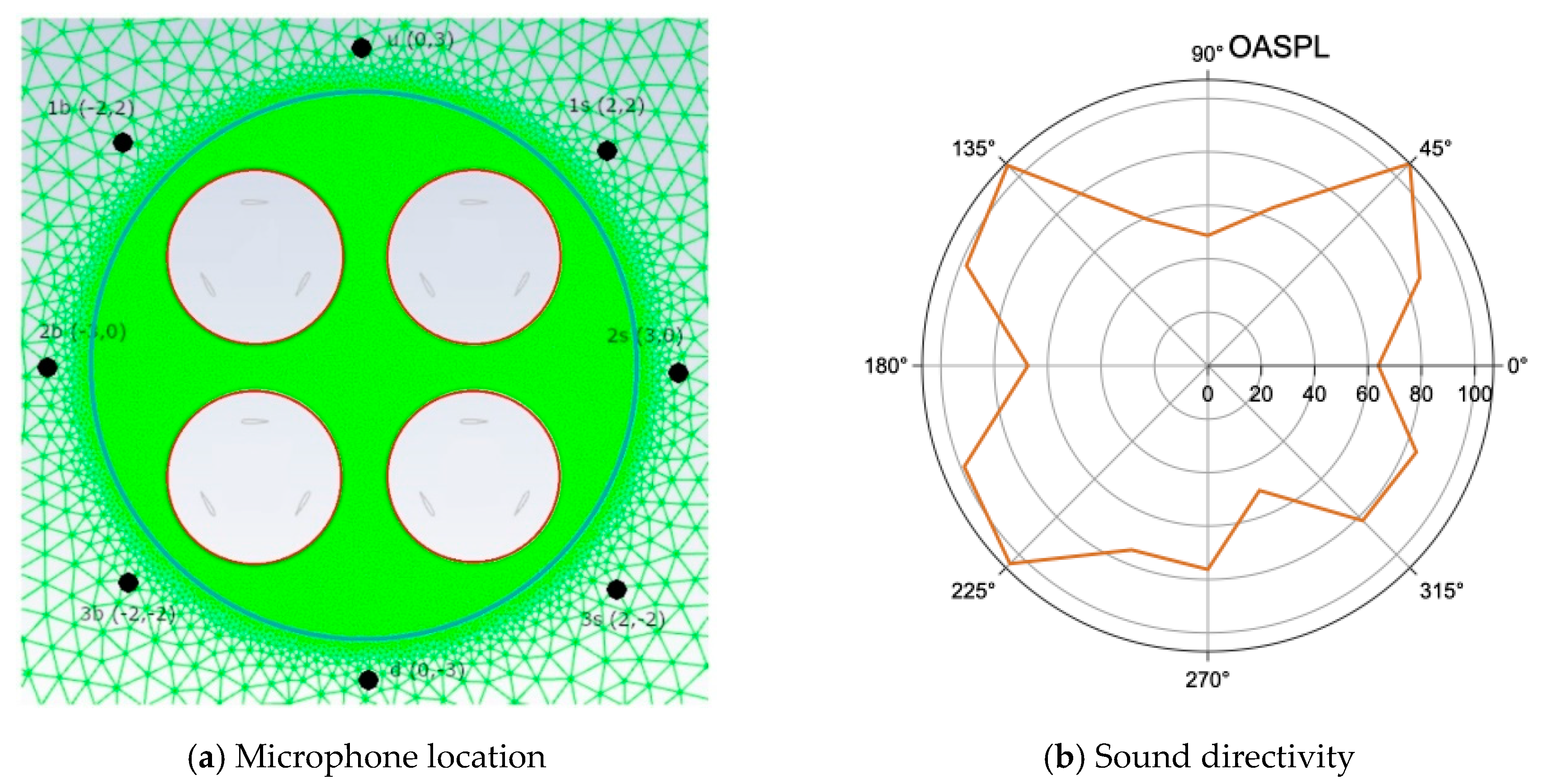
3.3. Aeroacoustic Sources for Four Vertical Axis Turbine in Close Proximity
3.4. Human Perception of the Farm Acoustics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. NACA0012 Airfoil and Tonal Frequency at Low Angles of Attack
Appendix B. Estimation of Flow Scales in Vertical Axis Wind Turbines

B.1. The Blade Scaling
| Length Scale | Time Scale | Velocity Scale | Reynolds Number |
|---|---|---|---|
B.2. Vortex Scaling and Blade-Vortex Interaction
| Length Scale | Time Scale | Velocity Scale | Reynolds Number |
|---|---|---|---|
B.3. Wake Scaling
| Length Scale | Time Scale | Velocity Scale | Reynolds Number |
|---|---|---|---|
B.4. Farm Scaling
| Length Scale | Time Scale | Velocity Scale | Reynolds Number |
|---|---|---|---|
B.5. VAWT Wake and Wake-Farm Scaling
References
- Bhutta, M.M.A.; Hayat, N.; Farooq, A.U.; Ali, Z.; Jamil, S.R.; Hussain, Z. Vertical axis wind turbine–A review of various configurations and design techniques. Renew. Sustain. Energy Rev. 2012, 16, 1926–1939. [Google Scholar] [CrossRef]
- Eriksson, S.; Bernhoff, H.; Leijon, M. Evaluation of different turbine concepts for wind power. Renew. Sustain. Energy Rev. 2008, 12, 1419–1434. [Google Scholar] [CrossRef]
- Kumar, R.; Raahemifar, K.; Fung, A.S. A critical review of vertical axis wind turbines for urban applications. Renew. Sustain. Energy Rev. 2018, 89, 281–291. [Google Scholar] [CrossRef]
- Ouro, P.; Runge, S.; Luo, Q.; Stoesser, T. Three-dimensionality of the wake recovery behind a vertical axis turbine. Renew. Energy 2019, 133, 1066–1077. [Google Scholar] [CrossRef] [Green Version]
- Posa, A. Dependence of the wake recovery downstream of a Vertical Axis Wind Turbine on its dynamic solidity. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104212. [Google Scholar] [CrossRef]
- Zanforlin, S.; Nishino, T. Fluid dynamic mechanisms of enhanced power generation by closely spaced vertical axis wind turbines. Renew. Energy 2016, 99, 1213–1226. [Google Scholar] [CrossRef] [Green Version]
- Alexander, A.S.; Santhanakrishnan, A. Mechanisms of power augmentation in two side-by-side vertical axis wind turbines. Renew. Energy 2020, 148, 600–610. [Google Scholar] [CrossRef]
- Brownstein, I.D.; Wei, N.J.; Dabiri, J.O. Aerodynamically Interacting Vertical-Axis Wind Turbines: Performance Enhancement and Three-Dimensional Flow. Energies 2019, 12, 2724. [Google Scholar] [CrossRef] [Green Version]
- Hezaveh, S.H.; Bou-Zeid, E.; Dabiri, J.; Kinzel, M.; Cortina, G.; Martinelli, L. Increasing the Power Production of Vertical-Axis Wind-Turbine Farms Using Synergistic Clustering. Bound. Layer Meteorol. 2018, 169, 275–296. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.D.; Zheng, X.; Zhao, S. Arrangement of clustered straight-bladed wind turbines. Energy 2020, 200, 117563. [Google Scholar] [CrossRef]
- Barnes, A.; Hughes, B. Determining the impact of VAWT farm configurations on power output. Renew. Energy 2019, 143, 1111–1120. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. A framework for preliminary large-scale urban wind energy potential assessment: Roof-mounted wind turbines. Energy Convers. Manag. 2020, 214, 112770. [Google Scholar] [CrossRef]
- Wagner, S.; Bareiss, R.; Guidati, G. Wind Turbine Noise; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Doolan, C.; Moreau, D.J.; Brooks, L.A. Wind turbine noise mechanisms and some concepts for its control. Acoust. Aust./Aust. Acoust. Soc. 2012, 40, 7–13. [Google Scholar]
- Ferrer, E.; Munduate, X. Wind turbine blade tip comparison using CFD. J. Phys. Conf. Ser. 2007, 75, 7–13. [Google Scholar] [CrossRef]
- Ferrer, E.; Willden, R.H. Blade-wake interactions in cross-flow turbines. Int. J. Mar. Energy 2015, 11, 71–83. [Google Scholar] [CrossRef] [Green Version]
- Bangga, G.; Dessoky, A.; Wu, Z.; Rogowski, K.; Hansen, M.O. Accuracy and consistency of CFD and engineering models for simulating vertical axis wind turbine loads. Energy 2020, 206, 118087. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E. A Reduced Order Model to Predict Transient Flows around Straight Bladed Vertical Axis Wind Turbines. Energies 2018, 11, 566. [Google Scholar] [CrossRef] [Green Version]
- Ferrer, E.; Browne, O.M.; Valero, E. Sensitivity Analysis to Control the Far-Wake Unsteadiness Behind Turbines. Energies 2017, 10, 599. [Google Scholar] [CrossRef] [Green Version]
- Ferrer, E.; Clainche, S.L. Simple Models for Cross Flow Turbines. In Recent Advances in CFD for Wind and Tidal Offshore Turbines; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Du, L.; Ingram, G.L.; Dominy, R.G. A review of H-Darrieus wind turbine aerodynamic research. Proceedings of the Institution of Mechanical Engineers, Part C. J. Mech. Eng. Sci. 2019, 233, 7590–7616. [Google Scholar] [CrossRef] [Green Version]
- Weber, J.; Tautz, M.; Becker, S.; Huppe, A.; Kaltenbacher, M. Computational Aeroacoustic Simulations of Small Vertical Axis Wind Turbine. In Proceedings of the Inter–Noise and Noise–Con Congress and Conference Proceedings, InterNoise16, Hamburg, Germany, 21–24 August 2016; pp. 3858–4854. [Google Scholar]
- Weber, J.; Becker, S.; Scheit, C.; Grabinger, J.; Kaltenbacher, M. Aeroacoustics of Darrieus wind turbine. Int. J. Aeroacoustics 2015, 14, 883–902. [Google Scholar] [CrossRef] [Green Version]
- Pearson, C. Vertical Axis Wind Turbine Acoustics. Ph.D. Thesis, Cambridge University Engineering Department, Cambridge, UK, 2013. [Google Scholar]
- Ottermo, F.; Möllerström, E.; Nordborg, A.; Hylander, J.; Bernhoff, H. Location of aerodynamic noise sources from a 200kW vertical-axis wind turbine. J. Sound Vib. 2017, 400, 154–166. [Google Scholar] [CrossRef]
- Pearson, C.E.; Graham, W. Investigation of The Noise Sources on A Vertical Axis Wind Turbine Using An Acoustic Array. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013. [Google Scholar]
- Möllerström, E.; Ottermo, F.; Hylander, J.; Bernhoff, H. Noise Emission of a 200 kW Vertical Axis Wind Turbine. Energies 2015, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- Ghasemian, M.; Nejat, A. Aero-acoustics prediction of a vertical axis wind turbine using Large Eddy Simulation and acoustic analogy. Energy 2015, 88, 711–717. [Google Scholar] [CrossRef]
- Mohamed, M. Aero-acoustics noise evaluation of H-rotor Darrieus wind turbines. Energy 2014, 65, 596–604. [Google Scholar] [CrossRef]
- Su, J.; Lei, H.; Zhou, D.; Han, Z.; Bao, Y.; Zhu, H.; Zhou, L. Aerodynamic noise assessment for a vertical axis wind turbine using Improved Delayed Detached Eddy Simulation. Renew. Energy 2019, 141, 559–569. [Google Scholar] [CrossRef]
- Mohamed, M. Reduction of the generated aero-acoustics noise of a vertical axis wind turbine using CFD (Computational Fluid Dynamics) techniques. Energy 2016, 96, 531–544. [Google Scholar] [CrossRef]
- Mohamed, M. Criticism study of J-Shaped Darrieus wind turbine: Performance evaluation and noise generation assessment. Energy 2019, 177, 367–385. [Google Scholar] [CrossRef]
- Botha, J.; Shahroki, A.; Rice, H. An implementation of an aeroacoustic prediction model for broadband noise from a vertical axis wind turbine using a CFD informed methodology. J. Sound Vib. 2017, 410, 389–415. [Google Scholar] [CrossRef] [Green Version]
- Lighthill, S.M.J. On Sound Generated Aerodynamically. In Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, London, UK, 20 March 1952; Royal Society: London, UK, 1952. [Google Scholar]
- Ffwocs Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philosophical Transactions of the Royal Society of London. Ser. A. Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- Goldstein, M.E. A Generalized Acoustic Theory. J. Fluid Mech. 2003, 488, 315–333. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Atlar, M.; Sampson, R. An experimental investigation on cavitation, noise, and slipstream characteristics of ocean stream turbines. Proceedings of the Institution of Mechanical Engineers-Part A. J. Power Energy 2006, 221, 219–231. [Google Scholar] [CrossRef]
- Jones, L.E.; Sandberg, R.D. Numerical analysis of tonal airfoil self-noise and acoustic feedback-loops. J. Sound Vib. 2011, 330, 6137–6152. [Google Scholar] [CrossRef]
- Paterson, R.W.; Vogt, P.; Fink, M.; Munch, C. Vortex Noise of Isolated Airfoils. J. Aircr. 1973, 10, 296–302. [Google Scholar] [CrossRef]
- Rodríguez, I.; Lehmkuhl, O.; Borrell, R.; Oliva, A. Direct numerical simulation of a NACA0012 in full stall.International. J. Heat Fluid Flow 2013, 43, 194–203. [Google Scholar] [CrossRef] [Green Version]
- Norberg, C. Fluctuating lift on a circular cylinder: Review and new measurements. J. Fluids Struct. 2003, 17, 57–96. [Google Scholar] [CrossRef]
- Möser, M. Engineering Acoustics: An Introduction to Noise Control; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Lowson, M.; Fiddes, S.; Nash, E. Laminar boundary layer aero-acoustic instabilities. In Proceedings of the 32nd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 22 August 2012. [Google Scholar] [CrossRef]
- Arbey, H.; Bataille, J. Noise generated by airfoil profiles placed in a uniform laminar flow. J. Fluid Mech. 1983, 134, 33–47. [Google Scholar] [CrossRef] [Green Version]
- Desquesnes, G.; Terracol, M.; Sagaut, P. Numerical investigation of the tone noise mechanism over laminar airfoils. J. Fluid Mech. 2007, 591, 155–182. [Google Scholar] [CrossRef]
- Ferrer, E. A high order Discontinuous Galerkin–Fourier Incompressible 3D Navier–Stokes Solver with Rotating Sliding Meshes for Simulating Cross-Flow Turbines. Ph.D. Thesis, University of Oxford, Oxford, UK, 2012. [Google Scholar]
- Ferrer, E.; Le Clainche, S. Flow Scales in Cross-Flow Turbines. In CFD for Wind and Tidal Offshore Turbines; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Anderson, J. Fundamentals of Aerodynamics, 4th ed.; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
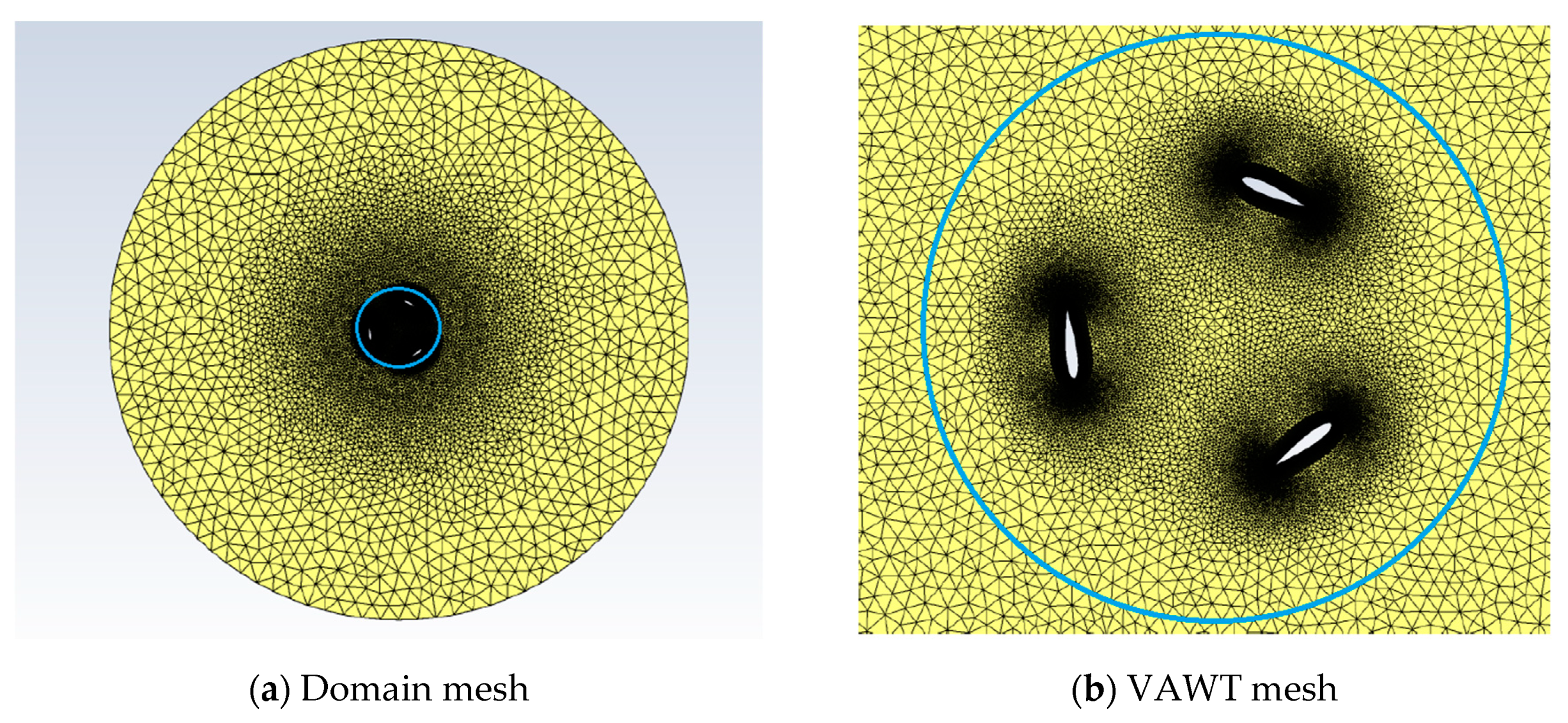

| NACA0012 (Sharp Trailing Edge) |
| Domain size (m): (C-type mesh) |
| Number of mesh elements: 253.080 |
| Reynolds number (chord based): |
| Blade Chord (m): |
| Angle of Attack (degrees): 0° |
| Isolated Vertical Axis Wind Turbine |
| Domain size (m): (O-type mesh) |
| Number of mesh elements: 460.740 |
| Reynolds number (Diameter based): |
| Profiles used for blades: NACA0018 (blunt trailing edge) |
| Turbine Diameter (m): |
| Number of blades: 3 |
| Blade Chord (m): |
| Rotational Velocity (rad/s): |
| Wind speed (m/s): |
| Tip speed ratio: |
| Range of Reynolds numbers (blade-chord based) for all azimuths: |
| Group of four Vertical Axis Wind Turbines (or farm) |
| Domain size (m): (O-type mesh) |
| Number of mesh elements: 5.053.400 |
| VAWT configuration: as for the individual turbine |
| Separation between turbines (m): 2 (square shape distribution) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viqueira-Moreira, M.; Ferrer, E. Insights into the Aeroacoustic Noise Generation for Vertical Axis Turbines in Close Proximity. Energies 2020, 13, 4148. https://doi.org/10.3390/en13164148
Viqueira-Moreira M, Ferrer E. Insights into the Aeroacoustic Noise Generation for Vertical Axis Turbines in Close Proximity. Energies. 2020; 13(16):4148. https://doi.org/10.3390/en13164148
Chicago/Turabian StyleViqueira-Moreira, Manuel, and Esteban Ferrer. 2020. "Insights into the Aeroacoustic Noise Generation for Vertical Axis Turbines in Close Proximity" Energies 13, no. 16: 4148. https://doi.org/10.3390/en13164148
APA StyleViqueira-Moreira, M., & Ferrer, E. (2020). Insights into the Aeroacoustic Noise Generation for Vertical Axis Turbines in Close Proximity. Energies, 13(16), 4148. https://doi.org/10.3390/en13164148






