Kinematics Measurement and Power Requirements of Fruitflies at Various Flight Speeds
Abstract
:1. Introduction
2. Materials and Methods
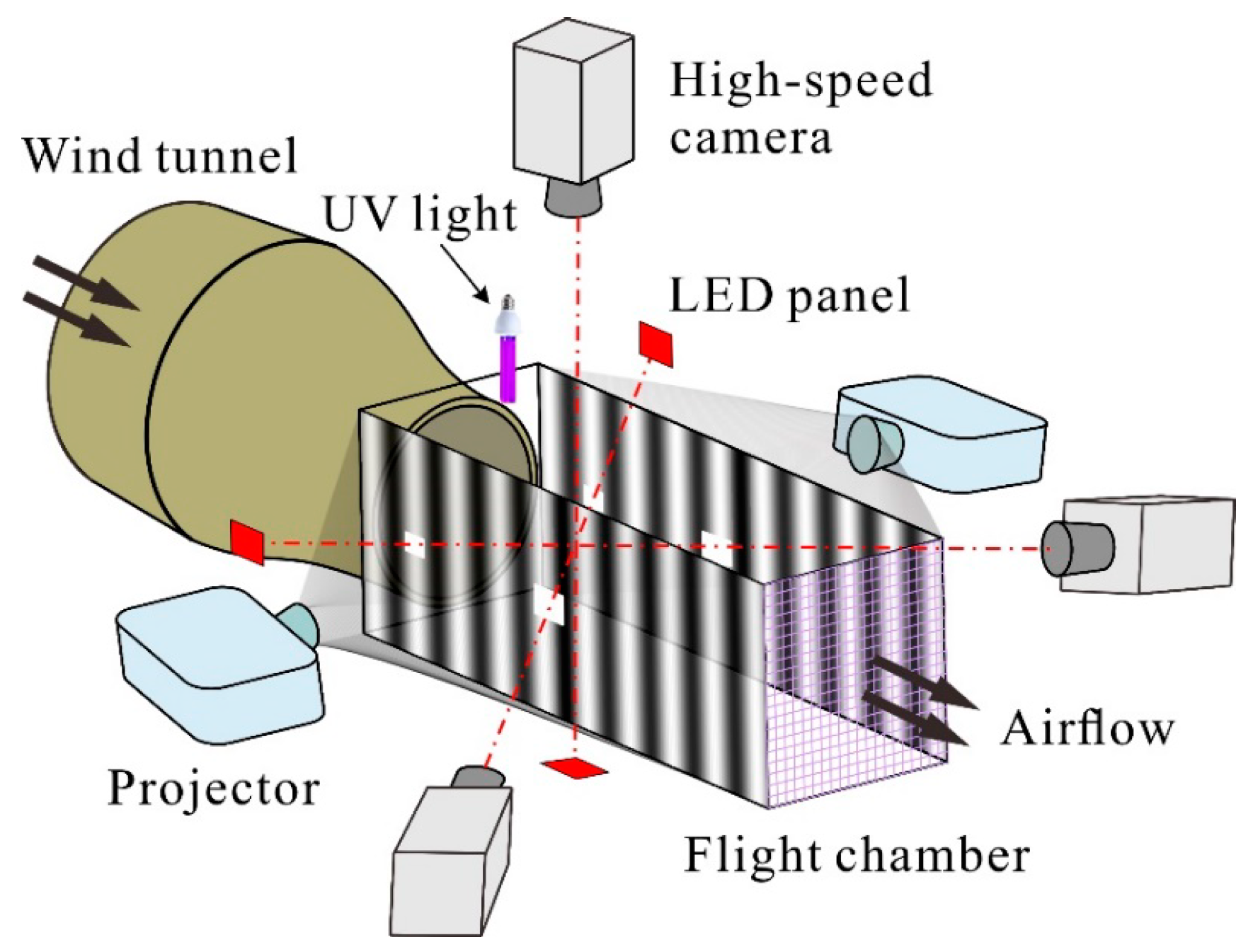
2.1. Insects and Experimental Setup
2.2. Filming Procedures
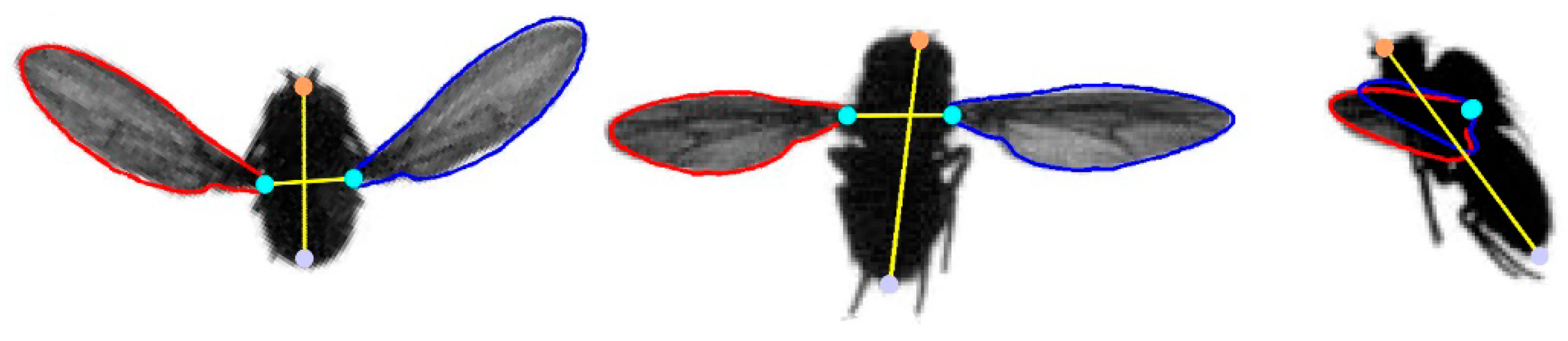
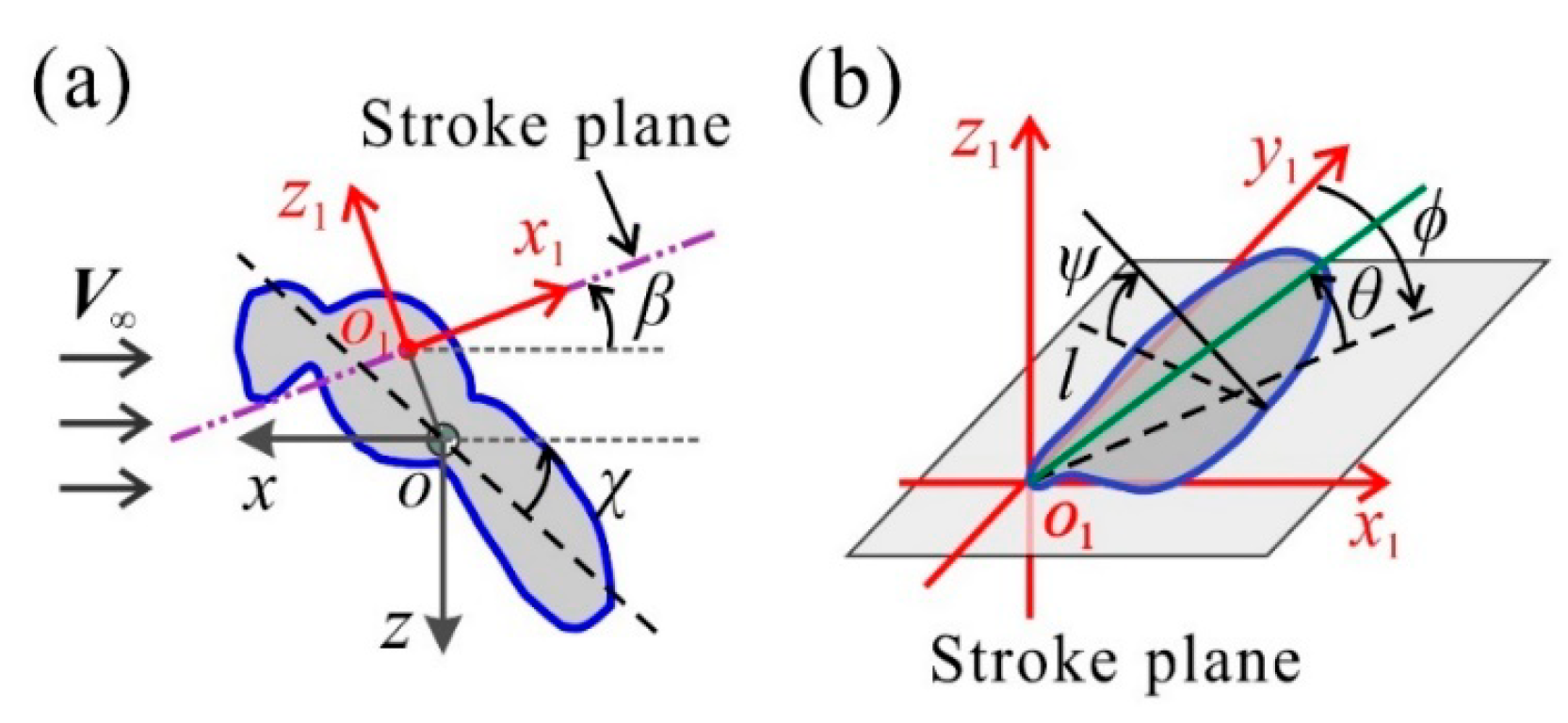
2.3. Measurement of Morphological and Kinematic Data
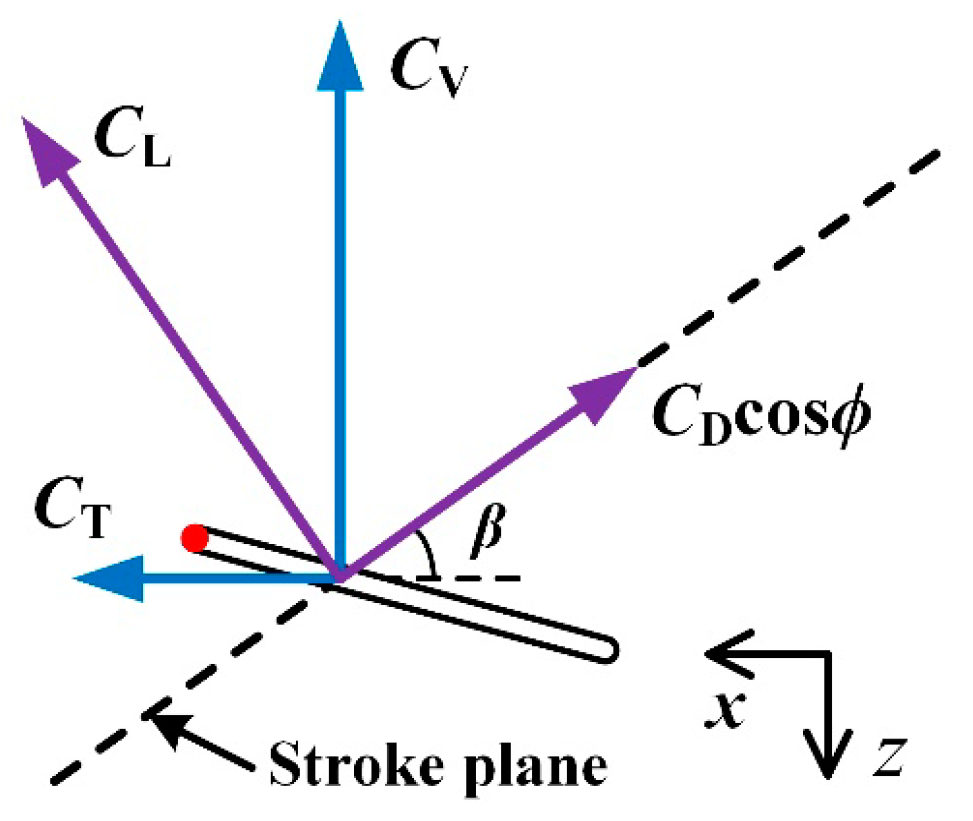
2.4. Evaluation of the Aerodynamic Forces and Mechanical Power
3. Results and Discussion
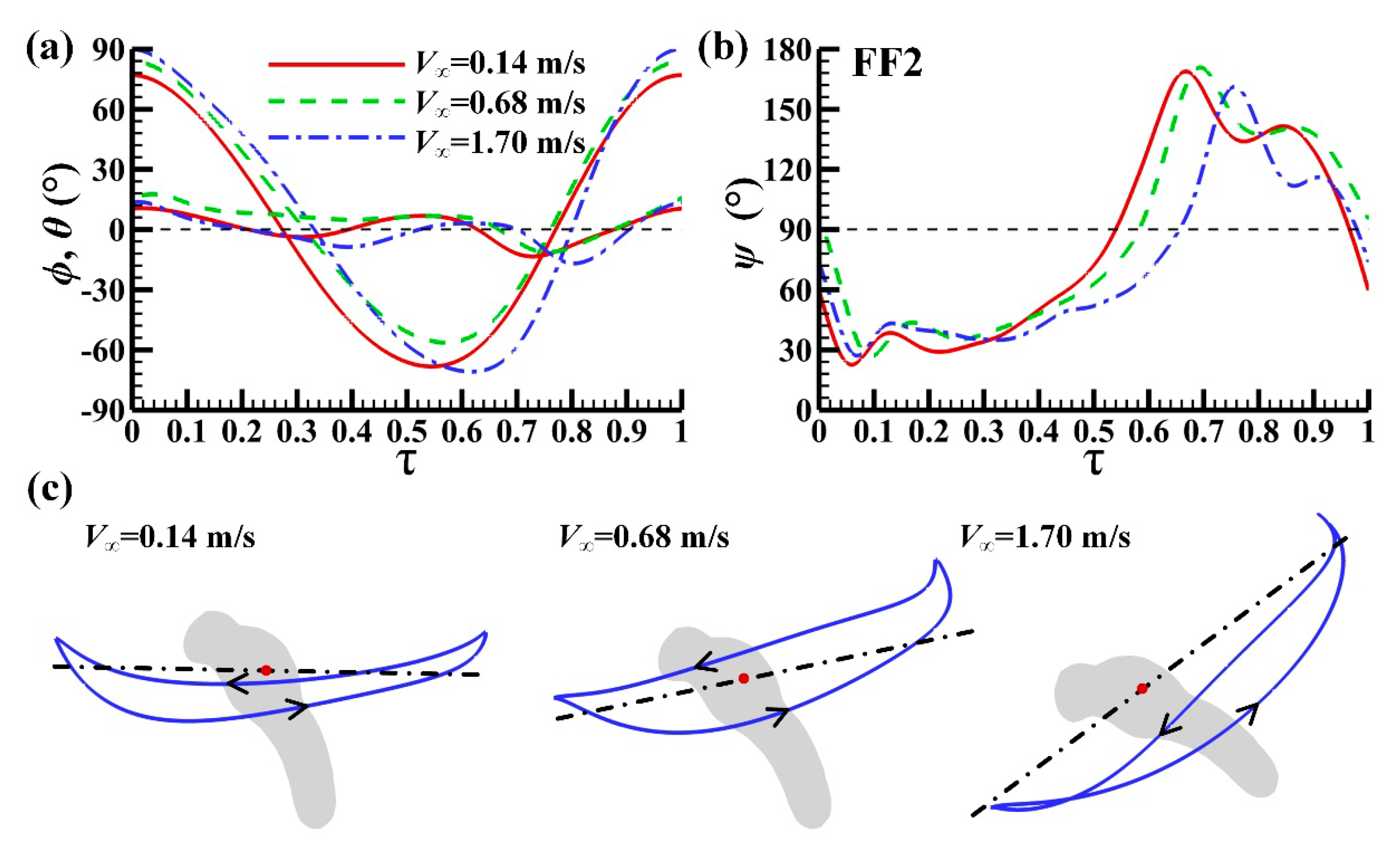
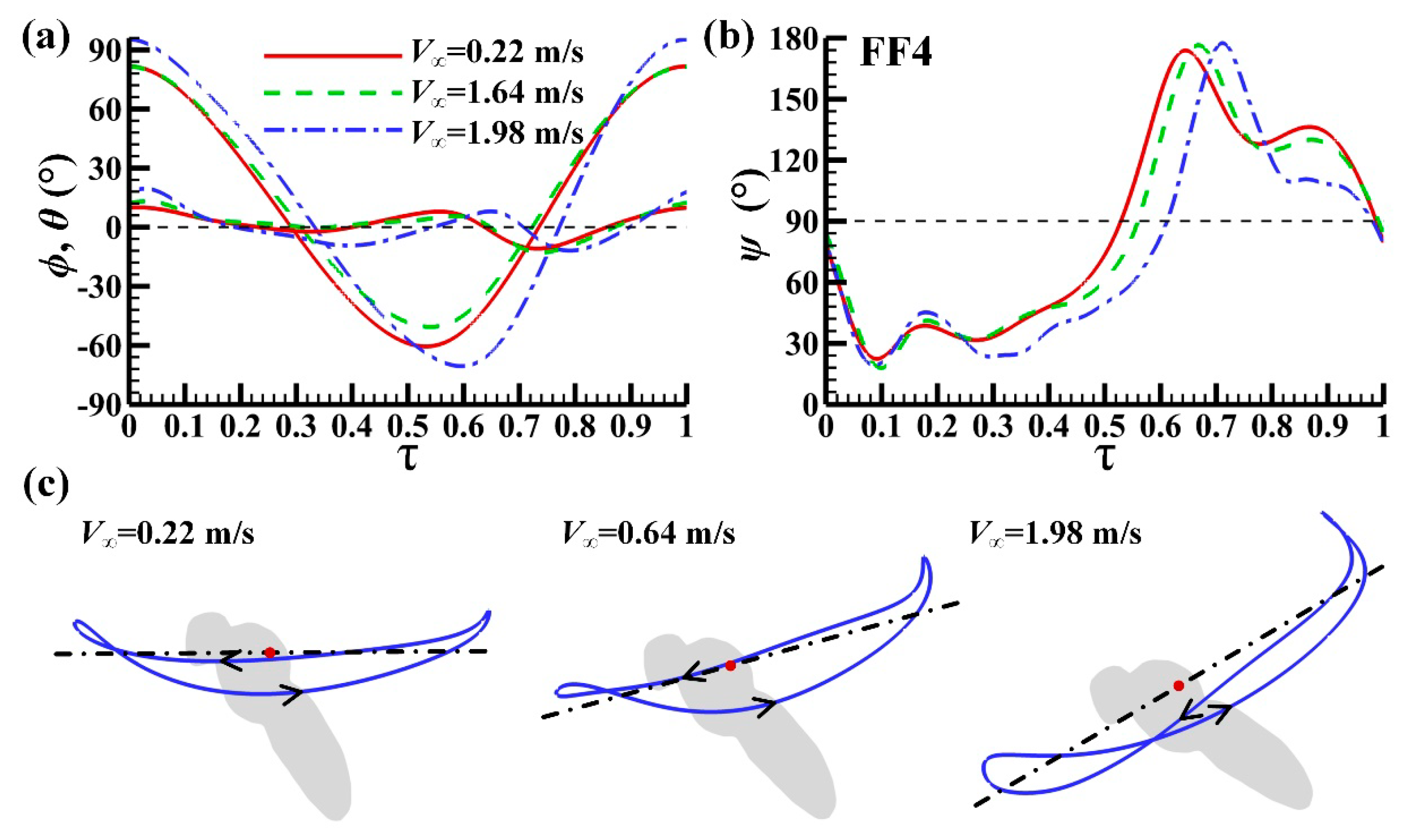
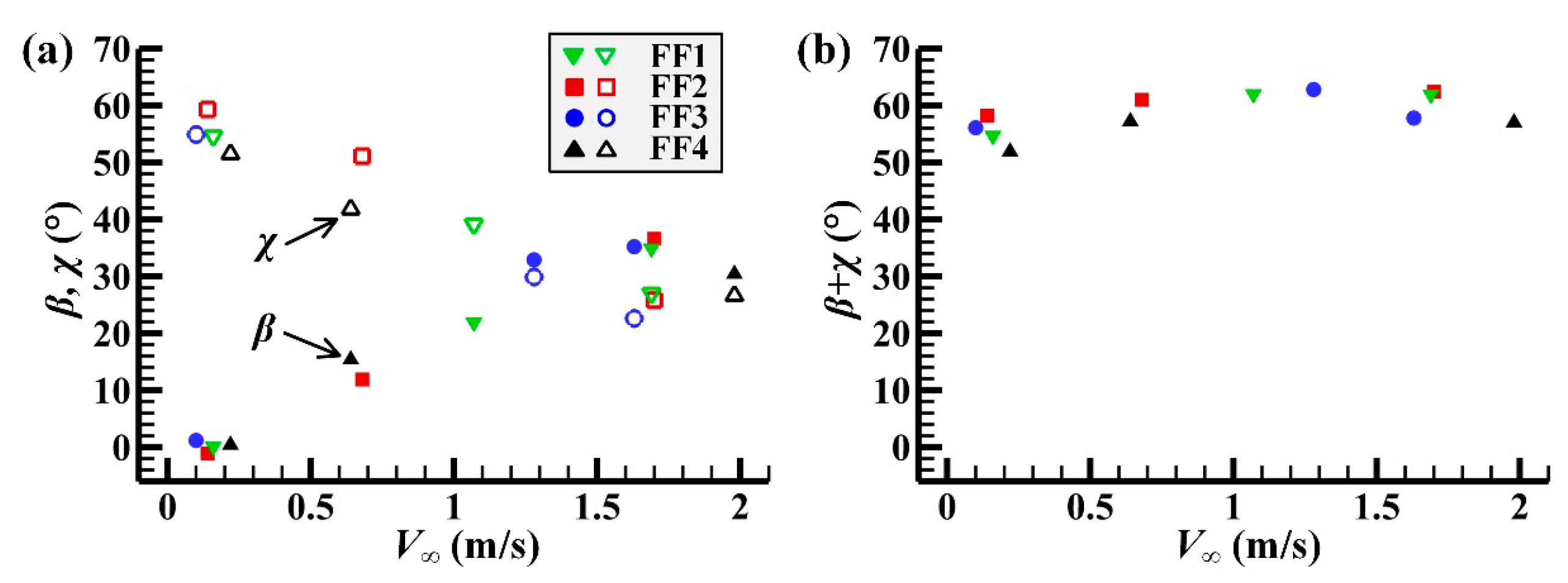
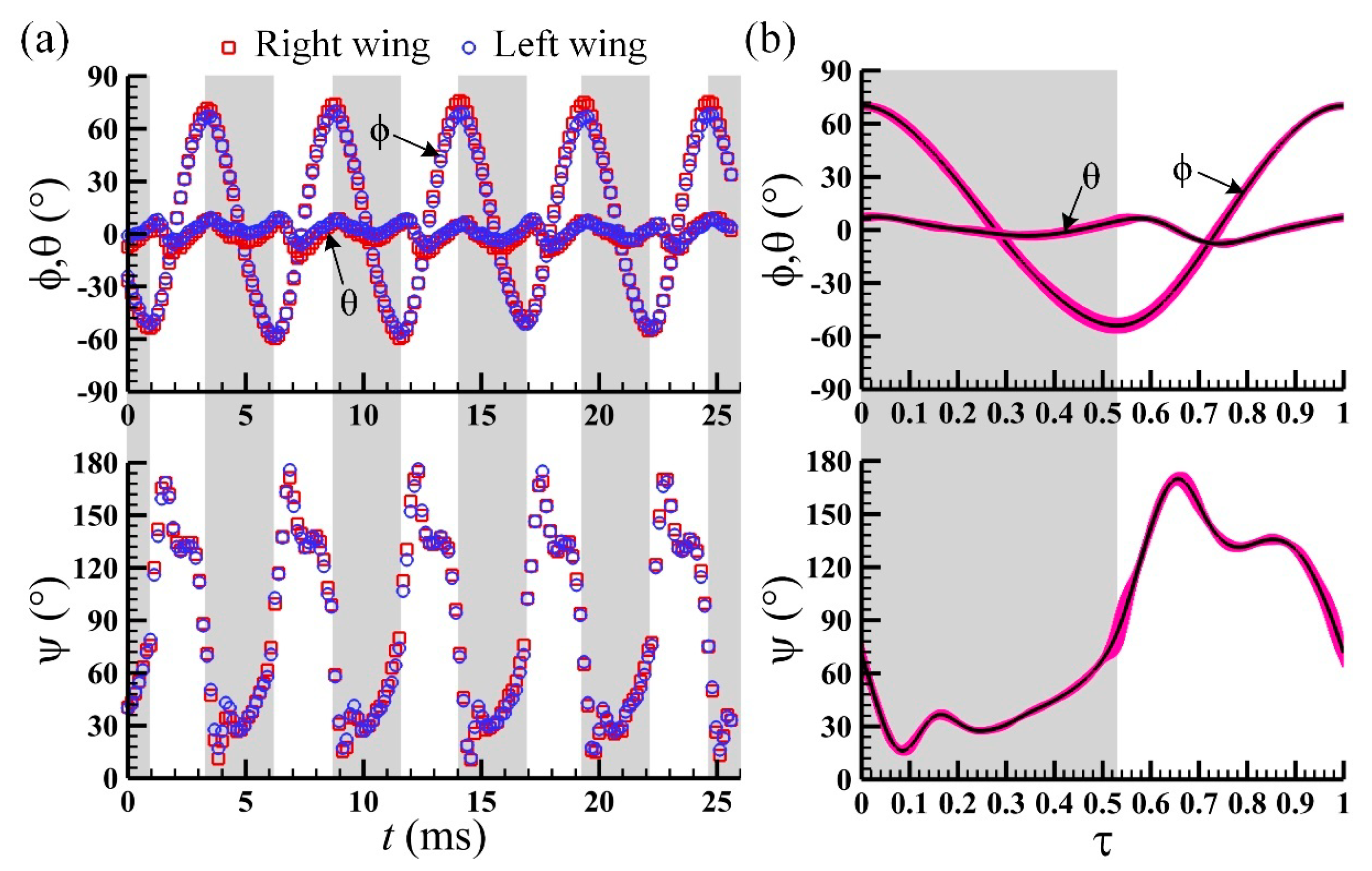
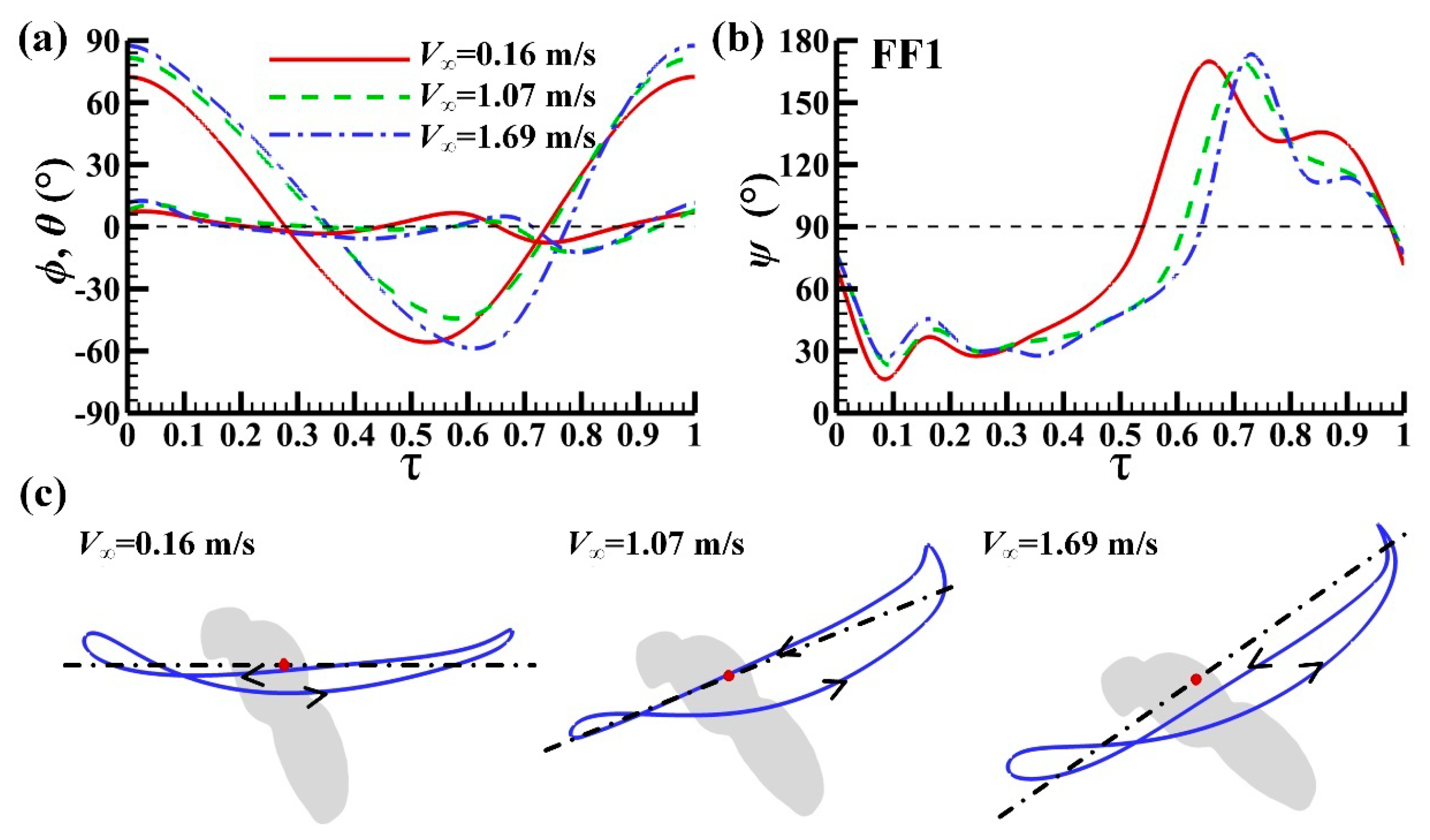
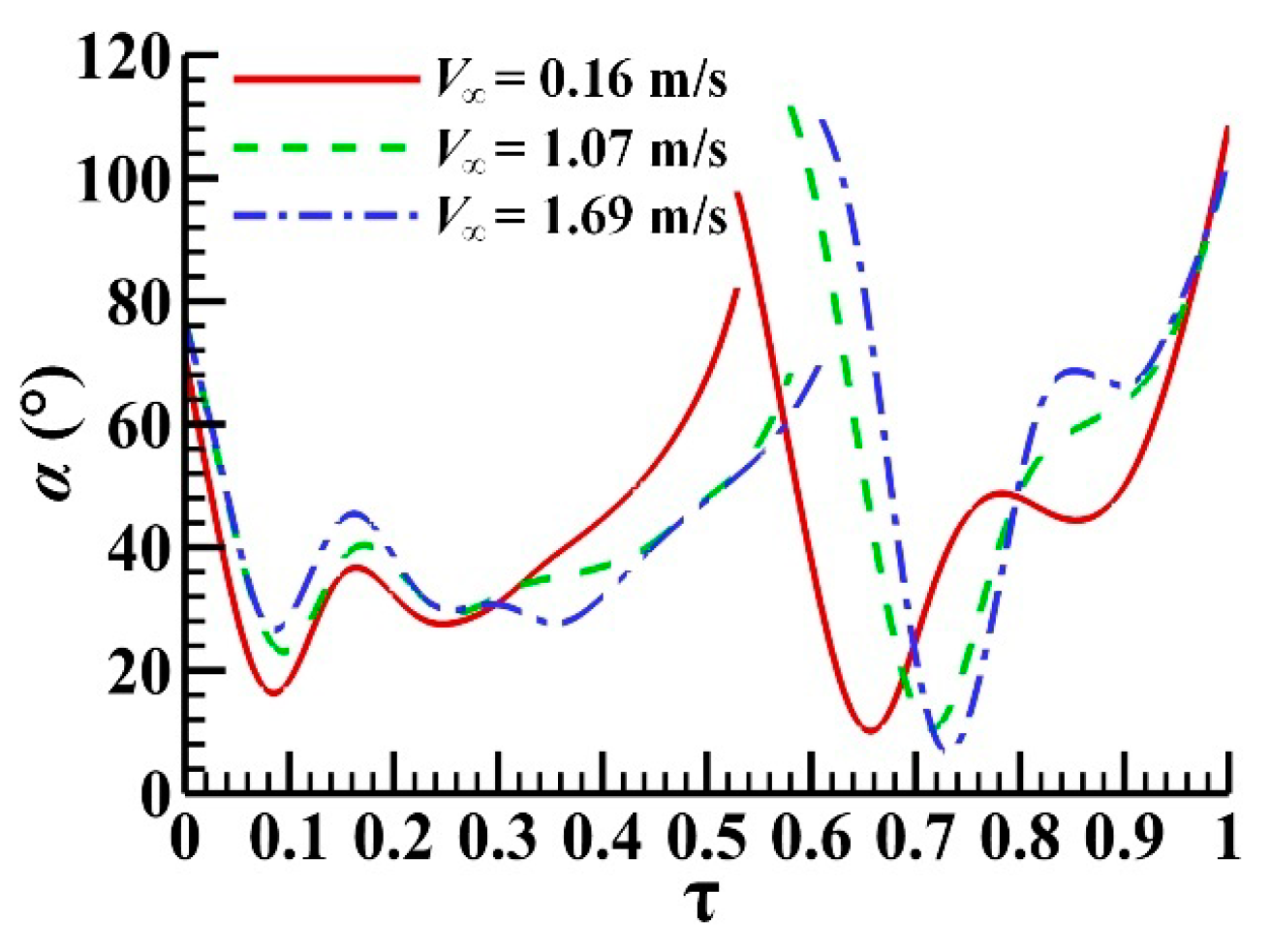
3.1. Measured Morphological Parameters and Wing and Body Motions
3.2. Aerodynamic Forces
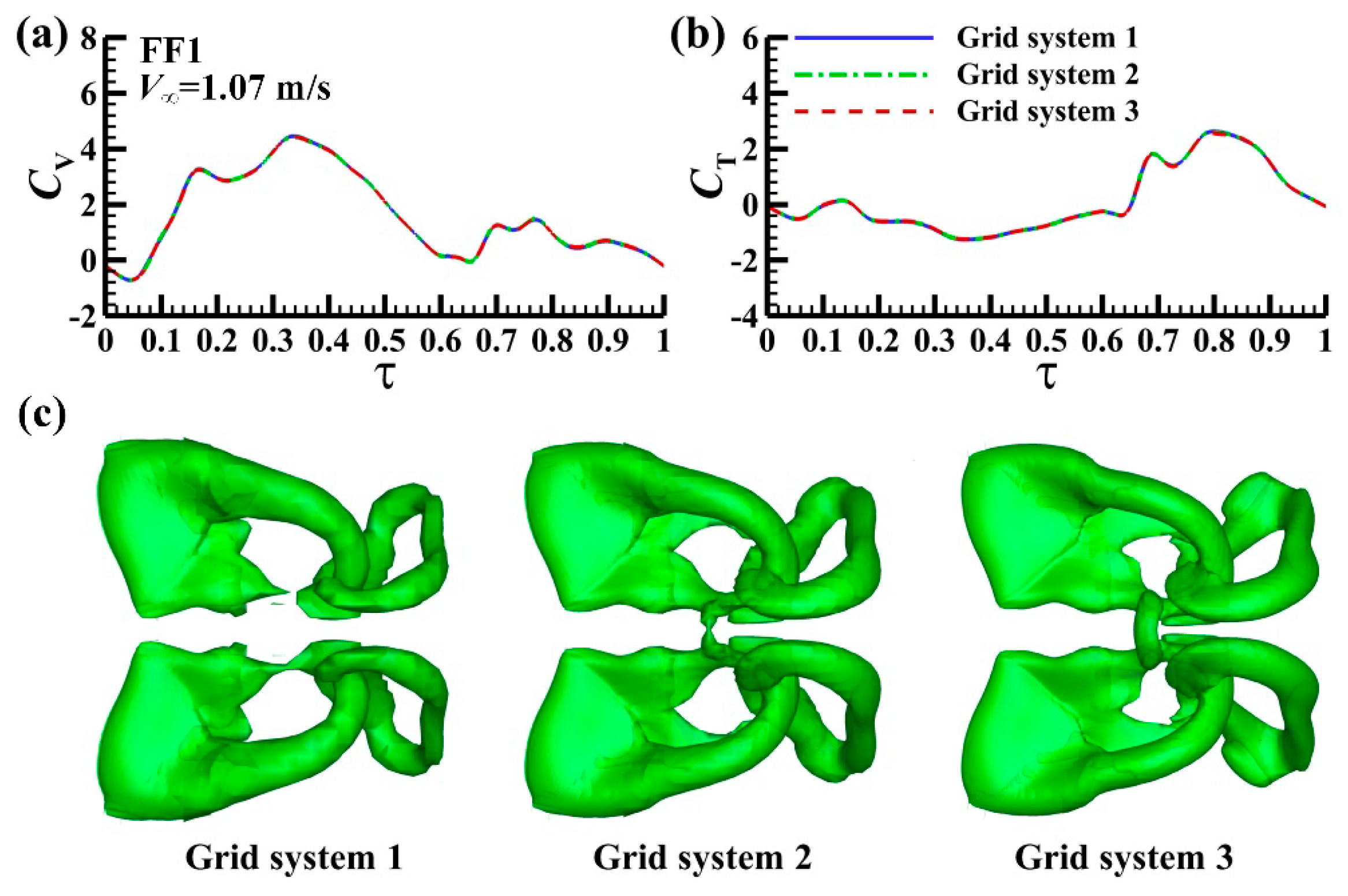
3.2.1. Code Validation and Grid Test
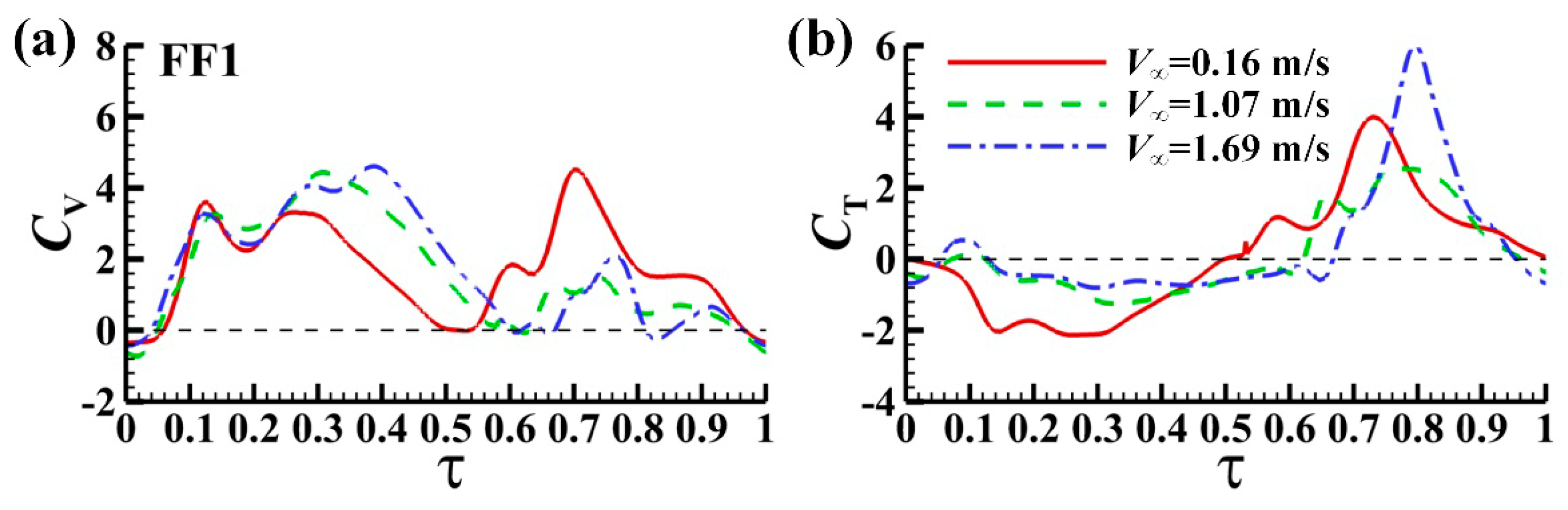
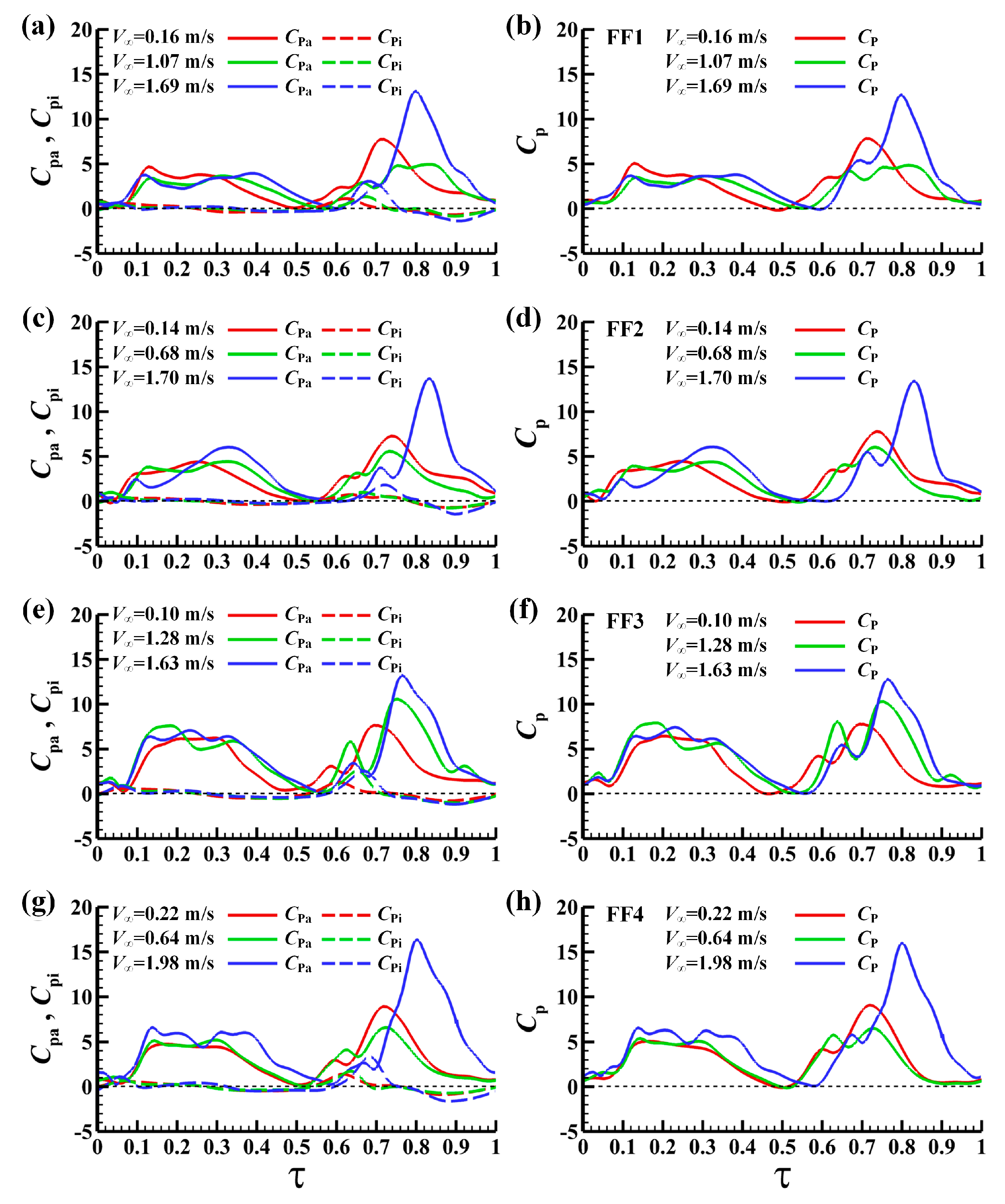
3.2.2. Computed Aerodynamic forces
3.3. Power Requirements
3.3.1. Computed Mechanical Power
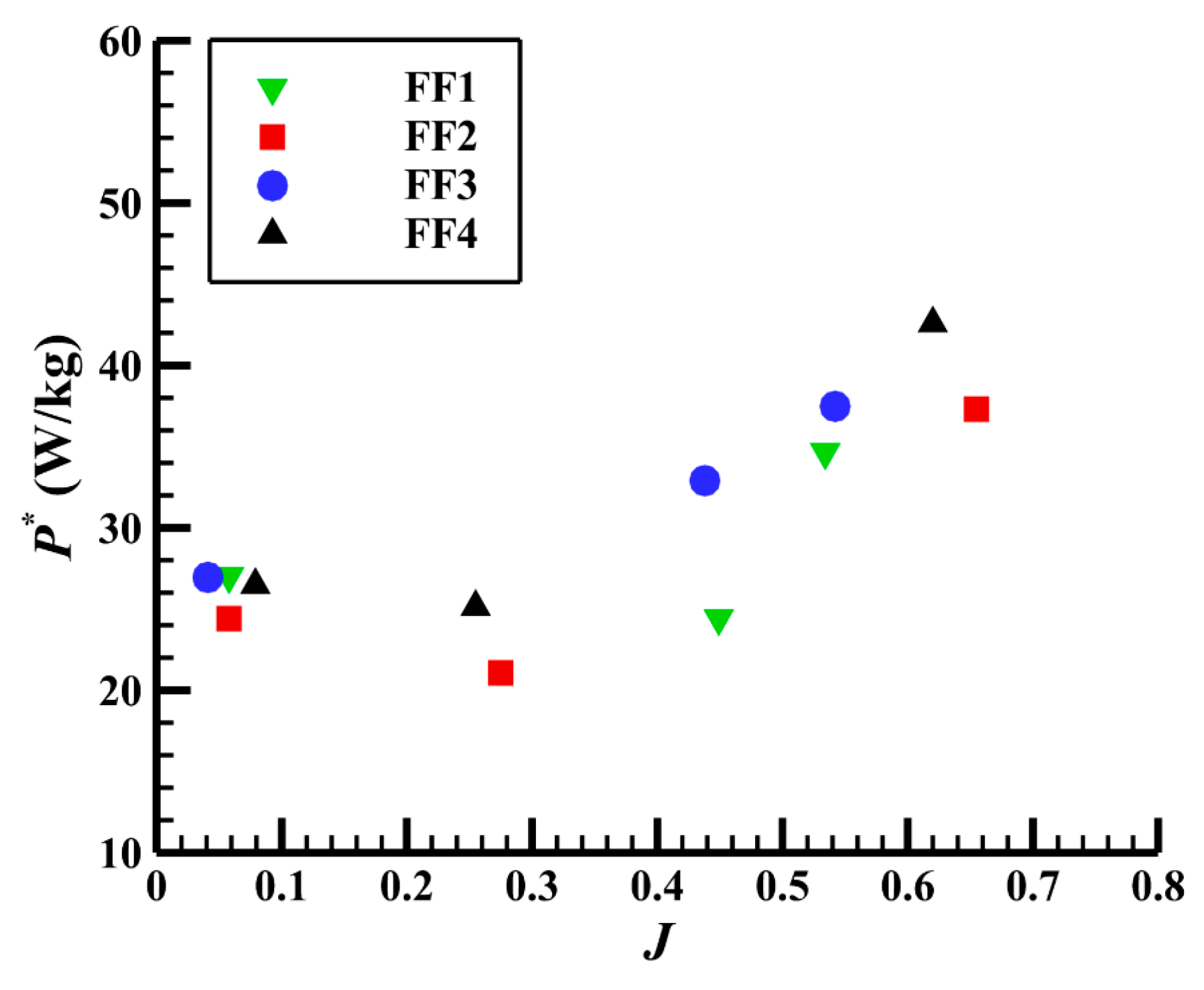
3.3.2. Specific power
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A



References
- Dudley, R. The Biomechanics of Insect Flight: Form, Function, Evolution; Princeton University Press: Princeton, NJ, USA, 2002; p. 496. [Google Scholar]
- Weis-Fogh, T. Energetics of hovering flight in hummingbirds and in Drosophila. J. Exp. Biol. 1972, 56, 79–104. [Google Scholar]
- Pennycuick, C.J. Power requirements for horizontal flight in the pigeon Columba Livia. J. Exp. Biol. 1968, 49, 527–555. [Google Scholar]
- Pennycuick, C.J. Mechanics of flight. In Avian Biology; Farner, D.S., King, J.R., Parkes, K.C., Eds.; Academic Press: New York, NY, USA, 1975; Volume 5, pp. 1–75. [Google Scholar]
- Dickinson, M.H.; Lehmann, F.-O.; Chan, W.P. The control of mechanical power in insect flight. Am. Zool. 1998, 38, 718–728. [Google Scholar] [CrossRef] [Green Version]
- Ellington, C.P.; Machin, K.E.; Casey, T.M. Oxygen consumption of bumblebees in forward flight. Nature 1990, 347, 472–473. [Google Scholar] [CrossRef]
- Warfvinge, K.; KleinHeerenbrink, M.; Hedenstrom, A. The power-speed relationship is U-shaped in two free-flying hawkmoths (Manduca sexta). J. R. Soc. Interface 2017, 14, 20170372. [Google Scholar] [CrossRef] [Green Version]
- Ellington, C.P. The aerodynamics of hovering insect flight. III. Kinematics. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1984, 305, 41–78. [Google Scholar] [CrossRef]
- Fry, S.N.; Sayaman, R.; Dickinson, M.H. The aerodynamics of hovering flight in Drosophila. J. Exp. Biol. 2005, 208, 2303–2318. [Google Scholar] [CrossRef] [Green Version]
- Ristroph, L.; Berman, G.J.; Bergou, A.J.; Wang, Z.J.; Cohen, I. Automated hull reconstruction motion tracking (HRMT) applied to sideways maneuvers of free-flying insects. J. Exp. Biol. 2009, 212, 1324–1335. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.P.; Sun, M. Wing kinematics measurement and aerodynamics of hovering droneflies. J. Exp. Biol. 2008, 211, 2014–2025. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.; Deng, X.Y.; Hedrick, T.L. The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta). J. Exp. Biol. 2011, 214, 4092–4106. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.G.; Sun, M. Aerodynamics and vortical structures in hovering fruitflies. Phys. Fluids 2015, 27, 031901. [Google Scholar] [CrossRef]
- Meng, X.G.; Sun, M. Wing kinematics, aerodynamic forces and vortex-wake structures in fruit-flies in forward flight. J. Bionic Eng. 2016, 13, 478–490. [Google Scholar] [CrossRef]
- Zou, P.Y.; Lai, Y.H.; Yang, J.T. Effects of phase lag on the hovering flight of damselfly and dragonfly. Phys. Rev. E 2019, 100, 063102. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Y.Z.; Zhu, H.J.; Sun, M. Flapping-mode changes and aerodynamic mechanisms in miniature insects. Phys. Rev. E 2019, 99, 012419. [Google Scholar] [CrossRef] [PubMed]
- Lyu, Y.Z.; Zhu, H.J.; Sun, M. Wing kinematic and aerodynamic compensations for unilateral wing damage in a small phorid fly. Phys. Rev. E 2020, 101, 012412. [Google Scholar] [CrossRef]
- Liu, L.G.; Du, G.; Sun, M. Aerodynamic-force production mechanisms in hovering mosquitoes. J. Fluid Mech. 2020, 898, A19. [Google Scholar] [CrossRef]
- Li, X.; Guo, C. Wing-kinematics measurement and flight modelling of the bamboo weevil C. buqueti. IET Nanobiotechnol. 2020, 14, 53–58. [Google Scholar] [CrossRef]
- Dudley, R.; Ellington, C.P. Mechanics of forward flight in bumblebees: I. Kinematics and morphology. J. Exp. Biol. 1990, 148, 19–52. [Google Scholar]
- Willmott, A.P.; Ellington, C.P. The mechanics of flight in the hawkmoth Manduca sexta. I. Kinematics of hovering and forward flight. J. Exp. Biol. 1997, 200, 2705–2722. [Google Scholar]
- Meng, X.G.; Sun, M. Wing and body kinematics of forward flight in drone-flies. Bioinspir. Biomim. 2016, 11, 056002. [Google Scholar] [CrossRef]
- Wu, J.H.; Sun, M. Unsteady aerodynamic forces and power requirements of a bumblebee in forward flight. Acta Mech. Sin. 2005, 21, 207–217. [Google Scholar] [CrossRef]
- David, C.T. Compensation for height in the control of groundspeed by Drosophila in a new, ‘barber’s pole’ wind tunnel. J. Comp. Physiol. A 1982, 147, 485–493. [Google Scholar] [CrossRef]
- Fry, S.N.; Rohrseitz, N.; Straw, A.D.; Dickinson, M.H. Visual control of flight speed in Drosophila melanogaster. J. Exp. Biol. 2009, 212, 1120–1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuller, S.B.; Straw, A.D.; Peek, M.Y.; Murray, R.M.; Dickinson, M.H. Flying Drosophila stabilize their vision-based velocity controller by sensing wind with their antennae. Proc. Natl. Acad. Sci. USA 2014, 111, 1182–1191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fry, S.N.; Sayaman, R.; Dickinson, M.H. The aerodynamics of free-flight maneuvers in Drosophila. Science 2003, 300, 495–498. [Google Scholar] [CrossRef] [Green Version]
- Vogel, S. Flight in Drosophila: I. Flight performance of tethered flies. J. Exp. Biol. 1966, 44, 567–578. [Google Scholar]
- Bartussek, J.; Lehmann, F.O. Proprioceptive feedback determines visuomotor gain in Drosophila. R. Soc. Open Sci. 2016, 3, 150562. [Google Scholar] [CrossRef] [Green Version]
- Mou, X.L.; Liu, Y.P.; Sun, M. Wing motion measurement and aerodynamics of hovering true hoverflies. J. Exp. Biol. 2011, 214, 2832–2844. [Google Scholar] [CrossRef] [Green Version]
- Aono, H.; Liang, F.; Liu, H. Near- and far-field aerodynamics in insect hovering flight: An integrated computational study. J. Exp. Biol. 2008, 211, 239–257. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Sun, M. A computational study of the wing-wing and wing-body interactions of a model insect. Acta Mech. Sin. 2009, 25, 421–431. [Google Scholar] [CrossRef]
- Liang, B.; Sun, M. Aerodynamic interactions between wing and body of a model insect in forward flight and maneuvers. J. Bionic Eng. 2013, 10, 19–27. [Google Scholar] [CrossRef]
- Rogers, S.E.; Kwak, D. Upwind differencing scheme for the time-accurate incompressible Navier-Stokes equations. AIAA J. 1990, 28, 253–262. [Google Scholar] [CrossRef]
- Rogers, S.; Kwak, D. Numerical solution of the incompressible Navier-Stokes equations for steady-state and time-dependent problems. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. [Google Scholar]
- Hilgenstock, A. A fast method for the elliptic generation of three-dimensional grids with full boundary control. In Proceedings of the 2nd International Conference on Numerical Grid Generation in Computational Fluid Mechanics, Miami, FL, USA, 5–9 December 1988; pp. 137–146. [Google Scholar]
- Sun, M. Insect flight dynamics: Stability and control. Rev. Mod. Phys. 2014, 86, 615–646. [Google Scholar] [CrossRef]
- Xiong, Y.; Sun, M. Dynamic flight stability of a bumblebee in forward flight. Acta Mech. Sin. 2008, 24, 25–36. [Google Scholar] [CrossRef]
- Xu, N.; Sun, M. Lateral dynamic flight stability of a model bumblebee in hovering and forward flight. J. Theor. Biol. 2013, 319, 102–115. [Google Scholar] [CrossRef]
- Zhu, H.J.; Meng, X.G.; Sun, M. Forward flight stability in a drone-fly. Sci. Rep. 2020, 10, 1975. [Google Scholar] [CrossRef]
- Yao, J.; Yeo, K.S. Forward flight and sideslip manoeuvre of a model hawkmoth. J. Fluid Mech. 2020, 896, A22. [Google Scholar] [CrossRef]
- Meng, X.G.; Sun, M. Aerodynamic effects of wing corrugation at gliding flight at low Reynolds numbers. Phys. Fluids 2013, 25, 071905. [Google Scholar] [CrossRef]
- Cheng, X.; Sun, M. Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J. Fluid Mech. 2018, 855, 646–670. [Google Scholar] [CrossRef] [Green Version]
- Ellington, C.P. The aerodynamics of hovering insect flight. VI. Lift and power requirements. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1984, 305, 145–181. [Google Scholar]
- Sun, M.; Tang, J. Lift and power requirements of hovering flight in Drosophila virilis. J. Exp. Biol. 2002, 205, 2413–2427. [Google Scholar] [PubMed]
- Sun, M.; Du, G. Lift and power requirements of hovering insect flight. Acta Mech. Sin. 2003, 19, 458–469. [Google Scholar]







| Individual | m (mg) | c (mm) | R (mm) | r2/R | lb (mm) | lr/lb | l1/lb | h1/lb | l2/lb |
|---|---|---|---|---|---|---|---|---|---|
| FF1 | 1.75 | 0.93 | 3.31 | 0.59 | 3.31 | 0.24 | 0.17 | 0.12 | 0.47 |
| FF2 | 1.22 | 0.89 | 3.05 | 0.59 | 3.33 | 0.28 | 0.15 | 0.10 | 0.45 |
| FF3 | 1.79 | 1.04 | 3.35 | 0.58 | 3.60 | 0.25 | 0.18 | 0.14 | 0.47 |
| FF4 | 2.07 | 0.98 | 3.30 | 0.58 | 3.68 | 0.27 | 0.21 | 0.15 | 0.47 |
| Individual | V∞ (m/s) | f (Hz) | Φ (°) | (°) | β (°) | χ (°) | d/u | J |
|---|---|---|---|---|---|---|---|---|
| FF1 | 0.16 | 187.9 ± 0.2 | 126.3 ± 2.4 | 8.2 ± 1.1 | 0.1 | 54.6 | 1.12 | 0.06 |
| 1.07 | 171.4 ± 0.1 | 126.8 ± 0.9 | 18.0 ± 0.8 | 21.9 | 39.1 | 1.38 | 0.45 | |
| 1.69 | 182.0 ± 0.1 | 147.1 ± 1.1 | 15.2 ± 0.8 | 34.9 | 27.0 | 1.57 | 0.53 | |
| FF2 | 014 | 161.2 ± 0.1 | 146.0 ± 2.2 | 5.1 ± 0.7 | −1.1 | 59.3 | 1.19 | 0.06 |
| 0.68 | 156.3 ± 0.2 | 140.9 ± 1.4 | 14.5 ± 1.2 | 11.9 | 51.1 | 1.33 | 0.27 | |
| 1.70 | 156.9 ± 0.1 | 161.9 ± 1.6 | 11.3 ± 0.6 | 36.6 | 25.8 | 1.59 | 0.65 | |
| FF3 | 0.10 | 184.0 ± 0.2 | 122.2 ± 1.6 | 6.7 ± 1.1 | 1.2 | 54.9 | 1.08 | 0.04 |
| 1.28 | 189.1 ± 0.1 | 134.3 ± 1.0 | 12.1 ± 0.5 | 32.9 | 29.9 | 1.27 | 0.44 | |
| 1.63 | 181.3 ± 0.1 | 144.2 ± 1.2 | 13.4 ± 0.8 | 35.2 | 22.6 | 1.34 | 0.54 | |
| FF4 | 0.22 | 172.5 ± 0.3 | 142.8 ± 2.8 | 10.8 ± 1.4 | 0.4 | 51.5 | 1.14 | 0.08 |
| 0.64 | 170.7 ± 0.1 | 133.5 ± 1.3 | 14.8 ± 1.3 | 15.4 | 41.8 | 1.18 | 0.25 | |
| 1.98 | 174.2 ± 0.2 | 164.0 ± 0.9 | 14.4 ± 0.9 | 30.4 | 26.6 | 1.44 | 0.62 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.J.; Sun, M. Kinematics Measurement and Power Requirements of Fruitflies at Various Flight Speeds. Energies 2020, 13, 4271. https://doi.org/10.3390/en13164271
Zhu HJ, Sun M. Kinematics Measurement and Power Requirements of Fruitflies at Various Flight Speeds. Energies. 2020; 13(16):4271. https://doi.org/10.3390/en13164271
Chicago/Turabian StyleZhu, Hao Jie, and Mao Sun. 2020. "Kinematics Measurement and Power Requirements of Fruitflies at Various Flight Speeds" Energies 13, no. 16: 4271. https://doi.org/10.3390/en13164271
APA StyleZhu, H. J., & Sun, M. (2020). Kinematics Measurement and Power Requirements of Fruitflies at Various Flight Speeds. Energies, 13(16), 4271. https://doi.org/10.3390/en13164271





