Solving the Optimal Reactive Power Dispatch Using Marine Predators Algorithm Considering the Uncertainties in Load and Wind-Solar Generation Systems

Abstract

The optimal reactive power dispatch (ORPD) problem is an important issue to assign the most efficient and secure operating point of the electrical system. The ORPD became a strenuous task, especially with the high penetration of renewable energy resources due to the intermittent and stochastic nature of wind speed and solar irradiance. In this paper, the ORPD is solved using a new natural inspired algorithm called the marine predators’ algorithm (MPA) considering the uncertainties of the load demand and the output powers of wind and solar generation systems. The scenario-based method is applied to handle the uncertainties of the system by generating deterministic scenarios from the probability density functions of the system parameters. The proposed algorithm is applied to solve the ORPD of the IEEE-30 bus system to minimize the power loss and the system voltage devotions. The result verifies that the proposed method is an efficient method for solving the ORPD compared with the state-of-the-art techniques.

1. Introduction

Solving the optimal reactive power dispatch (ORPD) problem plays a significant role in the efficient operation and planning of the power system. The aim of solving the ORPD is to determine the best operating point of system for maximizing the voltage stability, minimizing the system loss and the voltage deviations [1,2]. The best operating point includes the terminal voltages of the generators, taps of transformers and the injected reactive powers of the shunt compensators [3].

The ORPD is a nonconvex and nonlinear optimization problem. Several conventional techniques such as the quadratic programming method [4], the linear programming [5], the nonlinear programming [6], and the interior point [7] have solved the ORPD problem. However, although these techniques succeed in solving the problem for some cases, they suffer from stagnation at the local optimal for other cases, especially in solving optimal active and reactive power flows of the large-scale systems [8]. The shortages of the aforementioned techniques can be avoided by applying numerous optimization techniques, which can be classified based on their inspiration as follows:

• Swarm-based algorithms such as particle swarm optimization (PSO) [9], ant lion optimizer [10], whale optimization algorithm [11], improved social spider optimization algorithm [12], improved antlion optimization algorithm [13], and moth swarm algorithm [14];
• Evolutionary-based algorithms such as differential evolution [15], specialized genetic algorithm (SGA) [16], evolutionary programming [17], modified differential evolution [18], pareto evolutionary algorithm [19], comprehensive learning particle swarm optimization [20], and enhanced grey wolf optimizer (EGWO) [21];
• Human-based algorithms such as harmony search algorithm [22], teaching learning-based optimization [23], and biogeography-based optimization [24];
• Physical-based algorithms such as gravitational search algorithm [25], improved gravitational search algorithm [26], lightning attachment procedure optimization (LAPO) [27], modified sine cosine algorithm [28], and water cycle algorithm [29];
• Hybrid-based algorithms such as hybridization of the particle swarm optimization method and the tabu-search technique [30].

Renewable energy resources (RERs) widely incorporated in electrical systems provide an elegant solution from an economic, environmental and technical perspective. In other words, the inclusion of the RERs can effectively minimize the dependence of the generation obtained by fossil fuel, reduce the greenhouse gases and the harmful emissions, minimize the generation cost and enhance the system operation. The wind and solar power generation systems are the most applied technologies for RERs. However, some technical issues related to incorporating the wind and solar generation units, such as the wind speed and the solar irradiance, are continuously varied and intermittent in nature, which leads to increasing the uncertainties of the electrical power system, especially fluctuations in load demand [31,32]. Considering the uncertainties of the electrical power system is a strenuous task for the decision makers for efficient planning [33]. Thus, several approaches have been presented for modeling the uncertainty of the system including probabilistic methods [34], possibilistic methods [35], hybrid possibilistic–probabilistic methods [36], information gap theory [37], robust optimization [38], and interval analysis [39]. Moreover, the authors in [40] presented a comprehensive review of the stochastic techniques that have been implemented for optimization of solar-based renewable energy systems. In [41], a distributed operation strategy using a double deep Q-learning method is employed to manage the operation of the battery energy storage system considering the uncertainty of the renewable distributed generators. The authors in [42] proposed a robust optimization model for analyzing the interdependency of natural gas, coal and electricity infrastructures considering their operation constraints and wind power uncertainties.

A marine predators algorithm (MPA) is one of the newest optimization techniques that simulates the foraging behavior and movement of the marine predators proposed by A. Faramarzi et al. in 2020 [43]. The authors in [44] have applied the MPA to determine the optimal parameters for the adaptive neuro-fuzzy inference system to predict the spread of coronavirus (COVID-19). In [45], an improved version of the MPA was presented to assign the people infected by COVID-19 with X-ray image segmentation.

The aim of our study is to apply the newest algorithm, called the marine predators algorithm (MPA), in order to solve the ORPD problem for the first time to best of our knowledge. Then, the validity of the proposed MPA for minimizing the power loss and the total voltage deviations is investigated and compared with state-of-the-art techniques. The contributions of this paper can be summarized as follows:

• Solving the ORPD problem by utilizing one of the newest algorithms, called the marine predators algorithm (MPA);
• The validity of the proposed algorithm for minimizing the power loss and the total voltage deviations is investigated and compared with the state-of-the-art techniques;
• The ORPD problem is solved by incorporating the renewable energy resources, including wind turbine and solar PV systems;
• The ORPD problem is solved to minimize the expected power loss with considering the uncertainties of the load demand and the output powers of wind and solar generation systems;
• Weibull PDF, Beta PDF and normal PDF are utilized for modeling the uncertainties of wind speed, the solar irradiance and the load demand, respectively. In addition, the scenario-based method is used to model the combination of load-generation uncertainty.

The organization of paper is listed as follows: Section 2, illustrates the problem formulations of the ORPD problem. Section 3 models the uncertainty of the renewable sources and the load demand. Section 4 illustrates the step procedure of the MPA. Section 5 shows the obtained results and the corresponding discussion. Finally, the paper’s conclusion is presented in Section 6.

2. Problem Formulation

The solution of the ORPD problem is formulated as an optimization problem applied for assigning set control parameters for a certain objective function, satisfying the operating constraints of the system. Generally, the ORPD problem is represented as follows

$$Min F\left(x,u\right)$$

(1)

Subjected to

$$g_k\left(x,u\right)=0 k=1,2,\dots ,m$$

(2)

$$h_n\left(x,u\right)\le 0 n=1,2,\dots ,p$$

(3)

where $g_k$ and $h_n$ represent the equality and inequality constraints. u is a vector of the control parameters which includes the generator voltages, the compensators of injected reactive powers and the transformer taps while $x$ denotes the vector of the dependent variables which includes the slack bus power, the voltages of the load buses and the apparent power flow in transmission lines. $u$ and $x$ are vectors represented as follows

$$u=\left[V_G,Q_C,T_p\right]$$

(4)

$$x=\left[P_1,V_L,Q_G,S_T\right]$$

(5)

2.1. Objective Function

Power Loss

$$F_1=P_{Loss}={\displaystyle \sum }_{i=1}^{N_L}{G}_{ij}(V_i^2+V_j^2-2V_i{V}_{j}cos{\delta }_{ij})$$

(6)

Voltage Deviations

$$F_2=VD={\displaystyle \sum }_{i=1}^{N_Q}\left|\left(V_i-1\right)\right|$$

(7)

2.2. Constraints

Inequality Constraints

$$P_{Gk}^{min}\le P_{Gk}\le P_{Gk}^{max} k=1,2,\dots , N_G$$

(8)

$$Q_{Gk}^{min}\le Q_{Gk}\le Q_{Gk}^{max} k=1,2,\dots , N_G$$

(9)

$$V_{Gk}^{min}\le V_{Gk}\le V_{Gk}^{max} k=1,2,\dots , N_G$$

(10)

$$T_n^{min}\le T_n\le T_n^{max} n=1,2,\dots , N_Q$$

(11)

$$Q_{Cn}^{min}\le Q_{Cn}\le Q_{Cn}^{max} n=1,2,\dots , N_Q$$

(12)

$$S_{Ln}\le S_{Ln}^{min} n=1,2,\dots , N_Q$$

(13)

$$V_n^{min}\le V_n\le V_n^{max} n=1,2,\dots , N_Q$$

(14)

Quality Constraints

$$P_{Gi}-P_{Li}=\left|V_i\right|{\displaystyle \sum }_{j=1}^{Nb}\left|V_j\right| \left(G_{ij}cos{\delta }_{ij}+B_{ij}sin{\delta }_{ij}\right)$$

(15)

$$Q_{Gi}-Q_{Li}=\left|V_i\right|{\displaystyle \sum }_{j=1}^{Nb}\left|V_j\right| \left(G_{ij}sin{\delta }_{ij}-B_{ij}cos{\delta }_{ij}\right)$$

(16)

The system constraints should be considered to ensure that the obtained solution is at the suitable solution. This can be accomplished by using the concept of the weighted square variables as follows

$$F=F_i+{\chi }_1 {\left(P_{G1}-P_{G1}^{lim}\right)}^2+{\chi }_2{\displaystyle \sum }_{i=1}^{N_G} {\left(Q_{Gi}-Q_{Gi}^{lim}\right)}^2+{\chi }_3{\displaystyle \sum }_{i=1}^{N_Q} {\left(V_{Li}-V_{Li}^{lim}\right)}^2+{\chi }_4{\displaystyle \sum }_{i=1}^{N_{/}} {\left(S_{Li}-S_{Li}^{lim}\right)}^2$$

(17)

3. Uncertainty Modeling

To consider the uncertainties of the load demand and output powers of wind and solar photovoltaic (PV) generation systems, the continuous probability density function (PDF) is used for modeling the uncertainties of the system where the PDF is divided into subsections to obtain a number of scenarios from the load demand, wind speed and solar irradiance.

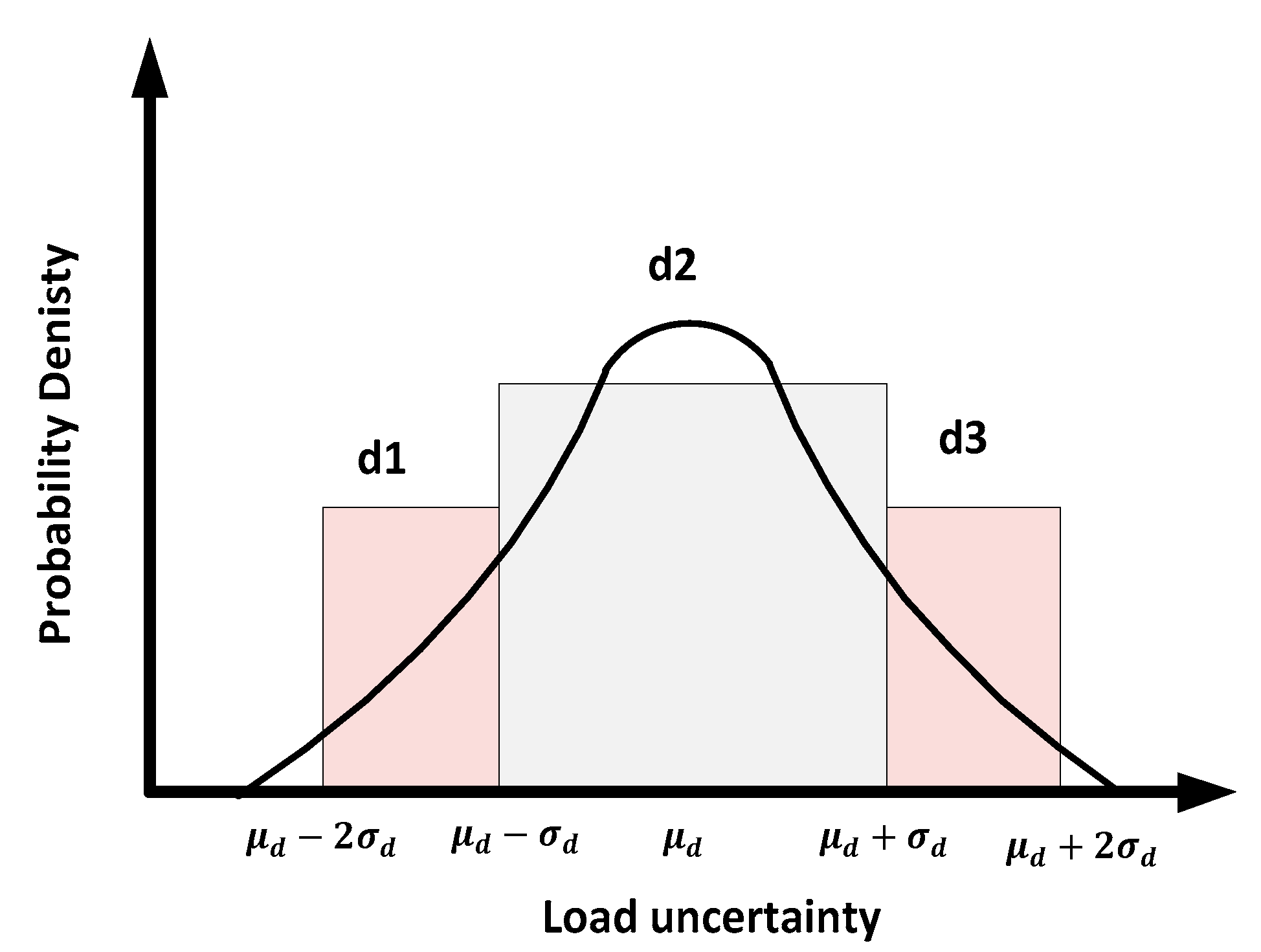
3.1. Modeling of Load Demand

Uncertainty of load demand is modeled using normal PDF [46] which can be described as

$$f_d\left(P_d\right)=\frac{1}{{\sigma }_d\sqrt{2\pi }}exp\left[-\frac{\left(P_d - {\mu }_d\right)2}{2{\sigma }_d{}^2}\right]$$

(18)

where $P_d$ is the probability density of normal distribution of the load while ${\sigma }_d$ and ${\mu }_d$ are the standard and mean deviation values, respectively. The portability of load demand and its corresponding expected load scenario can be calculated as follows [47]

$${\tau }_{d,i}=\underset{P_{d,i}^{min}}{\overset{P_{d,i}^{max}}{{\displaystyle \int }}}\frac{1}{{\sigma }_d\sqrt{2\pi }}exp\left[-\frac{\left(P_d - {\mu }_d\right)2}{2{\sigma }_d{}^2}\right]d{P}_d$$

(19)

$$P_{d,i}=\frac{1}{{\tau }_{d,i}}\underset{P_{d,i}^{min}}{\overset{P_{d,i}^{max}}{{\displaystyle \int }}}\frac{P_d}{{\sigma }_d\sqrt{2\pi }}exp\left[-\frac{\left(P_d - {\mu }_d\right)2}{2{\sigma }_d{}^2}\right]d{P}_d$$

(20)

where $P_{d,i}^{max}$ and $P_{d,i}^{min}$ are the minimum and the maximum limit of the selected interval i. In this paper, three scenarios of load demand are generated from the previous equations as depicted in Figure 1 and their corresponding mean values are ${\mu }_d-1.5259{\sigma }_d$ and ${\mu }_d+1.5259{\sigma }_d$, while their probabilities are 0.1587, 0.6826 and 0.1587, respectively. In this paper, the selected value of the ${\sigma }_d=0.02{\mu }_d$. The load scenarios and their corresponding probability are depicted in

Table 1. Load, wind and solar irradiance scenarios with the corresponding probabilities.

Load Scenario	${\mathit{\tau }}_{\mathit{d},\mathit{i}}$	Loading %
1	0.1587	96.9482
2	0.6826	100
3	0.1587	103.0518
Wind Scenario	${\tau }_{\mathit{w}\mathit{i}\mathit{n}\mathit{d},\mathit{k}}$	Wind Speed %
1	0.3	0
2	0.6	50
3	0.1	100
Irradiance Scenario	${\tau }_{\mathit{S}\mathit{o}\mathit{l}\mathit{a}\mathit{r},\mathit{m}}$	Solar Irradiance %
1	0.4	0
2	0.50	50
3	0.1	100

.

3.2. Modeling of Wind Speed

The uncertainty of wind speed is modeled by using the Weibull probability density function $f_v\left(v\right)$ which can be represented as follows [48]

$$f_v\left(v\right)=\left(\frac{\beta }{\alpha }\right){\left(\frac{v}{\alpha }\right)}^{\left(\beta -1\right)}exp\left[-{\left(\frac{v}{\alpha }\right)}^{\beta }\right]\hspace{1em}0\le v<\infty$$

(21)

where $\alpha$ and $\beta$ are the scale and the shape parameters of the Weibull PDF. The output power of wind turbine is defined as follows [49]

$$P_w\left(v_{\omega }\right)\hspace{0.17em}\hspace{0.17em}=\{\hspace{0.17em}\begin{array}{ccc}0& for& v_{\omega }<v_{\omega i} \& v_{\omega }>v_{\omega o}\\ P_{wr}\left(\frac{v_{\omega }-v_{\omega i}}{v_{\omega r}-v_{\omega i}}\right)& for& \left(v_{\omega i}\le v_{\omega }\le v_{\omega r}\right)\\ P_{wr}& for & \left(v_{\omega r}<v_{\omega }\le v_{\omega o}\right) \end{array}$$

(22)

where $P_{wr}$ is the rated output power of the wind turbine while $v_{\omega r}$, $v_{\omega i}$ and $v_{\omega o}$ are the rated, cut-in and the cut-out speeds of the wind turbine. In this paper, the wind farm consists of 25 turbines and the rated power of each turbine is 3 MW, while its rated speeds of $v_{\omega r}$, $v_{\omega i}$ and $v_{\omega o}$ are 16, 3 and 25 m/s, respectively [50]. The portability of wind speed for each scenario can be calculated as follows [32]

$${\tau }_{wind,k}={{\displaystyle \int }}_{v_k^{min}}^{v_k^{max}}{f}_v\left(v\right)dv$$

(23)

where ${\tau }_{wind,k}$ denotes the probability of the wind speed being in scenario k. In addition, $v_k^{min}$ and $v_k^{max}$ are the starting and ending points of wind speed’s interval at k-th scenario. In this paper, three scenarios are generated from the previous equations. The wind speed scenarios and their corresponding probability are depicted in Table 1.

3.3. Modeling of Solar Irradiance

The uncertainty of solar irradiance called (G) is modeled by the Beta PDF, which is used to describe the solar irradiance [51]. Thus, the Beta PDF is formulated as follows

$$f_G\left(G\right)=\{\begin{array}{c}\frac{\Gamma \left(\alpha +\beta \right)}{\Gamma \left(\alpha \right)+\Gamma \left(\beta \right)}\times G^{\propto -1}\\ \times {\left(1-G\right)}^{\beta -1}\\ 0 otherwise\end{array} If 0\le G\le 1, 0\le \alpha ,\beta$$

(24)

where $\alpha$ and $\beta$ are parameters of the beta probability function which can be calculated in terms of the mean (${\mu }_s$) and standard deviation (${\sigma }_s$) of the random variables as follows

$$\beta =\left(1-{\mu }_s\right)\times \left(\frac{{\mu }_s\times \left(1+{\mu }_s\right)}{{\sigma }_s{ }^2}\right)-1$$

(25)

$${\sigma }_s =\left(1-{\mu }_s\right)\times \left(\frac{{\mu }_s\times \beta }{\left(1-{\mu }_s\right)}\right)-1$$

(26)

The output power of the PV unit is calculated as a function of solar irradiance as follows [52,53]

$$P_s\left(G\right)\hspace{0.17em}\hspace{0.17em}=\{\begin{array}{ccc}{P}_{sr}\left(\frac{G^2}{G_{std }\times X_c }\right)\hfill & for & 0<G\le X_c\\ P_{sr}\left(\frac{G}{G_{std } }\right)\hfill & for & G\ge X_c\end{array}$$

(27)

where $P_{sr}$ is the rated power of the solar PV. $G_{std }$ denotes the standard solar irradiance which is set as 1000 $\mathrm{W}/{\mathrm{m}}^2$. Moreover, $X_c$ represents a certain irradiance point which is set as 120$\mathrm{W}/{\mathrm{m}}^2$ [50]. In this paper, the rated power of the PV system is 50 MW. The portability of solar irradiance for each scenario can be calculated as follows [32]

$${\tau }_{Solar,m}={{\displaystyle \int }}_{G_m^{min}}^{G_m^{min}}{f}_G\left(G\right)dG$$

(28)

where ${\tau }_{Solar,i}$ denotes the probability of the solar irradiance being in scenario m. $G_m^{min}$ and $G_m^{min}$ are the starting and ending points of solar irradiance’s interval at m-th scenario. In this paper, three scenarios are generated from the previous equations. The solar irradiance scenarios and their corresponding probability are depicted in Table 1. It should be highlighted here that the three most occurring scenarios and the corresponding probabilities (${\tau }_{d,i}$, ${\tau }_{wind,k}$, ${\tau }_{Solar,m}$) are selected similarly to [32] and [47].

3.4. The Combined Load-Generation Model

Combined scenarios of the load, wind speed and solar irradiance model are captured by multiplying the probabilities of (19), (23) and (28) together which result as

$${\tau }_S={\tau }_{d,i}\times {\tau }_{Solar,m}\times {\tau }_{wind,k}$$

(29)

4. Optimization Algorithm

The marine predators algorithm (MPA) is a new efficient algorithm that is conceptualized from the foraging behavior of the marine predators like marlines, tunas, sunfish, sharks, and swordfish with their prey in oceans. The foraging technique of the marine predators depends upon two random movements processes including the Lévy flight walk and the Brownian movements which are depicted in Figure 2. Humphries et al. indicated that Lévy motion is a widespread pattern among marine predators when searching for food; however, when it comes to foraging, the pattern is prevalently switched to Brownian type [54]. It should be highlighted here that the Lévy flight walk is a random process of transition of an object from one position to another based on the probability distribution factor [43].

The predator moves based on the Lévy flight at the food in a prey-sparse environment. On the other hands, the predator moves in a Brownian pattern when being located in a prey-abundant area. Another behavior related to the motion of the predators like sharks is recorded by the fish aggregating device (FAD), which reveals that the sharks move in a sudden vertical jump. The following steps describe the MPA:

Step 1: initialization

The initialization of the populations of the MPA randomly as follows

$$X_i=X_i^{min}+\left(X_i^{max}-X_i^{min}\right)\times rand$$

(30)

where $X_i^{max}$ and $X_i^{min}$ are the maximum and the minimum boundaries of the control variable; $\mathrm{rand}$ is a random number where $0\le rand\le 1$. The objective functions of the initial population are represented as follows

$$F_i=obj \left(X_i\right)$$

(31)

Step 2: Detecting top predator

First, the populations are arranged in a matrix called the prey matrix which can be represented as follows

$$X=\left[\begin{array}{cc}\begin{array}{cc}{X}_{1,1}& X_{1,2}\\ X_{2,1}& X_{22}\end{array}& \begin{array}{cc}\cdots & X_{1d}\\ \cdots & X_{2,1}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ X_{n,1}& X_{n,2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \dots & X_{n,d}\end{array}\end{array}\right]$$

(32)

where $n$ is the number of population, while $d$ denotes the number of control variables. In this step, the top predator is determined by the arrangement of the solutions based on their objective function values. A matrix is constructed that includes the top predator called the Elite matrix, which can be listed as follows

$$E=\left[\begin{array}{cc}\begin{array}{cc}{E}_{1,1}& E_{1,2}\\ E_{2,1}& E_{22}\end{array}& \begin{array}{cc}\cdots & E_{1d}\\ \cdots & E_{2,1}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ E_{n,1}& E_{n,2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \dots & E_{n,d}\end{array}\end{array}\right]$$

(33)

where $\overline{E}$ denotes the top predator vector.

Step 3: Lévy flight and the Brownian movements

In this step, the positions of the prey and the predators are updated based on three phases which depend upon the velocity ratio between the prey and predator velocity, which can be stated as follows:

Phase 1: This phase, representing the exploration phase of the algorithm, is applied at a high-velocity ratio. In other words, the velocity of the predator is higher than the velocity of the prey. In this phase, the prey and the predator are updated based on Brownian movement which can be mathematically represented as follows

$$\overline{S{Z}_i}=\overline{R_{Br}}\oplus \left(\overline{E_i}-\overline{R_{Br}}\oplus \overline{X_i}\right) if T\le T_{max}$$

(34)

$$\overline{X_i}=\overline{X_i}+P.\overline{R} \oplus \overline{S{Z}_i}$$

(35)

where $T$ and $T_{max}$ are the current iteration number and the maximum number of iterations, respectively; $\oplus$ denotes the entry wise multiplication; $\overline{R_{Br}}$ is a vector containing random numbers based on normal distribution representing the Brownian motion. In addition, $\overline{S{Z}_i}$ is the step size vector, and P is a constant number equal to 0.5.

Phase 2: This phase is an intermittent phase between the exploration and the exploitation phase that is applied when the velocity of predator equals the velocity of prey. In this section, the populations are divided into two groups. The first group is employed from exploitation and the other group for exploration, which can be represented as follows

$$if \frac{1}{3}{T}_{max}\le T\le \frac{2}{3}{T}_{max}$$

$$\overline{S{Z}_i}=\overline{R_{Levy}}\oplus \left(\overline{E_i}-\overline{R_{Levy}}\oplus \overline{X_i}\right) for i=1,2,3\dots , \frac{n}{2}$$

(36)

$$\overline{X_i}=\overline{X_i}+P.\overline{R} \oplus \overline{S{Z}_i}$$

(37)

The second group or exploration group

$$\overline{S{Z}_i}=\overline{R_{Br}}\oplus \left(\overline{E_i}-\overline{R_{Br}}\oplus \overline{X_i}\right) for i=\frac{n}{2},\dots , n$$

(38)

$$\overline{X_i}=\overline{X_i}+P.CF \oplus \overline{S{Z}_i}$$

(39)

where $R_{Levy}$ is a vector containing random numbers based on Lévy distribution which mimics the movement of prey in levy manner. $CF$ is an adaptive operator utilized to control the step size of predator’s movement.

Phase 3: This phase is a fully exploitation phase which is applied when the velocity of the predator is more than the velocity of the prey at the final iterations of the optimization technique.

$$\overline{S{Z}_i}=\overline{R_{Levy}}\oplus \left(\overline{R_{Levy}}\oplus \overline{E_i}-\overline{X_i}\right) for i=1,2,3\dots , \frac{n}{2}$$

(40)

$$\overline{X_i}=\overline{E_i}+P.\overline{R} \oplus \overline{S{Z}_i}$$

(41)

In this phase, the predator is moving in levy strategy and the previous equations describe the prey movement based on the elite vector.

Step 4: In eddy formation and FADs’ effect, the predator changes its movement behavior due to environmental issues, as mentioned before. These predators move in the eddy formation or fish aggregating devices which represent the local optima, while they take a longer jump to find a new environment that has abundant regions. This step can be represented as follows

$$\overline{X_i}=\{\begin{array}{c}\overline{X_i}+CF\left[X_i^{min}+R\left(X_i^{max}-X_i^{min}\right)\right] \oplus \overline{U} If r\le FADS\\ \overline{X_i}+\left[FADS\left(1-r\right)+r\right] \left(\overline{X_{r1}}-\overline{X_{r2}}\right) If r>FADS\end{array}$$

(42)

where $r$ is a random value within the range 0 to 1. $r1$ and $r2$ represent random indices from prey matrix. $\mathrm{FADS}$ represents FADs probability, which equals 0.2. $\overline{U}$ is a binary vector.

Step 5: Marine memory

The marine predators can efficiently remember the best location of foraging. Thus, in the MPA technique, the updated solution is compared with those in the previous iteration to capture the optimal solution.

5. Simulation Results

In this section, the MPA technique is utilized to solve the ORPD in IEEE 30-bus system with and without considering the uncertainty of system. The program code of the proposed algorithm of ORPD was written for the MATLAB R2018b programming software and run on a PC with Core I5 @ 1.7 GHz with 4GB RAM. The IEEE 30-bus system data are given in [55]. The boundaries of the control variables are listed in

Table 2. The optimal control variables for ${\mathrm{P}}_{\mathrm{Loss}}$ and $\mathrm{voltage} \mathrm{deviations}\left(\mathrm{VD}\right)$.

Control Variables	Min.	Max.	${\mathbf{P}}_{\mathbf{L}\mathbf{o}\mathbf{s}\mathbf{s}} \mathbf{Minimization}$	$\mathbf{V}\mathbf{D} \mathbf{Minimization}$
Generator Voltage
V1 (p.u)	1.1	0.9	1.1000	0.9971
V2 (p.u)	1.1	0.9	1.0949	0.9959
V5 (p.u)	1.1	0.9	1.0761	1.0164
V8 (p.u)	1.1	0.9	1.0780	0.9971
V11 (p.u)	1.1	0.9	1.0873	1.0387
V13 (p.u)	1.1	0.9	1.1000	1.0251
Transformer Tap Ratio
T11	1.1	0.9	0.9807	1.0556
T12	1.1	0.9	1.0222	1.0180
T15	1.1	0.9	0.9765	1.0230
T36	1.1	0.9	0.9707	0.9676
Capacitor Banks
Q10 (p.u)	0.05	0	0.0179	0.0450
Q12 (p.u)	0.05	0	0.0483	0.0497
Q15 (p.u)	0.05	0	0.0397	0.0499
Q17 (p.u)	0.05	0	0.0499	0.0240
Q20 (p.u)	0.05	0	0.0422	0.0463
Q21 (p.u)	0.05	0	0.0461	0.0499
Q23 (p.u)	0.05	0	0.0469	0.0426
Q24 (p.u)	0.05	0	0.0412	0.0499
Q29 (p.u)	0.05	0	0.0329	0.0193
Objective Function
${\mathrm{P}}_{\mathrm{Loss} }\left(\mathrm{MW}\right)$			4.5335	6.11680
$\mathrm{V}\mathrm{D} \left(\mathrm{p}.\mathrm{u}\right)$			2.06573	0.08514

. The studied cases of system are listed as follows.

5.1. Case 1: ORPD Solution without Considering the Uncertainty

In this case, the MPA is applied for solving the ORPD problem to minimize the power loss and the voltage deviations at a deterministic pattern. The selected number of populations, the maximum number of iterations and run trials of the MPA are 30, 100 and 25, respectively. It should be highlighted here that these parameters are selected empirically where the importance of this act is having a compromise between optimal solution and run time or minimum number of iterations, which is a necessary feature of the optimization algorithms. The initial power loss and the voltage deviations are 5.596 MW and 0.8691 p.u., respectively. The optimal control variables obtained by the application of MPA for power loss and voltage deviation minimization are listed in Table 2. The minimum power loss obtained by MPA is 4.5335 MW.

Table 3. Comparison of simulation results for ${\mathrm{P}}_{\mathrm{Loss}}$ minimization.

Algorithm	Best	Worst	Mean
MPA	4.5335	4.6006	4.55389
JA [56]	4.625	NA	NA
ALO [10]	4.5900	NA	NA
HSA [22]	4.9059	4.9653	4.924
PSO [22]	4.9239	5.0576	4.972
STGA [22]	4.9408	5.1651	5.0378
TLBO [23]	4.5629	4.57480	4.56950
QOTLBO [23]	4.5594	4.56170	4.56010
DE [15]	4.5550	NA	NA
SGA [16]	4.5692	NA	NA
FA [57]	4.5691	4.59	4.578
HPSO-TS [30]	4.5213	NA	NA
TS [30]	4.9203	NA	NA
PSO [30]	4.6862	NA	NA
WOA [11]	4.5943	NA	NA
PSO-TVAC [11]	4.6469	NA	NA
IDE [18]	4.5521	NA	NA
BBO [24]	4.5511	NA	NA
CLPSO [20]	4.6282	NA	NA
PSO [20]	4.5615	NA	NA
GSA [26]	5.00954	NA	NA
PSO [26]	4.91578	NA	NA
GSA-CSS [26]	4.79301	NA	NA
IGSA-CSS [26]	4.76601	NA	NA

shows the best, worst and mean values of the power losses obtained by application other optimization techniques. As can be seen from Table 3, the MPA algorithm outperforms other algorithms as it can achieve a power loss reduction of 21.7823% (from the initial power loss), compared with 20.2036% by JA [56], by 20.2036%% ALO [10], 21.2750% 20.8075% by HSA [22], 15.3571% by PSO [22], by 15.0466% STGA [22], by 14.7550% TLBO [23], 21.3354% by QOTLBO [23], 21.4113% by DE [15], 21.1663% by SGA [16], 21.1680% by FA [57], 21.9928% by HPSO-TS [30], 15.1087% by TS [30], 19.1477% by PSO [30], 20.7333% by WOA [11] 19.8257% by PSO-TVAC [11], by 21.4614% IDE [18], 21.4786% by BBO [24], 20.1484% by CLPSO [20], 21.2992% by PSO [20], 13.5690% by GSA [26], 15.1867% by PSO [26], 17.3049% by GSA-CSS [26] and by 17.7707% IGSA-CSS [26]. In case of minimizing the voltage deviations (VD), the minimum VD that obtained by application the MPA is 0.08514 p.u and the optimal values of control variables for this case are reported in the 5th column of Table 1.

Table 4. Comparison of simulation results for $\mathrm{VD}$ minimization.

Algorithm	Best	Worst	Mean
MPA	0.08513	0.09900	0.09454
QOTLBO [23]	0.0856	0.0907	0.0872
TLBO [23]	0.0913	0.0988	0.0934
PSO-TVIW [58]	0.1038	0.5791	0.1597
PSO-TVA [58]	0.2064	0.5796	0.2376
SPSO-TVAC [58]	0.1354	0.1833	0.1558
PSO-CF [58]	0.1287	0.4041	0.1557
PG-PSO [58]	0.1202	0.2593	0.1440
SWT-PSO [58]	0.1614	0.2296	0.1814
IPG-PSO [58]	0.0892	0.2518	0.1078
DE [15]	0.0911	NA	NA
ISSO [12]	0.08847	0.14938	0.11603
SSO [12]	0.19304	0.42681	0.2863
HSSSA [12]	0.174701	0.576439	0.308337
MSSA [12]	0.230087	1.860037	0.690254
SSA [12]	0.188411	0.941759	0.374529
CSA [12]	0.12692	0.2076	0.16432
IALO [13]	0.0881	NA	0.1012
ALO [13]	0.1192	NA	0.1575
GSA [26]	0.17241	NA	NA
PSO [26]	0.10462	NA	NA
GSA-CSS [26]	0.12394	NA	NA
IGSA-CSS [26]	0.08968	NA	NA

shows the voltage deviations that are obtained by application different algorithms. From Table 4, it is shown that the MPA algorithm outperforms other algorithms as it can achieve a voltage deviations reduction of 90.2048% (from the initial VD), compared with 90.1507% by QOTLBO [23], 89.4949% by TLBO [23], 88.0566% by PSO-TVIW [58], 76.2513% by PSO-TVA [58], 84.4207% by SPSO-TVAC [58], 85.1916% by PSO-CF [58], 86.1696% by PG-PSO [58], 81.4291% by SWT-PSO [58], 89.7365% by IPG-PSO [58], 89.5179% by DE [15], 89.8205% by ISSO [12], 77.7885% by SSO [12], 79.8986% by HSSSA [12], 73.5258% by MSSA [12], 78.3211% by SSA [12], 85.3964% by CSA [12], 89.8631% by IALO [13], 86.2847% by ALO [13], 80.1622% by GSA [26], 87.9623% by PSO [26], 85.7393% by GSA-CSS [26] and 89.6813% by IGSA-CSS [26]. According to Table 4, it is obvious that the minimum VD can be obtained by the MPA compared with the reported algorithms. Figure 3 and Figure 4 depict the convergence characteristics of the MPA for power loss and the VD, respectively. It is clear that MPA has stable convergence characteristics. For $P_{Loss}$, the MPA is converged at the 70th iteration, while the other algorithms are converged about or at 30th iteration JA [56], 70th iteration ALO [10], 2800th iteration HSA [22], 68th iteration TLBO [23], 60th iteration QOTLBO [23], 130th iteration DE [15], 280th iteration SGA [16], 130th iteration FA [57], 65th iteration HPSO-TS [30], 18th iteration TS [30], 25th iteration PSO [30], 130th iteration WOA [11], 90th iteration PSO-TVAC [11], 200th iteration IDE [18], 240th iteration BBO [24], 23th iteration CLPSO [20], 35th iteration PSO [20], 220th iteration GSA [26], 400th iteration PSO [26], 300th iteration GSA-CSS [26] and 150th iteration IGSA-CSS [26]. In terms of the VD, the MPA is converged at the 68th iteration, while the other algorithms are converged about or at 63th iteration QOTLBO [23], 70th iteration TLBO [23], 35th iteration PSO-TVIW [58], 65th iteration PSO-TVA [58], 95th iteration SPSO-TVAC [58], 35th iteration PSO-CF [58], 90th iteration PG-PSO [58], 30th iteration SWT-PSO [58], 40th iteration IPG-PSO [58], 430th iteration DE [15], 30th iteration IALO [13], 40th iteration ALO [13], 220th iteration GSA [26], 200th iteration PSO [26], 300th iteration GSA-CSS [26], 420th iteration IGSA-CSS [26].

5.2. Case 2: Solution of ORPD Problem Considering the Uncertainty

In this case, the ORPD is solved by considering the uncertainties of the wind and solar generation systems and load demand. To solve the ORPD with the stochastic natural of wind and solar generation resources, the IEEE 30-bus system is modified as depicted in Figure 5. A wind farm and solar PV system are incorporated with bus 5 and bus 8, respectively. The wind farm consists of 25 turbines and the rated power of each turbine is 3 MW, while the rated speeds of each turbine $v_{\omega r}$, $v_{\omega i}$ and $v_{\omega o}$ are 16, 3 and 25 m/s, respectively. The rated power of the PV system is 50 MW and the standard solar irradiance ($G_{std}$) is 1000 W/m² [50].

As depicted in Table 1, this shows three individual scenarios and their corresponding probabilities for modeling the uncertainties of the load, the solar irradiance and the wind speed. The number of the generated scenarios from combining the uncertainties of load, solar irradiance and the wind speed is 27 according to Section 3.4.

Table 5. Selected scenarios and the corresponding probabilities and parameters.

Scenario	Loading %	Solar Irradiance %	Wind Speed %	${\mathit{\tau }}_{\mathit{d},\mathit{i}}$	${\mathit{\tau }}_{\mathit{S}\mathit{o}\mathit{l}\mathit{a}\mathit{r},\mathit{m}}$	${\mathit{\tau }}_{\mathit{w}\mathit{i}\mathit{n}\mathit{d},\mathit{k}}$	${\mathit{\tau }}_{\mathit{S}}$
$\mathrm{S}1$	96.9482	0	0	0.1587	0.4	0.3	0.0190
$\mathrm{S}2$	96.9482	0	50	0.1587	0.4	0.6	0.0381
$\mathrm{S}3$	96.9482	0	100	0.1587	0.4	0.1	0.0063
$\mathrm{S}4$	96.9482	50	0	0.1587	0.5	0.3	0.0238
$\mathrm{S}5$	96.9482	50	50	0.1587	0.5	0.6	0.0476
$\mathrm{S}6$	96.9482	50	100	0.1587	0.5	0.1	0.0079
$\mathrm{S}7$	96.9482	100	0	0.1587	0.1	0.3	0.0048
$\mathrm{S}8$	96.9482	100	50	0.1587	0.1	0.6	0.0095
$\mathrm{S}9$	96.9482	100	100	0.1587	0.1	0.1	0.0016
$\mathrm{S}10$	100	0	0	0.6826	0.4	0.3	0.0819
$\mathrm{S}11$	100	0	50	0.6826	0.4	0.6	0.1638
$\mathrm{S}12$	100	0	100	0.6826	0.4	0.1	0.0273
$\mathrm{S}13$	100	50	0	0.6826	0.5	0.3	0.1024
$\mathrm{S}14$	100	50	50	0.6826	0.5	0.6	0.2048
$\mathrm{S}15$	100	50	100	0.6826	0.5	0.1	0.0341
$\mathrm{S}16$	100	100	0	0.6826	0.1	0.3	0.0205
$\mathrm{S}17$	100	100	50	0.6826	0.1	0.6	0.0410
$\mathrm{S}18$	100	100	100	0.6826	0.1	0.1	0.0068
$\mathrm{S}19$	103.0518	0	0	0.1587	0.4	0.3	0.0190
$\mathrm{S}20$	103.0518	0	50	0.1587	0.4	0.6	0.0381
$\mathrm{S}21$	103.0518	0	100	0.1587	0.4	0.1	0.0063
$\mathrm{S}22$	103.0518	50	0	0.1587	0.5	0.3	0.0238
$\mathrm{S}23$	103.0518	50	50	0.1587	0.5	0.6	0.0476
$\mathrm{S}24$	103.0518	50	100	0.1587	0.5	0.1	0.0079
$\mathrm{S}25$	103.0518	100	0	0.1587	0.1	0.3	0.0048
$\mathrm{S}26$	103.0518	100	50	0.1587	0.1	0.6	0.0095
$\mathrm{S}27$	103.0518	100	100	0.1587	0.1	0.1	0.0016

lists the combined scenarios and their probabilities along with the load, solar irradiance and the wind speed. It should be highlighted here that the wind speeds in Table 5 are a percentage of the rated wind speed (16 m/s) while the solar irradiances are a percentage of the standard solar irradiance (1000 W/m²). The aim of solving the ORPD is to minimize the expected the power loss over the whole scenarios which can be expressed as follows

$$TEPL={\displaystyle \sum }_{h=1}^{N_S}EP{L}_h ={\displaystyle \sum }_{h=1}^{N_S}{\tau }_{S,h}\times P_{Loss,h}$$

(43)

where $N_S$ is a number of the generated scenarios;${ \mathrm{EPL}}_{\mathrm{h}}$ is the expected power loss for the h-th scenario;$\mathrm{TEPL}$ describes the total expected power losses. The total expected power loss without incorporating the renewable energy resources in system is 10.746 MW, while it equals 7.1223 MW when incorporating the renewable energy resources and considering their probabilities. In other words, the TEPL is reduced to 33.72% with the inclusion of the renewable energy resources.

Table 6. Selected scenarios and the corresponding output powers of renewable systems and the expected power losses.

Scenario	${\mathit{P}}_{\mathit{s}}\left(\mathit{M}\mathit{W}\right)$	${\mathit{P}}_{\mathit{w}}\left(\mathit{M}\mathit{W}\right)$	${\mathit{P}}_{\mathit{L}\mathit{o}\mathit{s}\mathit{s}}\left(\mathit{M}\mathit{W}\right)$	${\mathit{\tau }}_{\mathit{S}}$	$\mathit{E}\mathit{P}\mathit{L}\left(\mathit{M}\mathit{W}\right)$
$\mathrm{S}1$	0	0	11.0584	0.0190	0.2101
$\mathrm{S}2$	0	28.8462	7.4343	0.0381	0.2832
$\mathrm{S}3$	0	75.0000	4.2777	0.0063	0.0269
$\mathrm{S}4$	25	0	8.4741	0.0238	0.2017
$\mathrm{S}5$	25	28.8462	5.4973	0.0476	0.2617
$\mathrm{S}6$	25	75.0000	3.1696	0.0079	0.0250
$\mathrm{S}7$	50	0	6.6682	0.0048	0.0320
$\mathrm{S}8$	50	28.8462	4.4733	0.0095	0.0425
$\mathrm{S}9$	50	75.0000	2.6388	0.0016	0.0042
$\mathrm{S}10$	0	0	10.4350	0.0819	0.8546
$\mathrm{S}11$	0	28.8462	7.4520	0.1638	1.2206
$\mathrm{S}12$	0	75.0000	4.9558	0.0273	0.1353
$\mathrm{S}13$	25	0	8.4523	0.1024	0.8655
$\mathrm{S}14$	25	28.8462	5.8801	0.2048	1.2042
$\mathrm{S}15$	25	75.0000	3.3202	0.0341	0.1132
$\mathrm{S}16$	50	0	7.0750	0.0205	0.1450
$\mathrm{S}17$	50	28.8462	4.7426	0.0410	0.1944
$\mathrm{S}18$	50	75.0000	2.4981	0.0068	0.0170
$\mathrm{S}19$	0	0	11.4607	0.0190	0.2178
$\mathrm{S}20$	0	28.8462	9.0704	0.0381	0.3456
$\mathrm{S}21$	0	75.0000	6.4350	0.0063	0.0405
$\mathrm{S}22$	25	0	9.1914	0.0238	0.2188
$\mathrm{S}23$	25	28.8462	6.9738	0.0476	0.3320
$\mathrm{S}24$	25	75.0000	4.3080	0.0079	0.0340
$\mathrm{S}25$	50	0	7.9091	0.0048	0.0380
$\mathrm{S}26$	50	28.8462	5.5830	0.0095	0.0530
$\mathrm{S}27$	50	75.0000	3.3066	0.0016	0.0053
					TEPL = 7.1223

shows the output power of wind turbine, solar PV unit and the corresponding probabilities as well as the expected power loss for each scenario. The IEEE 30-bus voltage profile for each scenario is depicted in Figure 6. It is clear that the system voltages are within limits.

6. Conclusions

This paper solved the ORPD problem efficiently using a new efficient algorithm called the marine predators algorithm (MPA) for losses and the voltage deviations minimization. The ORPD was solved with and without the uncertainties of the system. The proposed technique was validated in an IEEE 30-bus system and the obtained results were compared with well-known techniques. Three uncertainty parameters were considered, which are the uncertainty of load demands and uncertainties associated with renewable energy resources including the wind speed and solar irradiance. The uncertainties of load demands, wind speed and the solar irradiance were examined using normal PDF, Weibull PDF and Beta PDF. The scenario-based model has been applied to generate various scenarios using the individual scenarios of the uncertainty parameters of the system. The expected power loss is evaluated with numerous scenarios of load demands, wind and solar power. The obtained results confirmed that the proposed MPA is an efficient technique for solving the ORPD compared with other reported techniques. Furthermore, in cases solving the ORPD considering the uncertainty, the expected power loss reduced considerably with the inclusion of renewable energy resources, from 10.746 to 7.1223 MW.