Thermal Distortion of Signal Propagation Modes Due to Dynamic Loading in Medium-Voltage Cables
Abstract
:1. Introduction
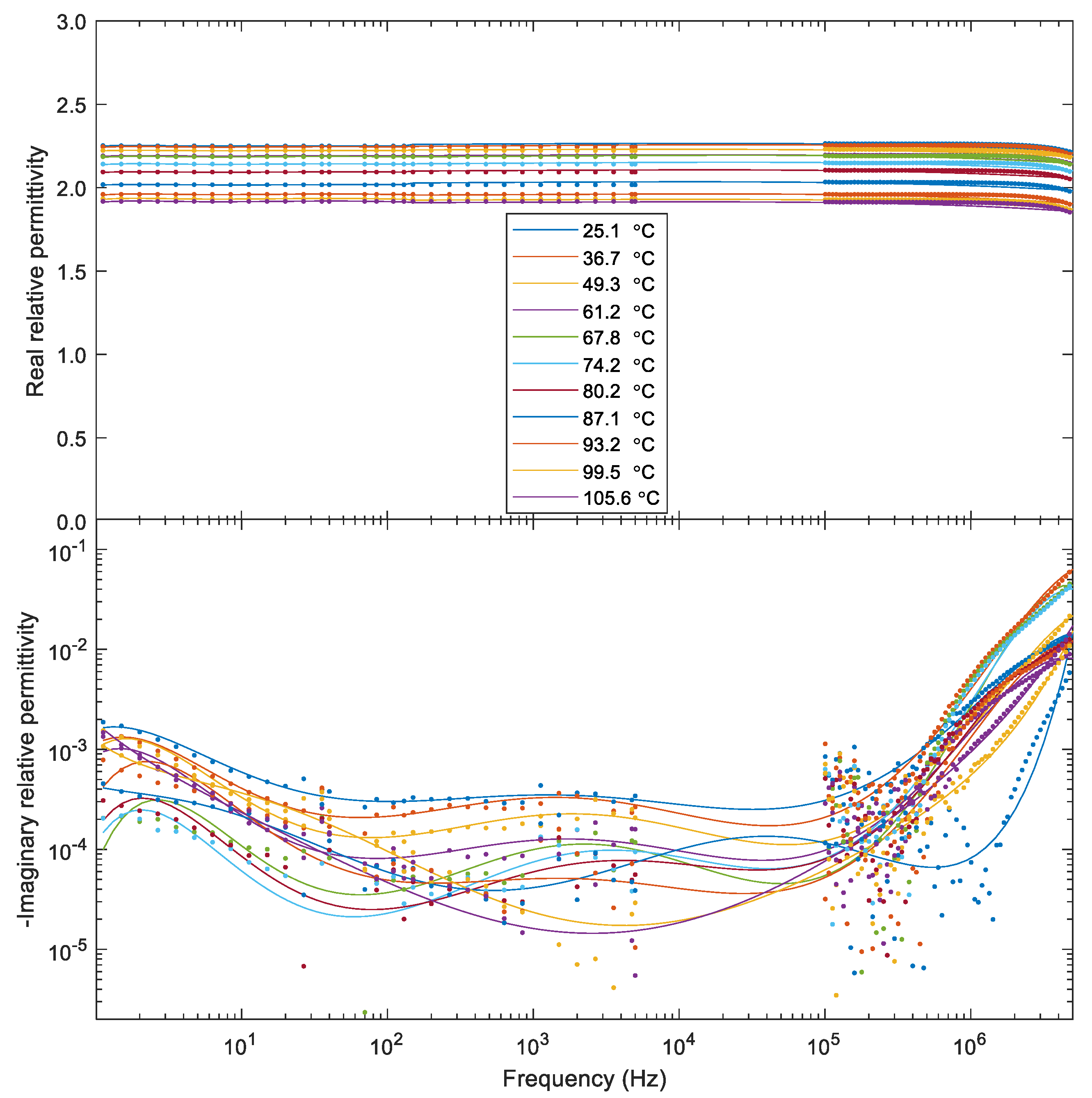
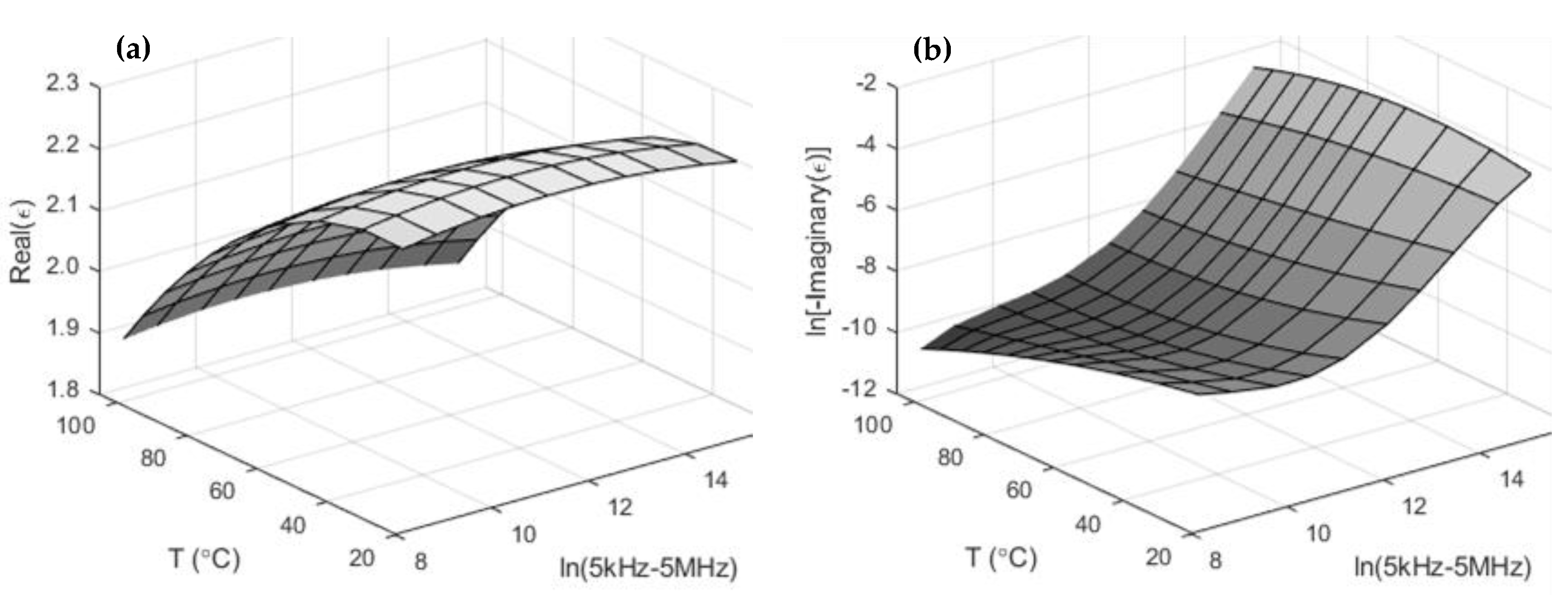
2. Complex Relative Permittivity of XLPE
- For frequencies up to 5 kHz, a dielectric material analyzer is employed (Spectano 100, test amplitude 200 V)
- A VNA is used for the higher frequency range, up to 5 MHz (Bode 100, test voltage 1 Vrms).
- The upper frequency is restricted by the dielectric sample holder design (DSH 100, temperature up to 125 °C).
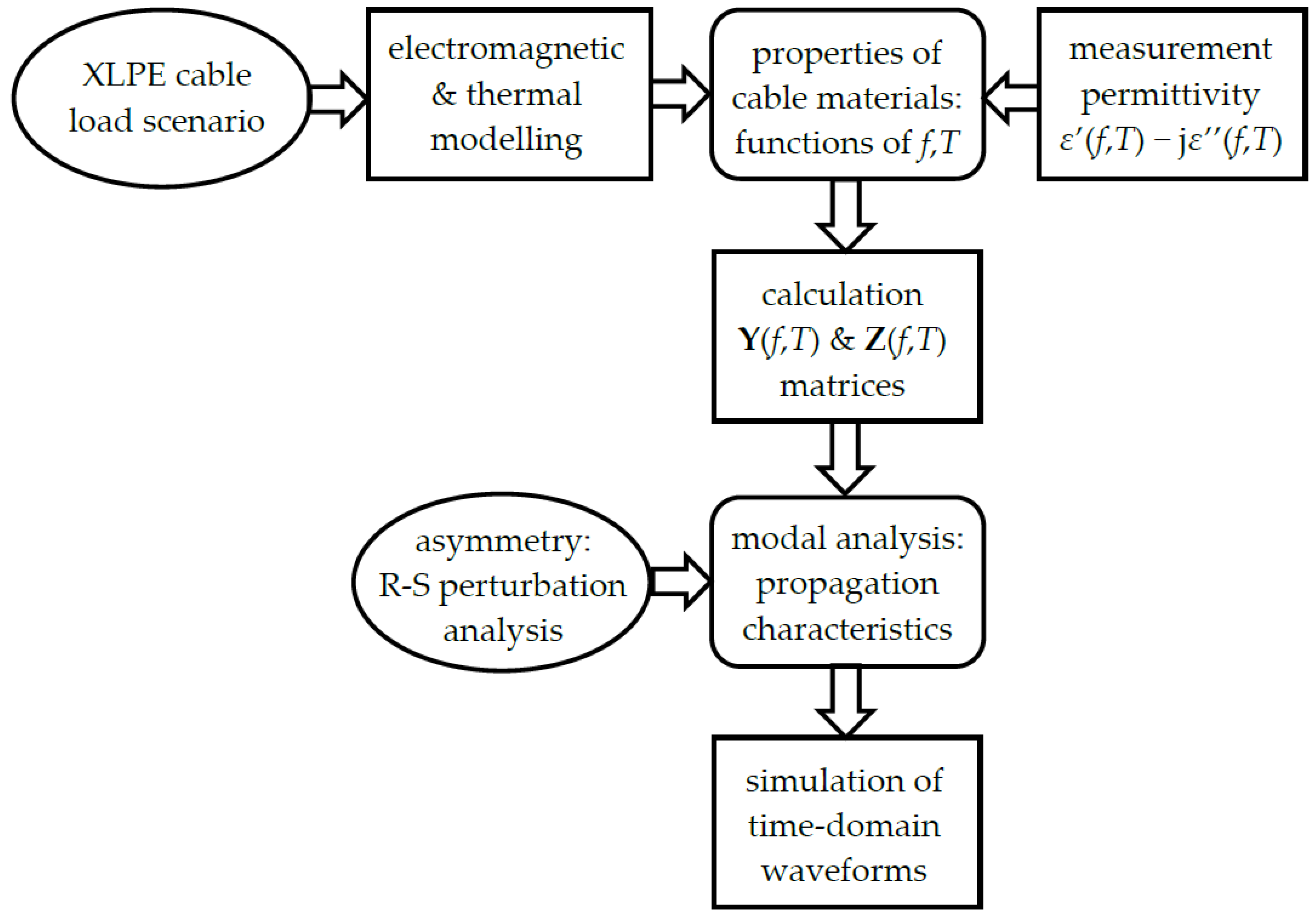
3. Propagation Mode Modeling
3.1. Electromagnetic and Thermal Modeling
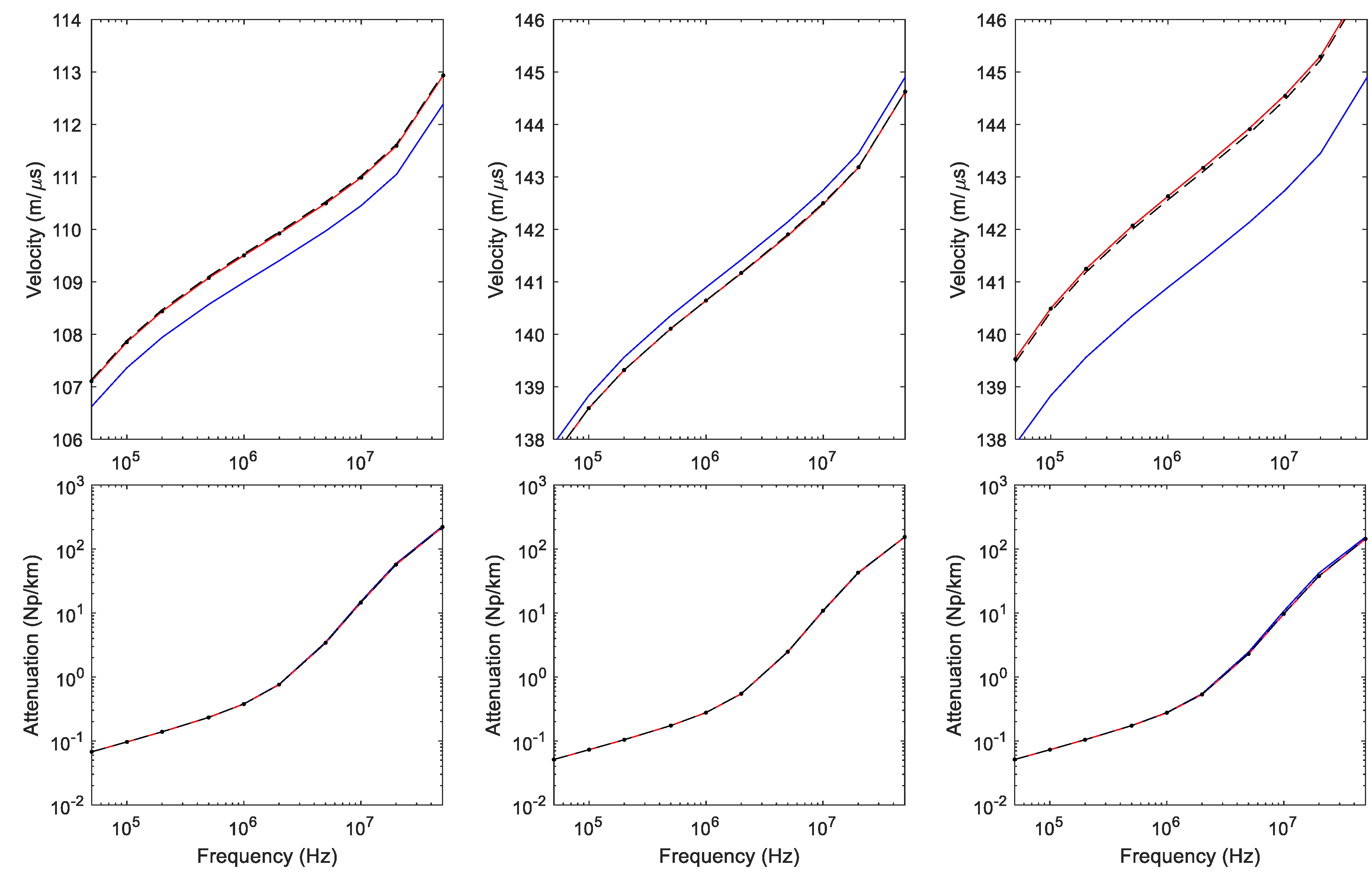
3.2. Modeling Material Properties
3.3. Modal Analysis
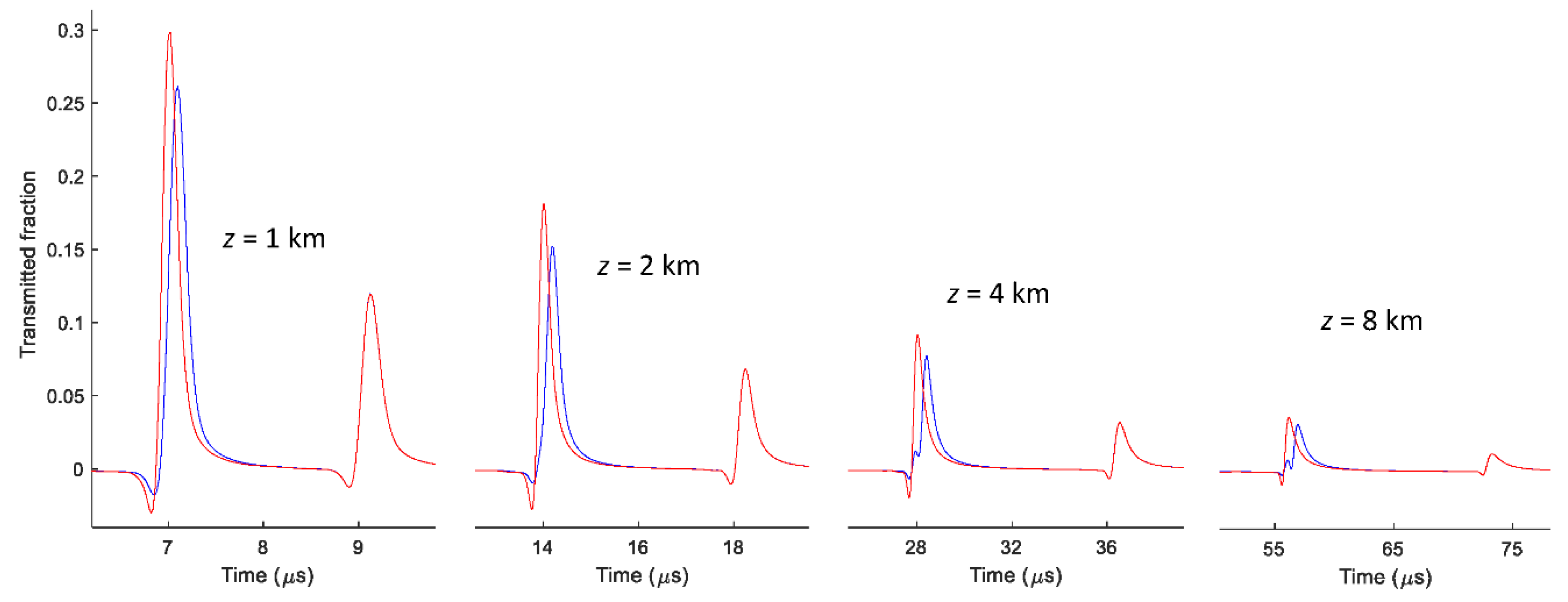
3.4. Time-Domain Response
- The initial signal at z = 0 is converted to the frequency domain by a Fourier transform
- The frequency-domain signal is decomposed in the modal components
- The modal components after traveling distance z are calculated
- The modal components are converted back to phase signals
- The phase signals are converted to the time domain with the inverse Fourier transform
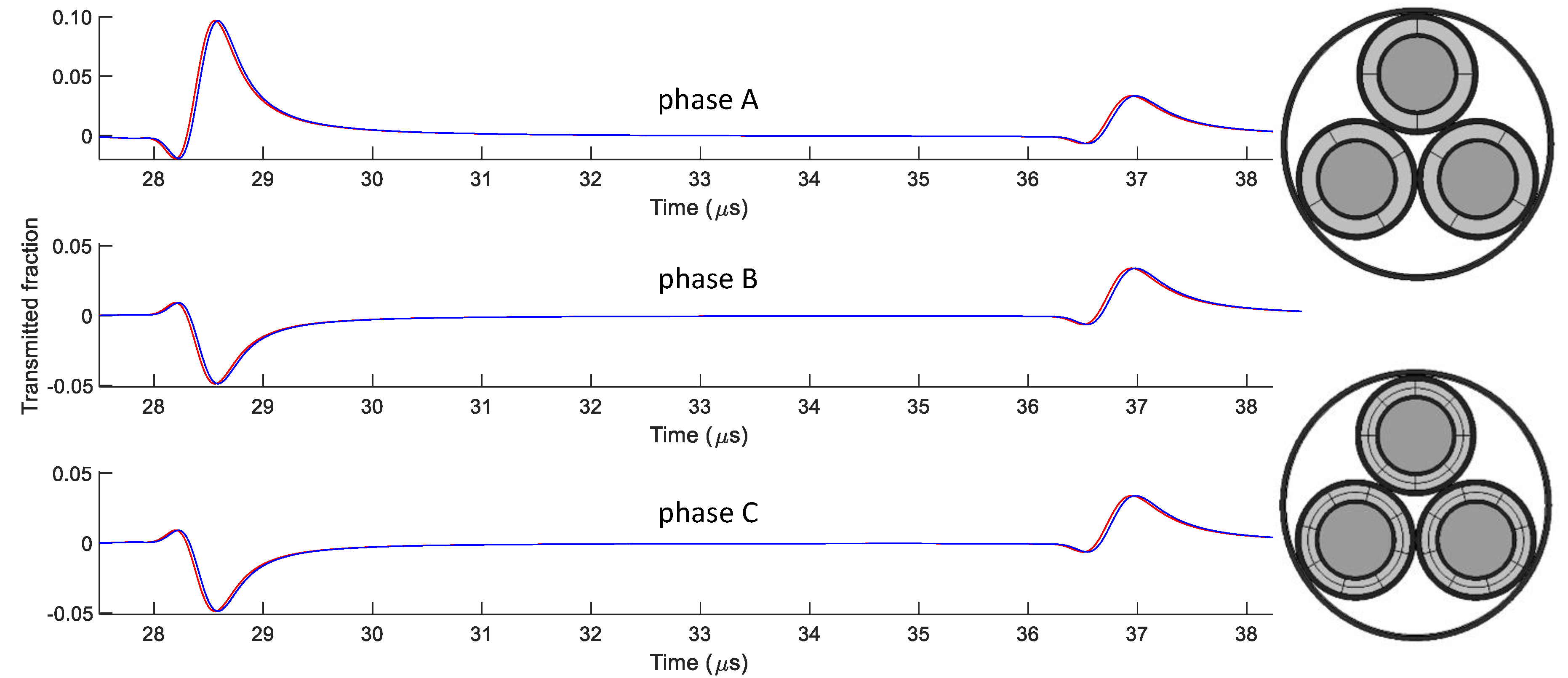
4. Discussion
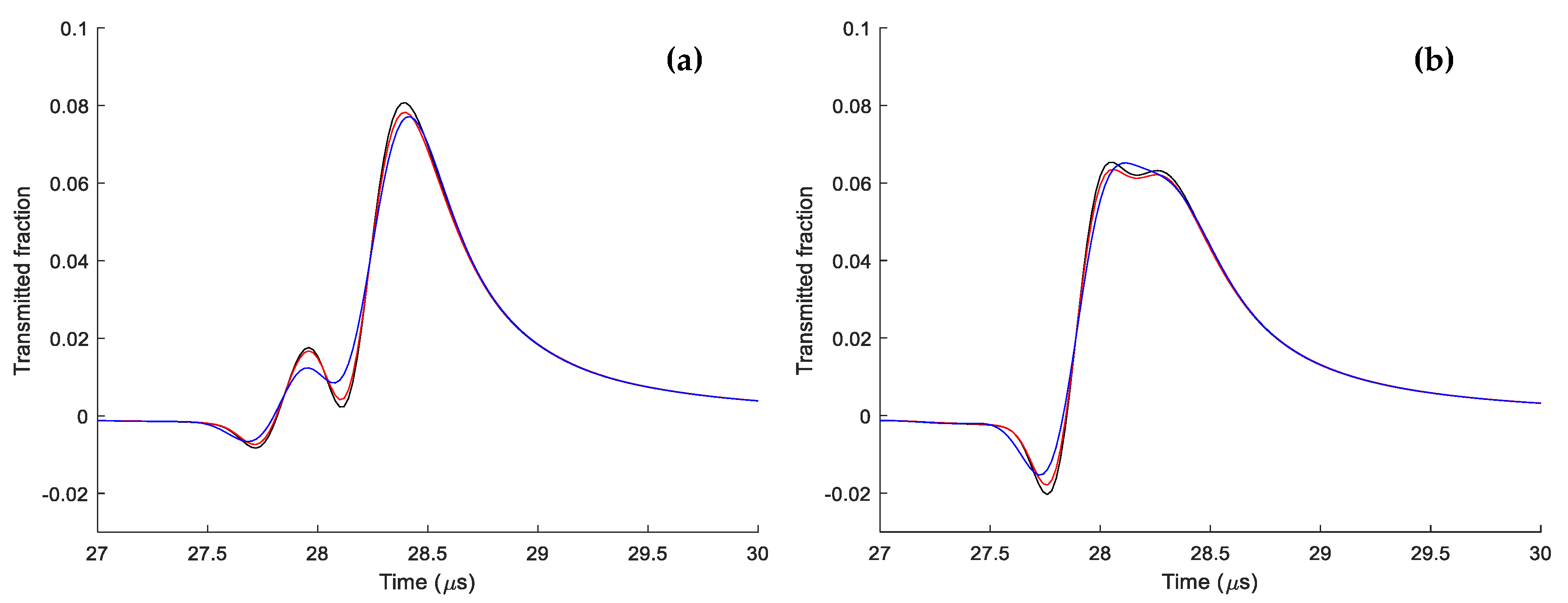
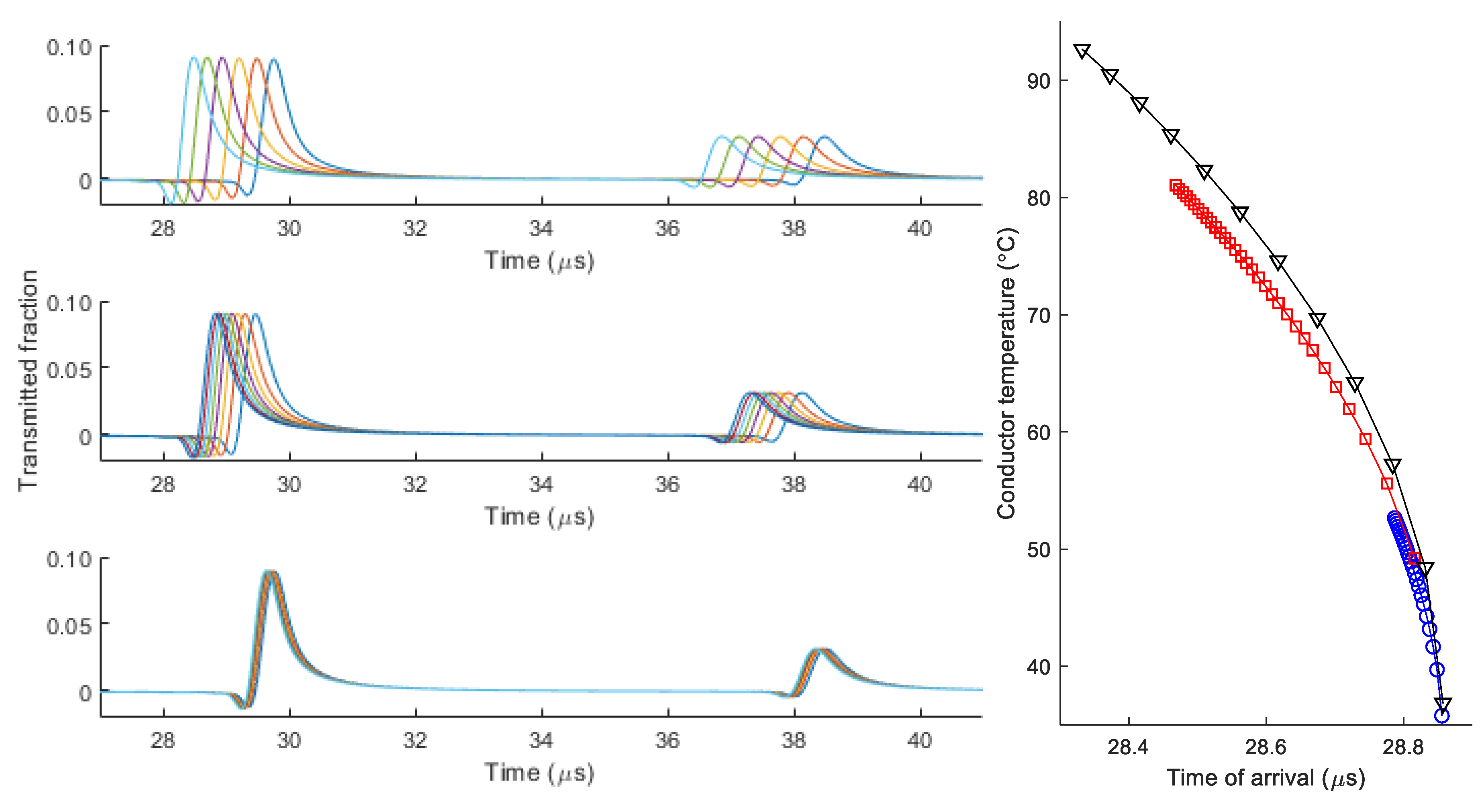
4.1. Sensitivity Analysis
4.2. Application Perspectives
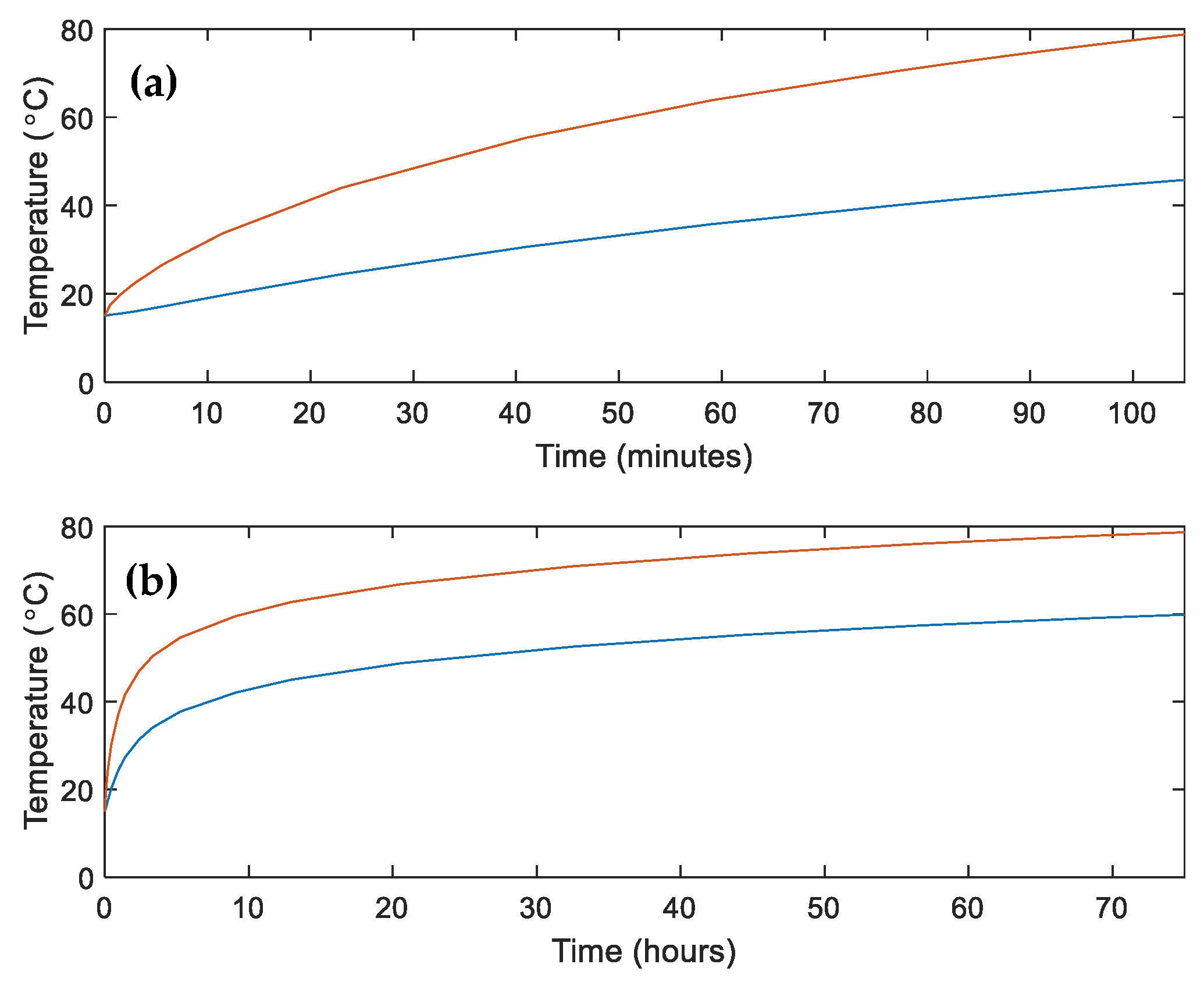
- When the load is 75% higher than nominal, the maximum temperature allowed is reached in three hours. This unrealistic load situation exemplifies the effect of large temperature differences in the cable cross-section.
- A 25% increase over the nominal current is more realistic. Such situations can arise, for instance, in which a parallel connection is temporarily out of service. The current level can be maintained as long as the cable temperature remains within safe operation range.
- For a nominal load, the cable temperature stays within a safe range. The change in the relative permittivity is low, resulting in only minor shifts in the waveform.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Coefficients pij | Coefficients qij | |
|---|---|---|
| p00 = 2.153 | q00 = −9.115 | q30 = 0.02546 |
| p10 = −0.006566 | q10 = 1.740 | q21 = -0.09336 |
| p01 = −0.1347 | q01 = −0.4192 | q12 = −0.03861 |
| p20 = −0.01064 | q20 = 1.547 | q40 = −0.1872 |
| p11 = −0.001949 | q11 = −0.08973 | q31 = 0.1121 |
| p02 = −0.04101 | q02 = 0.1624 | q22 = −0.1385 |
Appendix B

References
- Steennis, E.F.; Wagenaars, P.; van der Wielen, P.C.J.M.; Wouters, P.A.A.F.; Li, Y.; Broersma, T.; Harmsen, D.; Bleeker, P. Guarding MV cables on-line: With travelling wave based temperature monitoring, fault location, PD location and PD related remaining life aspects. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 1562–1569. [Google Scholar] [CrossRef] [Green Version]
- Van Deursen, A.; Wouters, P.A.A.F.; Steennis, E.F. Corrosion in low-voltage distribution networks and perspectives for online condition monitoring. IEEE Trans. Power Deliv. 2019, 34, 1423–1431. [Google Scholar] [CrossRef] [Green Version]
- Wouters, P.A.A.F.; Tong, A.; van Deursen, A.; van der Wielen, P.C.J.M.; Li, Y. Temperature dependency of transient signal propagation in underground power cables. In Proceedings of the International Conference on High Voltage Engineering and Application (ICHVE), Beijing, China, 6–10 September 2020. [Google Scholar]
- Dubickas, V.; Edin, H. On-line time domain reflectometry measurements of temperature variations of an XLPE power cable. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Kansas City, MI, USA, 15–18 October 2006; pp. 47–50. [Google Scholar] [CrossRef]
- Li, Y.; Wouters, P.A.A.F.; Wagenaars, P.; van der Wielen, P.C.J.M.; Steennis, E.F. Temperature dependent signal propagation velocity: Possible indicator for MV cable dynamic rating. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 665–672. [Google Scholar] [CrossRef]
- Nyamupangedengu, C.; Sotsaka, M.; Mlangeni, G.; Ndlovu, L.; Munilal, S. Effect of temperature variations om wave propagation characteristics in power cables. S. Afr. Inst. Electr. Eng. 2015, 106, 28–38. [Google Scholar] [CrossRef]
- Omicron Lab. Available online: www.omicron-lab.com (accessed on 15 August 2020).
- Dubickas, V. Development of on-Line Diagnostic Methods for Medium Voltage XLPE Power Cables. Ph.D. Thesis, Kungl Tekniska Högskolan, Stockholm, Sweden, 2009. [Google Scholar]
- Mugala, G.; Eriksson, R.; Pettersson, P. Dependence of XLPE insulated power cable wave propagation characteristics on design parameters. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 393–399. [Google Scholar] [CrossRef]
- Jung, C.-K.; Kim, J.-T.; Lee, J.-B. Partial discharge simulation and analysis based on experiment in underground distribution power cables. J. Electr. Eng. Technol. 2013, 8, 832–839. [Google Scholar] [CrossRef] [Green Version]
- Wouters, P.A.A.F.; van Deursen, A.; Li, Y. Rayleigh-Schrödinger perturbation analysis of signal propagation modes in inhomogeneous multi-conductor power cables. Int. J. Electr. Power Energy Syst. 2020, 121. [Google Scholar] [CrossRef]
- Plesch, J.; Pack, S.; Schort, H. Soil temperature profile due to stationary and transient operation of energy cables. In Proceedings of the International Conference on High Voltage Engineering and Application (ICHVE), Shanghai, China, 17–20 September 2012; pp. 47–50. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Available online: www.comsol.com (accessed on 15 August 2020).
- Integrated Engineering Software, Electro and Oersted. Available online: www.integratedsoft.com (accessed on 15 August 2020).
- Paul, C.R. Analysis of Multiconductor Transmission Lines, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0-470-13154-1. [Google Scholar]
- Da Silva, F.F.; Bak, C.L. Electromagnetic Transients in Power Cables, 1st ed.; Springer: London, UK, 2013; ISBN 978-1-4471-5236-1. [Google Scholar]
- Miano, G.; Maffucci, A. Transmission Lines and Lumped Circuits, 1st ed.; Elsevier Academic Press: Cambridge, MA, USA, 2001; ISBN 978-0-12-189710-9. [Google Scholar]
- Barnett, S. Matrices—Methods and Applications, 1st ed.; Oxford University Press: Oxford, UK, 1990; ISBN 978-0-19-859680-6. [Google Scholar]
- Davis, P.J. Circulant Matrices, 1st ed.; Wiley: Hoboken, NJ, USA, 1979; ISBN 978-0-471-05771-0. [Google Scholar]
- Strutt, J.W. The Theory of Sound; McMillan and Co.: London, UK, 1877. [Google Scholar]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 80, 437–490. [Google Scholar] [CrossRef]
- Cherukupalli, S.; Anders, G.J. Distributed Fiber Optic Sensing and Dynamic Rating of Power Cables, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2019; ISBN 978-1-119-48770-8. [Google Scholar]
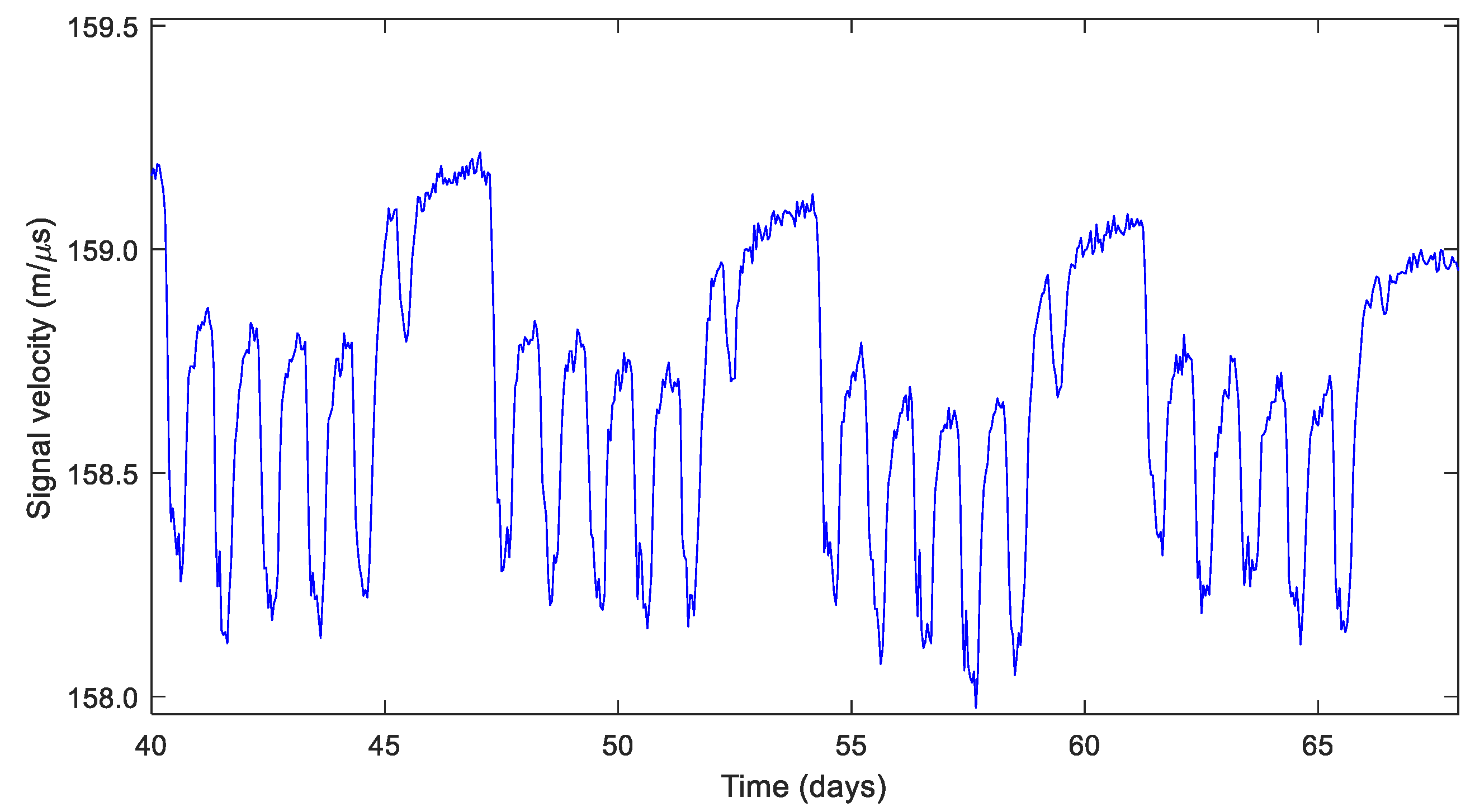
| Author | Temperature | Change Velocity | Rate of Change | Method |
|---|---|---|---|---|
| Dubickas et al., 2006 (Table 1 in [4], v~1/√ε’) | 20–40 °C 40–60 °C | 0.76% 0.92% | 0.038 %/°C 0.046 %/°C | TDR and VNA measurement |
| Li et al., 2015 (estimate from in [5]) | 25–36 °C 25–45 °C | 0.22% 0.90% | 0.020 %/°C 0.045 %/°C | TDR and VNA measurement |
| Nyamupangedengu et al., 2015 1 (abstract of [6]) | 22–58 °C | 4% | 0.11 %/°C | TDR measurement |
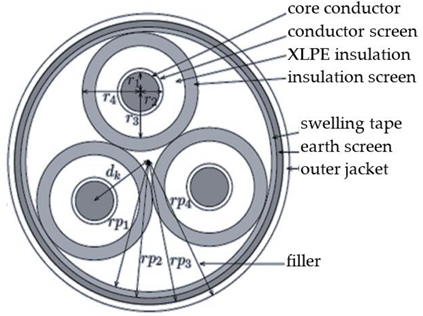
| Parameter | Value |
|---|---|
| radius aluminum conductors, r1 | 8.55 mm |
| radius conductor screens, r2 | 9.35 mm |
| radius XLPE insulation layers, r3 | 12.75 mm |
| radius insulation screens, r4 | 14.00 mm |
| distance conductors to center, dk | 16.16 mm |
| radius filler material, rp1 | 30.15 mm |
| radius swelling tape, rp2 | 30.50 mm |
| radius copper earth screen, rp3 | 31.50 mm |
| outer radius cable jacket, rp4 | 33.00 mm |
| Material Property 1 | Aluminum | Copper | XLPE | Filler | Jacket | Soil |
|---|---|---|---|---|---|---|
| electric resistivity in Ω·m | 2.65 × 10−8 | 1.72 × 10−8 | (∞) | (∞) | (∞) | (100) |
| at reference temperature | 20 °C | 25 °C | ||||
| relative permittivity | 1 | 1 | Figure 5 | 4 | (4) | (10) |
| specific heat capacity in J/kg·K | 900 | 385 | 2581 | 1700 | 1000 | 1470 |
| thermal conductivity in W/m·K | 238 | 400 | 0.29 | 0.26 | 0.19 | 1 |
| density in kg/m3 | 2700 | 8960 | 930 | 1150 | 1300 | 1300 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wouters, P.; van Deursen, A. Thermal Distortion of Signal Propagation Modes Due to Dynamic Loading in Medium-Voltage Cables. Energies 2020, 13, 4436. https://doi.org/10.3390/en13174436
Wouters P, van Deursen A. Thermal Distortion of Signal Propagation Modes Due to Dynamic Loading in Medium-Voltage Cables. Energies. 2020; 13(17):4436. https://doi.org/10.3390/en13174436
Chicago/Turabian StyleWouters, Peter, and Armand van Deursen. 2020. "Thermal Distortion of Signal Propagation Modes Due to Dynamic Loading in Medium-Voltage Cables" Energies 13, no. 17: 4436. https://doi.org/10.3390/en13174436
APA StyleWouters, P., & van Deursen, A. (2020). Thermal Distortion of Signal Propagation Modes Due to Dynamic Loading in Medium-Voltage Cables. Energies, 13(17), 4436. https://doi.org/10.3390/en13174436





