Optimal Design of Multi-Output LLC Resonant Converter with Independently Regulated Synchronous Single-Switched Power-Regulator ^†

Abstract

This paper presents a tightly regulated multi-output isolated converter that employs only an independently regulated synchronous Single-Switched Post-Regulator (SSPR). The proposed converter is a highly accurate single-ended secondary side post-regulator based on a Series Resonant Converter (SRC); furthermore, it has a voltage-doubler characteristic. The proposed post-regulator requires only one auxiliary switch, in contrast with a bulky and expensive non-isolated DC–DC converter. Moreover, the added voltage-doubler can tightly regulate the slave output current. In addition, the voltage-doubler can improve electromagnetic interference characteristics and reduce switching losses arising from the Zero Current Switching (ZCS) operation of all power switches. The validity of the proposed converter is verified using experimental results obtained via a prototype converter applicable to an LED 3D TV power supply.

1. Introduction

Liquid crystal display (LCD) TVs are witnessing a rapid change in backlighting technology, from cold cathode fluorescent lamps (CCFLs) to LEDs. There are several attributes of LEDs that justify this change: improved contrast ratios, mercury-free operation, and relatively low power consumption.

As internal power supply units are used in most LCD TVs, designing slim systems with high-efficiency power supplies at appropriate costs for the LCD TV consumer market continues to present a formidable challenge for the power electronics industry. LCDs are, by far, the most widely produced and sold television display type. LCD screens, which are energy efficient, are available in a wider range of screen sizes than cathode-ray tube and plasma displays. Each of the functional blocks in an LCD TV, such as the audio technology, backlighting, and video and audio signal processors, requires a particular power solution. Therefore, several voltage lines are required to power each of the functional blocks. The backlight is the most power consuming sub-system within a flat TV. Although there are several backlighting technologies, ranging from plasma technology to CCFL, the current trend is towards an LED backlight solution for LCD TVs that allows for slim cabinets. It is challenging for TV manufacturers to select an architecture that allows for design optimization without also increasing cost and circuit complexity. Generally, manufacturers employ a universal power supply that supports a voltage range of AC90–264 V. This allows one power supply design for a specific TV size to be used for a series of models, leading to reduced development costs.

A conventional front-end AC–DC power supply unit for an LCD TV is shown in Figure 1a. In addition, this illustrates the circuit for implementing the primary side inverter of the DC-DC stage. It has three outputs: an LED voltage to power the backlight; 12.8 V for the audio/T-con; and 5 V to power the system. The V_drv line powers the LED driver stage on the panel, then boosts the voltage to a string voltage to drive the three stages (PFC + DC/DC + B/L) of the power system that are needed to drive the lamps, further reducing the AC-to-backlight efficiency. Two additional stages of the power system are required to drive the LED strings: a non-isolated DC–DC boost stage to build up to the LED string voltage, and an LED-dimming current controller to regulate the string current. This can adversely affect the overall system efficiency.

With LCD TVs trending towards slimmer designs, a high end-to-end efficiency is paramount. Adding additional power processing stages limits the overall performance and adds overhead to the drive architecture. Accordingly, efficient and cost-effective LED driver circuits that eliminate intermediate stages have gained increased attention from the industry [1,2,3]. Additionally, with the continuous advancements in LED technology and performance, TV architectures (e.g., LED string voltages and current tolerances) are continuously changing; hence, a modular power supply solution that is easily adaptable to such changes can significantly reduce the design cycle time.

Figure 1 shows a schematic of a conventional multi-output LED driving circuit [4]. The resonant converter controls only one master output, and the slave output is not controllable. To manage this issue, a conventional LED application requires an additional power regulator, e.g., a buck converter or boost converter. However, adding the post-regulator results in increased power dissipation and cost.

Figure 2 shows the primary side of the proposed converter, which is the same as a conventional inductor–inductor–capacitor (LLC) resonator converter. However, the secondary side of the proposed converter consists of a rectifier diode, one output capacitor, and one auxiliary switch, instead of an expensive secondary post-regulator, i.e., boost converter, as shown in Figure 1 [5,6,7,8,9,10,11].

The secondary side of the proposed converter also comprises a single-switched post-regulator with voltage-doubler characteristics as shown in Figure 2, and the proposed voltage doubling method improves the stable cross-regulation performance under the high load conditions of LED Back Light Unit (BLU) power and low load conditions of image power. Thus, one simple control loop can be used to control the LED string currents to further simplify the design. An additional benefit of the proposed scheme is that it can be readily modified for a different number of LED strings/combinations.

In this paper, to overcome the aforementioned drawbacks, high efficiency and cost-effective current balance LED drivers are proposed, as shown in Figure 2. In addition, experimental results are presented to verify the theoretical analysis and effectiveness of the proposed converter.

2. Technical Work Preparation

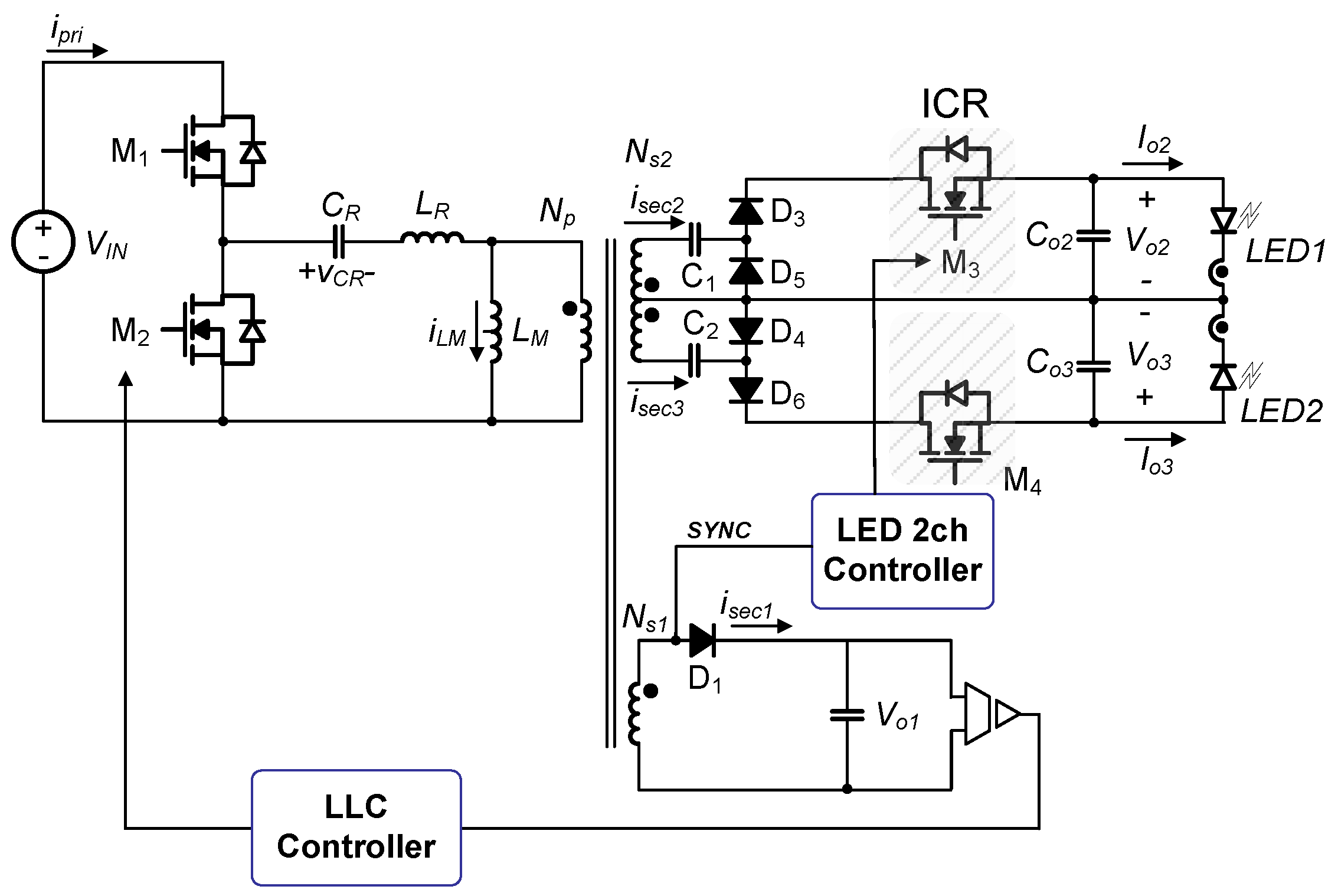
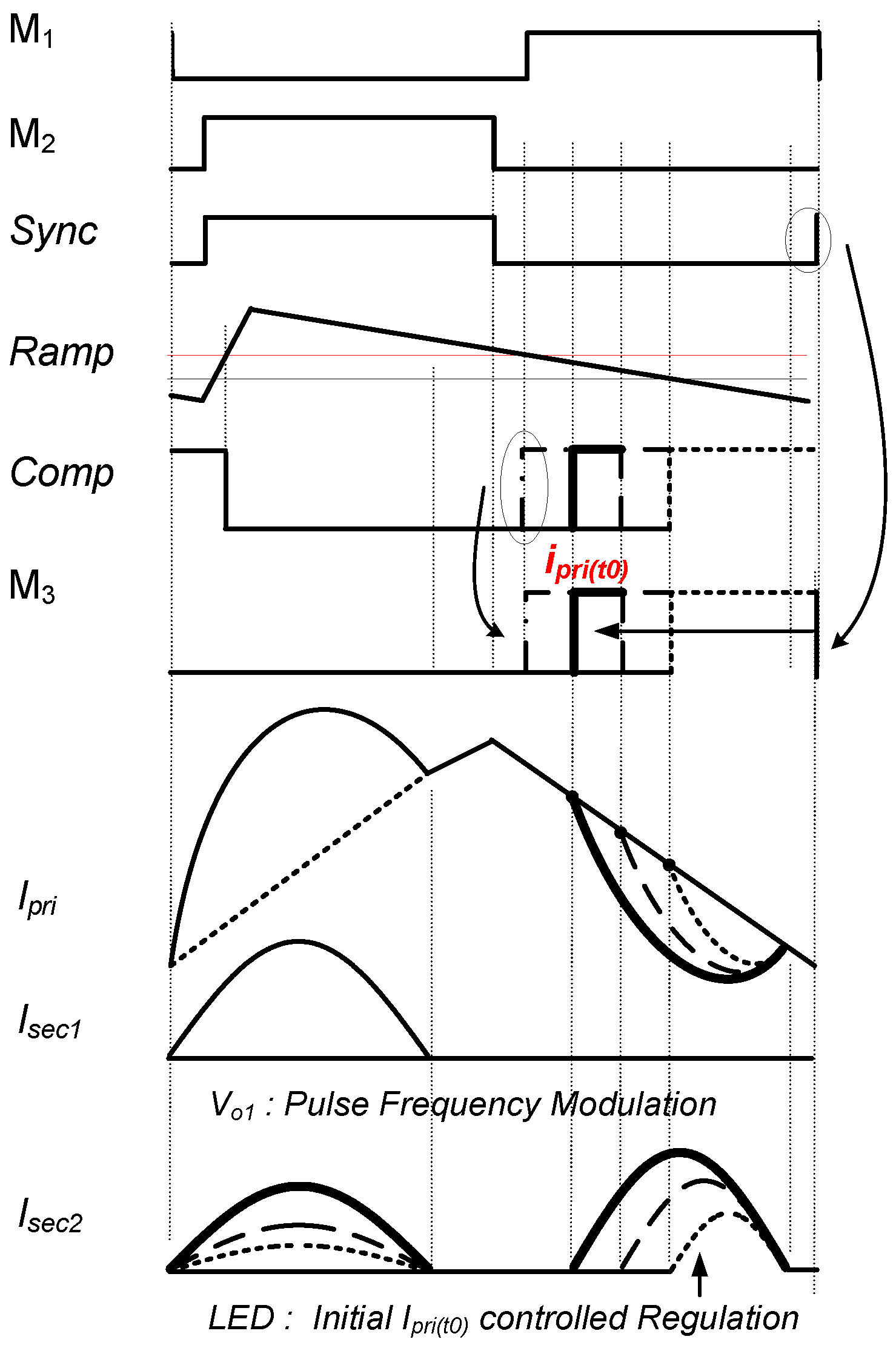
2.1. Control Method for Proposed Converter

The basic concept described in the paper is to supply the rectified secondary current directly driving the LED string and the regulated current to a single series transformer. As shown in Figure 2, the proposed post-regulator should be synchronized with the switching voltage of the secondary winding. Figure 3 shows the manner in which the proposed initial current control regulation is performed for one LED channel. The gating signal of the auxiliary switch is synchronized with the primary side switch to ensure zero voltage switching [12,13,14].

The output voltage V_o1 can be controlled by determining the switching frequencies of M₁ and M₂, as in a conventional LLC resonant converter [15,16,17,18]. However, i_o2 is controlled by the turn-on point of M₃ when M₂ is turned on. That is, although M₂ is conducting and −v_CR is applied to the primary side of the transformer, M₃, which is turned off, prevents the input power from being transferred to the output side. At this time, D₄ and D₅ are turned on and charged to C₁ and C₂, respectively. Therefore, resonance does not occur between C_R and L_R, i_sec2 is maintained at zero, and the initial current I_ini decreases with the slope of −v_CR/(L_R + L_M). When M₃ is turned on with M₁ conducting, the secondary-side diode D₃ is turned on, and simultaneously, the resonant current between C_R and L_R is transferred to the output side of the converter. At this point, in the case that M₃ is turned on earlier, the resonant current i_pri(t) is increased further, owing to the larger initial value I_ini, which causes the output current i_o2 to increase. In contrast, the resonant current i_pri(t) decreases more when M₃ is turned on later.

2.2. Analysis of Operational Modes

The main waveforms are shown in Figure 4. The proposed converter operates in five modes [19] according to the conduction state of each switch (M₁, M₂, and M₃), as shown in Figure 5.

For the expediency of mode analysis in a steady state, several assumptions are made, as follows.

(1)

The switch is ideal, except for the internal diode.

(2)

The transformer is ideal, except for the magnetizing inductance L_m and leakage inductance L_R.

(3)

The output capacitors C_o1 and C_o2 are large enough to be considered as constant DC voltage sources V_o1 and V_o2, respectively.

(4)

The switching transition interval between M₁ and M₂ is small enough to be ignored.

It is assumed that the switch M₁ is conducting before t₀ and that a transformer magnetizing current i_Lm flows through M₁, as shown in Figure 4.

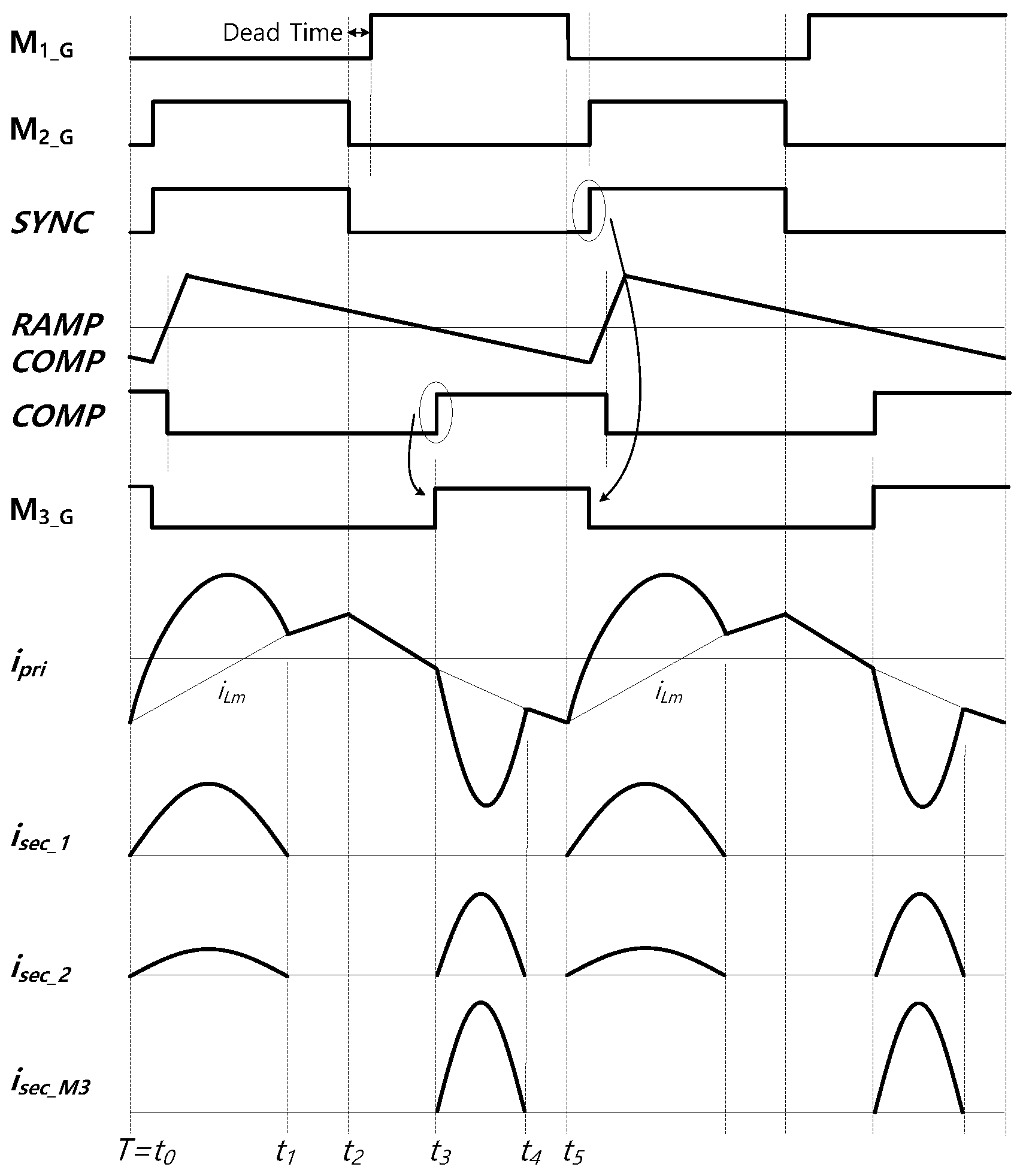
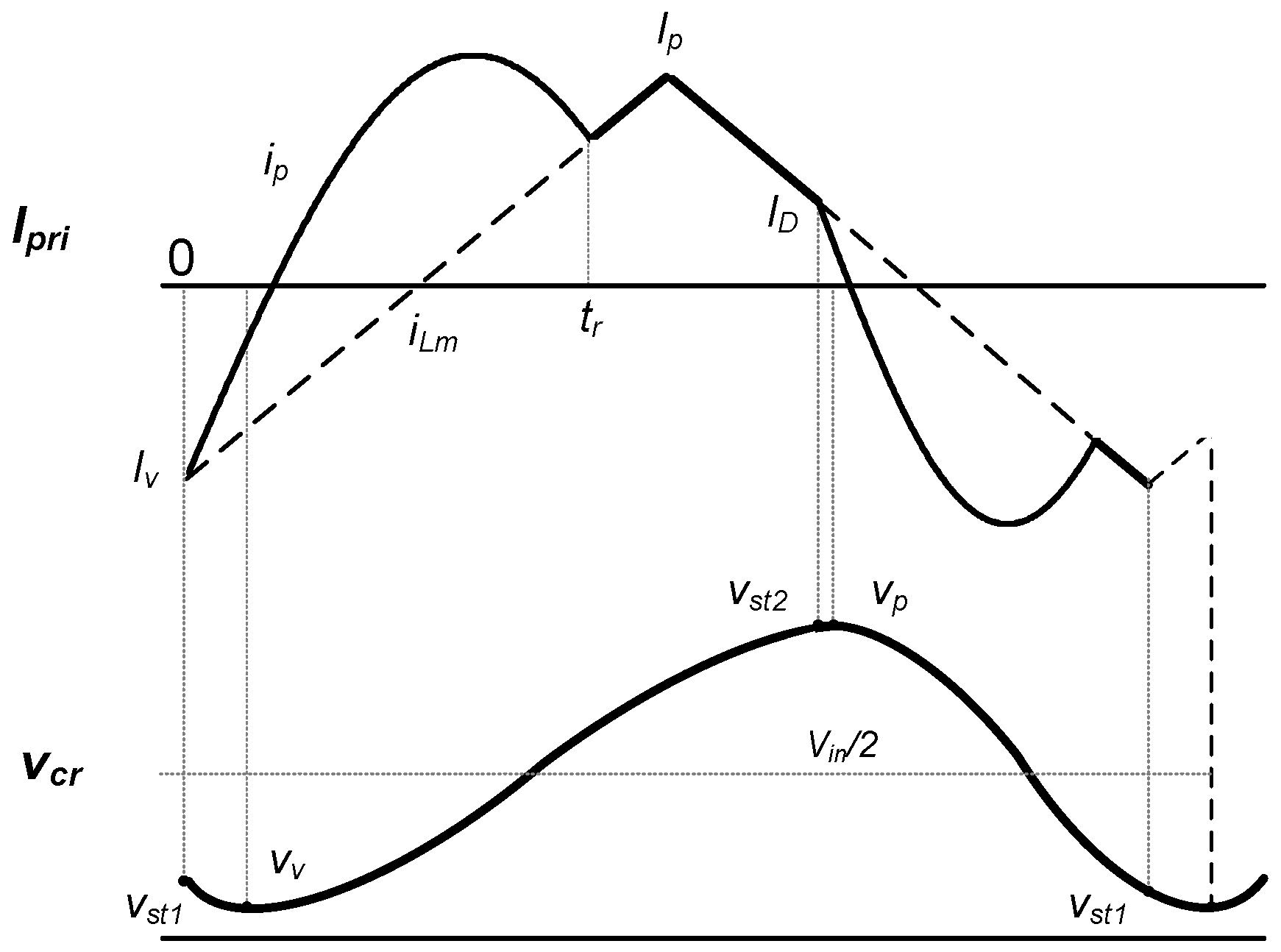
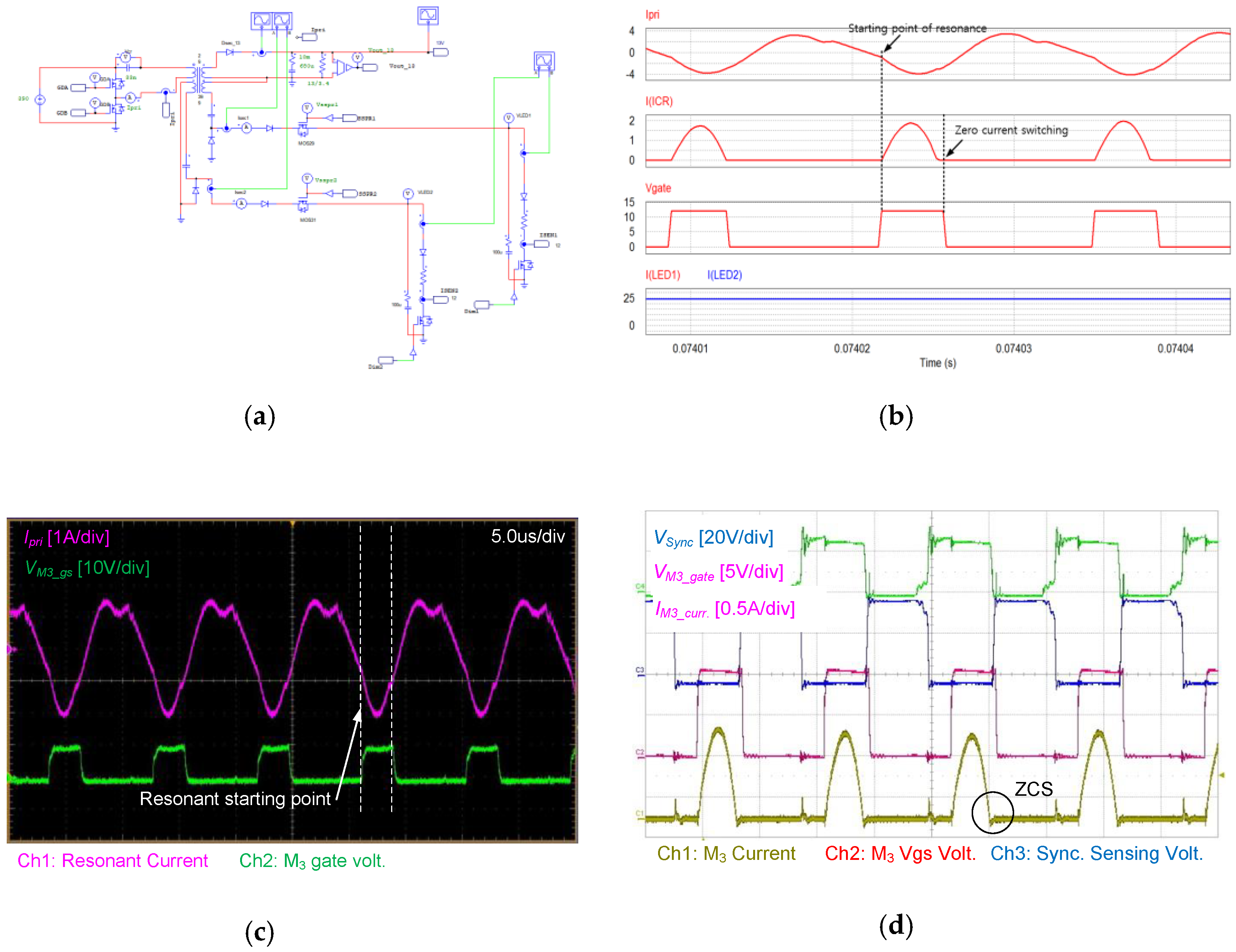
• Mode 1 [t₀–t₁]: This mode starts when M₁ is turned off at t₀. At this moment, the current of the resonant inductor L_R is negative; it will flow through the body diode of M₂, creating a zero-voltage switching (ZVS) condition for M₂. The gating signal of M₂ should be applied during this mode.
  When the current of the resonant inductor L_R flows through the body diode of M₂, I_pri starts to rise. As the voltage V_IN–v_CR across the primary side of the transformer is higher than the reflected output voltage (N_P/N_S1)V_o1, D₁ is turned on.
  Concurrently, the transformer primary current i_pri starts to increase, based on the resonance between C_R and L_R. The magnetic current i_Lm increases linearly as the reflected output voltage (N_P/N_S1)V_o1 is applied to L_m. Therefore, it does not participate in the resonance during this period. In this mode, the circuit operates as a series resonant converter (SRC), with a resonant inductor L_R and resonant capacitor C_R. This mode is terminated when the L_R current is the same as the L_m current.
• Mode 2 [t₁–t₂]: When the transformer primary current i_pri becomes equal to i_LM and i_sec1 reaches zero at t₁, Mode 2 begins. At this moment, D₁ is blocked, and V_IN–v_CR is applied to L_M + L_R. The value of i_pri is still increasing owing to the resonance between C_R and L_M + L_R, as shown in Figure 5c, and the primary current i_pri is still increasing, based on the resonance between C_R and L_m + L_R.
• Mode 3 [t₂–t₃]: When M₂ is turned off and M₁ is turned on at t₂, Mode 3 begins. Although M₁ is conducting and −v_CR is applied to the primary side of the transformer, the turned off M₃ prevents the input power from being transferred to the output side. Therefore, resonance does not occur between C_R and L_R, i_sec2 is maintained at zero, and the initial current I_ini decreases with the slope of −v_CR/(L_R + L_m). The primary current i_pri decreases in the same manner as the resonance between C_R and L_M + L_R.
• Mode 4 [t₃–t₄]: When M₃ is turned on at t₃, Mode 4 starts, as shown in Figure 4. D₃ is turned on because the voltage v_CR is higher than the reflected output voltage (N_P/N_S2)V_o2. Concurrently, the primary current begins to decrease owing to the resonance between C_R and L_R. In addition, the reflected output voltage −(N_P/N_S2)V_o2 is applied to L_M, causing the magnetizing current i_LM to decrease linearly.
• Mode 5 [t₄–t₅]: Mode 5 begins when the primary current i_pri becomes equal to the magnetizing current i_LM, and the secondary current of the transformer, i_sec2, reaches zero at t₄. At this moment, the primary current i_pri is still decreasing owing to the resonance between C_R and L_M + L_R, because D₃ and D₆ are blocked and −v_CR is applied to L_M + L_R, as shown in Figure 5e. If only M₃ and M₄ are turned off after t₅, M₃ and M₄ can be turned off to the Sync signal under the ZCS operation. This mode is terminated when M₁ is switched off at t₅. Then, the operations from t₀ to t₅ are repeated.

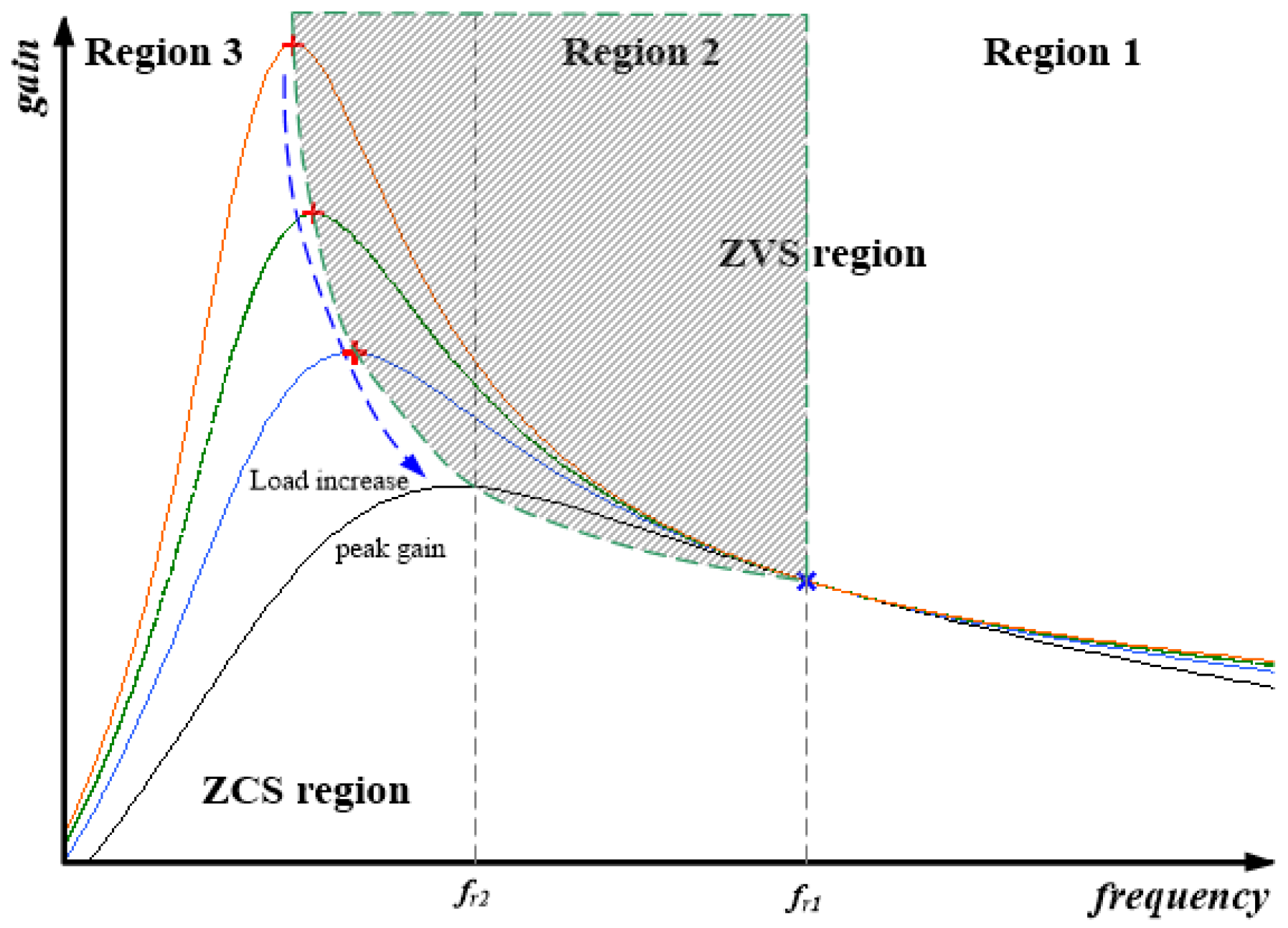
3. Analysis and Simplified Design Guidelines

3.1. Output Voltage Analysis

For convenience of analysis, it is assumed that the dead time between M₁ and M₂ is zero, and that i_LM linearly increases or decreases with the slope of V_o1/n₁L_M or −V_o2/n₂L_M, respectively.

As shown in Figure 6, the steady-state offset current i_LM through L_M can be obtained as:

$$i_{LM}=n_2{I}_{o2}-n_1{I}_{o1}$$

(1)

Here n₁ = N_s1/N_p and n₂ = N_s2/N_p, respectively.

From Equation (1), the values of I_p and I_v can be expressed as follows:

$$I_p=(n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o1}{T}_s}{4n_1{L}_M}$$

(2)

$$I_v=(n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o2}{T}_s}{4n_2{L}_M}$$

(3)

Here, T_s is the switching period.

Moreover, i_LM1 and i_LM2 can be obtained from Equations (4) and (5), as follows:

$$I_{vLM1}(t)=\frac{V_{o1}}{n_1{L}_M}t+((n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o2}{T}_s}{4n_2{L}_M})$$

(4)

$$I_{vLM2}(t)=\frac{V_{o2}}{n_2{L}_M}t+((n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o1}{T}_s}{4n_1{L}_M})$$

(5)

Furthermore, when M₂ is conducting, the difference between i_pri and i_LM1 is transferred to the output side as i_sec1. Similarly, when M₁ is conducting, the difference between i_pri and i_LM2 is transferred to the output side as i_sec2. From Equations (2), (6), and (7), i_sec1 during t₀–t₁ and i_sec2 during t₃–t₄ can be obtained as follows:

$$i_{\sec 1}=\frac{1}{n_1}\left|i_{pri}-i_{LM1}\right|=I_{ini1}\cos \omega t+\frac{V_{crini1}-V_{IN}+V_{o1}/n_1}{\sqrt{L_R/C_R}}\sin \omega t-\left\{\frac{V_{o1}}{n_1{L}_M}t+((n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o2}{T}_s}{4n_2{L}_M})\right\}$$

(6)

$$i_{\sec 2}=\frac{1}{n_2}\left|i_{pri}-i_{LM2}\right|=I_{ini2}\cos \omega t+\frac{V_{crini2}-V_{IN}+V_{o2}/n_2}{\sqrt{L_R/C_R}}\sin \omega t-\left\{\frac{V_{o2}}{n_2{L}_M}t+((n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o1}{T}_s}{4n_1{L}_M})\right\}$$

(7)

In the equations above, ω is the angular frequency.

Therefore, the output load currents I_o1 and I_o2 can be calculated from the mean values of i_sec1 and i_sec2, respectively, as follows:

$$I_{o1}=\frac{1}{n_1{T}_s}{\displaystyle {\int }_o^{t_r}{I}_{ini1}\cos \varpi t+\frac{V_{crini1}-V_{IN}+V_{o1}/n_1}{\sqrt{L_R/C_R}}\sin \varpi t}-\left\{\frac{V_{o1}}{n_1{L}_M}t+((n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o2}{T}_s}{4n_2{L}_M})\right\}dt=\frac{V_{o1}}{R_{o1}}$$

(8)

$$I_{o2}=\frac{1}{n_2{T}_s}{\displaystyle {\int }_o^{t_r-D\prime T_s}{I}_{ini2}\cos \varpi t+\frac{V_{crini2}-V_{IN}+V_{o2}/n_2}{\sqrt{L_R/C_R}}\sin \varpi t}-\left\{\frac{V_{o2}}{n_2{L}_M}t+((n_2{I}_{o2}-N_1{I}_{o1})+\frac{V_{o2}{T}_s}{4n_2{L}_M})\right\}dt=\frac{V_{o2}}{R_{o2}}$$

(9)

Here, D’ is the turn-off duty ratio of the switch M₃.

From Equations (10) and (11), where t_rs = t_r − D’T_s, the output voltages V_o1 and V_o2 can be obtained, as follows:

$$V_{o1}=\frac{\gamma (V_{crinis}-V_{IN})(\cos \varpi t_r-1)}{\left(\frac{n_1{T}_s}{R_{01}}-\frac{\beta }{\omega }\sin \omega t_{rs}-\frac{\gamma }{n_1}\right)\cdot (\cos \omega t_{rs}-1)+\frac{t^2{}_r}{2_{n1}{L}_M}+\alpha t_r}$$

(10)

$$V_{o2}=\frac{\gamma (V_{crinis2}-V_{IN})(\cos \omega t_r-1)}{\left(\frac{n_2{T}_s}{R_{02}}-\frac{\beta }{\omega }\sin \omega t_{rs}-\frac{\gamma }{n_2}\right)\cdot (\cos \omega t_{rs}-1)+\frac{t^2{}_r}{2_{n2}{L}_M}+\beta t_r}$$

(11)

Here, the variables α, β, γ are defined:

$$\begin{gathered} \alpha =-\left(\frac{n_1^2{R}_{o2}-n_2^2{R}_{o1}}{n_1{R}_{o1}{R}_{o2}}+\frac{T_s}{4_{n1}{L}_M}\right) \\ \beta =-\left(\frac{n_1^2{R}_{o2}-n_2^2{R}_{o1}}{n_1{R}_{o1}{R}_{o2}}+\frac{\left(4D^{\prime }-1\right)T_s}{4_{n1}{L}_M}\right) \\ \gamma =\frac{1}{\omega }\sqrt{\frac{C_R}{L_R}} \end{gathered}$$

3.2. Simplified Design Guidelines

The design of resonant components such as L_R, L_M, and C_R always involves a compromise between the maximum load variation, maximum allowable operating frequency deviation, maximum input voltage range, circulating energy in the resonant circuit, and short-circuit characteristics. The optimal operating point of the converter can be reached for a given input voltage and load resistance. Therefore, in practice, a converter is typically designed using operating conditions such as a high resonant frequency and maximum DC-link voltage. In the design of an LLC topology, it is crucial that the manufacturing tolerances of the inductors and capacitors are higher than those in standard productions.

(1)

Switching frequency (f_s)

The switching frequency of the converter is determined based on the total losses of the switches and transformer. Generally, a higher switching frequency selection results in a lower magnetic flux; thus, the core size, as well as the core loss, can be reduced. However, a higher switching frequency also results in a higher AC loss on the winding of the transformer and a turn-off loss on the switches, reducing the converter efficiency. As a result, the selection of the switching frequency is a trade-off between these two effects. The trade-off depends on the power rating, type of semiconductor, and operating range of the converter.

(2)

Resonant tank frequency (f_n)

One goal is to minimize the resistive losses in the duration of the circulating stages of Mode 2 and Mode 5, as shown in Figure 4. This can be achieved by setting the frequency ratio f_n of the switching frequency (f_s) to the resonant frequency of the resonant tank (f_r) smaller than (but close to) unity.

$$f_n=\frac{f_s}{f_r}<1$$

(12)

This frequency ratio is designed such that the converter can be operated at a switching frequency between f_r2 and f_r1, where f_r2 and f_r1 are determined by {(L_M + L_R) and C_R} and {L_R and C_R}, respectively. This operating point is located in Region 2, as shown in Figure 7 [19].

In Figure 7, Region 1 is the SRC operation region. The converter operates in this region when the switching frequency is higher than f_r1. The magnetizing inductance does not participate in the resonance, and a ZVS condition is naturally assured. Region 2 is the multi-resonant converter region. The load condition between f_r1 and f_r2 determines the operation of the converter under ZVS and zero current switching (ZCS) conditions.

In this region, the energy stored in the magnetic components triggers ZVS for the opposite Metal Oxide Semiconductor Field Effect Transistor (MOSFET). Region 3 is an overloaded region. In this area, the converter enters the ZCS mode. In general, the LLC resonant converter is designed to operate in Regions 1 and 2, owing to output regulation and ZVS operation. To ensure ZVS operation, the operating range of the converter should be above f_r2. Therefore, L_R and C_R are chosen to be guaranteed under a heavy load. The selection of L_M determines the switching frequency range and the MOSFET turn-off current. The smaller the value of L_M, the narrower the operating range. However, the MOSFET turn-off current will be higher, increasing the switching loss.

(3)

Magnetizing inductance of the transformer (L_M)

The ZVS operation of the MOSFETs and the ZCS operation of the output auxiliary switches are particularly important for the efficiency and optimal design of the LLC resonant converter. In Figure 6, the primary current is always negative at t₀, ensuring that M₂ operates under a ZVS condition. In addition, M₁ always operates under the ZVS condition, owing to the positive I_p. Therefore, the ZVS condition of the two power switches depends on the magnetizing inductance L_M and dead time duration t_dt, as follows:

$$t_{dt}>\frac{2V_{IN}{C}_{ds}}{I_{p\_\min }},t_{dt}>\frac{2V_{IN}{C}_{ds}}{\left|I_{v\_\min }\right|}$$

(13)

From Equation (6), the limitation of the magnetizing inductance can be derived as follows:

$$L_M\le \frac{t_{dt}}{16C_s{f}_{s\_\max }}$$

(14)

Here, t_dt is the dead time and C_ds is the equivalent capacitance of the MOSFETs.

The magnetizing inductor needs to be small enough to achieve the ZVS condition, and large enough to reduce the turn-off losses. Therefore, in an optimal design, L_M should have the maximum value that meets the ZVS requirement.

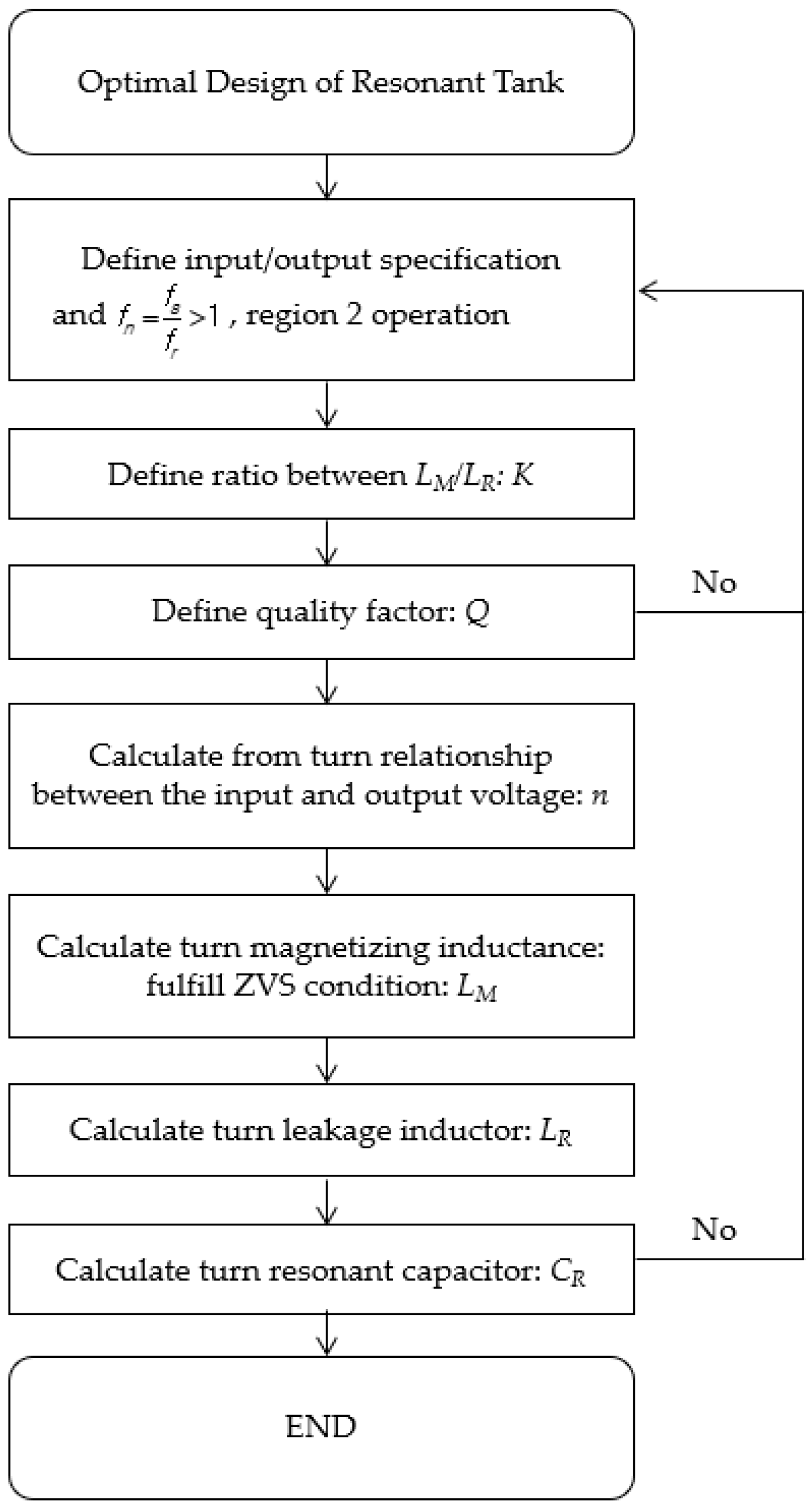
3.3. Optimal Design of the LLC Resonant Converter

Figure 8 shows a flow chart for the optimal design of inductor-inductor-capacitor (LLC) resonance tank. The following is the step-by-step design guide line.

Step 1. Refer to the above “(1) Switching frequency (f_s) (2) Resonant tank frequency (f_n)” and select the switching frequency range. The converter is designed to operate in Region 2 at high and low input voltages to minimize switching loss due to hard-switching. For ZCS operation of the secondary-side output rectifier, switching frequency f_s shall be lower than resonant frequency f_r1. The limit of f_r is defined as follows.

$$f_r=\frac{1}{2\pi \sqrt{L_R{C}_R}}$$

(15)

Step 2. When Q decreases (load decrease) higher peak gains are obtained. In addition, the important factor determining peak gain is the ratio between L_M/L_R. The ratio between L_M/L_R and quality factor is defined as follows.

$$K=\frac{L_M}{L_R}, Q=\frac{\sqrt{L_R/C_R}}{R_{ac}}$$

(16)

Step 3. The turn ratio n should be calculated from the relationship between the input and output voltages.

$$n\ge \frac{V_{in}/2}{V_{o1}+V_f}$$

(17)

Step 4. The magnetizing inductance needs to be small enough to achieve the ZVS condition, and large enough to reduce the turn-off losses. From Equation (14), the limitation of the magnetizing inductance can be derived as:

$$L_M\le \frac{t_{dt}}{16C_s{f}_{s\_\max }}$$

(18)

Step 5. The leakage inductance can be calculated from Equation (15) and as follows:

$$L_R=\frac{Q{R}_{ac}}{2\pi f_r}$$

(19)

Here, n is transformer turns ratio and R_ac is AC equivalent load resistance, $R_{ac}=\frac{8n^2}{{\pi }^2}{R}_o$, $n=\frac{N_P}{N_s}$.

Step 7. The resonant capacitor can be calculated from Equation (15) and as follows:

$$C_R=\frac{1}{2\pi f_{r}Q{R}_{ac}}$$

(20)

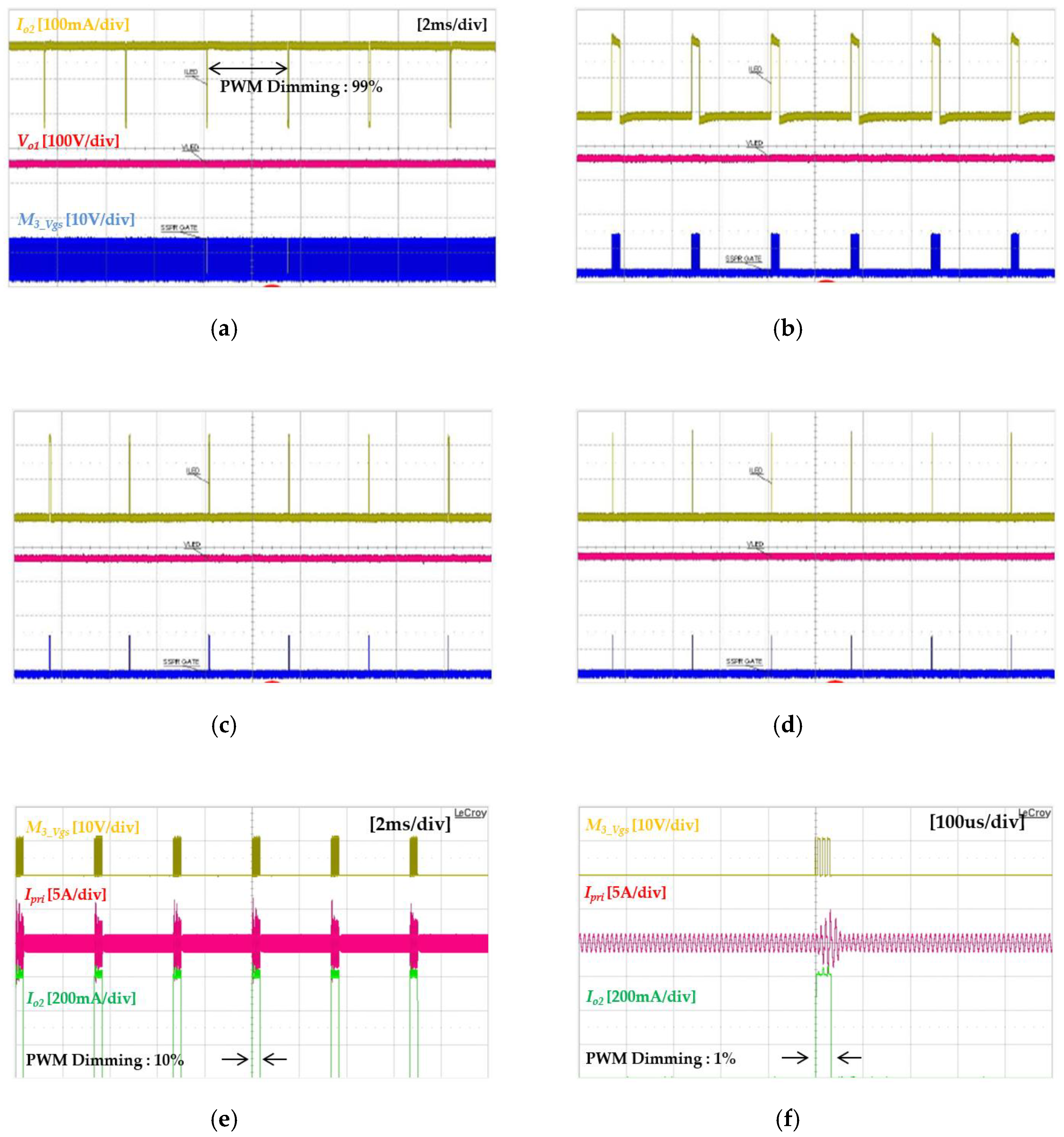
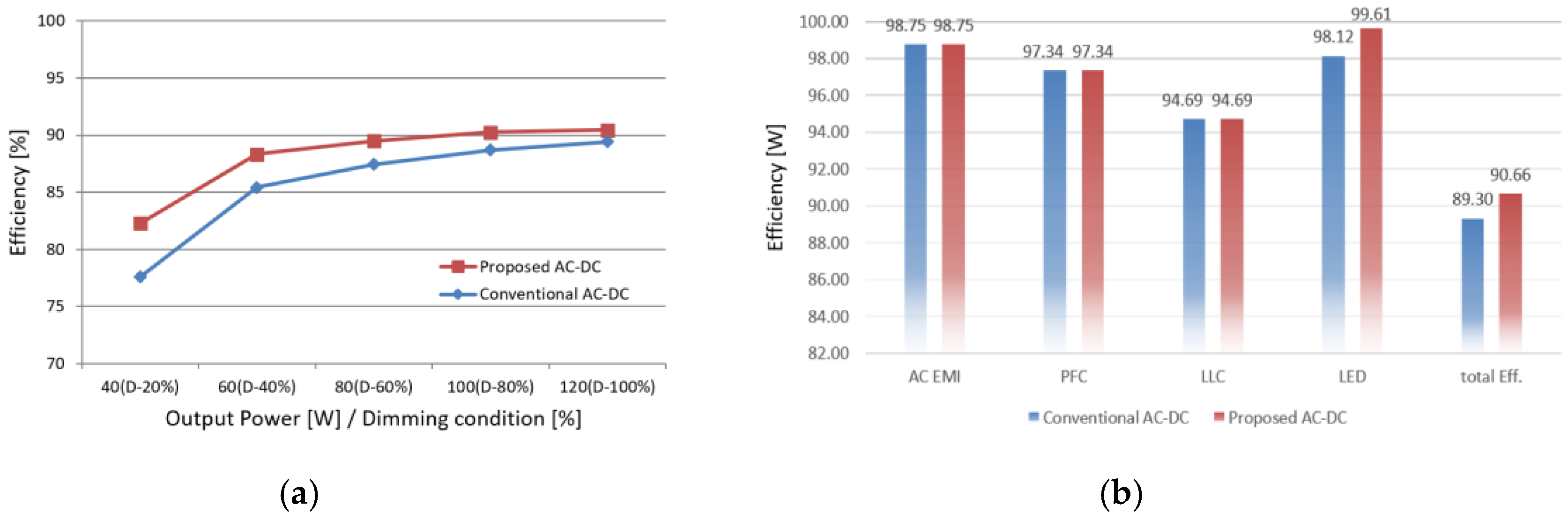
4. Experimental Results

To verify the feasibility of the proposed converter, a prototype of a 120 W output power converter for LED 3D TVs is implemented. The prototype of the proposed LED driver is shown in Figure 9.

Table 1. Design and circuit specification for power system.

Input Voltage, VIN	AC90–264V
Vvisual and Vamp	12.8 V/5.4 A
LED Output (2CH)	2D Mode_100V/240 mA
	3D Mode_122V/630 mA
Output Power, Po,max	120 W
Trans Turn Ratio, NP:NS1:NS2	39:2:32
Resonant Capacitor, Cr	33 nF
Leakage Inductance, Lr	94 uH
Magnetizing inductance, LM	470 uH
LLC Resonant Controller	FA6A00N, Fuji Electric, Japan

shows the design specifications and circuit parameters for the prototype.

Table 2. Comparisons between conventional and proposed converters (2CH).

Item	Conventional Circuit		Proposed Circuit
Rectifier Diode	4EA	SDURF1030 (TO-220)	4EA	SF38G (DO-201A)
Heat Sink	1EA	60 mm × 30 mm × 9 mm	−	−
Power Switch	2EA	AOD9N25 (D-PAK)	2EA	AOD5N40 (D-PAK)
Freewheeling Diode	2EA	MUR460 (DO-201A)	−	−
Elec. Capacitor	2EA	68 uF/160 V	−	−
	2EA	33 uF/200 V	2EA	47 uF/200 V
Film Capacitor	−	−	2EA	100 nF/330 V
Inductor	2EA	EFD2020	−	−

shows a comparison between the conventional and proposed circuits, in terms of the number of components. As shown in Table 2, the proposed converter has fewer components than the number of components in the conventional converter owing to the absence of the additional non-isolated DC-DC converter.

Figure 10 shows the ZCS operating waveforms of the proposed converter; when M₃ is turned on, the resonant current of the primary side starts flowing. It is clear that ZCS is ensured, based on the zero current at the end of the ICR switching.

Figure 11 shows the experimental waveforms at 2D (99%, 10%, 1%, and 0.2%) and 3D (10% and 1%) dimming ratios. As shown in Figure 11, the LED current becomes zero for the low dimming signal, and it is exactly controlled to be 2D_210 mA and 3D_630 mA for the high dimming signal. Moreover, although the proposed LED driver comprises only a few components, the current through the LED array is well-controlled and balanced according to all of the dimming ratios.

Based on Table 1, Figure 12 shows the total efficiency of the power system from AC to the final LED backlight (AC EMI + PFC + DC/DC + LED backlight driver) and the efficiency of each stage is also compared. Efficiency measurements are efficiency data according to LED dimming conditions as shown in Figure 11. This is a measure of operating from dark to full brightness on a TV screen. Assuming that the components not specified in Figure 12 have similar power consumptions, the proposed driver shows a lower consumption by approximately 1.74 W power loss than the conventional driver.

Probably of the most importance is the high efficiency with this LLC topology that allows slim power supply designs. LED string current control is achieved using the LLC resonant half bridge topology in current mode control. Typical efficiency for the proposed converter in TV application is shown in Figure 12; the total efficiency from AC to backlight can be achieved by more than 90% with this architecture.

5. Conclusions

In this paper, optimal design of a multi-output LLC resonant converter with an independently regulated synchronous single-switched power-regulator is proposed. As an isolated DC-DC converter and LED drivers are integrated into one power stage in the proposed LED driver system, it consists of two cascaded power stages. The proposed post-regulator requires only one auxiliary switch, in contrast with a bulky and expensive non-isolated DC-DC converter

Through the analysis of the control method for the proposed converter, the simplified design guidelines and magnetizing inductance are designed to obtain soft switching capability. The proposed driver system features a relatively low cost, simple structure, high efficiency, and high power density. In addition, it can ensure the ZVS operation of power switches and the ZCS operation of output auxiliary switches along the entire load range. It has highly desirable advantages, such as reduced switching losses and heat generation.

Finally, through the experimental results it can be seen that very fast LED rise and fall currents can be achieved with this control scheme that allow excellent linearity performance under any dimming conditions. The proposed converter is simple and achieves excellent dimming current control between multiple outputs, and the highest AC to backlight efficiency. The PSIM simulation and experimental results using the prototype converter verified the validity of the proposed architecture.