A Generalized Approach to the Steady-State Efficiency Analysis of Torque-Adding Transmissions Used in Renewable Energy Systems

Abstract

The paper presents a general approach to the steady-state efficiency analysis of one degree of freedom (1-DOF) speed increasers with one or two inputs, and one or two outputs, applicable to wind, hydro and marine-current power generating systems. The mechanical power flow, and the efficiency of this type of complex speed increasers, are important issues in the design and development of new power-generating systems. It is revealed that speed increases, with in-parallel transmission of the mechanical power from the wind or water rotors to the electric generator, have better efficiency than serial transmissions, but their efficiency calculus is still a challenging problem, solved in the paper by applying the decomposition method of complex speed increasers into simpler component planetary gear sets. Therefore, kinematic, steady-state torque and efficiency equations are derived for a generic 1-DOF speed increasers with two inputs and two outputs, obtained by connecting in parallel two gear mechanisms. These equations allow any speed increaser to be analysed with two inputs and one output, with one input and two outputs, and with one input and one output. We discuss a novel design of a patent-pending planetary-gear speed increaser, equipped with a two-way clutch, which can operate (in combination with the pitch adjustment of the rotors blades) in four distinct configurations. It was found that the mechanical efficiency of this speed increaser in the steady-state regime is influenced by the interior kinematic ratios, the input-torque ratio and by the meshing efficiency of its individual gear pairs. The efficiency of counter-rotating dual-rotor systems was found to be the highest, followed by systems with counter-rotating electric generator, and both have higher efficiency than conventional systems with one rotor and one electric generator with fixed-stator.

1. Introduction

Among the renewable energy technologies, hydro and wind energy conversion systems currently have the largest share of electrical power generation worldwide [1,2]. While, hydro-electric power is a more mature technology, improvements to wind, tidal-stream and marine-current energy conversion systems are reported every year [3,4]. The major research has looked at energy-conversion efficiency for the purpose of maximizing the use of the onsite renewable potential. Moreover, in the case of wind and hydro-power systems of medium and high capacity, power is transmitted from the wind or water turbine to the electric generator via a speed increaser, which amplifies the speed of the turbine shaft approximately three times in case of hydro-electric systems, and by around one hundred in case of wind power systems [5,6,7]. The best performing speed increasers in use, are one degree of freedom (1-DOF) or two degrees of freedom (2-DOF) planetary transmissions, which achieve higher efficiency, higher transmission ratios and smaller overall sizes than fixed-axis transmissions. However, these benefits come with added complexity, making the respective transmissions more difficult to design and optimize.

Many innovative solutions of wind and tidal turbines have been proposed in recent years (Figure 1), such as counter-rotating rotors [8,9,10,11,12,13,14,15,16,17,18,19], high-performance mechanical transmissions [3,20] and more compact and efficient electric generators, including the counter-rotating type [21,22]. Shin [8] proposed a large capacity wind turbine that uses multiple, smaller rotors in a spatial arrangement and a high-efficiency planetary speed increaser. Wacinski [11], Brander [12], Climescu et al. [13] and Oprina et al. [16] proposed different solutions of horizontal-axis wind turbines with two coaxial, counter-rotating rotors. Didane et al. [15,19] and West [18] evaluated the performance of new concepts of vertical-axis wind turbines with counter-rotating coaxial rotors. Designers of counter-rotating turbines (CRT) have resorted to a wide variety of innovative solutions of speed increasers, such as variable transmissions [23], differential transmissions with electric motor speed control [24], or novel planetary gears [25,26,27,28]. In spite of their larger size and lower efficiency, compared to their planetary counterparts, the most common solution of speed increasers implemented in wind, hydro and marine-current power generating systems, including of the CRT type, are fixed-axis gear mechanisms [29,30,31].

Planetary speed increasers are more appropriate for CRT applications because they ensure higher kinematic ratios and reduced overall size, at higher efficiency levels [11,13,25,26,32,33,34,35,36,37,38,39,40,41]. Furthermore, CRTs can employ 2-DOF transmissions to sum the input speeds [35,39] or 1-DOF planetary transmissions to sum the input torques of their two rotors [40,41]. The first type of speed increaser has been studied in conjunction with CRT and conventional generator [42,43,44,45,46,47,48], or with CRT and counter-rotating electric generator [41]. No generalization has been proposed. Rather, particular designs have been presented and analysed with respect to their performance. The 1-DOF planetary speed increasers with multiple inputs and outputs can operate both, with single or with counter-rotating wind or water rotors, and with conventional (fixed stator) or counter-rotating, (moving stator) electric generator [49,50,51]. Efficiency analysis of the mechanical transmissions used in wind, tidal-stream and marine-current energy conversion systems is an essential part of their design and development process [52,53].

Based on the literature survey, the authors concluded that a comprehensive analysis of two-input, one degree of freedom planetary transmissions applicable to wind and water turbines is necessary, aiming to model the speed increaser efficiency in steady-state regime.

The paper proposes a generic class of 1-DOF transmissions, with two inputs and two outputs, employing two planetary gear mechanisms connected in parallel. All four possible combinations, i.e., with one or two input rotors, and with one or two generator outputs can be obtained as particular cases. In Section 2, steady-state torque and efficiency equations are derived for this generic speed increaser class with two inputs and two outputs. Three other types of speed increasers, i.e., with two inputs and one output, with one input and two outputs, and with one input and one output are discussed in Section 3 as particular cases. A novel planetary speed increaser with cylindrical gears, which can operate in four variants by means of a two-way clutch [54], is analysed in Section 4 using bivariate three-dimensional (3D) plots. The paper ends with a summary of results and conclusions.

The main contributions of this paper involve the proposed 1-DOF speed increaser class that can operate in four functional cases. To the best of our knowledge, it is the first unifying modeling of transmission performance in different functional cases. The application example is done for a novel design of a patent-pending transmission [54]. The performance study of the transmission is outlined in this paper by using bivariate plots.

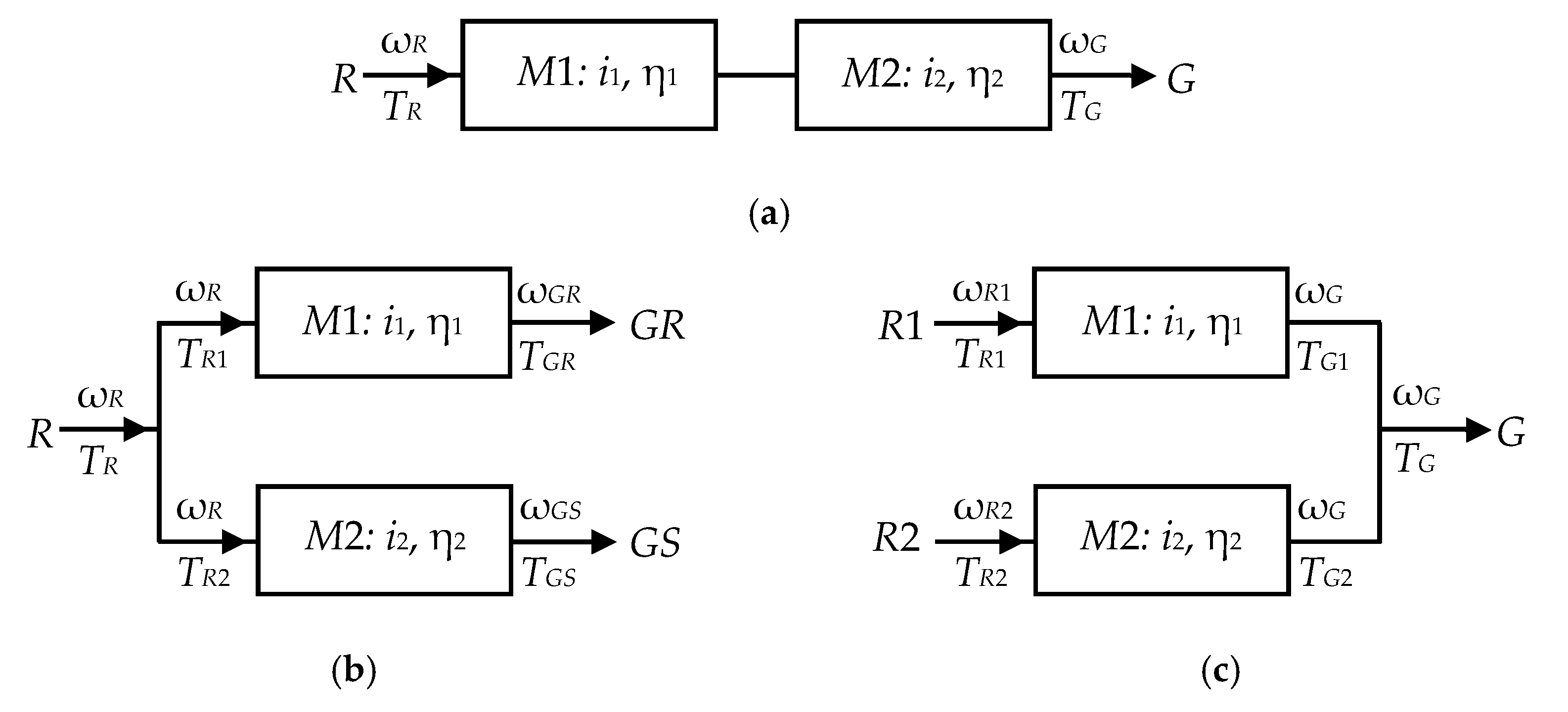
2. Problem Formulation

It is known that mechanical transmissions where power is transmitted in parallel, also known as split-power transmissions, have higher efficiency than transmissions formed with mechanisms connected in series [51]. The same applies to speed increasers used in wind, hydro and marine-current power generating systems that integrate two counter-rotating wind or water rotors and/or one counter-rotating electric generator. A 1-DOF transmission consisting of two 1-DOF mechanisms M1 and M2 is assumed, providing serial (Figure 2a) or in-parallel transmission (Figure 2b,c) of the mechanical power from one rotor (R) or from two counter-rotating rotors (R1 and R2) to a standard electric generator (G) with a fixed stator, or to a generator with counter-rotating rotor (GR) and moving stator (GS). Mechanisms M1 and M2 are characterized by their kinematic ratios i₁ and i₂, and efficiencies η₁ and η₂. Each shaft x has an angular velocity ω_x and transmits a torque T_x (where x is either R, R1, R2, G, GR or GS).

As explained in references [26,40,51], the efficiencies of the 1-DOF mechanical transmissions have been determined in closed-form, from kinematic, torque equilibrium and energy conservation considerations using Maple computer algebra system.

The efficiencies of the 1-DOF mechanical transmissions in Figure 2 are calculated as follows.

• Case A (Figure 2a): speed increaser with one input (R) and one output (G) for which,

  $${\omega }_G=\frac{{\mathsf{\omega }}_R}{i_1{i}_2}; T_G=-i_1{i}_2{\mathsf{\eta }}_1{\mathsf{\eta }}_2{T}_R$$

  (1)

  the efficiency is:

  $${\mathsf{\eta }}_A=\frac{-P_G}{P_R}=\frac{-T_G\cdot {\mathsf{\omega }}_G}{T_R\cdot {\mathsf{\omega }}_R}={\mathsf{\eta }}_1{\mathsf{\eta }}_2$$

  (2)
• Case B (Figure 2b): speed increaser with one input (R) and two outputs (GR and GS) with:

  $${\mathsf{\omega }}_{GR}=\frac{{\mathsf{\omega }}_R}{i_1}; {\mathsf{\omega }}_{GS}=\frac{{\mathsf{\omega }}_R}{i_2}; {\mathsf{\omega }}_G={\mathsf{\omega }}_{GR}-{\mathsf{\omega }}_{GS}=\frac{i_2-i_1}{i_1{i}_2}{\mathsf{\omega }}_R$$

  (3)

  $$T_{R1}=-\frac{T_{GR}}{i_1{\mathsf{\eta }}_1}; T_{R2}=-\frac{T_{GS}}{i_2{\mathsf{\eta }}_2}; T_R=T_{R1}+T_{R2}$$

  (4)

Knowing that the torques transmitted to the rotor and to the moving stator of the electric-generator are equal but of opposite signs (T_GS = ‒T_GR), the torque T_G = T_GR and mechanical power T_G ω_G delivered to the electric generator are:

$$T_G=T_R\frac{i_1{i}_2{\mathsf{\eta }}_1{\mathsf{\eta }}_2}{i_1{\mathsf{\eta }}_1-i_2{\mathsf{\eta }}_2} \mathrm{and} T_G\cdot {\mathsf{\omega }}_G={\mathsf{\eta }}_1{\mathsf{\eta }}_2\frac{i_2-i_1}{i_1{\mathsf{\eta }}_1-i_2{\mathsf{\eta }}_2}{T}_R\cdot {\mathsf{\omega }}_R$$

(5)

These equations allow the efficiency of the transmission to be calculated as:

$${\mathsf{\eta }}_B=\frac{-P_G}{P_R}=\frac{-T_G\cdot {\mathsf{\omega }}_G}{T_R\cdot {\mathsf{\omega }}_R}={\mathsf{\eta }}_1{\mathsf{\eta }}_2\frac{i_1-i_2}{i_1{\mathsf{\eta }}_1-i_2{\mathsf{\eta }}_2}$$

(6)

• Case C (Figure 2c): speed increaser with two inputs (R1 and R2) and one output (G).

  $${\mathsf{\omega }}_G=\frac{{\mathsf{\omega }}_{R1}}{i_1}=\frac{{\mathsf{\omega }}_{R2}}{i_2}; {\mathsf{\omega }}_{R2}=\frac{i_2}{i_1}{\mathsf{\omega }}_{R1}$$

  (7)

  $$T_{G1}=-i_1{\mathsf{\eta }}_1{T}_{R1}; T_{G2}=-i_2{\mathsf{\eta }}_2{T}_{R2}; T_G=T_{G1}+T_{G2}$$

  (8)

  $$T_G\cdot {\mathsf{\omega }}_G=-\frac{i_1{\mathsf{\eta }}_1{T}_{R1}+i_2{\mathsf{\eta }}_2{T}_{R2}}{i_1}{\mathsf{\omega }}_{R1}$$

  (9)

  from where the efficiency of the transmission is calculated as:

  $${\mathsf{\eta }}_C=\frac{-P_G}{P_R}=\frac{-T_G\cdot {\mathsf{\omega }}_G}{T_{R1}\cdot {\mathsf{\omega }}_{R1}+T_{R2}\cdot {\mathsf{\omega }}_{R2}}=\frac{i_1{\mathsf{\eta }}_1-i_2{\mathsf{\eta }}_2{k}_t}{i_1-i_2{k}_t}$$

  (10)

  where k_t is the input torque ratio:

  $$k_t=-\frac{T_{R2}}{T_{R1}}$$

  (11)

Assuming for convenience that the two component mechanisms M₁ and M₂ have equal efficiencies (η₁ = η₂ = η) Equations (2), (6) and (10) become:

$${\mathsf{\eta }}_A={\mathsf{\eta }}_{}^2; {\mathsf{\eta }}_B={\mathsf{\eta }}_{}; {\mathsf{\eta }}_C={\mathsf{\eta }}_{}$$

(12)

Equation (12) suggests that if mechanisms M₁ and M₂ have comparable efficiencies, the use of counter-rotating wind or water rotors, or of counter-rotating generator, results in better efficiencies compared to serial arrangements i.e., η_B > η_A and η_C > η_A. In the next section, a general model for the efficiency analysis of a class of 1-DOF planetary speed increasers with two inputs and two outputs, consisting of two in-parallel planetary gear sets will be presented.

3. Generalized Speed and Steady-State Torque Equations for 1-DOF Speed Increasers with Two Inputs and Two Outputs

Figure 3 shows a general case of a 1-DOF speed increaser with two inputs and two outputs, obtained by connecting in parallel two planetary gear sets M1 and M2. The main input will be from the primary wind or water-turbine rotor R1, while the main output will be the generator rotor GR. The two planetary gear sets are connected through two links, one to the frame (i.e., body 0), and the second to both the secondary input-rotor R2 and to stator GS of the electric generator. The other input is connected to the primary rotor R1, while the electric generator rotor (GR) is connected to the other output.

With either the sun gear or planet carrier hold fixed to the frame, the two planetary gear sets M1 and M2 become 1-DOF mechanisms. Due to the constraints introduced by connecting the output of M1 to the input of M2, the speed increaser with two inputs and two outputs (L = 4) will have one degree of freedom.

Four functional variants of the 1-DOF speed increaser in Figure 3 are possible, depending on how the inputs and the outputs of the mechanism are activated:

(1)

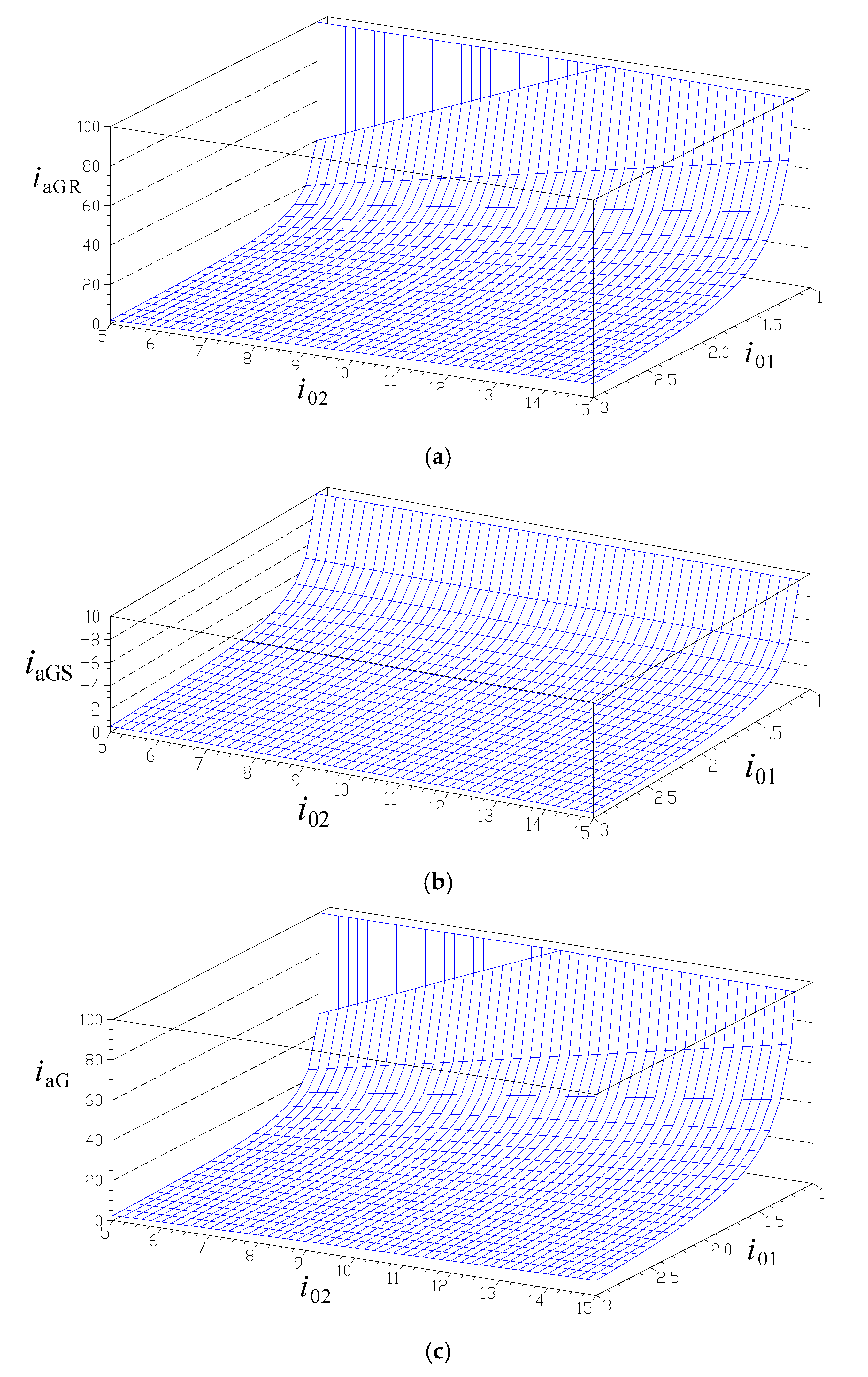
Variant V1: where both inputs R1 and R2, and both outputs GR and GS are active (L = 4). A system with two counter-rotating rotors and one counter-rotating electric generator is obtained.

(2)

Variant V2: where both inputs R1 and R2 and the electric-generator output GR are active (L = 3). In this case, a system with two counter-rotating rotors and a standard electric generator with ω_GS = 0 is obtained.

(3)

Variant V3: where the main input R1 and both outputs are active (L = 3), case in which a system with one rotor (T_R1 ≠ 0 and T_R2 = 0) and one counter-rotating electric generator is obtained.

(4)

Variant V4: where only the main input R1 and the main output to the generator rotor GR are active (L = 2). This results in a system with one rotor (T_R1 ≠ 0 and T_R2 = 0) and a standard electric generator with ω_GR ≠ 0 and ω_GS = 0.

A 1-DOF mechanism with two inputs and two outputs (L = 4) is characterized by the following kinematic and static properties [51]:

(1)

It has one independent external angular velocity, with ω_R1 assumed the independent kinematic parameter;

(2)

It has three angular-velocity transmission functions, i.e., three of the external angular velocities depend on the independent velocity i.e., ω_R2 = ω_R2 (ω_R1), ω_RG = ω_RG (ω_R1), ω_GS = ω_GS (ω_R1);

(3)

It has one torque-transmission function T_R1 = T_R1 (T_R2, T_GR, T_GS) i.e., one dependent external torque (the primary rotor torque T_R1) and three independent external torques i.e., T_R2, T_GR and T_GS.

It is also known that these transmission functions are linear, except for non-circular gears. As a result, the transmission functions for angular velocities can be written as,

$${\mathsf{\omega }}_{GR}=a\cdot {\mathsf{\omega }}_{R1}; {\mathsf{\omega }}_{R2}=b\cdot {\mathsf{\omega }}_{R1}; {\mathsf{\omega }}_{GS}=c\cdot {\mathsf{\omega }}_{R1}$$

(13)

where coefficients a, b and c are constant, and have meanings of kinematic ratios. The dependent torque T_R1 can be written as,

$$T_{R1}=A\cdot T_{GR}+B\cdot T_{R2}+C\cdot T_{GS}$$

(14)

where coefficients A, B and C are also constant and have meanings of torque ratios.

The counter-rotating electric generator is characterized by the relative angular velocity ω_G between the rotor and the stator, and by the property that the rotor torque T_GR and the stator torque T_GS are equal and of opposite signs:

$${\mathsf{\omega }}_G={\mathsf{\omega }}_{GR}-{\mathsf{\omega }}_{GS}=\left(a-c\right){\mathsf{\omega }}_{R1}; T_{GS}=-T_{GR}$$

(15)

The efficiency η of a 1-DOF speed increaser with two inputs and two outputs is defined as the ratio between the sum of output powers over the sum of input powers. Since efficiency must be positively, and since the output powers of a mechanism are always negative, the efficiency equation writes,

$$\mathsf{\eta }=-\frac{{\mathsf{\omega }}_{GR}{T}_{GR}+{\mathsf{\omega }}_{GS}{T}_{GS}}{{\mathsf{\omega }}_{R1}{T}_{R1}+{\mathsf{\omega }}_{R2}{T}_{R2}}$$

(16)

or by using coefficients a, b, c, A, B and C it becomes:

$$\mathsf{\eta }=-\frac{a-c}{A-C}\frac{T_{R1}-B{T}_{R2}}{T_{R1}+b{T}_{R2}}.$$

(17)

The input-torque ratio k_t in Equation (11) varies from zero (i.e., T_R2 = 0) to a maximum value, depending on the geometry of the two rotors R1 and R2, where the most common method of changing torque T_R2 is to adjust the pitch angle of the rotor blades. The efficiency of the above four variants V1 … V4 can be obtained by considering particular forms of Equations (11) and (17) as follows:

For variant V1 with two inputs (R1, R2) and two outputs (GR, GS):

$${\mathsf{\eta }}_{V1}=-\frac{\left(a-c\right)\left(1+k_{t}B\right)}{\left(A-C\right)\left(1-k_{t}b\right)}$$

(18)

For variant V2 with two inputs (R1, R2) and one output (GR), i.e., ω_GS = 0:

$${\mathsf{\eta }}_{V2}=-\frac{a\left(1+k_{t}B\right)}{A\left(1-k_{t}b\right)}.$$

(19)

For variant V3 with one input (R1), i.e., k_t = 0, and two outputs (GR, GS):

$${\mathsf{\eta }}_{V3}=-\frac{a-c}{A-C}$$

(20)

For variant V4 with one input (R1), i.e., k_t = 0, and one output (GR), i.e., ω_GS = 0:

$${\mathsf{\eta }}_{V4}=-\frac{a}{A}$$

(21)

Coefficients a, b, c and A, B, C in Equations (18)–(21) can be determined by applying the principle of superposition. An example on how these coefficients can be determined for the case of a planetary speed increaser with cylindrical gears will be presented next.

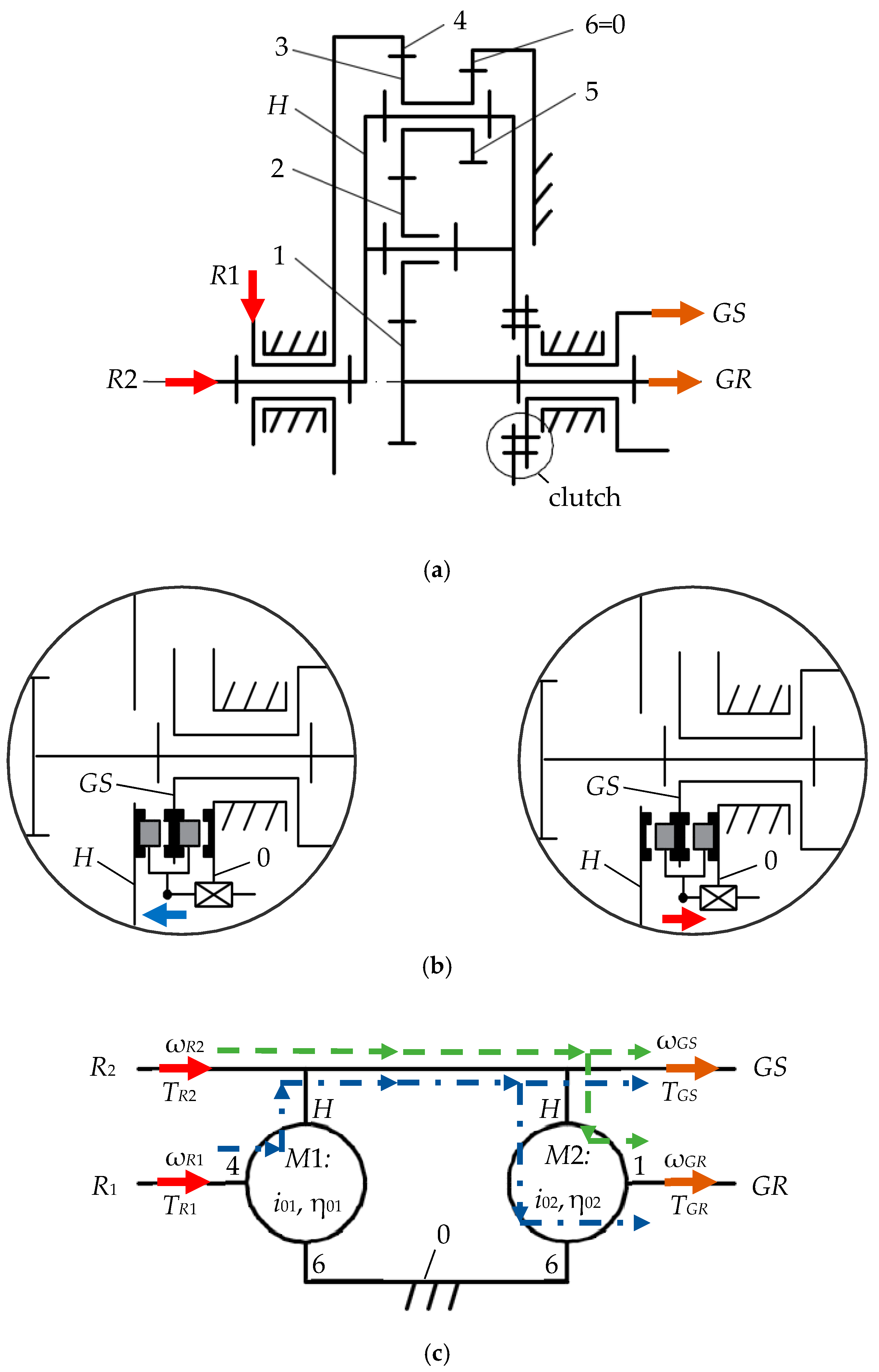
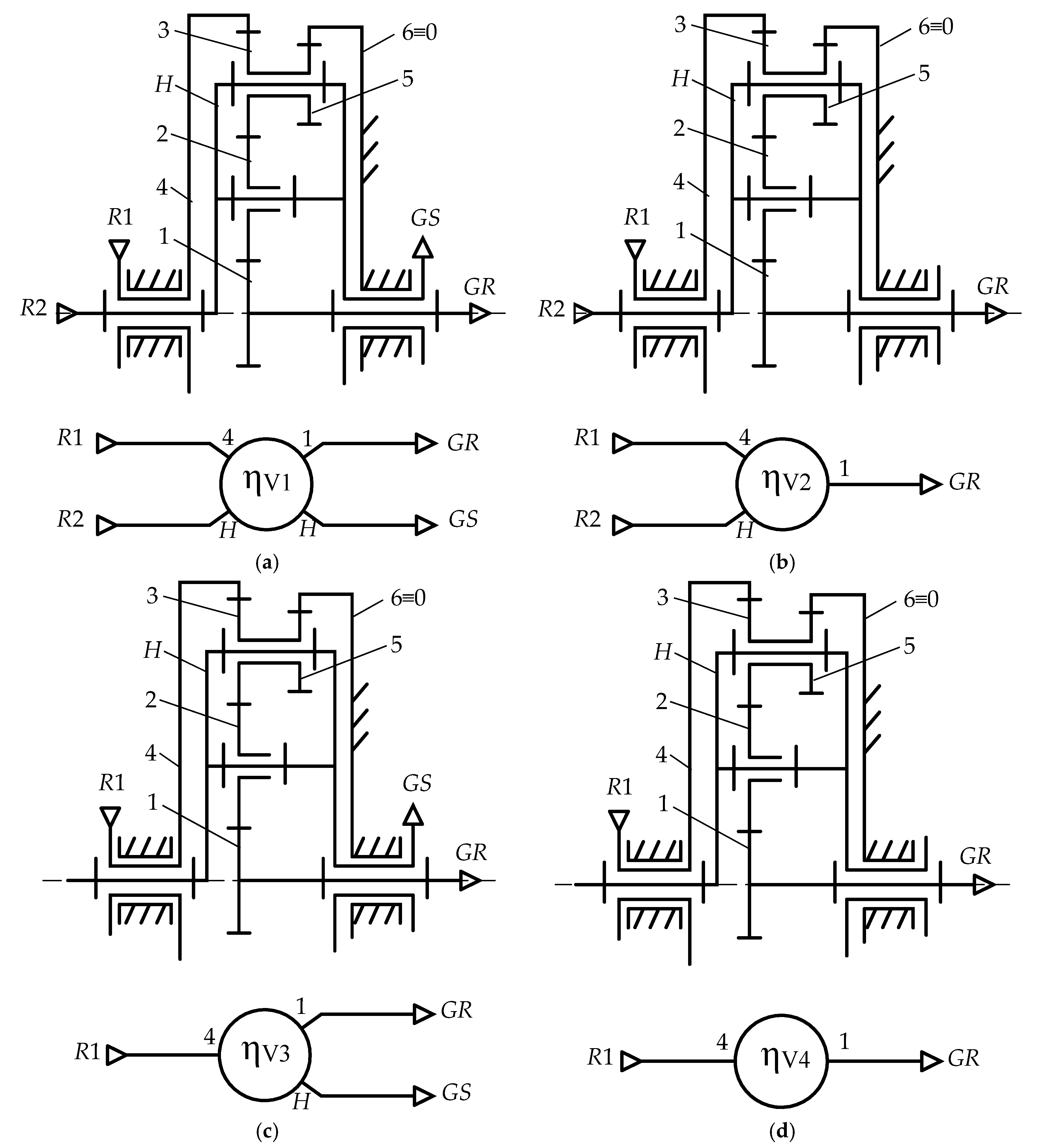
4. Case Study Analysis

In this section, a novel cylindrical-gear planetary speed increaser will be considered. Its unique feature is that the input and output motions have opposite directions, provided by planet gear 2 in series with planet gear 3 (see Figure 4a).

Ring gear 4, connected to the primary rotor R1 is the main input, and meshes with planet gear 3, while the secondary input is the planet carrier H. Ring gear 6 which is fixed, meshes with gear 5 of the compound planet 3–5. Sun gear 1 is connected to the electric-generator rotor (GR), while its stator is connected to carrier H through a two-way clutch. This clutch allows the transmission of the mechanical power to output shafts GS and GR (see Figure 4b-left) or, by holding fixed the stator of the electric generator, to output GR only (see Figure 4b-right).

According to the block diagram in Figure 4c, the speed increaser consists of planetary gear sets M1 and M2, of which M1 (4-3-5-6-H) contains a compound planet with internal - internal gearing, and M2 (1-2-3-5-6-H) has two planets in series with external-internal gearing. In this configuration, the two component mechanisms share the same moving carrier H and the same fixed gear 6.

In its general configuration with two inputs and two outputs, the four operating variants V1 to V4 become (see Figure 5):

(1)

Variant V1: a system with two inputs and two outputs (L = 4), in which both input R1 and R2 and both output GR and GS are active. The input-output torque ratio k_t > 0 is controlled by the blade-pitch angle of either or both rotors R1 and R2, while the clutch is set to connect carrier H to GS (see Figure 4b-left);

(2)

Variant V2: a system with two inputs and one output (L = 3), in which the output is connected to the electric-generator rotor GR, and stator GS is fixed by the clutch as shown in Figure 4b-right;

(3)

Variant V3: a system with one input and two outputs (L = 3), obtained from V1 by deactivating the secondary rotor R2 (k_t = 0);

(4)

Variant V4: a system with one input and one output (L = 2), obtained from variant V1 by deactivating the secondary rotor R2 (k_t = 0) and by connecting the electric-generator stator to the frame (see Figure 4b-right).

The two component planetary gear sets M1 and M2 are characterized by the interior kinematic ratios i₀₁ and i₀₂,

$$i_{01}=i_{46}^H=i_{43}^H\cdot i_{56}^H=\frac{z_3{z}_6}{z_4{z}_5}>0; i_{02}=i_{16}^H=i_{12}^H\cdot i_{23}^H\cdot i_{56}^H=\frac{z_3{z}_6}{z_1{z}_5}>0$$

(22)

where $i_{xy}^z$ is the angular speed ratio of body x and body y relative to body z.

For obvious reasons, the number of teeth z₄ of ring gear 4 has to be bigger than the number of teeth z₁ of sun gear 1 (i.e., z₄ > z₁), and according to Equation (22), inequality i₀₂ > i₀₁ should also hold true.

Efficiencies η₀₁ and η₀₂ are the internal efficiencies of mechanisms M1 and M2 associated to the respective planetary gear sets, when carrier H is fixed (see Equation (12), where η₀ is the efficiency of one gear pair, and efficiencies ${\mathsf{\eta }}_{xy}^z$ correspond to the power being transmitted from member x to member y when z is held fixed, and where x, y can be either 1, 2, 3, 4, 5 and H, while z can be either 6 and H).

$${\mathsf{\eta }}_{01}={\mathsf{\eta }}_{43}^H\cdot {\mathsf{\eta }}_{56}^H={({\mathsf{\eta }}_0^{})}^2; {\mathsf{\eta }}_{02}={\mathsf{\eta }}_{12}^H\cdot {\mathsf{\eta }}_{23}^H\cdot {\mathsf{\eta }}_{56}^H={({\mathsf{\eta }}_0^{})}^3$$

(23)

Coefficients a, b, c defined in Equation (13) can be calculated by applying a motion-inversion relative to planet carrier H [51]:

$$a=i_{14}^6=\frac{{\mathsf{\omega }}_{16}}{{\mathsf{\omega }}_{46}}=\frac{1-i_{02}}{1-i_{01}}; b=c=i_{H4}^6=\frac{{\mathsf{\omega }}_{H6}}{{\mathsf{\omega }}_{46}}=\frac{1}{1-i_{01}}$$

(24)

In turn, torque-transmission functions are also linear equations according to Equation (25)

$$T_{R1}=T_{R1}^{(GR)}+T_{R1}^{(R2)}+T_{R1}^{(GS)}; T_{R1}^{(GR)}=A\cdot T_{GR}; T_{R1}^{(R2)}=B\cdot T_{R2}; T_{R1}^{(GS)}=C\cdot T_{GS}$$

(25)

where $T_{R1}^{(x)}$ is the torque at the primary rotor shaft R1 obtained when all independent external torques are zero, except for T_x, and where coefficients A, B, C defined in Equation (14) are determined by applying the principle of superposition.

For example, torque $T_{R1}^{(GR)}$ is obtained for T_GR ≠ 0 (mechanical power is transmitted only to electric-generator rotor GR) and for T_R2 = T_GS = 0 (i.e., the secondary rotor R2 and the stator of the electric generator are idling).

Considering only the power flow from R1 to GR yields,

$$T_{R1}^{(GR)}\cdot {\mathsf{\omega }}_{46}\cdot {\mathsf{\eta }}_{41}^6+T_{GR}\cdot {\mathsf{\omega }}_{16}=0 => T_{R1}^{(GR)}=-T_{GR}\cdot \frac{a}{{\mathsf{\eta }}_{41}^6}$$

(26)

where,

$${\mathsf{\eta }}_{41}^6={\mathsf{\eta }}_{4H}^6\cdot {\mathsf{\eta }}_{H1}^6; {\mathsf{\eta }}_{4H}^6=\frac{1-\overline{i_{01}}}{1-i_{01}}; {\mathsf{\eta }}_{H1}^6=\frac{1-i_{02}}{1-\overline{i_{02}}}$$

(27)

and where $\overline{i_{01}}$ and $\overline{i_{02}}$ are torque ratios [51], defined as:

$$\overline{i_{01}}=i_{01}\cdot {\mathsf{\eta }}_{01}^{x_1}; x_1=sign \left(\frac{{\mathsf{\omega }}_{4H}}{{\mathsf{\omega }}_{46}}\right)=sign \left(\frac{i_{01}}{i_{01}-1}\right)$$

(28)

$$\overline{i_{02}}=i_{02}\cdot {\mathsf{\eta }}_{02}^{x_2}; x_2=sign \left(-\frac{{\mathsf{\omega }}_{1H}}{{\mathsf{\omega }}_{16}}\right)=sign \left(-\frac{i_{02}}{i_{02}-1}\right)$$

(29)

In the above equations, sign represents the sign function, and x₁ = −1 for i₀₁ < 1 and x₁ = +1 for i₀₁ > 1, x₂ = +1 for i₀₂ < 1 and x₂ = −1 for i₀₂ > 1, i₀₁ ≠ 1, i₀₂ ≠ 1. Because in a counter-rotating electric generator, the generator rotor must have a higher angular velocity than the stator i.e., |ω_GR| > |ω_GS|, then |a| > |c|, and as a result, i₀₂ > 2 and x₂ = −1.

From the condition that rotors R1 and R2 are counter-rotating, i.e., sign (ω_R1 ω_R2) = −1, and since b < 0, then i₀₁ > 1 and x₁ = +1 (see Equations (13) and (24)). It also implies that:

$$A=-\frac{a}{{\mathsf{\eta }}_{41}^6}=-\frac{1-\overline{i_{02}}}{1-\overline{i_{01}}}=-\frac{1-i_{02}\cdot {\mathsf{\eta }}_{02}^{-1}}{1-i_{01}\cdot {\mathsf{\eta }}_{01}^{}}$$

(30)

Coefficients B and C are determined similarly to coefficient A, by considering the power flow from R1 to R2 and from R1 to RS:

$$T_{R1}^{(R2)}\cdot {\mathsf{\omega }}_{46}\cdot {\mathsf{\eta }}_{4H}^6+T_{R2}\cdot {\mathsf{\omega }}_{H6}=0 => T_{R1}^{(R2)}=-T_{R2}\cdot \frac{b}{{\mathsf{\eta }}_{4H}^6}$$

(31)

$$T_{R1}^{(R\mathrm{S})}\cdot {\mathsf{\omega }}_{46}\cdot {\mathsf{\eta }}_{4H}^6+T_{R\mathrm{S}}\cdot {\mathsf{\omega }}_{H6}=0 => T_{R1}^{(R\mathrm{S})}=-T_{R\mathrm{S}}\cdot \frac{c}{{\mathsf{\eta }}_{4H}^6}$$

(32)

According to Equation (24), b = c which yields:

$$B=C=-\frac{b}{{\mathsf{\eta }}_{4H}^6}=-\frac{c}{{\mathsf{\eta }}_{4H}^6}=-\frac{1}{1-\overline{i_{01}}}=-\frac{1}{1-i_{01}\cdot {\mathsf{\eta }}_{01}^{}}$$

(33)

By employing Equations (18)–(21), the efficiencies of the four variants of the 1-DOF planetary speed increaser are obtained.

For variant V1: two inputs and two outputs (L = 4):

$${\mathsf{\eta }}_{V1}=\frac{i_{02}}{\overline{i_{02}}}\cdot \frac{1-\overline{i_{01}}-k_t}{1-i_{01}-k_t}={\mathsf{\eta }}_{02}^{}\cdot \frac{1-i_{01}{\mathsf{\eta }}_{01}^{}-k_t}{1-i_{01}-k_t}$$

(34)

For variant V2: two inputs and one output (L = 3, ${\mathsf{\omega }}_{GS}=0$):

$${\mathsf{\eta }}_{V2}=\frac{1-i_{02}}{1-i_{02}{\mathsf{\eta }}_{02}^{-1}}\cdot \frac{1-i_{01}{\mathsf{\eta }}_{01}^{}-k_t}{1-i_{01}-k_t}.$$

(35)

For variant V3: one input and two outputs (L = 3, $k_t=0$):

$${\mathsf{\eta }}_{V3}={\mathsf{\eta }}_{02}^{}\cdot \frac{1-i_{01}{\mathsf{\eta }}_{01}^{}}{1-i_{01}}$$

(36)

For variant V4: one input and one output (L = 2, ${\mathsf{\omega }}_{GS}=0$, $k_t=0$):

$${\mathsf{\eta }}_{V4}=\frac{1-i_{02}}{1-i_{02}{\mathsf{\eta }}_{02}^{-1}}\cdot \frac{1-i_{01}{\mathsf{\eta }}_{01}^{}}{1-i_{01}}$$

(37)

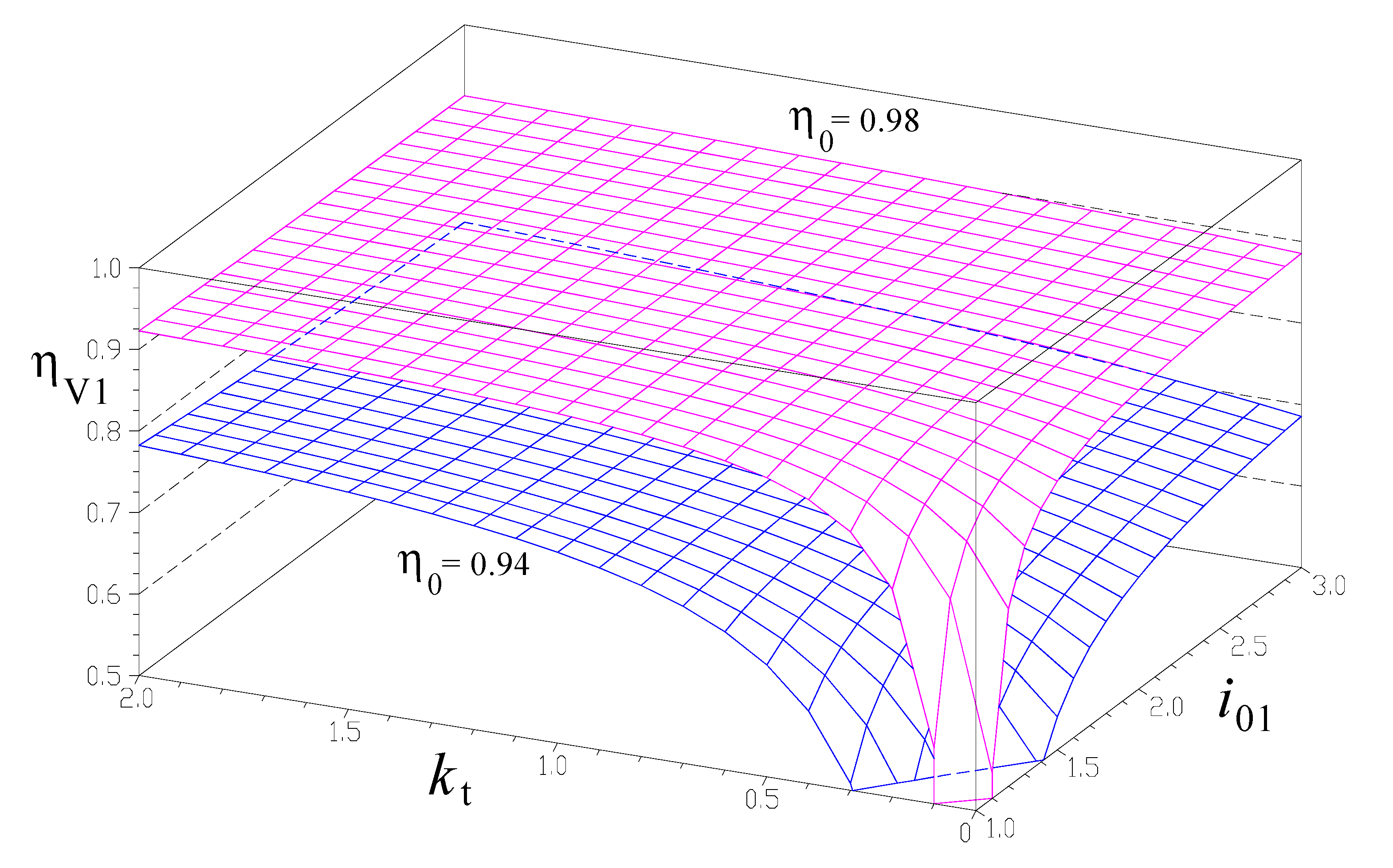
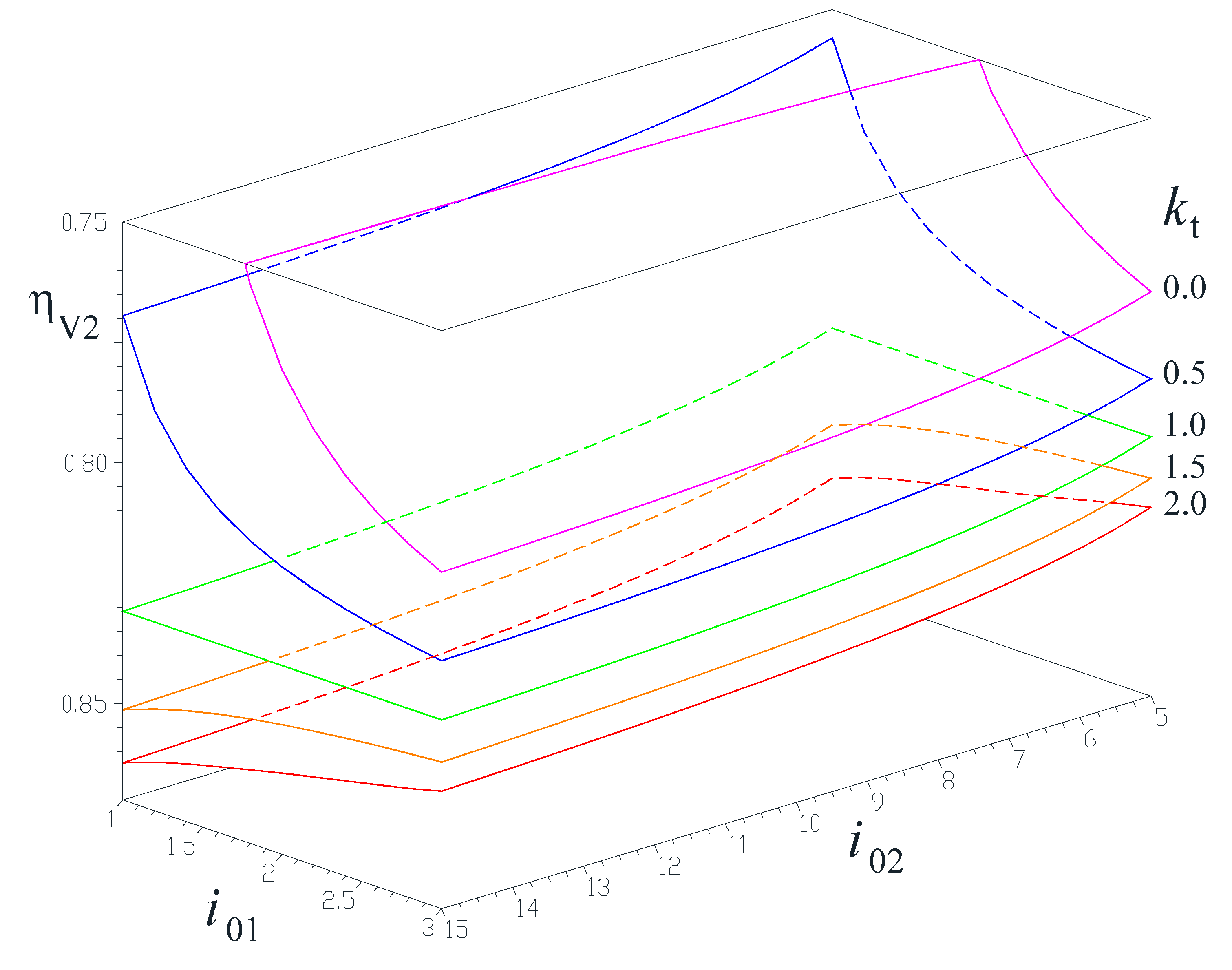
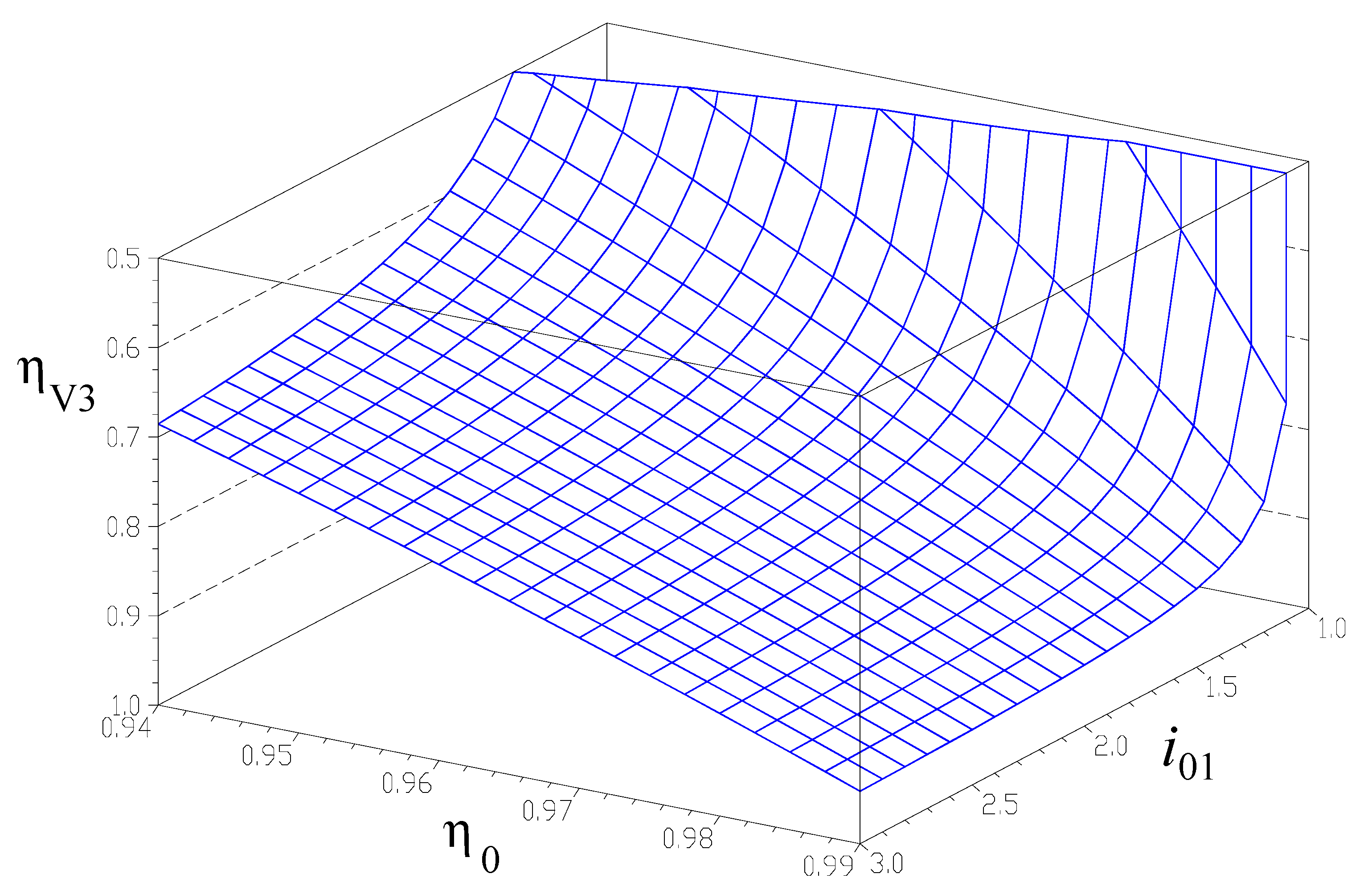
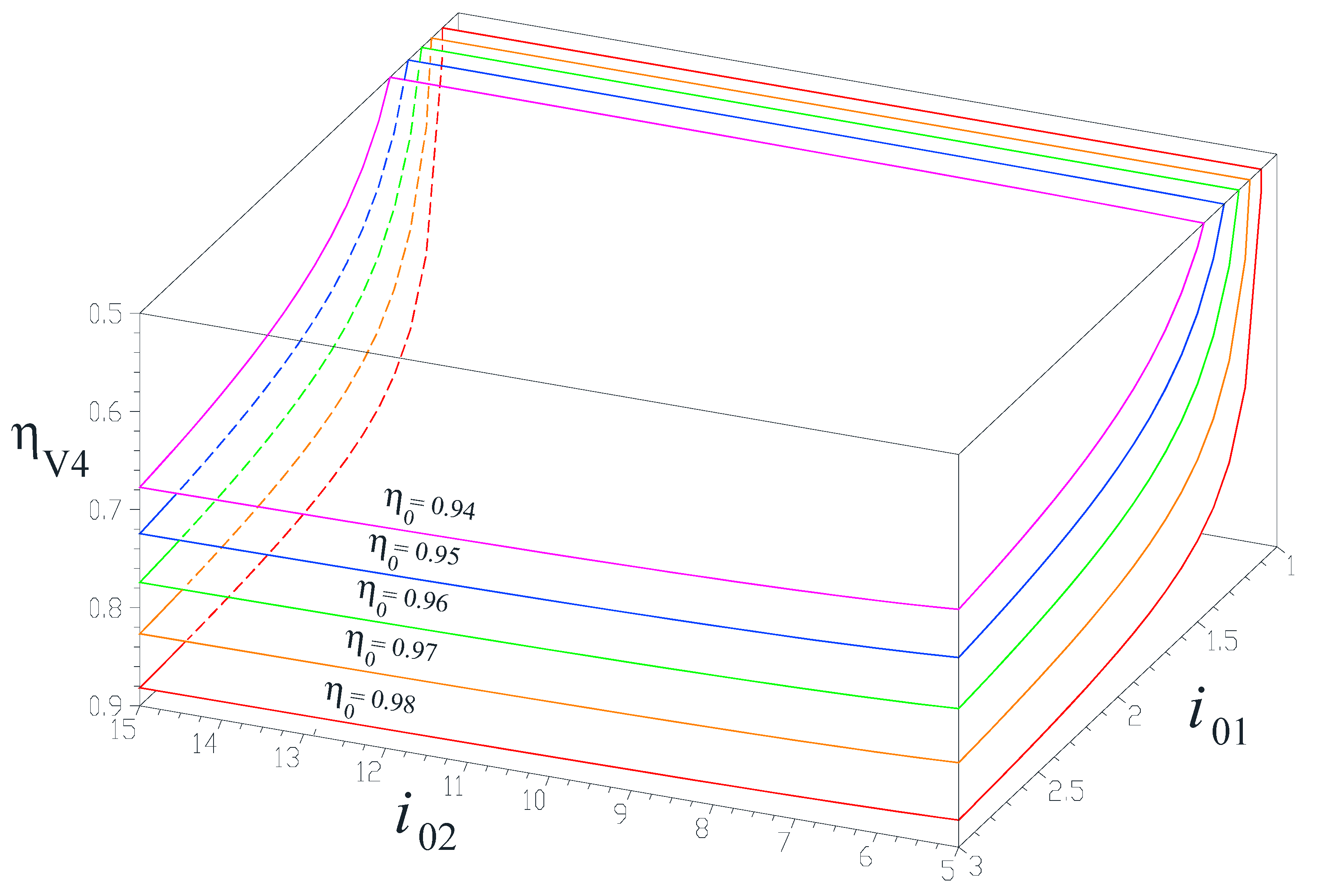
5. Numerical Simulations and Discussions

Four independent parameters, i.e., i₀₁, i₀₂, k_t and η₀ occur in the efficiency Equations (34)–(37) of the planetary speed increaser variants V1, V2, V3 and V4. The effects of these parameters upon overall efficiency and kinematic ratios of the respective speed increasers have been studied using bivariate plots as explained in [55,56] (see Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10; note that in some of these plots the z-axis has been reversed for clarity). The value ranges of these four parameters have been considered as follows: the kinematic ratio of the speed increaser i_aG = ω_G/ω_R1 ≥ 3, input torque ratio k_t < 2 and efficiency of a typical pair of gears η₀ > 0.94 [57].

According to Equation (34), the efficiency of a speed increasers with two counter-rotating wind or water rotors and counter-rotating electric generator (variant V1) depends on i₀₁, k_t and η₀, and it is not influenced by the interior kinematic ratio i₀₂. As the plot in Figure 6 shows, the efficiency η_V1 of the speed increaser is influenced the most by the efficiency η₀ of its constituent gear pairs, resulting in more than 12% increase, for only 4% improvement in η₀ i.e., from 94% to 98%. Consequently, care should be given to the manufacturing quality of the individual gears. Also, what is visible in Figure 7 is a rapid decrease of η_V1 with a reduction of parameters i₀₁ and k_t, most noticeable for i₀₁ < 1.75 and k_t < 0.75. From Figure 10c it additionally becomes apparent that for 1 < i₀₁ < 2, high values of the amplification ratio i_aG are obtained. During the operation of a power generating system equipped with such a transmission, torque ratio k_t will be adjusted via the pitch angles of the wind or water rotors. In the design stage, the anticipated range of k_t should be correlated with interior ratio i₀₁ and gear-pair efficiency η₀ to achieve best speed increaser efficiency and a high amplification ratio i_aG.

In case of variant V2 of gear increasers (which is the same as variant V1 but with a locked stator, i.e., ${\mathsf{\omega }}_{GS}=0$) Equation (35) indicates that the efficiency η_V2 of the increaser depends on all four parameters i₀₁, i₀₂, k_t and η₀. Assuming that each gear-pair of the transmission has the same efficiency η₀ and equal to 0.965, according to the plot in Figure 7, η_V2 is influenced manly by the interior kinematic ratio i₀₁ and by the torque ratio k_t, and less by the interior ratio i₀₂. As i₀₂ increases and for i₀₁ and k_t assumed constant, a slight increase of η_V2 is observed. Likewise, efficiency η_V2 increases for k_t < 1, and decreases slightly for k_t > 1 as i₀₁ increases. For k_t = 1, efficiency η_V2 no longer depends on i₀₁, which may be interesting when large kinematic amplification ratios i_aG are desired. Same as for variant V1, an increase of the torque ratio k_t is accompanied by an increase in efficiency η_V2. The increase of η_V2 with k_t is more significant for small values of i₀₁ than is for larger values of i₀₁.

The efficiency of gear transmission variant V3 with one input R1 and two counter-rotating outputs GR and GS, depends only on i₀₁ and η₀ (see Equation (36)). The internal gear ratio i₀₁ does not affect the efficiency η_V3 of the increaser and k_t = 0. The 3D plot in Figure 8 shows, for i₀₁ held constant, a linear correlation of efficiency η_V3 with η₀. Also apparent is a rapid drop of efficiency η_V3 with i₀₁, particularly for i₀₁ < 1.75.

Variant V4 of gear increaser is characterized by k_t = 0 (there is only one input i.e., R1) and by ${\mathsf{\omega }}_{GS}=0$ (the generator has a fixed stator). According to Equation (37) its efficiency η_V4 depends on parameters i₀₁, i₀₂ and η₀. Higher values of the efficiency η_V4 are obtained for larger values of these three parameters, of which η₀ has the most effect, Figure 9. Internal kinematic ratio i₀₂ has a smaller effect, however, a rapid drop in η_V4 is observed for i₀₁ approaching 1.

Based on the same plots in Figure 6, Figure 7, Figure 8 and Figure 9, the following additional conclusions can be drawn:

−

Efficiencies η_V1 and η_V2 increase as the input torque ratio k_t increases. This is explicable by the relative increase of the power from the secondary wind or water rotor R2. It is worth mentioning that the power flow from R1 passes entirely through mechanism M1 and then through part of mechanism M2, while the power flow generated by R2 passes only partially through M2 and the rest is transmitted directly to the generator stator GS;

−

The interior kinematic ratio i₀₁ influences strongly the speed-increaser efficiency in all four variants as k_t approaching 0, particularly if 1 < i₀₁ < 1.75. Furthermore, the mechanism locks (i.e., efficiency becomes negative) for i₀₁ approaching 1;

−

The interior kinematic ratio i₀₂ does not occur in the efficiency Equations (34) and (36) for the speed increaser variants V1 and V3 with counter-rotating electric generator. Instead, efficiencies η_V2 and η_V4 (the cases with electric generator with a fixed stator) have markedly lower values for small values of parameter i₀₂, but increase with the increase of i₀₂;

−

The quality of the component gears and therefore the individual gear pair efficiencies η₀, have a major influence upon the efficiency of the speed increaser, regardless of variant V1 to V4. Therefore, it is recommended that good quality gear pairs are used, in order to minimize losses and maximize the efficiency in transmitting mechanical power from wind or water rotors to the electric generator.

As a general conclusion, Figure 6, Figure 7, Figure 8 and Figure 9 confirm that split-power transmissions have higher efficiencies than serial transmission. Overall, the best efficiencies are provided by variant V1, which combines the split input power (Figure 2c) with the split output power (Figure 2b). The second most efficient is variant V2 with two inputs and one output (Figure 2c), followed by variant V3 with a single rotor and counter-rotating electric generator (Figure 2b). The least performing variant is V4 with serial transmission of mechanical power (Figure 2a). Thus, the efficiency of hydro/tidal/wind systems can be increased by adopting either a split-input power transmissions, a split-output power transmissions, or a transmissions with power split both at input and at output.

The interior kinematic ratios i₀₁ and i₀₂ of the component mechanisms M1 and M2, directly influence the transmission of input angular speed ω_R1 to the electric generator, and implicitly, the relative speed ω_G between the generator rotor and stator. The plots in Figure 10, depicted for variant V1 with two inputs and two outputs, indicate that the amplification ratio i_aG = ω_G/ω_R1 increases with the decrease of i₀₁ and with the increase of i₀₂. High kinematic ratios i_aG can be obtained at reduced internal ratios i₀₁ (e.g., i_aG = 50 for i₀₁ = 1.2 and i₀₂ = 10) and/or in combination with high values of internal ratio i₀₂ (e.g., i_aG = 30 for i₀₁ = 1.5 and i₀₂ = 15).

6. Conclusions

This paper presented a generalized model of efficiency calculation of 1-DOF speed increasers applicable to hydro and wind energy conversion systems with two gear mechanisms in parallel. Possible operating modes involve one input or two counter-rotating inputs, and with a single or two generator outputs. The inputs are provided by two counter-rotating wind or water rotors, while the outputs are linked to the counter-rotating rotor and the stator of an electric generator.

It was found that the in-parallel or split-power transmissions have higher efficiency compared to the serial transmissions. The in-parallel power transmission can be achieved, either by using two counter-rotating wind or water rotors, or by employing an electric generator with counter-rotating rotor and stator. As a result, counter-rotating systems have higher efficiencies than conventional single input, single output systems.

For the general case of a speed increaser with two inputs and two outputs, an efficiency analysis has been performed where transmissions with only two inputs and one output; one input and two outputs, and with one input and one output result as particular cases. This approach has then been applied to a novel planetary gear speed increaser, which can operate in all four possible combinations using a built-in two-way clutch, and by adjusting the pitch angle of the wind or water rotors.

The results reveal that the speed-increasers with two inputs and two outputs have higher efficiency. The results presented in this paper offer design engineers a useful approach for the analysis and synthesis of high-performance wind/tidal/hydro electrical systems.