Studies on Dynamic Properties of Ultracapacitors Using Infinite r–C Chain Equivalent Circuit and Reverse Fourier Transform
Abstract
:1. Introduction
2. Experimental Studies
2.1. Experimental Setup
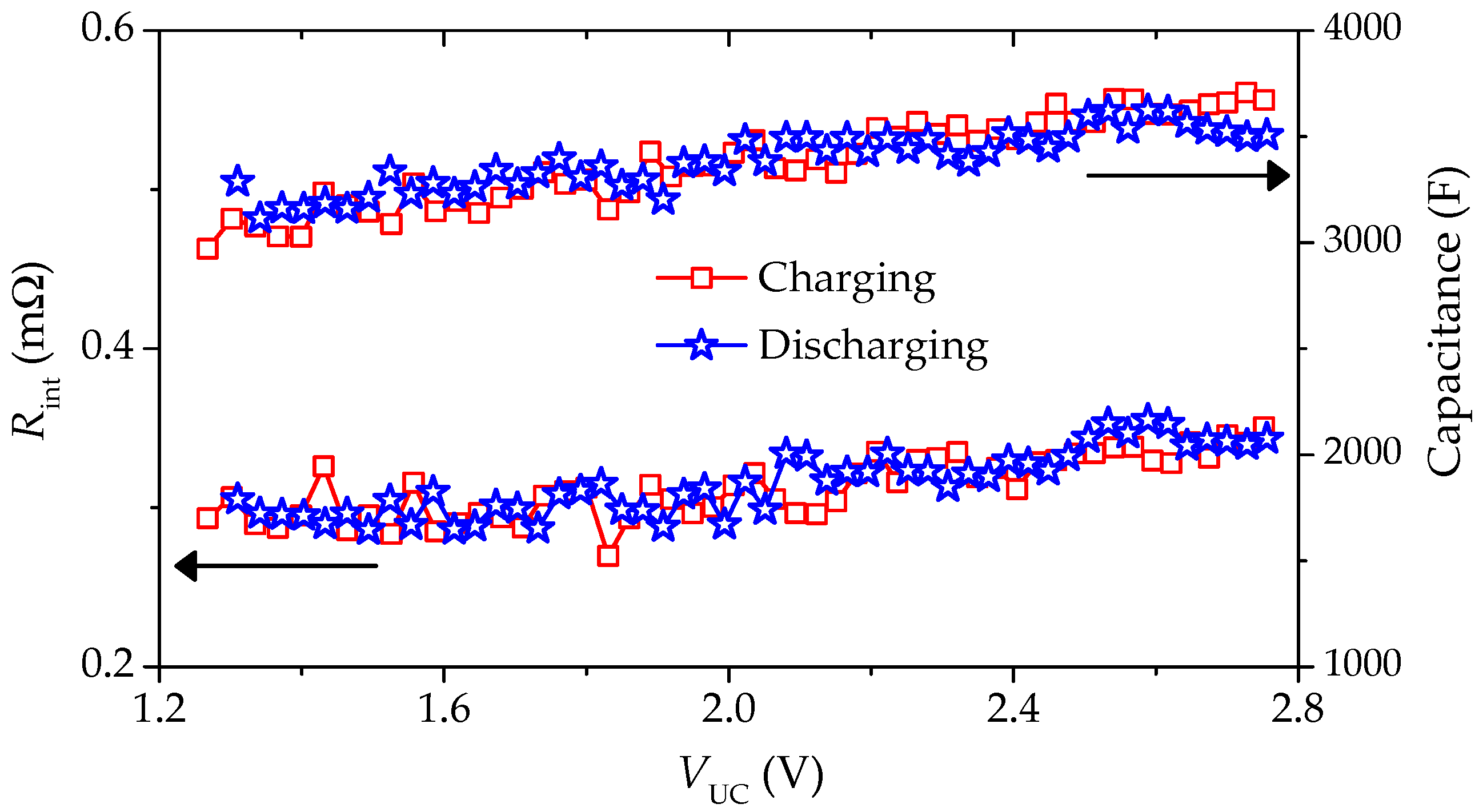
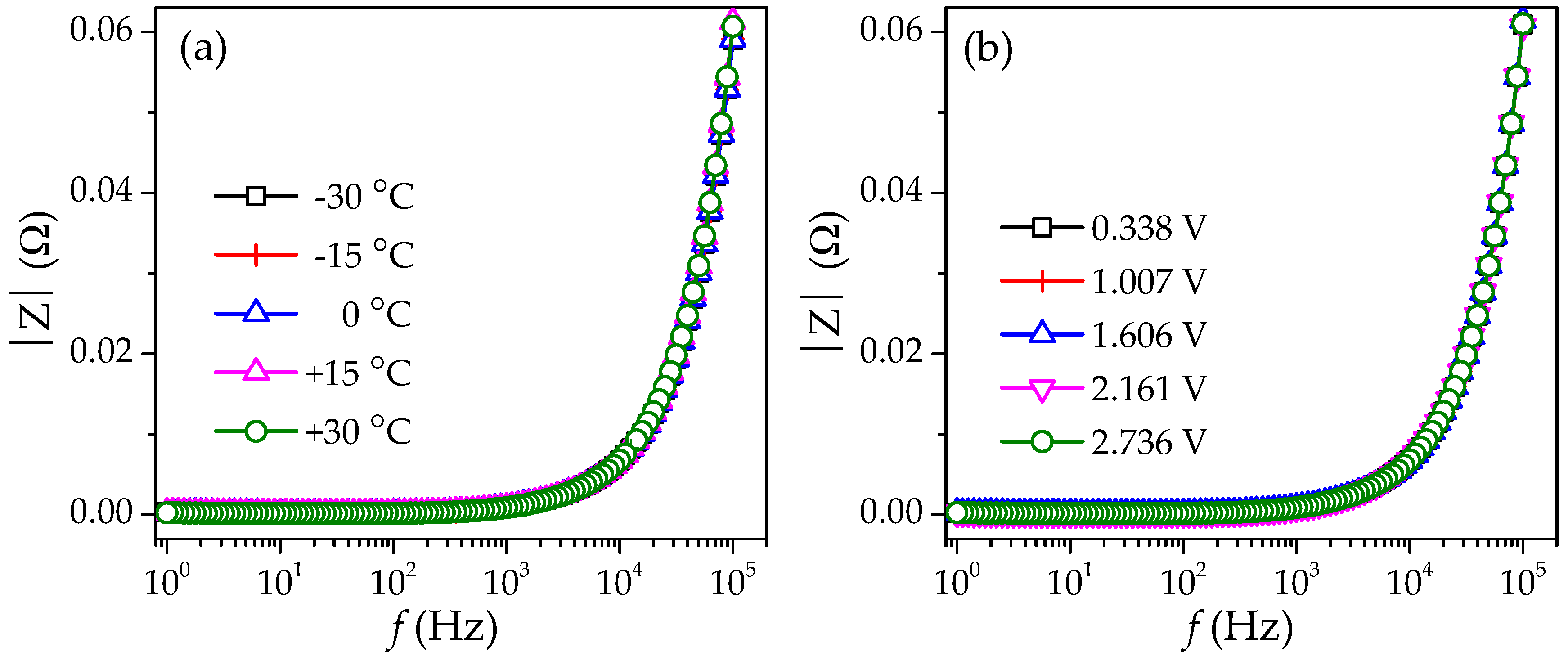
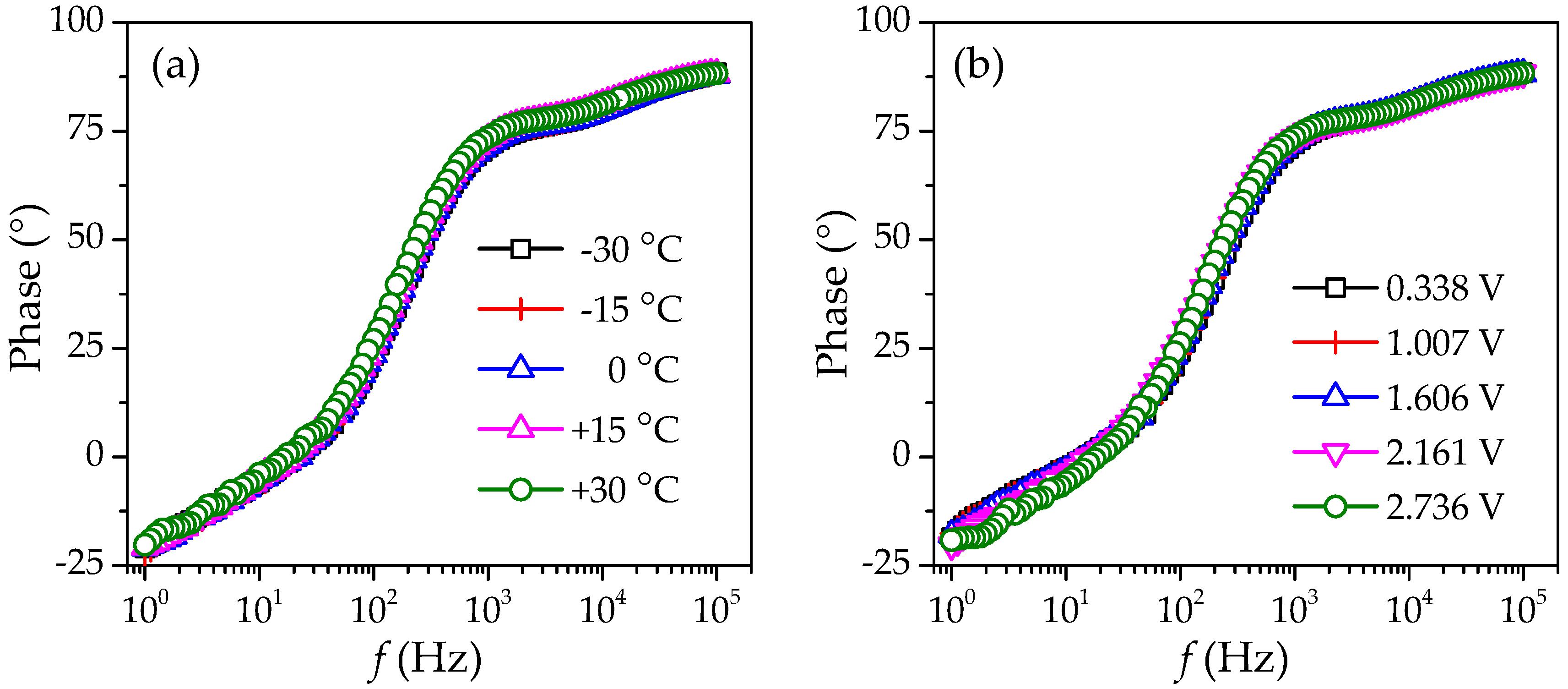
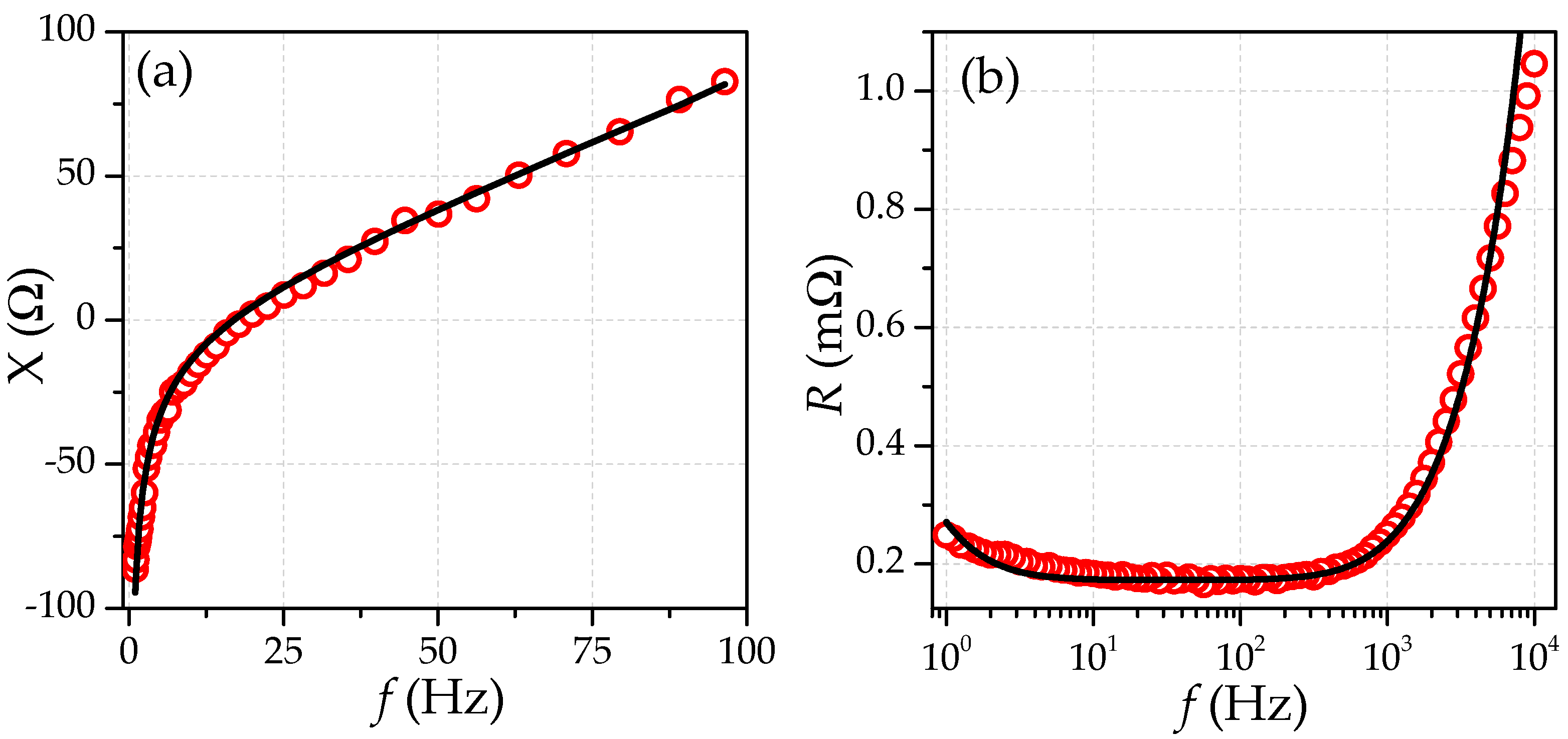
2.2. Results
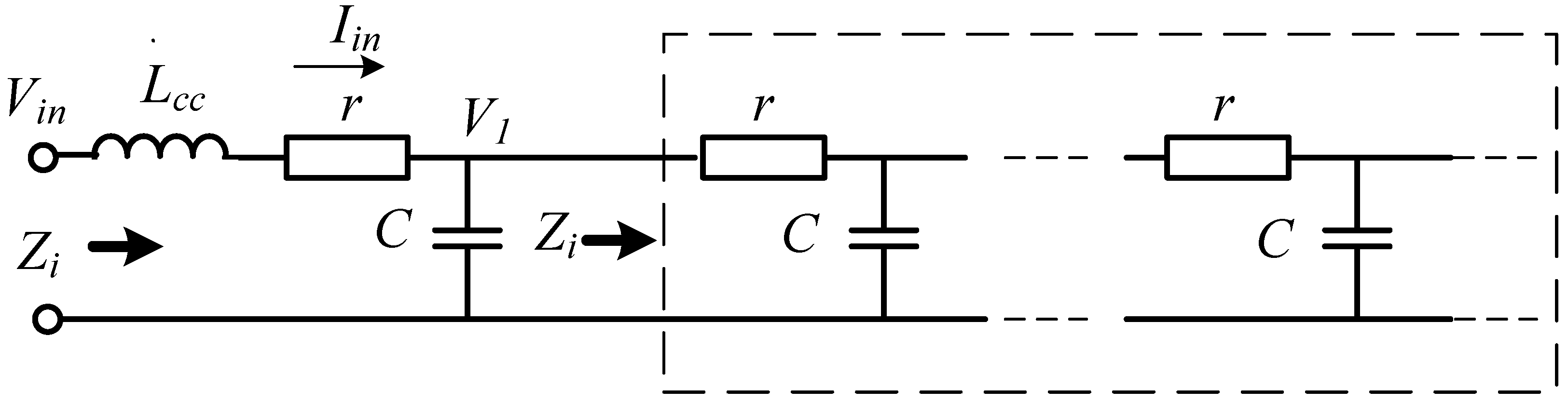
3. Equivalent Circuit Development
3.1. Mathematical Model
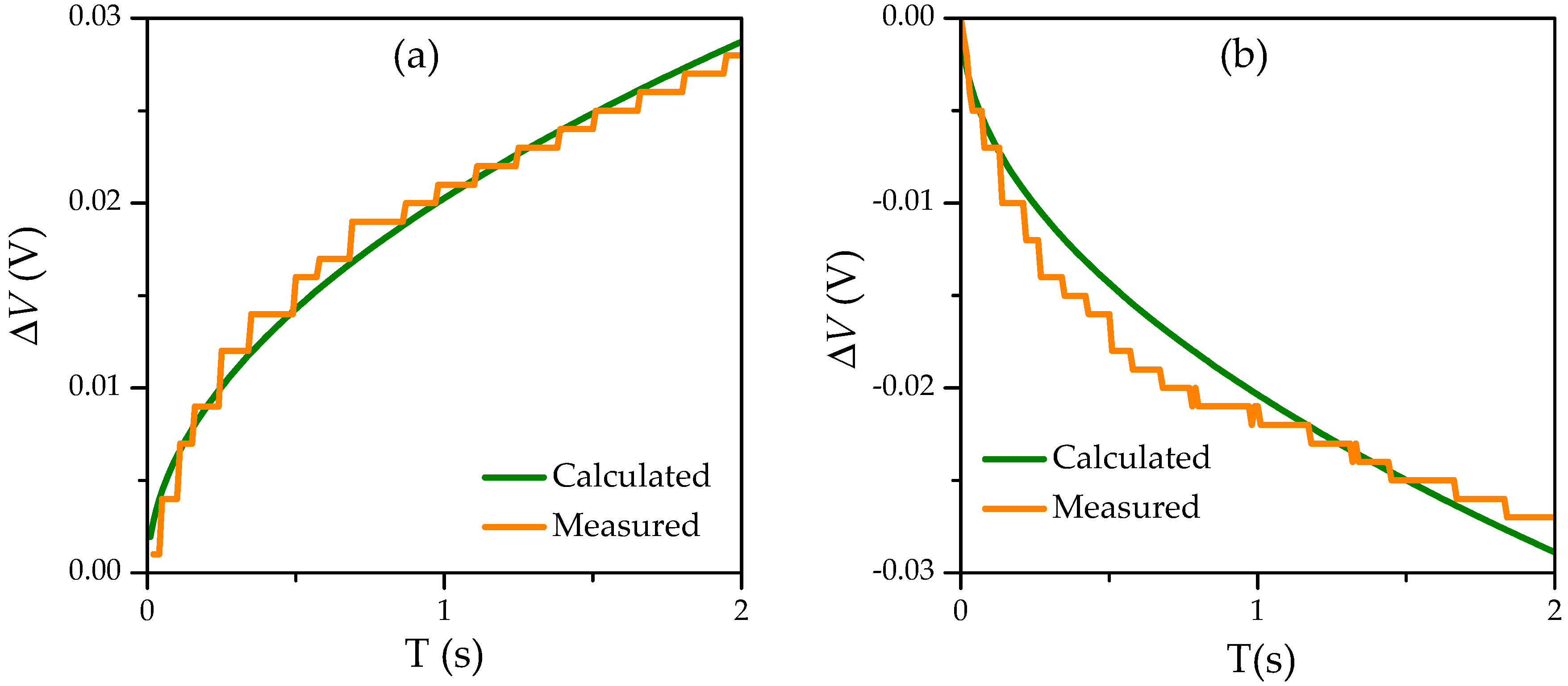
3.2. Representation of Dynamic UC Parameters Using Reverse Fourier Transform
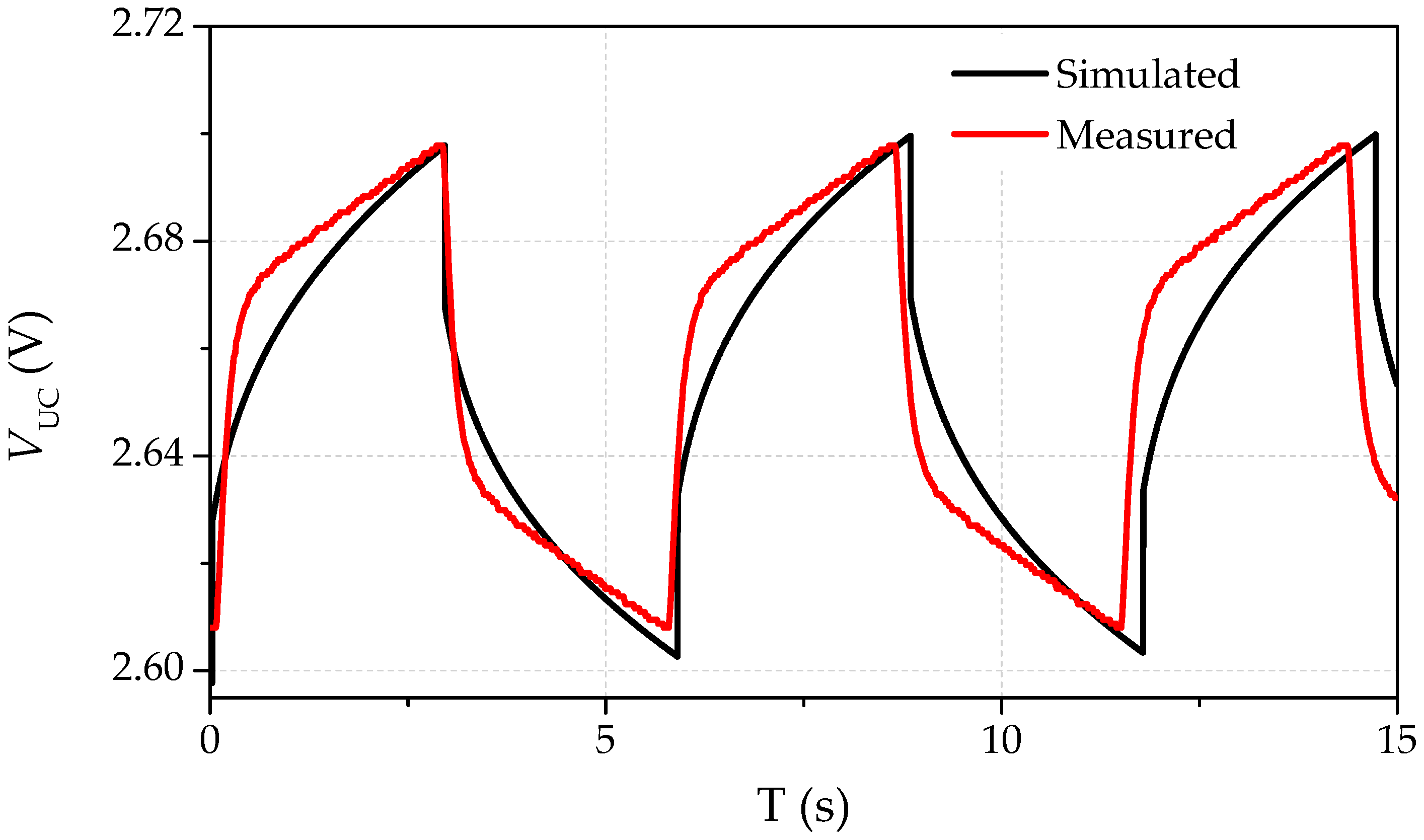
4. Equivalent Circuit Model with PSIM Software
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shtessel, Y.B.; Ghanes, M.; Ashok, R.S. Hydrogen Fuel Cell and Ultracapacitor Based Electric Power System Sliding Mode Control: Electric Vehicle Application. Energies 2020, 13, 2798. [Google Scholar] [CrossRef]
- Karden, E.; Ploumen, S.; Fricke, B.; Miller, T.; Snyder, K. Energy storage devices for future hybrid electric vehicles. J. Power Sources 2007, 168, 2–11. [Google Scholar] [CrossRef]
- Wong, L.A.; Ramachandaramurthy, V.K.; Taylor, P.; Ekanayake, J.B.; Walker, S.L.; Padmanaban, S. Review on the optimal placement, sizing and control of an energy storage system in the distribution network. J. Energy Storage 2019, 21, 489. [Google Scholar] [CrossRef]
- Rajput, S.; Amiel, I.; Sitbon, M.; Aharon, I.; Averbukh, M. Control the Voltage Instabilities of Distribution Lines using Capacitive Reactive Power. Energies 2020, 13, 875. [Google Scholar] [CrossRef] [Green Version]
- Sorkin, O.; Farber, E.; Averbukh, M. Selecting ultracapacitors for smoothing voltage deviations in local grids fed by transformer with tap-changer and distributed PV facilities. Electronics 2019, 8, 357. [Google Scholar] [CrossRef] [Green Version]
- Heard, B.P.; Brook, B.W.; Wigley, T.M.; Bradshaw, C.J. Burden of proof: A comprehensive review of the feasibility of 100% renewable-electricity systems. Renew. Sustain. Energy Rev. 2017, 76, 1122. [Google Scholar] [CrossRef]
- Rajput, S.; Averbukh, M.; Yahalom, A.; Minav, T. An Approval of MPPT Based on PV Cell’s Simplified Equivalent Circuit During Fast-Shading Conditions. Electronics 2019, 8, 1060. [Google Scholar] [CrossRef] [Green Version]
- Kumar, G.V.B.; Sarojini, R.K.; Palanisamy, K.; Padmanaban, S.; Holm-Nielsen, J.B. Large Scale Renewable Energy Integration: Issues and Solutions. Energies 2019, 12, 1996. [Google Scholar] [CrossRef] [Green Version]
- Averbukh, M.; Lineykin, S.; Kuperman, A. Portable ultracapacitor based power source for emergency starting of internal combustion engines. IEEE Trans. Power Electron. 2015, 30, 4283–4290. [Google Scholar] [CrossRef]
- Uno, M.; Iwasaki, K.; Hasegawa, K. Series-Parallel Reconfiguration Technique with Voltage Equalization Capability for Electric Double-Layer Capacitor Modules. Energies 2019, 12, 2741. [Google Scholar] [CrossRef] [Green Version]
- Ito, Y.; Yanagisawa, H.; inventors; Panasonic Intellectual Property Management Co Ltd. assignee. Electrolyte Solution for Electric Double Layer Capacitors, and Electric Double Layer Capacitor. U.S. Patent 10,199,179, 5 February 2019. [Google Scholar]
- Teuber, M.; Strautmann, M.; Drillkens, J.; Sauer, D.U. Lifetime and Performance Assessment of Commercial Electric Double-Layer Capacitors Based on Cover Layer Formation. ACS Appl. Mater. Interfaces 2019, 11, 18313. [Google Scholar] [CrossRef]
- Abetbool, Y.; Rajput, S.; Yahalom, A.; Averbukh, M. Comprehensive Study on Dynamic Parameters of Symmetric and Asymmetric Ultracapacitors. Electronics 2019, 8, 891. [Google Scholar] [CrossRef] [Green Version]
- Muzaffar, A.; Ahamed, M.B.; Deshmukh, K.; Thirumalai, J. A review on recent advances in hybrid supercapacitors: Design, fabrication and applications. Renew. Sustain. Energy Rev. 2019, 101, 123. [Google Scholar] [CrossRef]
- Jiya, I.N.; Gurusinghe, N.; Gouws, R. Electrical Circuit Modelling of Double Layer Capacitors for Power Electronics and Energy Storage Applications: A Review. Electronics 2018, 7, 268. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Liu, W.; Chu, L.; Zhao, J. Fractional-Order Modeling and Parameter Identification for Ultracapacitors with a New Hybrid SOA Method. Energies 2019, 12, 4251. [Google Scholar] [CrossRef] [Green Version]
- Skovranek, T.; Macias, M.; Sierociuk, D.; Malesza, W.; Dzielinski, A.; Podlubny, I.; Pocsova, J.; Petras, I. Anomalous diffusion modeling using ultracapacitors in domino ladder circuit. Microelectron. J. 2019, 84, 136. [Google Scholar] [CrossRef]
- Kang, J.; Wen, J.; Jayaram, S.H.; Yu, A.; Wang, X. Development of an equivalent circuit model for electrochemical double layer capacitors (EDLCs) with distinct electrolytes. Electrochim. Acta 2014, 115, 587. [Google Scholar] [CrossRef]
- Pozo, B.; Garate, J.I.; Ferreiro, S.; Fernandez, I.; de Gorostiza, E.F. Supercapacitor Electro-Mathematical and Machine Learning Modelling for Low Power Applications. Electronics 2018, 7, 44. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Zhang, X.; Li, C.; Wang, K.; Sun, X.; Huo, Q.; Wei, T.; Ma, Y. Equivalent circuit models and parameter identification methods for lithium-ion capacitors. J. Energy Storage 2019, 24, 100762. [Google Scholar] [CrossRef]
- Buller, S.; Karden, E.; Kok, D.; Doncker, R.W.D. Modeling the dynamic behavior of supercapacitors using impedance spectroscopy. IEEE Trans. Ind. Appl. 2002, 38, 1622. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Drummond, R.; Zhao, S.; Howey, D.A.; Duncan, S.R. Circuit synthesis of electrochemical supercapacitor models. J. Energy Storage 2017, 10, 48. [Google Scholar] [CrossRef] [Green Version]
- Yu, A.; Chabot, V.; Zhang, J. Electrochemical Supercapacitors for Energy Storage and Delivery: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Barbero, G.; Lelidis, I. Analysis of Warburg’s impedance and its equivalent electric circuits. Phys. Chem. Chem. Phys. 2017, 19, 24934. [Google Scholar] [CrossRef] [PubMed]
- De Pauli, M.; Gomes, A.M.; Cavalcante, R.L.; Serpa, R.B.; Reis, C.P.; Reis, F.T.; Sartorelli, M.L. Capacitance spectra extracted from EIS by a model-free generalized phase element analysis. Electrochim. Acta 2019, 320, 134366. [Google Scholar] [CrossRef]
- Belhachemi, F. Modélisation et Caractérisation des Supercondensateurs à Couche Double Électrique Utilisés en Électronique de Puissance (Doctoral Dissertation); National Polytechnic Institute of Lorraine (INPL): Lorraine, France, 2001. [Google Scholar]
- Logerais, P.O.; Camara, M.A.; Riou, O.; Djellad, A.; Omeiri, A.; Delaleux, F.; Durastanti, J.F. Modeling of a supercapacitor with a multibranch circuit. Int. J. Hydrog. Energy 2015, 40, 13725. [Google Scholar] [CrossRef]
- Berrueta, A.; Martin, I.S.; Hernández, A.; Ursúa, A.; Sanchis, P. Electro-thermal modelling of a supercapacitor and experimental validation. J. Power Sources 2014, 259, 154. [Google Scholar] [CrossRef]
- Belhachemi, F.; Rael, S.; Davat, B. A physical based model of power electric double-layer supercapacitors. In Proceedings of the Conference Record of the 2000 IEEE Industry Applications Conference, Rome, Italy, 8–12 October 2000; pp. 3069–3076. [Google Scholar]
- Navarro, G.; Nájera, J.; Torres, J.; Blanco, M.; Santos, M.; Lafoz, M. Development and Experimental Validation of a Supercapacitor Frequency Domain Model for Industrial Energy Applications Considering Dynamic Behaviour at High Frequencies. Energies 2020, 13, 1156. [Google Scholar] [CrossRef] [Green Version]
- Musolino, V.; Piegari, L.; Tironi, E. New full-frequency-range supercapacitor model with easy identification procedure. IEEE Trans. Ind. Electron. 2012, 60, 112. [Google Scholar] [CrossRef]
- Rafik, F.; Gualous, H.; Gallay, R.; Crausaz, A.; Berthon, A. Frequency, thermal and voltage supercapacitor characterization and modeling. J. Power Sources 2007, 165, 928. [Google Scholar] [CrossRef]
- K2 ULTRACAPACITORS: 2.85V/3400F. Available online: https://www.maxwell.com/images/documents/K2_2_85V_DS_3000619EN_3_.pdf (accessed on 7 January 2020).
- Charge/Discharge System Controller, PFX2532. Available online: https://www.kikusui.co.jp/en/product/detail.php?IdFamily=0118 (accessed on 19 January 2020).
- Variable-Switching MultiRange DC Power Supply PWR 1600W. Available online: https://www.kikusui.co.jp/en/product/detail.php?IdFamily=0064 (accessed on 19 January 2020).
- Multifunctional DC Electronic Load, PLZ-4W Series. Available online: https://www.kikusui.co.jp/en/product/detail.php?IdFamily=0011 (accessed on 19 January 2020).
- Midi Logger GL900. Available online: http://www.graphteccorp.com/instruments/gl900/index.html (accessed on 27 January 2020).
- EchemLab XM Potentiostat Galvanostat. Available online: https://www.ameteksi.com/products/potentiostats/single-channel/apps-xm-series/echemlab-xm-potentiostat-galvanostat (accessed on 1 March 2020).
- Lunaire Steady State Testing Chamber. Available online: https://www.thermalproductsolutions.com/brands/tenney-lunaire-environmental-test-chambers-and-rooms (accessed on 6 March 2020).
- Shenkman, A.L.; Zarudi, M. Circuit Analysis for Power Engineering Handbook; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- PSIM-Software for Power Electronics. Available online: https://powersimtech.com/products/psim/ (accessed on 10 May 2020).
- Zubieta, L.; Bonert, R. Characterization of double-layer capacitors for power electronics applications. IEEE Trans. Ind. Appl. 2000, 36, 199. [Google Scholar] [CrossRef] [Green Version]

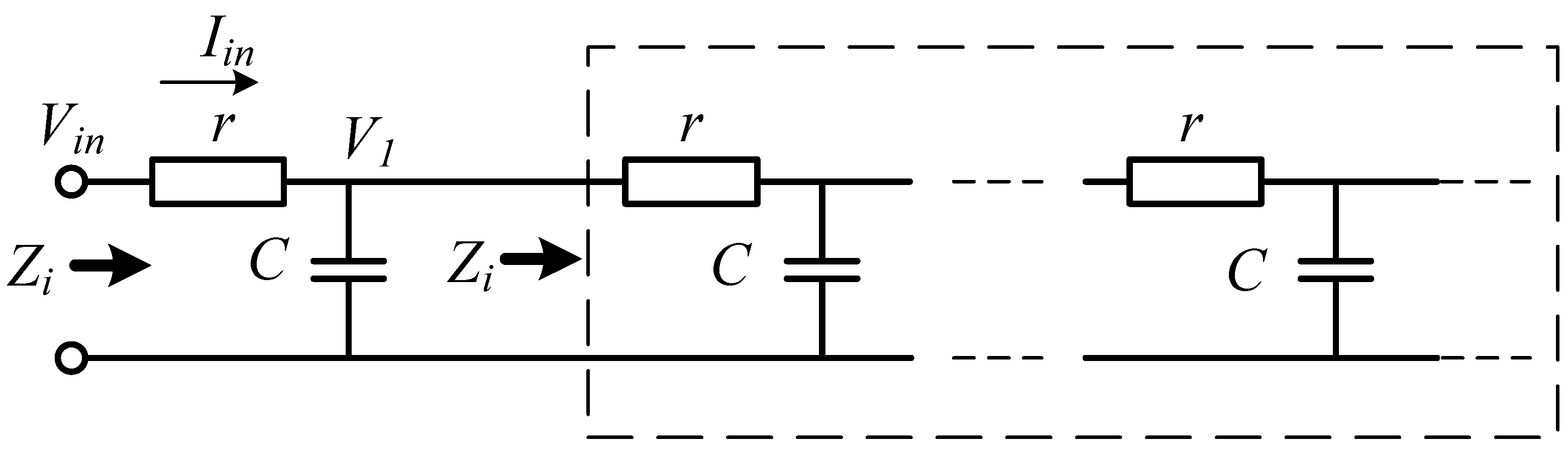

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajput, S.; Kuperman, A.; Yahalom, A.; Averbukh, M. Studies on Dynamic Properties of Ultracapacitors Using Infinite r–C Chain Equivalent Circuit and Reverse Fourier Transform. Energies 2020, 13, 4583. https://doi.org/10.3390/en13184583
Rajput S, Kuperman A, Yahalom A, Averbukh M. Studies on Dynamic Properties of Ultracapacitors Using Infinite r–C Chain Equivalent Circuit and Reverse Fourier Transform. Energies. 2020; 13(18):4583. https://doi.org/10.3390/en13184583
Chicago/Turabian StyleRajput, Shailendra, Alon Kuperman, Asher Yahalom, and Moshe Averbukh. 2020. "Studies on Dynamic Properties of Ultracapacitors Using Infinite r–C Chain Equivalent Circuit and Reverse Fourier Transform" Energies 13, no. 18: 4583. https://doi.org/10.3390/en13184583
APA StyleRajput, S., Kuperman, A., Yahalom, A., & Averbukh, M. (2020). Studies on Dynamic Properties of Ultracapacitors Using Infinite r–C Chain Equivalent Circuit and Reverse Fourier Transform. Energies, 13(18), 4583. https://doi.org/10.3390/en13184583







