Reliability and Network Performance Enhancement by Reconfiguring Underground Distribution Systems

Abstract

Contemporary distributions are now going to underground their overhead distribution lines due to techno-social reasons. Reliability and loss reduction are the two prime objectives for distribution system operation. Since failure rates of ungrounded cables are the function of Joules heating besides their physical lengths, the reliability evaluation of undergrounded distribution systems needs to be reviewed. This paper suggested a suitable modification in existing reliability indices in order to make them more appropriate for underground distribution systems. A multi-objective network reconfiguration problem is formulated to enhance the reliability and performance of distribution systems while duly addressing the variability and uncertainty in load demand and power generation from renewables. The application results on a standard test bench shift the paradigm of the well-known conflicting nature of reliability and network performance indices defined for overhead distribution systems.

1. Introductions

Owing to the higher request of reliability for customers incurred by the sustainable economic growth of the world, system reliability draws more and more attention, and thus becomes an important technical and economic indicator to distribution companies [1]. The deregulation in power distribution has introduced an intense competitive business environment. Distribution companies therefore have to run distribution systems at optimum performance while considering power losses and the node voltage profile, whereas every customer desires an uninterrupted quality power supply. The objective of a reliability-driven design of a distribution system is to reduce the frequency and duration of power interruptions to the customers [2]. However, the failure rates of overhead distribution lines are strictly governed by their physical lengths, whereas they also depend upon Joules heating in the case of undergrounded distribution lines, which is ignored while evaluating the reliability of overhead distribution systems. The objective of improving the reliability of distribution systems stands for the reduction in the frequency and the duration of power interruptions that affect the customers [3]. Therefore, distribution flows becomes crucial to evaluate the reliability of underground distribution systems.

Network performance of distribution systems can be enhanced by minimizing feeder power losses and node voltage deviations. This is accomplished by optimally varying the radial topology of the network via exchanging the status of sectionalizing and tie switches, and the process is known as network reconfiguration (NR). Since NR causes load balancing among feeders, it therefore affects distribution flows. Thus, reliability and network performance objectives can be enhanced simultaneously, which otherwise are well-known for their conflicting nature. In this context, existing reliability indices need modification and the effectiveness of NR to enhance both the reliability and performance of distribution systems needs investigation.

Optimal NR has many advantages like power losses reduction, voltage profile enhancement, reliability improvement and so on [4]. Kumar and Jayabarathi [5] used the bacterial foraging optimization algorithm to minimize losses, but the optimal configuration obtained is not radial. Kavousi-Fard et al. [6] solved a multi-objective NR problem to optimize losses, node voltage profile and total cost using modified teacher learning optimization. Zou et al. [7] assessed the reliability of a remote distribution system using NR, recloser installation, recloser replacement and distributed generation (DG) installation to minimize the reliability index. The authors of [8] employed NR to minimize customers’ interruption costs and enhance the reliability of electric power supplies and concluded that the method is effective to increase reliability and can bring larger economic benefits to society.

Niknam et al. [9] proposed a multi-objective NR problem to optimize power losses, total cost, total emissions of fuel cells and system reliability. Brown et al. [10] used the sequential feeder method to solve an NR problem of active distribution systems to enhance reliability using GA. In [4,11,12,13,14], an NR problem is solved to optimize the efficiency and reliability of distribution systems. An NR methodology is developed in [3] by considering probabilistic reliability models to optimize losses and reliability. Recently, Ref. [15] presented a computationally effective dynamic reliability network-equivalent approach (DRNEA) method for the reliability evaluation of active distribution systems. The authors of [16] presented a method to improve the power quality and reliability of distribution systems using NR, and NR and capacitor placement were employed in [17] to improve reliability.

In order to enhance reliability and customer satisfaction, electric utilities have begun to install automatic switching systems in their distribution systems [18]. Raoofat [19] adopted a GA-based method to allocate DGs and remote-controlled switches (RCSs) simultaneously in order to reduce energy losses and improve reliability considering a multilevel load. A differential search (DS) algorithm was proposed in [20] to solve a distribution system reliability problem by optimizing the number and location of RCSs. An enhancement in system efficiency and reliability was suggested by proposing a new solution methodology in [21] via optimal NR considering optimal switch and wind turbine placements.

Several important works have considered uncertainty in reliability data while addressing the problem. The authors of [22] investigated the role of a multi-objective NR problem to enhance typical reliability indices, energy efficiency and production cost in distribution systems while duly addressing uncertainty in wind turbines using the adaptive bat algorithm. The optimal NR problem has been solved for loss reduction and reliability enhancement considering uncertainty in reliability data using a robust approach [23], a modified cuckoo search algorithm [24] and interval analysis techniques [25].

From the abovementioned discussion, it has been observed that reliability or network performance can be enhanced by optimally reconfiguring distribution networks using metaheuristic techniques. Moreover, the network topology plays a crucial role in deciding the distribution flows. Distribution flows decide on Joules heating and thus become vital while considering the failure rates of underground distribution feeders. In this context, existing reliability indices need to be modified while considering the failure rates of feeders in underground distribution systems. NR causes more even distribution flows among distribution feeders that consequently results in lower failure rates, power loss reduction and better node voltage profiles. With these concerns, a more comprehensive NR problem may be formulated to optimize the reliability and network performance of distribution systems while duly addressing the issues and concerns that may affect distribution flows. Any strategy that can limit the current may have a positive impact on reliability and renders a more economical operation of the power system since active power losses are limited as well. [4].

This paper proposes a method to enhance the reliability and network performance of distribution systems by optimally reconfiguring the distribution network. Existing reliability indices have been modified by redefining failure rates in the context of undergrounded feeders. A more realistic formulation in a fuzzy framework is suggested to solve a multi-objective NR problem while considering variability and uncertainty in load demand and power generation from renewable DGs. The multi-objective NR problem is formulated in a fuzzy framework to optimize reliability indices, feeder power losses and node voltage deviations. The application results obtained on a modified 33-bus test distribution system are presented and investigated.

2. Proposed Reliability Indices

For a distribution network with N_c feeding nodes, the reliability indices for the ith radial topology, as adopted by the Chilean law, are defined by the Inter-American Committee of Regional Electricity-CIER [26] as

$$F(i)=\frac{{\displaystyle \sum _{j=1}^{N_c}KVA(j)\lambda (j)}}{{\displaystyle \sum _{j=1}^{N_c}KVA(j)}}$$

(1)

$$T(i)=\frac{{\displaystyle \sum _{j=1}^{N_c}KVA(j)\lambda (j)}r(j)}{{\displaystyle \sum _{j=1}^{N_c}KVA(j)}}$$

(2)

$$ENS(i)={\displaystyle \sum _{j=1}^{N_c}KW(j)\lambda (j)}r(j)$$

(3)

$$D(i)=\frac{T(i)}{F(i)}$$

(4)

$$U(j)=\lambda (j)r(j)$$

(5)

where F(i) is the system’s average interruption frequency index, T(i) is the system’s average interruption unavailability index, ENS(i) is the energy not supplied and D(i) is the system’s average duration interruption index for the ith candidate topology. These objectives are the function of active load demand KW(j) and apparent load demand KVA(j) of the N_c system load points as well as of the failure rate λ(j), repair time r(j) and the unavailability U(j) for each load point.

In the present scenario, most of the distribution feeders are transforming from overhead to undergrounded systems as this provides less susceptibility to line faults and accidents and also helps in the beautification of the city. However, a marked difference exists in these two systems while evaluating the failure rate and hence the reliability of distribution systems.

In overhead systems, it is a well-known fact that the design of distribution feeders is based upon mechanical parameters such as pole span, ice loading and permissible sag of the catenary, which primarily decide the cross-section and hence p.u. weight of the line conductor. The size of the line conductor obtained while considering mechanical strength is usually quite far beyond the thermal limit. Alternatively, mechanical strength becomes more prominent than Joules heating while designing line conductors for overhead distribution feeders. Moreover, the heat produced is continuously dissipated in the atmosphere. The failure rate of overhead distribution feeders, therefore, has been taken invariably proportional to their length and thus becomes static by nature. On the contrary, Joules heating is crucial in undergrounded cables, besides length. The former is the source of incipient faults which may grow with time, whereas the latter decides the probability of mechanical faults. Due to contemporary distribution systems facing dynamically varying distribution flows on account of stochastic load demand and intermittency in power generation from renewable DGs, the existing failure rates need modification by considering both Joules heating and the length of distribution feeders. Therefore, in the present work, the dynamic failure rate of the distribution feeder is proposed as below:

$$\zeta (i,j,n)=\lambda (j)(I(i,j,n)/{(I(b,j,nom))}^2$$

(6)

where ζ(i,j,n) and I(i,j,n) denote the failure rate and the current in the jth distribution feeder during the nth system state, respectively, while the distribution system is operating in the ith radial topology, whereas I(b,j,nom) is the current flows in the jth distribution feeder considering a nominal load condition for the base topology of the distribution network. The existing failure rate λ(j) is static as it only depends upon the length of the jth distribution feeder. However, the proposed failure rate depends upon the feeder length as well as distribution flows. Distribution flows decide cable heating and are primarily governed by load demand, local power generation from DERs, node voltage profiles and network topology. The proposed failure rate becomes the function of these state parameters and thus becomes dynamic, and so the reliability indices too become dynamic. Furthermore, ENS is of prime importance for distribution system operators as it directly affects their margin of profits. In the present scenario of a dynamic electricity market, the energy price also varies with time. In this context, the existing reliability index ENS will not provide a true signal as it is expressed in kWh, rather it should be expressed in terms of a monetary value that provides the economic loss against the energy not being supplied. The reliability index ENS therefore needs correction. With the aforementioned discussion, the reliability indices for the ith radial topology of the nth state of a distribution system are proposed as

$$F(i,n)=\frac{{\displaystyle \sum _{j=1}^{N_c}KVA(j,n)\zeta \left(i,j,n\right)}}{{\displaystyle \sum _{j=1}^{N_c}KVA(j,n)}};\forall j\in N_c,\forall n\in N$$

(7)

$$T(i,n)=\frac{{\displaystyle \sum _{j=1}^{N_c}KVA(j,n)\zeta \left(i,j,n\right)}r(j)}{{\displaystyle \sum _{j=1}^{N_c}KVA(j,n)}};\forall j\in N_c,\forall n\in N$$

(8)

$$ENS(i,n)=k_e\left(n\right){\displaystyle \sum _{j=1}^{N_c}KW(j,n)\zeta \left(i,j,n\right)r(j)};\forall j\in N_c,\forall n\in N$$

(9)

$$D(i,n)=\frac{T(i,n)}{F(i,n)};\forall n\in N$$

(10)

$$U(i,j,n)=\zeta \left(i,j,n\right)r(j);\forall j\in N_c,\forall n\in N$$

(11)

From practical aspects, the index D is not a good index to be used as an objective function because its minimization is also possible with maximization of F [26]. The maximization of the index F is not a desirable attribute. Therefore, in the present study, minimization of the index D is not considered as an objective.

3. Problem Formulation for Proposed NR

A multi-objective NR problem is formulated to enhance the reliability and network performance of distribution systems. The reliability objectives considered are to minimize the proposed reliability indices F(i,n), T(i,n) and ENS(i,n) defined by (7)–(9). However, the network performance objectives considered are to minimize the cost of energy losses and node voltage deviations. These objectives are formulated as shown below:

$$EL(i,n)=ke(n)LD(n){\displaystyle \sum _{j=1}^{N_c}{I}^2(i,j,n)R_j};\forall j\in N_c,\forall n\in N$$

(12)

$$DV(i,n)=Max\left(abs\left(abs\left(V_s\right)-abs\left(V_{jn}\right)\right)\right)\forall j\in N_c,\forall n\in N$$

(13)

where LD(n) and ke(n) denote load duration and the energy price being prevailed during the nth system state. It is desirable to minimize each of the functions defined by (7)–(9), (12) and (13) while satisfying several system operational constraints pertaining to the power flow and radial topology. Since these objectives have different units, the proposed multi-objective NR problem is therefore formulated in a fuzzy framework and is solved as a single objective optimization in order to get the most compromising solution. A linear fuzzy membership function is considered for each of these objectives as shown in Figure 1. The fuzzy membership function shown in the figure provides linear scaling to each of the objectives considered and makes them unitless, thus facilitating a suitable mathematical operation to combine various objective functions into a single objective function. In the present work, various objectives are combined by taking their geometrical mean. The advantage of this approach is that the overall fuzzy membership falls sharply if any of the objective function is found to be poor. The objective function of the proposed multi-objective NR problem is therefore formulated to maximize the overall fuzzy membership function as given below:

$$Max\mu (i,n)={({\mu }_F(i,n){\mu }_T(i,n){\mu }_{ENS}(i,n){\mu }_{EL}(i,n){\mu }_{DV}(i,n))}^{1/5}$$

(14)

In (14), i stands for the ith radial topology of the distribution network and n stands for the nth system state, whereas µ refers to the fuzzy membership functions of the respective objective, where

$${\mu }_F(i,n)=\{\begin{array}{ll}1.0& ;F\left(i,n\right)\le F_{\min }\\ -\frac{F\left(i,n\right)}{\left(F_{\max }-F_{\min }\right)}+\frac{F_{\max }}{\left(F_{\max }-F_{\min }\right)}& ;F_{\min }<F\left(i,n\right)<F_{\max }\\ 0.0& ;F\left(i,n\right)\ge F_{\max }\end{array}$$

(15)

$${\mu }_T(i,n)=\{\begin{array}{ll}1.0& ;T\left(i,n\right)\le T_{\min }\\ -\frac{T\left(i,n\right)}{\left(T_{\max }-T_{\min }\right)}+\frac{T_{\max }}{\left(T_{\max }-T_{\min }\right)}& ;T_{\min }<T\left(i,n\right)<T_{\max }\\ 0.0& ;T\left(i,n\right)\ge T_{\max }\end{array}$$

(16)

$${\mu }_{ENS}(i,n)=\{\begin{array}{ll}1.0& ;ENS\left(i,n\right)\le EN{S}_{\min }\\ -\frac{ENS\left(i,n\right)}{\left(EN{S}_{\max }-EN{S}_{\min }\right)}+\frac{EN{S}_{\max }}{\left(EN{S}_{\max }-EN{S}_{\min }\right)}& ;EN{S}_{\min }<ENS\left(i,n\right)<EN{S}_{\max }\\ 0.0& ;ENS\left(i,n\right)\ge EN{S}_{\max }\end{array}$$

(17)

$${\mu }_{EL}(i,n)=\{\begin{array}{ll}1.0& ;EL\left(i,n\right)\le E{L}_{\min }\\ -\frac{EL\left(i,n\right)}{\left(E{L}_{\max }-E{L}_{\min }\right)}+\frac{E{L}_{\max }}{\left(E{L}_{\max }-E{L}_{\min }\right)}& ;E{L}_{\min }<EL\left(i,n\right)<E{L}_{\max }\\ 0.0& ;EL\left(i,n\right)\ge E{L}_{\max }\end{array}$$

(18)

$${\mu }_{DV}(i,n)=\{\begin{array}{ll}1.0& ;DV\left(i,n\right)\le D{V}_{\min }\\ -\frac{DV\left(i,n\right)}{\left(D{V}_{\max }-D{V}_{\min }\right)}+\frac{D{V}_{\max }}{\left(D{V}_{\max }-D{V}_{\min }\right)}& ;D{V}_{\min }<DV\left(i,n\right)<D{V}_{\max }\\ 0.0& ;DV\left(i,n\right)\ge D{V}_{\max }\end{array}$$

(19)

Subjected to the following problem constraints:

• Power Flow Constraint

  $$g_j\left(i\right)=0;\forall j\in N_c$$

  (20)
• Node Voltage Constraint

  $$V_{\min }\le V_{jn}\le V_{\max };\forall n\in N;\forall j\in N_c$$

  (21)
• Feeder Current Limit Constraint

  $$I_{jn}\le I_j^{\max };\forall n\in N,\forall j\in N_c$$

  (22)
• Radial Topology Constraint

  $${\Phi }_n(i)=0;\forall n\in N$$

  (23)

Equation (20) deals with usual power flow constraints pertaining to satisfy Kirchhoff’s laws in the distribution network, where the node voltage and feeder current limits are constrained by (21) and (22), respectively, and (23) confirms the radial topology of the distribution network with no closed path and without de-energization of any system node. While dealing with the NR problem using any population-based optimization technique, the radiality constraint imposes the biggest hurdle as all tentative solutions must represent radial topologies without any islanding. In the present work, the codification proposed by [27] is used to handle the radiality constraint. This is rule-based codification to check and correct the infeasible radial topologies. The codification employs a graph theory-based method following three rules to identify and/or correct infeasible individuals whenever they appear in the computational process.

Rule 1: Each candidate switch must belong to its corresponding loop vector.

Rule 2: Only one candidate switch can be selected from one common branch vector.

Rule 3: All the common branch vectors of a prohibited group vector cannot participate simultaneously to form an individual. For further details about the loop vector, common branch vector and prohibited group vector, Ref. [27] may be referred to.

4. Handling Uncertainty in Load Demand and Renewable Power Generation

Several probabilistic and deterministic techniques have been suggested in the recent past to handle uncertainty in load demand and power generation from renewable DGs. Recently, Wang et al. [28] suggested deterministic polyhedral uncertainty sets to handle uncertain data, but the selection of data spread (DS) and budget of uncertainty (BOU) is a difficult task and thus needs a trade-off between the robustness and conservativeness of the solution. Recently, the same authors have extended the work of [28] by proposing self-adaptive polyhedral deterministic uncertainty sets (SPDUS) in [29]. They suggested SPDUS in such a way that both DS and BOU are automatically derived in accordance with the prevailing conditions using given annual historical uncertain data. According to this model, the hourly mean and deviation (SD) of the monthly data are employed to generate uncertainty sets where both DS and BOU are derived from these two statistical indices. The modeling may be briefly described as below:

The polyhedral uncertainty set $W_{m,st}^{ldr}$ for the load demand of residential node r at state st and month m is defined as

$$\begin{array}{r}\begin{array}{r}{W}_{m,st}^{ldr}=\left\{{\chi }_{n,m,st}^{ldr}\in R^{ldr}:{\underset{\_}{\omega }}_{r,m,st}^{ldr}\le {\chi }_{r,m,st}^{ldr}\le {\overline{\omega }}_{r,m,st}^{ldr}\right\}\\ \forall r\in N_r\\ {\underset{\_}{\omega }}_{r,m,st}^{ldr}={\omega }_{r,m,st}^{ldr}-k{\sigma }_{r,m,st}^{ld}\\ {\overline{\omega }}_{r,m,st}^{ldr}={\omega }_{r,m,st}^{ldr}+k{\sigma }_{r,m,st}^{ldr}\end{array}\}\\ s.t.{\widehat{\omega }}_{r,m}^{ldr}-k{\widehat{\sigma }}_{r,m}^{ldr}\le {\widehat{\chi }}_{r,m}^{ldr}\le {\widehat{\omega }}_{r,m}^{ldr}+k{\widehat{\sigma }}_{r,m}^{ldr}\end{array}$$

(24)

where ω-terms denote available data and χ-terms denote the synthetic data to be generated. The DS for the load demand of node r at state st for month m is described by the interval $[{\underset{\_}{\omega }}_{n,m,st}^{ldr},{\overline{\omega }}_{n,m,st}^{ldr}]$, say for the residential node. The uncertain load demand of node r at state st for month m is constrained by the DS $({\omega }_{r,m,st}^{ldr}\pm k{\sigma }_{r,m,st}^{ldr})$, where ${\sigma }_{r,m,st}^{ldr}$ is the SD of the hourly load demand over the month m for the node r at state st. The synthetic load data so far generated are further constrained using BOUs in the range $[{\widehat{\omega }}_{r,m}^{ldr}\pm k{\widehat{\sigma }}_{r,m}^{ldr}]$. Similarly, in uncertainty sets for industrial and commercial customers, SPVs and WTs can also be developed. Ref. [29] may be referred to for further explanations.

5. Simulation Results

The effectiveness of the proposed reliability indices has been investigated using the IEEE 33-bus test distribution system [30]. This is an 11 kV primary distribution system with 33 nodes and 37 lines including 5 tie-lines. The base configuration of the distribution network is obtained by opening all the tie-lines 33–37. The nominal system data of this system are given

Table 1. Brief data of the test systems.

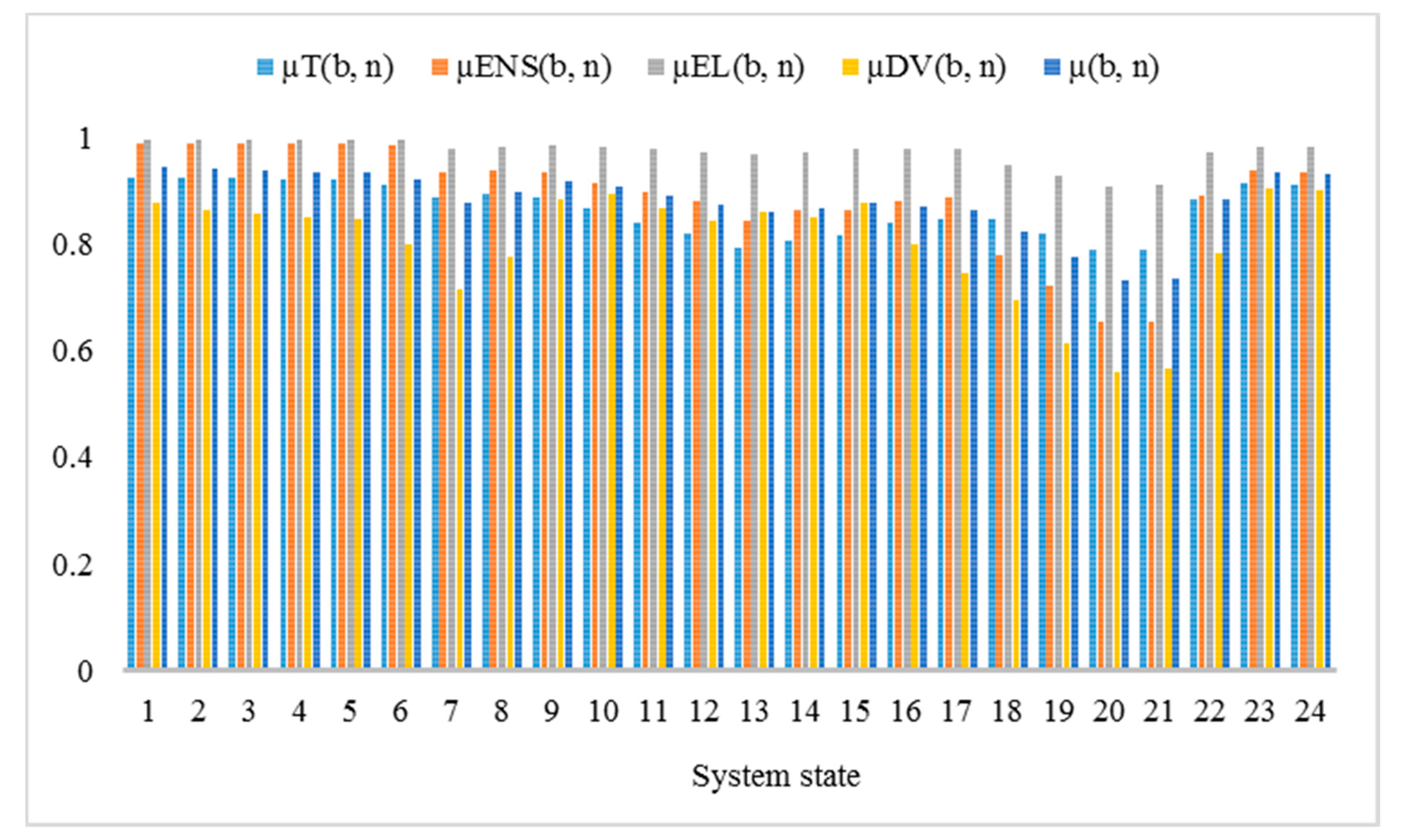
Particular	Value
Line voltage (kV)	12.66
Nominal active power demand (kW)	3715
Nominal reactive power demand (kVAr)	2300
Sectionalizing switches	1–32
Tie-switches	33–37
Base configuration with open lines	33 to 37
Power loss (kW)	202.5
Minimum node voltage (pu)	0.9131

and the detailed line and bus data may be referred to from the above-mentioned reference.

In order to show the difference between existing and proposed reliability indices, the distribution system is first assumed in base configuration. The existing and proposed reliability indices are determined for the distribution system at three different loading conditions, i.e., at nominal and ±10% of this loading. A comparison of the results obtained is presented in

Table 2. Comparison of existing and proposed reliability indices without distributed resources (DRs) before network reconfiguration (NR).

Reliability Index			F (Failure/yr)	T (hr/yr)	ENS (MWh/yr)
Load level	1	F(i)	3.18	1.86	437.67
		F(i,n)	3.18	1.86	437.67
		%ΔF	0	0	0
	1.1	T(i)	3.18	1.86	481.43
		T(i,n)	3.91	2.29	591.41
		%ΔT	22.97	22.89	22.84
	0.9	ENS(i)	3.18	1.86	393.9
		ENS(i,n)	2.53	1.49	314.41
		%ΔENS	–20.26	–20.20	–20.18

. It can be observed from the table that the proposed reliability indices depend upon system loading, where the higher the loading, the higher the value of indices, and vice-versa, however, they are exactly identical to the existing indices at nominal loading. It can also be observed that existing reliability indices do not vary with loading, so they are independent of concurrent Joules heating in distribution feeders. Moreover, the amount of variation is found to be consistent with the variation in system loading. This clearly highlights that the proposed reliability indices are different to existing indices, but are promising while dealing with dynamically changing system states. Interestingly, the index D remains almost unchanged. It happened because the index D(i,n) is the ratio of indices F(i,n) and T(i,n), so it nullifies the impact of the proposed dynamic failure rates.

In order to investigate the proposed method in a more realistic way, this test distribution system is modified by deploying diverse distributed resources (DRs) as shown in

Table 3. Existing distributed generation (DGs) and SCs assumed in a 33-bus test system.

SPV (Size in kWp/Site)	WT (Size in kWp/Site)	MT (Size in kW/Site)	SC (Size in kVAr/Site)
280/14, 840/24, 560/30	420/14, 700/24, 420/30	800/24	300/12, 300/25, 600/30

and Figure 2. The table shows the sizing and siting of SPVs, WTs, MT and shunt capacitors (SCs) which have been taken from [29]. The mean load and generation factors for 24 system states to represent a mean day are taken as shown in

Table 4. Load and generation factors used.

State	Load/Generation Factor			State	Load/Generation Factor
	Load	WT	SPV		Load	WT	SPV
1	0.5421	0.556	0	13	0.8711	0.896	0.967
2	0.5421	0.507	0	14	0.8000	0.894	0.921
3	0.5421	0.484	0	15	0.8711	0.799	0.820
4	0.5421	0.454	0	16	0.8711	0.688	0.625
5	0.5421	0.45	0	17	0.8711	0.704	0.398
6	0.6132	0.49	0	18	0.8711	0.728	0.158
7	0.6829	0.397	0.008	19	0.9303	0.763	0
8	0.6829	0.435	0.203	20	1.0000	0.784	0
9	0.6829	0.587	0.453	21	1.0000	0.806	0
10	0.7421	0.698	0.563	22	0.7513	0.823	0
11	0.7421	0.748	0.794	23	0.5421	0.88	0
12	0.7421	0.796	0.934	24	0.5421	0.911	0

. These factors are generated using (24). The dynamic energy charges in USD/kWh assumed for different time slots are shown in

Table 5. Dynamic electricity charges.

00AM-6AM	6AM-5PM	5PM-9PM	9PM-00AM
0.02	0.06	0.12	0.09

. GA is applied to solve the NR problem. For the application of the proposed method, the population size and maximum iterations are taken as 50 and 100, respectively, and the best solutions obtained after 100 trial runs are used for the study.

The application of the proposed method requires the determination of the lower and upper bounds of various fuzzy membership functions. The lower bound of these indices can be reasonably assumed to be zero, however, the upper bounds depend upon the particular network topology of the distribution network. The upper bounds are determined using single-objective NR optimization while considering only one objective at a time and the algorithm run to maximize the objective. The maximum value of each of the objectives so obtained is rounded-off to a higher side and presented in

Table 6. Maximum value of reliability indices obtained using optimal NR.

Fmax (Failure/yr)	Tmax (h/yr)	ENS max (USD/yr)	EL max (USD)	DVmax (p.u.)
5	3	800	70	0.10

. With these upper bounds, the multi-objective NR problem is formulated in a fuzzy framework.

Keeping the network topology in its base configuration, simulations are carried out for each of the 24 system states separately to optimize the objective function given by (14) and the results obtained are presented in Figure 3. It can be observed from the figure that all fuzzy member functions and hence the overall fuzzy member function also tend to reduce around the peak system loading. This is quite obvious as the failure rates of feeders, their power losses and node voltage deviations all increase with the increased power flows. The mean or minimum fuzzy membership functions, as the case may be, of the objectives and the corresponding de-fuzzified values are then determined as presented in

Table 7. Mean/minimum values of objectives before NR.

µFM(b)	µTM(b)	µENSM(b)	µELM(b)	µDVMIN(b)
0.8882	0.8660	0.8891	0.9743	0.5598
F(b) (failure/yr)	T(b) (hr/yr)	ENS(b) (USD/yr)	EL(b) (USD/yr)	DV(b) (p.u.)
0.5590	0.4021	88.7287	15757.7700	0.0440

. The distribution system is now optimally reconfigured to solve the multi-objective NR problem for each system state using GA and the best result obtained after 100 trial runs is presented in

Table 8. Optimal configurations obtained after NR.

State	Optimal Configuration	State	Optimal Configuration
1	33-37-35-13-36	13	20-37-35-13-8
2	33-37-35-13-36	14	20-37-33-10-34
3	33-37-35-13-36	15	33-37-35-9-34
4	33-37-35-13-36	16	33-37-35-11-34
5	33-37-35-13-36	17	33-37-35-12-36
6	33-37-35-13-36	18	33-37-35-12-36
7	33-37-35-14-36	19	33-37-35-14-36
8	33-37-35-13-36	20	33-37-35-14-36
9	33-37-35-13-36	21	33-37-35-14-36
10	20-37-11-34-36	22	33-37-35-12-36
11	20-37-8-12-36	23	20-37-35-34-36
12	20-37-8-12-36	24	20-37-35-34-36

and Figure 4.

The table shows the optimal network configuration for each system state and Figure 4 shows the fuzzy memberships and overall fuzzy membership function obtained for the respective optimal topology. A close comparison of Figure 4 with Figure 3 exhibits enhancement in all the objectives considered for each system state. The mean/minimum fuzzy membership functions of the objectives while considering all system states and the corresponding de-fuzzified values are determined as presented in

Table 9. Mean/minimum values of objectives after NR.

µFM(o)	µTM(o)	µENSM(o)	µELM(o)	µDVMIN(o)
0.8967	0.8732	0.8954	0.9812	0.5699
F(o) (failure/yr)	T(o) (hr/yr)	ENS(o) (USD/yr)	EL(o) (USD/yr)	DV(o) (p.u.)
0.5167	0.3804	83.6887	13122.48	0.0316
F(%)	T(%)	ENS (%)	EL(%)	DV(%)
7.57	5.40	5.68	16.72	28.18

. A comparison of Table 9 with Table 7 reveals enhancement in various objectives using NR which is quantified as percentage enhancement using NR and is also presented in Table 9. It can be observed from the table that the proposed NR methodology can simultaneously enhance reliability and network performance, though by different margins.

6. Discussion

Failure rates of different system components are the most crucial data for reliability analysis. Since accurate information of these failure rates is not available, most of the existing methods rely on average values of failure rates available in the literature. However, in real life, components would have different failure rates due to exposure to different factors such as the loading level. If a component is overloaded for a longer duration, its failure rate will increase due to increased Joules heating. In this context, the existing failure rates and related reliability indices need modifications. The reliability indices are also greatly affected by the presence of DRs in distribution systems as their presence changes the power flow among distribution feeders. The reliability indices that have been defined in the literature are based upon the average failure rate and average duration of an interruption that might occur for a system or its components in general. However, with the penetration of DRs and due to the frequent reconfiguration of distribution systems, the dynamics of the power flow is changed and therefore the use of the average failure rate will provide erroneous results for different reliability indices. The distribution system consists of various components such as distribution transformers, distribution feeders and switchgears. The useful life of each of these components depends upon the amount of current flows during the operation of distribution systems. The higher the magnitude of the current, the higher the heat produced on account of Joules heating, so more wear and tear occur, causing an increase in the failure rate. Therefore, failure rates of distribution components may be taken as proportional to the amount of Joules heating produced. Therefore, the failure rates need to be modified to take into account the heating effect of the actual feeder currents. In the present work, the failure rates are proposed to be redefined by considering the Joules heating of the distribution feeders. The Joules heating is proportional to the magnitude of the current flowing through the given feeder. Since the current flowing through the distribution feeders varies with the dynamically changing states, the failure rates of distribution feeders shall be made dynamic. In a dynamic electricity market, the electricity price depends upon the magnitude of system loading in a somewhat proportional manner. In such a scenario, the same amount of energy may have different costs during different hours of the day. In this context, the existing reliability index may not be a useful index in terms of economy.

Conventionally, the failure rate of distribution feeders is taken as proportional to their physical lengths, as in [31]. It implies that while maximizing system reliability using optimal NR, the radial topology would be probably obtained by opening most of the lengthy line sections, irrespective of the system’s feeder power losses. On the contrary, the optimal radial topology for loss minimization ought to open the lines causing feeder load balancing. This selection of lines is quite independent of their physical lengths. Therefore, reliability and network performance objectives are, in general, conflicting in nature. This has been well pointed out in [32]. However, this behavior will not sustain while considering the proposed dynamic failure rates of distribution feeders. It happened because the proposed failure rates are the function of the length of distribution feeders as well as distribution flows, i.e., Joules heating in the feeders. Since NR balances distribution flows among feeders, it thus reduces power losses, node voltage deviations and the dynamic failure rates of the feeders. In this way, both the reliability and performance of the distribution system can be enhanced simultaneously using NR. This fact can be observed from Figure 5 that compares the difference in the results of Table 7 and Table 9. The figure shows a negative change in all fuzzy membership functions for almost all system states. This implies that system reliability and performance has been improved using NR, thus shifting the paradigm of the conflicting nature of reliability and network performance objectives while considering underground distribution systems.

The proposed approach of redefining the failure rate is more realistic because distribution flows are crucial besides their physical lengths while considering a failure of undergrounded cables. The fairness of the proposed reliability indices is based upon the fact that overheated cables due to Joules heating are more prone to insulation puncture, whereas lengthy cables are more prone to fail on account of mechanical reasons. The proposed dynamic failure rate considers both electrical and mechanical reasons behind the failure of underground distribution feeders.

It is important to note that reliability and power quality parameters are the reflections of network operating conditions. For example, the optimal sitting and sizing of different DRs along with their kW/Var dispatch affect the power flows and power quality in the network [33]. Therefore, in the case where the distribution system is equipped with optimally placed DRs, the effect of NR on the power quality and reliability attributes is marginal. This is perhaps due to the fact that optimally placed DRs optimize the flow of power in all the lines and very small scope is left for further improvement. This is why the NR strategy is causing only marginal improvement in the system reliability and power quality parameters. For more clear differentiation, the percentage enhancements are determined with respect to the base condition of the distribution network and the results obtained are presented in

Table 10. Comparison results.

Scenario	Network Topology	F (Failure/yr)	T (h/yr)	ENS (USD/yr)	EL (USD/yr)	DV (p.u.)
Distribution system without DR	Before NR	1.7123	1.0055	229.0578	70722.99	0.0869
	After NR	1.5300	0.9123	207.92	66282.78	0.0803
Distribution system with DR	Before NR	0.5590	0.4021	88.7287	15757.77	0.0440
	After NR	0.5167	0.3804	83.6887	13122.48	0.0316

. It can be observed from the table that an enhancement of about 10% is obtained using NR in distribution systems without DRs. After DR placement, the effectiveness of NR is found to be increased marginally by about 2–3%.

7. Conclusions

This paper addresses a new methodology for the reliability evaluation of underground distribution systems by proposing dynamic failure rates of feeders and suggests network reconfiguration to enhance the reliability and performance of distribution systems. The proposed failure rates depend upon the feeder length as well as distribution flows and thus become dynamic. The study on a modified 33-bus distribution system reveals that the reliability and performance of distribution systems can be simultaneously enhanced using NR. The proposed failure rates provide true pictures for the reliability assessment of underground distribution systems as they duly address Joules heating in distribution feeders. The application results reveal a paradigm shift in the conflicting nature of reliability and network performance objectives while attempting a reconfiguration problem of distribution systems. In present study, the dynamic nature of the failure rate is explicitly considered by assuming a proportional relationship between the failure rate and Joules heating, however, the work can be extended using an exact relationship. Distributed energy storage devices are not considered to avoid complexity, but the work can be extended and investigated in their presence.