Analysis of V-Gutter Reacting Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions
Abstract
:1. Introduction
2. Algorithm for Post-Processing Methods
2.1. POD Algorithm
2.2. DMD Algorithm
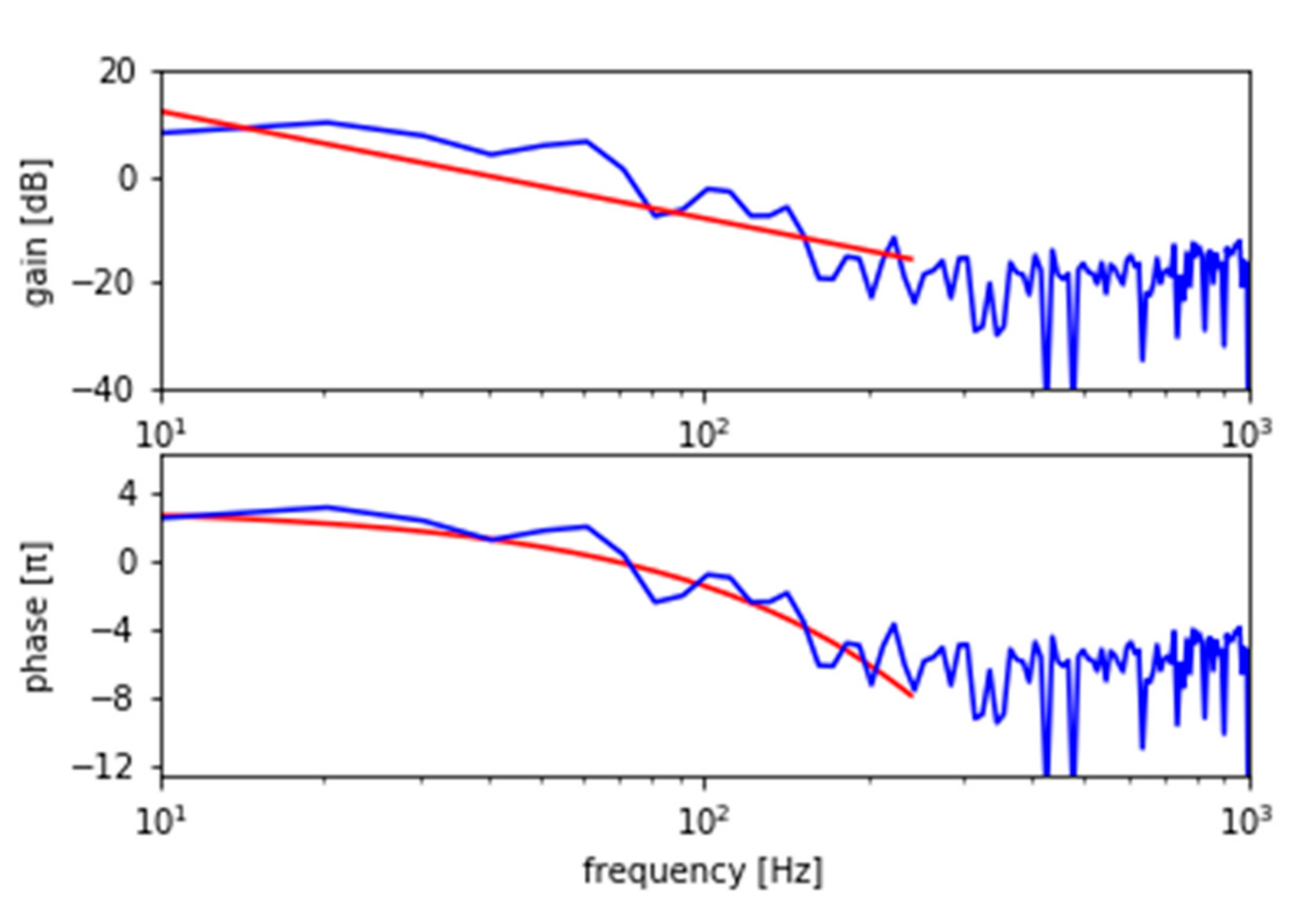
2.3. FTF Procedure
3. V-Gutter Geometry and the Numerical Method
4. Results
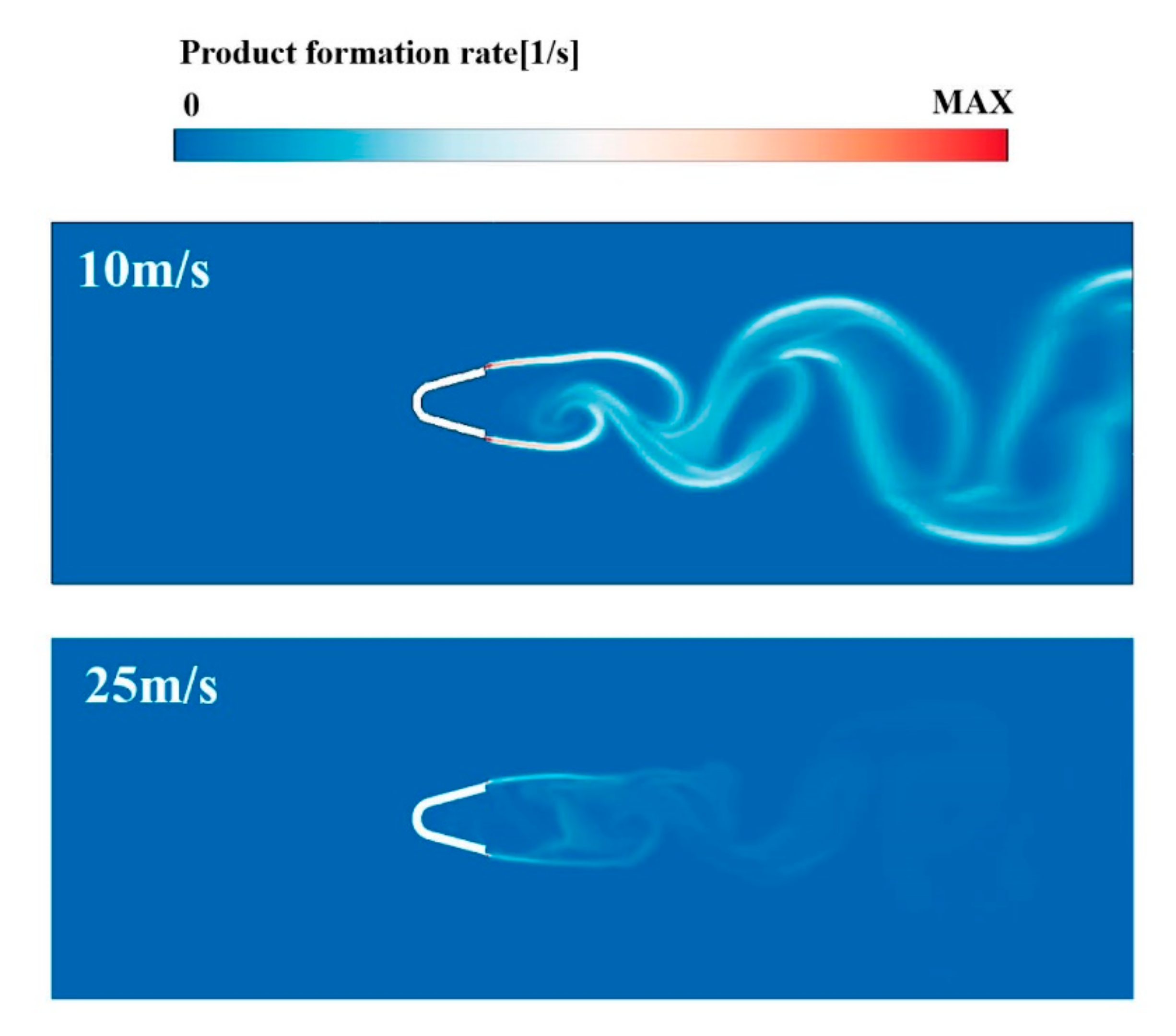
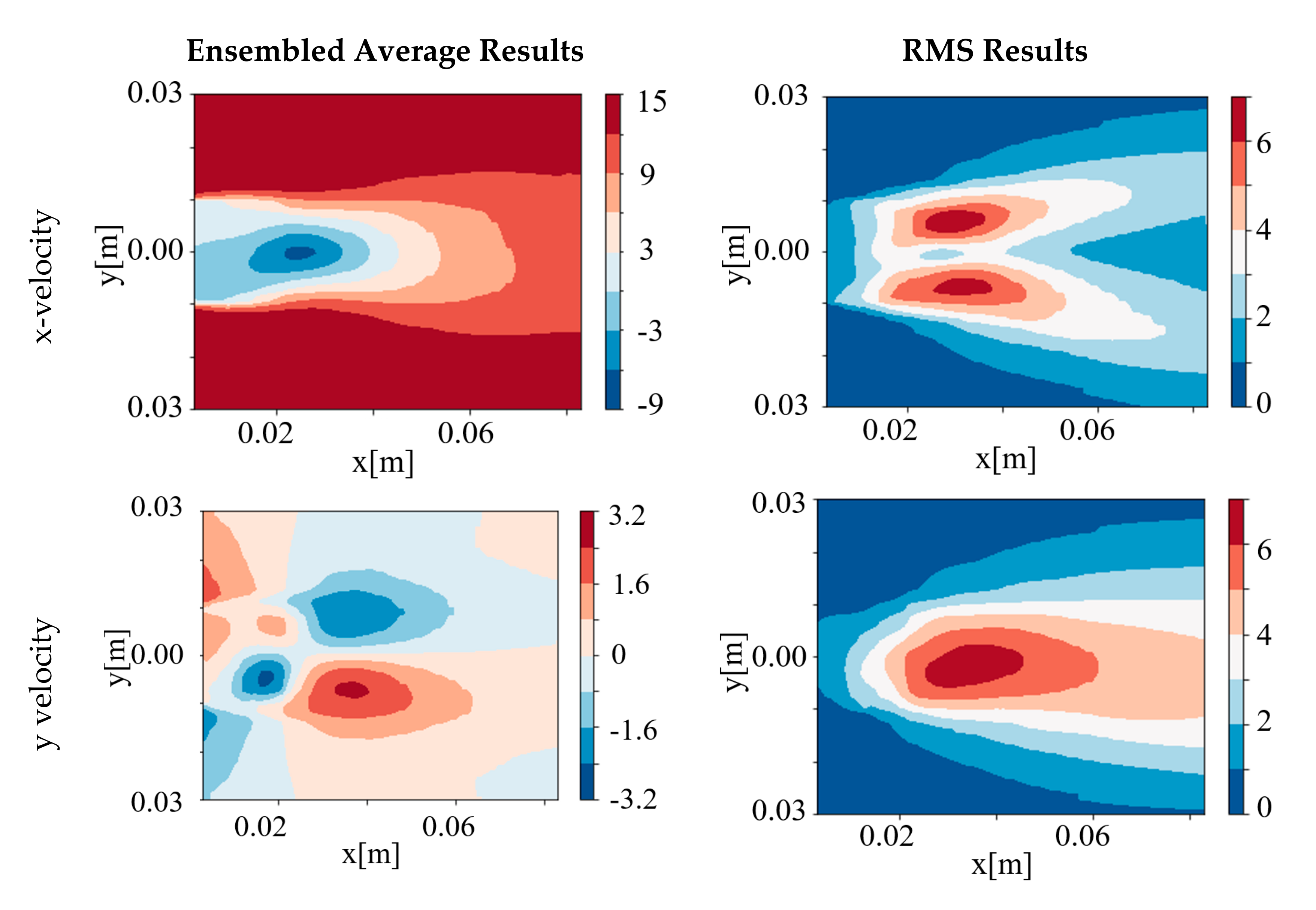
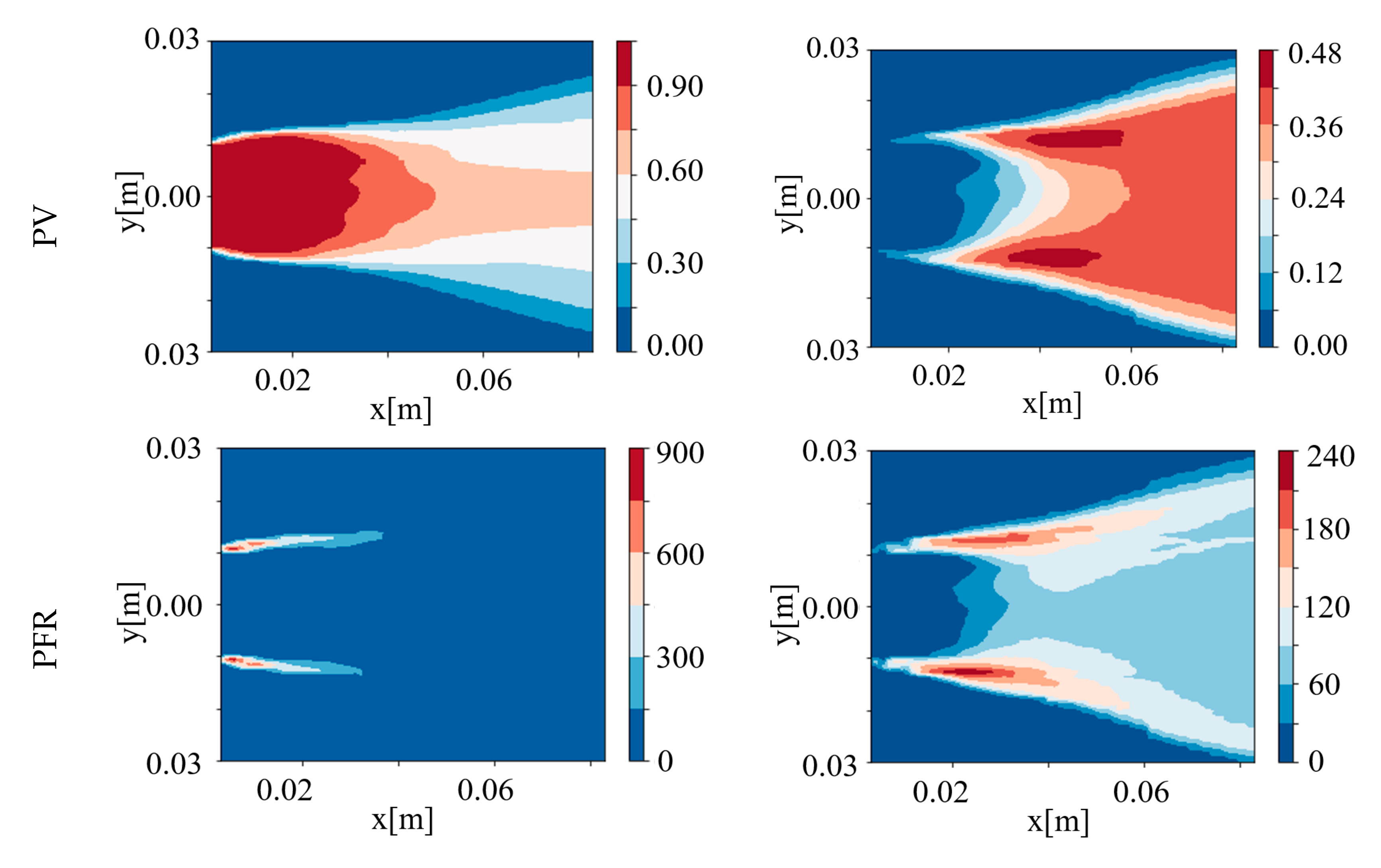
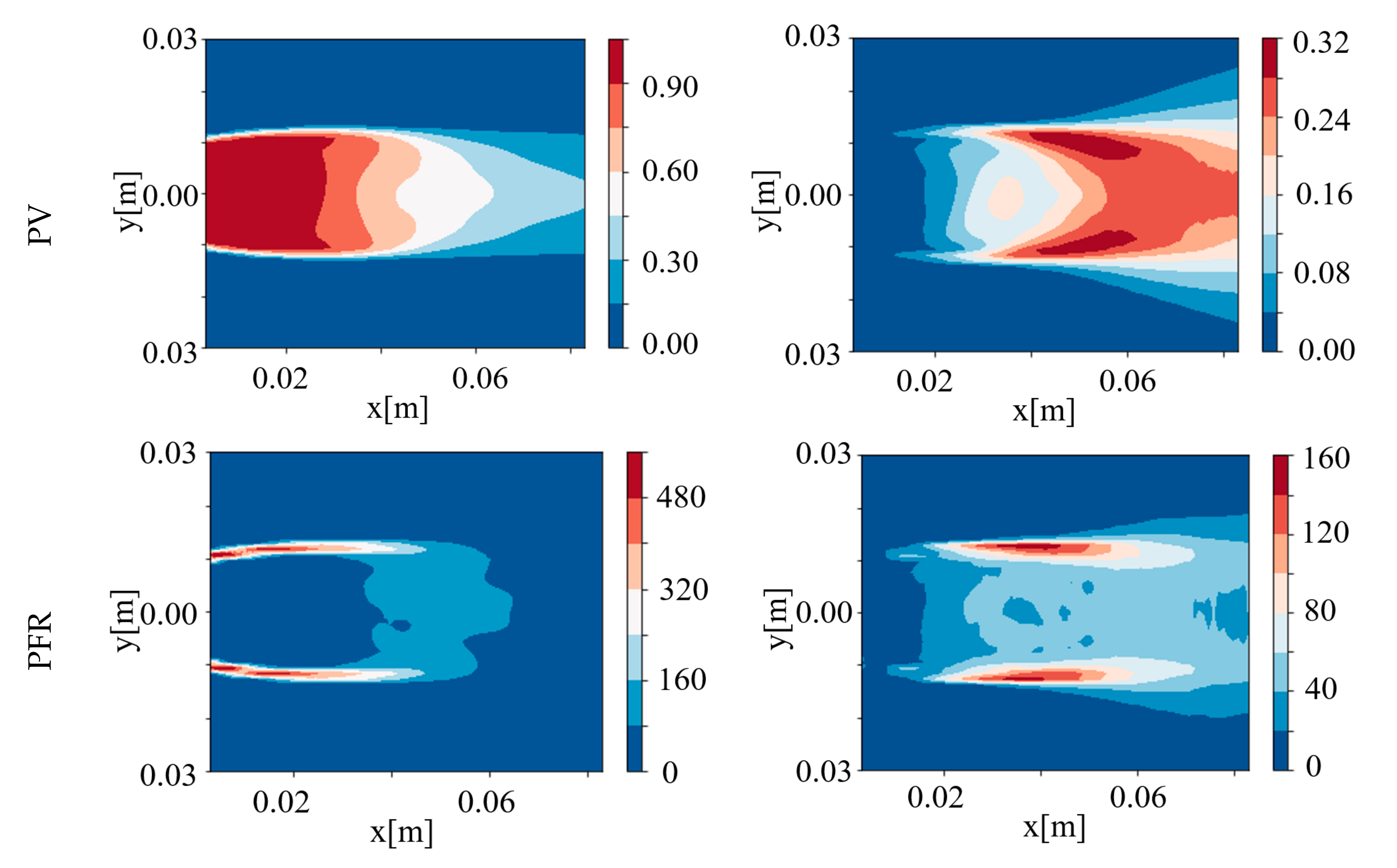
4.1. Instantaneous and Averaged Results
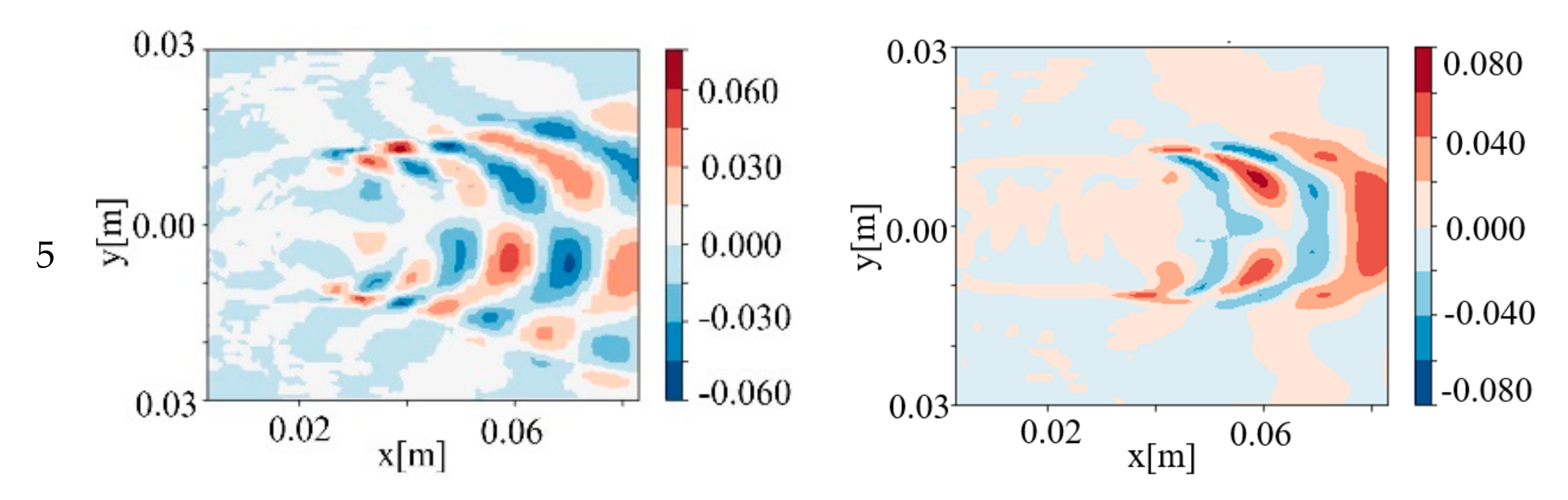
4.2. POD Results
4.3. DMD and FTF Results
4.3.1. Flame Dynamics and Dynamic Mode in Condition 1
- (1)
- The higher growth rate DMD modes.
- (2)
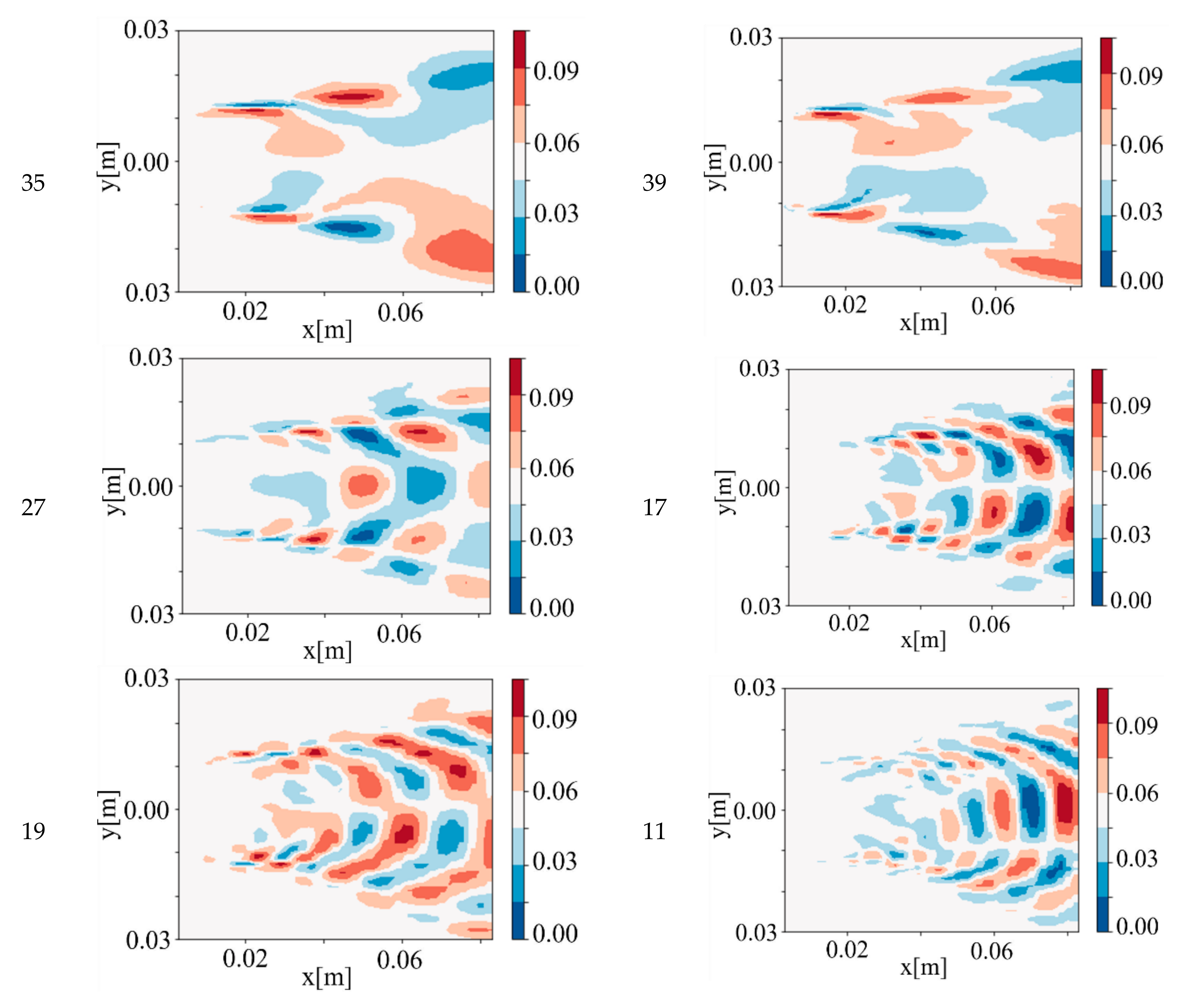
- The 35th and 39th DMD modes.
- (3)
- The 27th, 17th, and 19th DMD modes.
- (4)
- The 11th DMD mode is the second order of the 27th DMD mode.
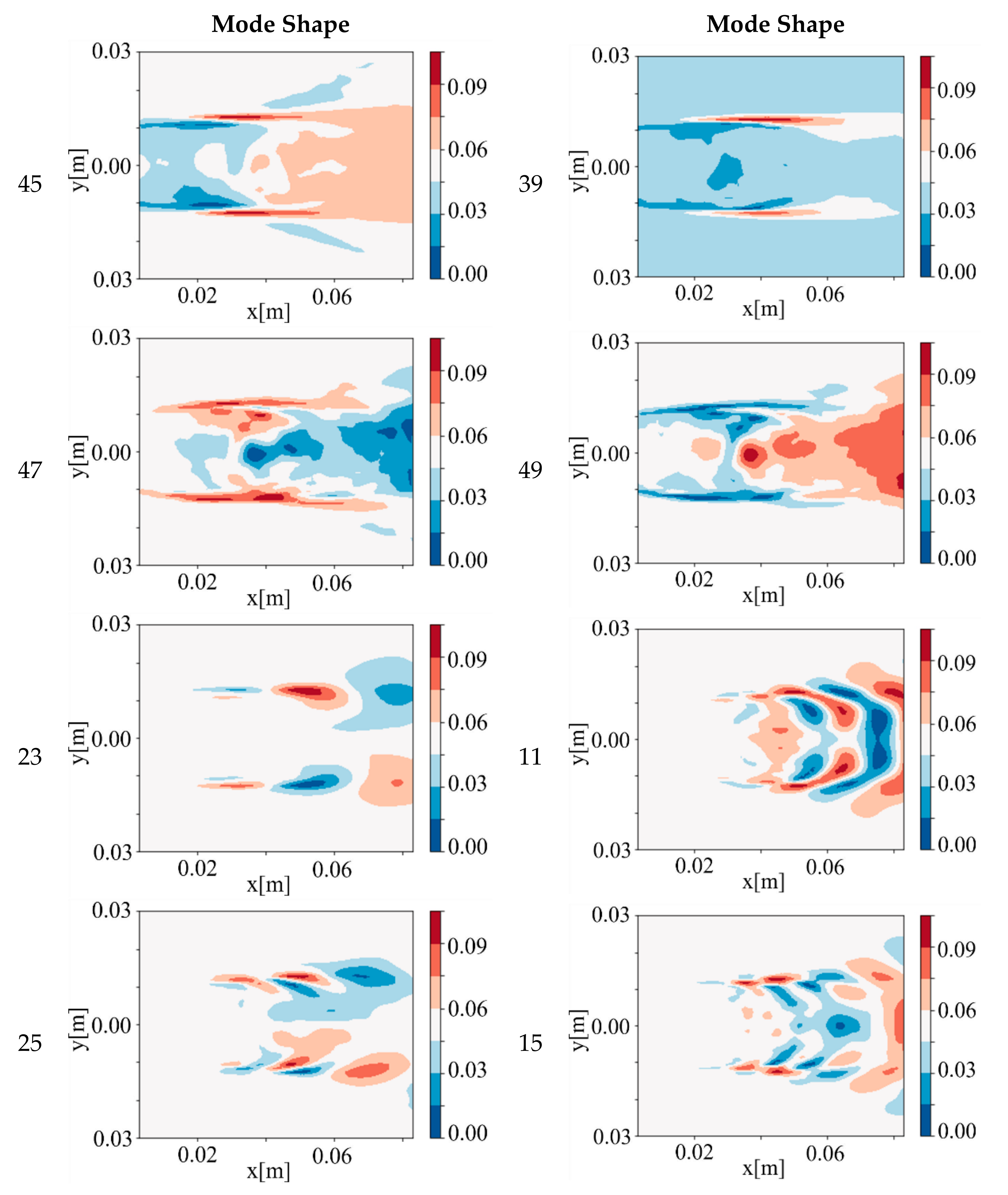
4.3.2. Flame Dynamics and Dynamic Mode in Condition 2
- (1)
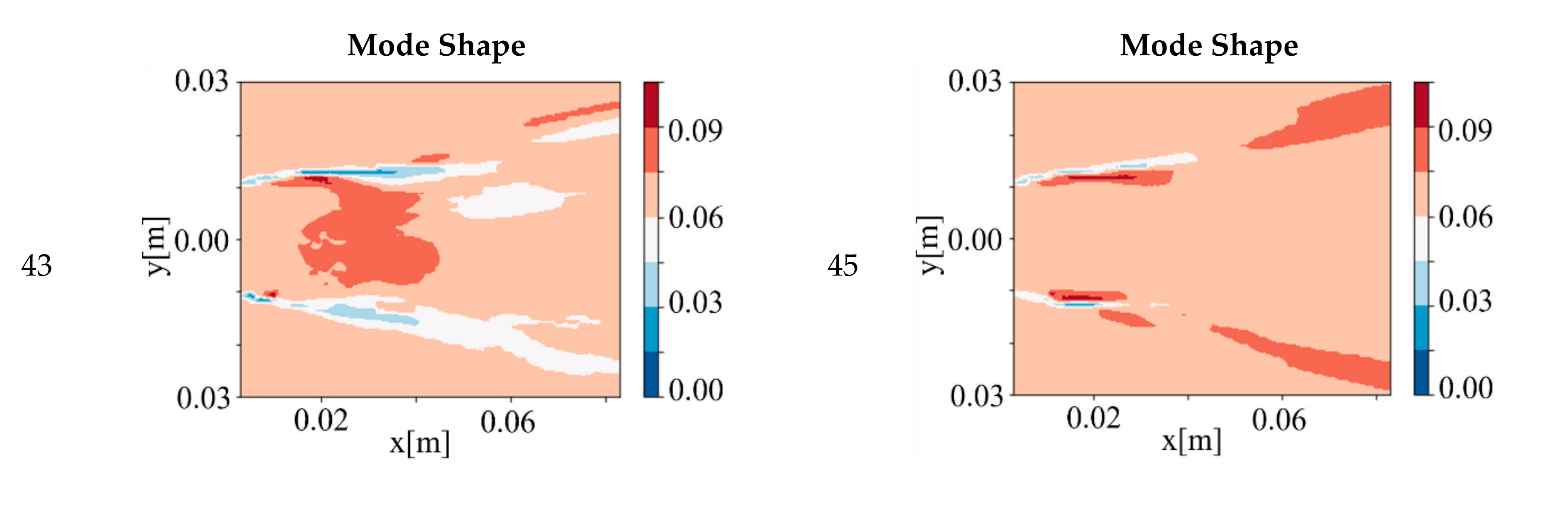
- The 47th and 49th DMD modes.
- (2)
- The 45th and 39th DMD modes.
- (3)
- The 23rd–25th DMD modes.
- (4)
- The 11th and 15th DMD modes.
5. Conclusions
- (1)
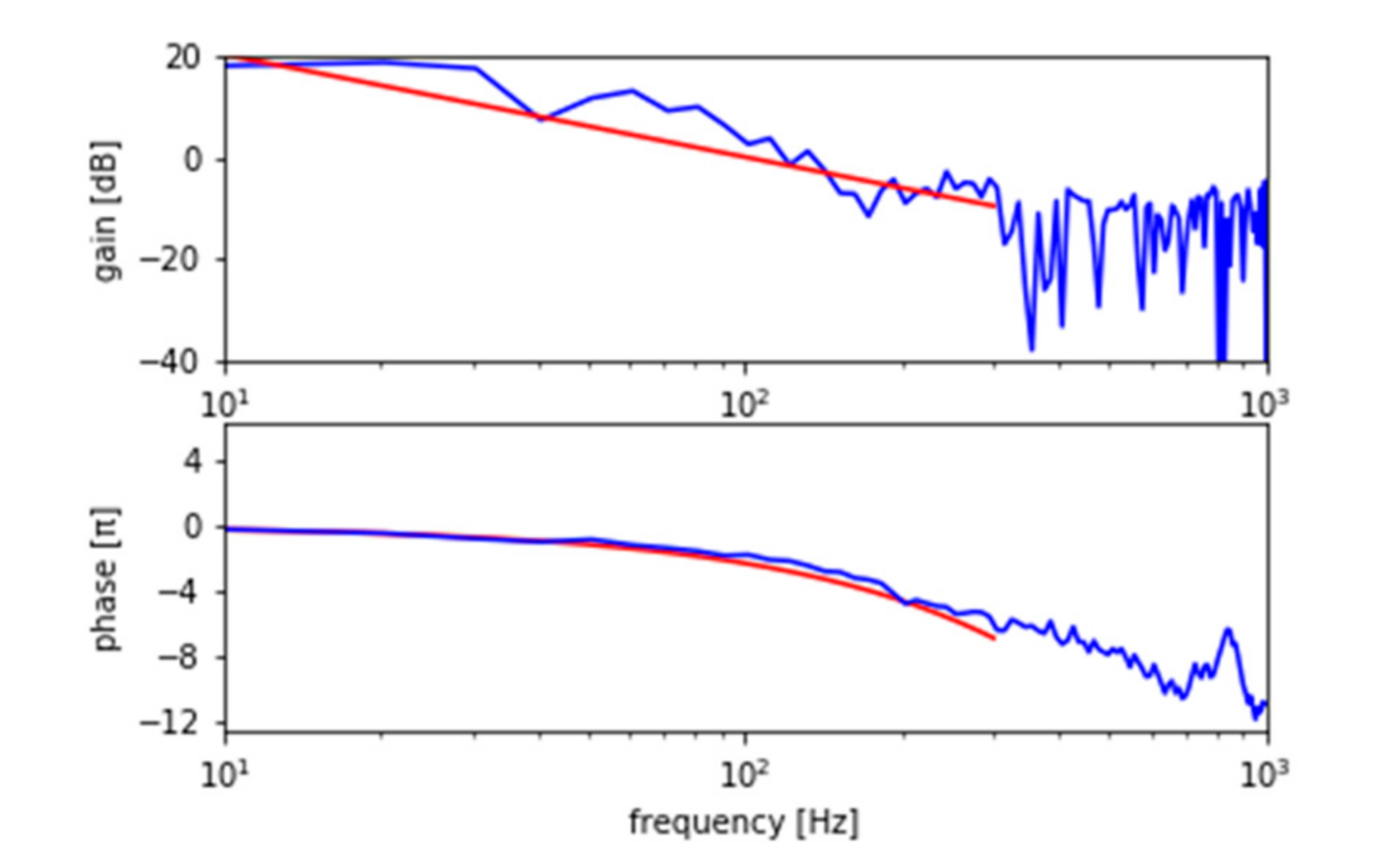
- The FTF results show that both flames behave as if the systems have proportional, inertial, and delay components. The time delays, which are simply estimated by curve fitting, indicate that the fluctuating flame fronts are shear layer flame fronts.
- (2)
- The shedding wake motion (BVK instability) and shear layer motion (KH instability) can then be captured from the POD post-processing method. The results indicate that the dominant frequencies of wake motion are different from those predicted using the literature method.
- (3)
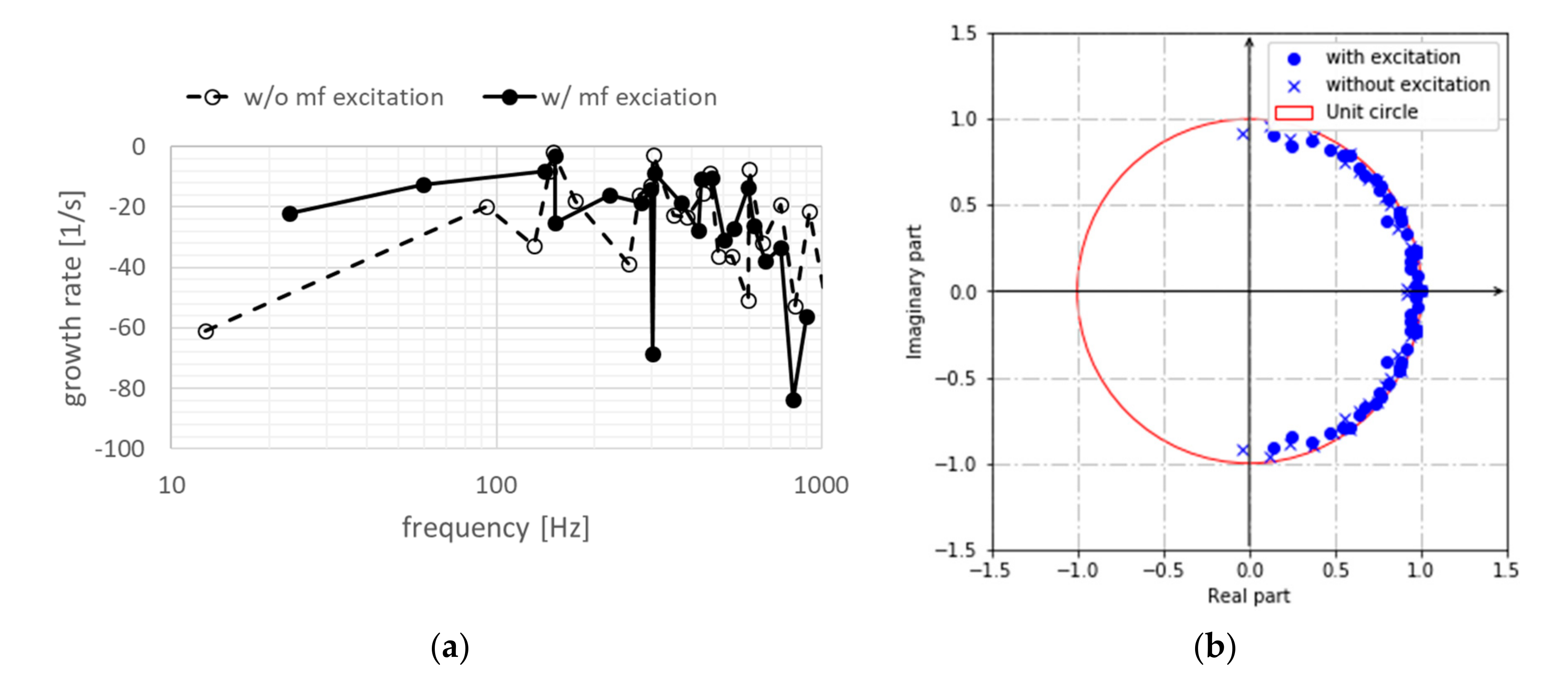
- Subsequently, the DMD method was performed. In order to understand which flame structures are responding, with and without inlet excitation, inflow boundary conditions were used for each condition. The excited DMD modes correspond to the shear layer flames swing and convect in the x-direction. Other DMD modes, which have a higher growth rate, are found to be in agreement with the first several POD modes.
- (4)
- Making a comparison between two inflow conditions, the negative growth rates for the two conditions confirm that the shear layer stabilized flame (condition 2) is more stable than the flame having wake instability (condition 1).
- (1)
- POD, which is essentially a dimensionality reduction method, its efficiency depends on the relevance of the selected dataset. For example, in condition 1, if the velocity only field is considered, the first two modes contain more accumulated energy than that for the flame only dataset. When the flame only data are considered, the accumulated energy drops.
- (2)
- When considering both flow and flame data in the same matrix, the standardization procedure should be taken. Actually, this step helps to eliminate the impact from different units andorder of magnitudes. However, this step has been rarely mentioned in the literature.
- (3)
- Single POD mode might contain multiple flow/flame structures, which are not separated since the variance of such a mode is large. Therefore, the POD cannot be used to distinguish these fine structures.
- (4)
- Due to uncertainty of the physical significance of higher order POD modes, only the first five modes are shown in this paper. The reason is that the point of inflection is already present in the scree plot. In the analysis, a cumulative variance contribution rate of 80% is considered.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| POD | proper orthogonal decomposition |
| DMD | dynamic mode decomposition |
| CFD | Computational fluid dynamics |
| LES | large-eddy simulation |
| RANS | reynolds-averaged Navier-Stokes equations |
| FTF | flame transfer function |
| DLN | dry low NOx |
| NOx | nitrogen oxides |
| HRR | heat release rate |
| LTI | linear time-invariant |
| KH | Kelvin Helmholtz |
| BVK | Bérnard von Karman |
| SVD | singular vector decomposition |
| PFR | product formation rate |
| WALE | wall-adapting local eddy viscosity |
| SGS | subgrid-scale |
| TFC | turbulent flame speed closure |
| PV | progress variable |
| RZ | recirculation zone |
| DRBS | discrete random binary signal |
| PSD | power spectrum density |
| DoE | design of experiment |
| RMS | root mean square |
| RSM | Reynolds stress mode |
| TKE | turbulent kinetic energy |
References
- Schlein, B.C.; Anderson, D.A.; Beukenberg, M.; Mohr, K.D.; Leiner, H.L.; Träptau, W. Development history and field experiences of the first FT8 gas turbine with dry low NOx combustion system. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar]
- Peter, B.; Hoffmann, S. Suppression of dynamic combustion instabilities by passive and active means. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000. [Google Scholar]
- Strutt, J. The Theory of Sound (Cambridge Library Collection—Physical Sciences); Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Sundaram, S.S.; Babu, V. Numerical Investigation of Combustion Instability in a V-Gutter Stabilized Combustor. J. Eng. Gas Turbines Power 2013, 135, 501–510. [Google Scholar] [CrossRef]
- Lieuwen, T.C.; Vigor, Y. Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms, and Modeling; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. [Google Scholar]
- Bloxsidge, G.J.; Dowling, A.P.; Langhorne, P.J. Reheat buzz: An acoustically coupled combustion instability. part 2. Theory. J. Fluid Mech. 1988, 193, 445–473. [Google Scholar] [CrossRef]
- Dowling, A.P. The calculation of thermoacoustic oscillations. J. Sound Vib. 1995, 180, 557–581. [Google Scholar] [CrossRef]
- Lacombe, R.; Föller, S.; Jasor, G.; Polifke, W.; Aurégan, Y.; Moussou, P. Identification of aero-acoustic scattering matrices from large eddy simulation: Application to whistling orifices in duct. J. Sound Vib. 2013, 332, 5059–5067. [Google Scholar] [CrossRef]
- Schuermans, B.; Guethe, F.; Pennell, D.; Guyot, D.; Paschereit, C.O. Thermoacoustic modeling of a gas turbine using transfer functions measured under full engine pressure. J. Eng. Gas Turbines Power 2010, 132, 503–514. [Google Scholar] [CrossRef]
- Noiray, N.; Durox, D.; Schuller, T.; Candel, S. Self-induced instabilities of premixed flames in a multiple injection configuration. Combust. Flame 2006, 145, 435–446. [Google Scholar] [CrossRef]
- Durox, D.; Schuller, T.; Candel, S. Combustion dynamics of inverted conical flames. Proc. Combust. Inst. 2005, 30, 1717–1724. [Google Scholar] [CrossRef]
- Huber, A.; Polifke, W. Dynamics of Practical Premixed Flames, Part I: Model Structure and Identification. Int. J. Spray Combust. Dyn. 2009, 1, 199–228. [Google Scholar] [CrossRef]
- Biagioli, F.; Wysocki, S.; Alemela, R.; Srinivasan, S.; Denisov, A. Experimental and LES analysis of a premix swirl burner under acoustic excitation. In Proceedings of the ASME Turbo Expo: Turbomachinery Technical Conference and Exposition Charlotte, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Biagioli, F.; Lachaux, T.; Narendran, S. Investigation of the Dynamic Response of Swirling Flows Based on LES and Experiments. Flow Turbul. Combust. 2014, 93, 521–536. [Google Scholar] [CrossRef]
- Biagioli, F.; Guethe, F. Effect of pressure and fuel-air unmixedness on NOx emissions from industrial gas turbine burners. Combust. Flame. 2007, 151, 274–288. [Google Scholar] [CrossRef]
- Biagioli, F.; Paikert, B.; Genin, F.; Noiray, N.; Bernero, S.; Syed, K. Dynamic response of turbulent low emission flames at different vortex breakdown conditions. Flow Turbul. Combust. 2013, 90, 343–372. [Google Scholar] [CrossRef]
- Dolan, B.J.; Gomez, R.V.; Zink, G.; Pack, S.; Gutmark, E.J. High-Speed imaging of combustion oscillations in a multiple nozzle staged combustor. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Huang, C.; Anderson, W.E.; Harvazinski, M.E.; Sankaran, V.S. Analysis of self-excited combustion instabilities using decomposition techniques. AIAA J. 2016, 54, 2791–2807. [Google Scholar] [CrossRef]
- Wysocki, S.; Syed, K.J.; Biagioli, F. Frequency response of turbulent partially premixed flame stabilized in free-standing vortex breakdown. Combust. Sci. Technol. 2019, 191, 797–832. [Google Scholar] [CrossRef]
- Schmid, P.; Sesterhenn, J. Dynamic Mode Decomposition of numerical and experimental data. J. Fluid Mech. 2008, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.W.; MeziĆ, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Son, J.; Sohn, C.H.; Yoon, J.; Bae, J.; Yoon, Y. Combustion Instability Analysis of a Model Gas Turbine by Application of Dynamic Mode Decom-position. J. Korean Combust. 2019, 24, 51–56. [Google Scholar] [CrossRef]
- Palies, P.; Ilak, M.; Cheng, R. Transient and limit cycle combustion dynamics analysis of turbulent premixed swirling flames. J. Fluid Mech. 2017, 830, 681–707. [Google Scholar] [CrossRef]
- Wilhite, J.M.; Dolan, B.J.; Gomez, R.V.; Kabiraj, L.; Gutmark, E.J. Analysis of combustion oscillations in a staged MLDI burner using decomposition methods and recurrence analysis. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Ebrahimi, H. Overview of gas turbine augmentor design, operation, and combustion oscillation. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Sacramento, CA, USA, 9–12 July 2006. [Google Scholar]
- Lovett, J.; Brogan, T.; Philippona, D.; Keil, B.; Thompson, T. Development needs for advanced afterburner designs. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar]
- Hanbhogue, S.J.; Husain, S.; Lieuwen, T. Lean blowoff of bluff body stabilized flames: Scaling and dynamics. Prog. Energy Combust. Sci. 2009, 35, 98–120. [Google Scholar] [CrossRef]
- Cardell, G.S. Flow Past a Circular Cylinder with a Permeable Splitter Plate. Ph.D. Thesis, California Insititute of Technology, Pasadena, CA, USA, 1993. [Google Scholar]
- Lieuwen, T.; Shanbhogue, S.; Khosla, S.; Smith, C. Dynamics of Bluff Body Flames Near Blowoff. In Proceedings of the 45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Smith, C.; Nickolaus, D.; Leach, T.; Kiel, B.; Garwick, K. LES blowout analysis of premixed flow past v-gutter flameholder. In Proceedings of the 45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Bothien, M.; Demian, L.; Yang, Y.; Alessandro, S. Reconstruction and analysis of the acoustic transfer matrix of a reheat flame from large-eddy simulations. J. Eng. Gas Turbines Power 2019, 141, 021018. [Google Scholar] [CrossRef]
- Yang, Y.; Noiray, N.; Scarpato, A.; Schulz, O.; Bothien, M. Numerical analysis of the dynamic flame response in alstom reheat combustion systems. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. Part I: Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Chong, T.W.; Komarek, T.; Kaess, R.; Föller, P. Identification of Flame Transfer Functions from LES of a Premixed Swirl Burner; ASME Turbo Expo: Glasgow, UK, 18 June 2010. [Google Scholar]
- Lennart, L. System Identification: Theory for the User, 2nd ed.; Pearson: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Celik, I.; Klein, M.; Janicka, J. Assessment measures for engineering LES applications. J. Fluids Eng. 2009, 131, 031102. [Google Scholar] [CrossRef]
- Pope, S.B. Ten Questions Concerning the Large-Eddy Simulation of Turbulent Flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef] [Green Version]
- Geurts Bernard, J. A framework for predicting accuracy limitations in large-eddy simulation. Phys. Fluids 2002, 14, L41–L44. [Google Scholar] [CrossRef] [Green Version]
- Celik, I.B.; Cehreli, Z.N.; Yavuz, I. Index of Quality for Large Eddy Simulations. J. Fluids Eng. 2005, 127, 949–958. [Google Scholar] [CrossRef]
- Klein, M. An Attempt to Assess the Quality of Large Eddy Simulations in the Context of Implicit Filtering. Flow Turbul. Combust. 2005, 75, 131–147. [Google Scholar] [CrossRef]
- Wang, S.; Hsieh, S.-Y.; Vigor, Y. Unsteady flow evolution in swirl injector with radial entry. I. Stationary conditions. Phys. Fluids. 2005, 17, 045106. [Google Scholar] [CrossRef] [Green Version]
- Davidson, L. Large Eddy Simulations: How to evaluate resolution. Int. J. Heat Fluid Flow 2009, 30, 1016–1025. [Google Scholar] [CrossRef] [Green Version]
- Freitag, M.; Klein, M. Direct Numerical Simulation of a Recirculating, Swirling Flow. Flow Turbul. Combust. 2005, 75, 51–66. [Google Scholar] [CrossRef]
- Berkeley Mechnical Engineering. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 12 June 2019).
- Zimont, V.; Lipatnikov, A.N. A numerical model of premixed turbulent combustion of gases. Chem. Phys. Rep. 1995, 14, 993–1025. [Google Scholar]
- Zimont, V.; Polifke, W.; Bettelini, M.; Weisenstein, W. An efficient computational model for premixed turbulent combustion at high Reynolds numbers based on a turbulent flame speed closure. J. Eng. Gas Turbines Power. 1998, 120, 526–532. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zhang, Z.H. Large eddy simulation calculated flame dynamics of one F-class gas turbine combustor. Fuel 2020, 261, 116451. [Google Scholar] [CrossRef]
- Eriksson, P. The Zimont TFC model applied to premixed bluff body stabilized combustion using four different RANS turbulence models. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
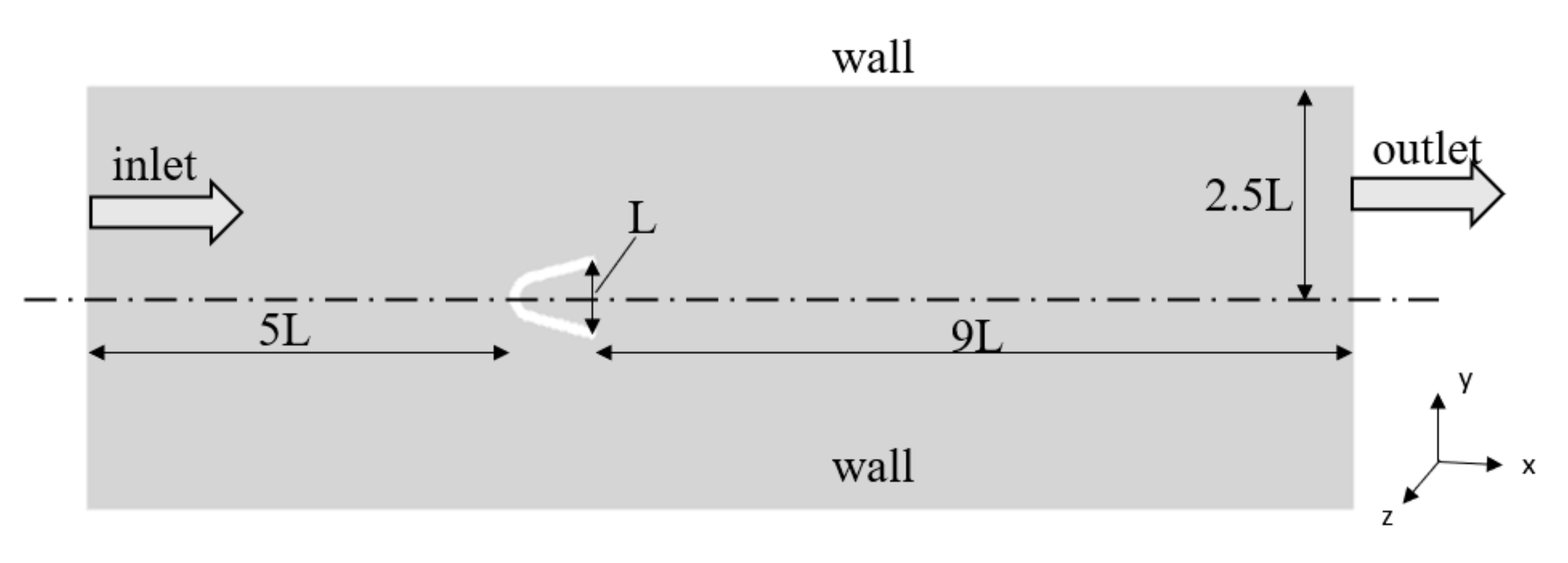

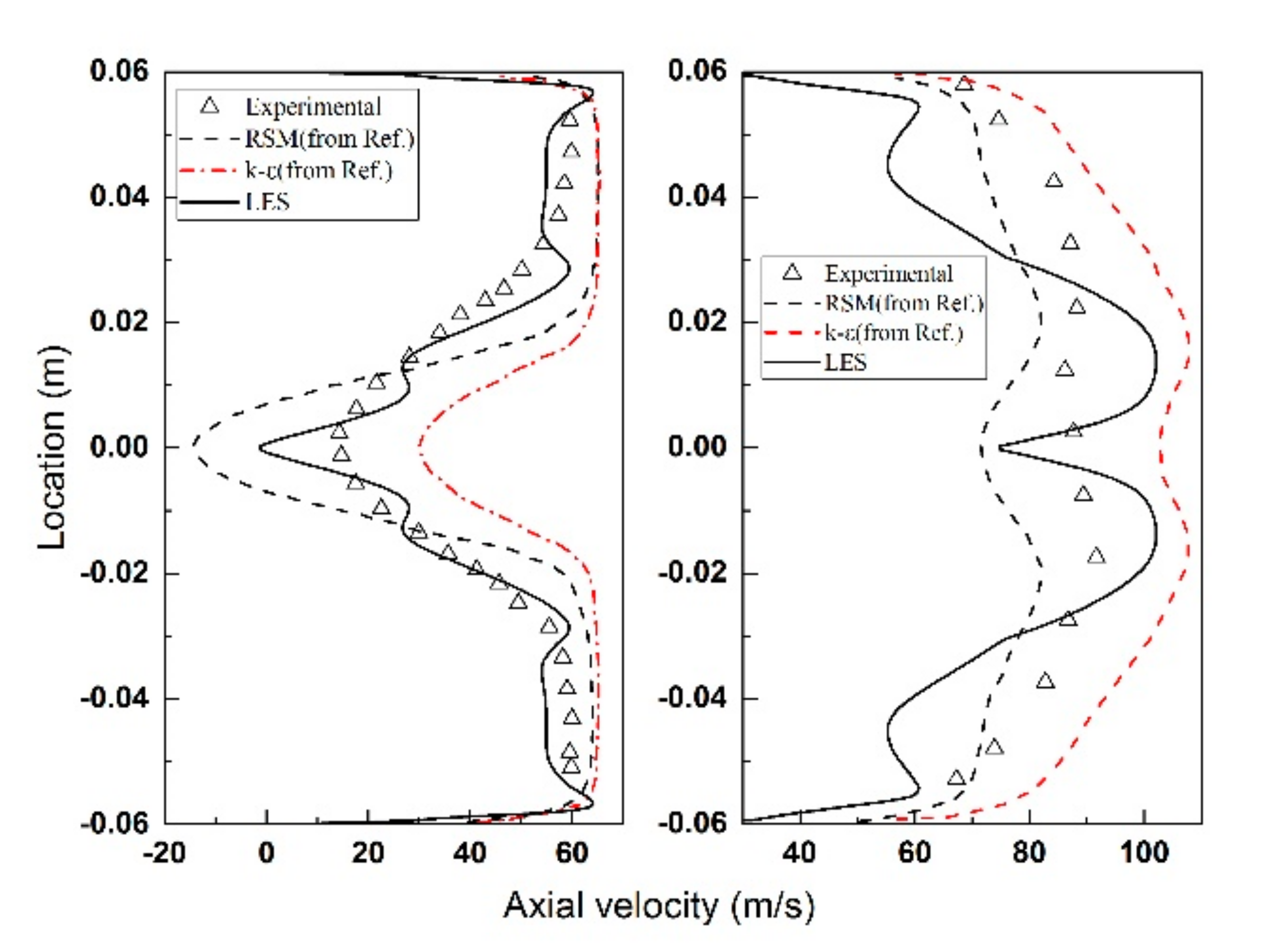
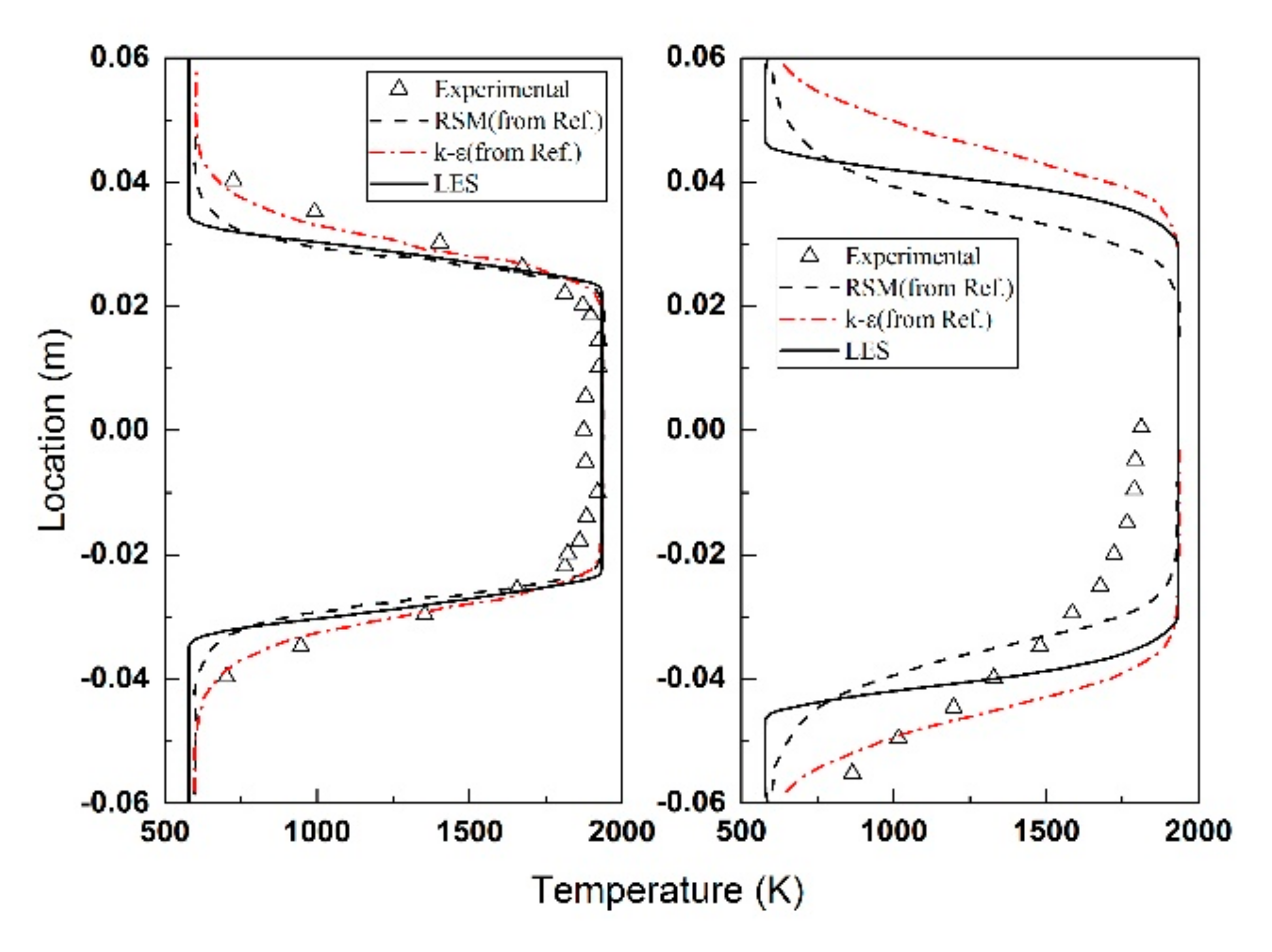


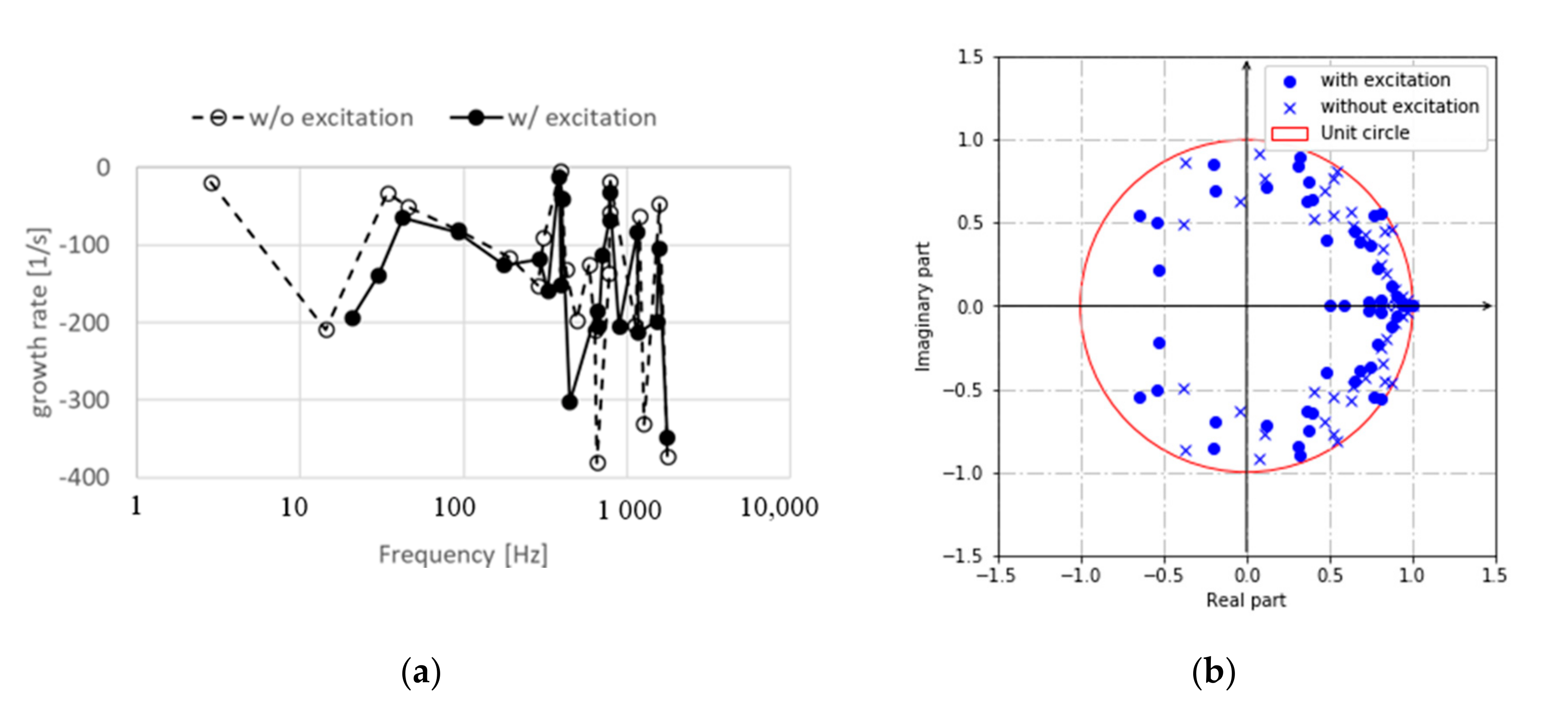
| V-Gutter Opening Angle () | Inflow Velocity U (m/s) | Equivalence Ratio () | |
|---|---|---|---|
| Condition 1 | 30 | 10 | 0.5148 |
| Condition 2 | 30 | 25 | 0. 5148 |
| POD | DMD | |||
|---|---|---|---|---|
| Mode Number | Frequency [Hz] | Mode Number | Frequency [Hz] | Growth Rate [1/s] |
| No corresponding modes in the first five POD modes | 43 | 23 | −22 | |
| 45 | 60 | −12 | ||
| 1 | 150 | 35 | 152 | −3 |
| 2 | 39 | 141 | −8 | |
| 3 | 300 | 27 | 307 | −9 |
| 4 | ||||
| 5 | 420–470 | 17 | 460 | −10 |
| 19 | 429 | −11 | ||
| No corresponding modes in the first five POD modes | 11 | 594 | −13 | |
| POD | DMD | |||
|---|---|---|---|---|
| Mode Number | Frequency [Hz] | Mode Number | Frequency [Hz] | Growth Rate [1/s] |
| No corresponding modes in the first five POD modes | 45 | 42 | −65 | |
| 39 | 92 | −83 | ||
| 47 | 21 | −194 | ||
| 49 | 30 | −139 | ||
| 2, 3 | 400 | 23 | 383 | −11 |
| No corresponding modes in the first five POD modes | 25 | 394 | −39 | |
| 5 | 800 | 11 | 782 | −32 |
| 15 | 778 | −68 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Liu, X.; Zhang, Z. Analysis of V-Gutter Reacting Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions. Energies 2020, 13, 4886. https://doi.org/10.3390/en13184886
Yang Y, Liu X, Zhang Z. Analysis of V-Gutter Reacting Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions. Energies. 2020; 13(18):4886. https://doi.org/10.3390/en13184886
Chicago/Turabian StyleYang, Yang, Xiao Liu, and Zhihao Zhang. 2020. "Analysis of V-Gutter Reacting Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions" Energies 13, no. 18: 4886. https://doi.org/10.3390/en13184886
APA StyleYang, Y., Liu, X., & Zhang, Z. (2020). Analysis of V-Gutter Reacting Flow Dynamics Using Proper Orthogonal and Dynamic Mode Decompositions. Energies, 13(18), 4886. https://doi.org/10.3390/en13184886




