Measuring the Risk of Supply and Demand Imbalance at the Monthly to Seasonal Scale in France
Abstract
1. Introduction
2. Methodology
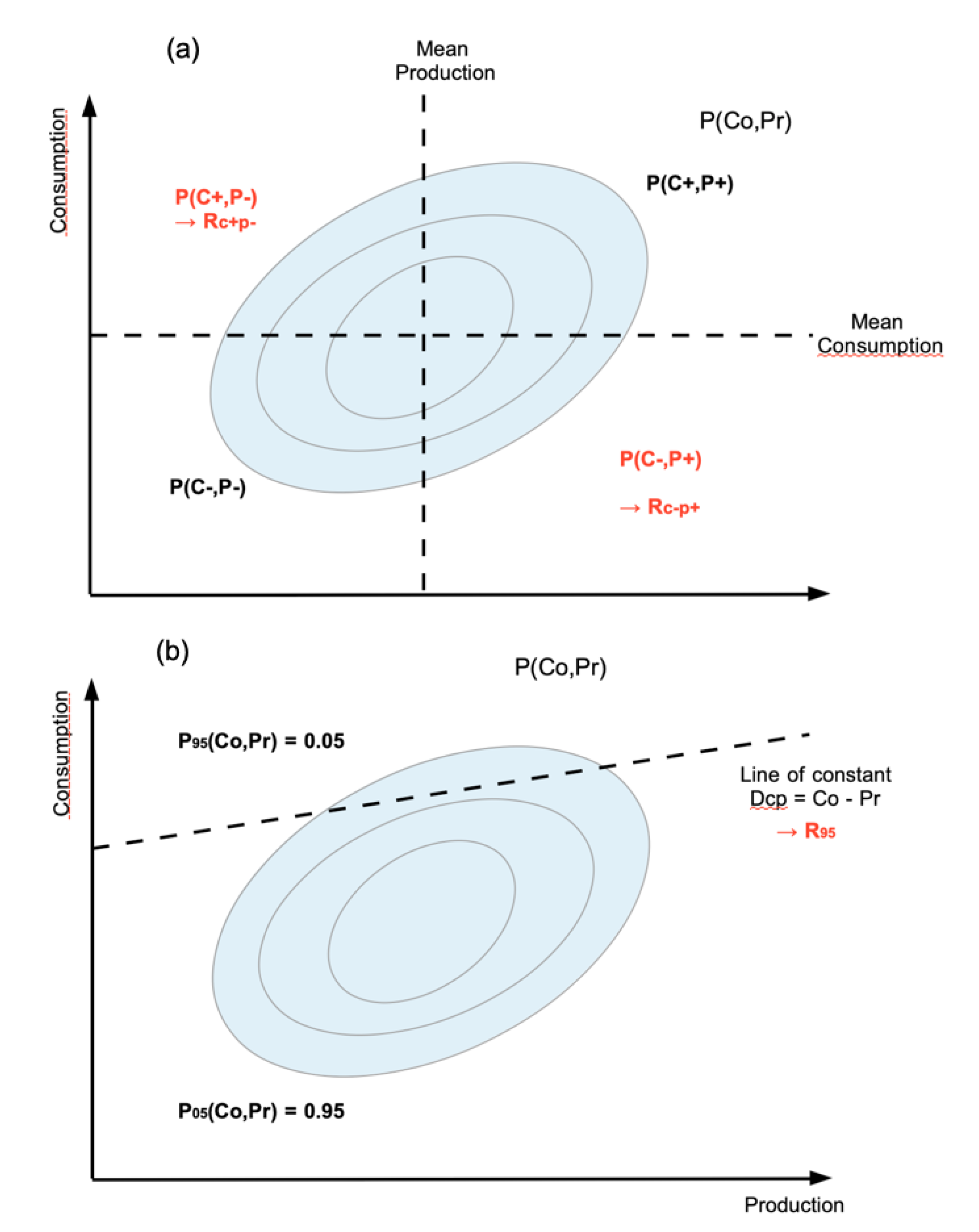
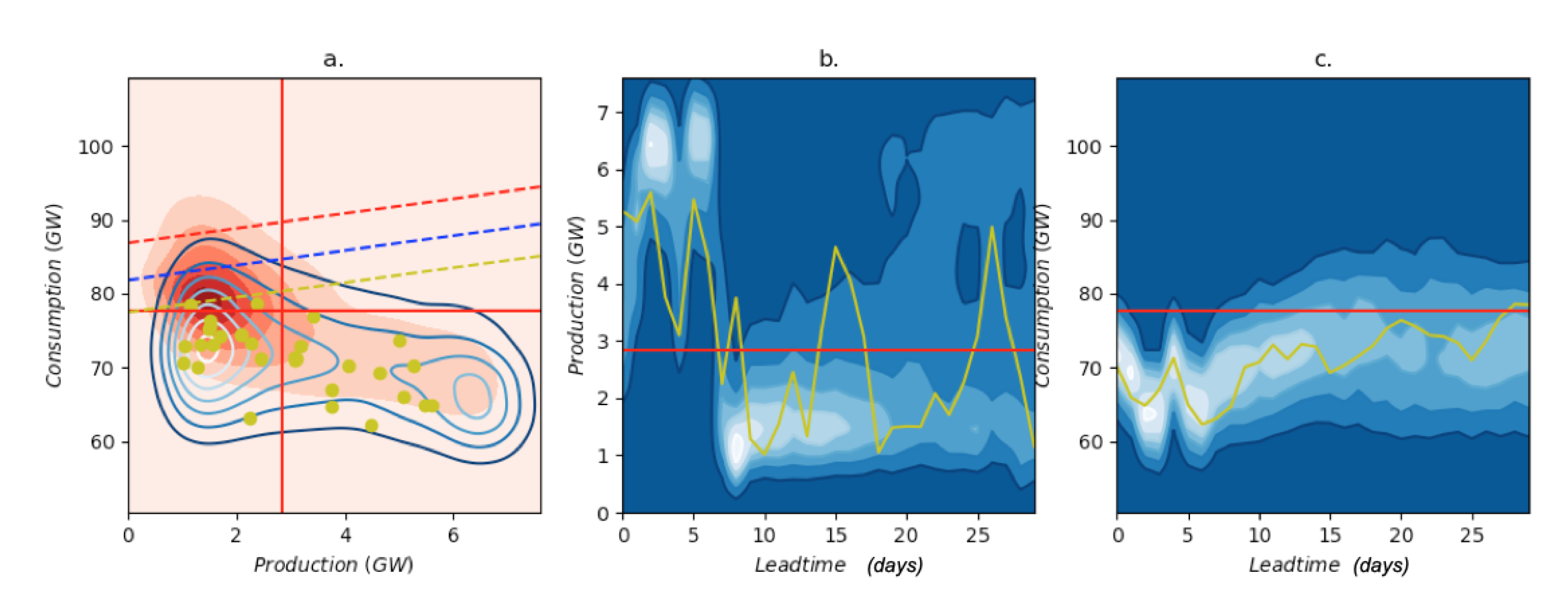
2.1. Risk Measures
- the upper-left quadrant, where and , corresponds to a risk of high consumption and low production. It is referred in the following as .
- the lower-right quandrant, where and , orresponds to a risk of low consumption and high production. It is referred in the following as .
- a seasonal climatology estimated over a long period of observed consumption and production (typically 30 years or more)
- a ‘real’ seasonal joint distribution estimated on the sample of observed or inferred consumption and production for the specific season
- a reconstructed (or forecasted) seasonal joint distribution using the model detailed in Section 2.2
2.2. Modelling the Joint PDF of Consumption and Production
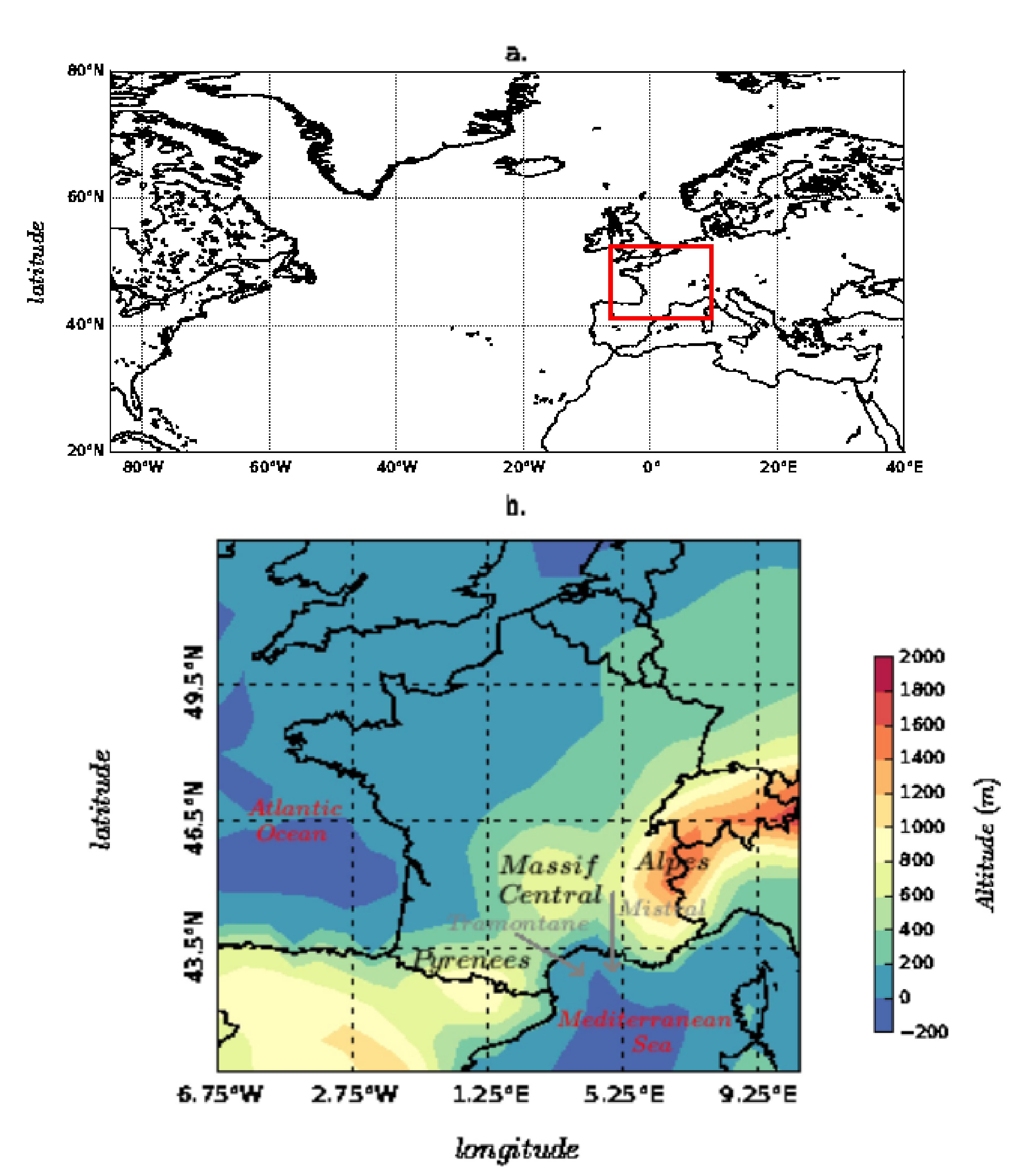
2.2.1. Explanatory Variables
2.2.2. Consumption () and production ()
2.3. Calibration of the Model
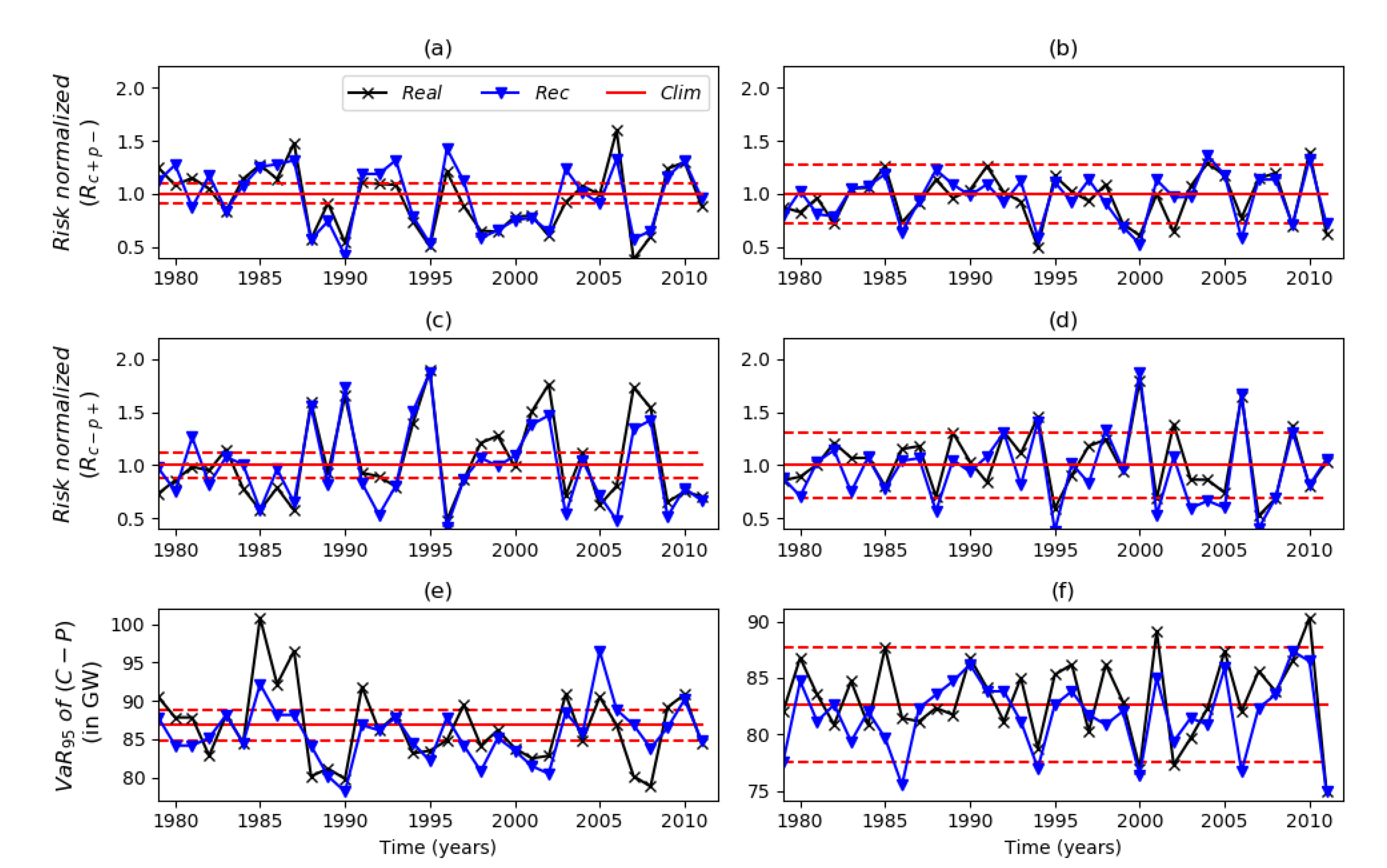
3. Model Performance Assessment
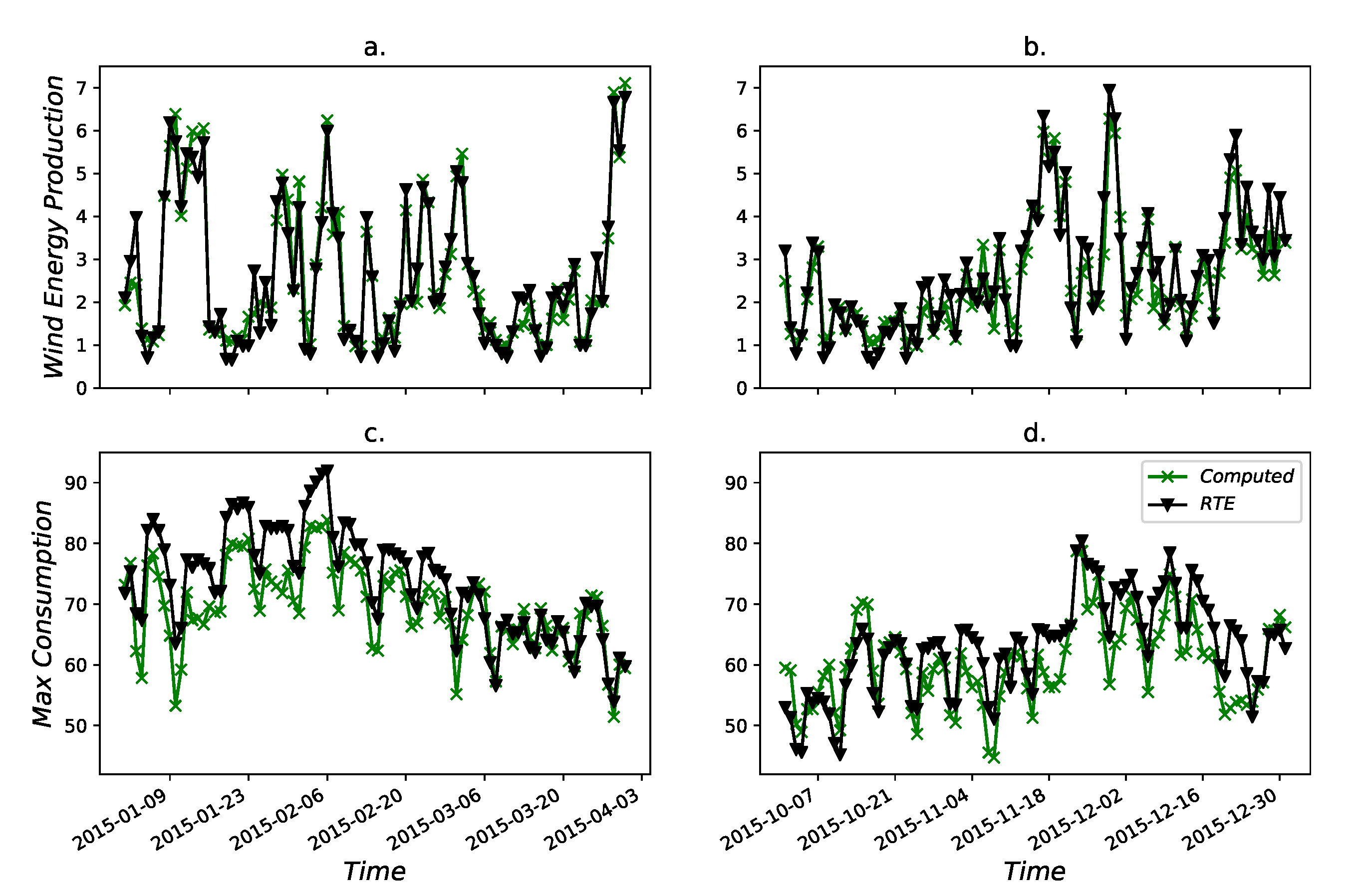
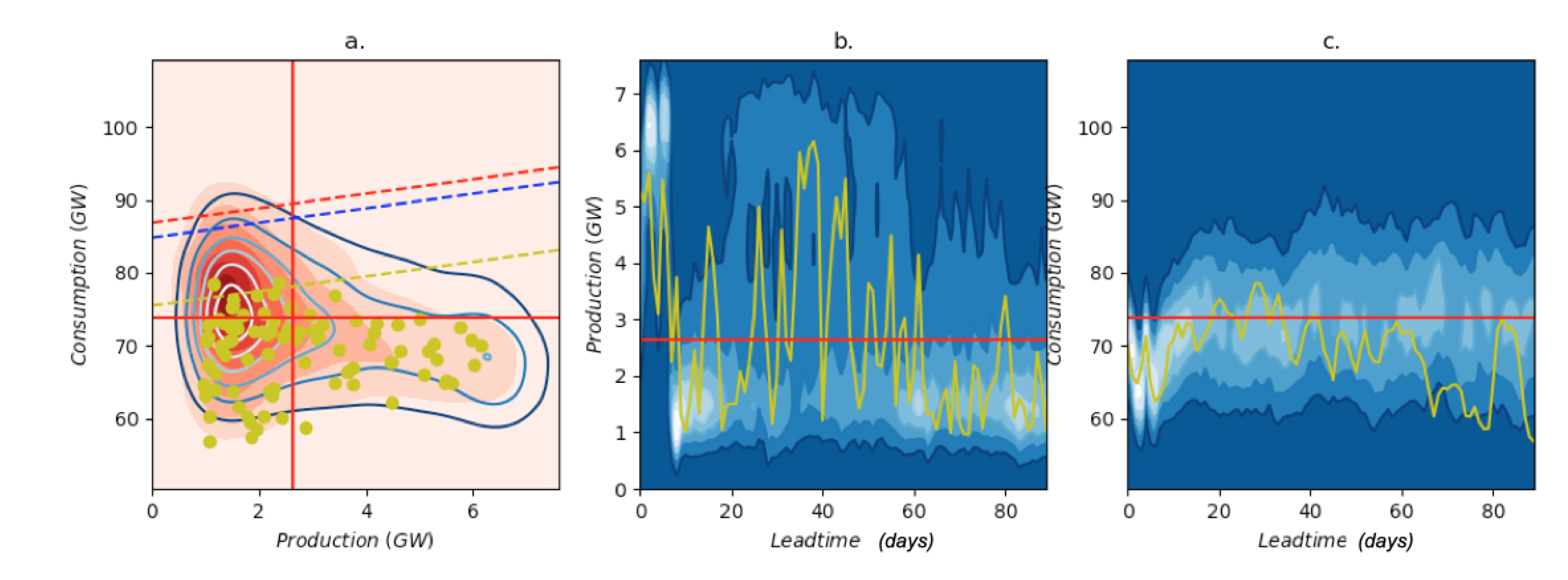
3.1. Modelling Results
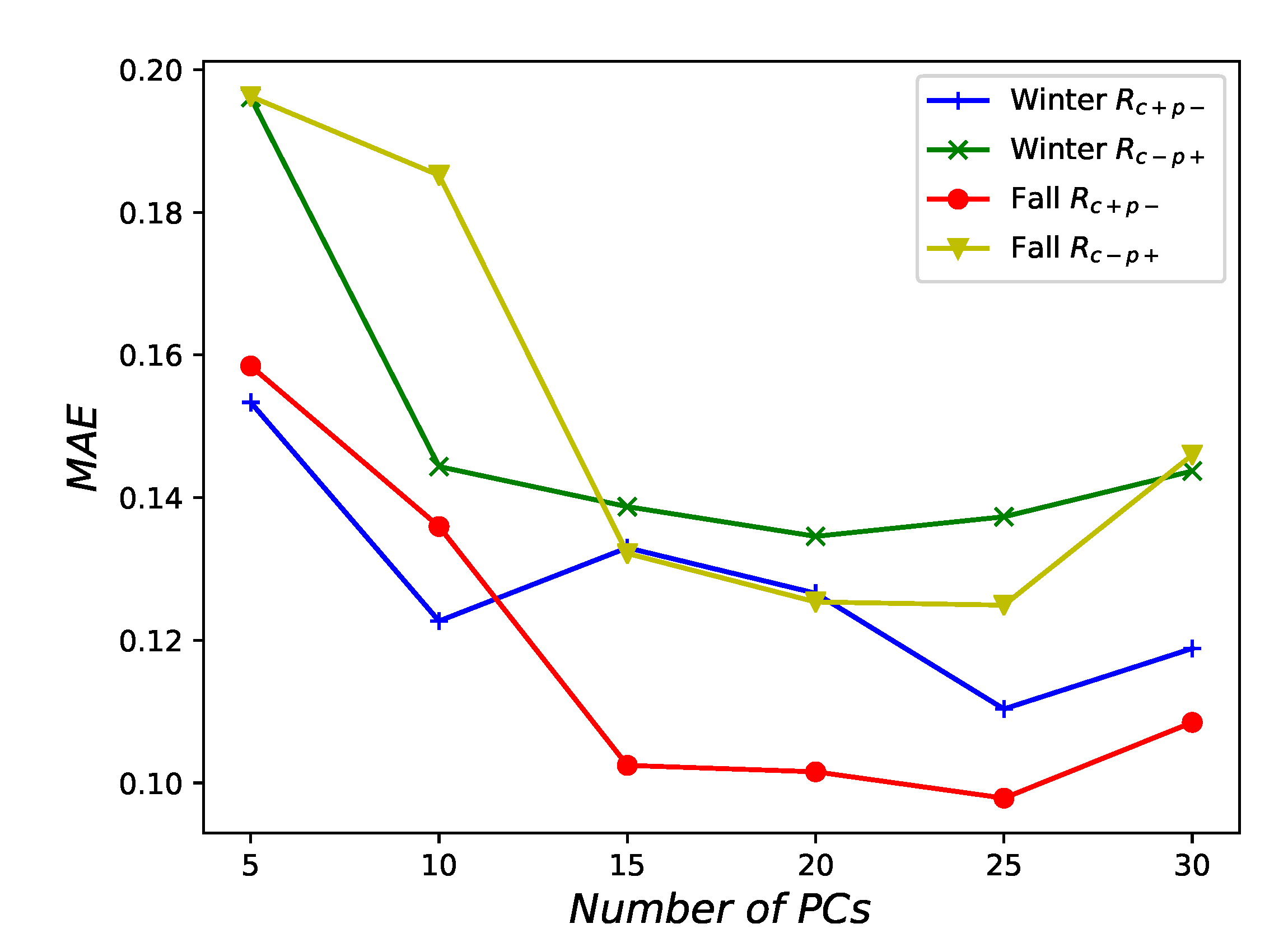
3.2. Explanatory Value of the First PCs
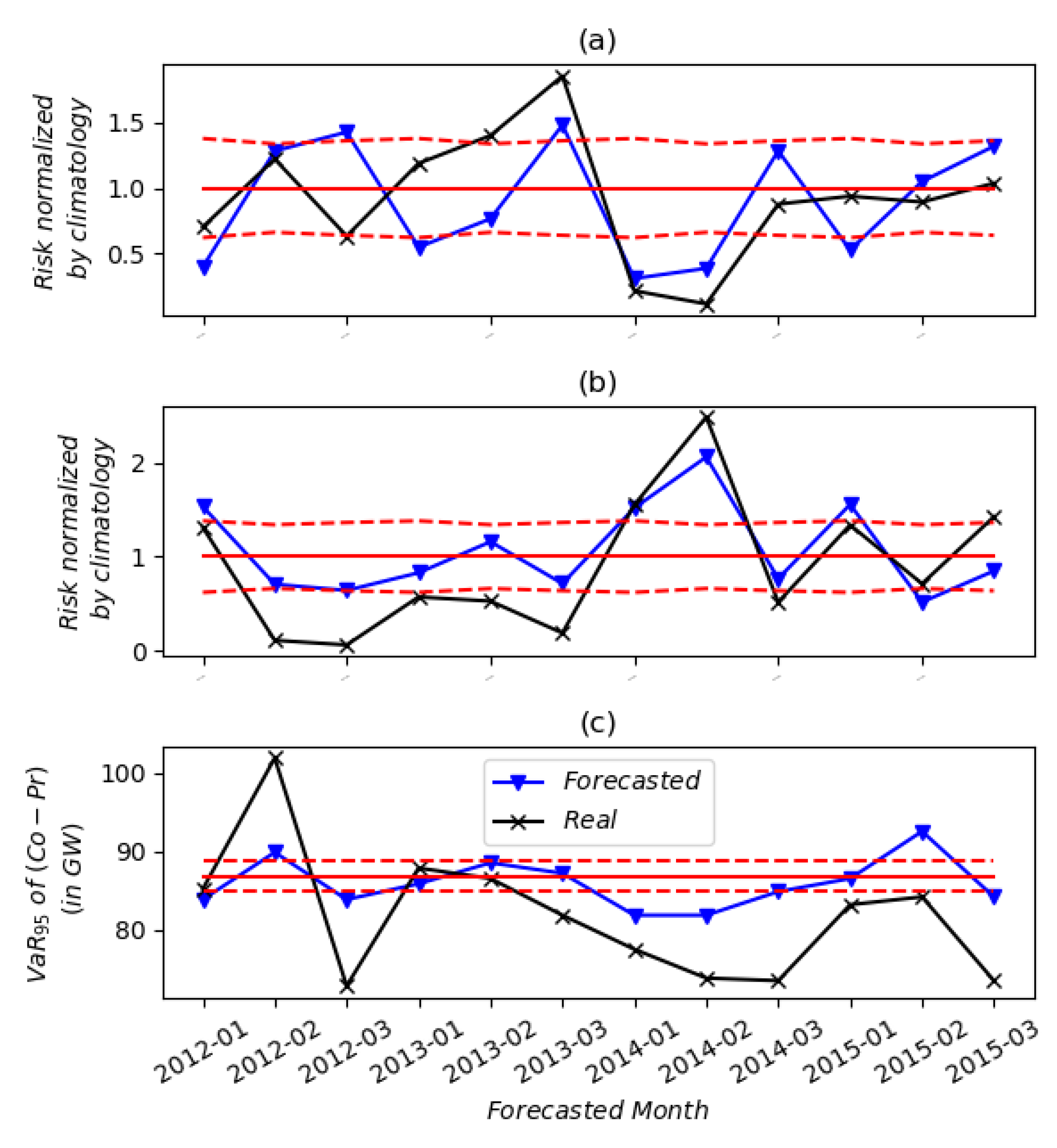
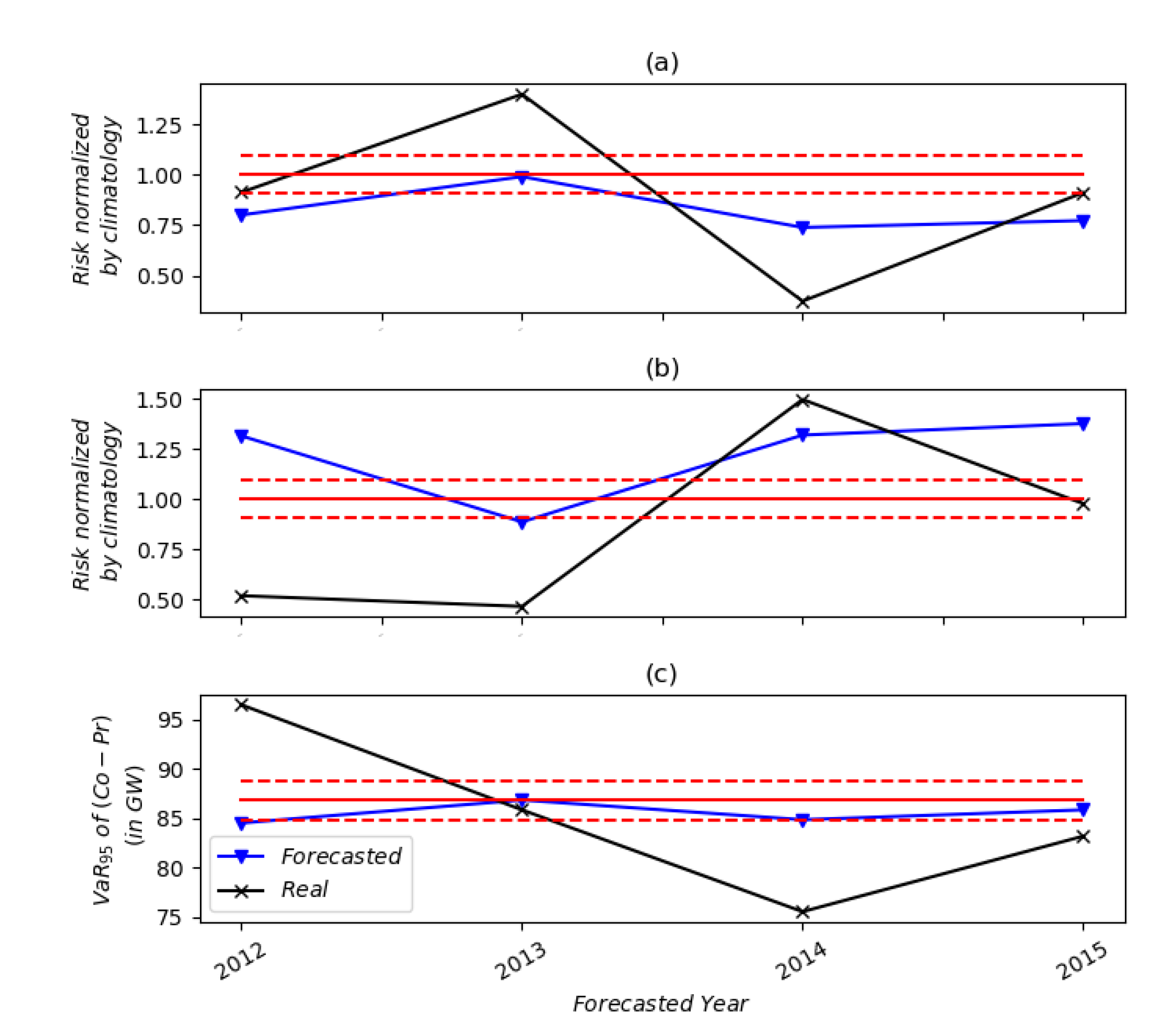
4. Risk Forecasting
4.1. Integration over the Seasonal Ensemble Forecasts of the ECMWF
4.2. Monthly and Seasonal Forecasts
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Sensitivity of the Model to the Number of PCs Used to Fit the Indexes
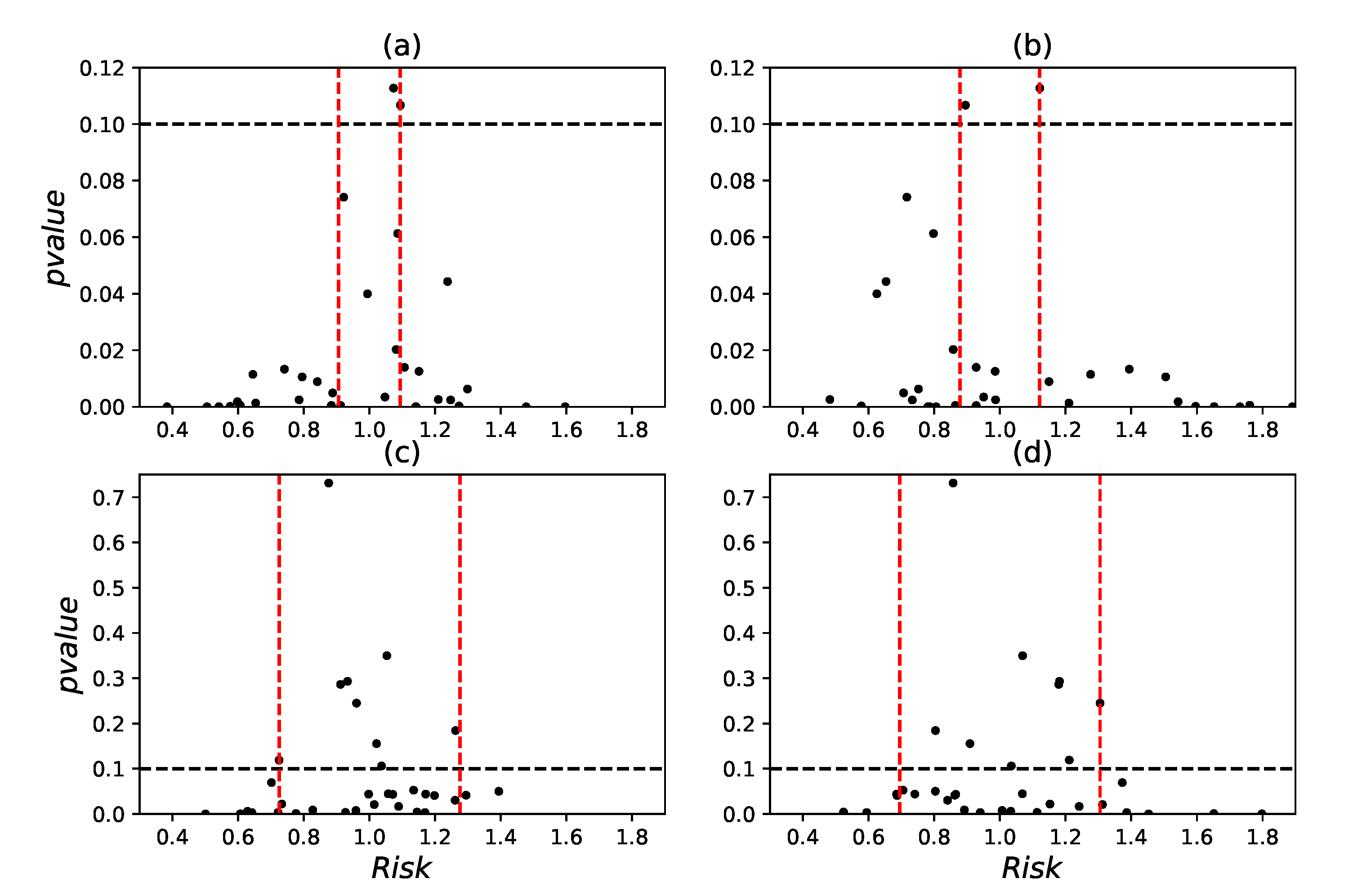
Appendix B. Significance Levels for the Risk Measures

References
- RTE, Bilan électricique; RTE Report; Réseau de transport d’électricité de France: Paris, France, 2017.
- WindEurope. WindEurope, Wind Energy in Europe: Scenarios for 2030; Wind Europe Report; WindEurope: Brussels, Belgium, 2017. [Google Scholar]
- Alain Burtin and Vera Silva, Technical and Economic Analysis of the European Electricity System with 60% RES; EDF R&D Report; 2015. Available online: https://www.edf.fr/sites/default/files/Lot%203/CHERCHEURS/Portrait%20de%20chercheurs/summarystudyres.pdf (accessed on 6 August 2020).
- ENTSOE. ENTSOE, Winter Outlook Report—2016; ENTSOE Report; ENTSOE: Brussels, Belgium, 2016. [Google Scholar]
- RTE, Annual Electricity Report—2016; RTE Report; Réseau de transport d’électricité de France: Paris, France, 2016.
- Scaife, A.A.; Arribas, A.; Blockley, E.; Brookshaw, A.; Clark, R.T.; Dunstone, N.; Eade, R.; Fereday, D.; Folland, C.K.; Gordon, M.; et al. Skillful long-range prediction of European and North American winters. Geophys. Res. Lett. 2014, 41, 2514–2519. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Cohan, D.S. Interannual Variability and Seasonal Predictability of Wind and Solar Resources. Resources 2017, 6, 29. [Google Scholar] [CrossRef]
- Clark, R.T.; Bett, P.E.; Thornton, H.E.; Scaife, A.A. Skilful seasonal predictions for the European energy industry. Environ. Res. Lett. 2017, 12, 1–9. [Google Scholar] [CrossRef]
- Torralba, V.; Doblas-Reyes, F.J.; Macleod, D.; Christel, I.; Davis, M. Seasonal Climate Prediction: A New Source of Information for the Management of Wind Energy Resources. J. Appl. Meteorol. Climatol. 2017, 56, 1231–1247. [Google Scholar] [CrossRef]
- Soret, A.; Torralba, V.; Cortesi, N.; Christel, I.; Palma, L.; Manrique-Sunen, A.; Lledo, L.; Gonzalez-Reviriego, N.; Doblas- Reyes, F.J. Sub-seasonal to seasonal climate predictions for wind energy forecasting. J. Phys. Conf. Ser. 2019, 1222, 012009. [Google Scholar] [CrossRef]
- Alonzo, B.; Tankov, P.; Drobinski, P.; Plougonven, R. Probabilistic wind forecasting up to 3 months ahead using ensemble predictions for geopotential height. Int. J. Forecast. 2020, 36, 515–530. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E.; Troccoli, A.; De-Felice, M.; Suckling, E.; Dubus, L.; Saint-Drenan, Y.M.; Brayshaw, D.J. A Simplified Seasonal Forecasting Strategy, Applied to Wind and Solar Power in Europe. 2019. Available online: https://ideas.repec.org/p/osf/eartha/kzwqx.html (accessed on 2 February 2019).
- Lledo, L.; Torralba, V.; Soret, A.; Ramon, J.; Doblas-Reyes, F.J. Seasonal forecasts of wind power generation. Renew. Energy 2019, 143, 91–100. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E. The climatological relationships between wind and solar energy supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. The increasing impact of weather on electricity supply and demand. Energy 2018, 145, 65–78. [Google Scholar] [CrossRef]
- de-Queiroz, A.R.; Mulcahy, D.; Sankarasubramanian, A.; Deane, J.P.; Mahinthakumar, G.; Lu, N.; DeCarolis, J.F. Repurposing an energy system optimization model for seasonal power generation planning. Energy 2019, 181, 1321–1330. [Google Scholar] [CrossRef]
- Parka, H.; Baldick, R. Optimal capacity planning of generation system integrating uncertain solar and wind energy with seasonal variability. Electr. Power Syst. Res. 2020, 180, 106072. [Google Scholar] [CrossRef]
- Schroeder, R.; Joyeau, A.; Carlini, E.M. Seasonal Adequacy Risks: Getting prepared for seasonal adequacy risks on regional level. In Proceedings of the IEEE international Conference on Environement and Electrical Engineering and IEEE Industrial and Comercial Power System Europe, Palermo, Italy, 12 June 2018; pp. 1–6. [Google Scholar]
- Orlov, A.; Silmann, J.; Vigo, I. Better seasonal forecasts for renewable energy industry. Nat. Energy 2020, 5, 108–110. [Google Scholar] [CrossRef]
- Prior, J.; Kendon, M. The UK winter of 2009/2010 compared with severe winters of the last 100 years. Weather 2011, 66, 4–10. [Google Scholar] [CrossRef]
- Brayshaw, D.J.; Dent, C.; Zachary, S. Wind generation’s contribution to supporting peak electricity demand - meteorological insights. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2012, 226, 44–50. [Google Scholar] [CrossRef]
- Leahy, P.G.; Foley, A.M. Wind generation output during cold weather-driven electricity demand peaks in Ireland. Energy 2012, 39, 48–53. [Google Scholar] [CrossRef]
- Cradden, L.C.; McDermott, F. A weather regime characterisation of Irish wind generation and electricity demand in winters 2009–2011. Environ. Res. Lett. 2018, 13. [Google Scholar] [CrossRef]
- Fasano, G.; Franceschini, A. A multidimensional version of the Kolmogorov-Smirnov test. Mon. Not. R. Astron. Soc. 1986, 225, 155–170. [Google Scholar] [CrossRef]
- Bueh, C.; Nakamura, H. Scandinavian pattern and its climatic impact. Q. J. R. Meteorol. Soc. 2007, 133, 2117–2131. [Google Scholar] [CrossRef]
- Jourdier, B. Wind Resource in Metropolitan France: Assessment Methods, Variability and Trends. Ph.D. Thesis, Ecole Polytechnique, Palaiseau, France, 2015. [Google Scholar]



| Variable | Data Source | Time Period | Time Resolution | Computation | Result |
|---|---|---|---|---|---|
| 10 m wind speed | ERA-I | 01-01-1979 31-12-2015 | 6-hourly | - Averaged daily - Compute Pr | Pr (1979 to 2015) |
| French Production | RTE | 01-01-2015 31-12-2015 | hourly | ||
| 2 m temperature | ERA-I | 01-01-1979 31-12-2015 | 6-hourly | - Averaged daily - Average in France - Compute Max Co | Co (1979 to 2015) |
| French consumption | RTE | 01-01-2015 31-12-2015 | hourly | ||
| Z500 | ERA-I | 01-01-1979 31-12-2015 | 6-hourly | - Averaged daily - PCA - Select several PCs | (1979 to 2015) |
| Z500 | ECMWF seasonal ensemble forecasts | 01-01-2012 31-12-2015 | 6-hourly Available every month | - Averaged daily - Apply PCA - Select horizon | Ensemble of (2012 to 2015) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonzo, B.; Drobinski, P.; Plougonven, R.; Tankov, P. Measuring the Risk of Supply and Demand Imbalance at the Monthly to Seasonal Scale in France. Energies 2020, 13, 4888. https://doi.org/10.3390/en13184888
Alonzo B, Drobinski P, Plougonven R, Tankov P. Measuring the Risk of Supply and Demand Imbalance at the Monthly to Seasonal Scale in France. Energies. 2020; 13(18):4888. https://doi.org/10.3390/en13184888
Chicago/Turabian StyleAlonzo, Bastien, Philippe Drobinski, Riwal Plougonven, and Peter Tankov. 2020. "Measuring the Risk of Supply and Demand Imbalance at the Monthly to Seasonal Scale in France" Energies 13, no. 18: 4888. https://doi.org/10.3390/en13184888
APA StyleAlonzo, B., Drobinski, P., Plougonven, R., & Tankov, P. (2020). Measuring the Risk of Supply and Demand Imbalance at the Monthly to Seasonal Scale in France. Energies, 13(18), 4888. https://doi.org/10.3390/en13184888






