Abstract
The industry 4.0 concepts are moving towards flexible and energy efficient factories. Major flexible production lines use battery-based automated guided vehicles (AGVs) to optimize their handling processes. However, optimal AGV battery management can significantly shorten lead times. In this paper, we address the scheduling problem in an AGV-based job-shop manufacturing facility. The considered schedule concerns three strands: jobs affecting machines, product transport tasks’ allocations and AGV fleet battery management. The proposed model supports outcomes expected from Industry 4.0 by increasing productivity through completion time minimization and optimizing energy by managing battery replenishment. Experimental tests were conducted on extended benchmark literature instances to evaluate the efficiency of the proposed approach.
1. Introduction
In manufacturing systems, owners try always to improve profits and optimize production resource use. They also aim to eliminate wastes of time and energy in order to reduce costs and align with current standards. In this context, industry 4.0 has been adopted as a revolutionary industrial paradigm to ensure that production concepts will adapt effectively to operative changes with a more intensive focus on sustainability in industrial contexts while increasing economic and ecological efficiency [1]. The key element for such a concept is the implementation of a highly flexible manufacturing process that allows better resource management.
Governments announced, through the United Nations General Assembly in September 2015, that they would demonstrate the scale and ambition needed to develop the knowledge and technological innovations to increase the use of sustainable energy in multiple areas of critical importance, including transport systems [2]. In this field, urban transport systems [3], freight transport systems [4] and industrial material handling systems [5] are nowadays a major stake (e.g., Figure 1 presents a fully automated material handling based sortation plant in an e-commerce company). Nevertheless, sustainability must be taken into account not only at the strategic level, but also at the operational level in which scheduling is one of the key factors [6].

Figure 1.
A material handling system for e-commerce product sortation (Indian Flipkart [7]).
Modern flexible manufacturing systems use automated guided vehicles (AGVs) as a part of their material handling system [8]. In fact, AGVs are driverless, their routes can be redefined and transport request fulfillments can be reviewed without the infrastructure changes, which offers faster and more intuitive ways of adapting an existing system to new business rules [9]. Battery management on AGVs has an impact on the overall performance of the manufacturing system [8]; however, previous studies omitted this factor [10] which led us to consider it through this work. More precisely, this paper presents a scheduling approach that supports processing, transport and vehicles’ battery replenishment tasks. The main question that arises is: how can we maintain the economic cost (i.e., makespan) and optimize energy consumption onboard AGV while considering all these tasks?. From our perspective, the key to reaching the resolution of this scheduling problem easier is to decompose it into three assignment sub-problems: production tasks to processing machines, transport tasks to AGVs and battery replenishment tasks to handling trips. Consequently, it is important to address adequately the battery management to run an AGV system efficiently [11]. Furthermore, this study led us to present a more real view of previous research and should be more reliable when applied in the real world.
Our paper is organized as follows: in the current section, we describe the treated problem and review the state of the art of the related works to position our contribution in this context. Next, the proposed approach is presented, the developed model is described and related algorithms are listed. Section 3 is dedicated to detail experiments and Section 4 reports numerical results which are later discussed in Section 5. Finally, Section 6 presents conclusions and highlights our perspectives for future research.
1.1. Problem Description
In our target job-shop scheduling problem (JSP), production is represented as a sequence of jobs j entering and leaving the system through a loading/unloading station (L/U). Each job j represents an occurrence of a product type manufacturing process and consists of an ordered list of tasks i. Every is executed on a specific uninterruptible mono-task machine m according to a predefined process route. Thus, a manufacturing plan of a job j can be considered as a sequential series of (i,j,m) combinations that have to be scheduled efficiently.
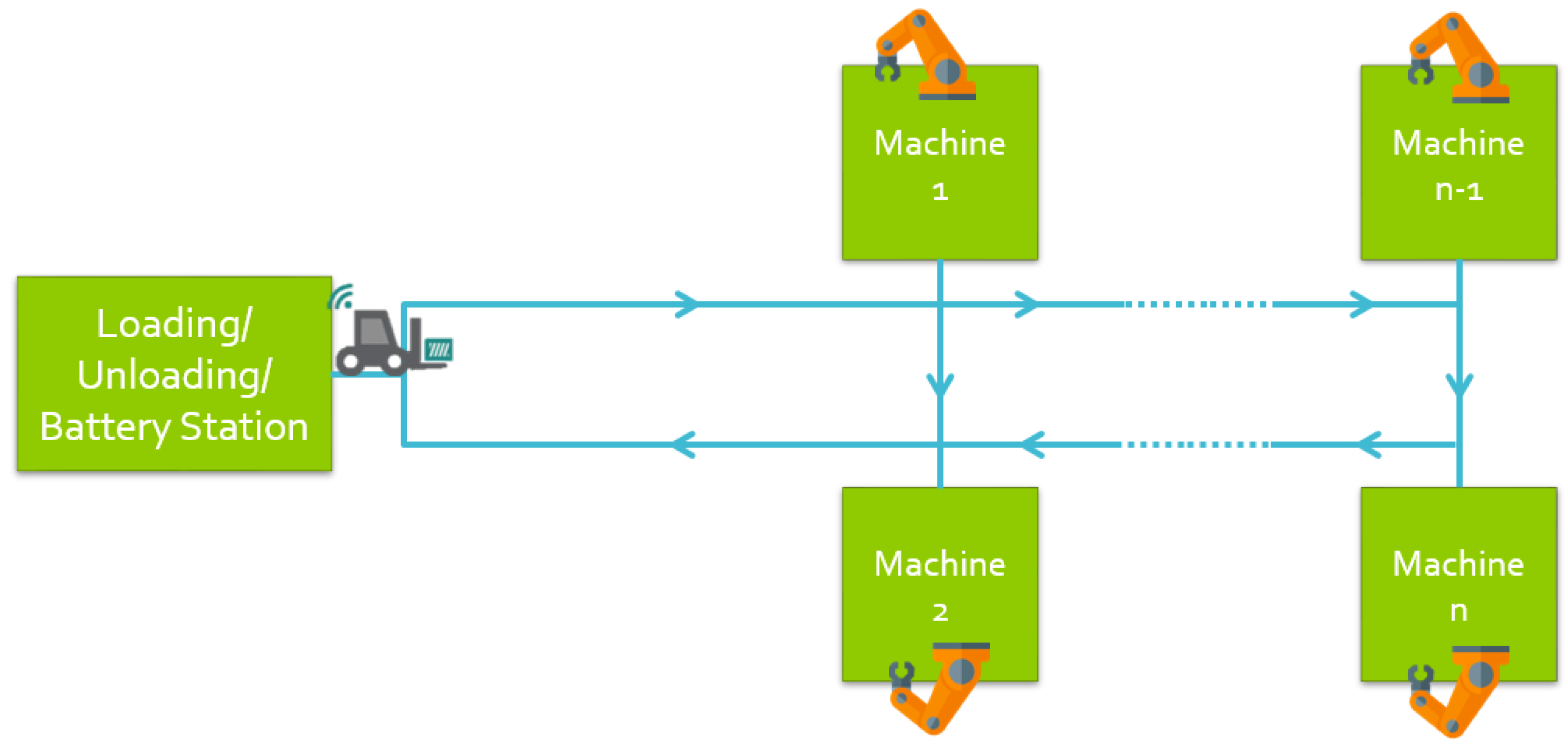
The transport fleet has a limited number of battery-based uni-charge AGVs starting their first transportation jobs from the L/U station at time t = 0 with fully charged batteries. A transportation job managed by an AGV v to carry a combination is composed of two sequential transport sub-tasks performed on unidirectional routes to avoid collision: the moving of empty task v from its current position, which can be either the L/U station if it is the first job or the last delivery station otherwise, to the call node m’ with (m’), and the moving of the loaded combination to its target station m. During these sub-tasks, the AGV can be redirected to the L/U station to replace its battery before it has a deep discharge; i.e., the detected level at L/U station should never go below a certain value (called also maximum discharge capacity in [12] or threshold level charge in [11]). A typical layout of the studied job-shop problem is provided by Figure 2 which tallies up Bilge and Ulusoy benchmark specifications from [13] with an additional battery station at the L/U node.
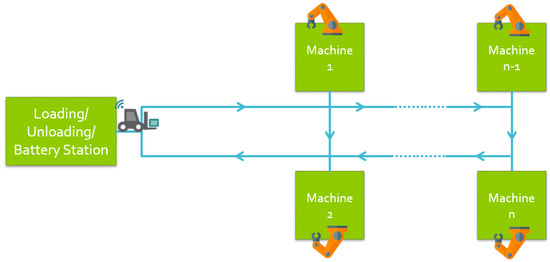
Figure 2.
Target job-shop manufacturing problem.
Generally, constraints related to AGV battery replenishment are omitted from the literature [14] and the some papers that exist consider them only in dynamic behavior. Thus, a static scheduling approach (i.e., predictive behavior) that integrates transport, battery replenishment and task affectation into machine constraints will be defined in this paper.
Integrating transport constraints into JSP is an NP-hard problem [15] because of the dependence between task allocation and the availability of both machines and AGVs. Our objective is to schedule tasks optimally on machines, AGVs and battery stations to minimize the makespan while keeping the maximum discharge capacity of each AGV battery higher than level. Thus, it is necessary to choose the battery management technique meeting the desired optimization objectives.
In the next subsection, works related to JSP with transport constraints and AGV battery management approaches are described, and our contribution is positioned in this context.
1.2. Related Works
JSP with transport constraints is an optimization problem in which resources are allocated to perform a predetermined set of tasks. A great deal of effort has been spent while developing methods in this context. The first benchmarks in this field were introduced by Bilge and Ulusoy in [13], and Knust and Huring in [16]. Both provided referential instances for simultaneous material transfer between machines in identical uni-charge AGV based JSP. Reference [13] proposed an approach based on AGV trips time window constraints that depends on machine operations’ completion times. They provided an iterative heuristic procedure to optimize the maximum completion time of job sets in two AGV based problem examples. The benchmark proposed by [16] addresses the same problem in new instances using a single robot-based material handling system. They used the tabu search metaheuristic to minimize the sum of all traveling and waiting times and proposed an appropriate technique to accelerate solution evaluation in the used context. Both benchmarks consider conflict-free unidirectional manufacturing layouts with predetermined shortest paths routing problem and are widely used and enhanced in the literature. Reference [17] implemented three metaheuristics based on iterated local search, and simulated annealing and their hybridization to deal with transport and processing allocations to resources. They obtained new upper bounds for Bilge and Ulusoy instances, and provided new results for minimizing the exit time of the last job after extending the same benchmark instances. Later on, reference [18] developed an approach composed of a disjunctive graph-based framework to model the joint scheduling problem and a mimetic algorithm for representing machines and AGVs scheduling. Their results on both [13,16] instances came up with new enhancements on both makespan and exit time minimization. Reference [19] used a hybrid heuristic search algorithm based on a timed colored Petri net to optimize both the makespan and exit time of the last job. Reference [20] explored a biologically inspired whale optimization algorithm in a mono transport robot JSP to minimize seven fitness functions (makespan, robot finishing time, transport time, balanced level of robot utilization, robot waiting time, job waiting time and total robot and job waiting time). They provided also a novel mathematical formulation and compared the obtained results with five meta-heuristic algorithms. All the papers listed above have omitted battery constraints from their studies.
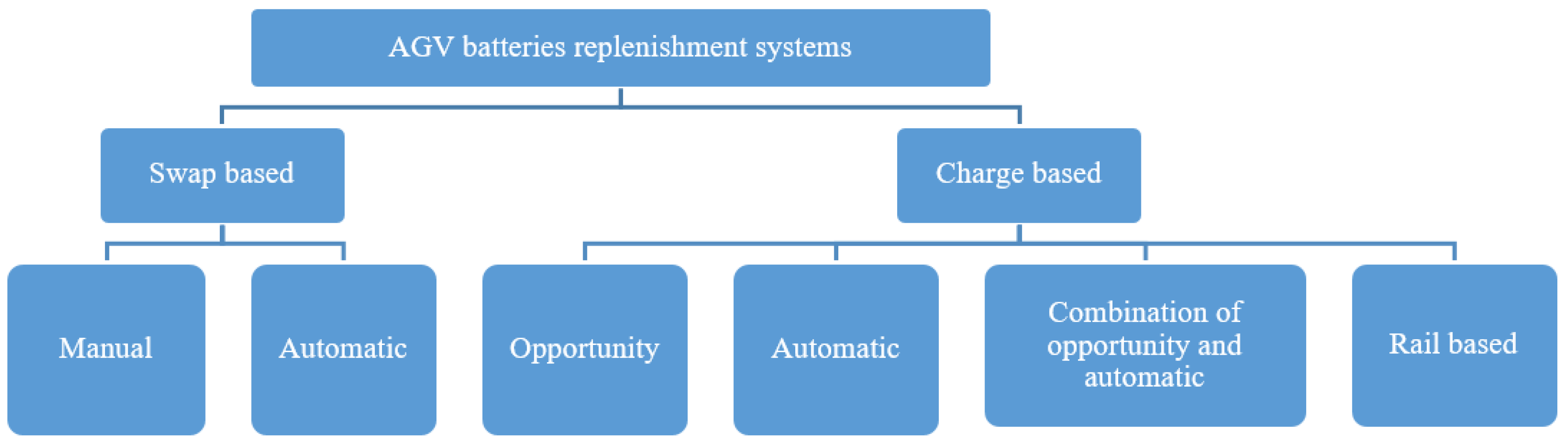
Since most AGVs rely on batteries as sources of energy, battery depletion rates can become limiting factors [12]. In fact, additional traveling times required to charge or change a depleted battery can significantly affect manufacturing costs. Thus, battery management constraints must be considered in order to get as close as possible to the real behavior of the studied system. Reference [12] presented an overview dictating the way battery replenishment should be implemented in AGV systems (see Figure 3). The author presented two techniques: a battery charging technique, in which AGVs are coupled with chargers until each depleted battery reaches a predefined level, and the replacement technique where the battery is being replaced by a new one. Battery replacement can either be manual, through a handling agent, or automatic in a battery swap station. Meanwhile, the battery charging covers four possible scenarios: (1) Opportunity charge during AGV idle time. (2) Automatic charge in which the AGV is redirected to a charging station until its battery level recovered. (3) A combination of both. (4) Rail based charging where the AGV remains coupled to a charge rail while traveling through a specific area in the manufacturing plant.
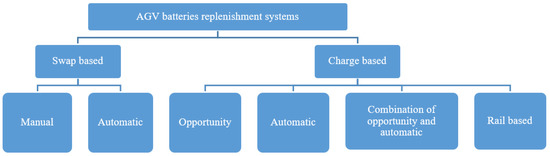
Figure 3.
AGV battery replenishment systems according to [12].
Battery replenishment techniques have a large influence on the operational times of AGVs. In fact, recharging the battery inside the vehicle until replenishment means that it will not be available for the charging process’s duration, which exceeds, in general, its possible working time [21] and can vary from a battery type to another. On the other hand, the battery swap technique has a limited impact on the operational time of the AGV as batteries are recharged outside the vehicle before being replaced.
To ensure the planned throughput while using these techniques, replenishment (or charging) strategies were developed. They are part of the vehicle dispatching module of the transport order processing and depend on the used battery type and the replenishment method [22]. They are used to prevent too many vehicles from entering the replenishment process at the same time and thus reduce vehicle unavailability while managing battery replenishment. Reference [21] listed four strategies an AGV can use to change its battery in a multi battery station environment. They take into account the position of the battery station regarding the route within the current transport job:
- The nearest battery station;
- The farthest reachable battery station on the current route;
- The first battery station encountered on the current route;
- The battery station that leads to minimum delay.
Reference [11] implemented those four routing heuristics in a battery swap-based AGV system and performed a comparative analysis between them in large scale manufacturing plant. Their proposed approach ensures that the battery charge will not go below a threshold level (20% for strategies 1 and 4, 28% for strategy 3 and 33% for strategy 2) by the time the depleted battery is swapped. AGVs are redirected to the battery station when traveling to the pickup node or after getting loaded with the affected part. The obtained simulation results proved that the strategy 4 outperforms all others by giving the largest number of total outputs for the used instances.
A common rule between all the previous strategies is that the residual charge of an AGV battery should not go below a certain level . This is because a deep battery discharge under the recommended level can affect the battery’s life cycle greatly [23]. To highlight the relation between the residual charge and time required for replenishment, reference [24] proposed three regression formulas to calculate the time required to charge a valve regulated lead acid battery (commonly VRLA) based on the current depth of discharge (DoD) and the desired state of charge (SoC) (the first refers to the quantity of energy lost from the battery while the second identifies the quantity of energy available in the battery (or residual charge) with SoC = full battery capacity—DoD). They state in their study that the level of charge that a battery receives is not proportional to the time it gets charged for, and batteries receive most of their charge during the initial phase of charging, as opposed to the later phase. Thus, they proposed these formulas to calculate the recharging time t in minutes while targeting 90%, 95% and 100% of DoD respectively (d):
They mentioned also that targeting a lower SoC may have undesirable consequences on battery live cycle (Over-discharge and deep-discharge both have terrible effects on life performance of the battery grid structure and are in the origin of poor life cycles [23,25].), but they prove the efficiency of targeting a lower SoC through saving time and increasing system outputs. In a same way, Reference [26] proposed three formulas for calculating recharging time for 90%, 95% and 100% targeted DoD (d) in lithium-ion batteries:
Previous listed works used the AGV battery management constraints in non-deterministic production processes (i.e., the list of jobs to be processed is not known before the production process starts); few papers considered deterministic ones. Reference [14] presented a graph based linear programming heuristic in the vehicle routing problem (VRP) environment to minimize the time needed to schedule AGV deadlined pickup/drop-off transportation jobs while using a charging strategy (machine scheduling is not considered in his work). AGVs move from a charging location; perform transportation between two points according to request and finish times; and go back to the charging location without exceeding the battery capacity. The authors in [27] used a genetic algorithm, particle swarm optimization and hybridization of both in an AGV-based flexible manufacturing system to minimize makespan and the total AGV count while considering battery charges. The proposed approach tries to add an AGV to the fleet if the battery charge of the available AGVs cannot allow responding to current demands. They considered both automatic and opportunity battery charging, in which an AGV charges for 10–12 min every hour, and integrates a parameter that can be changed to adopt to any battery type. To validate their approach, they used two random layouts and implemented their model in a simulation to prove its feasibility. Reference [28] solved the optimal battery swap station location in respect to AGV routing and machine scheduling in JSP facility. In that study, they fixed a duration of time after which an AGV battery was considered elapsed and the AGV stopped in a planned horizon h. In fact, in their model, AGVs transfer parts from a pickup point to a delivery point and return back to a home station, and an AGV is not assigned to a part if its battery charge is not sufficient; however, it can stop while returning home due to battery discharging. The mathematical model they proposed tries to minimize the distance between the optimal location of the battery swap station and the stop point for all warehouse AGVs while optimizing the makespan. It has been tested on seven instances using CPLEX to validate the proposed model with different numbers of AGVs.
The particularity of our approach is in using the variable neighborhood search metaheuristic to rearrange a deterministic task scheduling (i.e., processing, transport and battery swap tasks). We also consider real AGV battery characteristics and use a widely explored benchmark in manufacturing systems with some additional parameters to cover battery constraints. The next section presents the details of our proposed model.
2. Problem Modeling and Solving Approach
In the proposed approach, an unexplored metaheuristic in the context of JSP with transport constraints is used to represent a model that encompasses the three sub-problems treated by this study: task allocation to machines, transportation assignment of parts to AGVs and battery swap scheduling during the manufacturing process in a production cell identical to that described in previous sections.
The variable neighborhood search algorithm (VNS) is a metaheuristic for solving combinatorial and global optimization problems [29]. It was firstly introduced by N. Mladenovic and P. Hansen in 1997 [30]. Since the majority of metaheuristics make use of just one type of neighborhood structure, there exists a high probability of them getting trapped in local optima after a certain number of iterations [31]. VNS inventors tried to bypass this shortcoming by proposing a technique that diversifies, systematically, the type of neighborhood structure while searching for the solution and thus escaping the local optima. It consists of proposing different neighborhood structures for the problem and randomly jumping from one to another until reaching a stop condition (fixed number of neighborhoods, maximum running time, maximum loops within a local search, etc.).
As metaheuristics work on encoding spaces, an encoding technique is used to define different parts of our problem schedule efficiently. It allows describing the three studied sub-problems for our schedule and distinguishing different neighborhood structures explored by VNS. In the next section, the used coding space is described.
2.1. Schedule Representation
To present different parts of our problem, the schedule representation will include three parts:
- The JSP-string: representing the schedule of production tasks on their related processing machines;
- The transport string (or AGV-string), representing the AGV IDs selected for transporting the processing tasks of the JSP-string;
- The battery swap string (or BS string), enumerating AGVs behaviors regarding the battery replenishment during the transport of the affected task.
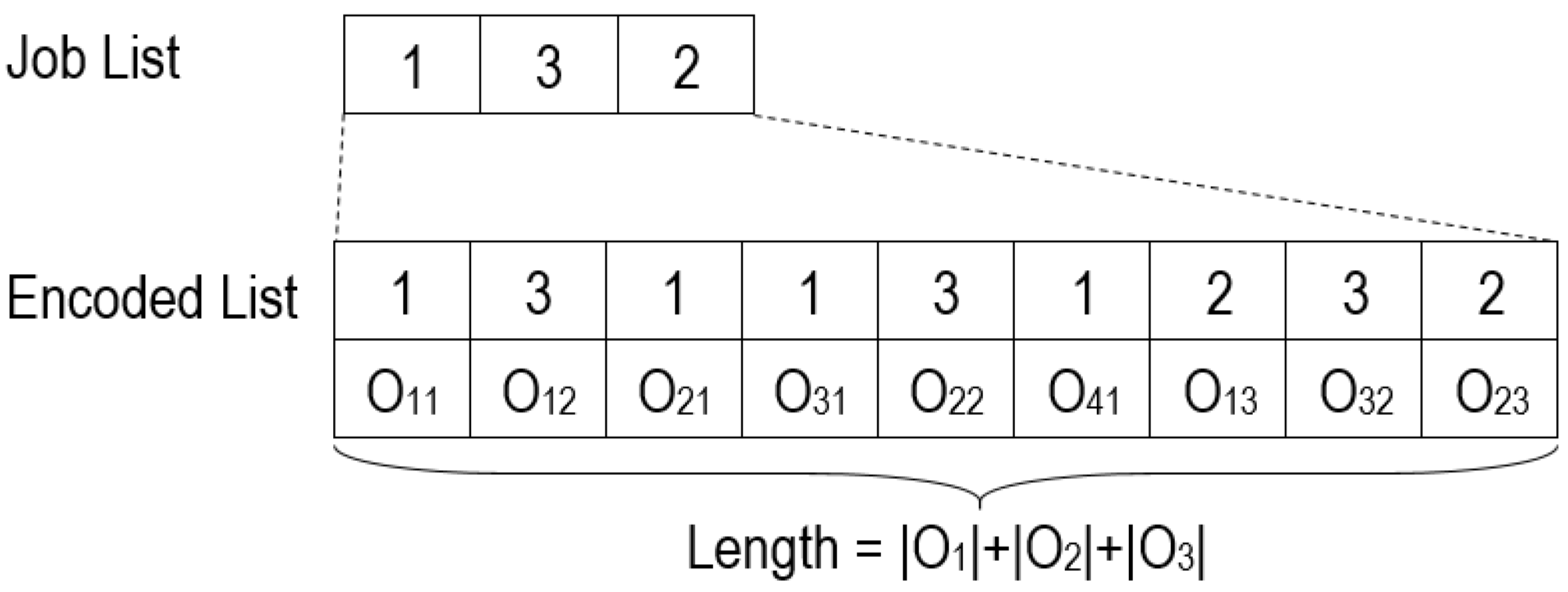
In the first part, the system receives an entry list of n integers representing the requested job-list to be manufactured where each number refers to a product type; for example, the job list “132” refers to three products or jobs, one of type “1”, a second of type “3” and a last type “2”. From this job-list, a JSP-string is generated by repeating each job type from the job-list according to the size of its task set (i.e., if the job type “1” has four tasks, it will be repeated four times in the JSP-string). To differentiate tasks of the same job we employ the appearance order; hence, all tasks take their names from their parent jobs but they are interpreted according to their appearance order in the JSP-string (i.e., the first “1” in the JSP-string corresponds to the first task of the job “1”; the second “1” refers to the second task of the job “1” and vice versa; see the example in Figure 4 where is the task i of the job j and is the number of tasks of the job j). This is called operation (or task)-based representation, as detailed in [32].
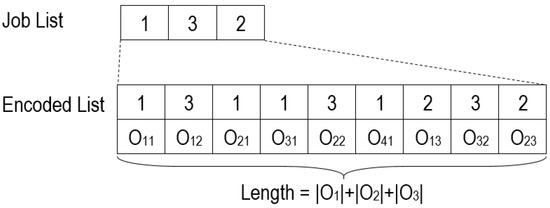
Figure 4.
JSP schedule representation.
The second part is the representation needed to select AGV for transporting tasks between machines. The simplest way has been utilized by reproducing the same JSP-string from previous steps, and substituting task numbers with AGV IDs to generate the AGV-string. Interpreting the new string highly depends on the JSP-string, as an AGV id in a position p indicates that this AGV is selected to transport the task in the same position p from the JSP-string (see Figure 5; for example, the third column states that AGV with id = 0 is selected to transport the second task of the job “1”). As described in previous sections, a task trip covers two moves: from the current AGV position to the pickup node of the task, and from this last one to the delivery node. Tasks’ pickup and delivery nodes are static data stored in a separate dictionary queried for that purpose.

Figure 5.
A JSP, transport and battery swap representation example in a two-AGV-based facility.
In a same way, the last part of the representation corresponds to the behavior of the AGV while transporting the task from the pickup to the drop-off node. The BS string is generated with the same number of elements as JSP and AGV strings. Each element of the BS string describes the route that the AGV of the same position from the AGV-string will seek during its transport task. We consider three possible scenarios in our study and thus three possible values for each element of the BS string: a zero “0” indicates that the transport task is realized from source to destination without interruption (i.e., no battery swap is performed during the whole AGV trip); a one “1” forces the AGV to perform a battery swap before reaching the pickup station (i.e., AGV travels from its current position to the battery station, makes a battery switch and then is redirected to the pickup station to perform its transporting task); and finally a two “2” make the AGV change its battery whilst transporting the job to its next destination (i.e., AGV travels to the pickup node, loads the corresponding part, is redirected to the battery station with loaded part onboard, makes a battery switch and then moves to the drop-off node). Still for our example from Figure 5, the third column states that AGV with an ID of 0 will move to the BS station to perform a battery swap, and then travel to the pickup node of the second task of the job “1” in order to transport it to its destination.
Using this 3-string based representation, infeasible solutions for our schedule have been avoided, and thus, an additional cleaning step in our metaheuristic has been omitted [33]. Additionally, our approach incorporates three local search stages, one for each sub-string, which operate together to find better task allocation while keeping the makespan minimized and the minimum battery levels for the whole AGV fleet higher than a particular level. In the next subsection, we detail the proposed approach.
2.2. The Proposed Approach
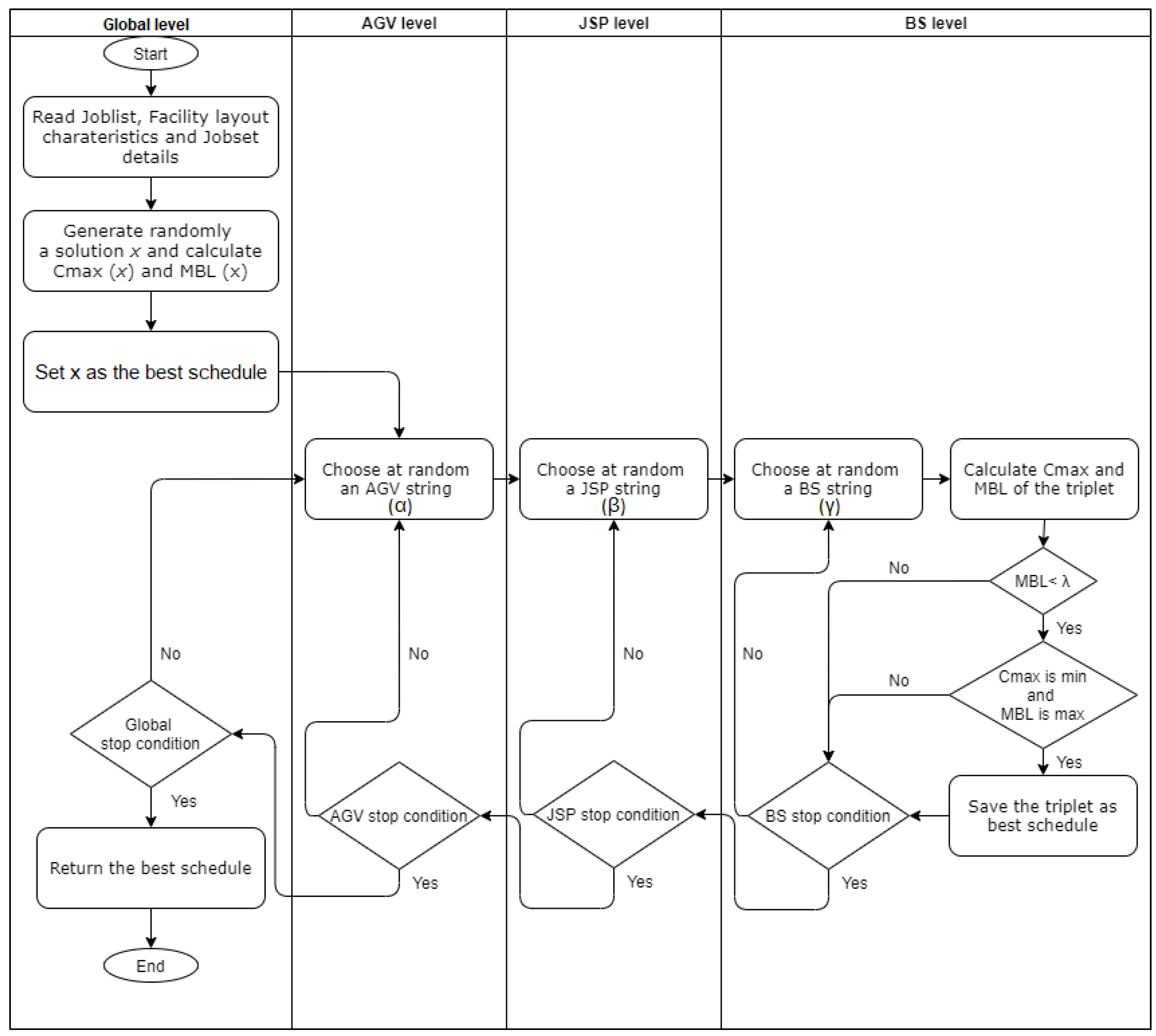
The flowchart of the Figure 6 presents our model’s behavior. The objective is to find the combination of three sub-strings (i.e., JSP, AGV and BS strings) producing the best schedule for the studied problem; thus, a cost function is used, at the end of each research step, to calculate both the makespan () and the minimum detected battery level (MBL) for all available AGVs. A schedule is accepted if MBL is greater or equal to pre-specified battery charge level ; otherwise it will be ignored and a new BS string search is restarted.
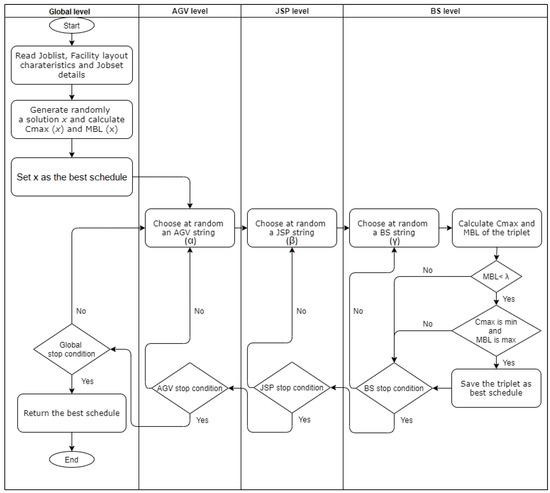
Figure 6.
The proposed VNS model flowchart.
Three types of neighborhoods are used in the searching process according to the representation string of each sub-problem, as detailed in previous sections: JSP, AGV and BS neighborhoods. Since JSP schedule structure has fixed letter enumeration (i.e., only the order of letters can change within all possible JSP strings), only neighborhood structures that operate on elements orders are allowed (see Figure 7). On the other hand, both AGV and BS schedules can have several neighborhood structures.
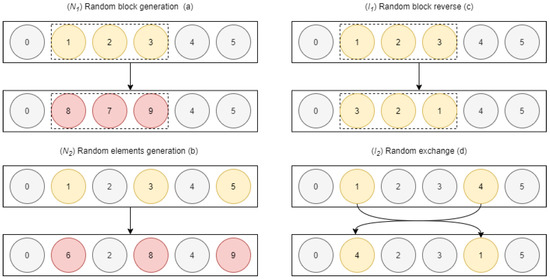
Figure 7.
Exploring techniques inside local search routines.
At the start of the process, an initial random solution x is generated from the input data (i.e., the requested job list, processing orders of each job and layout characteristics) having three strings with the same length l and a BS strings that gives an MBL . At this stage, this solution is considered as the best schedule.
The exploration process uses three nested local search levels to look for the best triplet strings composing the schedule: initially, an AGV-string is chosen randomly; then a JSP string is picked by random; and finally, a random BS string is generated and sent, together with aforementioned strings, to the cost function to calculate and MBL. If the resulting MBL is lower than , the exploration process passes to the next BS string; however, if the triplet cost has the lowest and the highest MBL (in the case of equal ), it will be saved as the best schedule. Otherwise, the searching process is repeated likewise with a new random BS string to find a better cost until reaching the BS stop condition.
When knocked out by a stop condition, at BS, JSP or AGV levels, the searching process steps back to upper levels to try with new random elements till reaching the global stop condition which can refer generally to a maximum CPU time or number of iterations. AGV, JSP and BS levels’ stop conditions are fixed to exit the related level if no improvement of the is detected within pre-defined number of loops.
At VNS exit, the best triplet selected corresponds to the best schedule having the minimum and the maximum MBL value.
2.3. VNS Implementation
When experiencing VNS, we realized that its implementation is mainly based on small details which can greatly influence the quality of the obtained results. After choosing the appropriate representation and neighborhood types, it is necessary to well determine both neighborhood structures and local search heuristics. We chose using general VNS (GVNS), one of the most successful VNS variants [34], and variable neighborhood descendant (VND) as a local search routine for both AGV and BS schedules. VND can significantly increase the chance of reaching the global minimum as it gives the possibility of jumping to another neighborhood structure during the local searching process, despite only a single neighborhood structure being explored in the classic local search concept [35]. VND is used only in both AGV and BS schedules for the same reason that differentiates the JSP neighborhood described in Section 2.2. The VNDs’ pieces of pseudocode are shown in Algorithms 1 and 2 respectively, in which four neighborhood structures are used to allow exploring different regions of the feasible solutions space:
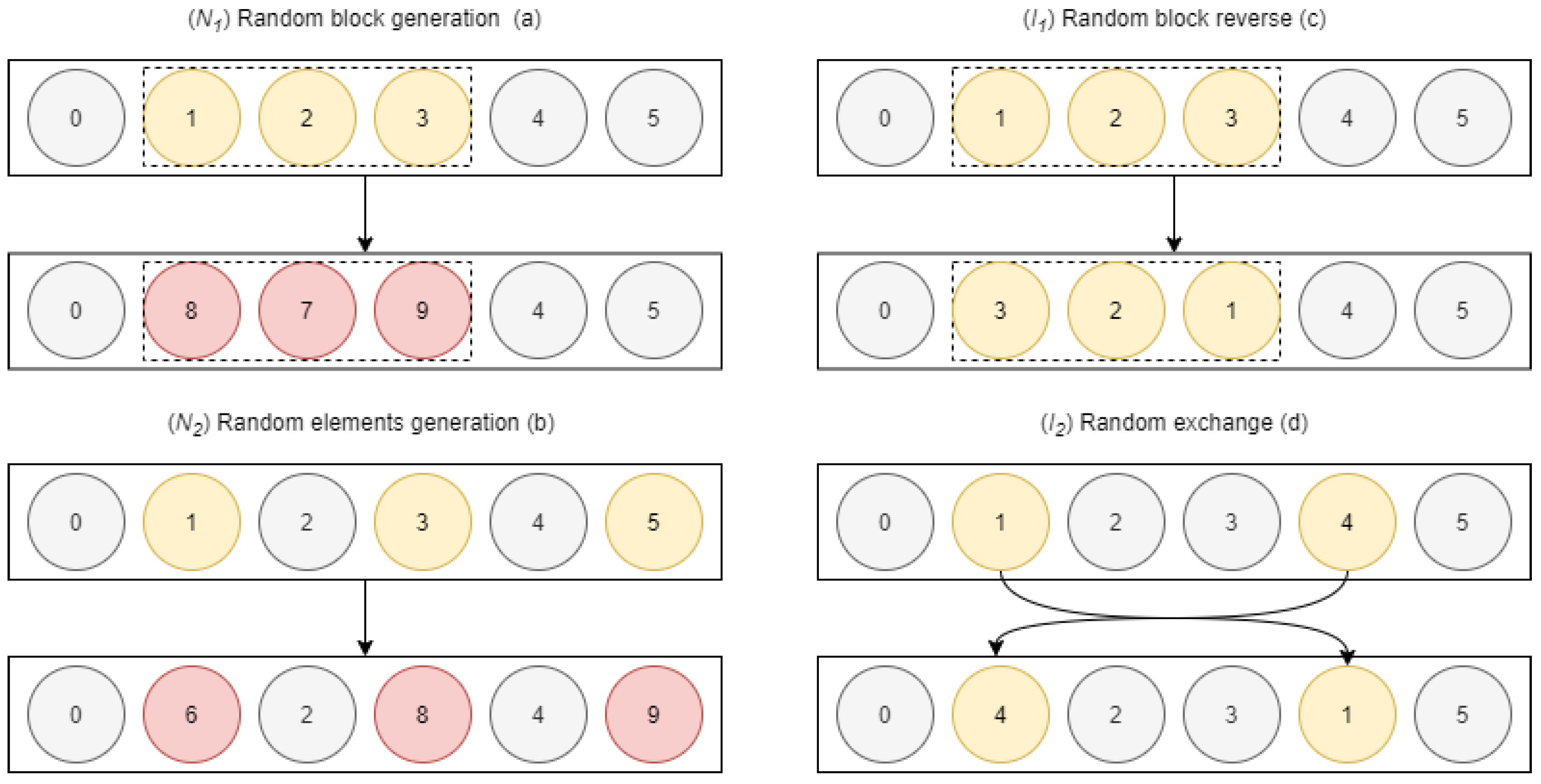
- : Select a random block and generate randomly new values for it (Figure 7a).
- : Select random indexes and generate randomly new elements in these indexes (Figure 7b).
- : Random block reverse: select a random block and reverse it (Figure 7c).
- : Substitute between two randomly selected adjacent or not adjacent elements (Figure 7d).
| Algorithm 1: AGV VND. |
 |
In both VND algorithms, neighborhood changes are used and a loop is initialized to allow exploration. Initially, a neighbor is randomly selected from the current neighborhood using either or technique (the choice depends on the value of the variable noImprovementCount which represents the number of iterations without the solution x ameliorates). Afterwards, the heuristic requests other levels’ strings to calculate the triplet (where represents the AGV-string, the JSP-string and the BS string). If the new cost is better, the best solution x is updated and the noImprovementCount variable is reinitialized. Otherwise, noImprovementCount is incremented and a neighborhood change is performed using either or technique according to the new value of noImprovementCount. Note that, in each loop, , , or are always applied equitable during the exploration process on the best solution x (which explains the use of the modulo(noImprovementCount, 4) in AGV_VND and BS_VNS, and modulo(noImprovementCount, 2) in JSP_LS).
On the other hand, the JSP local search function JSP_LS, described in Algorithm 3, uses only and neighborhood structures to explore possible JSP schedules.
| Algorithm 2: BS VND. |
 |
| Algorithm 3: JSP LS. |
 |
3. Experimentation
3.1. Instance Description
To validate our approach, a series of tests has been held on the Bilge and Ulusoy manufacturing benchmark presented in [13] which is a common reference for JSP with transport constraints. This benchmark has been extended to cover energy behavior onboard AGV (or battery constraints) and additionally for machine and transport scheduling. We used 40 test instances with two AGVs to assure transport in four different manufacturing layouts exploring 10 separate job-sets. The following assumptions and parameters were considered to align with our study’s objectives:
- One time unit in the benchmark corresponds to one minute in the real world;
- L/U times are included in the travel duration;
- L/U were automatically performed upon AGV destination arrival;
- Travel durations were constant either traveling empty or loaded;
- AGVs were unicharge vehicles;
- Battery swap operation was performed in the L/U station and took 4 min to achieve (authors in [36] state that this operation takes less than 5 min; thus we choose the first integer value which met this requirement).
Instance nomination code uses EX (abbreviation of example) followed by job set and layout digits. For example: EX61 represents instance using the job set 6 with layout 1.
3.2. Energy Characteristics
To reflect the real behavior of battery discharge onboard AGVs, we distinguished various AGV activities and their related consumed energy rates using data collected from existing AGV systems [12]. Table 1 lists amperes consumed by our AGV model in one time unit by activity type, as described in [12] for unit load AGVs:

Table 1.
AGV activities ampere draws.
For example, an AGV that is traveling loaded during six minutes consumes energy equal to: 6 min × 60 amperes = 360 ampere-min = 6 ampere-h. The battery capacity was fixed to 100 Ah, which is equivalent to 6 h discharge rate, as mentioned by [12].
Energy consumed when L/U parts is considered null; in the assumed layouts, AGV passes by a special area that loads/unloads parts on/from the vehicle automatically at node arrival.
4. Numerical Results
In the first experiment, two possible cases for energy onboard AGVs have been studied: no battery management and opportunity charging (see Section 1.2). First, the energy consumption is monitored by measuring the MBL during the manufacturing process. This allowed us to highlight the gain through using a battery management strategy while applying an AGV scheduling approach in the real world. Then, the behaviors of two different types of batteries have been monitored in an opportunity charge based system in which AGVs were automatically coupled to battery chargers upon station arrival, during their idle time (i.e., AGV still charging while parking in the last drop-off station). The AGV battery still charged till the next call, and the quantity of energy replenished depended on several parameters: battery type, idle time duration, the targeted state of charge (SoC) and the current depth of discharge (DoD). Thus, three possible target SoCs for each studied battery type were tested, by exploring jointly the six equations detailed in Section 1.2 and a new Equation (7), to calculate the quantity of replenished energy. The obtained results are presented in Table 2.

Table 2.
GVNS results using opportunity charge for two battery types and different SoC targets.
Experiments within that table were conducted on a modified version of the proposed GVNS by omitting the battery switch level. The used benchmark instances’ referential lower bound and upper bound enhancements provided by Zheng et al. 2014 in [37] are presented in “LB” and “BK” columns respectively. The “BF” column contains the best found makespan results obtained by the modified GVNS approach, while both “BK” and “BF” are expressed in minutes to comply with the assumptions of Section 3.1. Furthermore, seven columns are used to express MBLs during the whole working process in seven cases: one case column to express the obtained results without using a charging strategy, and six cases columns to display findings when employing an opportunity charging strategy on two different battery types (lead acid and lithium-ion) and targeting three different SoCs for each battery type (90%, 95% and 100%).
In the last part of the experiments, given by Table 3, all the three scheduling levels of our GVNS model were used (i.e., JSP, AGV and BS schedules). In this series of tests, was minimized while keeping the MBL superior to 28% as per [11]. Consequently, benchmark instances in which the MBL value already reached this level without being battery replenished were not included in these tests (i.e., if the value in the 5th column of Table 2 is greater or equal to 28%, then the related instance was not considered for this second part of the study). Two different groups of data are provided in this table:

Table 3.
GVNS results with battery swap extension.
- Results without battery replenishment: This part reproduces the values obtained in Table 2 for comparison purposes, where columns “” and “MBL” refer to “BF” and “MBL without charging” columns respectively.
- Results with battery swap technique: This presents our GVNS model outputs. In addition to and MBL columns, the “BS count” column refers to number of battery switches performed to reach level; “” indicates the ID of the AGV concerned by the battery switch’s operation, and “Status in BS” column describes the status of the AGV while swapping its battery (two values are possible: Empty (or “1”), Loaded (or “2”) as described in the BS string representation in Section 2.1).
5. Results Discussion
Several remarks can be drawn from the results obtained in Table 2. Initially, values gathered by using GVNS were almost identical to the best known solution (BK). The analysis of variance through one-way ANOVA confirmed that there was no significant difference between our GVNS results and BK, as the calculated p-value was almost 90%—greatly superior to 5%.
Additionally, MBLs without a replenishment technique substantiate previous findings in the literature and further support the idea that battery constraints have a great impact on system throughput [12]. In fact, lines EX103, EX74 and EX104 state that omitting energy usage while scheduling various tasks may cause one or both AGVs stop in the middle of a transport operation (as MBL is lower than zero) involving a huge delay in production, route congestion, onboard battery characteristics’ degradation and extra cost for troubleshooting failed AGV(s). Furthermore, adopting the opportunity charging technique provides further evidence for our previous deductions. As a matter of fact, the last six columns show that an optimal can be maintained by choosing the right battery type. Additionally, it can be clearly observed that the charge level in lead acid batteries did not improve much when adopting the opportunity charge technique.
Note that stable battery levels for some instances, such as in EX73, were due to the lack of blocking time at the pickup/drop-off stations.
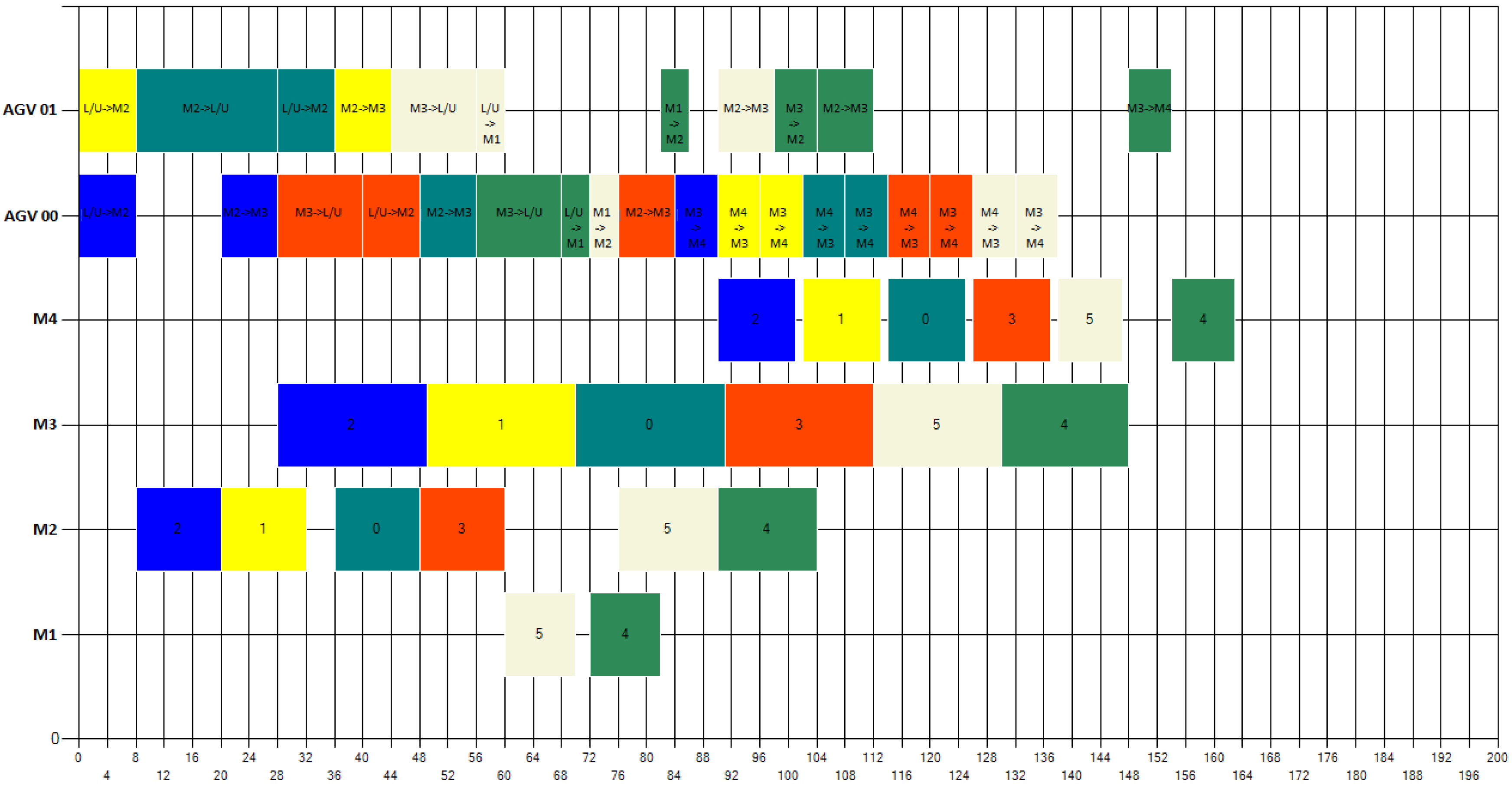
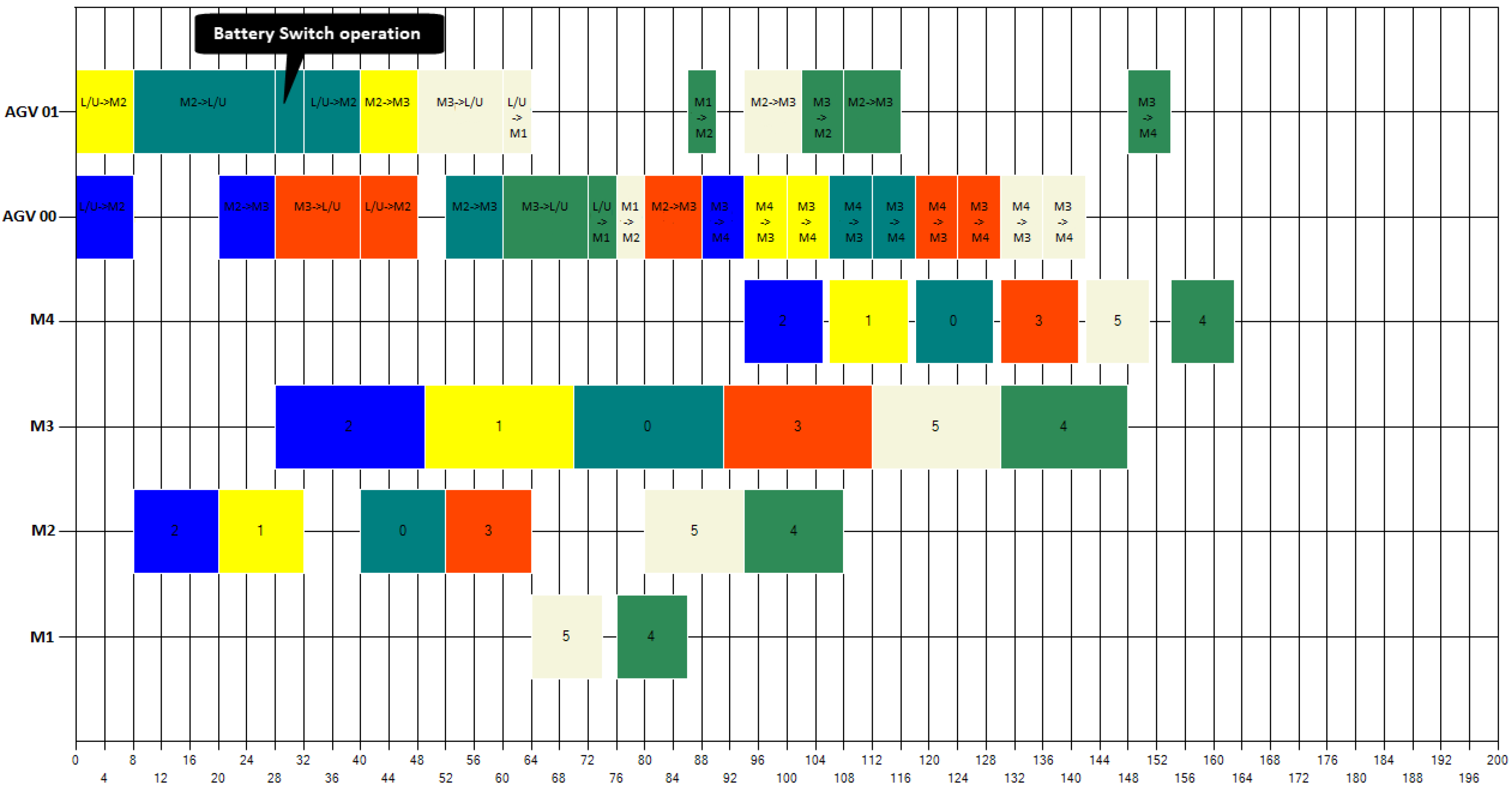
On the other hand, results of Table 3 have further strengthened the effectiveness of considering battery management method. Lines EX84 and EX94 stress just how possible it is to preserve the same scheduling qualities while managing energy: was unchanged and remained the same while adopting a battery replacement strategy. Figure 8 and Figure 9 show, respectively, Gantt diagrams of the instance EX84 before and after using a battery management policy and demonstrate that the schedule system has maintained the same in both situations.
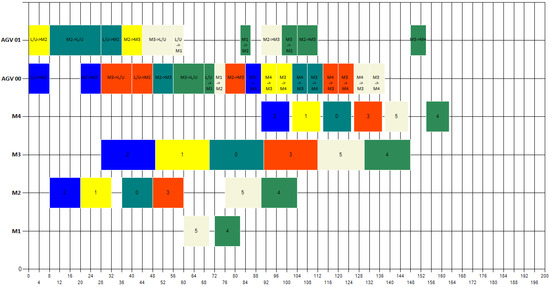
Figure 8.
Gantt diagram of EX84 instance without a battery management strategy with makespan = 163.
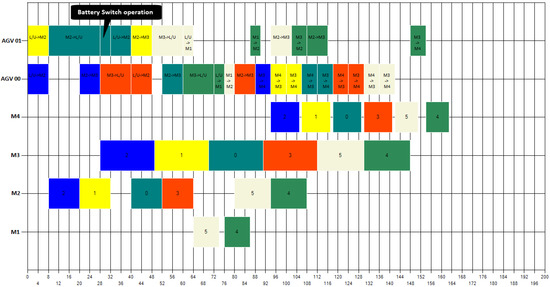
Figure 9.
Gantt diagram of EX84 instance using a battery management strategy with makespan = 163.
Furthermore, the analysis of variance (one-way ANOVA) has been conducted to evaluate whether a significant statistical difference exists between and MBL data groups before and after using a battery swap technique. The obtained p-values (see the last line of Table 3) demonstrate that results have not been significantly changed before and after using a battery swap technique (p-value ), while MBL values have been meaningfully enhanced after using our approach (p-value ). This confirms that our GVNS has improved MBL values while keeping makespan in steady state.
Finally, the proposed approach demonstrates its ability to minimize the number of battery switch operations: all the proposed schedules have only one BS operation. Additionally, using a single BS station is more beneficial, in terms of installation and maintenance costs, than using a battery charging station in each node which can presents a valuable economic factor.
6. Conclusions
In this paper, we have addressed a novel approach to resolve the JSP in an AGV-based manufacturing facility with battery constraints. We have studied previous works to highlight their limitations and proposed a GVNS-based metaheuristic that has succeeded to preserve the economical quality of the production cells while significantly optimizing energy consumption.
The provided numerical results show that the obtained makespan is very close to the best known solutions. We complemented the existing literature on the topic with new energy consumption related results, and enhanced our understanding on the feasibility or unfeasibility of previous findings when considering energy aspects. Our results also put forward the possibility of using an opportunity charge or a battery swap strategy while saving money.
The proposed model is useful to managers for the decision making at the operational level, although some potential limitations need to be considered. First, the maximum battery capacity is not constant and it is subject to degradation during the charging process [38]; thus, future studies should take into consideration the dynamic nature of this parameter while highlighting battery properties such as the maximum allowable charging/discharging current, allowable warming and balancing cells. Additionally, the battery threshold level parameter (), to prevent batteries from being deeply discharged, was fixed with an arbitrary value while it should be carefully chosen, as it can highly influence the economic factor by reducing battery cost, which is significant in comparison with energy prices [39]. Finally, it would be wise to integrate other factors such as battery degradation rates, AGVs workloads or battery stations’ installation and maintenance costs.
Considerable insight has been gained with regard to AGV systems and their usage in different industry types. Some modern companies try to bypass the limitations and logistical problems of battery charging and switch techniques by employing other replenishment systems, such as rail based charging [40], which can be a very interesting field of investigation, even if this choice still depends on technical and economical factors of the target system. Additionally, a reactive behavior study, allowing AGVs to manage their own energy replenishment operations in regard to system outlined objectives, will also be helpful. Furthermore, additional battery parameters can be monitored, during the manufacturing process, when considering the opportunity charge strategy, such as the issue of balancing cells and their operating parameters (temperature, charging/discharging currents, service life, etc.
Author Contributions
Conceptualization, M.A., A.B., D.T., N.A. and K.B.; data curation, M.A. and A.B.; formal analysis, M.A. and A.B.; funding acquisition, M.A. and K.B.; investigation, M.A. and A.B.; methodology, M.A. and A.B.; project administration, N.A. and K.B.; resources, A.B., D.T., N.A. and K.B.; software, M.A.; supervision, D.T. and K.B.; validation, A.B.; visualization, A.B., D.T., N.A. and K.B.; writing—original draft, M.A. and A.B.; Writing—review and editing, M.A., A.B., D.T., N.A. and K.B. All authors have read and agreed to the published version of the manuscript.
Funding
The first author of this work has been funded by the Algerian Ministry of Higher Education and Scientific Research through the Exceptional National Program scholarship under: 97/PNE/enseignant/France/2018–2019. The work described in this paper was conducted within the framework of the joint laboratory “SurferLab” founded by Bombardier, Prosyst and the Université Polytechnique Hauts-de-France. This Joint Laboratory is supported by the CNRS, the European Union (ERDF) and the Hauts-de-France region.
Acknowledgments
The authors would like to thank the Directorate General for Scientific Research and Technological Development (DGRSDT), an institution of the Algerian Ministry of Higher Education and Scientific Research, for their support on this work.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AGV | Automated Guided Vehicle |
| BS | Battery Switch |
| GVNS | General Variable Neighborhood Search |
| JSP | Job-shop Scheduling Problem |
| L/U | Loading/Unloading |
| MBL | Minimum detected Battery Level |
| VND | Variable Neighborhood Descendant |
| VNS | Variable Neighborhood Search |
| VRP | Vehicle Routing Problem |
References
- Lasi, H.; Fettke, P.; Kemper, H.-G.; Feld, T.; Hoffmann, M. Industry 4.0. Bus. Inf. Syst. Eng. 2014, 6, 239–242. [Google Scholar] [CrossRef]
- General Assembly of the United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; A/RES/70/1; Division for Sustainable Development Goals: New York, NY, USA, 2015; pp. 1–35. [Google Scholar]
- Pojani, D.; Stead, D. Policy design for sustainable urban transport in the global south. Policy Des. Pract. 2018, 1, 90–102. [Google Scholar] [CrossRef]
- Muñoz-Villamizar, A.; Montoya-Torres, J.R.; Faulin, J. Impact of the use of electric vehicles in collaborative urban transport networks: A case study. Transp. Res. Part D Transp. Environ. 2017, 50, 40–54. [Google Scholar] [CrossRef]
- Bechtsis, D.; Tsolakis, N.; Vouzas, M.; Vlachos, D. Industry 4.0: Sustainable material handling processes in industrial environments. Comput. Aided Chem. Eng. 2017, 40, 2281–2286. [Google Scholar]
- Giret, A.; Trentesaux, D.; Prabhu, V. Sustainability in manufacturing operations scheduling: A state of the art review. J. Manuf. Syst. 2015, 37, 126–140. [Google Scholar] [CrossRef]
- CIOL Bureau. Flipkart Introduces India-first Automation Initiative: Automated Guided Vehicles. 2019. Available online: https://www.ciol.com/flipkart-introduces-india-first-automation-initiative-automated-guided-vehicles/ (accessed on 1 September 2020).
- Vis, I.F.A. Survey of research in the design and control of automated guided vehicle systems. Eur. J. Oper. Res. 2006, 170, 677–709. [Google Scholar] [CrossRef]
- Weber, A. AGVs vs. Conveyors. In Assembly Magazine; BNP Media: Troy, MI, USA, 2 October 2008. [Google Scholar]
- De Ryck, M.; Versteyhe, M.; Debrouwere, F. Automated guided vehicle systems, state-of-the-art control algorithms and techniques. J. Manuf. Syst. 2020, 54, 152–173. [Google Scholar] [CrossRef]
- Kabir, Q.S.; Suzuki, Y. Comparative analysis of different routing heuristics for the battery management of automated guided vehicles. Int. J. Prod. Res. 2018, 57, 624–641. [Google Scholar] [CrossRef]
- McHANEY, R. Modelling battery constraints in discrete event automated guided vehicle simulations. Int. J. Prod. Res. 1995, 33, 3023–3040. [Google Scholar] [CrossRef]
- Bilge, Ü.; Ulusoy, G. A Time Window Approach to Simultaneous Scheduling of Machines and Material Handling System in an FMS. Oper. Res. 1995, 43, 1058–1070. [Google Scholar] [CrossRef]
- Fatnassi, E.; Chaouachi, J. Scheduling automated guided vehicle with battery constraints. In Proceedings of the 2015 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 24–27 August 2015; IEEE: Miedzyzdroje, Poland, 2015; pp. 1010–1015. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Appendix: List of NP-Complete Problems. In Computers and Intractability: A Guide to the Theory of NP-Completeness, 1st ed.; Series of Books in the Mathematical Sciences; W. H. Freeman: Kearny, NJ, USA, 1979; p. 242. [Google Scholar]
- Hurink, J.; Knust, S. A tabu search algorithm for scheduling a single robot in a job-shop environment. Discret. Appl. Math. 2002, 119, 181–203. [Google Scholar] [CrossRef]
- Deroussi, L.; Gourgand, M.; Tchernev, N. A simple metaheuristic approach to the simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Res. 2008, 46, 2143–2164. [Google Scholar] [CrossRef]
- Lacomme, P.; Larabi, M.; Tchernev, N. Job-shop based framework for simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Econ. 2013, 143, 24–34. [Google Scholar] [CrossRef]
- Baruwa, O.T.; Piera, M.A. A coloured Petri net-based hybrid heuristic search approach to simultaneous scheduling of machines and automated guided vehicles. Int. J. Prod. Res. 2016, 54, 4773–4792. [Google Scholar] [CrossRef]
- Petrović, M.; Miljković, Z.; Jokić, A. A novel methodology for optimal single mobile robot scheduling using whale optimization algorithm. Appl. Soft Comput. 2019, 81, 105520. [Google Scholar] [CrossRef]
- Ebben, M. Logistic Control in Automated Transportation Networks. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2001. [Google Scholar]
- Colling, D.; Oehler, J.; Furmans, K. Battery Charging Strategies for AGV Systems. Logist. J. Proc. 2019. [Google Scholar] [CrossRef]
- Tsubota, M.; Osumi, S.; Kosai, M. Characteristics of valve-regulated lead/acid batteries for automotive applications under deep-discharge duty. J. Power Sources 1991, 33, 105–116. [Google Scholar] [CrossRef]
- Kabir, Q.S.; Suzuki, Y. Increasing manufacturing flexibility through battery management of automated guided vehicles. Comput. Ind. Eng. 2018, 117, 225–236. [Google Scholar] [CrossRef]
- Kawakami, T.; Takata, S. Battery Life Cycle Management for Automatic Guided Vehicle Systems. In Design for Innovative Value Towards a Sustainable Society; Matsumoto, M., Umeda, Y., Masui, K., Fukushige, S., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 403–408. [Google Scholar]
- Zhan, X.; Xu, L.; Zhang, J.; Li, A. Study on AGVs battery charging strategy for improving utilization. Procedia CIRP 2019, 81, 558–563. [Google Scholar] [CrossRef]
- Mousavi, M.; Yap, H.J.; Musa, S.N.; Tahriri, F.; Md Dawal, S.Z. Multi-objective AGV scheduling in an FMS using a hybrid of genetic algorithm and particle swarm optimization. PLoS ONE 2017, 12, e0169817. [Google Scholar] [CrossRef]
- Dehnavi-Arani, S.; Sabaghian, A.; Fazli, M. A Job Shop Scheduling and Location of Battery Charging Storage for the Automated Guided Vehicles (AGVs). J. Optim. Ind. Eng. 2019, 12, 121–129. [Google Scholar]
- Hansen, P.; Mladenović, N. Variable Neighborhood Search. In Handbook of Heuristics; Martí, R., Pardalos, P.M., Resende, M.G.C., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 759–787. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Roshanaei, V.; Naderi, B.; Jolai, F.; Khalili, M. A variable neighborhood search for job shop scheduling with set-up times to minimize makespan. Future Gener Comput. Syst. 2009, 25, 654–661. [Google Scholar] [CrossRef]
- Cheng, R.; Gen, M.; Tsujimura, Y. A tutorial survey of job-shop scheduling problems using genetic algorithms—I. representation. Comput. Ind. Eng. 1996, 30, 983–997. [Google Scholar] [CrossRef]
- Optimization and Big Data. In Metaheuristics for Big Data; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 1–21.
- Lusa, A.; Potts, C.N. A variable neighbourhood search algorithm for the constrained task allocation problem. J. Oper. Res. Soc. 2008, 59, 812–822. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. Variable Neighborhood Search. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; Kluwer Academic Publishers: Boston, MA, USA, 2003; Volume 57, pp. 145–184. [Google Scholar]
- Bruce, B. Unit load carriers. In Materials Handling Handbook; Kulwiec, R.A., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1985; p. 302. [Google Scholar]
- Zheng, Y.; Xiao, Y.; Seo, Y. A tabu search algorithm for simultaneous machine/AGV scheduling problem. Int. J. Prod. 2014, 52, 5748–5763. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, X.; Li, X.; Xiao, R.; Shen, J. LiFePO4 battery charging strategy design considering temperature rise minimization. J. Renew. Sustain. Energy 2017, 9, 064103. [Google Scholar] [CrossRef]
- Petrik, M.; Wu, X. Optimal Threshold Control for Energy Arbitrage with Degradable Battery Storage. In Proceedings of the UAI, Amsterdam, The Netherlands, 12–16 July 2015; AUAI Press: Corvallis, OR, USA, 2015; pp. 692–701. [Google Scholar]
- Automatic Fast Charging of Automated Guided Vehicles (AGVs). Available online: https://www.azom.com/article.aspx?ArticleID=15531 (accessed on 8 July 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).