A Combined Multi-Level Perspective and Agent-Based Modeling in Low-Carbon Transition Analysis
Abstract
:1. Introduction
2. Challenges and Analytical Approaches to Low-Carbon Transition
2.1. Low-Carbon Transition Challenges
2.2. Agent-Based Modeling and Multi-Level Perspective
2.3. Advantages and Disadvantages
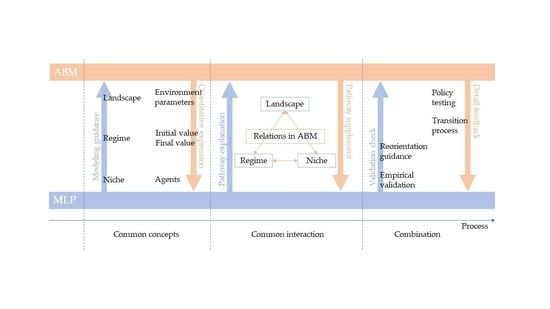
3. Toward a Combined Analytical Framework
3.1. Common Concepts
3.1.1. High-Carbon States
- Niche dynamics and system stability can explain the interactions between participants or actors and social groups in MLP. The analysis of the MLP focuses on qualitative factors, such as distributed energy systems, energy networks, and evolution processes, that span multiple dimensions, such as the social, economic, technological, or political dimensions. This explains the emergence of niche innovation in that it competes with established degrees of the developmental trajectory.
- In ABM, the concepts of niche dynamics and system stability are applied to show the predicted rate of change in various quantitative indicators over time. ABM uses complexity theory to model the system through internally and externally consistent parameters and rules to investigate and explain the fundamental role of some key elements and their interaction in the low-carbon transition process. Different scenarios can be examined using various initial conditions and parameter settings that represent niche innovation and system conditions within their evolution. With landscape institutions and actors at the regime or niche levels modeled as agents, a specific value in the initial or final stage can be used to determine the status of the system. Parameter settings are usually implications of landscape and regime environments.
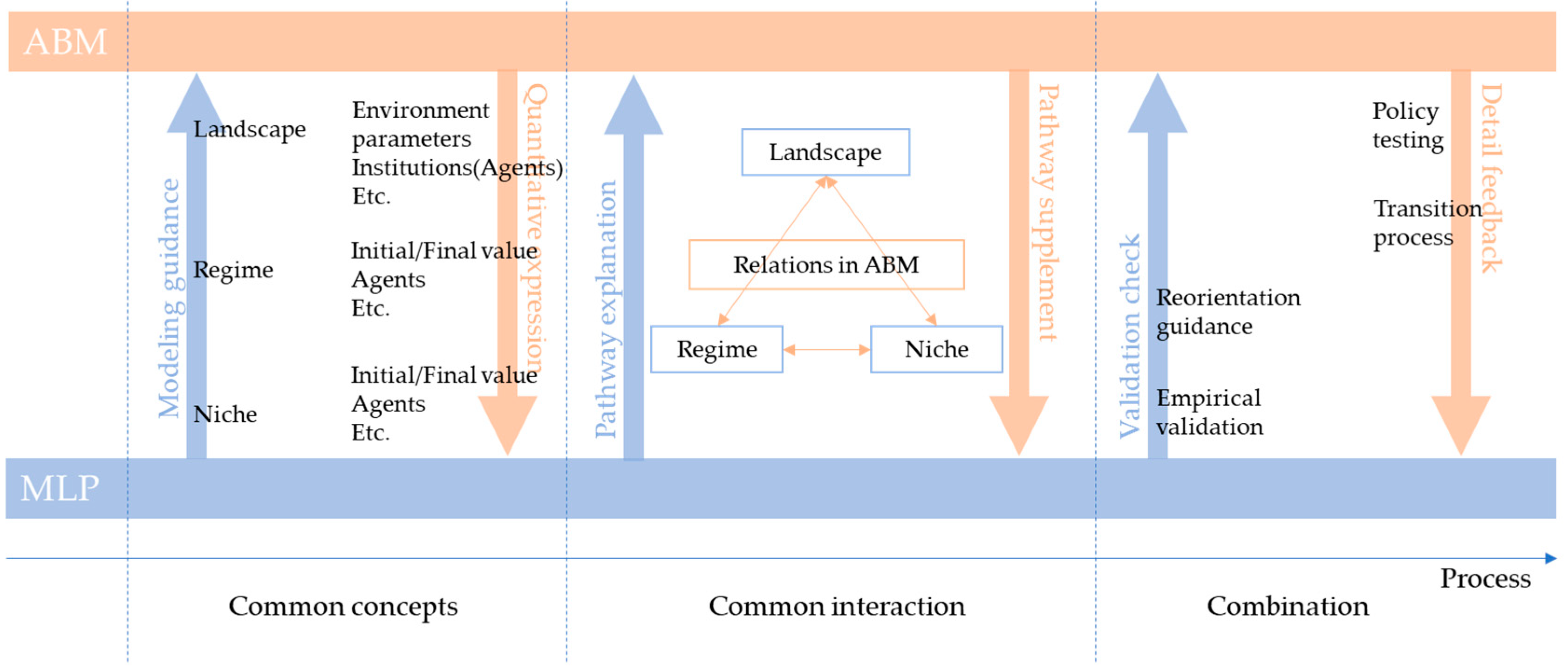
3.1.2. Pathways of the Low-Carbon Transition
- The pathway description in the MLP concentrates on the interactions between different levels. By providing a comprehensive interpretation of sociotechnical complexity, the pathway description provides a method to describe a general pathway that reflects social phenomena and technical changes. The efficiency of policy selections and actions relies on a description based on an introduced strategy and patterns.
- For ABM, the pathway description is often designed using applied mathematics and parameterization based on complexity theory, and the scenario-based pathway description offers the chance to obtain specific interaction phenomena between different levels. With respect to policy concerns, first, policy actions are mainly analyzed through parameter settings and regulatory tools. Second, clear model-based transition recommendations for policy intervention choices can be provided. Third, a specific policy can be suggested on the basis of the phase diagram obtained from the ABM simulation by confirming key factors and actors as control parameters.
3.1.3. Low-Carbon States
- The concepts of system dynamics and stability in low-carbon states, used to interpret system stability and the impact of an existing regime that could explain a successful transition in interactions between actors and social groups, are applied in MLP. In addition, the analysis focuses on qualitative factors such as niche innovation in a low-carbon state, and the uncertainty of the future can be briefly interpreted through system evolution patterns.
- ABM applies the concepts of system stability and dynamics in low-carbon states so that various quantitative indicators reflect the expected rate of change over time. ABM can provide a detailed representation of system information such as niche innovation in low-carbon states and scenario simulations, therefore allowing system complexities in low-carbon states to be explored under specific constraints and policy actions as numerical instruments in models.
3.2. From Common Concepts to Conceptual Interaction
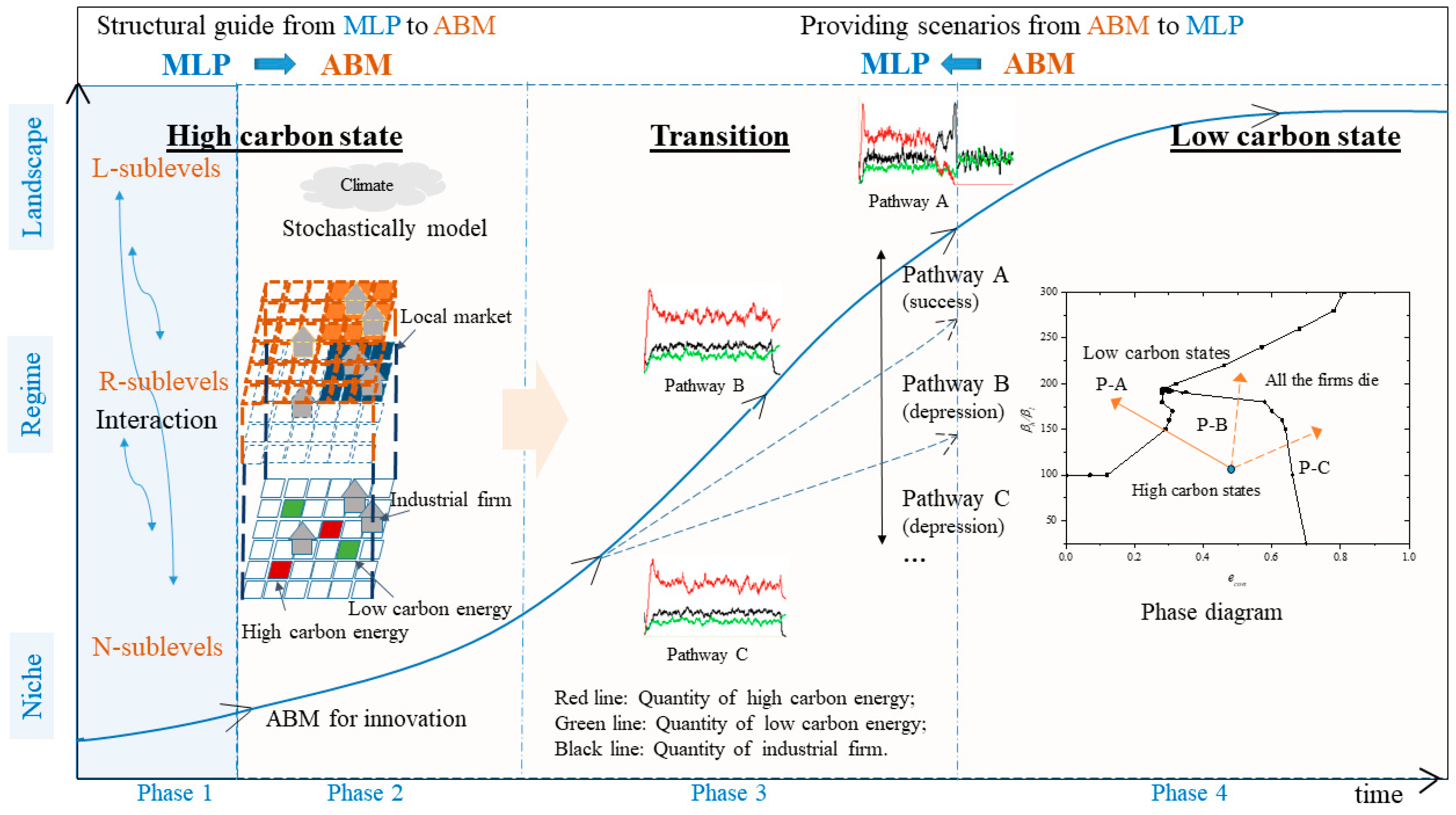
3.3. Combination
3.4. Combination Flow of the Low-Carbon Transitions
4. Application of the Combined Approach
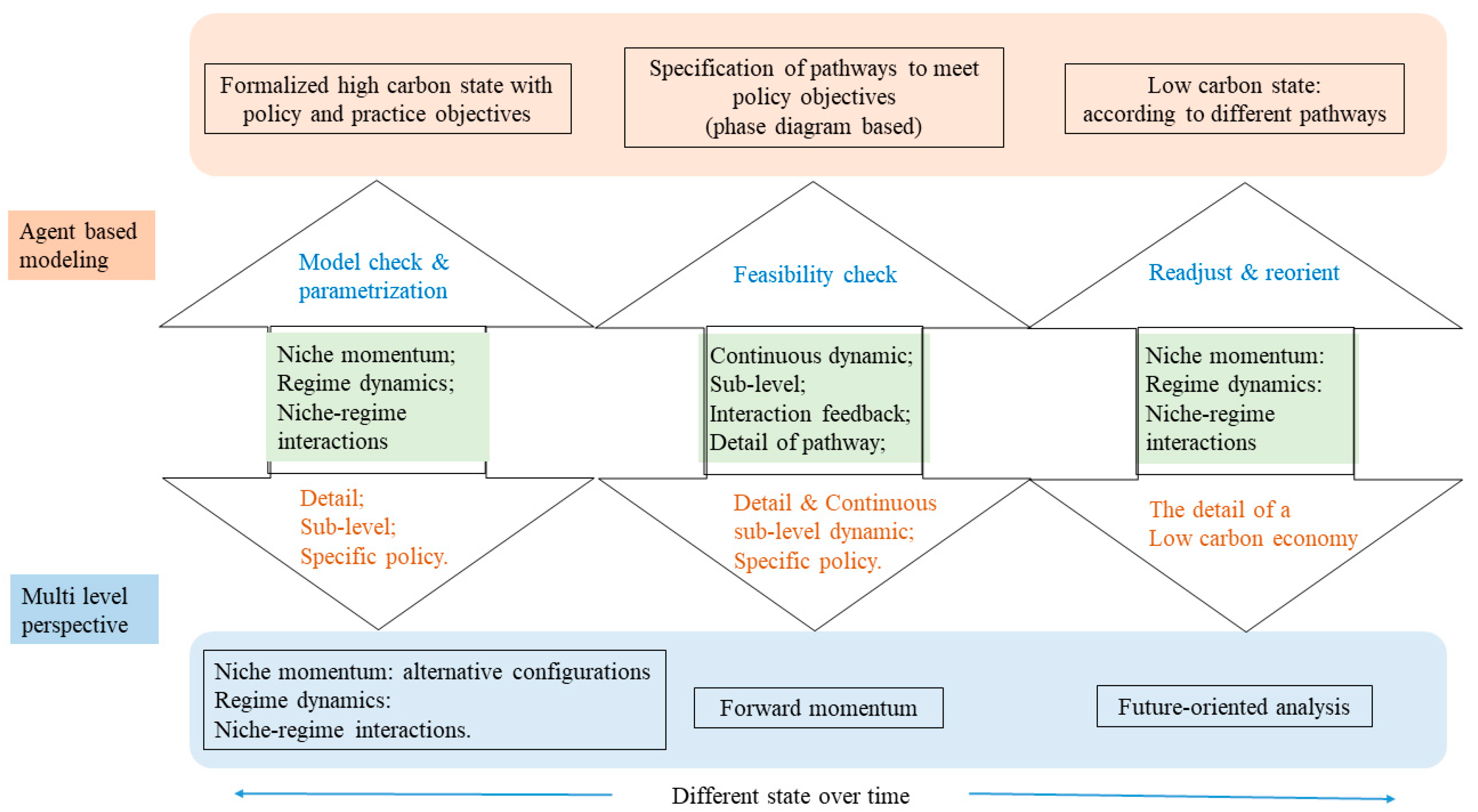
5. Agent-Based Model Verification and Validation
5.1. Structural Verification
5.2. Behavioral Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Xu, Y.; Lou, Y.; Chen, Y. Low carbon transition in a distributed energy system regulated by localized energy markets. Energy Policy 2018, 122, 474–485. [Google Scholar] [CrossRef]
- Song, M.; Niu, F.; Mao, N.; Hu, Y.; Deng, S.S. Review on building energy performance improvement using phase change materials. Energy Build. 2018, 158, 776–793. [Google Scholar] [CrossRef]
- Song, M.; Deng, S.S.; Dang, C.; Mao, N.; Wang, Z. Review on improvement for air source heat pump units during frosting and defrosting. Appl. Energy 2018, 211, 1150–1170. [Google Scholar] [CrossRef]
- David, F.; Hatef, M. On heat pumps in smart grids: A review. Renew. Sustain. Energy Rev. 2017, 70, 342–357. [Google Scholar]
- Wu, X.; Cao, J.; Jiang, C.; Lou, Y.; Zhao, S.; Madani, H.; Chen, Y. Low carbon transition in climate policy linked distributed energy System. Glob. Transit. Proc. 2020, 1, 1–6. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, X.; Zhao, S.; Madani, H.; Chen, Y. Economic crisis impact on low carbon transition in economy-ecosystem. Glob. Transit. Proc. 2020, 1, 7–12. [Google Scholar] [CrossRef]
- Liu, H. Biofuel’s sustainable development under the trilemma of energy, environment and economy. Probl. Ekorozwoju 2015, 10, 55–59. [Google Scholar]
- Raphael, J.; Darren, M.; Benjamin, K. Resolving society’s energy trilemma through the Energy Justice Metric. Energy Policy 2015, 87, 168–176. [Google Scholar]
- Geels, F.W. Technological transitions as evolutionary reconfiguration processes: A multi-level perspective and a case-study. Res. Policy 2002, 31, 1257–1274. [Google Scholar] [CrossRef] [Green Version]
- Geels, F.W.; Schot, J. Typology of sociotechnical transition pathways. Res. Policy 2007, 36, 399–417. [Google Scholar] [CrossRef]
- Mariësse, A.; Andries, F.; Samuel, C.; Frank, G.; Måns, N.; Karoline, R.; Bruno, T.; Detlef, P. Aligning integrated assessment modelling with socio-technical transition insights: An application to low-carbon energy scenario analysis in Europe. Technol. Forecast. Soc. Chang. 2017, 119117. [Google Scholar]
- Bruno, T.; Frans, B.; Frank, G.; Andries, H.; Andy, M.; Björn, N.; Detlefvan, V. Evaluating sustainability transitions pathways: Bridging analytical approaches to address governance challenges. Glob. Environ. Chang. 2015, 35, 239–253. [Google Scholar]
- Frank, W.; Frans, B.; Detlef, P. Bridging analytical approaches for low-carbon transitions. Nat. Clim. Chang. 2016, 6, 576–583. [Google Scholar]
- Macal, C.; North, M.J. Agent-based modeling and simulation. In Proceedings of the 2009 Winter Simulation Conference (WSC), Austin, TX, USA, 13–16 December 2009; pp. 86–98. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [Green Version]
- Smith, E.R.; Conrey, F.R. Agent-based modeling: A new approach for theory building in Social psychology. Pers. Soc. Psychol. Rev. 2007, 11, 87–104. [Google Scholar] [CrossRef]
- Marsella, S.C.; Pynadath, D.V.; Read, S.J. PsychSim: Agent-based modeling of social interactions and influence. Proc. Internat. Conf. Cognit. Model. 2004, 36, 243–248. [Google Scholar]
- Climate Change 2014: Impacts, Adaptation, and Vulnerability; IPCC: Nairobi, Kenya, 2014.
- Frank, G. Ontologies, socio-technical transitions (to sustainability), and the multi-level perspective. Res. Policy 2010, 39, 495–510. [Google Scholar]
- Macal, C.M.; North, M.J. Tutorial on agent-based modelling and simulation. J. Simul. 2010, 4, 151–162. [Google Scholar] [CrossRef]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Sharon, J.; Stephanie, C. Building a sustainable energy future, one community at a time. Renew. Sustain. Energy Rev. 2016, 60, 867–880. [Google Scholar]
- Yuan, C.; Liu, L.; Ye, J.; Ren, G.; Zhuo, D.; Qi, X. Assessing the effects of rural livelihood transition on non-point source pollution: A coupled ABM–IECM model. Environ. Sci. Pollut. Res. 2017, 24, 12899–12917. [Google Scholar] [CrossRef]
- Evans, T.P.; Kelley, H. Assessing the transition from deforestation to forest regrowth with an agent-based model of land cover change for south-central Indiana (USA). Geoforum 2008, 39, 819–832. [Google Scholar] [CrossRef]
- Tesfatsion, L. Electric power markets in transition: Agent-based modeling tools for transactive energy support. Handb. Comput. Econ. 2018, 4, 715–766. [Google Scholar] [CrossRef]
- Kathleen, A. The emerging field of energy transitions: Progress, challenges, and opportunities. Energy Res. Soc. Sci. 2014, 112–121. [Google Scholar]
- Nurtaj, V.; Elchin, S.; Cihan, B.; Ceyhun, M. Transition to renewable energy and sustainable energy development in Azerbaijan. Renew. Sustain. Energy Rev. 2017, 80, 1153–1161. [Google Scholar]
- Andrew, C.; Kenshi, I. Energy transition to a future low-carbon energy society in Japan’s liberalizing electricity market: Precedents, policies and factors of successful transitions. Renew. Sustain. Energy Rev. 2018, 81, 2019–2027. [Google Scholar]
- Hansen, P.; Liu, X.; Morrison, G.M. Agent-based modelling and socio-technical energy transitions: A systematic literature review. Energy Res. Soc. Sci. 2019, 49, 41–52. [Google Scholar] [CrossRef]
- Hinker, J.; Hemkendreis, C.; Drewing, E.; März, S.; Rodríguez, D.I.H.; Myrzik, J.M. A novel conceptual model facilitating the derivation of agent-based models for analyzing socio-technical optimality gaps in the energy domain. Energy 2017, 137, 1219–1230. [Google Scholar] [CrossRef]
- Bergek, A.; Jacobsson, S. The emergence of a growth industry: A comparative analysis of the German, Dutch and Swedish wind turbine industries. Chang. Transform. Dev. Physica 2003, 197–227. [Google Scholar] [CrossRef]
- Carlsson, B.; Jacobsson, S.; Holmén, M.; Rickne, A. Innovation systems: Analytical and methodological issues. Res. Policy 2002, 31, 233–245. [Google Scholar] [CrossRef]
- Hekkert, M.P.; Suurs, R.; Negro, S.O.; Kuhlmann, S.; Smits, R. Functions of innovation systems: A new approach for analysing technological change. Technol. Forecast. Soc. Chang. 2007, 74, 413–432. [Google Scholar] [CrossRef] [Green Version]
- Johnson, A. Functions in innovation system approaches. In Proceedings of the Nelson and Winter Conference, Aalborg, Denmark, 12–15 June 2001. [Google Scholar]
- Geels, F.W.; Raven, R. Non-linearity and expectations in niche-development trajectories: Ups and downs in Dutch biogas development (1973–2003). Technol. Anal. Strat. Manag. 2006, 18, 375–392. [Google Scholar] [CrossRef]
- Casti, J.L. BizSim: The world of business—In a box. Artif. Life Robot. 2000, 4, 125–129. [Google Scholar] [CrossRef]
- Markard, J.; Truffer, B. Actor-oriented analysis of innovation systems: Exploring micro–meso level linkages in the case of stationary fuel cells. Technol. Anal. Strat. Manag. 2008, 20, 443–464. [Google Scholar] [CrossRef]
- Papachristos, G.; Sofianos, A.; Adamides, E. System interactions in socio-technical transitions: Extending the multi-level perspective. Environ. Innov. Soc. Transit. 2013, 7, 53–69. [Google Scholar] [CrossRef]
- Busch, J.; Roelich, K.; Bale, C.S.; Knoeri, C. Scaling up local energy infrastructure; An agent-based model of the emergence of district heating networks. Energy Policy 2017, 100, 170–180. [Google Scholar] [CrossRef] [Green Version]
- Frank, W.; Benjamin, K.S.; Tim, S.; Steve, S. The socio-technical dynamics of low-carbon transitions. Joule 2017, 1, 463–479. [Google Scholar]
- Liu, Y. Relationship between industrial firms, high-carbon and low-carbon energy: An agent-based simulation approach. Appl. Math. Comput. 2013, 219, 7472–7479. [Google Scholar] [CrossRef]
- Stavins, R. World’s largest carbon market is scheduled for 2020 launch in China. Environ. Forum. 2018, 35, 15. [Google Scholar]
- Liu, L.; Chen, C.; Zhao, Y.; Zhao, E. China׳s carbon-emissions trading: Overview, challenges and future. Renew. Sustain. Energy Rev. 2015, 49, 254–266. [Google Scholar] [CrossRef]
- Qudrat-Ullah, H.; Seong, B.S. How to do structural validity of a system dynamics type simulation model: The case of an energy policy model. Energy Policy 2010, 38, 2216–2224. [Google Scholar] [CrossRef]
- Senge, P.; Forrester, J. Tests for building confidence in system dynamics models. Syst. Dyn. TIMS Stud. Manag. Sci. 1980, 14, 209–228. [Google Scholar]
- Schot, J.; Kanger, L.; Verbong, G. The roles of users in shaping transitions to new energy systems. Nat. Energy 2016, 1, 16054. [Google Scholar] [CrossRef] [Green Version]
- Geels, F.W.; Sovacool, B.K.; Schwanen, T.; Sorrell, S. Sociotechnical transitions for deep decarbonization. Science 2017, 357, 1242–1244. [Google Scholar] [CrossRef]
- Borup, M.; Brown, N.; Konrad, K.; Van Lente, H. The sociology of expectations in science and technology. Technol. Anal. Strat. Manag. 2006, 18, 285–298. [Google Scholar] [CrossRef]
- Hughes, L.; Urpelainen, J. Interests, institutions, and climate policy: Explaining the choice of policy instruments for the energy sector. Environ. Sci. Policy 2015, 54, 52–63. [Google Scholar] [CrossRef]
- Trancik, J.E. Renewable energy: Back the renewables boom. Nature 2014, 507, 300–302. [Google Scholar] [CrossRef] [Green Version]
- Goldthau, A. The G20 must govern the shift to low-carbon energy. Nature 2017, 546, 203–205. [Google Scholar] [CrossRef] [Green Version]
- Lund, H.; Mathiesen, B.V. Energy system analysis of 100% renewable energy systems—The case of Denmark in years 2030 and 2050. Energy 2009, 34, 524–531. [Google Scholar] [CrossRef]
- Dominković, D.F.; Bačeković, I.; Sveinbjörnsson, D.; Pedersen, A.S.; Krajačić, G. On the way towards smart energy supply in cities: The impact of interconnecting geographically distributed district heating grids on the energy system. Energy 2017, 137, 941–960. [Google Scholar] [CrossRef] [Green Version]
- Reuters. Available online: https://www.energylivenews.com/2020/03/10/denmark-needs-higher-carbon-tax-to-hit-2030-net-zero-goal/ (accessed on 1 July 2020).
- International Energy Agency. Energy Policies of IEA Countries: Denmark Review; OECD Publishing: Paris, France, 2002. [Google Scholar]
- World Bank. State and Trends of Carbon Pricing 2020; World Bank: Washington, DC, USA, 2020. [Google Scholar]
- Meibom, P.; Vinther, D.; Hilger, K.B.; Madsen, H. Energy comes together in Denmark: The key to a future fossil-free Danish power system. IEEE Power Energy Mag. 2013, 11, 46–55. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Tambo, T. Comparing consumer perceptions of energy security, policy, and low-carbon technology: Insights from Denmark. Energy Res. Soc. Sci. 2016, 11, 79–91. [Google Scholar] [CrossRef]
- Frede, H.; Søren, D. Consumer ownership, natural monopolies and transition to 100% renewable energy systems. Energy 2019, 181, 440–449. [Google Scholar]
- Parajuli, R. Looking into the Danish energy system: Lesson to be learned by other communities. Renew. Sustain. Energy Rev. 2012, 16, 2191–2199. [Google Scholar] [CrossRef]
- Downie, C. Strategies for Survival: The International Energy Agency’s response to a new world. Energy Policy 2020, 141, 111452. [Google Scholar] [CrossRef]
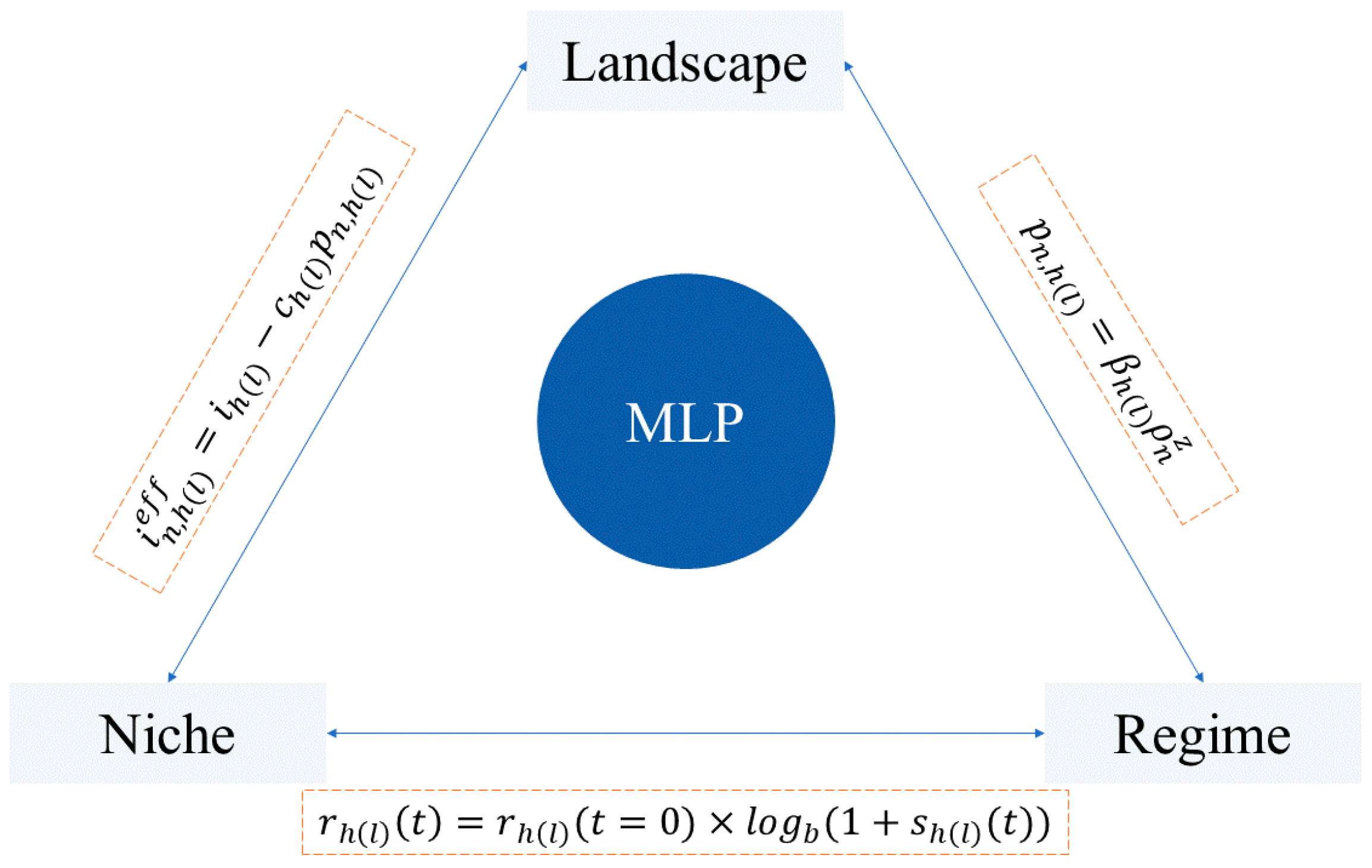
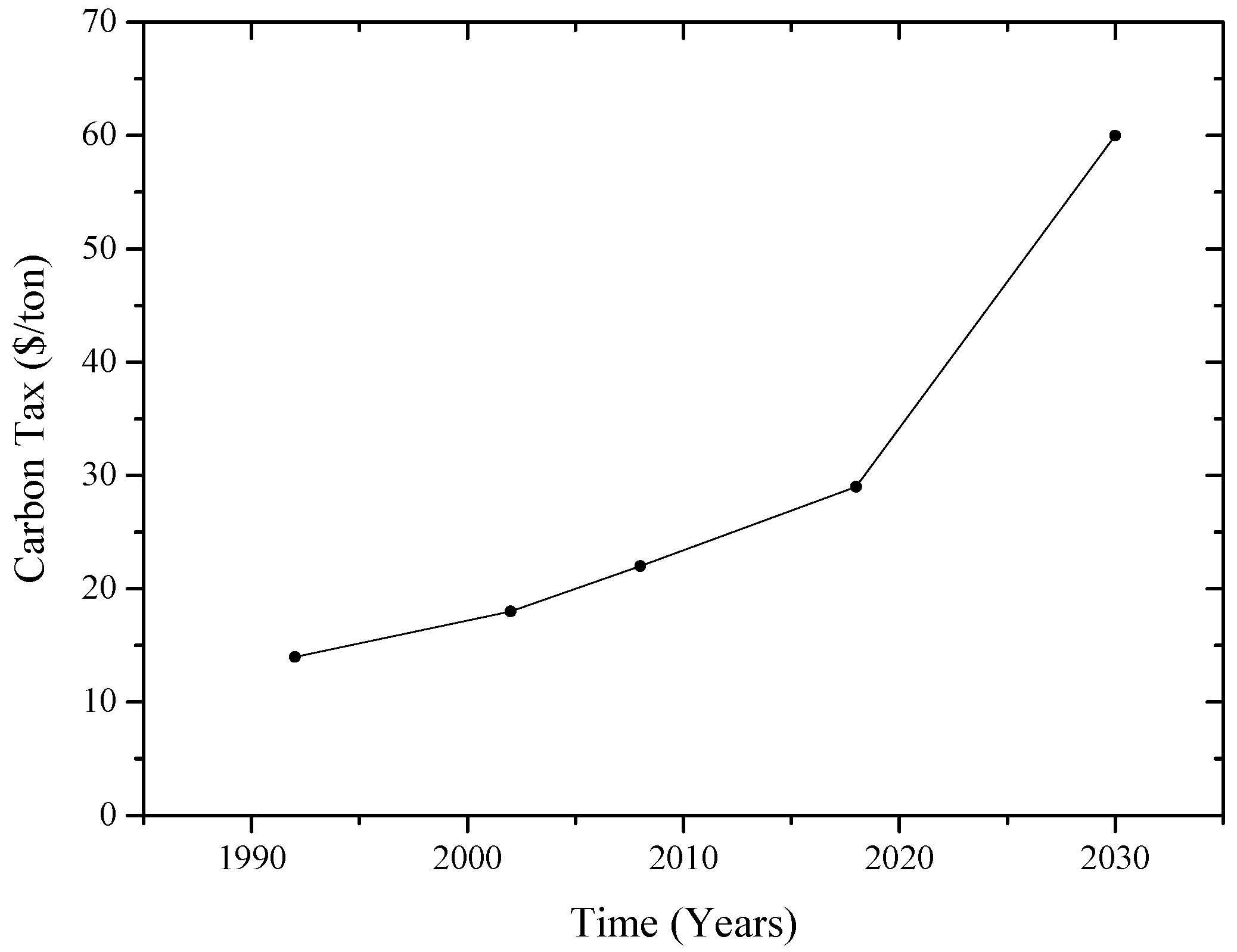

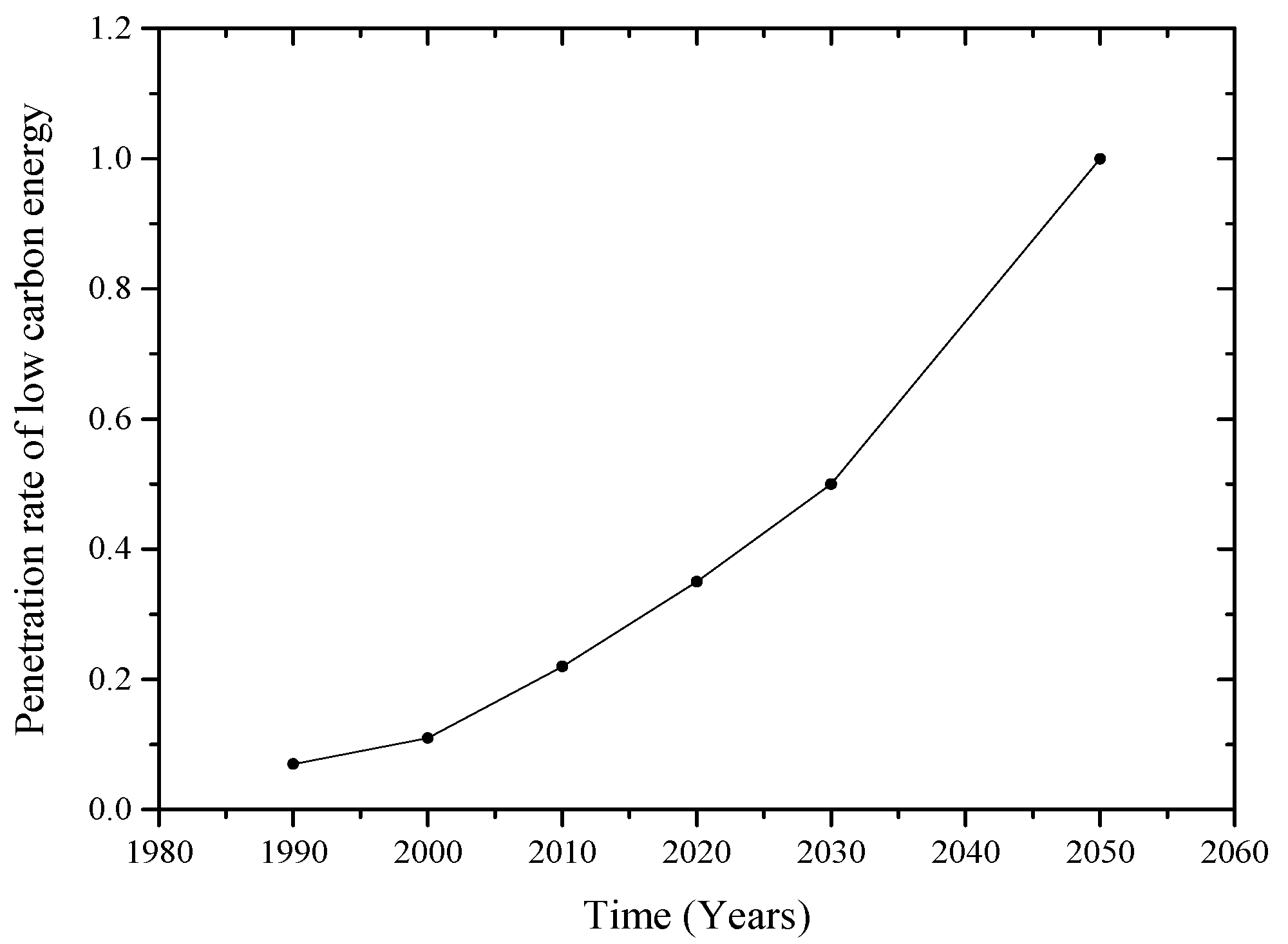
| MLP | ABM Model Parameters | ABM Model Assumptions | ||
|---|---|---|---|---|
| Landscape | Environmental pressure for carbon emission mitigation | (), carbon emission pressure for high-carbon (low-carbon) energy consumption | Environmental pressure impacts the regime level and market sensitivity coefficient for high (low)-carbon energy | |
| Technological development for emission reduction [9,10] | Long-term technical innovation supported for high (low) energy capacity | Technological development impacts the niche level, cultivating distributed energy systems, etc. [46] | ||
| Regime | Localized market, carbon tax, and subsidy policies [47] | Localized energy market | : Low-carbon energy is thought to be less sensitive to market performance in distributed energy systems [50,51] : The local firm number represents the potential demand | |
| , | Participant’s market property | : Real demand (number of firms that purchase high-carbon (low-carbon) energy). : Effective high-carbon (low-carbon) energy capacity reflects the firm’s real gains | ||
| Participant’s nature property | : Energy consumption reflects the efficiency and life cost. : Amount of energy retained by a firm | |||
| Niche | Niche innovation and distributed energy system [46] | The amount of energy provided by one unit of high-carbon (low-carbon) energy | & : Supply (at this time, high-carbon energy can perform with higher efficiency) [1] | |
| Rate of high-carbon (low-carbon) energy development | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Zhao, S.; Shen, Y.; Madani, H.; Chen, Y. A Combined Multi-Level Perspective and Agent-Based Modeling in Low-Carbon Transition Analysis. Energies 2020, 13, 5050. https://doi.org/10.3390/en13195050
Wu X, Zhao S, Shen Y, Madani H, Chen Y. A Combined Multi-Level Perspective and Agent-Based Modeling in Low-Carbon Transition Analysis. Energies. 2020; 13(19):5050. https://doi.org/10.3390/en13195050
Chicago/Turabian StyleWu, Xifeng, Sijia Zhao, Yue Shen, Hatef Madani, and Yu Chen. 2020. "A Combined Multi-Level Perspective and Agent-Based Modeling in Low-Carbon Transition Analysis" Energies 13, no. 19: 5050. https://doi.org/10.3390/en13195050
APA StyleWu, X., Zhao, S., Shen, Y., Madani, H., & Chen, Y. (2020). A Combined Multi-Level Perspective and Agent-Based Modeling in Low-Carbon Transition Analysis. Energies, 13(19), 5050. https://doi.org/10.3390/en13195050