Simulation of Heat and Mass Transfer Characteristics for the Optimal Operating Conditions of a Gas-to-Gas Membrane Humidifier with Porous Metal Foam
Abstract
:1. Introduction
2. Methods
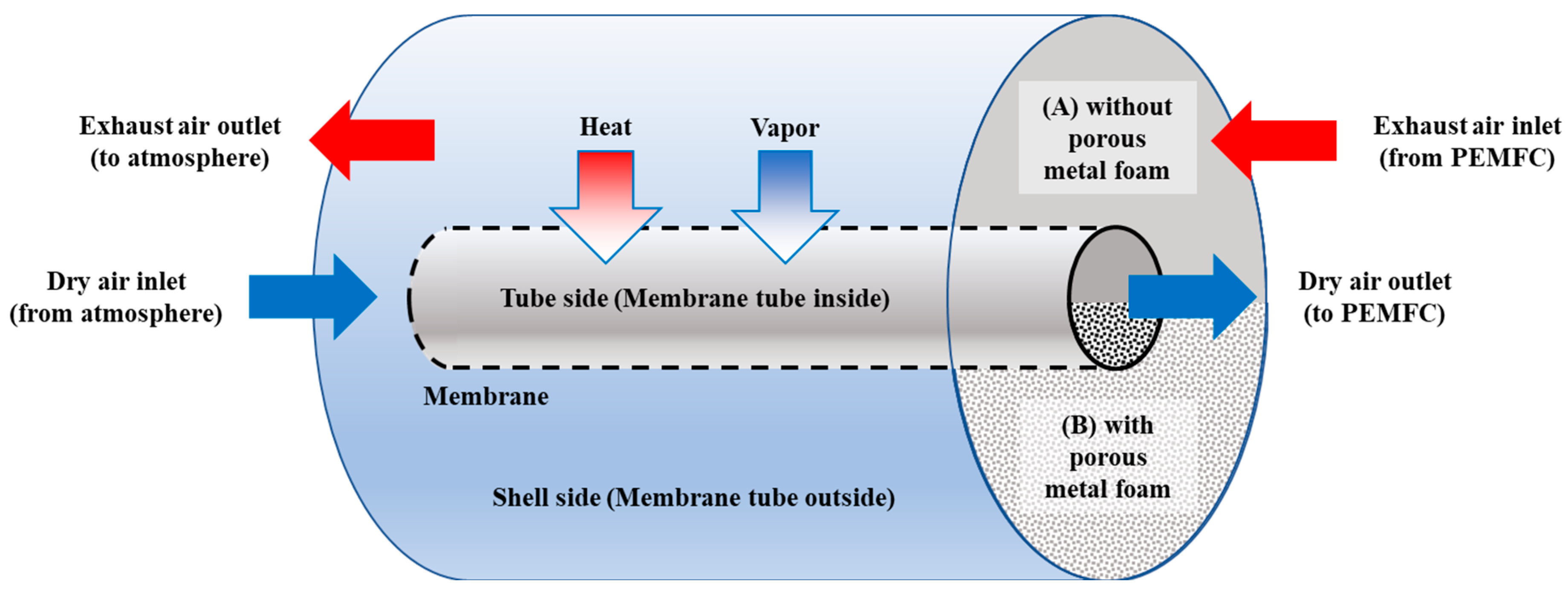
2.1. Model Description
- Air is an ideal gas because its density and pressure are low, and temperature is high enough to use the ideal state equation.
- Only water transfer occurs in the membrane because it is difficult for air molecules to pass it, owing to its diminutive pores.
- Heat loss to the atmosphere is ignored by regarding it as a complete insulation condition.
- Changes in the specific heat of the fluid above the operating temperature range are ignored.
- No phase change occurs, and the fluid is gaseous.
- The control volume is constant, as the expansion and contraction effect of the membrane according to the water content and differential pressure is much smaller than the control volume.
2.2. Modeling Approach
2.2.1. Thermodynamic Equation
2.2.2. Heat Transfer Equation
2.2.3. Mass Transfer Equation
2.3. Simulation Parameters
3. Results and Discussions
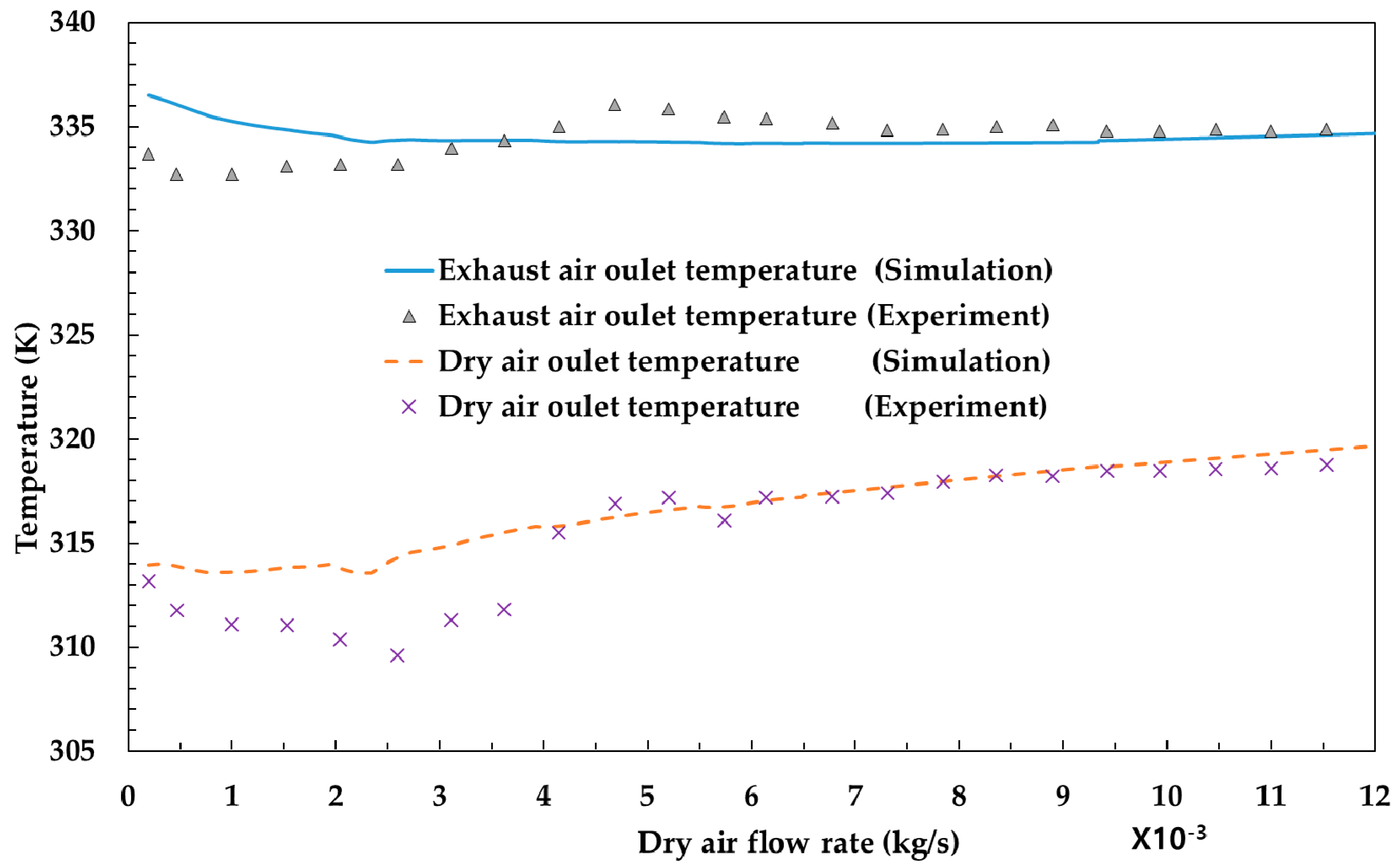
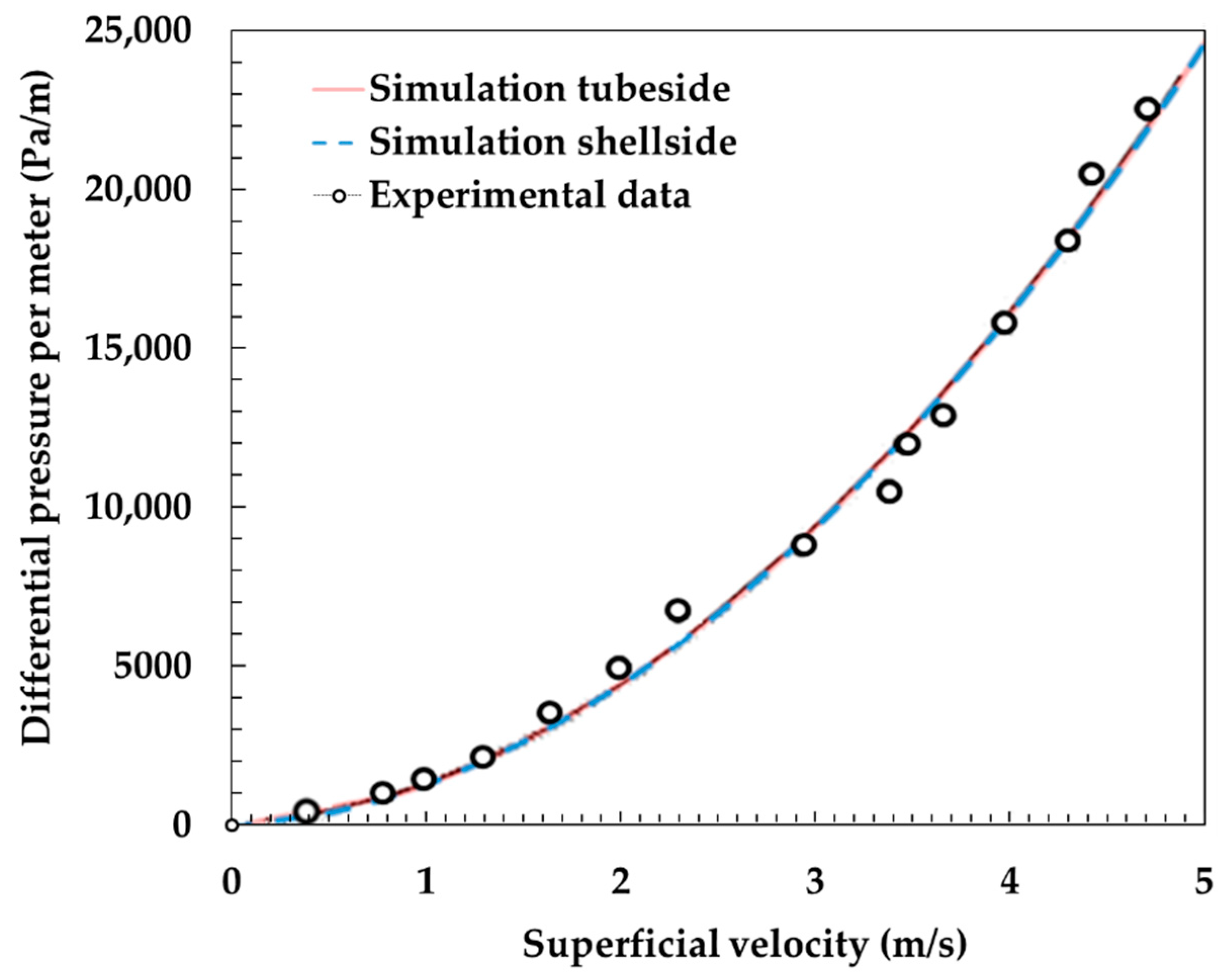
3.1. Model Validation
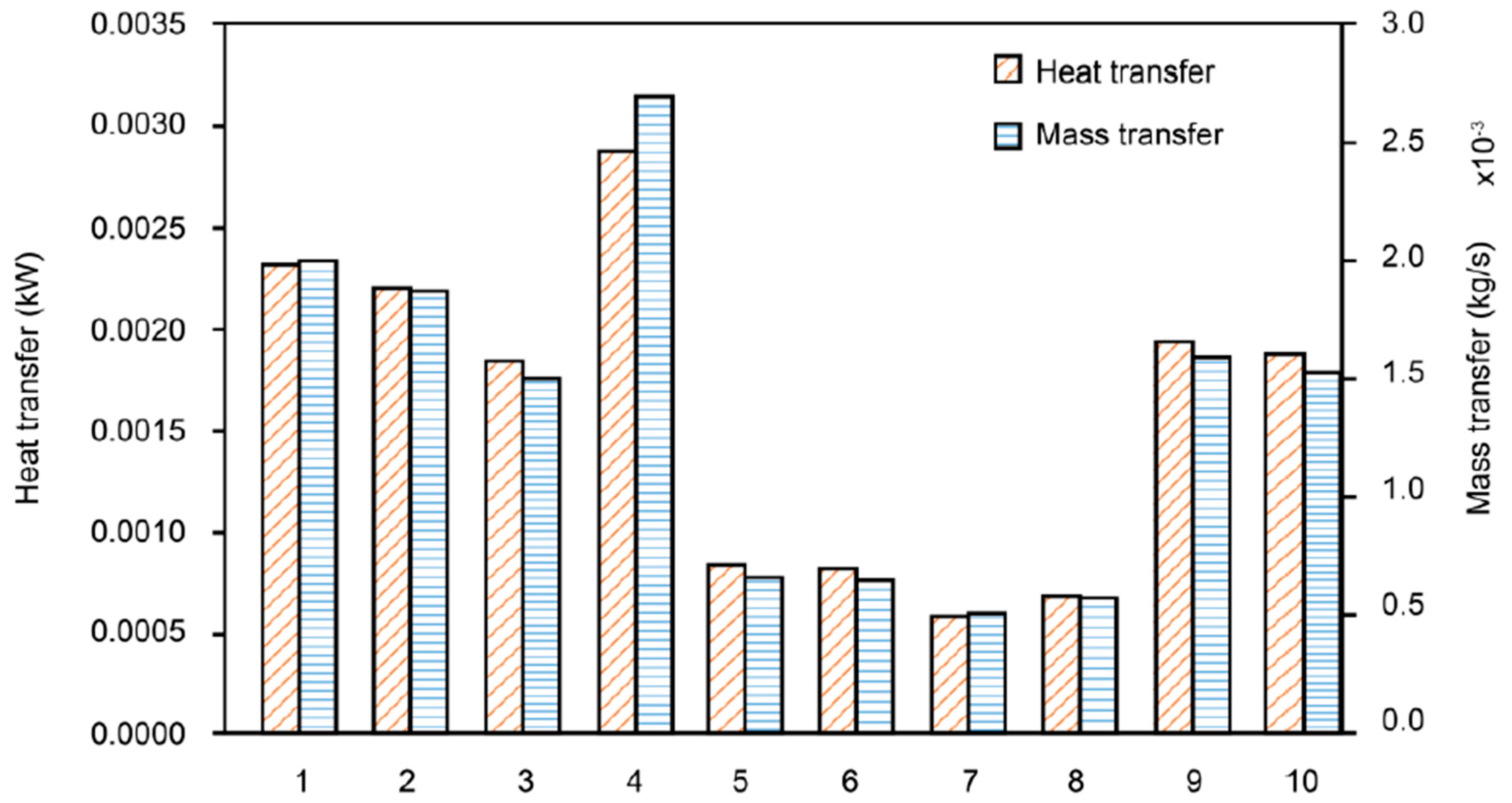
3.2. Effects of Metal Foam Types on Humidifier Performance
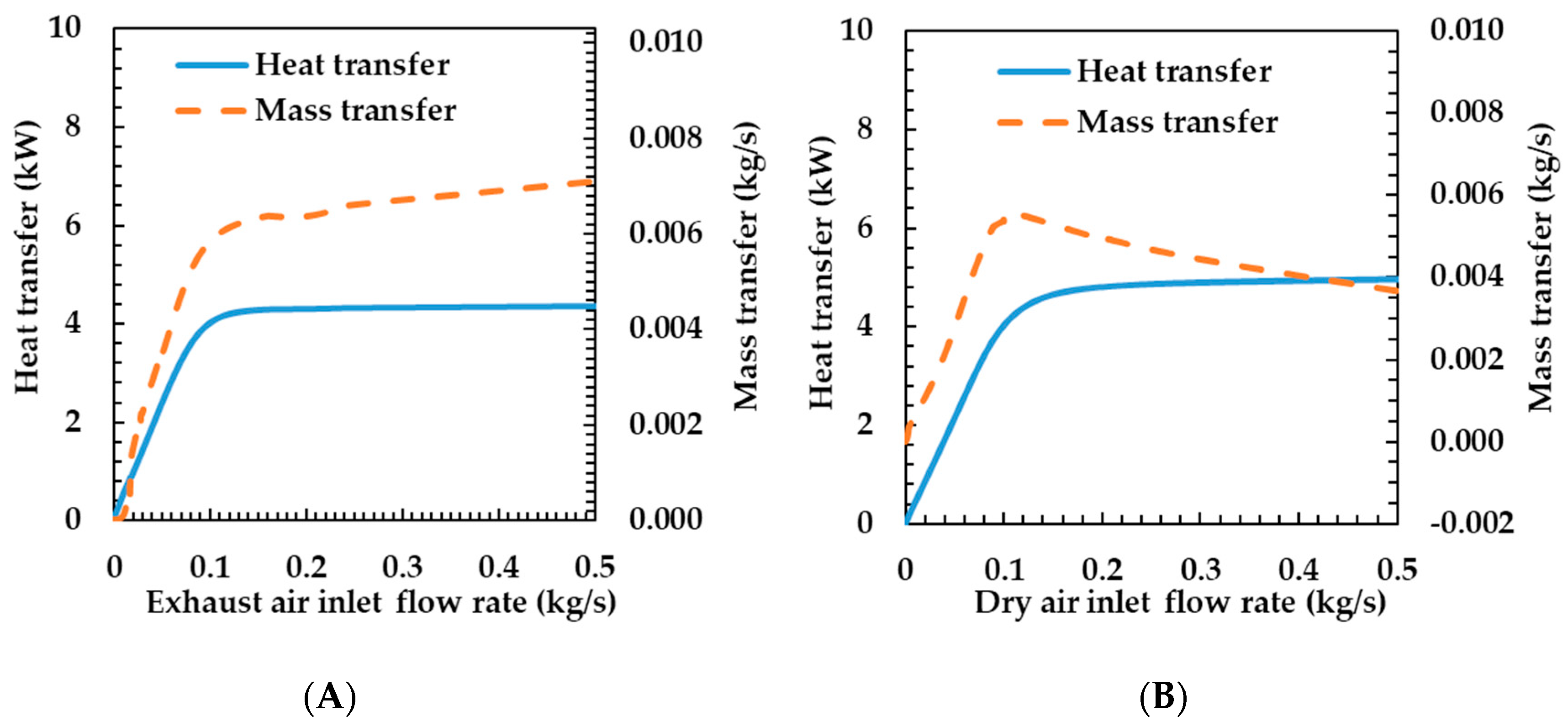
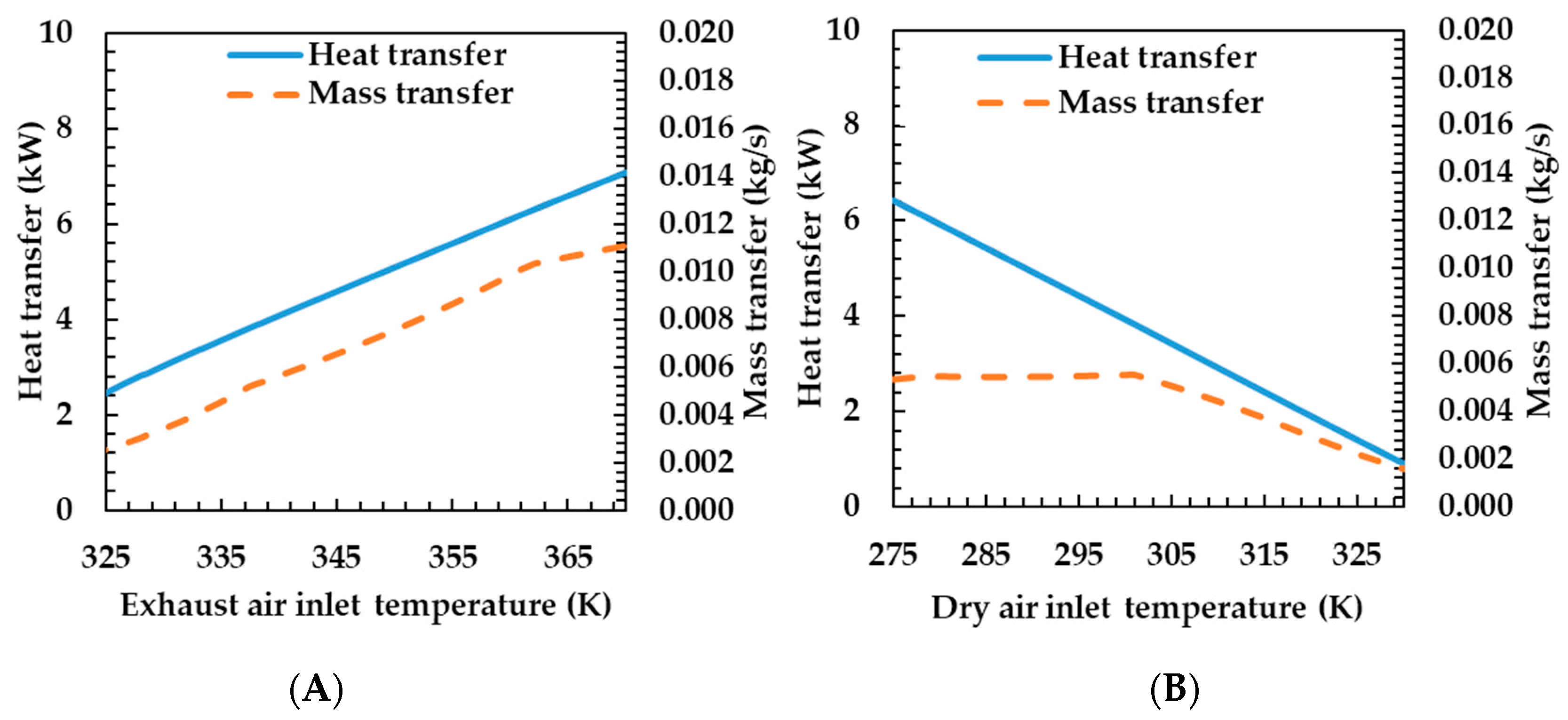
3.3. Effects of Operating Conditions on Humidifier Performance
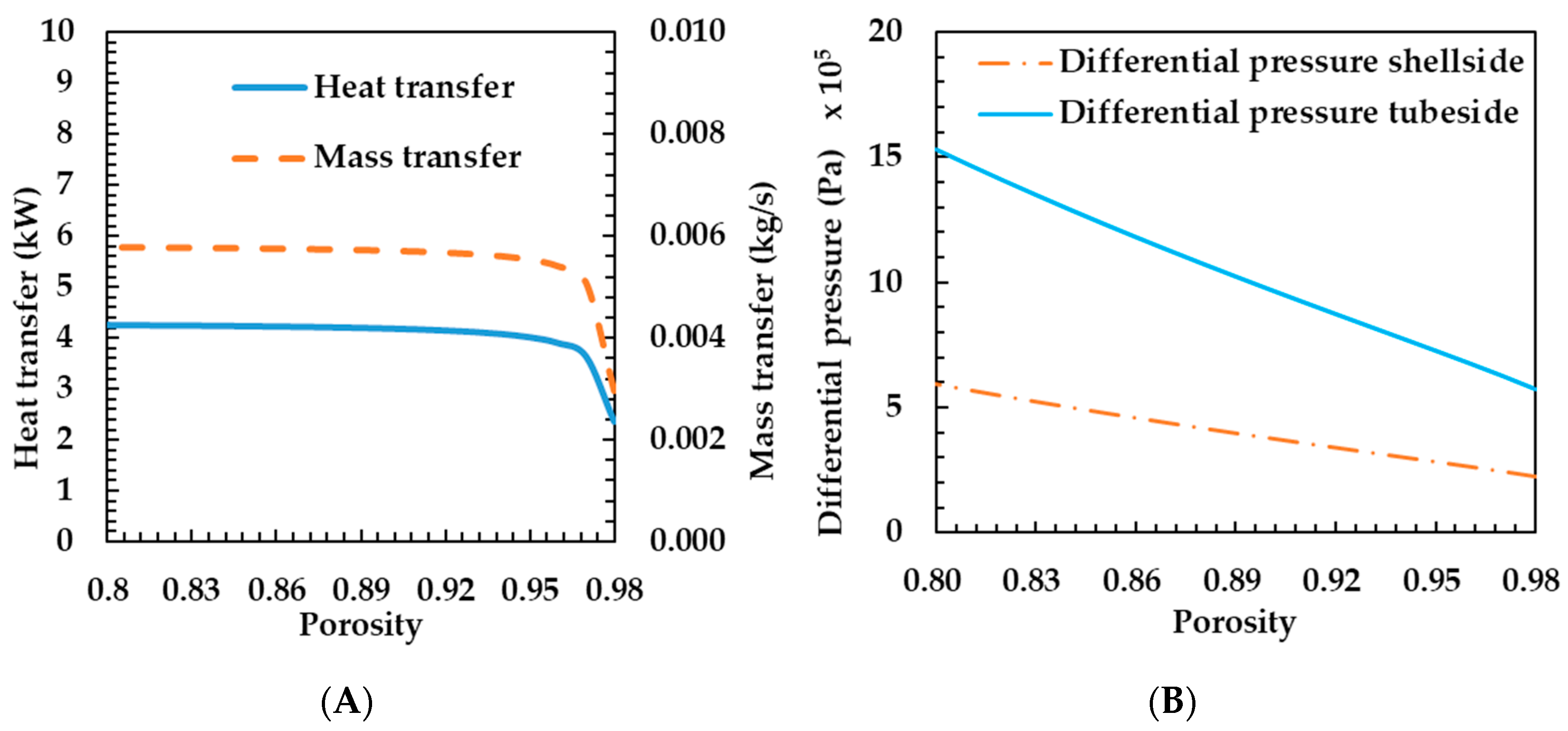
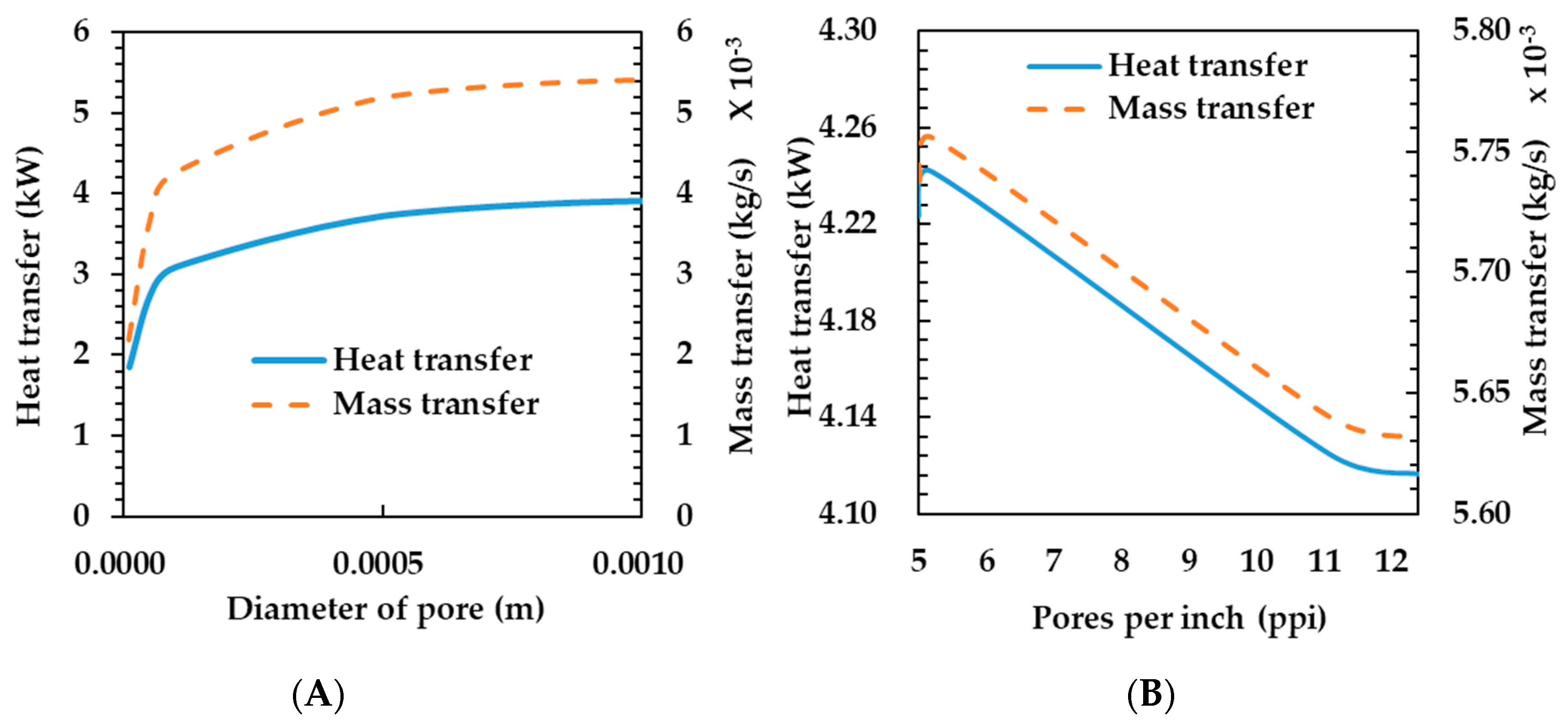
3.4. Effects of Geometric Parameters on Humidifier Performance
4. Conclusions
- Effective heat conductivity—as the metal foam’s effective heat conductivity increased, the heat and mass transfer rates of the humidifier increased proportionally.
- Compression ratio—as the metal foam compression ratio increased, the pore diameter became smaller and the porosity increased. As the metal foam compression ratio increased, the heat and mass transfer rates decreased.
- Flow rate—as the exhaust gas flow rate increased, the heat and mass transfer rates increased logarithmically. As the dry air flow rate increased, the heat transfer rate increased logarithmically and the mass transfer rate increased and then decreased.
- Temperature—as the exhaust gas temperature increased, the heat and mass transfer rate increased. As the drying air temperature increased, the heat and mass transfer rates decreased.
- Relative humidity—as the exhaust gas relative humidity increased, the heat and mass transfer rates also increased. As the dry air relative humidity increased, the mass transfer rate decreased.
- Thickness—as the membrane thickness increased, the heat and mass transfer rates decreased.
- Diameter—as tube diameter increased, the heat and mass transfer rates increased. As shell diameter increased, the heat and mass transfer rates decreased.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Alphabet: | ||
| A | Area | m2 |
| Ae | Area density | m2 m−3 |
| A | Activity | Pa Pa−1 |
| C | Specific heat | kJ kg−1 K−1 |
| Concentration | kmol m−3 | |
| Coefficient | (-) | |
| D | Hydraulic diameter | m |
| d | Diameter | m |
| e | Coefficient | (-) |
| h | Convection Coefficient | W m−2 K−1 |
| Enthalpy | kJ | |
| K | Hydraulic permeability | m2 |
| k | Conductivity Coefficient | W m−1 K−1 |
| M | Molar mass | kg kmol−1 |
| m | Mass | kg |
| Nu | Nusselt number | (-) |
| P | Pressure | Pa |
| Pr | Prandtl number | (-) |
| Q | Heat transfer | kJ |
| q | Heat transfer rate | kW |
| RH | Relative humidity | (-) |
| Re | Reynolds number | (-) |
| T | Temperature | K |
| t | Thickness | m |
| U | Overall heat transfer coefficient | W m−2 K−1 |
| u | Internal energy | kJ |
| Superscripts, subscripts: | ||
| A | Pore | |
| C | Cool | |
| D | Dry side | |
| E | Exhaust side | |
| Eff | Effective | |
| F | fluid | |
| H | High | |
| I | Inlet | |
| M | Mean, Membrane | |
| mem-dry | Membrane dried | |
| O | Outlet | |
| P | Constant pressure | |
| S | Solid, Superficial, Strut, Shape | |
| Sat | Saturation | |
| T | Empiricism | |
| Tr | Transfer | |
| V | Constant volume | |
| V | Vapor | |
| W | Membrane diffusion | |
| ˙ | Rate of change d/dt | |
| 0 | Standard condition | |
| Greek symbols: | ||
| α | Thermal diffusivity | m2 s−1 |
| ε | Porosity | (-) |
| μ | Viscosity | m2 s−1 |
| υ | Velocity | m s−1 |
| ν | Dynamic viscosity | m2 s−1 |
| △ | Differential | (-) |
| λ | Water content | kg kg−1 |
| ρ | Density | kg m−3 |
References
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained, 2nd ed.; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Sabharwal, M.; Duelk, C.; Bhatia, D. Two-dimensional modeling of a cross flow plate and frame membrane humidifier for fuel cell applications. J. Membr. Sci. 2012, 409, 285–301. [Google Scholar] [CrossRef]
- Khazaee, I.; Sabadbafan, H. Effect of humidity content and direction of the flow of reactant gases on water management in the 4-serpentine and 1-serpentine flow channel in a PEM (proton exchange membrane) fuel cell. Energy 2016, 10, 252–265. [Google Scholar] [CrossRef]
- Maricle, D.L.; Nagle, D.C. Carbon Foam Fuel Cell Components. U.S. Patent 4125676, 14 November 1978. [Google Scholar]
- Zhang, G.; Bao, Z.; Xie, B.; Wang, Y.; Jiao, K. Three-dimensional multi-phase simulation of PEM fuel cell considering the full morphology of metal foam flow field. Int. J. Hydrogen Energy 2020. [Google Scholar] [CrossRef]
- Afshari, E. Computational analysis of heat transfer in a PEM fuel cell with metal foam as a flow field. J. Therm. Anal. Calorim. 2020, 139, 2423–2434. [Google Scholar] [CrossRef]
- Kang, D.G.; Lee, D.K.; Choi, J.M.; Shin, D.K.; Kim, M.S. Study on the metal foam flow field with porosity gradient in the polymer electrolyte membrane fuel cell. Renew. Energy 2020, 156, 931–941. [Google Scholar] [CrossRef]
- Tsai, B.T.; Tseng, C.J.; Liu, Z.S.; Wang, C.H.; Lee, C.I.; Yang, C.C.; Lo, S.K. Effects of flow field design on the performance of a PEM fuel cell with metal foam as the flow distributor. Int. J. Hydrogen Energy 2012, 37, 13060–13066. [Google Scholar] [CrossRef]
- Afshari, E.; Houreh, N.B. Performance analysis of a membrane humidifier containing porous metal foam as flow distributor in a PEM fuel cell system. Energy Convers. Manag. 2014, 88, 612–621. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lu, T.J.; Hodson, H.P. Natural convection in metal foams with open cells. Int. J. Heat Mass Transf. 2005, 48, 2452–2463. [Google Scholar] [CrossRef]
- Hwang, J.J.; Hwang, G.J.; Yeh, R.H.; Chao, C.H. Measurement of interstitial convective heat transfer and frictional drag for flow across metal foams. J. Heat Transf. 2002, 124, 120–129. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.Y. Simulation of flow and transport phenomena in a polymer electrolyte fuel cell under low-humidity operation. J. Power Sources 2005, 47, 148–161. [Google Scholar] [CrossRef]
- Park, S.K.; Choe, S.Y.; Choi, S.H. Dynamic modeling and analysis of a shell-and-tube type gas-to-gas membrane humidifier for PEM fuel cell applications. Int. J. Hydrogen Energy 2008, 33, 2273–2282. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zhao, C.Y. Review on thermal transport in high porosity cellular metal foams with open cells. J. Heat Mass Transf. 2012, 55, 3618–3632. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. Forced convection in high porosity metal foam. J. Heat Transf. 2000, 122, 557–565. [Google Scholar] [CrossRef]
- Dukhan, N.; Patel, P. Equivalent particle diameter and length scale for pressure drop in porous metals. Exp. Therm. Fluid Sci. 2008, 32, 1059–1067. [Google Scholar] [CrossRef]
- Lacroix, M.; Nguyen, P.; Schweich, D.; Huu, C.P.; Sabine, S.P.; Edouard, D. Pressure drop measurements and modeling on SiC foams. Chem. Eng. Sci. 2007, 62, 3259–3267. [Google Scholar] [CrossRef]
- Pukrushpan, J.T.; Peng, H.; Stefanopoulou, A.G. Simulation and analysis of transient fuel cell system performance based on a dynamic reactant flow model. ASME Int. Mech. Eng. Congr. Expo. 2002, 637–648. [Google Scholar] [CrossRef] [Green Version]
- Coquard, R.; Rochais, D.; Baillis, D. Experimental investigations of the coupled conductive and radiative heat transfer in metallic/ceramic foams. J. Heat Mass Transf. 2009, 52, 4907–4918. [Google Scholar] [CrossRef]
- Giani, L.; Groppi, G.; Tronconi, E. Mass-transfer characterization of metallic foams as supports for structured catalysts. Ind. Eng. Chem. Res. 2005, 44, 4993–5002. [Google Scholar] [CrossRef]
- Nguyen, T.V.; White, R.E. A water and heat management model for proton-exchange-membrane fuel cells. J. Electrochem. Soc. 1993, 140, 2178–2186. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Thickness of the membrane | 0.000050 (m) |
| Dry equivalent weight of membrane | 1.0 (kg mol−1) |
| Dry density of membrane | 0.1 (kg m−3) |
| Inner diameter of the tube | 0.048000 (m) |
| Overall length of the tube | 0.381000 (m) |
| Inner diameter of the humidifier housing | 0.182880 (m) |
| Porosity of metal foam | 0.95 |
| Pore diameter of metal foam | 0.001747 (m) |
| Thermal conductivity of metal foam stem | 0.218 (kW m−1∙K) |
| Parameters | Value 1 | Value 2 |
|---|---|---|
| Flow rate of dry air inlet | 0.1 (kg s−1) | 0.004 (kg s−1) |
| Temperature of dry air inlet | 299.15 (K) | 298.15 (K) |
| Pressure of dry air inlet | 297,809 (Pa) | 131,722 (Pa) |
| Relative humidity of dry air inlet | 40 (%) | 30 (%) |
| Fraction of oxygen of dry air inlet | 21 (%) | 21 (%) |
| Flow rate of exhaust air inlet | 0.1 (kg s−1) | 0.003 (kg s−1) |
| Temperature of exhaust air inlet | 339.15 (K) | 343.15 (K) |
| Pressure of exhaust air inlet | 241,969 (Pa) | 131,722 (Pa) |
| Relative humidity of exhaust air inlet | 100 (%) | 100 (%) |
| Fraction of oxygen of exhaust air inlet | 0.21 (%) | 0.21 (%) |
| Material | Effective Conductivity (W m−1 K−1) | Density (kg m−3) | Diameter of Pore (mm) | Porosity | Specific Heat (J kg−1 K−1) | |
|---|---|---|---|---|---|---|
| 1 | NiCrAl | 0.266 | 537 | 1.4 | 0.937 | 501 |
| 2 | NiCrAl | 0.257 | 503 | 1.2/0.6 | 0.941 | 501 |
| 3 | NiCrAl | 0.246 | 587 | 0.8/0.4 | 0.931 | 501 |
| 4 | NiCrAl | 0.308 | 665 | 2.8/1.4 | 0.922 | 501 |
| 5 | FeCrAlY | 0.098 | 230 | 0.423 | 0.968 | 487 |
| 6 | FeCrAlY | 0.096 | 230 | 0.423 | 0.968 | 487 |
| 7 | FeCrAlY | 0.076 | 253 | 0.32 | 0.965 | 487 |
| 8 | FeCrAlY | 0.093 | 270 | 0.32 | 0.963 | 486 |
| 9 | Mullite | 0.279 | 534 | 1.2 | 0.809 | 950 |
| 10 | Zirconia | 0.257 | 966 | 1.2 | 0.832 | 451 |
| Samples | Pores per Inch | Diameter of Pore (m) | Porosity |
|---|---|---|---|
| A | 5.4 | 0.0047 | 0.927 |
| B | 5.6 | 0.0046 | 0.911 |
| C | 11.5 | 0.0022 | 0.938 |
| D | 12.8 | 0.0020 | 0.937 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, H.; Kim, M.-H.; Park, S.-K.; Kim, Y.-S.; Choi, B.C. Simulation of Heat and Mass Transfer Characteristics for the Optimal Operating Conditions of a Gas-to-Gas Membrane Humidifier with Porous Metal Foam. Energies 2020, 13, 5110. https://doi.org/10.3390/en13195110
Jang H, Kim M-H, Park S-K, Kim Y-S, Choi BC. Simulation of Heat and Mass Transfer Characteristics for the Optimal Operating Conditions of a Gas-to-Gas Membrane Humidifier with Porous Metal Foam. Energies. 2020; 13(19):5110. https://doi.org/10.3390/en13195110
Chicago/Turabian StyleJang, Hyesoo, Myoung-Hwan Kim, Sang-Kyun Park, Yul-Seong Kim, and Byung Chul Choi. 2020. "Simulation of Heat and Mass Transfer Characteristics for the Optimal Operating Conditions of a Gas-to-Gas Membrane Humidifier with Porous Metal Foam" Energies 13, no. 19: 5110. https://doi.org/10.3390/en13195110
APA StyleJang, H., Kim, M.-H., Park, S.-K., Kim, Y.-S., & Choi, B. C. (2020). Simulation of Heat and Mass Transfer Characteristics for the Optimal Operating Conditions of a Gas-to-Gas Membrane Humidifier with Porous Metal Foam. Energies, 13(19), 5110. https://doi.org/10.3390/en13195110





