Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow
Abstract
:1. Introduction
2. Numerical Methodology
2.1. Lattice Boltzmann Method
2.1.1. Octree Lattice Structure
2.1.2. Collision Operator
2.2. Turbulence Modeling
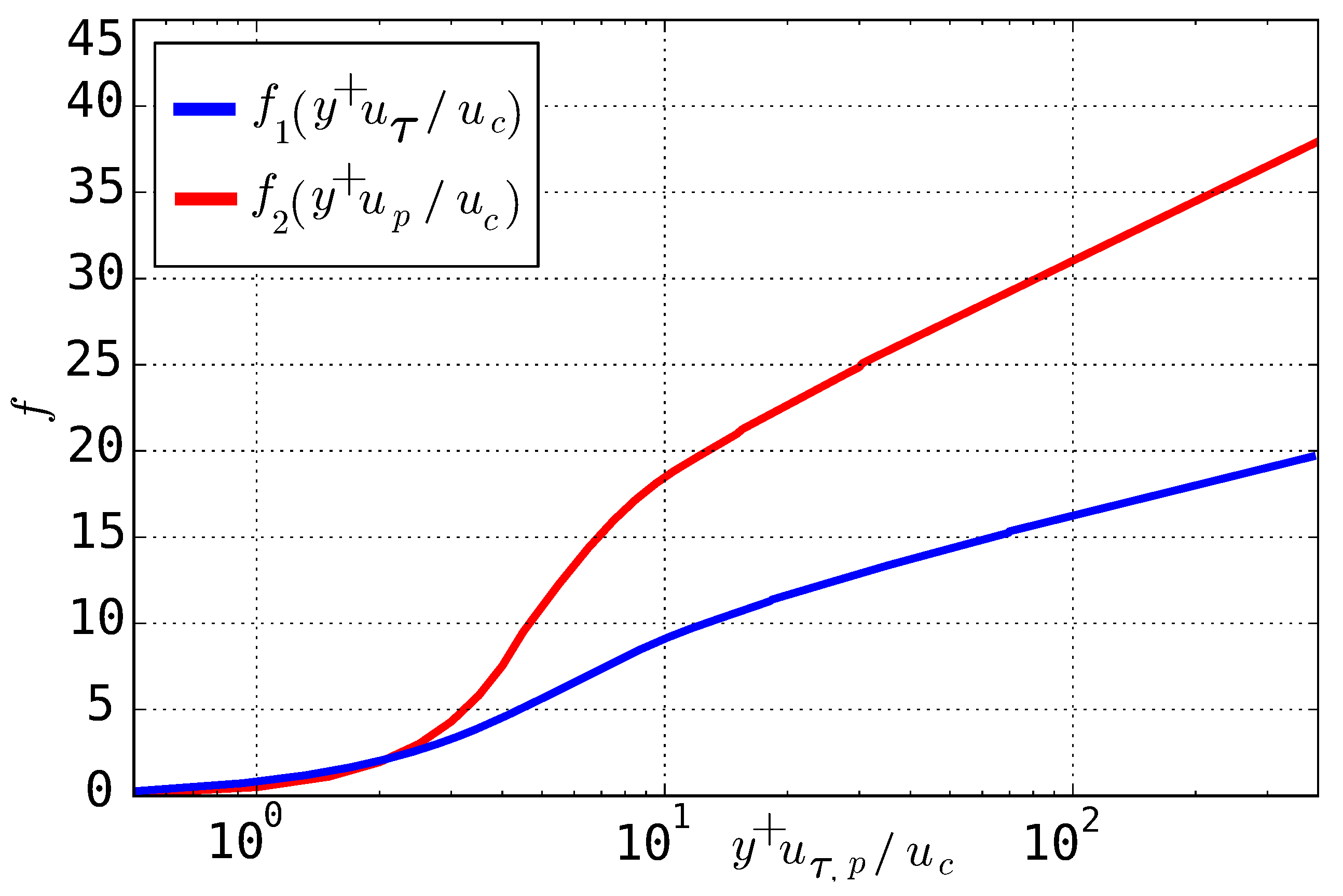
2.3. Near-Wall Treatment
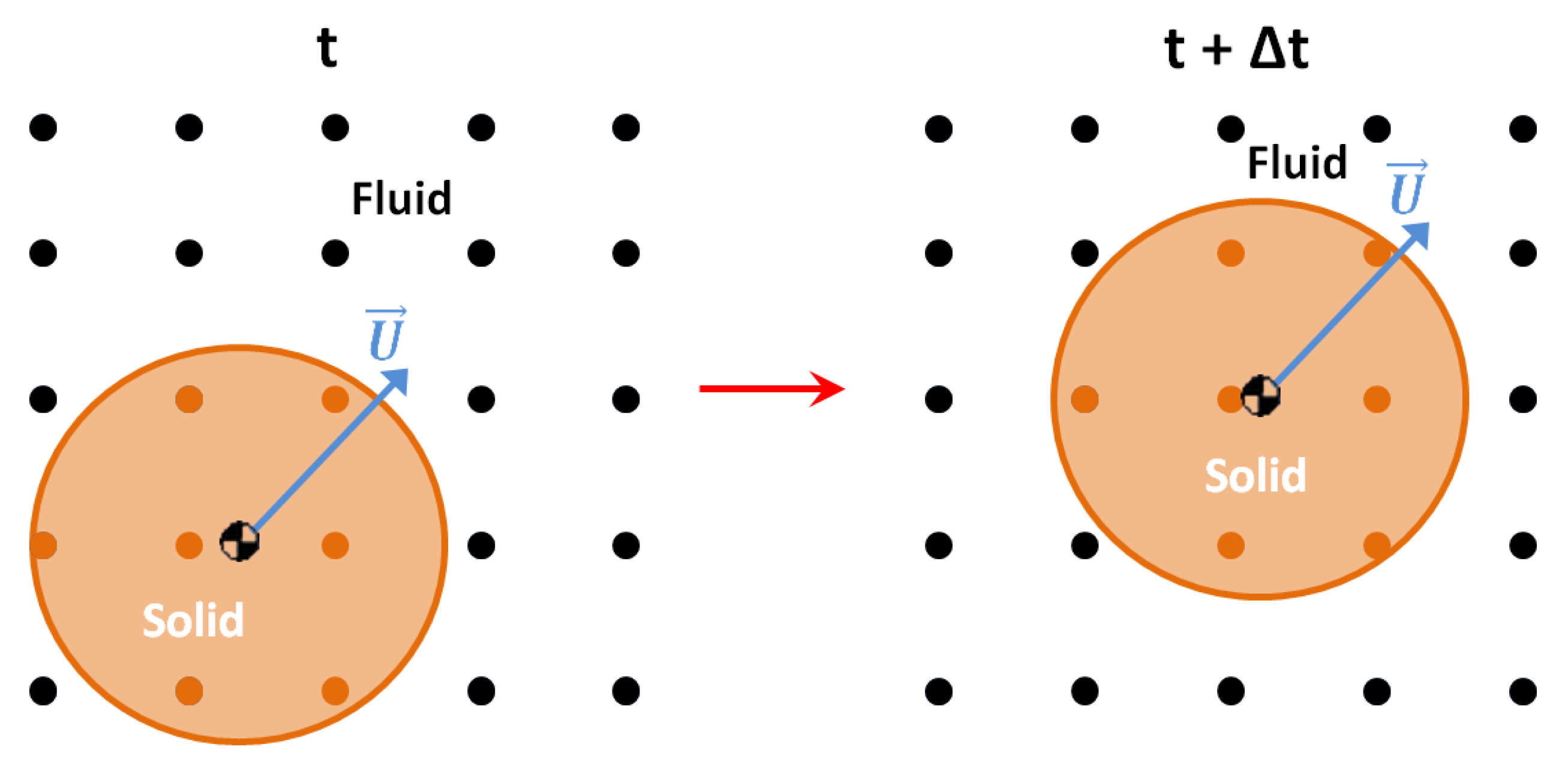
Dynamic Geometries
3. Simulations
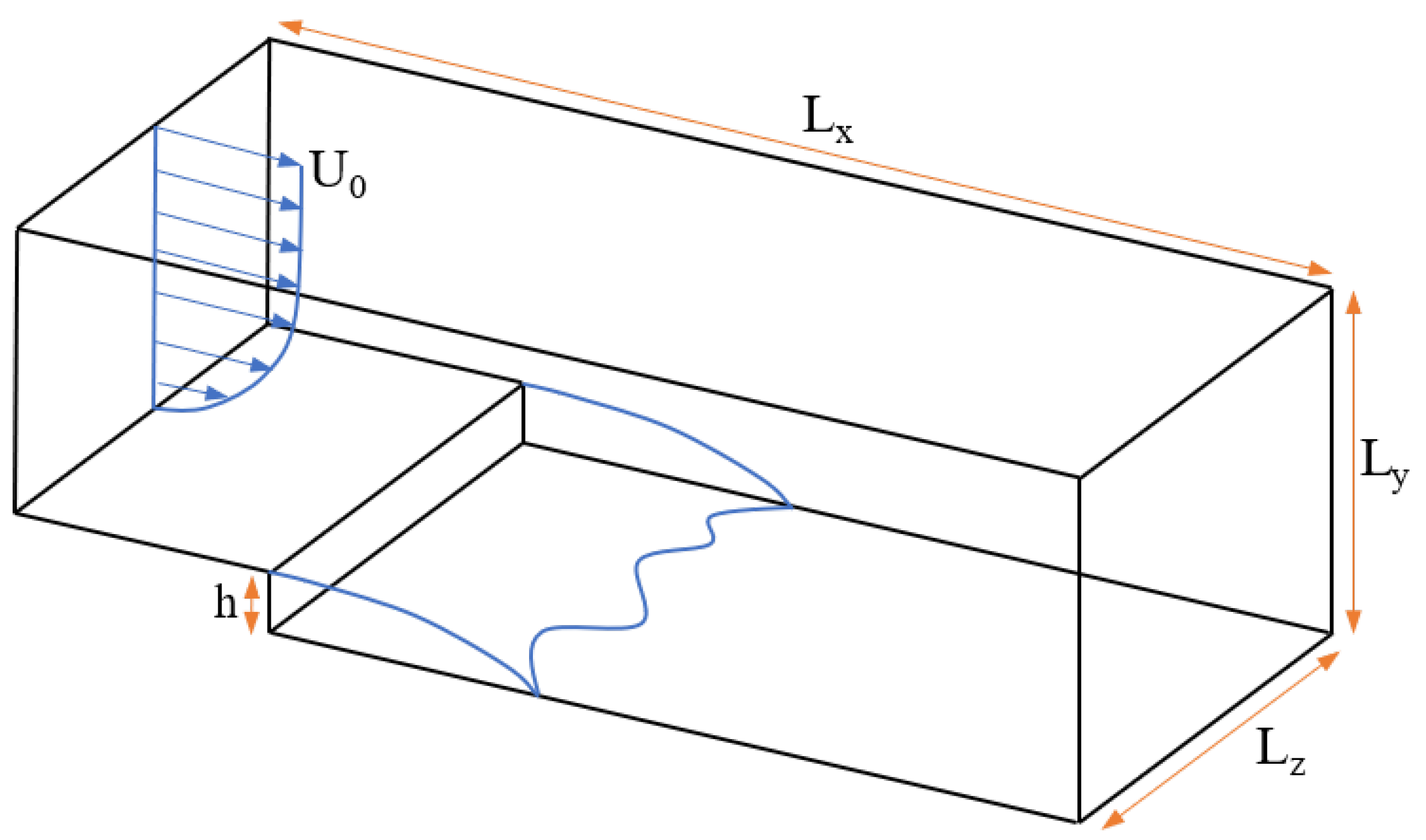
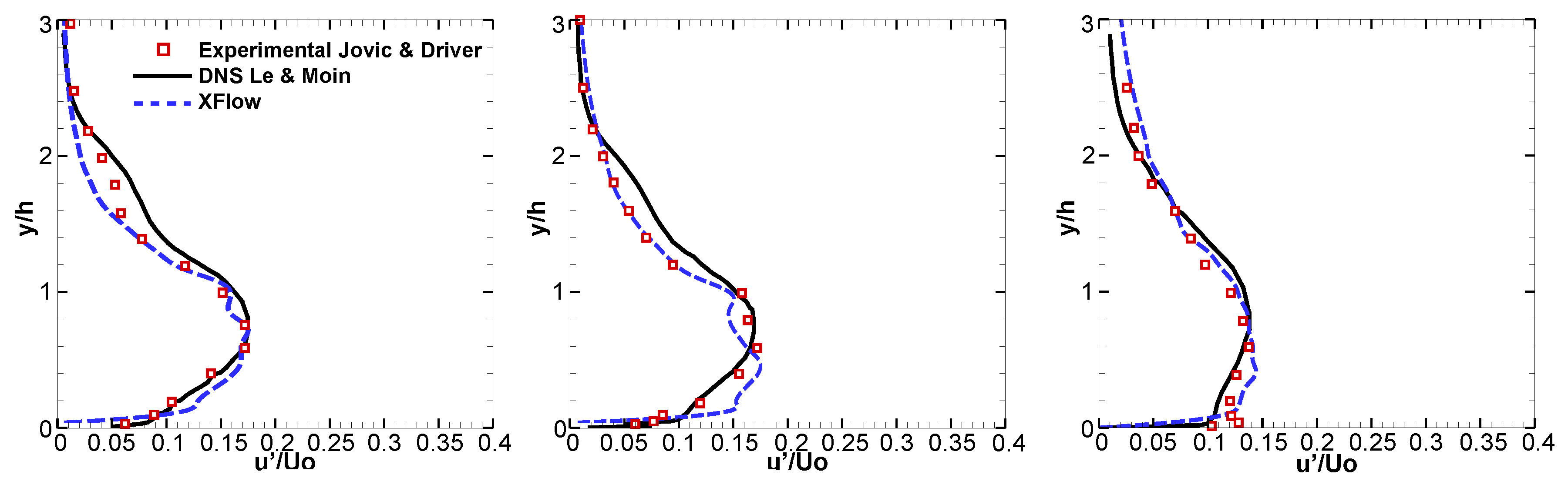
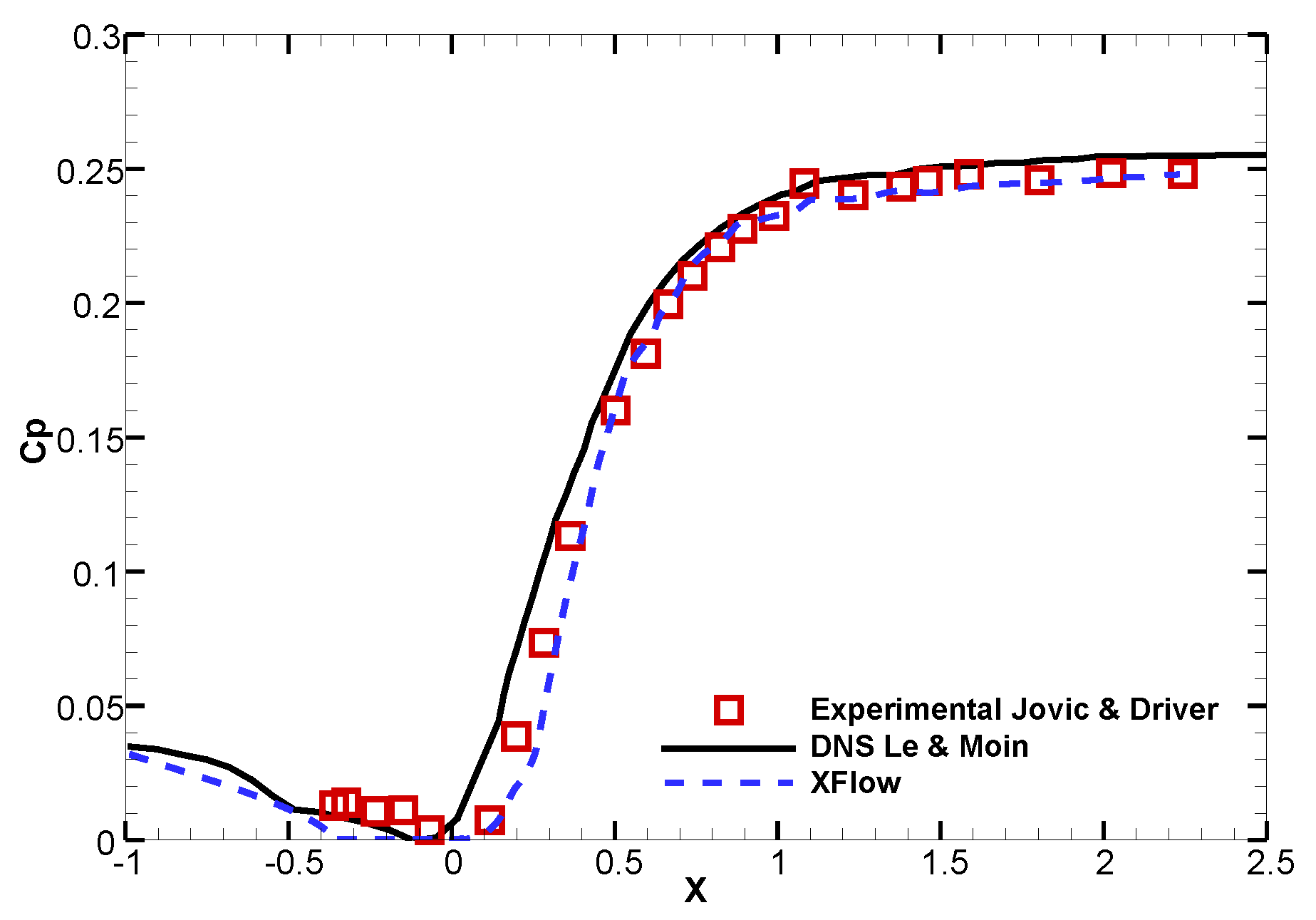
3.1. Backward-Facing Step
3.1.1. Introduction
3.1.2. Setup and Mesh Convergence
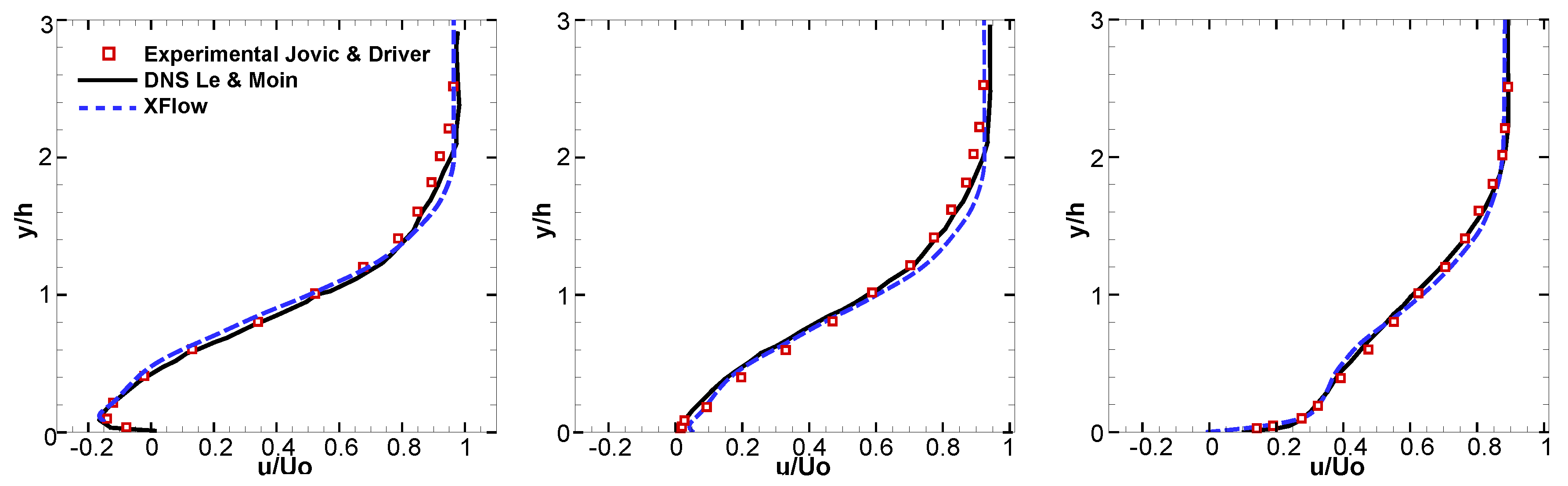
3.1.3. Results
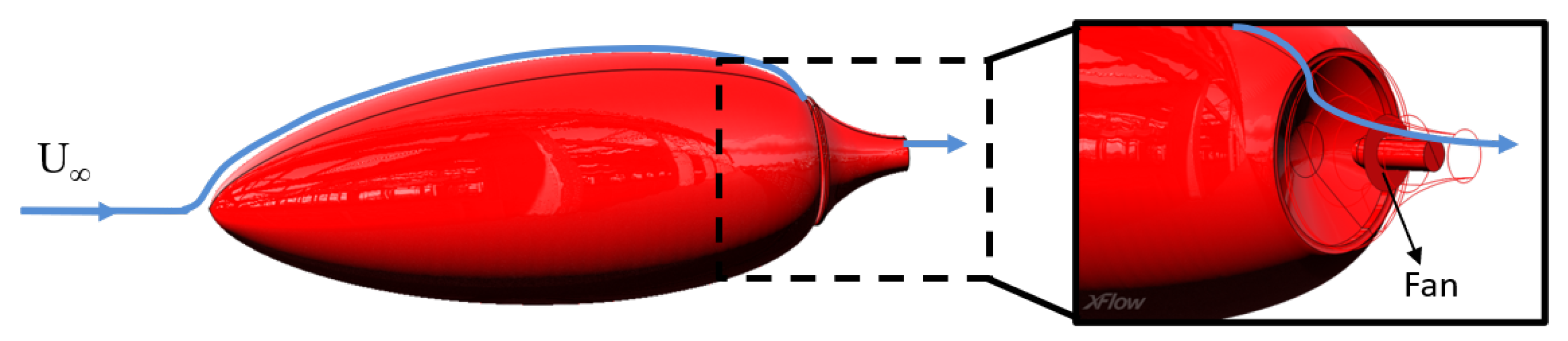
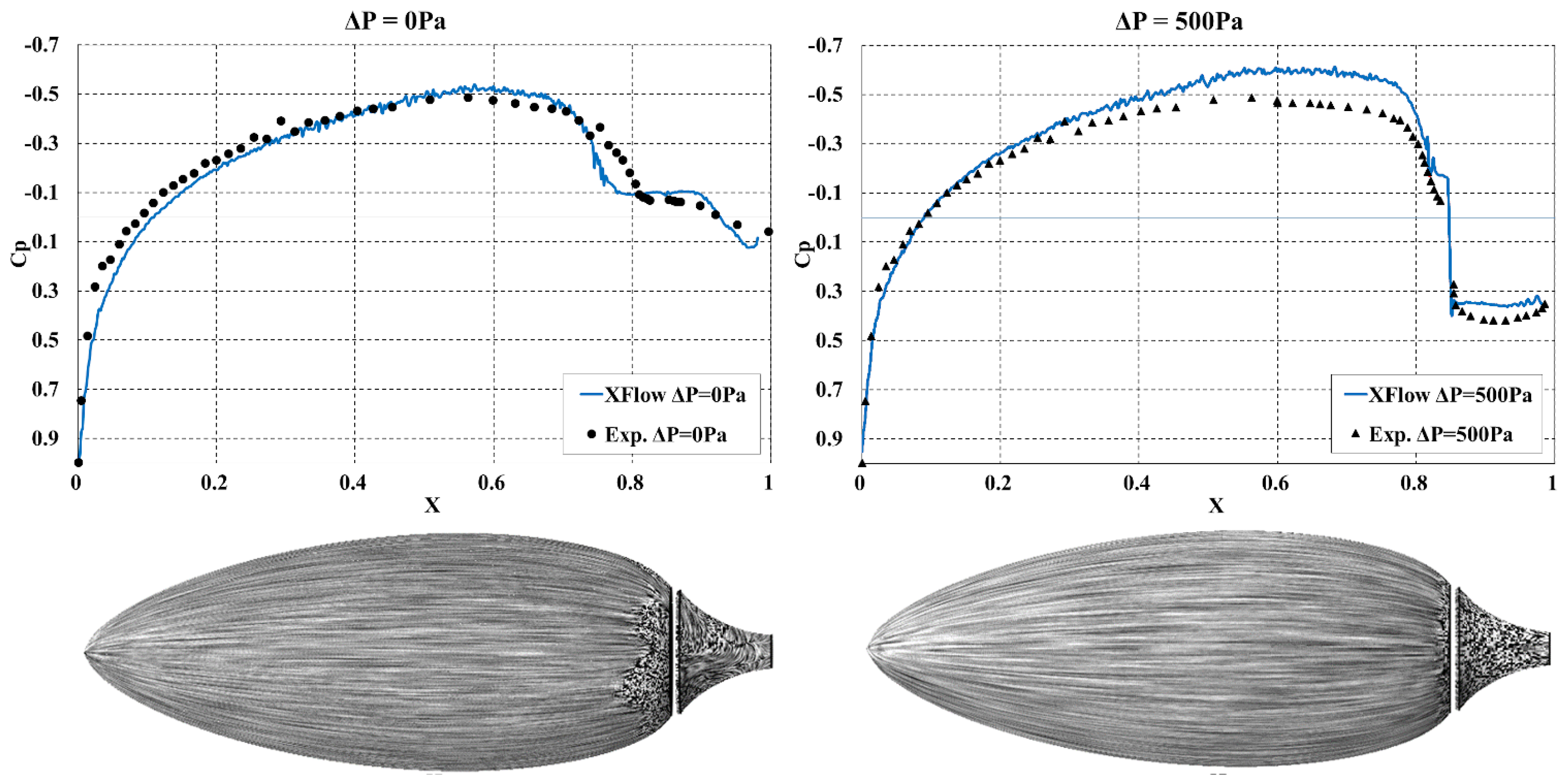
3.2. Goldschmied Body
3.2.1. Introduction
3.2.2. Setup and Mesh Convergence
3.2.3. Results
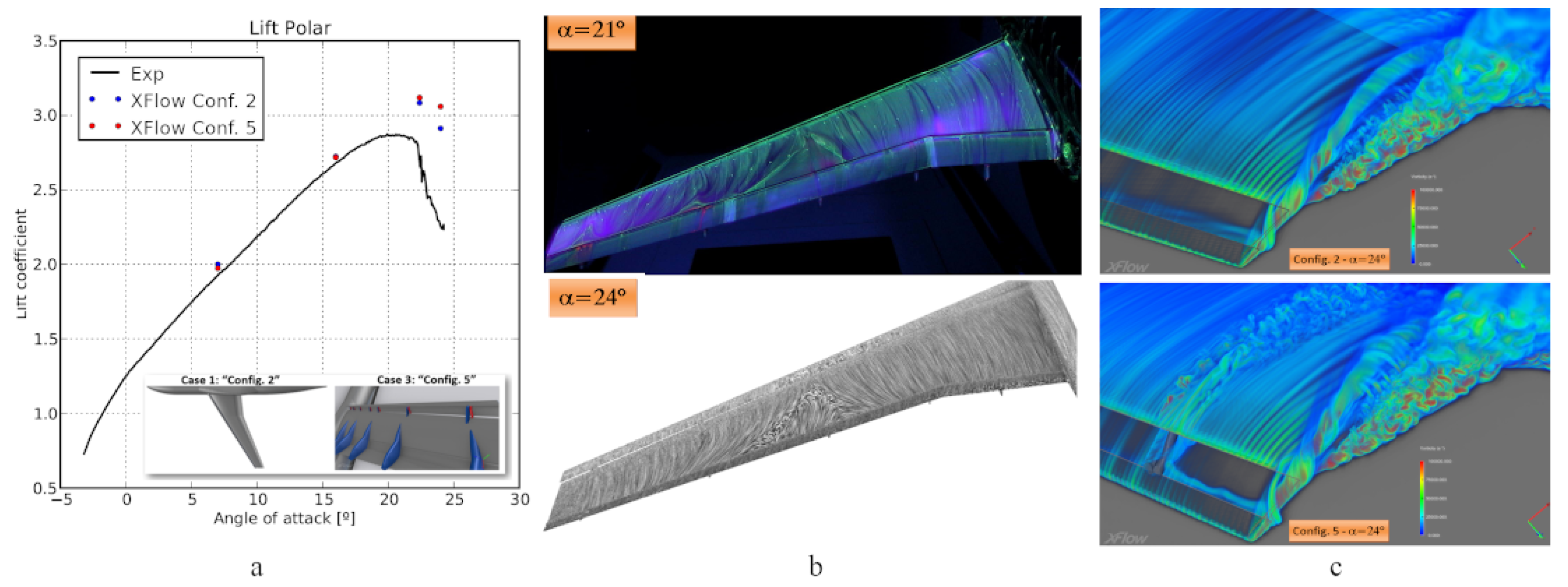
3.3. 2nd High-Lift Prediction Workshop
3.3.1. Introduction
3.3.2. Setup and Mesh Convergence
3.3.3. Results
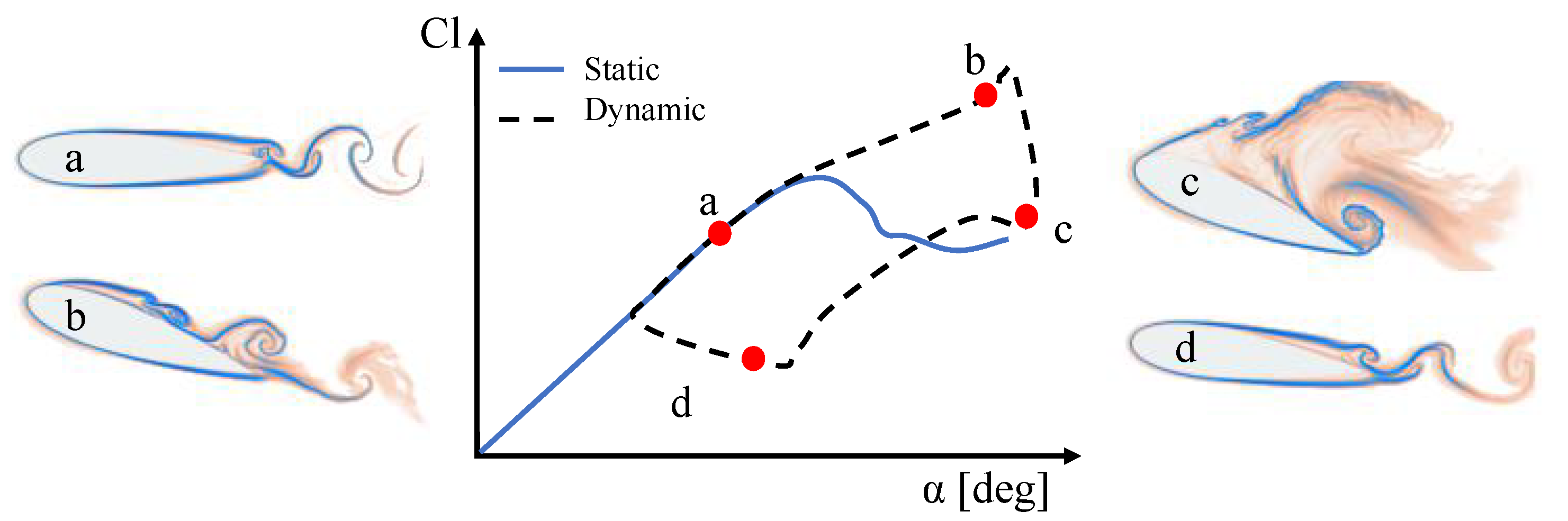
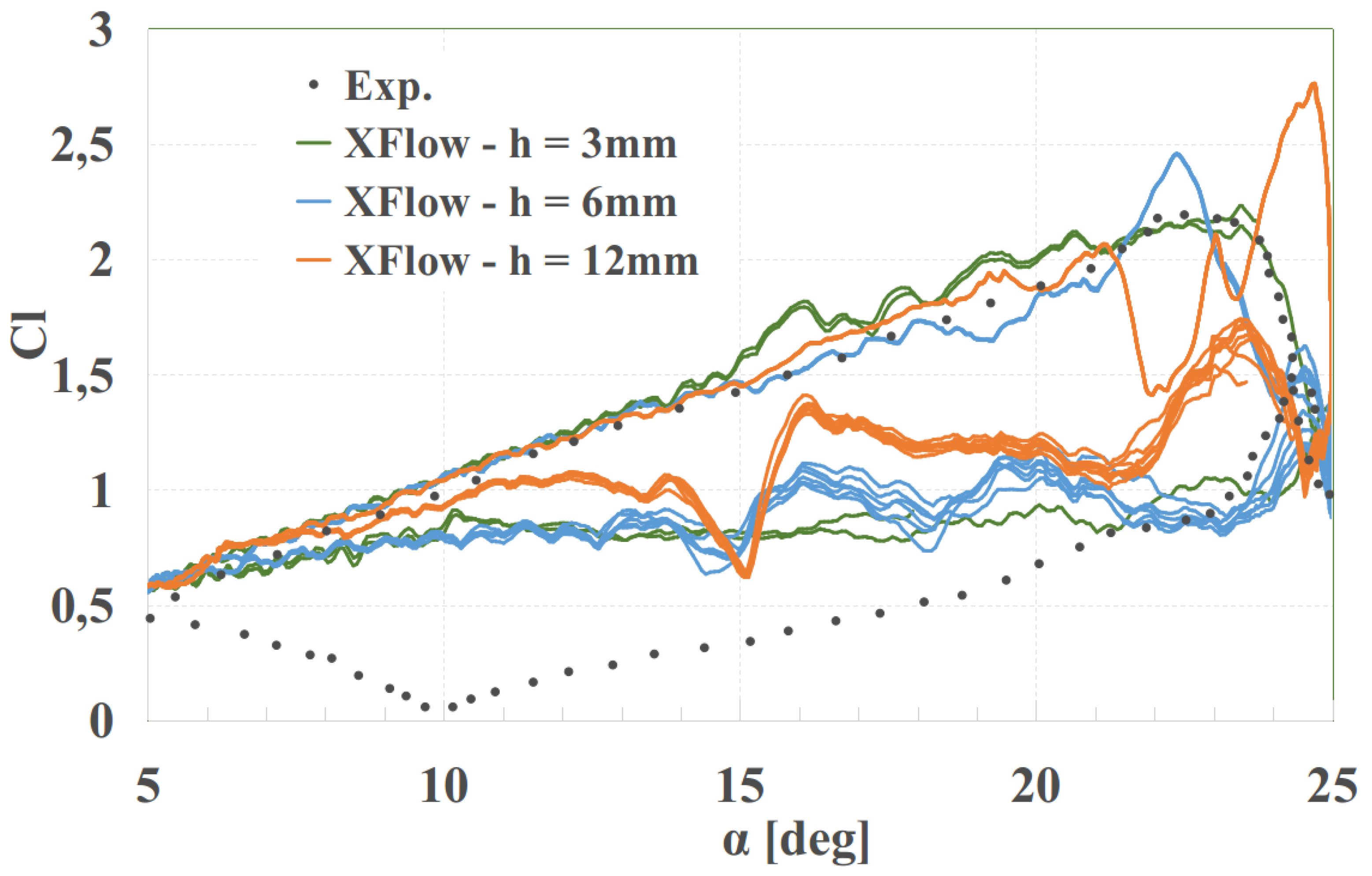
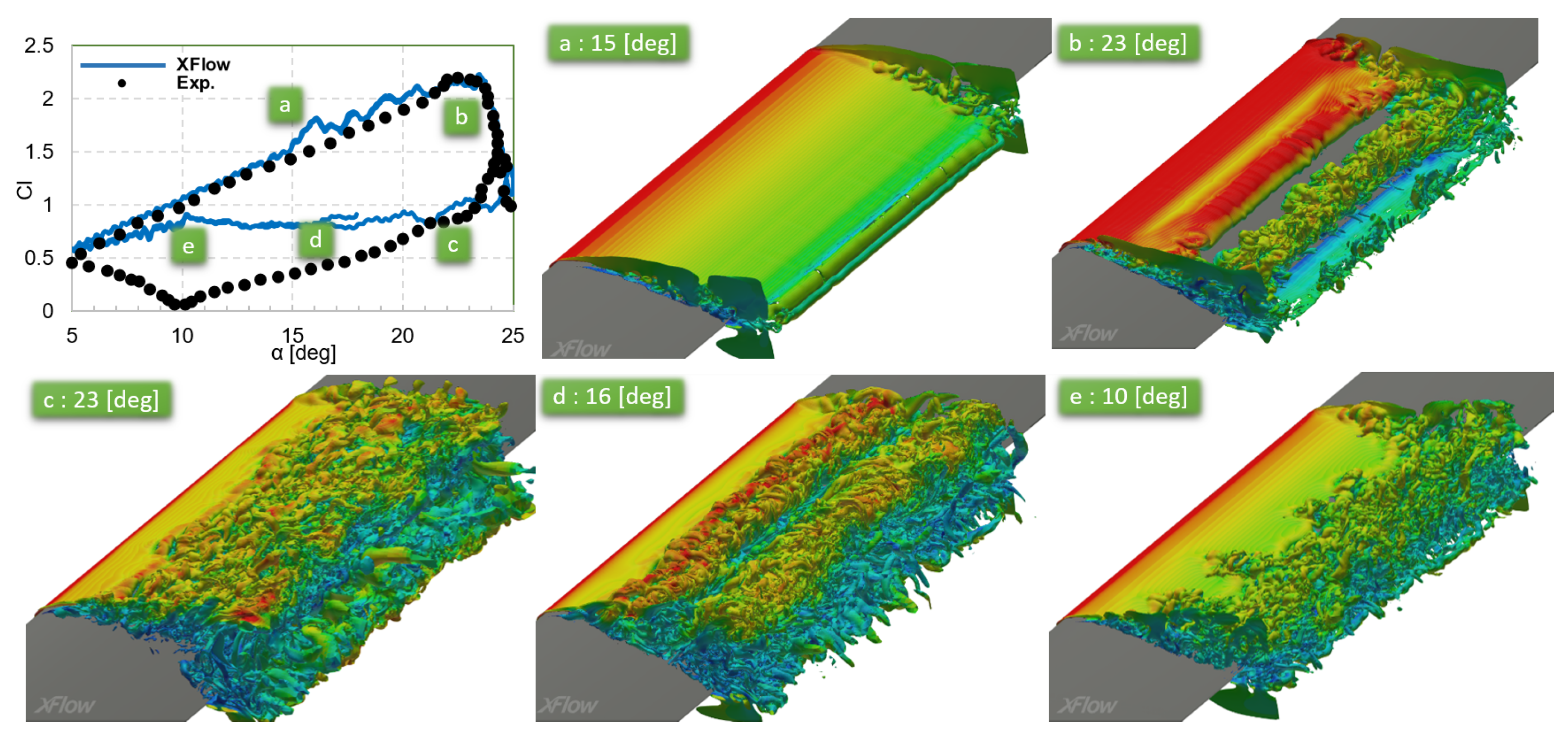
3.4. Dynamic Stall: NACA0012
3.4.1. Introduction
3.4.2. Setup and Mesh Convergence
3.4.3. Results
3.5. Wing with Leading-Edge Tubercles
3.5.1. Introduction
- Wavelength, : defines the non-dimensional wavelength (or equivalently the spatial frequency) of the tubercles, with c being the local chord.
- Amplitude, : defines the amplitude of the tubercles. It is also made non-dimensional using the local chord c.
- Span section, : defines the wing span section where the tubercles start. Please note that b is the total wing span.
3.5.2. Setup and Mesh Convergence
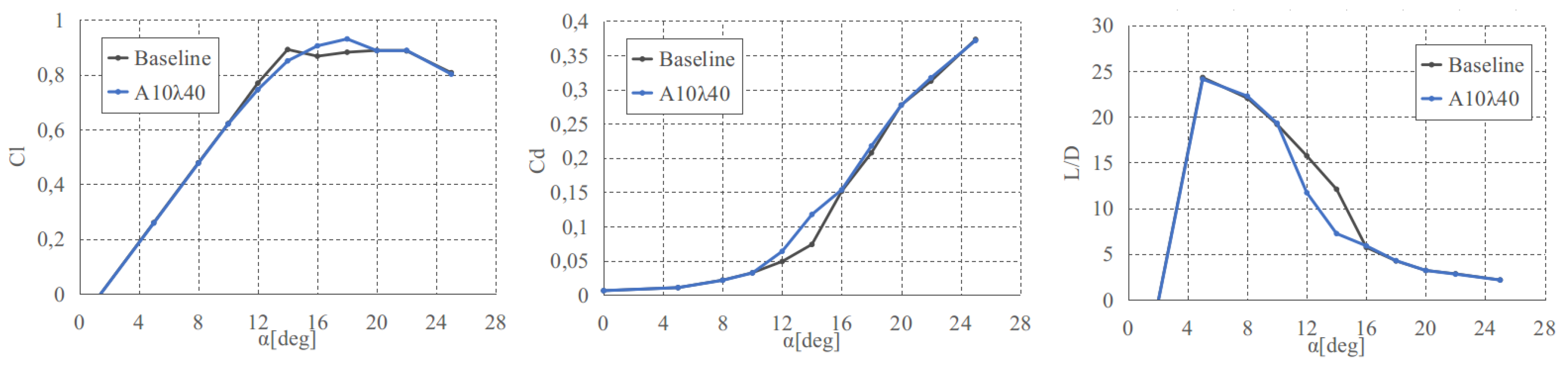
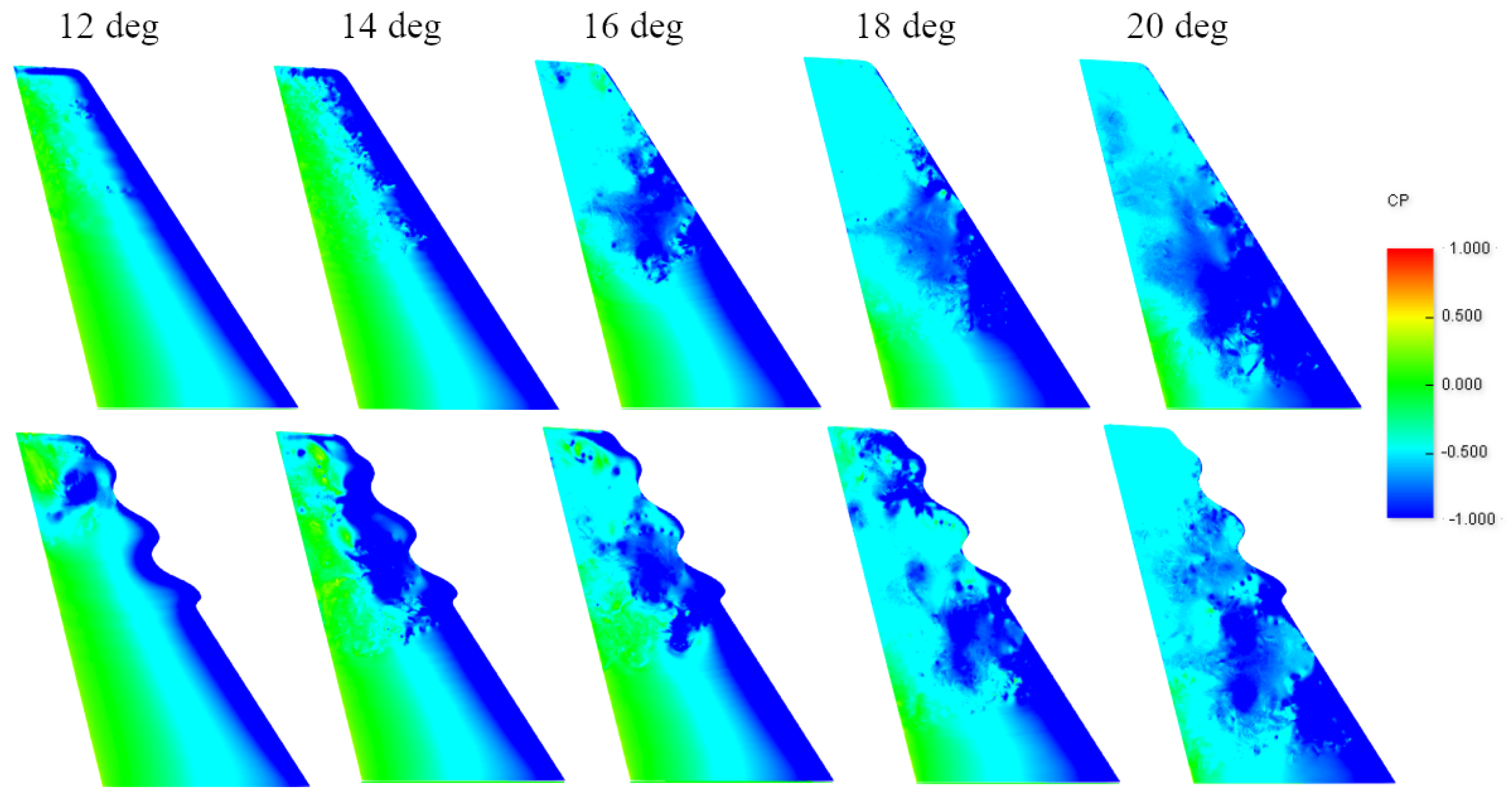
3.5.3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vincent, P.E.; Jameson, A. Facilitating the adoption of unstructured high-order methods amongst a wider community of fluid dynamicists. Math. Model. Nat. Phenom. 2011, 6, 97–140. [Google Scholar] [CrossRef]
- Allahyari, M.; Esfahanian, V.; Yousefi, K. The Effects of Grid Accuracy on Flow Simulations: A Numerical Assessment. Fluids 2020, 5, 110. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 54–73. [Google Scholar]
- Jacqmin, D. Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Allahyari, M.; Mohseni, K. Numerical simulation of flows with shocks and turbulence using observable methodology. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0066. [Google Scholar]
- Holman, D.M.; Brionnaud, R.M.; Chávez-Modena, M.; Sánchez, E.V. Lattice Boltzmann method contribution to the second high-lift prediction workshop. J. Aircr. 2015, 52, 1122–1135. [Google Scholar] [CrossRef]
- Brionnaud, R.; Chávez Modena, M.; Trapani, G.; Holman, M.D. Direct noise computation with a Lattice-Boltzmann method and application to industrial test cases. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; p. 2969. [Google Scholar]
- Sanders, L.; Manoha, E.; Murayama, M.; Yokokawa, Y.; Yamamoto, K.; Hirai, T. Lattice-Boltzmann flow simulation of a two-wheel landing gear. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; p. 2767. [Google Scholar]
- Trapani, G.; Brionnaud, R.; Holman, D. XFlow contribution to the third high-lift prediction workshop. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 2847. [Google Scholar]
- Thibault, S.; Holman, D.; Garcia, S.; Trapani, G. CFD Simulation of a quad-rotor UAV with rotors in motion explicitly modeled using an LBM approach with adaptive refinement. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0583. [Google Scholar]
- Grondeau, M.; Guillou, S.; Mercier, P.; Poizot, E. Wake of a Ducted Vertical Axis Tidal Turbine in Turbulent Flows, LBM Actuator-Line Approach. Energies 2019, 12, 4273. [Google Scholar] [CrossRef] [Green Version]
- Trapani, G.; Brionnaud, R.M.; Holman, D.M. Non-linear fluid-structure interaction using a partitioned lattice Boltzmann-FEA approach. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3636. [Google Scholar]
- Armaly, B.F.; Durst, F.; Pereira, J.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473–496. [Google Scholar] [CrossRef]
- Goldschmied, F.R. On the aerodynamic optimization of mini-RPV and small GA aircraft. In Proceedings of the 2nd American Institute of Aeronautics and Astronautics, Applied Aerodynamics Conference, Seattle, WA, USA, 21–23 August 1984; Volume 21. [Google Scholar]
- Rudnik, R.; Huber, K.; Melber-Wilkending, S. EUROLIFT test case description for the 2nd high lift prediction workshop. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012; p. 2924. [Google Scholar]
- McCroskey, W.J.; McAlister, K.W.; Carr, L.W.; Pucci, S. An Experimental Study of Dynamic Stall on Advanced Airfoil Sections; Technical Report; Volume 1: Summary of the Experiment; NASA: Washington, DC, USA, 1982. [Google Scholar]
- Miklosovic, D.; Murray, M.; Howle, L.; Fish, F. Leading-edge tubercles delay stall on humpback whale (Megaptera novaeangliae) flippers. Phys. Fluids 2004, 16, L39–L42. [Google Scholar] [CrossRef] [Green Version]
- Boltzmann, L. Weitere studien über das wärmegleichgewicht unter gasmolekülen. In Kinetische Theorie II; Springer: Berlin/Heidelberg, Germany, 1970; pp. 115–225. [Google Scholar]
- Premnath, K.N.; Banerjee, S. Incorporating forcing terms in cascaded Lattice Boltzmann approach by method of central moments. Phys. Rev. E 2009, 80, 036702. [Google Scholar] [CrossRef] [Green Version]
- Chávez-Modena, M.; Ferrer, E.; Rubio, G. Improving the stability of multiple-relaxation lattice Boltzmann methods with central moments. Comput. Fluids 2018, 172, 397–409. [Google Scholar] [CrossRef]
- Coreixas, C.; Chopard, B.; Latt, J. Comprehensive comparison of collision models in the lattice Boltzmann framework: Theoretical investigations. Phys. Rev. E 2019, 100, 033305. [Google Scholar] [CrossRef] [Green Version]
- Geier, M.; Greiner, A.; Korvink, J.G. Bubble functions for the lattice Boltzmann method and their application to grid refinement. Eur. Phys. J. Spec. Top. 2009, 171, 173–179. [Google Scholar] [CrossRef]
- Imamura, T.; Suzuki, K.; Nakamura, T.; Yoshida, M. Acceleration of steady-state lattice Boltzmann simulations on non-uniform mesh using local time step method. J. Comput. Phys. 2005, 202, 645–663. [Google Scholar] [CrossRef]
- Arnone, A.; Liou, M.S.; Povinelli, L.A. Integration of Navier-Stokes equations using dual time stepping and a multigrid method. AIAA J. 1995, 33, 985–990. [Google Scholar] [CrossRef]
- Bhaskaran, R.; Lele, S.K. Large eddy simulation of free-stream turbulence effects on heat transfer to a high-pressure turbine cascade. J. Turbul. 2010, 11, N6. [Google Scholar] [CrossRef]
- Gardner, M. Taxicab geometry. In The Last Recreations; Springer: Berlin/Heidelberg, Germany, 1997; pp. 159–175. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Zhao, T. A lattice BGK scheme with general propagation. J. Sci. Comput. 2001, 16, 569–585. [Google Scholar] [CrossRef]
- D’Humieres, D. Generalized lattice-Boltzmann equations. Prog. Astronaut. Aeronaut. 1994, 159, 450. [Google Scholar]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546. [Google Scholar] [CrossRef] [Green Version]
- Geier, M.; Greiner, A.; Korvink, J.G. Cascaded digital lattice Boltzmann automata for high Reynolds number flow. Phys. Rev. E 2006, 73, 066705. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J. A factorized central moment lattice Boltzmann method. Eur. Phys. J. Spec. Top. 2009, 171, 55–61. [Google Scholar] [CrossRef]
- Premnath, K.; Banerjee, S. On the Three-Dimensional Central Moment Lattice Boltzmann Method. J. Stat. Phys. 2011, 143, 747–794. [Google Scholar] [CrossRef] [Green Version]
- Chávez-Modena, M.; Martí-nez Cava, A.; Rubio, G.; Ferrer, E. Optimizing free parameters in the D3Q19 Multiple-Relaxation lattice Boltzmann methods to simulate under-resolved turbulent flows. J. Comput. Sci. 2020, 45, 101170. [Google Scholar] [CrossRef]
- Coreixas, C.; Wissocq, G.; Chopard, B.; Latt, J. Impact of collision models on the physical properties and the stability of lattice Boltzmann methods. arXiv 2020, arXiv:2002.05265. [Google Scholar] [CrossRef]
- Ducros, F.; Nicoud, F.; Poinsot, T. Wall-adapting local eddy-viscosity models for simulations in complex geometries. In Numerical Methods for Fluid Dynamics VI; 1998; Available online: https://www.researchgate.net/profile/Nicoud_Franck/publication/248366844_Wall-Adapting_Local_Eddy-Viscosity_Models_for_Simulations_in_Complex_Geometries/links/5501a2ea0cf2d60c0e5f946f.pdf (accessed on 2 October 2020).
- Chai, Z.; Shi, B.; Guo, Z.; Rong, F. Multiple-relaxation-time lattice Boltzmann model for generalized Newtonian fluid flows. J. Non-Newton. Fluid Mech. 2011, 166, 332–342. [Google Scholar] [CrossRef]
- Barad, M.F.; Kocheemoolayil, J.G.; Kiris, C.C. Lattice Boltzmann and navier-stokes Cartesian CFD approaches for airframe noise predictions. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef] [Green Version]
- Shih, T.; Povinelli, L.; Liu, N.; Potapczuk, M.; Lumley, J. A Generalized Wall Function; TM 113112 NASA Technical Report; Glenn Research Center: Cleveland, OH, USA, 1999. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Strack, O.E.; Cook, B.K. Three-dimensional immersed boundary conditions for moving solids in the lattice-Boltzmann method. Int. J. Numer. Methods Fluids 2007, 55, 103–125. [Google Scholar] [CrossRef]
- Jovic, S.; Driver, D.M. Backward-Facing Step Measurements at Low Reynolds Number, Reh = 5000; NASA Technical Reports Server (NTRS): Moffett Field, CA, USA, 1994. [Google Scholar]
- Le, H.; Moin, P. Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef] [Green Version]
- Spalart, P.R. Direct simulation of a turbulent boundary layer up to Rθ = 1410. J. Fluid Mech. 1988, 187, 61–98. [Google Scholar] [CrossRef]
- Thomason, N.M. Experimental Investigation of Suction Slot Geometry on a Goldschmied Propulsor. Ph.D. Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2012. [Google Scholar]
- Rumsey, C.L.; Slotnick, J.P. Overview and summary of the second AIAA High Lift Prediction Workshop. In Proceedings of the 52nd Aerospace Sciences Meeting, Harbor, MD, USA, 13–17 January 2014; p. 0747. [Google Scholar]
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircr. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Ekaterinaris, J.A.; Platzer, M.F. Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 1998, 33, 759–846. [Google Scholar] [CrossRef]
- Ribeiro, A.F.; Casalino, D.; Fares, E. Lattice-Boltzmann simulations of an oscillating NACA0012 airfoil in dynamic stall. In Advances in Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2016; pp. 179–192. [Google Scholar]
- Aftab, S.; Razak, N.; Rafie, A.M.; Ahmad, K. Mimicking the humpback whale: An aerodynamic perspective. Prog. Aerosp. Sci. 2016, 84, 48–69. [Google Scholar] [CrossRef]
- Johari, H.; Henoch, C.W.; Custodio, D.; Levshin, A. Effects of leading-edge protuberances on airfoil performance. AIAA J. 2007, 45, 2634–2642. [Google Scholar] [CrossRef]
- Custodio, D.S. The Effect of Humpback Whale-like Protuberances on Hydrofoil Performance. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2007. [Google Scholar]
- Wei, Z.; New, T.H.; Cui, Y. Aerodynamic performance and surface flow structures of leading-edge tubercled tapered swept-back wings. AIAA J. 2018, 56, 423–431. [Google Scholar] [CrossRef]




| Lattice Resolution (mm) | Elements | Simulation Time (s) | Comp. Time (h) | Cores | ||
|---|---|---|---|---|---|---|
| Coarse | 78.1 | 0.5 | 9.16 | 0.3 | 8 | |
| Medium | 58.6 | 0.5 | 7.42 | 0.8 | 8 | |
| Fine | 48.8 | 0.5 | 6.81 | 2.1 | 8 | |
| Extra-Fine | 38.8 | 0.5 | 6.33 | 3.5 | 8 | |
| Le and Moin [43] | - | - | 6.28 | - | - | |
| Jovic and Driver [42] | - | - | - | 6.00 | - | - |
| Lattice Resolution (mm) | Elements | Simulation Time (s) | Cd | Comp. Time (h) | Cores | |
|---|---|---|---|---|---|---|
| Coarse | 4 | 0.5 | 0.24 | 3.2 | 16 | |
| Medium | 2 | 0.5 | 0.091 | 10 | 32 | |
| Fine | 1.5 | 0.5 | 0.066 | 25 | 64 | |
| Experimental | - | - | - | 0.055 | - | - |
| Grid | Fuselage (mm) | Wing (mm) | Elements | Sim. Time (s) | Cd | Cl | Comp. Time (h) | Cores |
|---|---|---|---|---|---|---|---|---|
| Extra-Coarse | 4 | 4 | 0.1 | 0.262 | 1.95 | 160 | ||
| Coarse | 2 | 2 | 0.1 | 0.295 | 2.16 | 5.2 | 160 | |
| Medium | 1 | 1 | 0.1 | 0.296 | 2.51 | 33.8 | 160 | |
| Fine | 2 | 0.5 | 0.1 | 0.310 | 2.67 | 84 | 256 | |
| Experimental | - | - | - | - | 0.275 | 2.68 | - | - |
| Lattice Resolution (mm) | Elements | Simulation Time (s) | Comp. Time (h) | Cores | |
|---|---|---|---|---|---|
| Coarse | 12 | 2 | 3.8 | 8 | |
| Medium | 6 | 2 | 24.5 | 8 | |
| Fine | 3 | 2 | 100 | 40 |
| Baseline | 2.702 m | 6.225 m | ||
|---|---|---|---|---|
| 0.025 | 0.05 | 0.1 | ||
| 0.1 | A02510 | A0510 | A1010 | |
| 0.2 | A02520 | A0520 | A1020 | |
| 0.4 | A02540 | A0540 | A1040 | |
| Lattice Resolution (mm) | Elements | Simulation Time (s) | Cd | Cl | Comp. Time (h) | Cores | |
|---|---|---|---|---|---|---|---|
| Extra Coarse | 40 | 3 | 0.254 | 0.780 | 19 | 8 | |
| Coarse | 20 | 3 | 0.242 | 0.872 | 28 | 8 | |
| Medium | 10 | 3 | 0.218 | 0.930 | 25 | 32 | |
| Fine | 5 | 3 | 0.215 | 0.941 | 155 | 32 |
| Baseline | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cd [%] | 0 | −8.3 | −4.9 | −3.5 | −4.9 | −2.6 | −1.8 | −1.7 | 2.8 | −1.9 |
| Cl [%] | 0 | −2.0 | 0.1 | −1.7 | 0.4 | 0.0 | 0.1 | 4.1 | 5.5 | 0.8 |
| L/D [%] | 0 | 6.8 | 5.2 | 1.8 | 5.5 | 2.7 | 2.0 | 5.9 | 2.7 | 2.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chávez-Modena, M.; Martínez, J.L.; Cabello, J.A.; Ferrer, E. Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow. Energies 2020, 13, 5146. https://doi.org/10.3390/en13195146
Chávez-Modena M, Martínez JL, Cabello JA, Ferrer E. Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow. Energies. 2020; 13(19):5146. https://doi.org/10.3390/en13195146
Chicago/Turabian StyleChávez-Modena, M., J. L. Martínez, J. A. Cabello, and E. Ferrer. 2020. "Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow" Energies 13, no. 19: 5146. https://doi.org/10.3390/en13195146
APA StyleChávez-Modena, M., Martínez, J. L., Cabello, J. A., & Ferrer, E. (2020). Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow. Energies, 13(19), 5146. https://doi.org/10.3390/en13195146






