The Influence of Winglet Pitching on the Performance of a Model Wind Turbine: Aerodynamic Loads, Rotating Speed, and Wake Statistics
Abstract
:1. Introduction
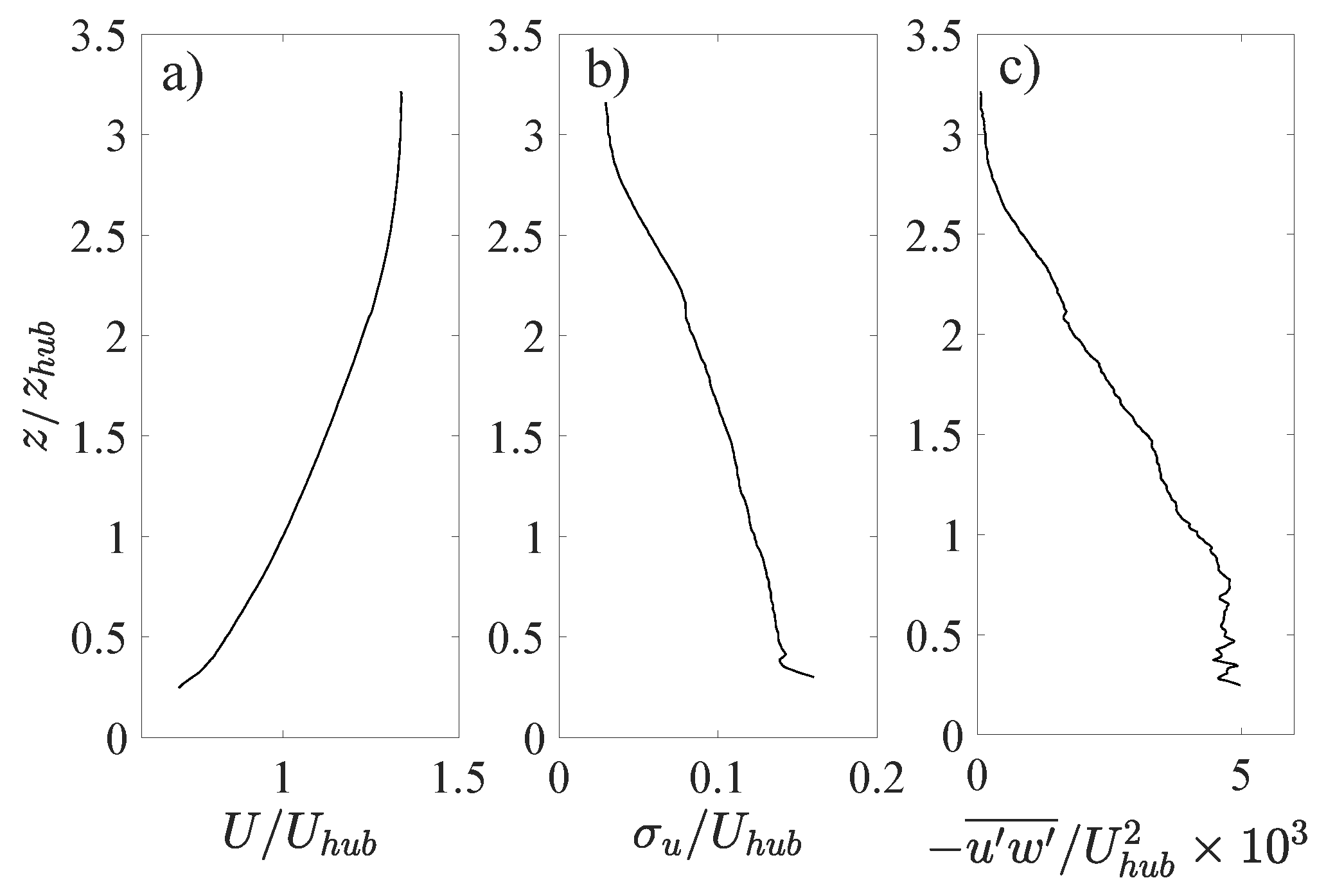
2. Experimental Setup
3. Results and Discussion
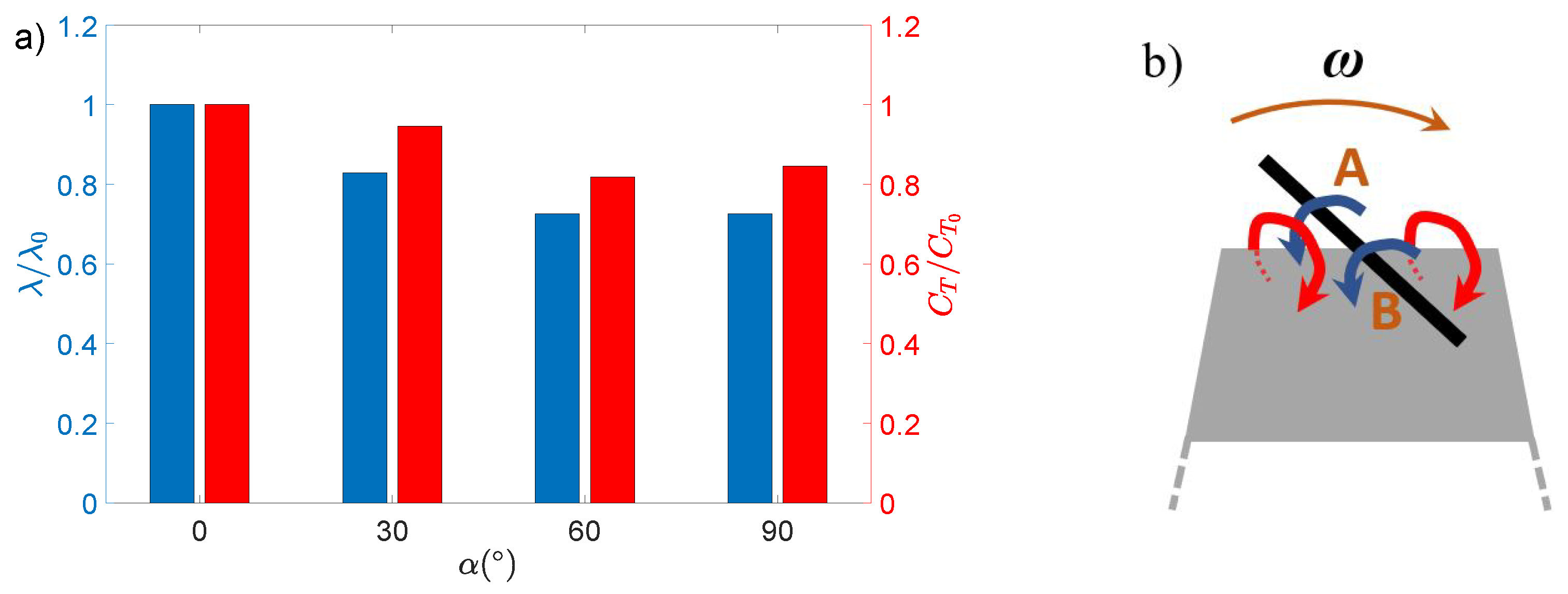
3.1. Rotation Speed and Thrust Force
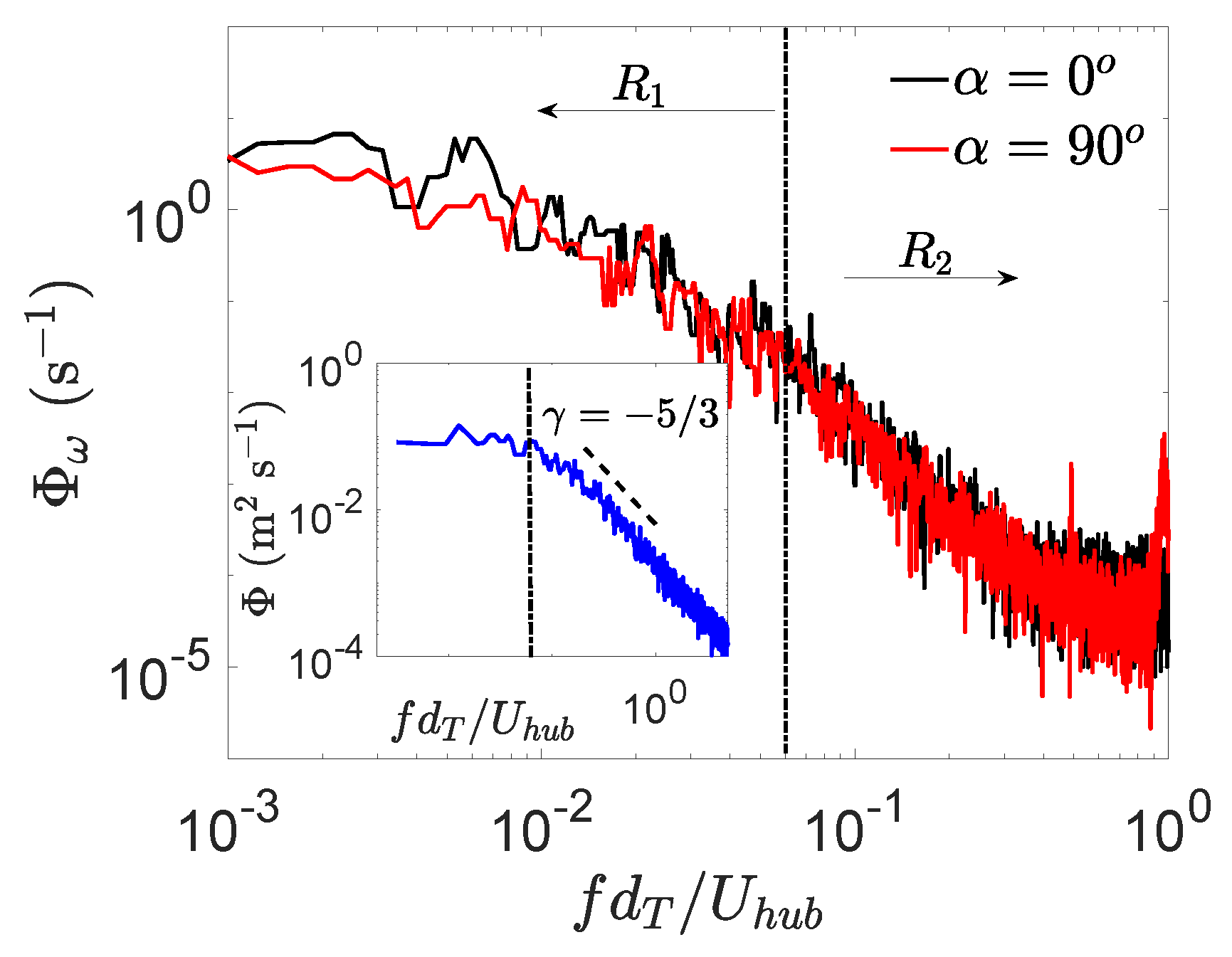
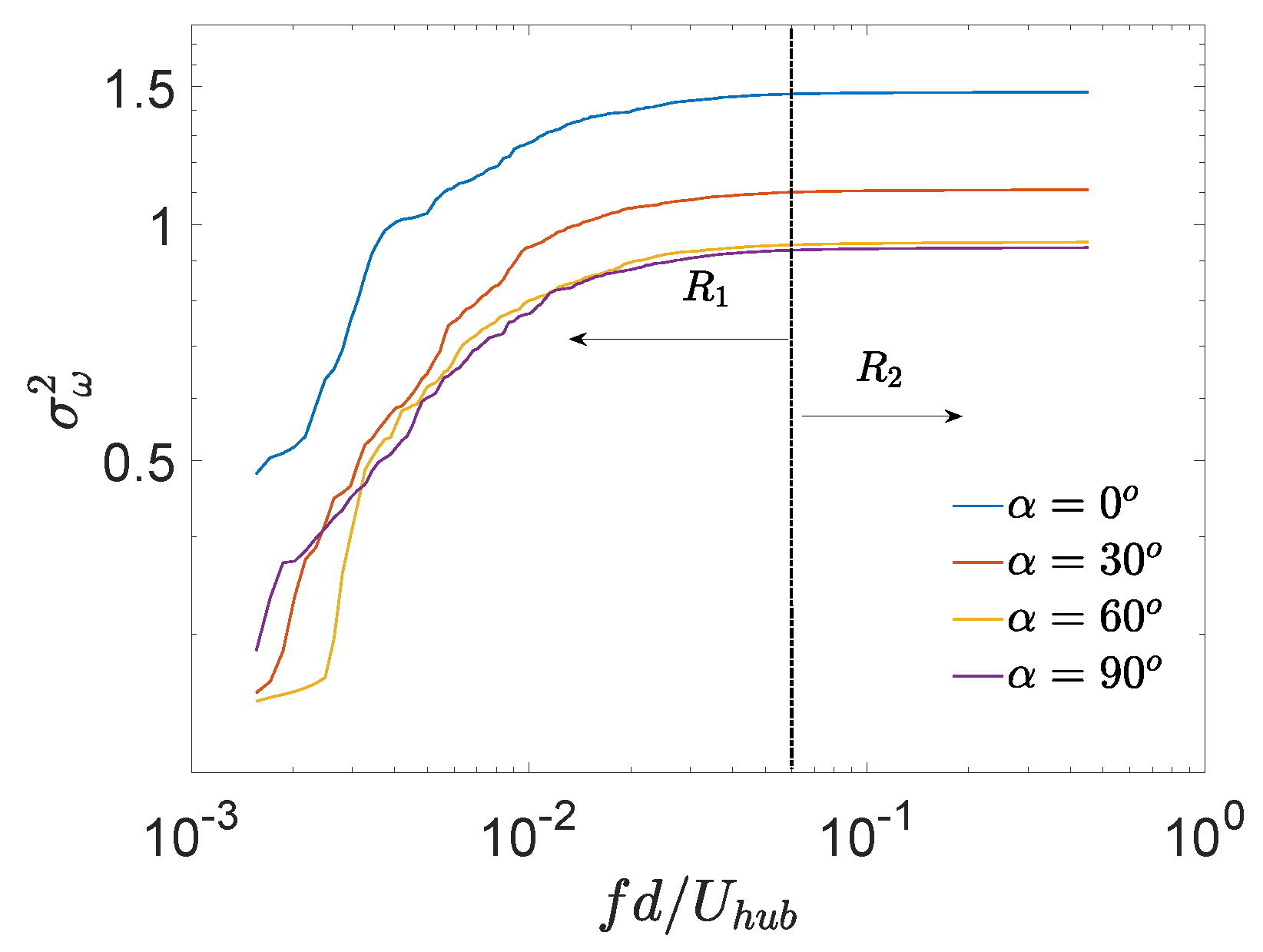
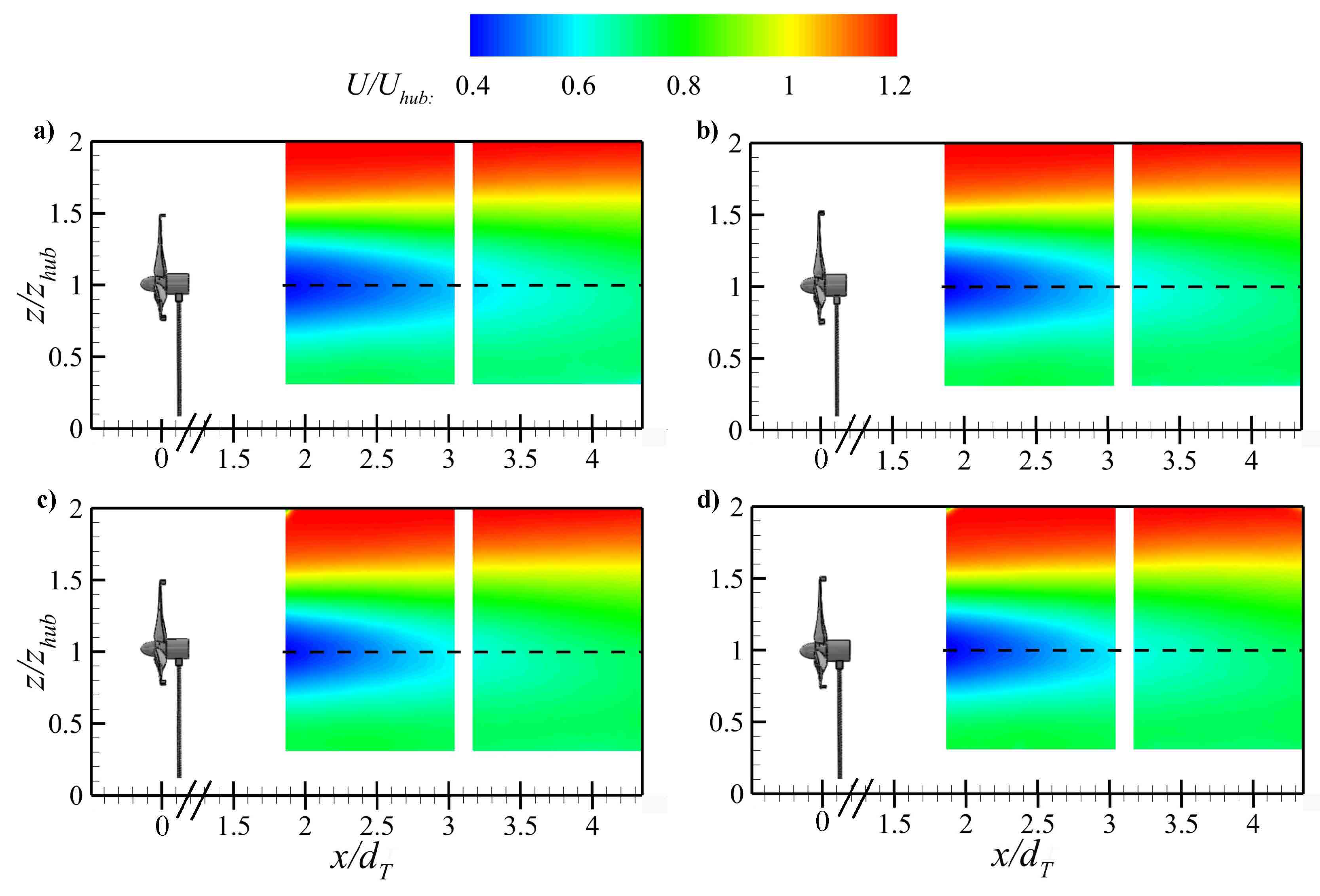
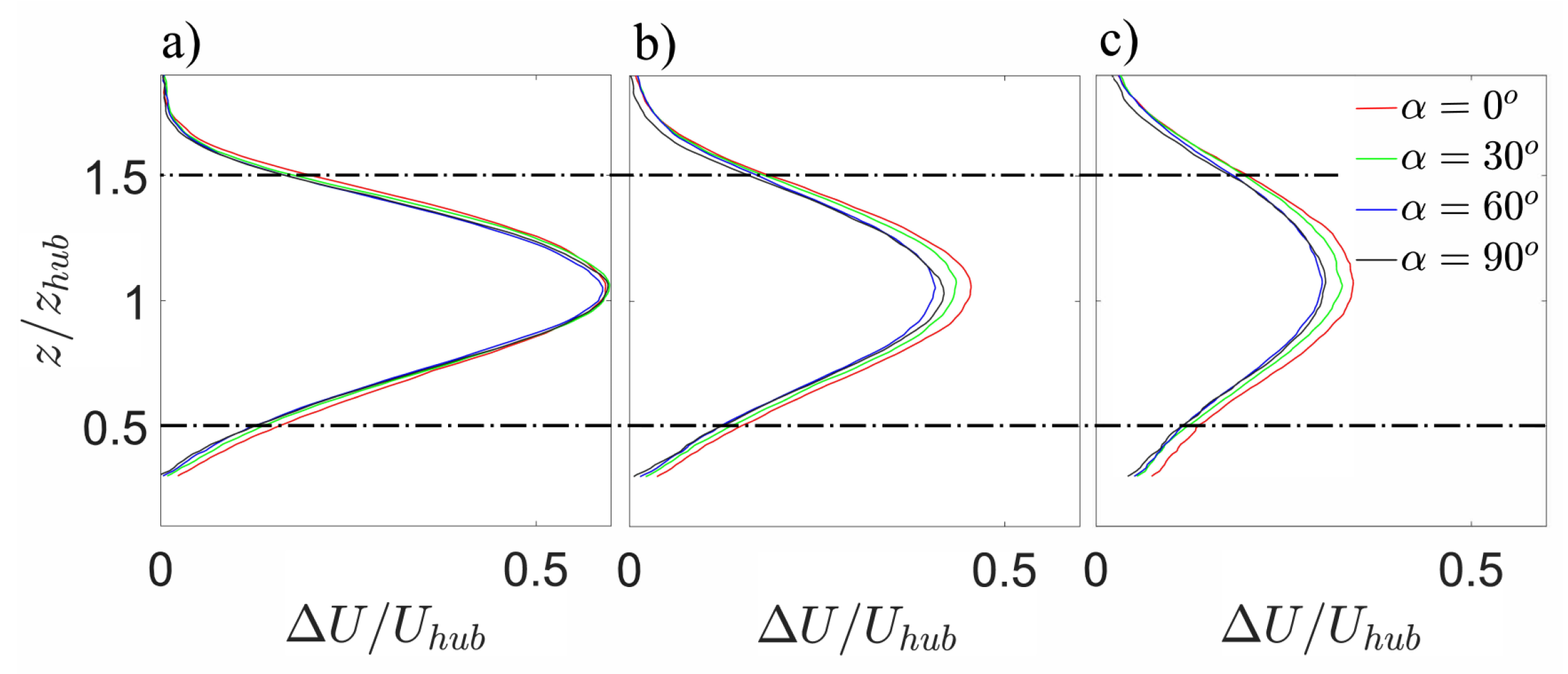
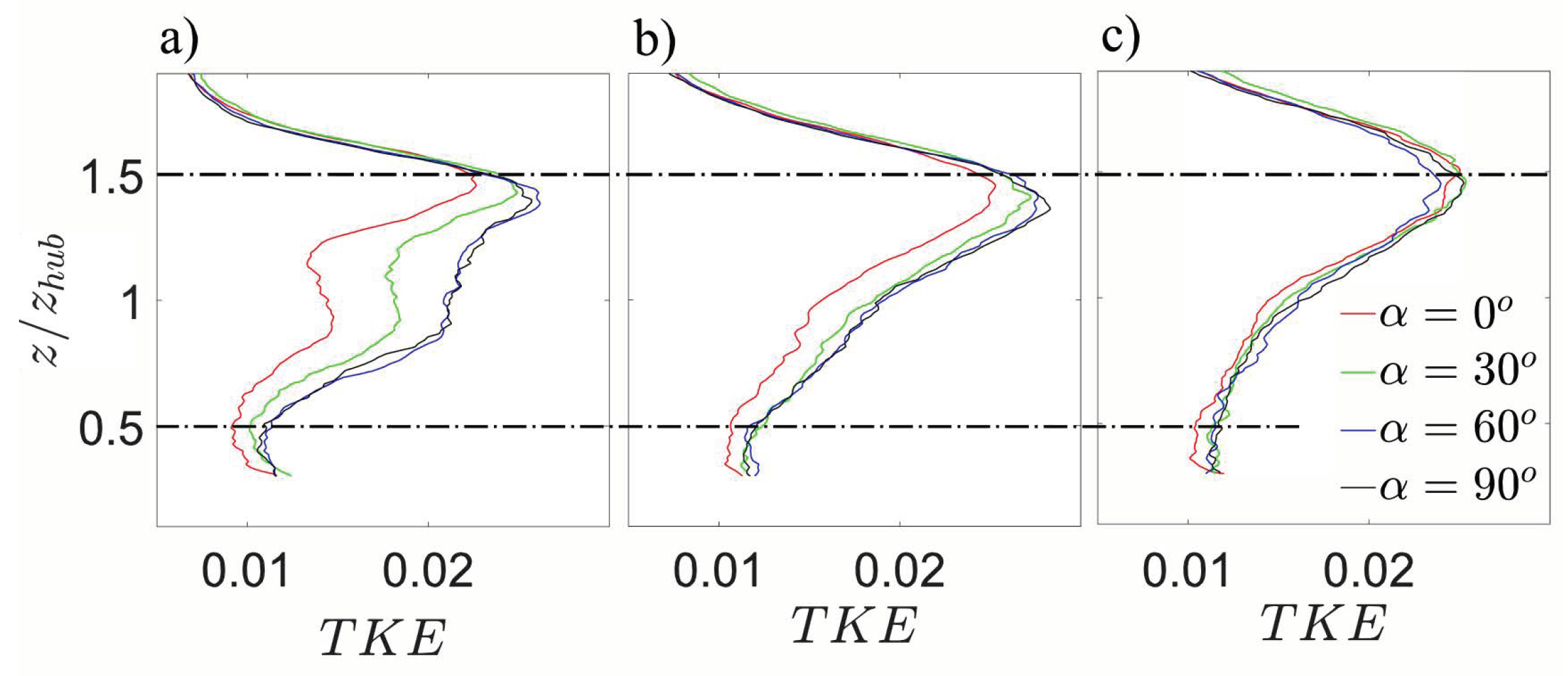
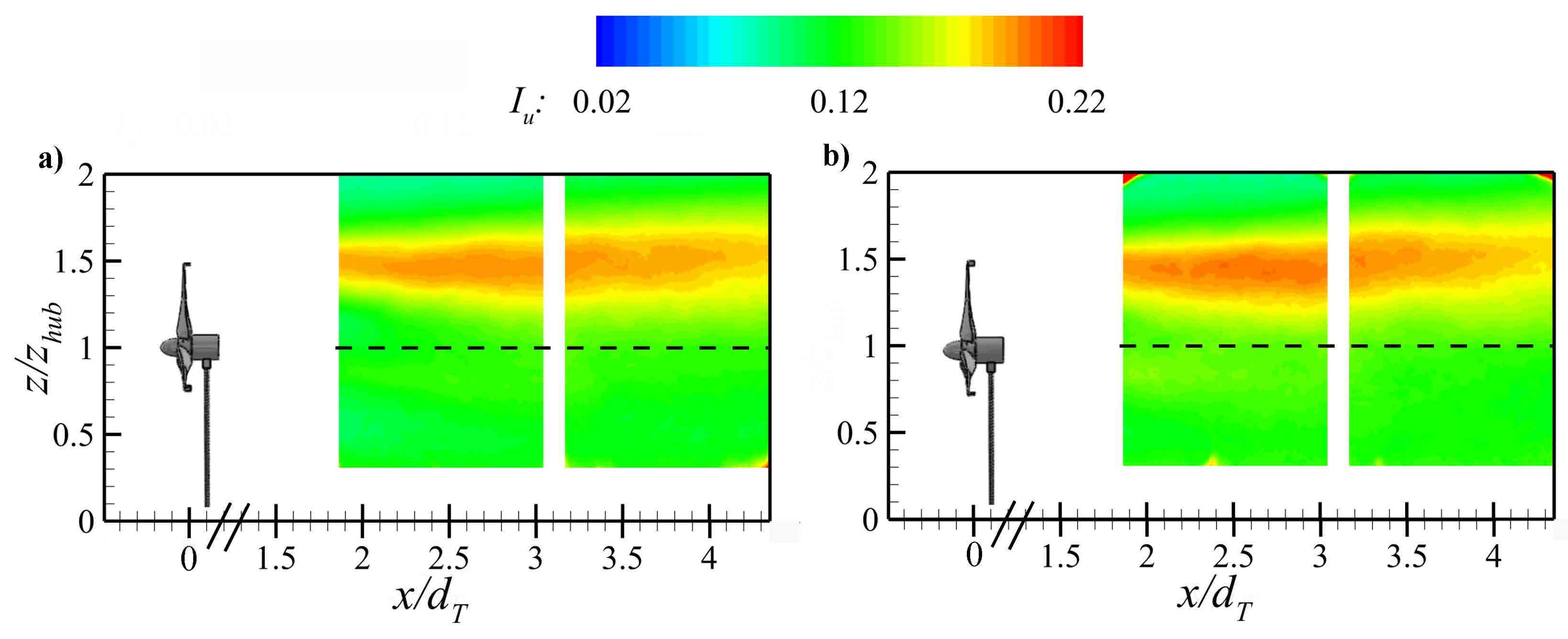
3.2. Wake Characteristics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Electricity in the United States-Energy Explained, Your Guide To Understanding Energy (EIA, 2019). Available online: https://www.eia.gov/energyexplained/index.cfm?page=electricityintheunitedstates (accessed on 3 January 2020).
- Cost and Performance Characteristics of New Generating Technologies, Annual Energy Outlook 2019. U.S. Energy Information Administration. Available online: https://www.eia.gov/outlooks/aeo/assumptions/pdf/table_8.2.pdf (accessed on 3 January 2020).
- Barthelmie, R.; Hansen, O.F.; Enevoldsen, K.; Højstrup, J.; Frandsen, S.; Pryor, S.; Larsen, S.; Motta, M.; Sanderhoff, P. Ten years of meteorological measurements for offshore wind farms. J. Sol. Energy Eng. 2005, 127, 170–176. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J. Flow characteristics in the coastal zone. In European Seminar Offshore Wind Energy in Mediterranean and Other European Seas; ENEA: Paris, France, 2000; pp. 29–43. [Google Scholar]
- Akpinar, E.K.; Akpinar, S. An assessment on seasonal analysis of wind energy characteristics and wind turbine characteristics. Energy Convers. Manag. 2005, 46, 1848–1867. [Google Scholar] [CrossRef]
- Gökçek, M.; Bayülken, A.; Bekdemir, S. Investigation of wind characteristics and wind energy potential in Kirklareli, Turkey. Renew. Energy 2007, 32, 1739–1752. [Google Scholar] [CrossRef]
- Guo, H.; Xu, M.; Hu, Q. Changes in near-surface wind speed in China: 1969–2005. Int. J. Climatol. 2011, 31, 349–358. [Google Scholar] [CrossRef]
- Ouammi, A.; Dagdougui, H.; Sacile, R.; Mimet, A. Monthly and seasonal assessment of wind energy characteristics at four monitored locations in Liguria region (Italy). Renew. Sustain. Energy Rev. 2010, 14, 1959–1968. [Google Scholar] [CrossRef]
- Tobin, N.; Zhu, H.; Chamorro, L.P. Spectral behaviour of the turbulence-driven power fluctuations of wind turbines. J. Turbul. 2015, 16, 832–846. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, H.; Aggarwal, R.; Singh, A.; Chamorro, L.P. Effects of freestream turbulence in a model wind turbine wake. Energies 2016, 9, 830. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Jin, Y.; Tobin, N.; Chamorro, L.P. Towards uncovering the structure of power fluctuations of wind farms. Phys. Rev. E 2017, 96, 063117. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Hayat, I.; Jin, Y.; Chamorro, L. On the evolution of the integral time scale within wind farms. Energies 2018, 11, 93. [Google Scholar] [CrossRef] [Green Version]
- Hau, E. Commercial Applications of Wind Turbines. In Wind Turbines: Fundamentals, Technologies, Application, Economics; Springer Science & Business Media: Munich, Germany, 2006; pp. 563–614. [Google Scholar]
- Nagai, B.M.; Ameku, K.; Roy, J.N. Performance of a 3 kW wind turbine generator with variable pitch control system. Appl. Energy 2009, 86, 1774–1782. [Google Scholar] [CrossRef]
- Muljadi, E.; Butterfield, C.P. Pitch-controlled variable-speed wind turbine generation. IEEE Trans. Ind. 2001, 37, 240–246. [Google Scholar] [CrossRef] [Green Version]
- Gao, R.; Gao, Z. Pitch control for wind turbine systems using optimization, estimation and compensation. Renew. Energy 2016, 91, 501–515. [Google Scholar] [CrossRef]
- Van Wingerden, J.W.; Hulskamp, A.W.; Barlas, T.; Marrant, B.; van Kuik, G.A.M.; Molenaar, D.P.; Verhaegen, M. On the proof of concept of a ‘smart’ wind turbine rotor blade for load alleviation. Wind Energy 2008, 11, 265–280. [Google Scholar] [CrossRef]
- Barlas, T.K.; Van Kuik, G.A.M. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Barlas, T.K.; Van der Veen, G.J.; Van Kuik, G.A.M. Model predictive control for wind turbines with distributed active flaps: Incorporating inflow signals and actuator constraints. Wind Energy 2012, 15, 757–771. [Google Scholar] [CrossRef]
- Whitcomb, R.T. A Design Approach and Selected Wind Tunnel Results at High Subsonic Speeds for Wing-Tip Mounted Winglets; NASA TN D-8260; Natl. Aeronaut. Space Admin: Washington, DC, USA, 1976.
- Johansen, J.; Sørensen, N.N. Aerodynamic Investigation of Winglets on Wind Turbine Blades Using CFD Risø-R-1543(EN); Risø National Laboratory: Roskilde, Denmark, 2006. [Google Scholar]
- Imamura, H.; Hasegawa, Y.; Kikuyama, K. Numerical analysis of the horizontal axis wind turbine with wihglets. JSME Int. J. Ser. B Fluids Therm. Eng. 1998, 41, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Gaunaa, M.; Johansen, J. Determination of the maximum aerodynamic efficiency of wind turbine rotors with winglets. J. Phys. Conf. Ser. 2007, 75, 012006. [Google Scholar] [CrossRef] [Green Version]
- Saravanan, P.; Parammasivam, K.M.; Selvi Rajan, S. Pressure distribution of rotating small wind turbine blades with winglet using wind tunnel. J. Sci. Ind. Res. 2012, 71, 425–429. [Google Scholar]
- Saravanan, P.; Parammasivam, K.M.; Selvi Rajan, S. Experimental investigation on small horizontal axis wind turbine rotor using winglets. J. Eng. Appl. 2013, 16, 159–164. [Google Scholar]
- Belferhat, S.; Meftah, S.M.A.; Yahiaoui, T.; Imine, B. Aerodynamic Optimization of a Winglet Design. In EPJ Web of Conferences; EDP Sciences: Paris, France, 2013; Volume 45, p. 01010. [Google Scholar]
- Tobin, N.; Hamed, A.M.; Chamorro, L.P. An Experimental Study on the Effects ofWinglets on the Wake and Performance of a ModelWind Turbine. Energies 2015, 8, 11955–11972. [Google Scholar] [CrossRef] [Green Version]
- Zhu, B.; Sun, X.; Wang, Y.; Huang, D. Performance characteristics of a horizontal axis turbine with fusion winglet. Energy 2017, 120, 431–440. [Google Scholar] [CrossRef]
- Khaled, M.; Ibrahim, M.M.; Hamed, H.E.A.; AbdelGwad, A.F. Investigation of a small Horizontal–Axis wind turbine performance with and without winglet. Energy 2019, 187, 115921. [Google Scholar] [CrossRef]
- Mühle, F.; Bartl, J.; Hansen, T.; Adaramola, M.S.; Sætran, L. An experimental study on the effects of winglets on the tip vortex interaction in the near wake of a model wind turbine. Wind Energy 2020, 23, 1286–1300. [Google Scholar] [CrossRef]
- Mourad, M.G.; Shahin, I.; Ayad, S.S.; Abdellatif, O.E.; Mekhail, T.A. Effect of winglet geometry on horizontal axis wind turbine performance. Eng. Rep. 2020, 2, e12101. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Lee, S.J.; Olsen, D.; Milliren, C.; Marr, J.; Arndt, R.; Sotiropoulos, F. Turbulence effects on a full-scale 2.5 MW horizontal-axis wind turbine under neutrally stratified conditions. Wind Energy 2015, 18, 339–349. [Google Scholar] [CrossRef]
- Shiu, H.; Johnson, E.; Barone, M.; Phillips, R.; Straka, W.; Fontaine, A.; Jonson, M. A design of a hydrofoil family for current-driven marine-hydrokinetic turbines. In International Conference on Nuclear Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 44984, pp. 839–847. [Google Scholar]
- Johnson, E.; Fontaine, A.A.; Jonson, M.L.; Meyer, R.S.; Straka, W.A.; Young, S.; van Dam, C.P.; Shiu, H.; Barone, M. A1: 8.7 scale water tunnel test of an axial flow water turbine. In Proceedings of the 1st Marine Energy Technology Symposium, METS13, Washington, DC, USA, 10–11 April 2013; pp. 10–11. [Google Scholar]
- Cheng, S.; Jin, Y.; Chamorro, L.P. Wind Turbines with Truncated Blades May Be a Possibility for Dense Wind Farms. Energies 2020, 13, 1810. [Google Scholar] [CrossRef] [Green Version]
- Mao, Z.; Jin, Y.; Wang, Z.; Chamorro, L.P. On the Unsteady Wake of a Rigid Plate Under Constant Acceleration and Deceleration. J. Fluids Eng. 2020, 142, 051301. [Google Scholar] [CrossRef]
- Modi, V.J.; Wiland, E.; Dikshit, A.K.; Yokomizo, T. On the fluid dynamics of elliptic cylinders. Int. J. Offshore Polar Eng. 1992, 2, 267–280. [Google Scholar]
- Jin, Y.; Ji, S.; Chamorro, L.P. Spectral Energy Cascade of Body Rotations and Oscillations under Turbulence. Phys. Rev. E 2016, 94, 063105. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Abkar, M.; Sørensen, J.N.; Porté-Agel, F. An analytical model for the effect of vertical wind veer on wind turbine wakes. Energies 2018, 11, 1838. [Google Scholar] [CrossRef] [Green Version]
- Archer, C.L.; Vasel-Be-Hagh, A.; Yan, C.; Wu, S.; Pan, Y.; Brodie, J.F.; Maguire, A.E. Review and evaluation of wake loss models for wind energy applications. Appl. Energy 2018, 226, 1187–1207. [Google Scholar] [CrossRef]
- Campagnolo, F.; Petrović, V.; Bottasso, C.L.; Croce, A. Wind tunnel testing of wake control strategies. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 513–518. [Google Scholar]
- Annoni, J.; Gebraad, P.M.O.; Scholbrock, A.K.; Fleming, P.A.; van Wingerden, J.W. Analysis of axial- induction-based wind plant control using an engineering and a high-order wind plant model. Wind Energy 2016, 19, 1135–1150. [Google Scholar] [CrossRef]
- Fu, S.; Jin, Y.; Zheng, Y.; Chamorro, L.P. Wake and power fluctuations of a model wind turbine subjected to pitch and roll oscillations. Appl. Energ 2019, 253, 113605. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Atmospheric turbulence effects on wind-turbine wakes: An LES study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Kang, S.; Yang, X.; Sotiropoulos, F. On the onset of wake meandering for an axial flow turbine in a turbulent open channel flow. J. Fluid Mech. 2014, 744, 376–403. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Guala, M.; Arndt, R.E.A.; Sotiropoulos, F. On the evolution of turbulent scales in the wake of a wind turbine model. J. Turbul. 2012, 13, 1–13. [Google Scholar] [CrossRef]
- Tobin, N.; Chamorro, L.P. Turbulence coherence and its impact on wind-farm power fluctuations. J. Fluid Mech. 2018, 855, 1116–1129. [Google Scholar] [CrossRef] [Green Version]



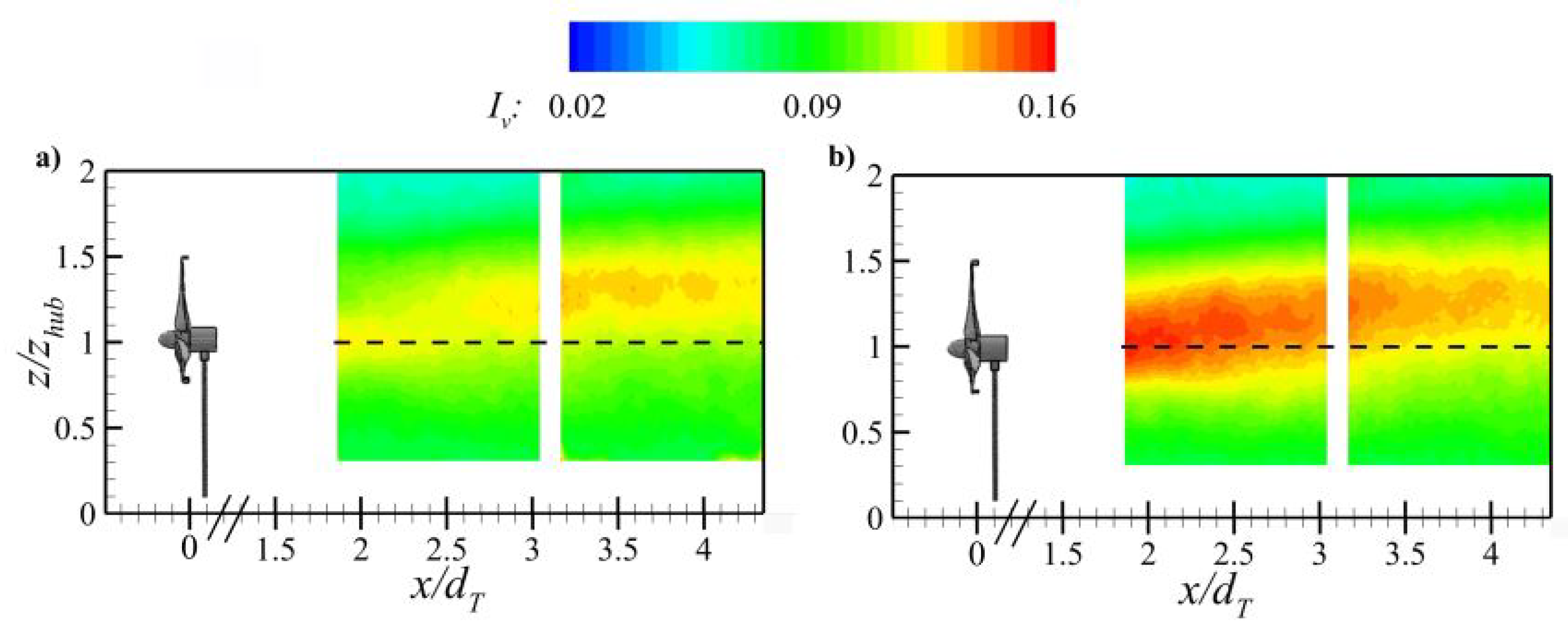
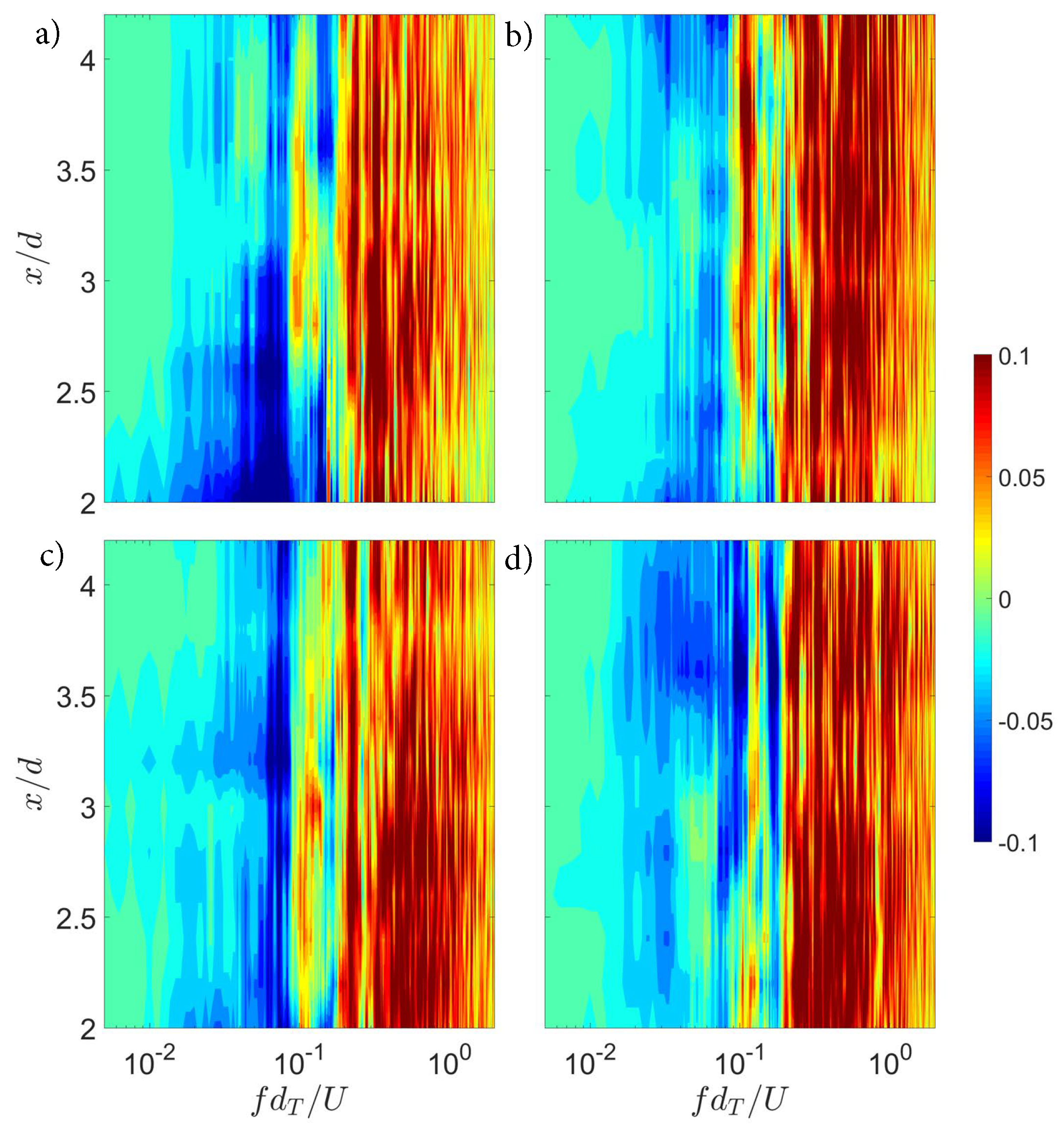
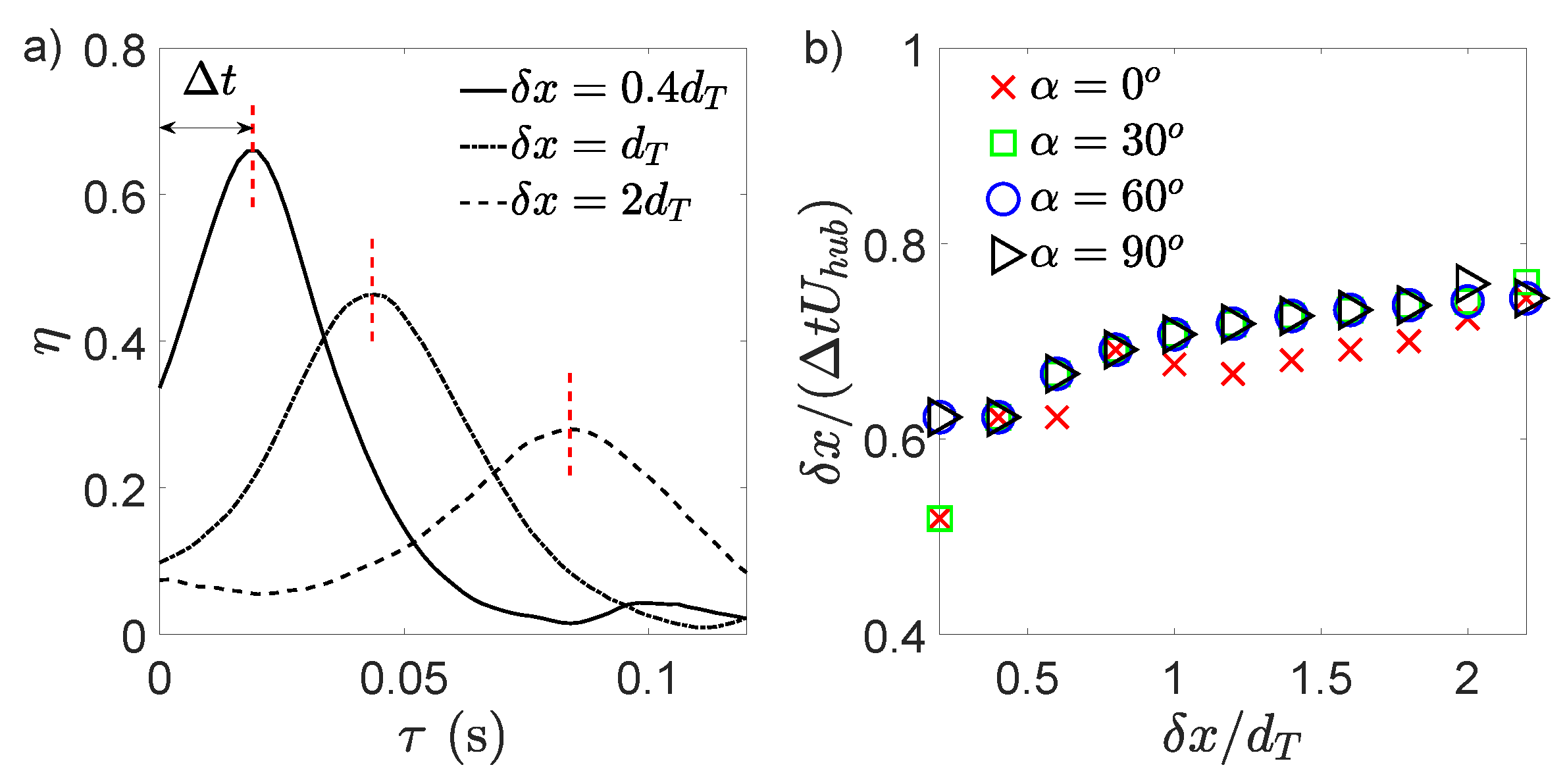
| (Mea) | 0.100 | 0.097 | 0.091 | 0.097 |
| (Mod) | 0.0893 | 0.0812 | 0.0724 | 0.0747 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aju, E.J.; Suresh, D.B.; Jin, Y. The Influence of Winglet Pitching on the Performance of a Model Wind Turbine: Aerodynamic Loads, Rotating Speed, and Wake Statistics. Energies 2020, 13, 5199. https://doi.org/10.3390/en13195199
Aju EJ, Suresh DB, Jin Y. The Influence of Winglet Pitching on the Performance of a Model Wind Turbine: Aerodynamic Loads, Rotating Speed, and Wake Statistics. Energies. 2020; 13(19):5199. https://doi.org/10.3390/en13195199
Chicago/Turabian StyleAju, Emmanuvel Joseph, Dhanush Bhamitipadi Suresh, and Yaqing Jin. 2020. "The Influence of Winglet Pitching on the Performance of a Model Wind Turbine: Aerodynamic Loads, Rotating Speed, and Wake Statistics" Energies 13, no. 19: 5199. https://doi.org/10.3390/en13195199
APA StyleAju, E. J., Suresh, D. B., & Jin, Y. (2020). The Influence of Winglet Pitching on the Performance of a Model Wind Turbine: Aerodynamic Loads, Rotating Speed, and Wake Statistics. Energies, 13(19), 5199. https://doi.org/10.3390/en13195199







